Στοιχεῖα Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ις΄. [16]
Εἰκοσάεδρον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὰ προειρημένα σχήματα, καὶ δεῖξαι, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ καὶ τετμήσθω κατὰ τὸ Γ ὥστε τετραπλῆν εἶναι τὴν ΑΓ τῆς ΓΒ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἤχθω ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς γωνίας εὐθεῖα γραμμὴ ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἐκκείσθω κύκλος ὁ ΕΖΗΘΚ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἔστω τῇ ΔΒ, καὶ ἐγγεγράφθω εἰς τὸν ΕΖΗΘΚ κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον τὸ ΕΖΗΘΚ, καὶ τετμήσθωσαν αἱ ΕΖ, ΖΗ, ΗΘ, ΘΚ, ΚΕ περιφέρειαι δίχα κατὰ τὰ Λ, Μ, Ν, Ξ, Ο σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΛΜ, ΜΝ, ΝΞ, ΞΟ, ΟΛ, ΕΟ. ἰσόπλευρον ἄρα ἐστὶ καὶ τὸ ΛΜΝΞΟ πεντάγωνον, καὶ δεκαγώνου ἡ ΕΟ εὐθεῖα. καὶ ἀνεστάτωσαν ἀπὸ τῶν Ε, Ζ, Η, Θ, Κ σημείων τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς γωνίας εὐθεῖαι αἱ ΕΠ, ΖΡ, ΗΣ, ΘΤ, ΚΥ ἴσαι οὖσαι τῇ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου, καὶ ἐπεζεύχθωσαν αἱ ΠΡ, ΡΣ, ΣΤ, ΤΥ, ΥΠ, ΠΛ, ΛΡ, ΡΜ, ΜΣ, ΣΝ, ΝΤ, ΤΞ, ΞΥ, ΥΟ, ΟΠ. καὶ ἐπεὶ ἑκατέρα τῶν ΕΠ, ΚΥ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, παράλληλος ἄρα ἐστὶν ἡ ΕΠ τῇ ΚΥ. ἔστι δὲ αὐτῇ καὶ ἴση· αἱ δὲ τὰς ἴσας τε καὶ παραλλήλους ἐπιζευγνύουσαι ἐπὶ τὰ αὐτὰ μέρη εὐθεῖαι ἴσαι τε καὶ παράλληλοί εἰσιν. ἡ ΠΥ ἄρα τῇ ΕΚ ἴση τε καὶ παράλληλός ἐστιν. πενταγώνου δὲ ἰσοπλεύρου ἡ ΕΚ· πενταγώνου ἄρα ἰσοπλεύρου καὶ ἡ ΠΥ τοῦ εἰς τὸν ΕΖΗΘΚ κύκλον ἐγγραφομένου. διὰ τὰ αὐτὰ δὴ καὶ ἑκάστη τῶν ΠΡ, ΡΣ, ΣΤ, ΤΥ πενταγώνου ἐστὶν ἰσοπλεύρου τοῦ εἰς τὸν ΕΖΗΘΚ κύκλον ἐγγραφομένου· ἰσόπλευρον ἄρα τὸ ΠΡΣΤΥ πεντάγωνον. καὶ ἐπεὶ ἑξαγώνου μέν ἐστιν ἡ ΠΕ, δεκαγώνου δὲ ἡ ΕΟ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΠΕΟ, πενταγώνου ἄρα ἐστὶν ἡ ΠΟ· ἡ γὰρ τοῦ πενταγώνου πλευρὰ δύναται τήν τε τοῦ ἑξαγώνου καὶ τὴν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΟΥ πενταγώνου ἐστὶ πλευρά. ἔστι δὲ καὶ ἡ ΠΥ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΟΥ τρίγωνον.
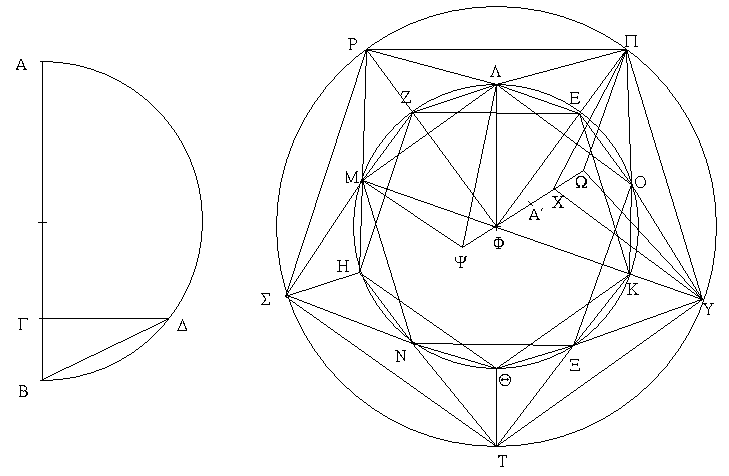
διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν ΠΛΡ, ΡΜΣ, ΣΝΤ, ΤΞΥ ἰσόπλευρόν ἐστιν. καὶ ἐπεὶ πενταγώνου ἐδείχθη ἑκατέρα τῶν ΠΛ, ΠΟ, ἔστι δὲ καὶ ἡ ΛΟ πενταγώνου, ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΛΟ τρίγωνον. διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν ΛΡΜ, ΜΣΝ, ΝΤΞ, ΞΥΟ τριγώνων ἰσόπλευρόν ἐστιν. εἰλήφθω τὸ κέντρον τοῦ ΕΖΗ ΘΚ κύκλου τὸ Φ σημεῖον· καὶ ἀπὸ τοῦ Φ τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἀνεστάτω ἡ ΦΩ, καὶ ἐκβεβλήσθω ἐπὶ τὰ ἕτερα μέρη ὡς ἡ ΦΨ, καὶ ἀφῃρήσθω ἑξαγώνου μὲν ἡ ΦΧ, δεκαγώνου δὲ ἑκατέρα τῶν ΦΨ, ΧΩ, καὶ ἐπεζεύχθωσαν αἱ ΠΩ, ΠΧ, ΥΩ, ΕΦ, ΛΦ, ΛΨ, ΨΜ. καὶ ἐπεὶ ἑκατέρα τῶν ΦΧ, ΠΕ τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, παράλληλος ἄρα ἐστὶν ἡ ΦΧ τῇ ΠΕ. εἰσὶ δὲ καὶ ἴσαι· καὶ αἱ ΕΦ, ΠΧ ἄρα ἴσαι τε καὶ παράλληλοί εἰσιν. ἑξαγώνου δὲ ἡ ΕΦ· ἑξαγώνου ἄρα καὶ ἡ ΠΧ. καὶ ἐπεὶ ἑξαγώνου μέν ἐστιν ἡ ΠΧ, δεκαγώνου δὲ ἡ ΧΩ, καὶ ὀρθή ἐστιν ἡ ὑπὸ ΠΧΩ γωνία, πενταγώνου ἄρα ἐστὶν ἡ ΠΩ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΥΩ πενταγώνου ἐστίν, ἐπειδήπερ, ἐὰν ἐπιζεύξωμεν τὰς ΦΚ, ΧΥ, ἴσαι καὶ ἀπεναντίον ἔσονται, καί ἐστιν ἡ ΦΚ ἐκ τοῦ κέντρου οὖσα ἑξαγώνου· ἑξαγώνου ἄρα καὶ ἡ ΧΥ. δεκαγώνου δὲ ἡ ΧΩ, καὶ ὀρθὴ ἡ ὑπὸ ΥΧΩ· πενταγώνου ἄρα ἡ ΥΩ. ἔστι δὲ καὶ ἡ ΠΥ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΥΩ τρίγωνον. διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ ΠΡ, ΡΣ, ΣΤ, ΤΥ εὐθεῖαι, κορυφὴ δὲ τὸ Ω σημεῖον, ἰσόπλευρόν ἐστιν. πάλιν, ἐπεὶ ἑξαγώνου μὲν ἡ ΦΛ, δεκαγώνου δὲ ἡ ΦΨ, καὶ ὀρθή ἐστιν ἡ ὑπὸ ΛΦΨ γωνία, πενταγώνου ἄρα ἐστὶν ἡ ΛΨ. διὰ τὰ αὐτὰ δὴ ἐὰν ἐπιζεύξωμεν τὴν ΜΦ οὖσαν ἑξαγώνου, συνάγεται καὶ ἡ ΜΨ πενταγώνου. ἔστι δὲ καὶ ἡ ΛΜ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΛΜΨ τρίγωνον. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ ΜΝ, ΝΞ, ΞΟ, ΟΛ, κορυφὴ δὲ τὸ Ψ σημεῖον, ἰσόπλευρόν ἐστιν. συνέσταται ἄρα εἰκοσάεδρον ὑπὸ εἴκοσι τριγώνων ἰσοπλεύρων περιεχόμενον.
Δεῖ δὴ αὐτὸ καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Ἐπεὶ γὰρ ἑξαγώνου ἐστὶν ἡ ΦΧ, δεκαγώνου δὲ ἡ ΧΩ, ἡ ΦΩ ἄρα ἄκρον καὶ μέσον λόγον τέμηται κατὰ τὸ Χ, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΦΧ· ἔστιν ἄρα ὡς ἡ ΩΦ πρὸς τὴν ΦΧ, οὕτως ἡ ΦΧ πρὸς τὴν ΧΩ. ἴση δὲ ἡ μὲν ΦΧ τῇ ΦΕ, ἡ δὲ ΧΩ τῇ ΦΨ· ἔστιν ἄρα ὡς ἡ ΩΦ πρὸς τὴν ΦΕ, οὕτως ἡ ΕΦ πρὸς τὴν ΦΨ. καί εἰσιν ὀρθαὶ αἱ ὑπὸ ΩΦΕ, ΕΦΨ γωνίαι· ἐὰν ἄρα ἐπιζεύξωμεν τὴν ΕΩ εὐθεῖαν, ὀρθὴ ἔσται ἡ ὑπὸ ΨΕΩ γωνία διὰ τὴν ὁμοιότητα τῶν ΨΕΩ, ΦΕΩ τριγώνων. διὰ τὰ αὐτὰ δὴ ἐπεί ἐστιν ὡς ἡ ΩΦ πρὸς τὴν ΦΧ, οὕτως ἡ ΦΧ πρὸς τὴν ΧΩ, ἴση δὲ ἡ μὲν ΩΦ τῇ ΨΧ, ἡ δὲ ΦΧ τῇ ΧΠ, ἔστιν ἄρα ὡς ἡ ΨΧ πρὸς τὴν ΧΠ, οὕτως ἡ ΠΧ πρὸς τὴν ΧΩ. καὶ διὰ τοῦτο πάλιν ἐὰν ἐπιζεύξωμεν τὴν ΠΨ, ὀρθὴ ἔσται ἡ πρὸς τῷ Π γωνία· τὸ ἄρα ἐπὶ τῆς ΨΩ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Π. καὶ ἐὰν μενούσης τῆς ΨΩ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἥξει καὶ διὰ τοῦ Π καὶ τῶν λοιπῶν σημείων τοῦ εἰκοσαέδρου, καὶ ἔσται σφαίρᾳ περιειλημμένον τὸ εἰκοσάεδρον. λέγω δή, ὅτι καὶ τῇ δοθείσῃ. τετμήσθω γὰρ ἡ ΦΧ δίχα κατὰ τὸ Α#. καὶ ἐπεὶ εὐθεῖα γραμμὴ ἡ ΦΩ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Χ, καὶ τὸ ἔλασσον αὐτῆς τμῆμά ἐστιν ἡ ΩΧ, ἡ ἄρα ΩΧ προσλαβοῦσα τὴν ἡμίσειαν τοῦ μείζονος τμήματος τὴν ΧΑ# πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τοῦ μείζονος τμήματος· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΩΑ# τοῦ ἀπὸ τῆς Α#Χ. καί ἐστι τῆς μὲν ΩΑ# διπλῆ ἡ ΩΨ, τῆς δὲ Α#Χ διπλῆ ἡ ΦΧ· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΩΨ τοῦ ἀπὸ τῆς ΧΦ. καὶ ἐπεὶ τετραπλῆ ἐστιν ἡ ΑΓ τῆς ΓΒ, πενταπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΔ· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΩΨ πενταπλάσιον τοῦ ἀπὸ τῆς ΦΧ. καί ἐστιν ἴση ἡ ΔΒ τῇ ΦΧ· ἑκατέρα γὰρ αὐτῶν ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου· ἴση ἄρα καὶ ἡ ΑΒ τῇ ΨΩ. καί ἐστιν ἡ ΑΒ ἡ τῆς δοθείσης σφαίρας διάμετρος· καὶ ἡ ΨΩ ἄρα ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ. τῇ ἄρα δοθείσῃ σφαίρᾳ περιείληπται τὸ εἰκοσάεδρον.
Λέγω δή, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων. ἐπεὶ γὰρ ῥητή ἐστιν ἡ τῆς σφαίρας διάμετρος, καί ἐστι δυνάμει πενταπλασίων τῆς ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου, ῥητὴ ἄρα ἐστὶ καὶ ἡ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου· ὥστε καὶ ἡ διάμετρος αὐτοῦ ῥητή ἐστιν. ἐὰν δὲ εἰς κύκλον ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων. ἡ δὲ τοῦ ΕΖΗΘΚ πενταγώνου πλευρὰ ἡ τοῦ εἰκοσαέδρου ἐστίν. ἡ ἄρα τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει πενταπλασίων ἐστὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου, ἀφ' οὗ τὸ εἰκοσάεδρον ἀναγέγραπται, καὶ ὅτι ἡ τῆς σφαίρας διάμετρος σύγκειται ἔκ τε τῆς τοῦ ἑξαγώνου καὶ δύο τῶν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων. ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου