ΜΕ ΕΣΩΤΕΡΙΚΗ ΠΛΟΗΓΗΣΗ
5 Αιτηματα
9 Κοιναι εννοιαι
465 Προτασεισ
Στοιχεῖα Εὐκλείδου
Βιβλία I-XIII
Στοιχεῖα Εὐκλείδου α΄
Βιβλίον I
Ὅροι κγ΄ 23
α΄ 1. Σημεῖόν ἐστιν, οὗ μέρος οὐθέν.
β΄ 2. Γραμμὴ δὲ μῆκος ἀπλατές.
γ΄ 3. Γραμμῆς δὲ πέρατα σημεῖα.
δ΄ 4. Εὐθεῖα γραμμή ἐστιν, ἥτις ἐξ ἴσου τοῖς ἐφ' ἑαυτῆς σημείοις κεῖται.
ε΄ 5. Ἐπιφάνεια δέ ἐστιν, ὃ μῆκος καὶ πλάτος μόνον ἔχει.
ς΄ 6. Ἐπιφανείας δὲ πέρατα γραμμαί.
ζ΄ 7. Ἐπίπεδος ἐπιφάνειά ἐστιν, ἥτις ἐξ ἴσου ταῖς ἐφ' ἑαυτῆς εὐθείαις κεῖται.
η΄ 8. Ἐπίπεδος δὲ γωνία ἐστὶν ἡ ἐν ἐπιπέδῳ δύο γραμμῶν ἁπτομένων ἀλλήλων καὶ μὴ ἐπ᾿ εὐθείας κειμένων πρὸς ἀλλήλας τῶν γραμμῶν κλίσις.
θ΄ 9. Ὅταν δὲ αἱ περιέχουσαι τὴν γωνίαν γραμμαὶ εὐθεῖαι ὦσιν, εὐθύγραμμος καλεῖται ἡ γωνία.
ι΄ 10. Ὅταν δὲ εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα τὰς ἐφεξῆς γωνίας ἴσας ἀλλήλαις ποιῇ, ὀρθὴ ἑκατέρα τῶν ἴσων γωνιῶν ἐστι, καὶ ἡ ἐφεστηκυῖα εὐθεῖα κάθετος καλεῖται, ἐφ' ἣν ἐφέστηκεν.
ια΄ 11. Ἀμβλεῖα γωνία ἐστὶν ἡ μείζων ὀρθῆς.
ιβ΄ 12. Ὀξεῖα δὲ ἡ ἐλάσσων ὀρθῆς.
ιγ΄ 13. Ὅρος ἐστίν, ὅ τινός ἐστι πέρας.
ιδ΄ 14. Σχῆμά ἐστι τὸ ὑπό τινος ἤ τινων ὅρων περιεχόμενον.
ιε΄ 15. Κύκλος ἐστὶ σχῆμα ἐπίπεδον ὑπὸ μιᾶς γραμμῆς περιεχόμενον [ἣ καλεῖται περιφέρεια], πρὸς ἣν ἀφ' ἑνὸς σημείου τῶν ἐντὸς τοῦ σχήματος κειμένων πᾶσαι αἱ προσπίπτουσαι εὐθεῖαι [πρὸς τὴν τοῦ κύκλου περιφέρειαν] ἴσαι ἀλλήλαις εἰσίν.
ις΄ 16. Κέντρον δὲ τοῦ κύκλου τὸ σημεῖον καλεῖται.
ιζ΄ 17. Διάμετρος δὲ τοῦ κύκλου ἐστὶν εὐθεῖά τις διὰ τοῦ κέντρου ἠγμένη καὶ περατουμένη ἐφ' ἑκάτερα τὰ μέρη ὑπὸ τῆς τοῦ κύκλου περιφερείας, ἥτις καὶ δίχα τέμνει τὸν κύκλον.
ιη΄ 18. Ἡμικύκλιον δέ ἐστι τὸ περιεχόμενον σχῆμα ὑπό τε τῆς διαμέτρου καὶ τῆς ἀπολαμβανομένης ὑπ' αὐτῆς περιφερείας. κέντρον δὲ τοῦ ἡμικυκλίου τὸ αὐτό, ὃ καὶ τοῦ κύκλου ἐστίν.
ιθ΄ 19. Σχήματα εὐθύγραμμά ἐστι τὰ ὑπὸ εὐθειῶν περιεχόμενα, τρίπλευρα μὲν τὰ ὑπὸ τριῶν, τετράπλευρα δὲ τὰ ὑπὸ τεσσάρων, πολύπλευρα δὲ τὰ ὑπὸ πλειόνων ἢ τεσσάρων εὐθειῶν περιεχόμενα.
κ΄ 20. Τῶν δὲ τριπλεύρων σχημάτων ἰσόπλευρον μὲν τρίγωνόν ἐστι τὸ τὰς τρεῖς ἴσας ἔχον πλευράς, ἰσοσκελὲς δὲ τὸ τὰς δύο μόνας ἴσας ἔχον πλευράς, σκαληνὸν δὲ τὸ τὰς τρεῖς ἀνίσους ἔχον πλευράς.
κα΄ 21. Ἔτι δὲ τῶν τριπλεύρων σχημάτων ὀρθογώνιον μὲν τρίγωνόν ἐστι τὸ ἔχον ὀρθὴν γωνίαν, ἀμβλυγώνιον δὲ τὸ ἔχον ἀμβλεῖαν γωνίαν, ὀξυγώνιον δὲ τὸ τὰς τρεῖς ὀξείας ἔχον γωνίας.
κβ΄ 22. Τῶν δὲ τετραπλεύρων σχημάτων τετράγωνον μέν ἐστιν, ὃ ἰσόπλευρόν τέ ἐστι καὶ ὀρθογώνιον, ἑτερόμηκες δέ, ὃ ὀρθογώνιον μέν, οὐκ ἰσόπλευρον δέ, ῥόμβος δέ, ὃ ἰσόπλευρον μέν, οὐκ ὀρθογώνιον δέ, ῥομβοειδὲς δὲ τὸ τὰς ἀπεναντίον πλευράς τε καὶ γωνίας ἴσας ἀλλήλαις ἔχον, ὃ οὔτε ἰσόπλευρόν ἐστιν οὔτε ὀρθογώνιον: τὰ δὲ παρὰ ταῦτα τετράπλευρα τραπέζια καλείσθω.
κγ΄ 23. Παράλληλοί εἰσιν εὐθεῖαι, αἵτινες ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι καὶ ἐκβαλλόμεναι εἰς ἄπειρον ἐφ' ἑκάτερα τὰ μέρη ἐπὶ μηδέτερα συμπίπτουσιν ἀλλήλαις.
Στοιχεῖα Εὐκλείδου α΄
Βιβλίον I
Αἰτήματα ε΄ 5
α΄ 1. Ἠιτήσθω ἀπὸ παντὸς σημείου ἐπὶ πᾶν σημεῖον εὐθεῖαν γραμμὴν ἀγαγεῖν.
β΄ 2. Καὶ πεπερασμένην εὐθεῖαν κατὰ τὸ συνεχὲς ἐπ᾿ εὐθείας ἐκβαλεῖν.
γ΄ 3. Καὶ παντὶ κέντρῳ καὶ διαστήματι κύκλον γράφεσθαι.
δ΄ 4. Καὶ πάσας τὰς ὀρθὰς γωνίας ἴσας ἀλλήλαις εἶναι.
ε΄ 5. Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ᾿ ἄπειρον συμπίπτειν, ἐφ' ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες.
Στοιχεῖα Εὐκλείδου α΄
Βιβλίον I
Κοιναί Ἒνοιαι θ΄ 9
α΄ 1. Τὰ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα.
β΄ 2. Καὶ ἐὰν ἴσοις ἴσα προστεθῇ, τὰ ὅλα ἐστὶν ἴσα.
γ΄ 3. Καὶ ἐὰν ἀπὸ ἴσων ἴσα ἀφαιρεθῇ, τὰ καταλειπόμενά ἐστιν ἴσα.
δ΄ 4. Καὶ ἐὰν ἀνίσοις ἴσα προστεθῇ, τὰ ὅλα ἐστὶν ἄνισα.
ε΄ 5. Καὶ τὰ τοῦ αὐτοῦ διπλάσια ἴσα ἀλλήλοις ἐστίν.
ς΄ 6. Καὶ τὰ τοῦ αὐτοῦ ἡμίση ἴσα ἀλλήλοις ἐστίν.]
ζ΄ 7. Καὶ τὰ ἐφαρμόζοντα ἐπ᾿ ἄλληλα ἴσα ἀλλήλοις ἐστίν.
η΄ 8. Καὶ τὸ ὅλον τοῦ μέρους μεῖζον [ἐστιν].
θ΄ 9. Καὶ δύο εὐθεῖαι χωρίον οὐ περιέχουσιν.
Στοιχεῖα Εὐκλείδου α΄
Βιβλίον I
Προτάσεις μη΄ 48 Βιβλίον I
Πρότασις α΄ 1 Βιβλίον I
Ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης τρίγωνον ἰσόπλευρον συστήσασθαι.
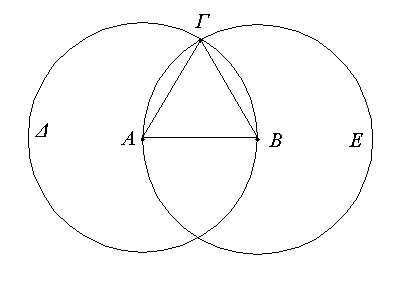
Ἔστω ἡ δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ. Δεῖ δὴ ἐπὶ τῆς ΑΒ εὐθείας τρίγωνον ἰσόπλευρον συστήσασθαι. Κέντρῳ μὲν τῷ Α διαστήματι δὲ τῷ ΑΒ κύκλος γεγράφθω ὁ ΒΓΔ, καὶ πάλιν κέντρῳ μὲν τῷ Β διαστήματι δὲ τῷ ΒΑ κύκλος γεγράφθω ὁ ΑΓΕ, καὶ ἀπὸ τοῦ Γ σημείου, καθ᾿ ὃ τέμνουσιν ἀλλήλους
οἱ κύκλοι, ἐπὶ τὰ Α, Β σημεῖα ἐπεζεύχθωσαν εὐθεῖαι αἱ ΓΑ, ΓΒ. Καὶ ἐπεὶ τὸ Α σημεῖον κέντρον ἐστὶ τοῦ ΓΔΒ κύκλου, ἴση ἐστὶν ἡ ΑΓ τῇ ΑΒ· πάλιν, ἐπεὶ τὸ Β σημεῖον κέντρον ἐστὶ τοῦ ΓΑΕ κύκλου, ἴση ἐστὶν ἡ ΒΓ τῇ ΒΑ. ἐδείχθη δὲ καὶ ἡ ΓΑ τῇ ΑΒ ἴση· ἑκατέρα ἄρα τῶν ΓΑ, ΓΒ τῇ ΑΒ ἐστὶν ἴση. τὰ δὲ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ ἡ ΓΑ ἄρα τῇ ΓΒ ἐστὶν ἴση· αἱ τρεῖς ἄρα αἱ ΓΑ, ΑΒ, ΒΓ ἴσαι ἀλλήλαις εἰσίν. Ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον, καὶ συνέσταται ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης τῆς ΑΒ. [Ἐπὶ τῆς δοθείσης ἄρα εὐθείας πεπερασμένης τρίγωνον ἰσόπλευρον συνέσταται]· ὅπερ ἔδει ποιῆσαι.
Πρότασις β΄ 2 Βιβλίον I
Πρὸς τῷ δοθέντι σημείῳ τῇ δοθείσῃ εὐθείᾳ ἴσην εὐθεῖαν θέσθαι.
Ἔστω τὸ μὲν δοθὲν σημεῖον τὸ Α, ἡ δὲ δοθεῖσα εὐθεῖα ἡ ΒΓ· δεῖ δὴ πρὸς τῷ Α σημείῳ τῇ δοθείσῃ εὐθείᾳ τῇ ΒΓ ἴσην εὐθεῖαν θέσθαι.
Ἐπεζεύχθω γὰρ ἀπὸ τοῦ Α σημείου ἐπὶ τὸ Β σημεῖον εὐθεῖα ἡ ΑΒ, καὶ συνεστάτω ἐπ᾿ αὐτῆς τρίγωνον ἰσόπλευρον τὸ ΔΑΒ, καὶ ἐκβεβλήσθωσαν ἐπ᾿ εὐθείας ταῖς ΔΑ, ΔΒ εὐθεῖαι αἱ ΑΕ, ΒΖ, καὶ κέντρῳ μὲν τῷ Β διαστήματι δὲ τῷ ΒΓ κύκλος γεγράφθω ὁ ΓΗΘ, καὶ πάλιν κέντρῳ τῷ Δ καὶ διαστήματι τῷ ΔΗ κύκλος γεγράφθω ὁ ΗΚΛ.
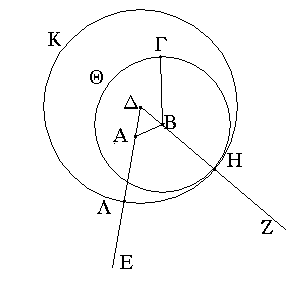
Ἐπεὶ οὖν τὸ Β σημεῖον κέντρον ἐστὶ τοῦ ΓΗΘ κύκλου, ἴση ἐστὶν ἡ ΒΓ τῇ ΒΗ. πάλιν, ἐπεὶ τὸ Δ σημεῖον κέντρον ἐστὶ τοῦ ΚΛΗ κύκλου, ἴση ἐστὶν ἡ ΔΛ τῇ ΔΗ, ὧν ἡ ΔΑ τῇ ΔΒ ἴση ἐστίν. λοιπὴ ἄρα ἡ ΑΛ λοιπῇ τῇ ΒΗ ἐστὶν ἴση. ἐδείχθη δὲ καὶ ἡ ΒΓ τῇ ΒΗ ἴση· ἑκατέρα ἄρα τῶν ΑΛ, ΒΓ τῇ ΒΗ ἐστὶν ἴση. τὰ δὲ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ ἡ ΑΛ ἄρα τῇ ΒΓ ἐστὶν ἴση.
Πρὸς ἄρα τῷ δοθέντι σημείῳ τῷ Α τῇ δοθείσῃ εὐθείᾳ τῇ ΒΓ ἴση εὐθεῖα κεῖται ἡ ΑΛ· ὅπερ ἔδει ποιῆσαι.
Πρότασις γ΄ 3 Βιβλίον I
Δύο δοθεισῶν εὐθειῶν ἀνίσων ἀπὸ τῆς μείζονος τῇ ἐλάσσονι ἴσην εὐθεῖαν ἀφελεῖν.
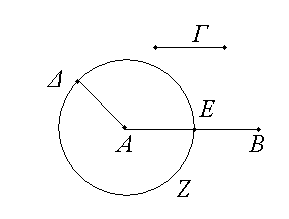
Ἔστωσαν αἱ δοθεῖσαι δύο εὐθεῖαι ἄνισοι αἱ ΑΒ, Γ, ὧν μείζων ἔστω ἡ ΑΒ· δεῖ δὴ ἀπὸ τῆς μείζονος τῆς ΑΒ τῇ ἐλάσσονι τῇ Γ ἴσην εὐθεῖαν ἀφελεῖν. Κείσθω πρὸς τῷ Α σημείῳ τῇ Γ εὐθείᾳ ἴση ἡ ΑΔ· καὶ κέντρῳ μὲν τῷ Α διαστήματι δὲ τῷ ΑΔ κύκλος γεγράφθω ὁ ΔΕΖ. Καὶ ἐπεὶ τὸ Α σημεῖον κέντρον ἐστὶ τοῦ ΔΕΖ κύκλου, ἴση ἐστὶν ἡ ΑΕ τῇ ΑΔ· ἀλλὰ καὶ ἡ Γ τῇ ΑΔ ἐστιν ἴση. ἑκατέρα ἄρα τῶν ΑΕ, Γ τῇ ΑΔ ἐστιν ἴση· ὥστε καὶ ἡ ΑΕ τῇ Γ ἐστιν ἴση. Δύο ἄρα δοθεισῶν εὐθειῶν ἀνίσων τῶν ΑΒ, Γ ἀπὸ τῆς μείζονος τῆς ΑΒ τῇ ἐλάσσονι τῇ Γ ἴση ἀφῄρηται ἡ ΑΕ· ὅπερ ἔδει ποιῆσαι.
Πρότασις δ΄ 4 Βιβλίον I
Ἐὰν δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δυσὶ πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἔχῃ τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην, καὶ τὴν βάσιν τῇ βάσει ἴσην ἕξει, καὶ τὸ τρίγωνον τῷ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν.
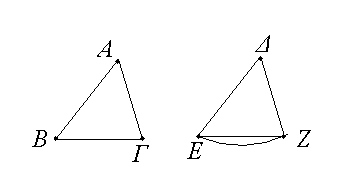
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ τὰς δύο πλευρὰς τὰς ΑΒ, ΑΓ ταῖς δυσὶ πλευραῖς ταῖς ΔΕ, ΔΖ ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ τὴν μὲν ΑΒ τῇ ΔΕ τὴν δὲ ΑΓ τῇ ΔΖ καὶ γωνίαν τὴν ὑπὸ ΒΑΓ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἴσην. λέγω, ὅτι καὶ βάσις ἡ ΒΓ βάσει τῇ ΕΖ ἴση ἐστίν, καὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν, ἡ μὲν ὑπὸ ΑΒΓ τῇ ὑπὸ ΔΕΖ, ἡ δὲ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΖΕ. Ἐφαρμοζομένου γὰρ τοῦ ΑΒΓ τριγώνου ἐπὶ τὸ ΔΕΖ τρίγωνον καὶ τιθεμένου τοῦ μὲν Α σημείου ἐπὶ τὸ Δ σημεῖον τῆς δὲ ΑΒ εὐθείας ἐπὶ τὴν ΔΕ, ἐφαρμόσει καὶ τὸ Β σημεῖον ἐπὶ τὸ Ε διὰ τὸ ἴσην εἶναι τὴν ΑΒ τῇ ΔΕ· ἐφαρμοσάσης δὴ τῆς ΑΒ ἐπὶ τὴν ΔΕ ἐφαρμόσει καὶ ἡ ΑΓ εὐθεῖα ἐπὶ τὴν ΔΖ διὰ τὸ ἴσην εἶναι τὴν ὑπὸ ΒΑΓ γωνίαν τῇ ὑπὸ ΕΔΖ· ὥστε καὶ τὸ Γ σημεῖον ἐπὶ τὸ Ζ σημεῖον ἐφαρμόσει διὰ τὸ ἴσην πάλιν εἶναι τὴν ΑΓ τῇ ΔΖ. ἀλλὰ μὴν καὶ τὸ Β ἐπὶ τὸ Ε ἐφηρμόκει· ὥστε βάσις ἡ ΒΓ ἐπὶ βάσιν τὴν ΕΖ ἐφαρμόσει. εἰ γὰρ τοῦ μὲν Β ἐπὶ τὸ Ε ἐφαρμόσαντος τοῦ δὲ Γ ἐπὶ τὸ Ζ ἡ ΒΓ βάσις ἐπὶ τὴν ΕΖ οὐκ ἐφαρμόσει, δύο εὐθεῖαι χωρίον περιέξουσιν· ὅπερ ἐστὶν ἀδύνατον. ἐφαρμόσει ἄρα ἡ ΒΓ βάσις ἐπὶ τὴν ΕΖ καὶ ἴση αὐτῇ ἔσται· ὥστε καὶ ὅλον τὸ ΑΒΓ τρίγωνον ἐπὶ ὅλον τὸ ΔΕΖ τρίγωνον ἐφαρμόσει καὶ ἴσον αὐτῷ ἔσται, καὶ αἱ λοιπαὶ γωνίαι ἐπὶ τὰς λοιπὰς γωνίας ἐφαρμόσουσι καὶ ἴσαι αὐταῖς ἔσονται, ἡ μὲν ὑπὸ ΑΒΓ τῇ ὑπὸ ΔΕΖ ἡ δὲ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΖΕ. Ἐὰν ἄρα δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δύο πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἔχῃ τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην, καὶ τὴν βάσιν τῇ βάσει ἴσην ἕξει, καὶ τὸ τρίγωνον τῷ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον I
Τῶν ἰσοσκελῶν τριγώνων αἱ πρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ προσεκβληθεισῶν τῶν ἴσων εὐθειῶν αἱ ὑπὸ τὴν βάσιν γωνίαι ἴσαι ἀλλήλαις ἔσονται.
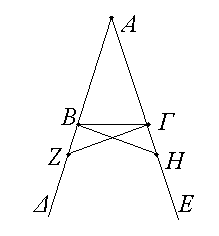
Ἔστω τρίγωνον ἰσοσκελὲς τὸ ΑΒΓ ἴσην ἔχον τὴν ΑΒ πλευρὰν τῇ ΑΓ πλευρᾷ, καὶ προσεκβεβλήσθωσαν ἐπ᾿ εὐθείας ταῖς ΑΒ, ΑΓ εὐθεῖαι αἱ ΒΔ, ΓΕ· λέγω, ὅτι ἡ μὲν ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΑΓΒ ἴση ἐστίν, ἡ δὲ ὑπὸ ΓΒΔ τῇ ὑπὸ ΒΓΕ. Εἰλήφθω γὰρ ἐπὶ τῆς ΒΔ τυχὸν σημεῖον τὸ Ζ, καὶ ἀφῃρήσθω ἀπὸ τῆς μείζονος τῆς ΑΕ τῇ ἐλάσσονι τῇ ΑΖ ἴση ἡ ΑΗ, καὶ ἐπεζεύχθωσαν αἱ ΖΓ, ΗΒ εὐθεῖαι. Ἐπεὶ οὖν ἴση ἐστὶν ἡ μὲν ΑΖ τῇ ΑΗ ἡ δὲ ΑΒ τῇ ΑΓ, δύο δὴ αἱ ΖΑ, ΑΓ δυσὶ ταῖς ΗΑ, ΑΒ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνίαν κοινὴν περιέχουσι τὴν ὑπὸ ΖΑΗ· βάσις ἄρα ἡ ΖΓ βάσει τῇ ΗΒ ἴση ἐστίν, καὶ τὸ ΑΖΓ τρίγωνον τῷ ΑΗΒ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν, ἡ μὲν ὑπὸ ΑΓΖ τῇ ὑπὸ ΑΒΗ, ἡ δὲ ὑπὸ ΑΖΓ τῇ ὑπὸ ΑΗΒ. καὶ ἐπεὶ ὅλη ἡ ΑΖ ὅλῃ τῇ ΑΗ ἐστιν ἴση, ὧν ἡ ΑΒ τῇ ΑΓ ἐστιν ἴση, λοιπὴ ἄρα ἡ ΒΖ λοιπῇ τῇ ΓΗ ἐστιν ἴση. ἐδείχθη δὲ καὶ ἡ ΖΓ τῇ ΗΒ ἴση· δύο δὴ αἱ ΒΖ, ΖΓ δυσὶ ταῖς ΓΗ, ΗΒ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΒΖΓ γωνίᾳ τῇ ὑπὸ ΓΗΒ ἴση, καὶ βάσις αὐτῶν κοινὴ ἡ ΒΓ· καὶ τὸ ΒΖΓ ἄρα τρίγωνον τῷ ΓΗΒ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἐστὶν ἡ μὲν ὑπὸ ΖΒΓ τῇ ὑπὸ ΗΓΒ ἡ δὲ ὑπὸ ΒΓΖ τῇ ὑπὸ ΓΒΗ. ἐπεὶ οὖν ὅλη ἡ ὑπὸ ΑΒΗ γωνία ὅλῃ τῇ ὑπὸ ΑΓΖ γωνίᾳ ἐδείχθη ἴση, ὧν ἡ ὑπὸ ΓΒΗ τῇ ὑπὸ ΒΓΖ ἴση, λοιπὴ ἄρα ἡ ὑπὸ ΑΒΓ λοιπῇ τῇ ὑπὸ ΑΓΒ ἐστιν ἴση· καί εἰσι πρὸς τῇ βάσει τοῦ ΑΒΓ τριγώνου. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΖΒΓ τῇ ὑπὸ ΗΓΒ ἴση· καί εἰσιν ὑπὸ τὴν βάσιν. Τῶν ἄρα ἰσοσκελῶν τριγώνων αἱ πρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ προσεκβληθεισῶν τῶν ἴσων εὐθειῶν αἱ ὑπὸ τὴν βάσιν γωνίαι ἴσαι ἀλλήλαις ἔσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον I
Ἐὰν τριγώνου αἱ δύο γωνίαι ἴσαι ἀλλήλαις ὦσιν, καὶ αἱ ὑπὸ τὰς ἴσας γωνίαις ὑποτείνουσαι πλευραὶ ἴσαι ἀλλήλαις ἔσονται.
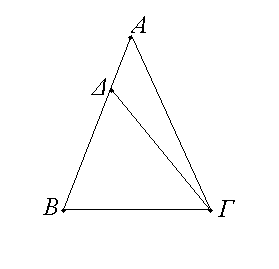
Ἔστω τρίγωνον τὸ ΑΒΓ ἴσην ἔχον τὴν ὑπὸ ΑΒΓ γωνίαν τῇ ὑπὸ ΑΓΒ γωνίᾳ· λέγω, ὅτι καὶ πλευρὰ ἡ ΑΒ πλευρᾷ τῇ ΑΓ ἐστιν ἴση. Εἰ γὰρ ἄνισός ἐστιν ἡ ΑΒ τῇ ΑΓ, ἡ ἑτέρα αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ΑΒ, καὶ ἀφῃρήσθω ἀπὸ τῆς μείζονος τῆς ΑΒ τῇ ἐλάττονι τῇ ΑΓ ἴση ἡ ΔΒ, καὶ ἐπεζεύχθω ἡ ΔΓ. Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΔΒ τῇ ΑΓ κοινὴ δὲ ἡ ΒΓ, δύο δὴ αἱ ΔΒ, ΒΓ δύο ταῖς ΑΓ, ΓΒ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ γωνία ἡ ὑπὸ ΔΒΓ γωνίᾳ τῇ ὑπὸ ΑΓΒ ἐστιν ἴση· βάσις ἄρα ἡ ΔΓ βάσει τῇ ΑΒ ἴση ἐστίν, καὶ τὸ ΔΒΓ τρίγωνον τῷ ΑΓΒ τριγώνῳ ἴσον ἔσται, τὸ ἔλασσον τῷ μείζονι· ὅπερ ἄτοπον· οὐκ ἄρα ἄνισός ἐστιν ἡ ΑΒ τῇ ΑΓ· ἴση ἄρα. Ἐὰν ἄρα τριγώνου αἱ δύο γωνίαι ἴσαι ἀλλήλαις ὦσιν, καὶ αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι πλευραὶ ἴσαι ἀλλήλαις ἔσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον I
Ἐπὶ τῆς αὐτῆς εὐθείας δύο ταῖς αὐταῖς εὐθείαις ἄλλαι δύο εὐθεῖαι ἴσαι ἑκατέρα ἑκατέρᾳ οὐ συσταθήσονται πρὸς ἄλλῳ καὶ ἄλλῳ σημείῳ ἐπὶ τὰ αὐτὰ μέρη τὰ αὐτὰ πέρατα ἔχουσαι ταῖς ἐξ ἀρχῆς εὐθείαις.
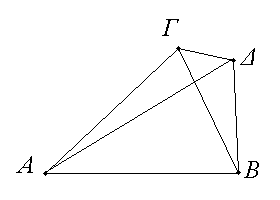
Εἰ γὰρ δυνατόν, ἐπὶ τῆς αὐτῆς εὐθείας τῆς ΑΒ δύο ταῖς αὐταῖς εὐθείαις ταῖς ΑΓ, ΓΒ ἄλλαι δύο εὐθεῖαι αἱ ΑΔ, ΔΒ ἴσαι ἑκατέρα ἑκατέρᾳ συνεστάτωσαν πρὸς ἄλλῳ καὶ ἄλλῳ σημείῳ τῷ τε Γ καὶ Δ ἐπὶ τὰ αὐτὰ μέρη τὰ αὐτὰ πέρατα ἔχουσαι, ὥστε ἴσην εἶναι τὴν μὲν ΓΑ τῇ ΔΑ τὸ αὐτὸ πέρας ἔχουσαν αὐτῇ τὸ Α, τὴν δὲ ΓΒ τῇ ΔΒ τὸ αὐτὸ πέρας ἔχουσαν αὐτῇ τὸ Β, καὶ ἐπεζεύχθω ἡ ΓΔ. Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΑΓ τῇ ΑΔ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΑΓΔ τῇ ὑπὸ ΑΔΓ· μείζων ἄρα ἡ ὑπὸ ΑΔΓ τῆς ὑπὸ ΔΓΒ· πολλῷ ἄρα ἡ ὑπὸ ΓΔΒ μείζων ἐστὶ τῆς ὑπὸ ΔΓΒ. πάλιν ἐπεὶ ἴση ἐστὶν ἡ ΓΒ τῇ ΔΒ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΓΔΒ γωνίᾳ τῇ ὑπὸ ΔΓΒ. ἐδείχθη δὲ αὐτῆς καὶ πολλῷ μείζων· ὅπερ ἐστὶν ἀδύνατον. Οὐκ ἄρα ἐπὶ τῆς αὐτῆς εὐθείας δύο ταῖς αὐταῖς εὐθείαις ἄλλαι δύο εὐθεῖαι ἴσαι ἑκατέρα ἑκατέρᾳ συσταθήσονται πρὸς ἄλλῳ καὶ ἄλλῳ σημείῳ ἐπὶ τὰ αὐτὰ μέρη τὰ αὐτὰ πέρατα ἔχουσαι ταῖς ἐξ ἀρχῆς εὐθείαις· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον I
Ἐὰν δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δύο πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρα, ἔχῃ δὲ καὶ τὴν βάσιν τῇ βάσει ἴσην, καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἕξει τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην.
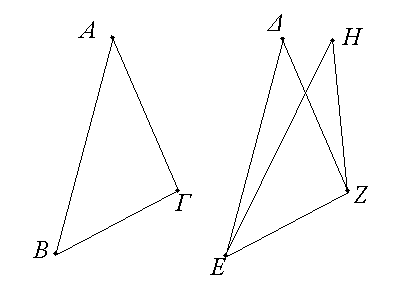
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ τὰς δύο πλευρὰς τὰς ΑΒ, ΑΓ ταῖς δύο πλευραῖς ταῖς ΔΕ, ΔΖ ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ, τὴν μὲν ΑΒ τῇ ΔΕ τὴν δὲ ΑΓ τῇ ΔΖ· ἐχέτω δὲ καὶ βάσιν τὴν ΒΓ βάσει τῇ ΕΖ ἴσην· λέγω, ὅτι καὶ γωνία ἡ ὑπὸ ΒΑΓ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἐστιν ἴση. Ἐφαρμοζομένου γὰρ τοῦ ΑΒΓ τριγώνου ἐπὶ τὸ ΔΕΖ τρίγωνον καὶ τιθεμένου τοῦ μὲν Β σημείου ἐπὶ τὸ Ε σημεῖον τῆς δὲ ΒΓ εὐθείας ἐπὶ τὴν ΕΖ ἐφαρμόσει καὶ τὸ Γ σημεῖον ἐπὶ τὸ Ζ διὰ τὸ ἴσην εἶναι τὴν ΒΓ τῇ ΕΖ· ἐφαρμοσάσης δὴ τῆς ΒΓ ἐπὶ τὴν ΕΖ ἐφαρμόσουσι καὶ αἱ ΒΑ, ΓΑ ἐπὶ τὰς ΕΔ, ΔΖ. εἰ γὰρ βάσις μὲν ἡ ΒΓ ἐπὶ βάσιν τὴν ΕΖ ἐφαρμόσει, αἱ δὲ ΒΑ, ΑΓ πλευραὶ ἐπὶ τὰς ΕΔ, ΔΖ οὐκ ἐφαρμόσουσιν ἀλλὰ παραλλάξουσιν ὡς αἱ ΕΗ, ΗΖ, συσταθήσονται ἐπὶ τῆς αὐτῆς εὐθείας δύο ταῖς αὐταῖς εὐθείαις ἄλλαι δύο εὐθεῖαι ἴσαι ἑκατέρα ἑκατέρᾳ πρὸς ἄλλῳ καὶ ἄλλῳ σημείῳ ἐπὶ τὰ αὐτὰ μέρη τὰ αὐτὰ πέρατα ἔχουσαι. οὐ συνίστανται δέ· οὐκ ἄρα ἐφαρμοζομένης τῆς ΒΓ βάσεως ἐπὶ τὴν ΕΖ βάσιν οὐκ ἐφαρμόσουσι καὶ αἱ ΒΑ, ΑΓ πλευραὶ ἐπὶ τὰς ΕΔ, ΔΖ. ἐφαρμόσουσιν ἄρα· ὥστε καὶ γωνία ἡ ὑπὸ ΒΑΓ ἐπὶ γωνίαν τὴν ὑπὸ ΕΔΖ ἐφαρμόσει καὶ ἴση αὐτῇ ἔσται. Ἐὰν ἄρα δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δύο πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ τὴν βάσιν τῇ βάσει ἴσην ἔχῃ, καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἕξει τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον I
Τὴν δοθεῖσαν γωνίαν εὐθύγραμμον δίχα τεμεῖν.
Ἔστω ἡ δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΒΑΓ. δεῖ δὴ αὐτὴν δίχα τεμεῖν.
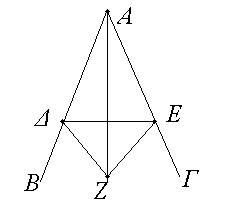
Εἰλήφθω ἐπὶ τῆς ΑΒ τυχὸν σημεῖον τὸ Δ, καὶ ἀφῃρήσθω ἀπὸ τῆς ΑΓ τῇ ΑΔ ἴση ἡ ΑΕ, καὶ ἐπεζεύχθω ἡ ΔΕ, καὶ συνεστάτω ἐπὶ τῆς ΔΕ τρίγωνον ἰσόπλευρον τὸ ΔΕΖ, καὶ ἐπεζεύχθω ἡ ΑΖ· λέγω, ὅτι ἡ ὑπὸ ΒΑΓ γωνία δίχα τέτμηται ὑπὸ τῆς ΑΖ εὐθείας. Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΑΔ τῇ ΑΕ, κοινὴ δὲ ἡ ΑΖ, δύο δὴ αἱ ΔΑ, ΑΖ δυσὶ ταῖς ΕΑ, ΑΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ. καὶ βάσις ἡ ΔΖ βάσει τῇ ΕΖ ἴση ἐστίν· γωνία ἄρα ἡ ὑπὸ ΔΑΖ γωνίᾳ τῇ ὑπὸ ΕΑΖ ἴση ἐστίν. Ἡ ἄρα δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΒΑΓ δίχα τέτμηται ὑπὸ τῆς ΑΖ εὐθείας· ὅπερ ἔδει ποιῆσαι.
Πρότασις ι΄ 10 Βιβλίον I
Τὴν δοθεῖσαν εὐθεῖαν πεπερασμένην δίχα τεμεῖν.
Ἔστω ἡ δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ· δεῖ δὴ τὴν ΑΒ εὐθεῖαν πεπερασμένην δίχα τεμεῖν.
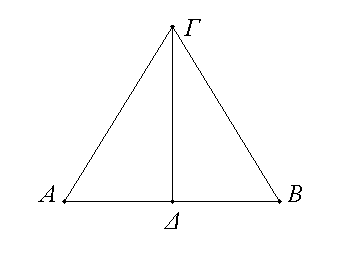
Συνεστάτω ἐπ᾿ αὐτῆς τρίγωνον ἰσόπλευρον τὸ ΑΒΓ, καὶ τετμήσθω ἡ ὑπὸ ΑΓΒ γωνία δίχα τῇ ΓΔ εὐθείᾳ· λέγω, ὅτι ἡ ΑΒ εὐθεῖα δίχα τέτμηται κατὰ τὸ Δ σημεῖον. Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, κοινὴ δὲ ἡ ΓΔ, δύο δὴ αἱ ΑΓ, ΓΔ δύο ταῖς ΒΓ, ΓΔ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΓΔ γωνίᾳ τῇ ὑπὸ ΒΓΔ ἴση ἐστίν· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΒΔ ἴση ἐστίν. Ἡ ἄρα δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ δίχα τέτμηται κατὰ τὸ Δ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ια΄11 Βιβλίον I
Τῇ δοθείσῃ εὐθείᾳ ἀπὸ τοῦ πρὸς αὐτῇ δοθέντος σημείου πρὸς ὀρθὰς γωνίας εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ τὸ δὲ δοθὲν σημεῖον ἐπ᾿ αὐτῆς τὸ Γ· δεῖ δὴ ἀπὸ τοῦ Γ σημείου τῇ ΑΒ εὐθείᾳ πρὸς ὀρθὰς γωνίας εὐθεῖαν γραμμὴν ἀγαγεῖν.
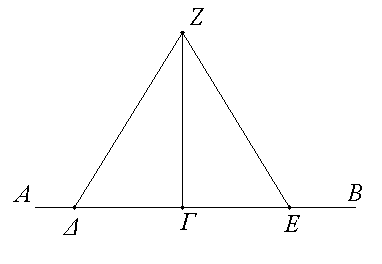
Εἰλήφθω ἐπὶ τῆς ΑΓ τυχὸν σημεῖον τὸ Δ, καὶ κείσθω τῇ ΓΔ ἴση ἡ ΓΕ, καὶ συνεστάτω ἐπὶ τῆς ΔΕ τρίγωνον ἰσόπλευρον τὸ ΖΔΕ, καὶ ἐπεζεύχθω ἡ ΖΓ· λέγω, ὅτι τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ ἀπὸ τοῦ πρὸς αὐτῇ δοθέντος σημείου τοῦ Γ πρὸς ὀρθὰς γωνίας εὐθεῖα γραμμὴ ἦκται ἡ ΖΓ. Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΔΓ τῇ ΓΕ, κοινὴ δὲ ἡ ΓΖ, δύο δὴ αἱ ΔΓ, ΓΖ δυσὶ ταῖς ΕΓ, ΓΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΔΖ βάσει τῇ ΖΕ ἴση ἐστίν· γωνία ἄρα ἡ ὑπὸ ΔΓΖ γωνίᾳ τῇ ὑπὸ ΕΓΖ ἴση ἐστίν· καί εἰσιν ἐφεξῆς. ὅταν δὲ εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα τὰς ἐφεξῆς γωνίας ἴσας ἀλλήλαις ποιῇ, ὀρθὴ ἑκατέρα τῶν ἴσων γωνιῶν ἐστιν· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν ὑπὸ ΔΓΖ, ΖΓΕ. Τῇ ἄρα δοθείσῃ εὐθείᾳ τῇ ΑΒ ἀπὸ τοῦ πρὸς αὐτῇ δοθέντος σημείου τοῦ Γ πρὸς ὀρθὰς γωνίας εὐθεῖα γραμμὴ ἦκται ἡ ΓΖ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιβ΄ 12 Βιβλίον I
Ἐπὶ τὴν δοθεῖσαν εὐθεῖαν ἄπειρον ἀπὸ τοῦ δοθέντος σημείου, ὃ μή ἐστιν ἐπ᾿ αὐτῆς, κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἄπειρος ἡ ΑΒ τὸ δὲ δοθὲν σημεῖον, ὃ μή ἐστιν ἐπ᾿ αὐτῆς, τὸ Γ· δεῖ δὴ ἐπὶ τὴν δοθεῖσαν εὐθεῖαν ἄπειρον τὴν ΑΒ ἀπὸ τοῦ δοθέντος σημείου τοῦ Γ, ὃ μή ἐστιν ἐπ᾿ αὐτῆς, κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
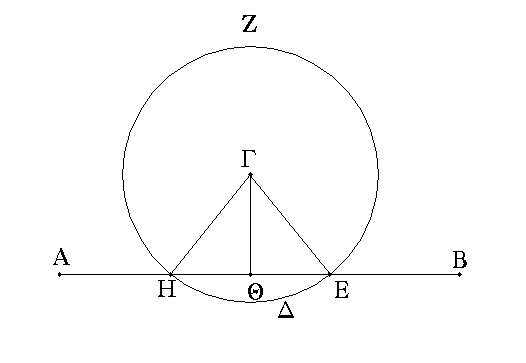
Εἰλήφθω γὰρ ἐπὶ τὰ ἕτερα μέρη τῆς ΑΒ εὐθείας τυχὸν σημεῖον τὸ Δ, καὶ κέντρῳ μὲν τῷ Γ διαστήματι δὲ τῷ ΓΔ κύκλος γεγράφθω ὁ ΕΖΗ, καὶ τετμήσθω ἡ ΕΗ εὐθεῖα δίχα κατὰ τὸ Θ, καὶ ἐπεζεύχθωσαν αἱ ΓΗ, ΓΘ, ΓΕ εὐθεῖαι· λέγω, ὅτι ἐπὶ τὴν δοθεῖσαν εὐθεῖαν ἄπειρον τὴν ΑΒ ἀπὸ τοῦ δοθέντος σημείου τοῦ Γ, ὃ μή ἐστιν ἐπ᾿ αὐτῆς, κάθετος ἦκται ἡ ΓΘ. Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΗΘ τῇ ΘΕ, κοινὴ δὲ ἡ ΘΓ, δύο δὴ αἱ ΗΘ, ΘΓ δύο ταῖς ΕΘ, ΘΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΓΗ βάσει τῇ ΓΕ ἐστιν ἴση· γωνία ἄρα ἡ ὑπὸ ΓΘΗ γωνίᾳ τῇ ὑπὸ ΕΘΓ ἐστιν ἴση. καί εἰσιν ἐφεξῆς. ὅταν δὲ εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα τὰς ἐφεξῆς γωνίας ἴσας ἀλλήλαις ποιῇ, ὀρθὴ ἑκατέρα τῶν ἴσων γωνιῶν ἐστιν, καὶ ἡ ἐφεστηκυῖα εὐθεῖα κάθετος καλεῖται ἐφ' ἣν ἐφέστηκεν. Ἐπὶ τὴν δοθεῖσαν ἄρα εὐθεῖαν ἄπειρον τὴν ΑΒ ἀπὸ τοῦ δοθέντος σημείου τοῦ Γ, ὃ μή ἐστιν ἐπ᾿ αὐτῆς, κάθετος ἦκται ἡ ΓΘ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιγ΄ 13 Βιβλίον I
Ἐὰν εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα γωνίας ποιῇ, ἤτοι δύο ὀρθὰς ἢ δυσὶν ὀρθαῖς ἴσας ποιήσει.
Εὐθεῖα γάρ τις ἡ ΑΒ ἐπ᾿ εὐθεῖαν τὴν ΓΔ σταθεῖσα γωνίας ποιείτω τὰς ὑπὸ ΓΒΑ, ΑΒΔ· λέγω, ὅτι αἱ ὑπὸ ΓΒΑ, ΑΒΔ γωνίαι ἤτοι δύο ὀρθαί εἰσιν ἢ δυσὶν ὀρθαῖς ἴσαι.
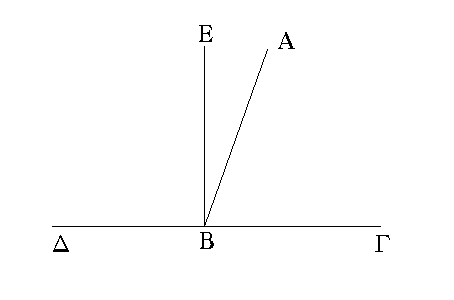
Εἰ μὲν οὖν ἴση ἐστὶν ἡ ὑπὸ ΓΒΑ τῇ ὑπὸ ΑΒΔ, δύο ὀρθαί εἰσιν. εἰ δὲ οὔ, ἤχθω ἀπὸ τοῦ Β σημείου τῇ ΓΔ [εὐθείᾳ] πρὸς ὀρθὰς ἡ ΒΕ· αἱ ἄρα ὑπὸ ΓΒΕ, ΕΒΔ δύο ὀρθαί εἰσιν· καὶ ἐπεὶ ἡ ὑπὸ ΓΒΕ δυσὶ ταῖς ὑπὸ ΓΒΑ, ΑΒΕ ἴση ἐστίν, κοινὴ προσκείσθω ἡ ὑπὸ ΕΒΔ· αἱ ἄρα ὑπὸ ΓΒΕ, ΕΒΔ τρισὶ ταῖς ὑπὸ ΓΒΑ, ΑΒΕ, ΕΒΔ ἴσαι εἰσίν. πάλιν, ἐπεὶ ἡ ὑπὸ ΔΒΑ δυσὶ ταῖς ὑπὸ ΔΒΕ, ΕΒΑ ἴση ἐστίν, κοινὴ προσκείσθω ἡ ὑπὸ ΑΒΓ· αἱ ἄρα ὑπὸ ΔΒΑ, ΑΒΓ τρισὶ ταῖς ὑπὸ ΔΒΕ, ΕΒΑ, ΑΒΓ ἴσαι εἰσίν. ἐδείχθησαν δὲ καὶ αἱ ὑπὸ ΓΒΕ, ΕΒΔ τρισὶ ταῖς αὐταῖς ἴσαι· τὰ δὲ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ αἱ ὑπὸ ΓΒΕ, ΕΒΔ ἄρα ταῖς ὑπὸ ΔΒΑ, ΑΒΓ ἴσαι εἰσίν· ἀλλὰ αἱ ὑπὸ ΓΒΕ, ΕΒΔ δύο ὀρθαί εἰσιν? καὶ αἱ ὑπὸ ΔΒΑ, ΑΒΓ ἄρα δυσὶν ὀρθαῖς ἴσαι εἰσίν. Ἐὰν ἄρα εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα γωνίας ποιῇ, ἤτοι δύο ὀρθὰς ἢ δυσὶν ὀρθαῖς ἴσας ποιήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον I
Ἐὰν πρός τινι εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ δύο εὐθεῖαι μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιῶσιν, ἐπ᾿ εὐθείας ἔσονται ἀλλήλαις αἱ εὐθεῖαι.
Πρὸς γάρ τινι εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Β δύο εὐθεῖαι αἱ ΒΓ, ΒΔ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας τὰς ὑπὸ ΑΒΓ, ΑΒΔ δύο ὀρθαῖς ἴσας ποιείτωσαν· λέγω, ὅτι ἐπ᾿ εὐθείας ἐστὶ τῇ ΓΒ ἡ ΒΔ.
Εἰ γὰρ μή ἐστι τῇ ΒΓ ἐπ᾿ εὐθείας ἡ ΒΔ, ἔστω τῇ ΓΒ ἐπ᾿ εὐθείας ἡ ΒΕ.
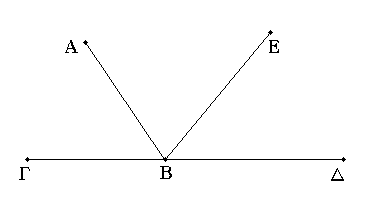
Ἐπεὶ οὖν εὐθεῖα ἡ ΑΒ ἐπ᾿ εὐθεῖαν τὴν ΓΒΕ ἐφέστηκεν, αἱ ἄρα ὑπὸ ΑΒΓ, ΑΒΕ γωνίαι δύο ὀρθαῖς ἴσαι εἰσίν· εἰσὶ δὲ καὶ αἱ ὑπὸ ΑΒΓ, ΑΒΔ δύο ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΓΒΑ, ΑΒΕ ταῖς ὑπὸ ΓΒΑ, ΑΒΔ ἴσαι εἰσίν. κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΓΒΑ· λοιπὴ ἄρα ἡ ὑπὸ ΑΒΕ λοιπῇ τῇ ὑπὸ ΑΒΔ ἐστιν ἴση, ἡ ἐλάσσων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐπ᾿ εὐθείας ἐστὶν ἡ ΒΕ τῇ ΓΒ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἄλλη τις πλὴν τῆς ΒΔ· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΓΒ τῇ ΒΔ.
Ἐὰν ἄρα πρός τινι εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ δύο εὐθεῖαι μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιῶσιν, ἐπ᾿ εὐθείας ἔσονται ἀλλήλαις αἱ εὐθεῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον I
Ἐὰν δύο εὐθεῖαι τέμνωσιν ἀλλήλας, τὰς κατὰ κορυφὴν γωνίας ἴσας ἀλλήλαις ποιοῦσιν.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΓΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε σημεῖον· λέγω, ὅτι ἴση ἐστὶν ἡ μὲν ὑπὸ ΑΕΓ γωνία τῇ ὑπὸ ΔΕΒ, ἡ δὲ ὑπὸ ΓΕΒ τῇ ὑπὸ ΑΕΔ.
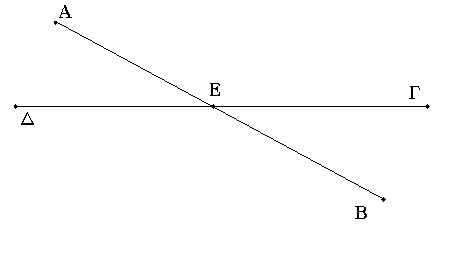
Ἐπεὶ γὰρ εὐθεῖα ἡ ΑΕ ἐπ᾿ εὐθεῖαν τὴν ΓΔ ἐφέστηκε γωνίας ποιοῦσα τὰς ὑπὸ ΓΕΑ, ΑΕΔ, αἱ ἄρα ὑπὸ ΓΕΑ, ΑΕΔ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. πάλιν, ἐπεὶ εὐθεῖα ἡ ΔΕ ἐπ᾿ εὐθεῖαν τὴν ΑΒ ἐφέστηκε γωνίας ποιοῦσα τὰς ὑπὸ ΑΕΔ, ΔΕΒ, αἱ ἄρα ὑπὸ ΑΕΔ, ΔΕΒ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. ἐδείχθησαν δὲ καὶ αἱ ὑπὸ ΓΕΑ, ΑΕΔ δυσὶν ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΓΕΑ, ΑΕΔ ταῖς ὑπὸ ΑΕΔ, ΔΕΒ ἴσαι εἰσίν. κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΑΕΔ· λοιπὴ ἄρα ἡ ὑπὸ ΓΕΑ λοιπῇ τῇ ὑπὸ ΒΕΔ ἴση ἐστίν· ὁμοίως δὴ δειχθήσεται, ὅτι καὶ αἱ ὑπὸ ΓΕΒ, ΔΕΑ ἴσαι εἰσίν.
Ἐὰν ἄρα δύο εὐθεῖαι τέμνωσιν ἀλλήλας, τὰς κατὰ κορυφὴν γωνίας ἴσας ἀλλήλαις ποιοῦσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον I
Παντὸς τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον γωνιῶν μείζων ἐστίν.
Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ προσεκβεβλήσθω αὐτοῦ μία πλευρὰ ἡ ΒΓ ἐπὶ τὸ Δ· λέγω, ὅτι ἡ ἐκτὸς γωνία ἡ ὑπὸ ΑΓΔ μείζων ἐστὶν ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον τῶν ὑπὸ ΓΒΑ, ΒΑΓ γωνιῶν.
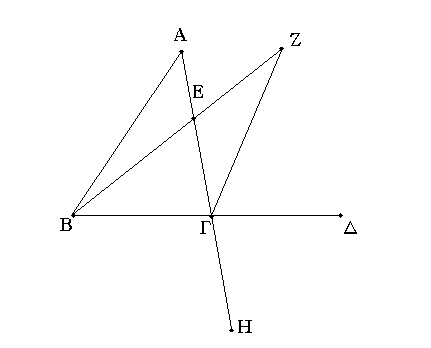
Τετμήσθω ἡ ΑΓ δίχα κατὰ τὸ Ε, καὶ ἐπιζευχθεῖσα ἡ ΒΕ ἐκβεβλήσθω ἐπ᾿ εὐθείας ἐπὶ τὸ Ζ, καὶ κείσθω τῇ ΒΕ ἴση ἡ ΕΖ, καὶ ἐπεζεύχθω ἡ ΖΓ, καὶ διήχθω ἡ ΑΓ ἐπὶ τὸ Η.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ μὲν ΑΕ τῇ ΕΓ, ἡ δὲ ΒΕ τῇ ΕΖ, δύο δὴ αἱ ΑΕ, ΕΒ δυσὶ ταῖς ΓΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΕΒ γωνίᾳ τῇ ὑπὸ ΖΕΓ ἴση ἐστίν· κατὰ κορυφὴν γάρ· βάσις ἄρα ἡ ΑΒ βάσει τῇ ΖΓ ἴση ἐστίν, καὶ τὸ ΑΒΕ τρίγωνον τῷ ΖΕΓ τριγώνῳ ἐστὶν ἴσον, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΑΕ τῇ ὑπὸ ΕΓΖ. μείζων δέ ἐστιν ἡ ὑπὸ ΕΓΔ τῆς ὑπὸ ΕΓΖ· μείζων ἄρα ἡ ὑπὸ ΑΓΔ τῆς ὑπὸ ΒΑΕ. ὁμοίως δὴ τῆς ΒΓ τετμημένης δίχα δειχθήσεται καὶ ἡ ὑπὸ ΒΓΗ, τουτέστιν ἡ ὑπὸ ΑΓΔ, μείζων καὶ τῆς ὑπὸ ΑΒΓ.
Παντὸς ἄρα τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον γωνιῶν μείζων ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον I
Παντὸς τριγώνου αἱ δύο γωνίαι δύο ὀρθῶν ἐλάσσονές εἰσι πάντῃ μεταλαμβανόμεναι.
Ἔστω τρίγωνον τὸ ΑΒΓ· λέγω, ὅτι τοῦ ΑΒΓ τριγώνου αἱ δύο γωνίαι δύο ὀρθῶν ἐλάττονές εἰσι πάντῃ μεταλαμβανόμεναι.
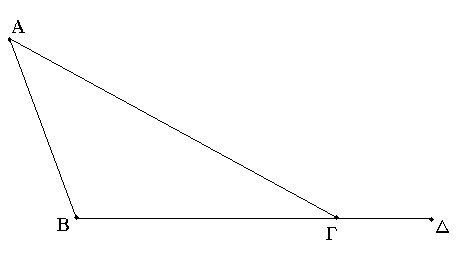
Ἐκβεβλήσθω γὰρ ἡ ΒΓ ἐπὶ τὸ Δ.
Καὶ ἐπεὶ τριγώνου τοῦ ΑΒΓ ἐκτός ἐστι γωνία ἡ ὑπὸ ΑΓΔ, μείζων ἐστὶ τῆς ἐντὸς καὶ ἀπεναντίον τῆς ὑπὸ ΑΒΓ. κοινὴ προσκείσθω ἡ ὑπὸ ΑΓΒ· αἱ ἄρα ὑπὸ ΑΓΔ, ΑΓΒ τῶν ὑπὸ ΑΒΓ, ΒΓΑ μείζονές εἰσιν. ἀλλ' αἱ ὑπὸ ΑΓΔ, ΑΓΒ δύο ὀρθαῖς ἴσαι εἰσίν· αἱ ἄρα ὑπὸ ΑΒΓ, ΒΓΑ δύο ὀρθῶν ἐλάσσονές εἰσιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ὑπὸ ΒΑΓ, ΑΓΒ δύο ὀρθῶν ἐλάσσονές εἰσι καὶ ἔτι αἱ ὑπὸ ΓΑΒ, ΑΒΓ.
Παντὸς ἄρα τριγώνου αἱ δύο γωνίαι δύο ὀρθῶν ἐλάσσονές εἰσι πάντῃ μεταλαμβανόμεναι· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον I
Παντὸς τριγώνου ἡ μείζων πλευρὰ τὴν μείζονα γωνίαν ὑποτείνει.
Ἔστω γὰρ τρίγωνον τὸ ΑΒΓ μείζονα ἔχον τὴν ΑΓ πλευρὰν τῆς ΑΒ· λέγω, ὅτι καὶ γωνία ἡ ὑπὸ ΑΒΓ μείζων ἐστὶ τῆς ὑπὸ ΒΓΑ.
Ἐπεὶ γὰρ μείζων ἐστὶν ἡ ΑΓ τῆς ΑΒ, κείσθω τῇ ΑΒ ἴση ἡ ΑΔ, καὶ ἐπεζεύχθω ἡ ΒΔ.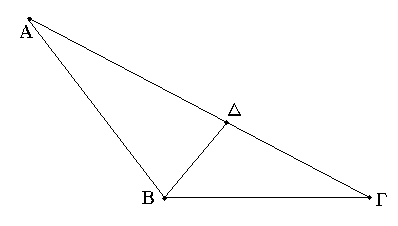
Καὶ ἐπεὶ τριγώνου τοῦ ΒΓΔ ἐκτός ἐστι γωνία ἡ ὑπὸ ΑΔΒ, μείζων ἐστὶ τῆς ἐντὸς καὶ ἀπεναντίον τῆς ὑπὸ ΔΓΒ· ἴση δὲ ἡ ὑπὸ ΑΔΒ τῇ ὑπὸ ΑΒΔ, ἐπεὶ καὶ πλευρὰ ἡ ΑΒ τῇ ΑΔ ἐστιν ἴση· μείζων ἄρα καὶ ἡ ὑπὸ ΑΒΔ τῆς ὑπὸ ΑΓΒ· πολλῷ ἄρα ἡ ὑπὸ ΑΒΓ μείζων ἐστὶ τῆς ὑπὸ ΑΓΒ.
Παντὸς ἄρα τριγώνου ἡ μείζων πλευρὰ τὴν μείζονα γωνίαν ὑποτείνει· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον I
Παντὸς τριγώνου ὑπὸ τὴν μείζονα γωνίαν ἡ μείζων πλευρὰ ὑποτείνει.
Ἔστω τρίγωνον τὸ ΑΒΓ μείζονα ἔχον τὴν ὑπὸ ΑΒΓ γωνίαν τῆς ὑπὸ ΒΓΑ· λέγω, ὅτι καὶ πλευρὰ ἡ ΑΓ πλευρᾶς τῆς ΑΒ μείζων ἐστίν.
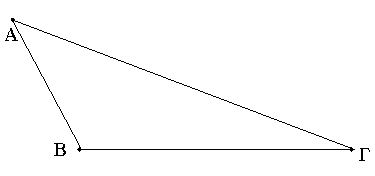
Εἰ γὰρ μή, ἤτοι ἴση ἐστὶν ἡ ΑΓ τῇ ΑΒ ἢ ἐλάσσων· ἴση μὲν οὖν οὐκ ἔστιν ἡ ΑΓ τῇ ΑΒ· ἴση γὰρ ἂν ἦν καὶ γωνία ἡ ὑπὸ ΑΒΓ τῇ ὑπὸ ΑΓΒ· οὐκ ἔστι δέ· οὐκ ἄρα ἴση ἐστὶν ἡ ΑΓ τῇ ΑΒ. οὐδὲ μὴν ἐλάσσων ἐστὶν ἡ ΑΓ τῆς ΑΒ· ἐλάσσων γὰρ ἂν ἦν καὶ γωνία ἡ ὑπὸ ΑΒΓ τῆς ὑπὸ ΑΓΒ· οὐκ ἔστι δέ· οὐκ ἄρα ἐλάσσων ἐστὶν ἡ ΑΓ τῆς ΑΒ. ἐδείχθη δέ, ὅτι οὐδὲ ἴση ἐστίν. μείζων ἄρα ἐστὶν ἡ ΑΓ τῆς ΑΒ.
Παντὸς ἄρα τριγώνου ὑπὸ τὴν μείζονα γωνίαν ἡ μείζων πλευρὰ ὑποτείνει· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον I
Παντὸς τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι.
Ἔστω γὰρ τρίγωνον τὸ ΑΒΓ· λέγω, ὅτι τοῦ ΑΒΓ τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι, αἱ μὲν ΒΑ, ΑΓ τῆς ΒΓ, αἱ δὲ ΑΒ, ΒΓ τῆς ΑΓ, αἱ δὲ ΒΓ, ΓΑ τῆς ΑΒ.
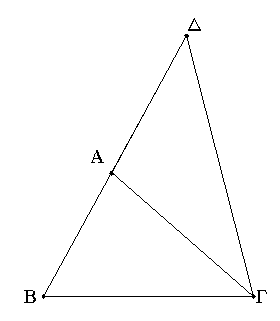
Διήχθω γὰρ ἡ ΒΑ ἐπὶ τὸ Δ σημεῖον, καὶ κείσθω τῇ ΓΑ ἴση ἡ ΑΔ, καὶ ἐπεζεύχθω ἡ ΔΓ. Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΔΑ τῇ ΑΓ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΑΔΓ τῇ ὑπὸ ΑΓΔ· μείζων ἄρα ἡ ὑπὸ ΒΓΔ τῆς ὑπὸ ΑΔΓ· καὶ ἐπεὶ τρίγωνόν ἐστι τὸ ΔΓΒ μείζονα ἔχον τὴν ὑπὸ ΒΓΔ γωνίαν τῆς ὑπὸ ΒΔΓ, ὑπὸ δὲ τὴν μείζονα γωνίαν ἡ μείζων πλευρὰ ὑποτείνει, ἡ ΔΒ ἄρα τῆς ΒΓ ἐστι μείζων. ἴση δὲ ἡ ΔΑ τῇ ΑΓ· μείζονες ἄρα αἱ ΒΑ, ΑΓ τῆς ΒΓ· ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ μὲν ΑΒ, ΒΓ τῆς ΓΑ μείζονές εἰσιν, αἱ δὲ ΒΓ, ΓΑ τῆς ΑΒ.
Παντὸς ἄρα τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι· ὅπερ ἔδει δεῖξαι.
Πρότασις κα΄ 21 Βιβλίον I
Ἐὰν τριγώνου ἐπὶ μιᾶς τῶν πλευρῶν ἀπὸ τῶν περάτων δύο εὐθεῖαι ἐντὸς συσταθῶσιν, αἱ συσταθεῖσαι τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν ἐλάττονες μὲν ἔσονται, μείζονα δὲ γωνίαν περιέξουσιν.
Τριγώνου γὰρ τοῦ ΑΒΓ ἐπὶ μιᾶς τῶν πλευρῶν τῆς ΒΓ ἀπὸ τῶν περάτων τῶν Β, Γ δύο εὐθεῖαι ἐντὸς συνεστάτωσαν αἱ ΒΔ, ΔΓ· λέγω, ὅτι αἱ ΒΔ, ΔΓ τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν τῶν ΒΑ, ΑΓ ἐλάσσονες μέν εἰσιν, μείζονα δὲ γωνίαν περιέχουσι τὴν ὑπὸ ΒΔΓ τῆς ὑπὸ ΒΑΓ.
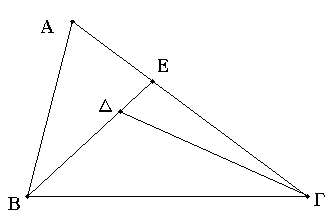
Διήχθω γὰρ ἡ ΒΔ ἐπὶ τὸ Ε. καὶ ἐπεὶ παντὸς τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσιν, τοῦ ΑΒΕ ἄρα τριγώνου αἱ δύο πλευραὶ αἱ ΑΒ, ΑΕ τῆς ΒΕ μείζονές εἰσιν· κοινὴ προσκείσθω ἡ ΕΓ· αἱ ἄρα ΒΑ, ΑΓ τῶν ΒΕ, ΕΓ μείζονές εἰσιν. πάλιν, ἐπεὶ τοῦ ΓΕΔ τριγώνου αἱ δύο πλευραὶ αἱ ΓΕ, ΕΔ τῆς ΓΔ μείζονές εἰσιν, κοινὴ προσκείσθω ἡ ΔΒ· αἱ ΓΕ, ΕΒ ἄρα τῶν ΓΔ, ΔΒ μείζονές εἰσιν. ἀλλὰ τῶν ΒΕ, ΕΓ μείζονες ἐδείχθησαν αἱ ΒΑ, ΑΓ· πολλῷ ἄρα αἱ ΒΑ, ΑΓ τῶν ΒΔ, ΔΓ μείζονές εἰσιν.
Πάλιν, ἐπεὶ παντὸς τριγώνου ἡ ἐκτὸς γωνία τῆς ἐντὸς καὶ ἀπεναντίον μείζων ἐστίν, τοῦ ΓΔΕ ἄρα τριγώνου ἡ ἐκτὸς γωνία ἡ ὑπὸ ΒΔΓ μείζων ἐστὶ τῆς ὑπὸ ΓΕΔ. διὰ ταὐτὰ τοίνυν καὶ τοῦ ΑΒΕ τριγώνου ἡ ἐκτὸς γωνία ἡ ὑπὸ ΓΕΒ μείζων ἐστὶ τῆς ὑπὸ ΒΑΓ. ἀλλὰ τῆς ὑπὸ ΓΕΒ μείζων ἐδείχθη ἡ ὑπὸ ΒΔΓ· πολλῷ ἄρα ἡ ὑπὸ ΒΔΓ μείζων ἐστὶ τῆς ὑπὸ ΒΑΓ.
Ἐὰν ἄρα τριγώνου ἐπὶ μιᾶς τῶν πλευρῶν ἀπὸ τῶν περάτων δύο εὐθεῖαι ἐντὸς συσταθῶσιν, αἱ συσταθεῖσαι τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν ἐλάττονες μέν εἰσιν, μείζονα δὲ γωνίαν περιέχουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον I
Ἐκ τριῶν εὐθειῶν, αἵ εἰσιν ἴσαι τρισὶ ταῖς δοθείσαις [εὐθείαις], τρίγωνον συστήσασθαι· δεῖ δὲ τὰς δύο τῆς λοιπῆς μείζονας εἶναι πάντῃ μεταλαμβανομένας [διὰ τὸ καὶ παντὸς τριγώνου τὰς δύο πλευρὰς τῆς λοιπῆς μείζονας εἶναι πάντῃ μεταλαμβανομένας].
Ἔστωσαν αἱ δοθεῖσαι τρεῖς εὐθεῖαι αἱ Α, Β, Γ, ὧν αἱ δύο τῆς λοιπῆς μείζονες ἔστωσαν πάντῃ μεταλαμβανόμεναι, αἱ μὲν Α, Β τῆς Γ, αἱ δὲ Α, Γ τῆς Β, καὶ ἔτι αἱ Β, Γ τῆς Α· δεῖ δὴ ἐκ τῶν ἴσων ταῖς Α, Β, Γ τρίγωνον συστήσασθαι.
Ἐκκείσθω τις εὐθεῖα ἡ ΔΕ πεπερασμένη μὲν κατὰ τὸ Δ ἄπειρος δὲ κατὰ τὸ Ε, καὶ κείσθω τῇ μὲν Α ἴση ἡ ΔΖ, τῇ δὲ Β ἴση ἡ ΖΗ, τῇ δὲ Γ ἴση ἡ ΗΘ· καὶ κέντρῳ μὲν τῷ Ζ, διαστήματι δὲ τῷ ΖΔ κύκλος γεγράφθω ὁ ΔΚΛ· πάλιν κέντρῳ μὲν τῷ Η, διαστήματι δὲ τῷ ΗΘ κύκλος γεγράφθω ὁ ΚΛΘ, καὶ ἐπεζεύχθωσαν αἱ ΚΖ, ΚΗ· λέγω, ὅτι ἐκ τριῶν εὐθειῶν τῶν ἴσων ταῖς Α, Β, Γ τρίγωνον συνέσταται τὸ ΚΖΗ.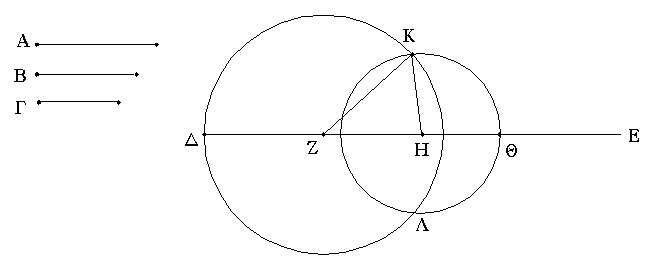
Ἐπεὶ γὰρ τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ ΔΚΛ κύκλου, ἴση ἐστὶν ἡ ΖΔ τῇ ΖΚ· ἀλλὰ ἡ ΖΔ τῇ Α ἐστιν ἴση. καὶ ἡ ΚΖ ἄρα τῇ Α ἐστιν ἴση. πάλιν, ἐπεὶ τὸ Η σημεῖον κέντρον ἐστὶ τοῦ ΛΚΘ κύκλου, ἴση ἐστὶν ἡ ΗΘ τῇ ΗΚ· ἀλλὰ ἡ ΗΘ τῇ Γ ἐστιν ἴση· καὶ ἡ ΚΗ ἄρα τῇ Γ ἐστιν ἴση. ἐστὶ δὲ καὶ ἡ ΖΗ τῇ Β ἴση· αἱ τρεῖς ἄρα εὐθεῖαι αἱ ΚΖ, ΖΗ, ΗΚ τρισὶ ταῖς Α, Β, Γ ἴσαι εἰσίν.
Ἐκ τριῶν ἄρα εὐθειῶν τῶν ΚΖ, ΖΗ, ΗΚ, αἵ εἰσιν ἴσαι τρισὶ ταῖς δοθείσαις εὐθείαις ταῖς Α, Β, Γ, τρίγωνον συνέσταται τὸ ΚΖΗ· ὅπερ ἔδει ποιῆσαι.
Πρότασις κγ΄ 23 Βιβλίον I
Πρὸς τῇ δοθείσῃ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ ἴσην γωνίαν εὐθύγραμμον συστήσασθαι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ πρὸς αὐτῇ σημεῖον τὸ Α, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΔΓΕ· δεῖ δὴ πρὸς τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ ὑπὸ ΔΓΕ ἴσην γωνίαν εὐθύγραμμον συστήσασθαι.
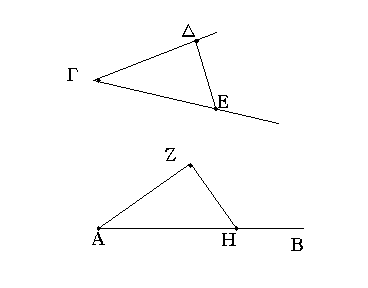
Εἰλήφθω ἐφ' ἑκατέρας τῶν ΓΔ, ΓΕ τυχόντα σημεῖα τὰ Δ, Ε, καὶ ἐπεζεύχθω ἡ ΔΕ· καὶ ἐκ τριῶν εὐθειῶν, αἵ εἰσιν ἴσαι τρισὶ ταῖς ΓΔ, ΔΕ, ΓΕ, τρίγωνον συνεστάτω τὸ ΑΖΗ, ὥστε ἴσην εἶναι τὴν μὲν ΓΔ τῇ ΑΖ, τὴν δὲ ΓΕ τῇ ΑΗ, καὶ ἔτι τὴν ΔΕ τῇ ΖΗ.
Ἐπεὶ οὖν δύο αἱ ΔΓ, ΓΕ δύο ταῖς ΖΑ, ΑΗ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ βάσις ἡ ΔΕ βάσει τῇ ΖΗ ἴση, γωνία ἄρα ἡ ὑπὸ ΔΓΕ γωνίᾳ τῇ ὑπὸ ΖΑΗ ἐστιν ἴση.
Πρὸς ἄρα τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ ὑπὸ ΔΓΕ ἴση γωνία εὐθύγραμμος συνέσταται ἡ ὑπὸ ΖΑΗ· ὅπερ ἔδει ποιῆσαι.
Πρότασις κδ΄ 24 Βιβλίον I
Πρὸς τῇ δοθείσῃ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ ἴσην γωνίαν εὐθύγραμμον συστήσασθαι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ πρὸς αὐτῇ σημεῖον τὸ Α, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΔΓΕ· δεῖ δὴ πρὸς τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ ὑπὸ ΔΓΕ ἴσην γωνίαν εὐθύγραμμον συστήσασθαι.

Εἰλήφθω ἐφ' ἑκατέρας τῶν ΓΔ, ΓΕ τυχόντα σημεῖα τὰ Δ, Ε, καὶ ἐπεζεύχθω ἡ ΔΕ· καὶ ἐκ τριῶν εὐθειῶν, αἵ εἰσιν ἴσαι τρισὶ ταῖς ΓΔ, ΔΕ, ΓΕ, τρίγωνον συνεστάτω τὸ ΑΖΗ, ὥστε ἴσην εἶναι τὴν μὲν ΓΔ τῇ ΑΖ, τὴν δὲ ΓΕ τῇ ΑΗ, καὶ ἔτι τὴν ΔΕ τῇ ΖΗ.
Ἐπεὶ οὖν δύο αἱ ΔΓ, ΓΕ δύο ταῖς ΖΑ, ΑΗ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ βάσις ἡ ΔΕ βάσει τῇ ΖΗ ἴση, γωνία ἄρα ἡ ὑπὸ ΔΓΕ γωνίᾳ τῇ ὑπὸ ΖΑΗ ἐστιν ἴση.
Πρὸς ἄρα τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ ὑπὸ ΔΓΕ ἴση γωνία εὐθύγραμμος συνέσταται ἡ ὑπὸ ΖΑΗ· ὅπερ ἔδει ποιῆσαι.
Πρότασις κε΄ 25 Βιβλίον I
Ἐὰν δύο τρίγωνα τὰς δύο πλευρὰς δυσὶ πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ, τὴν δὲ βάσιν τῆς βάσεως μείζονα ἔχῃ, καὶ τὴν γωνίαν τῆς γωνίας μείζονα ἕξει τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ τὰς δύο πλευρὰς τὰς ΑΒ, ΑΓ ταῖς δύο πλευραῖς ταῖς ΔΕ, ΔΖ ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ, τὴν μὲν ΑΒ τῇ ΔΕ, τὴν δὲ ΑΓ τῇ ΔΖ· βάσις δὲ ἡ ΒΓ βάσεως τῆς ΕΖ μείζων ἔστω· λέγω, ὅτι καὶ γωνία ἡ ὑπὸ ΒΑΓ γωνίας τῆς ὑπὸ ΕΔΖ μείζων ἐστίν·
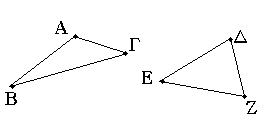
Εἰ γὰρ μή, ἤτοι ἴση ἐστὶν αὐτῇ ἢ ἐλάσσων· ἴση μὲν οὖν οὐκ ἔστιν ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ· ἴση γὰρ ἂν ἦν καὶ βάσις ἡ ΒΓ βάσει τῇ ΕΖ· οὐκ ἔστι δέ. οὐκ ἄρα ἴση ἐστὶ γωνία ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ· οὐδὲ μὴν ἐλάσσων ἐστὶν ἡ ὑπὸ ΒΑΓ τῆς ὑπὸ ΕΔΖ· ἐλάσσων γὰρ ἂν ἦν καὶ βάσις ἡ ΒΓ βάσεως τῆς ΕΖ· οὐκ ἔστι δέ· οὐκ ἄρα ἐλάσσων ἐστὶν ἡ ὑπὸ ΒΑΓ γωνία τῆς ὑπὸ ΕΔΖ. ἐδείχθη δὲ ὅτι οὐδὲ ἴση· μείζων ἄρα ἐστὶν ἡ ὑπὸ ΒΑΓ τῆς ὑπὸ ΕΔΖ.
Ἐὰν ἄρα δύο τρίγωνα τὰς δύο πλευρὰς δυσὶ πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκάτερᾳ, τὴν δὲ βάσιν τῆς βάσεως μείζονα ἔχῃ, καὶ τὴν γωνίαν τῆς γωνίας μείζονα ἕξει τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην· ὅπερ ἔδει δεῖξαι.
Πρότασις κς΄ 26 Βιβλίον I
Ἐὰν δύο τρίγωνα τὰς δύο γωνίας δυσὶ γωνίαις ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην ἤτοι τὴν πρὸς ταῖς ἴσαις γωνίαις ἢ τὴν ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν, καὶ τὰς λοιπὰς πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει [ἑκατέραν ἑκατέρᾳ] καὶ τὴν λοιπὴν γωνίαν τῇ λοιπῇ γωνίᾳ.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ τὰς δύο γωνίας τὰς ὑπὸ ΑΒΓ, ΒΓΑ δυσὶ ταῖς ὑπὸ ΔΕΖ, ΕΖΔ ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ, τὴν μὲν ὑπὸ ΑΒΓ τῇ ὑπὸ ΔΕΖ, τὴν δὲ ὑπὸ ΒΓΑ τῇ ὑπὸ ΕΖΔ· ἐχέτω δὲ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην, πρότερον τὴν πρὸς ταῖς ἴσαις γωνίαις τὴν ΒΓ τῇ ΕΖ· λέγω, ὅτι καὶ τὰς λοιπὰς πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει ἑκατέραν ἑκατέρᾳ, τὴν μὲν ΑΒ τῇ ΔΕ τὴν δὲ ΑΓ τῇ ΔΖ, καὶ τὴν λοιπὴν γωνίαν τῇ λοιπῇ γωνίᾳ, τὴν ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ.
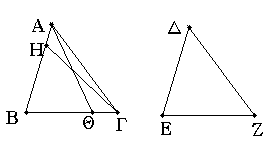
Εἰ γὰρ ἄνισός ἐστιν ἡ ΑΒ τῇ ΔΕ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ΑΒ, καὶ κείσθω τῇ ΔΕ ἴση ἡ ΒΗ, καὶ ἐπεζεύχθω ἡ ΗΓ.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ μὲν ΒΗ τῇ ΔΕ, ἡ δὲ ΒΓ τῇ ΕΖ, δύο δὴ αἱ ΒΗ, ΒΓ δυσὶ ταῖς ΔΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΗΒΓ γωνίᾳ τῇ ὑπὸ ΔΕΖ ἴση ἐστίν· βάσις ἄρα ἡ ΗΓ βάσει τῇ ΔΖ ἴση ἐστίν, καὶ τὸ ΗΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἡ ὑπὸ ΗΓΒ γωνία τῇ ὑπὸ ΔΖΕ. ἀλλὰ ἡ ὑπὸ ΔΖΕ τῇ ὑπὸ ΒΓΑ ὑπόκειται ἴση· καὶ ἡ ὑπὸ ΒΓΗ ἄρα τῇ ὑπὸ ΒΓΑ ἴση ἐστίν, ἡ ἐλάσσων τῇ μείζονι· ὅπερ ἀδύνατον. οὐκ ἄρα ἄνισός ἐστιν ἡ ΑΒ τῇ ΔΕ. ἴση ἄρα. ἔστι δὲ καὶ ἡ ΒΓ τῇ ΕΖ ἴση· δύο δὴ αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΔΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση· βάσις ἄρα ἡ ΑΓ βάσει τῇ ΔΖ ἴση ἐστίν, καὶ λοιπὴ γωνία ἡ ὑπὸ ΒΑΓ τῇ λοιπῇ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἴση ἐστίν.
Ἀλλὰ δὴ πάλιν ἔστωσαν αἱ ὑπὸ τὰς ἴσας γωνίας πλευραὶ ὑποτείνουσαι ἴσαι, ὡς ἡ ΑΒ τῇ ΔΕ· λέγω πάλιν, ὅτι καὶ αἱ λοιπαὶ πλευραὶ ταῖς λοιπαῖς πλευραῖς ἴσαι ἔσονται, ἡ μὲν ΑΓ τῇ ΔΖ, ἡ δὲ ΒΓ τῇ ΕΖ καὶ ἔτι ἡ λοιπὴ γωνία ἡ ὑπὸ ΒΑΓ τῇ λοιπῇ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἴση ἐστίν.
Εἰ γὰρ ἄνισός ἐστιν ἡ ΒΓ τῇ ΕΖ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων, εἰ δυνατόν, ἡ ΒΓ, καὶ κείσθω τῇ ΕΖ ἴση ἡ ΒΘ, καὶ ἐπεζεύχθω ἡ ΑΘ. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΒΘ τῇ ΕΖ ἡ δὲ ΑΒ τῇ ΔΕ, δύο δὴ αἱ ΑΒ, ΒΘ δυσὶ ταῖς ΔΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνίας ἴσας περιέχουσιν· βάσις ἄρα ἡ ΑΘ βάσει τῇ ΔΖ ἴση ἐστίν, καὶ τὸ ΑΒΘ τρίγωνον τῷ ΔΕΖ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΘΑ γωνία τῇ ὑπὸ ΕΖΔ. ἀλλὰ ἡ ὑπὸ ΕΖΔ τῇ ὑπὸ ΒΓΑ ἐστιν ἴση· τριγώνου δὴ τοῦ ΑΘΓ ἡ ἐκτὸς γωνία ἡ ὑπὸ ΒΘΑ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΒΓΑ· ὅπερ ἀδύνατον. οὐκ ἄρα ἄνισός ἐστιν ἡ ΒΓ τῇ ΕΖ· ἴση ἄρα. ἐστὶ δὲ καὶ ἡ ΑΒ τῇ ΔΕ ἴση. δύο δὴ αἱ ΑΒ, ΒΓ δύο ταῖς ΔΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνίας ἴσας περιέχουσι· βάσις ἄρα ἡ ΑΓ βάσει τῇ ΔΖ ἴση ἐστίν, καὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ ἴσον καὶ λοιπὴ γωνία ἡ ὑπὸ ΒΑΓ τῇ λοιπῇ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἴση.
Ἐὰν ἄρα δύο τρίγωνα τὰς δύο γωνίας δυσὶ γωνίαις ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην ἤτοι τὴν πρὸς ταῖς ἴσαις γωνίαις, ἢ τὴν ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν, καὶ τὰς λοιπὰς πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει καὶ τὴν λοιπὴν γωνίαν τῇ λοιπῇ γωνίᾳ· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον I
Ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐναλλὰξ γωνίας ἴσας ἀλλήλαις ποιῇ, παράλληλοι ἔσονται ἀλλήλαις αἱ εὐθεῖαι.
Εἰς γὰρ δύο εὐθείας τὰς ΑΒ, ΓΔ εὐθεῖα ἐμπίπτουσα ἡ ΕΖ τὰς ἐναλλὰξ γωνίας τὰς ὑπὸ ΑΕΖ, ΕΖΔ ἴσας ἀλλήλαις ποιείτω· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ.
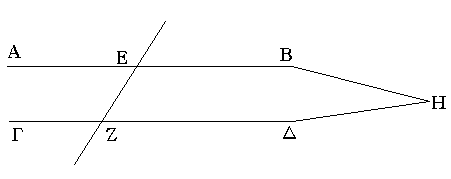
Εἰ γὰρ μή, ἐκβαλλόμεναι αἱ ΑΒ, ΓΔ συμπεσοῦνται ἤτοι ἐπὶ τὰ Β, Δ μέρη ἢ ἐπὶ τὰ Α, Γ. ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν ἐπὶ τὰ Β, Δ μέρη κατὰ τὸ Η. τριγώνου δὴ τοῦ ΗΕΖ ἡ ἐκτὸς γωνία ἡ ὑπὸ ΑΕΖ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΕΖΗ· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα αἱ ΑΒ, ΓΔ ἐκβαλλόμεναι συμπεσοῦνται ἐπὶ τὰ Β, Δ μέρη. ὁμοίως δὴ δειχθήσεται, ὅτι οὐδὲ ἐπὶ τὰ Α, Γ· αἱ δὲ ἐπὶ μηδέτερα τὰ μέρη συμπίπτουσαι παράλληλοί εἰσιν· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ.
Ἐὰν ἄρα εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐναλλὰξ γωνίας ἴσας ἀλλήλαις ποιῇ, παράλληλοι ἔσονται αἱ εὐθεῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον I
Ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὴν ἐκτὸς γωνίαν τῇ ἐντὸς καὶ ἀπεναντίον καὶ ἐπὶ τὰ αὐτὰ μέρη ἴσην ποιῇ ἢ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη δυσὶν ὀρθαῖς ἴσας, παράλληλοι ἔσονται ἀλλήλαις αἱ εὐθεῖαι.
Εἰς γὰρ δύο εὐθείας τὰς ΑΒ, ΓΔ εὐθεῖα ἐμπίπτουσα ἡ ΕΖ τὴν ἐκτὸς γωνίαν τὴν ὑπὸ ΕΗΒ τῇ ἐντὸς καὶ ἀπεναντίον γωνίᾳ τῇ ὑπὸ ΗΘΔ ἴσην ποιείτω ἢ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη τὰς ὑπὸ ΒΗΘ, ΗΘΔ δυσὶν ὀρθαῖς ἴσας· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ.
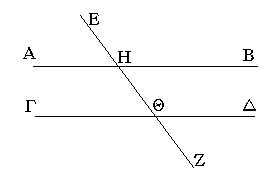
Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ὑπὸ ΕΗΒ τῇ ὑπὸ ΗΘΔ, ἀλλὰ ἡ ὑπὸ ΕΗΒ τῇ ὑπὸ ΑΗΘ ἐστιν ἴση, καὶ ἡ ὑπὸ ΑΗΘ ἄρα τῇ ὑπὸ ΗΘΔ ἐστιν ἴση· καί εἰσιν ἐναλλάξ· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ.
Πάλιν, ἐπεὶ αἱ ὑπὸ ΒΗΘ, ΗΘΔ δύο ὀρθαῖς ἴσαι εἰσίν, εἰσὶ δὲ καὶ αἱ ὑπὸ ΑΗΘ, ΒΗΘ δυσὶν ὀρθαῖς ἴσαι, αἱ ἄρα ὑπὸ ΑΗΘ, ΒΗΘ ταῖς ὑπὸ ΒΗΘ, ΗΘΔ ἴσαι εἰσίν· κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΒΗΘ· λοιπὴ ἄρα ἡ ὑπὸ ΑΗΘ λοιπῇ τῇ ὑπὸ ΗΘΔ ἐστιν ἴση· καί εἰσιν ἐναλλάξ· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ.
Ἐὰν ἄρα εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὴν ἐκτὸς γωνίαν τῇ ἐντὸς καὶ ἀπεναντίον καὶ ἐπὶ τὰ αὐτὰ μέρη ἴσην ποιῇ ἢ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη δυσὶν ὀρθαῖς ἴσας, παράλληλοι ἔσονται αἱ εὐθεῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον I
Ἡ εἰς τὰς παραλλήλους εὐθείας εὐθεῖα ἐμπίπτουσα τάς τε ἐναλλὰξ γωνίας ἴσας ἀλλήλαις ποιεῖ καὶ τὴν ἐκτὸς τῇ ἐντὸς καὶ ἀπεναντίον ἴσην καὶ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη δυσὶν ὀρθαῖς ἴσας.
Εἰς γὰρ παραλλήλους εὐθείας τὰς ΑΒ, ΓΔ εὐθεῖα ἐμπιπτέτω ἡ ΕΖ· λέγω, ὅτι τὰς ἐναλλὰξ γωνίας τὰς ὑπὸ ΑΗΘ, ΗΘΔ ἴσας ποιεῖ καὶ τὴν ἐκτὸς γωνίαν τὴν ὑπὸ ΕΗΒ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΗΘΔ ἴσην καὶ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη τὰς ὑπὸ ΒΗΘ, ΗΘΔ δυσὶν ὀρθαῖς ἴσας.
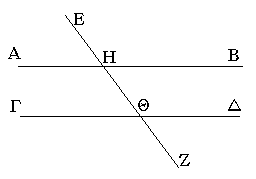
Εἰ γὰρ ἄνισός ἐστιν ἡ ὑπὸ ΑΗΘ τῇ ὑπὸ ΗΘΔ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ὑπὸ ΑΗΘ· κοινὴ προσκείσθω ἡ ὑπὸ ΒΗΘ· αἱ ἄρα ὑπὸ ΑΗΘ, ΒΗΘ τῶν ὑπὸ ΒΗΘ, ΗΘΔ μείζονές εἰσιν. ἀλλὰ αἱ ὑπὸ ΑΗΘ, ΒΗΘ δυσὶν ὀρθαῖς ἴσαι εἰσίν. [καὶ] αἱ ἄρα ὑπὸ ΒΗΘ, ΗΘΔ δύο ὀρθῶν ἐλάσσονές εἰσιν. αἱ δὲ ἀπ' ἐλασσόνων ἢ δύο ὀρθῶν ἐκβαλλόμεναι εἰς ἄπειρον συμπίπτουσιν· αἱ ἄρα ΑΒ, ΓΔ ἐκβαλλόμεναι εἰς ἄπειρον συμπεσοῦνται· οὐ συμπίπτουσι δὲ διὰ τὸ παραλλήλους αὐτὰς ὑποκεῖσθαι· οὐκ ἄρα ἄνισός ἐστιν ἡ ὑπὸ ΑΗΘ τῇ ὑπὸ ΗΘΔ· ἴση ἄρα. ἀλλὰ ἡ ὑπὸ ΑΗΘ τῇ ὑπὸ ΕΗΒ ἐστιν ἴση· καὶ ἡ ὑπὸ ΕΗΒ ἄρα τῇ ὑπὸ ΗΘΔ ἐστιν ἴση. κοινὴ προσκείσθω ἡ ὑπὸ ΒΗΘ· αἱ ἄρα ὑπὸ ΕΗΒ, ΒΗΘ ταῖς ὑπὸ ΒΗΘ, ΗΘΔ ἴσαι εἰσίν. ἀλλὰ αἱ ὑπὸ ΕΗΒ, ΒΗΘ δύο ὀρθαῖς ἴσαι εἰσίν· καὶ αἱ ὑπὸ ΒΗΘ, ΗΘΔ ἄρα δύο ὀρθαῖς ἴσαι εἰσίν.
Ἡ ἄρα εἰς τὰς παραλλήλους εὐθείας εὐθεῖα ἐμπίπτουσα τάς τε ἐναλλὰξ γωνίας ἴσας ἀλλήλαις ποιεῖ καὶ τὴν ἐκτὸς τῇ ἐντὸς καὶ ἀπεναντίον ἴσην καὶ τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη δυσὶν ὀρθαῖς ἴσας· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον I
Αἱ τῇ αὐτῇ εὐθείᾳ παράλληλοι καὶ ἀλλήλαις εἰσὶ παράλληλοι.
Ἔστω ἑκατέρα τῶν ΑΒ, ΓΔ τῇ ΕΖ παράλληλος· λέγω, ὅτι καὶ ἡ ΑΒ τῇ ΓΔ ἐστι παράλληλος. Ἐμπιπτέτω γὰρ εἰς αὐτὰς εὐθεῖα ἡ ΗΚ.
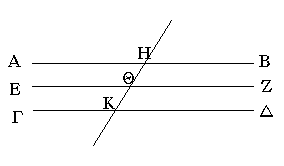
Καὶ ἐπεὶ εἰς παραλλήλους εὐθείας τὰς ΑΒ, ΕΖ εὐθεῖα ἐμπέπτωκεν ἡ ΗΚ, ἴση ἄρα ἡ ὑπὸ ΑΗΚ τῇ ὑπὸ ΗΘΖ. πάλιν, ἐπεὶ εἰς παραλλήλους εὐθείας τὰς ΕΖ, ΓΔ εὐθεῖα ἐμπέπτωκεν ἡ ΗΚ, ἴση ἐστὶν ἡ ὑπὸ ΗΘΖ τῇ ὑπὸ ΗΚΔ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΑΗΚ τῇ ὑπὸ ΗΘΖ ἴση. καὶ ἡ ὑπὸ ΑΗΚ ἄρα τῇ ὑπὸ ΗΚΔ ἐστιν ἴση· καί εἰσιν ἐναλλάξ. παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ.
[Αἱ ἄρα τῇ αὐτῇ εὐθείᾳ παράλληλοι καὶ ἀλλήλαις εἰσὶ παράλληλοι·] ὅπερ ἔδει δεῖξαι.
Πρότασις λα΄ 31 Βιβλίον I
Διὰ τοῦ δοθέντος σημείου τῇ δοθείσῃ εὐθείᾳ παράλληλον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω τὸ μὲν δοθὲν σημεῖον τὸ Α, ἡ δὲ δοθεῖσα εὐθεῖα ἡ ΒΓ· δεῖ δὴ διὰ τοῦ Α σημείου τῇ ΒΓ εὐθείᾳ παράλληλον εὐθεῖαν γραμμὴν ἀγαγεῖν.
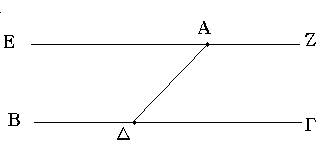
Εἰλήφθω ἐπὶ τῆς ΒΓ τυχὸν σημεῖον τὸ Δ, καὶ ἐπεζεύχθω ἡ ΑΔ· καὶ συνεστάτω πρὸς τῇ ΔΑ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΑΔΓ γωνίᾳ ἴση ἡ ὑπὸ ΔΑΕ· καὶ ἐκβεβλήσθω ἐπ᾿ εὐθείας τῇ ΕΑ εὐθεῖα ἡ ΑΖ.
Καὶ ἐπεὶ εἰς δύο εὐθείας τὰς ΒΓ, ΕΖ εὐθεῖα ἐμπίπτουσα ἡ ΑΔ τὰς ἐναλλὰξ γωνίας τὰς ὑπὸ ΕΑΔ, ΑΔΓ ἴσας ἀλλήλαις πεποίηκεν, παράλληλος ἄρα ἐστὶν ἡ ΕΑΖ τῇ ΒΓ.
Διὰ τοῦ δοθέντος ἄρα σημείου τοῦ Α τῇ δοθείσῃ εὐθείᾳ τῇ ΒΓ παράλληλος εὐθεῖα γραμμὴ ἦκται ἡ ΕΑΖ· ὅπερ ἔδει ποιῆσαι.
Πρότασις λβ΄ 32 Βιβλίον I
Παντὸς τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία δυσὶ ταῖς ἐντὸς καὶ ἀπεναντίον ἴση ἐστίν, καὶ αἱ ἐντὸς τοῦ τριγώνου τρεῖς γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν.
Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ προσεκβεβλήσθω αὐτοῦ μία πλευρὰ ἡ ΒΓ ἐπὶ τὸ Δ· λέγω, ὅτι ἡ ἐκτὸς γωνία ἡ ὑπὸ ΑΓΔ ἴση ἐστὶ δυσὶ ταῖς ἐντὸς καὶ ἀπεναντίον ταῖς ὑπὸ ΓΑΒ, ΑΒΓ, καὶ αἱ ἐντὸς τοῦ τριγώνου τρεῖς γωνίαι αἱ ὑπὸ ΑΒΓ, ΒΓΑ, ΓΑΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν.
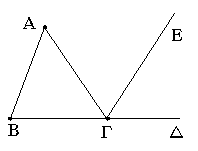
Ἤχθω γὰρ διὰ τοῦ Γ σημείου τῇ ΑΒ εὐθείᾳ παράλληλος ἡ ΓΕ.
Καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΕ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΑΓ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΒΑΓ, ΑΓΕ ἴσαι ἀλλήλαις εἰσίν. πάλιν, ἐπεὶ παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΕ, καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΒΔ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΕΓΔ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΑΒΓ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΑΓΕ τῇ ὑπὸ ΒΑΓ ἴση· ὅλη ἄρα ἡ ὑπὸ ΑΓΔ γωνία ἴση ἐστὶ δυσὶ ταῖς ἐντὸς καὶ ἀπεναντίον ταῖς ὑπὸ ΒΑΓ, ΑΒΓ.
Κοινὴ προσκείσθω ἡ ὑπὸ ΑΓΒ· αἱ ἄρα ὑπὸ ΑΓΔ, ΑΓΒ τρισὶ ταῖς ὑπὸ ΑΒΓ, ΒΓΑ, ΓΑΒ ἴσαι εἰσίν. ἀλλ' αἱ ὑπὸ ΑΓΔ, ΑΓΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν· καὶ αἱ ὑπὸ ΑΓΒ, ΓΒΑ, ΓΑΒ ἄρα δυσίν ὀρθαῖς ἴσαι εἰσίν.
Παντὸς ἄρα τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία δυσὶ ταῖς ἐντὸς καὶ ἀπεναντίον ἴση ἐστίν, καὶ αἱ ἐντὸς τοῦ τριγώνου τρεῖς γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον I
Αἱ τὰς ἴσας τε καὶ παραλλήλους ἐπὶ τὰ αὐτὰ μέρη ἐπιζευγνύουσαι εὐθεῖαι καὶ αὐταὶ ἴσαι τε καὶ παράλληλοί εἰσιν.
Ἔστωσαν ἴσαι τε καὶ παράλληλοι αἱ ΑΒ, ΓΔ, καὶ ἐπιζευγνύτωσαν αὐτὰς ἐπὶ τὰ αὐτὰ μέρη εὐθεῖαι αἱ ΑΓ, ΒΔ· λέγω, ὅτι καὶ αἱ ΑΓ, ΒΔ ἴσαι τε καὶ παράλληλοί εἰσιν.
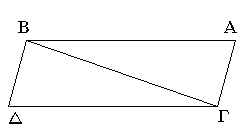
Ἐπεζεύχθω ἡ ΒΓ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΒΓ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΑΒΓ, ΒΓΔ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΓΔ κοινὴ δὲ ἡ ΒΓ, δύο δὴ αἱ ΑΒ, ΒΓ δύο ταῖς ΒΓ, ΓΔ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΒΓΔ ἴση· βάσις ἄρα ἡ ΑΓ βάσει τῇ ΒΔ ἐστιν ἴση, καὶ τὸ ΑΒΓ τρίγωνον τῷ ΒΓΔ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἡ ὑπὸ ΑΓΒ γωνία τῇ ὑπὸ ΓΒΔ. καὶ ἐπεὶ εἰς δύο εὐθείας τὰς ΑΓ, ΒΔ εὐθεῖα ἐμπίπτουσα ἡ ΒΓ τὰς ἐναλλὰξ γωνίας ἴσας ἀλλήλαις πεποίηκεν, παράλληλος ἄρα ἐστὶν ἡ ΑΓ τῇ ΒΔ. ἐδείχθη δὲ αὐτῇ καὶ ἴση.
Αἱ ἄρα τὰς ἴσας τε καὶ παραλλήλους ἐπὶ τὰ αὐτὰ μέρη ἐπιζευγνύουσαι εὐθεῖαι καὶ αὐταὶ ἴσαι τε καὶ παράλληλοί εἰσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις λδ΄ 34 Βιβλίον I
Τῶν παραλληλογράμμων χωρίων αἱ ἀπεναντίον πλευραί τε καὶ γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ ἡ διάμετρος αὐτὰ δίχα τέμνει.
Ἔστω παραλληλόγραμμον χωρίον τὸ ΑΓΔΒ, διάμετρος δὲ αὐτοῦ ἡ ΒΓ· λέγω, ὅτι τοῦ ΑΓΔΒ παραλληλογράμμου αἱ ἀπεναντίον πλευραί τε καὶ γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ ἡ ΒΓ διάμετρος αὐτὸ δίχα τέμνει.
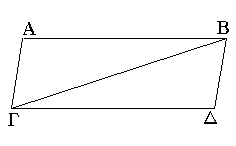
Ἐπεὶ γὰρ παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΒΓ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΑΒΓ, ΒΓΔ ἴσαι ἀλλήλαις εἰσίν. πάλιν, ἐπεὶ παράλληλός ἐστιν ἡ ΑΓ τῇ ΒΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΒΓ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΑΓΒ, ΓΒΔ ἴσαι ἀλλήλαις εἰσίν. δύο δὴ τρίγωνά ἐστι τὰ ΑΒΓ, ΒΓΔ τὰς δύο γωνίας τὰς ὑπὸ ΑΒΓ, ΒΓΑ δυσὶ ταῖς ὑπὸ ΒΓΔ, ΓΒΔ ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν πρὸς ταῖς ἴσαις γωνίαις κοινὴν αὐτῶν τὴν ΒΓ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς ἴσας ἕξει ἑκατέραν ἑκατέρᾳ καὶ τὴν λοιπὴν γωνίαν τῇ λοιπῇ γωνίᾳ· ἴση ἄρα ἡ μὲν ΑΒ πλευρὰ τῇ ΓΔ, ἡ δὲ ΑΓ τῇ ΒΔ, καὶ ἔτι ἴση ἐστὶν ἡ ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΓΔΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΒΓΔ, ἡ δὲ ὑπὸ ΓΒΔ τῇ ὑπὸ ΑΓΒ, ὅλη ἄρα ἡ ὑπὸ ΑΒΔ ὅλῃ τῇ ὑπὸ ΑΓΔ ἐστιν ἴση. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΓΔΒ ἴση.
Τῶν ἄρα παραλληλογράμμων χωρίων αἱ ἀπεναντίον πλευραί τε καὶ γωνίαι ἴσαι ἀλλήλαις εἰσίν.
Λέγω δή, ὅτι καὶ ἡ διάμετρος αὐτὰ δίχα τέμνει. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΑΒ τῇ ΓΔ, κοινὴ δὲ ἡ ΒΓ, δύο δὴ αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΓΔ, ΒΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΒΓΔ ἴση. καὶ βάσις ἄρα ἡ ΑΓ τῇ ΔΒ ἴση. καὶ τὸ ΑΒΓ [ἄρα] τρίγωνον τῷ ΒΓΔ τριγώνῳ ἴσον ἐστίν.
Ἡ ἄρα ΒΓ διάμετρος δίχα τέμνει τὸ ΑΒΓΔ παραλληλόγραμμον· ὅπερ ἔδει δεῖξαι.
Πρότασις λε΄ 35 Βιβλίον I
Τὰ παραλληλόγραμμα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν.
Ἔστω παραλληλόγραμμα τὰ ΑΒΓΔ, ΕΒΓΖ ἐπὶ τῆς αὐτῆς βάσεως τῆς ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΑΖ, ΒΓ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓΔ τῷ ΕΒΓΖ παραλληλογράμμῳ.
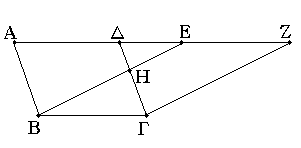
Ἐπεὶ γὰρ παραλληλόγραμμόν ἐστι τὸ ΑΒΓΔ, ἴση ἐστὶν ἡ ΑΔ τῇ ΒΓ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΕΖ τῇ ΒΓ ἐστιν ἴση· ὥστε καὶ ἡ ΑΔ τῇ ΕΖ ἐστιν ἴση· καὶ κοινὴ ἡ ΔΕ· ὅλη ἄρα ἡ ΑΕ ὅλῃ τῇ ΔΖ ἐστιν ἴση. ἔστι δὲ καὶ ἡ ΑΒ τῇ ΔΓ ἴση· δύο δὴ αἱ ΕΑ, ΑΒ δύο ταῖς ΖΔ, ΔΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΖΔΓ γωνίᾳ τῇ ὑπὸ ΕΑΒ ἐστιν ἴση ἡ ἐκτὸς τῇ ἐντός· βάσις ἄρα ἡ ΕΒ βάσει τῇ ΖΓ ἴση ἐστίν, καὶ τὸ ΕΑΒ τρίγωνον τῷ ΔΖΓ τριγώνῳ ἴσον ἔσται· κοινὸν ἀφῃρήσθω τὸ ΔΗΕ· λοιπὸν ἄρα τὸ ΑΒΗΔ τραπέζιον λοιπῷ τῷ ΕΗΓΖ τραπεζίῳ ἐστὶν ἴσον· κοινὸν προσκείσθω τὸ ΗΒΓ τρίγωνον· ὅλον ἄρα τὸ ΑΒΓΔ παραλληλόγραμμον ὅλῳ τῷ ΕΒΓΖ παραλληλογράμμῳ ἴσον ἐστίν.
Τὰ ἄρα παραλληλόγραμμα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον I
Τὰ παραλληλόγραμμα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν.
Ἔστω παραλληλόγραμμα τὰ ΑΒΓΔ, ΕΖΗΘ ἐπὶ ἴσων βάσεων ὄντα τῶν ΒΓ, ΖΗ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΑΘ, ΒΗ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓΔ παραλληλόγραμμον τῷ ΕΖΗΘ.
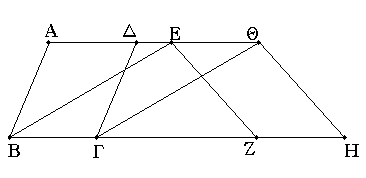
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΓΘ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΓ τῇ ΖΗ, ἀλλὰ ἡ ΖΗ τῇ ΕΘ ἐστιν ἴση, καὶ ἡ ΒΓ ἄρα τῇ ΕΘ ἐστιν ἴση. εἰσὶ δὲ καὶ παράλληλοι. καὶ ἐπιζευγνύουσιν αὐτὰς αἱ ΕΒ, ΘΓ· αἱ δὲ τὰς ἴσας τε καὶ παραλλήλους ἐπὶ τὰ αὐτὰ μέρη ἐπιζευγνύουσαι ἴσαι τε καὶ παράλληλοί εἰσι· [καὶ αἱ ΕΒ, ΘΓ ἄρα ἴσαι τέ εἰσι καὶ παράλληλοι]. παραλληλόγραμμον ἄρα ἐστὶ τὸ ΕΒΓΘ. καί ἐστιν ἴσον τῷ ΑΒΓΔ· βάσιν τε γὰρ αὐτῷ τὴν αὐτὴν ἔχει τὴν ΒΓ, καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστὶν αὐτῷ ταῖς ΒΓ, ΑΘ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΕΖΗΘ τῷ αὐτῷ τῷ ΕΒΓΘ ἐστιν ἴσον· ὥστε καὶ τὸ ΑΒΓΔ παραλληλόγραμμον τῷ ΕΖΗΘ ἐστιν ἴσον.
Τὰ ἄρα παραλληλόγραμμα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λζ΄ 37 Βιβλίον I
Τὰ τρίγωνα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν.
Ἔστω τρίγωνα τὰ ΑΒΓ, ΔΒΓ ἐπὶ τῆς αὐτῆς βάσεως τῆς ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΑΔ, ΒΓ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΒΓ τριγώνῳ.
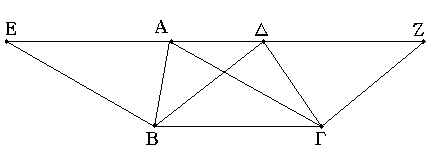
Ἐκβεβλήσθω ἡ ΑΔ ἐφ' ἑκάτερα τὰ μέρη ἐπὶ τὰ Ε, Ζ, καὶ διὰ μὲν τοῦ Β τῇ ΓΑ παράλληλος ἤχθω ἡ ΒΕ, διὰ δὲ τοῦ Γ τῇ ΒΔ παράλληλος ἤχθω ἡ ΓΖ. παραλληλόγραμμον ἄρα ἐστὶν ἑκάτερον τῶν ΕΒΓΑ, ΔΒΓΖ· καί εἰσιν ἴσα· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΓ, ΕΖ· καί ἐστι τοῦ μὲν ΕΒΓΑ παραλληλογράμμου ἥμισυ τὸ ΑΒΓ τρίγωνον· ἡ γὰρ ΑΒ διάμετρος αὐτὸ δίχα τέμνει· τοῦ δὲ ΔΒΓΖ παραλληλογράμμου ἥμισυ τὸ ΔΒΓ τρίγωνον· ἡ γὰρ ΔΓ διάμετρος αὐτὸ δίχα τέμνει. [τὰ δὲ τῶν ἴσων ἡμίση ἴσα ἀλλήλοις ἐστίν]. ἴσον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΒΓ τριγώνῳ.
Τὰ ἄρα τρίγωνα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λη΄ 38 Βιβλίον I
Τὰ τρίγωνα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν.
Ἔστω τρίγωνα τὰ ΑΒΓ, ΔΕΖ ἐπὶ ἴσων βάσεων τῶν ΒΓ, ΕΖ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΖ, ΑΔ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
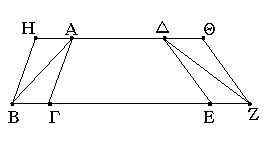
Ἐκβεβλήσθω γὰρ ἡ ΑΔ ἐφ' ἑκάτερα τὰ μέρη ἐπὶ τὰ Η, Θ, καὶ διὰ μὲν τοῦ Β τῇ ΓΑ παράλληλος ἤχθω ἡ ΒΗ, διὰ δὲ τοῦ Ζ τῇ ΔΕ παράλληλος ἤχθω ἡ ΖΘ. παραλληλόγραμμον ἄρα ἐστὶν ἑκάτερον τῶν ΗΒΓΑ, ΔΕΖΘ· καὶ ἴσον τὸ ΗΒΓΑ τῷ ΔΕΖΘ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΒΓ, ΕΖ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΖ, ΗΘ· καί ἐστι τοῦ μὲν ΗΒΓΑ παραλληλογράμμου ἥμισυ τὸ ΑΒΓ τρίγωνον. ἡ γὰρ ΑΒ διάμετρος αὐτὸ δίχα τέμνει· τοῦ δὲ ΔΕΖΘ παραλληλογράμμου ἥμισυ τὸ ΖΕΔ τρίγωνον· ἡ γὰρ ΔΖ διάμετρος αὐτὸ δίχα τέμνει· [τὰ δὲ τῶν ἴσων ἡμίση ἴσα ἀλλήλοις ἐστίν]. ἴσον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
Τὰ ἄρα τρίγωνα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λθ΄ 39 Βιβλίον I
Τὰ ἴσα τρίγωνα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐπὶ τὰ αὐτὰ μέρη καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν.
Ἔστω ἴσα τρίγωνα τὰ ΑΒΓ, ΔΒΓ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐπὶ τὰ αὐτὰ μέρη τῆς ΒΓ· λέγω, ὅτι καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν.
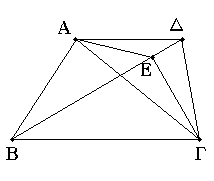
Ἐπεζεύχθω γὰρ ἡ ΑΔ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΔ τῇ ΒΓ.
Εἰ γὰρ μή, ἤχθω διὰ τοῦ Α σημείου τῇ ΒΓ εὐθείᾳ παράλληλος ἡ ΑΕ, καὶ ἐπεζεύχθω ἡ ΕΓ. ἴσον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΕΒΓ τριγώνῳ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς ἐστιν αὐτῷ τῆς ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις. ἀλλὰ τὸ ΑΒΓ τῷ ΔΒΓ ἐστιν ἴσον· καὶ τὸ ΔΒΓ ἄρα τῷ ΕΒΓ ἴσον ἐστὶ τὸ μεῖζον τῷ ἐλάσσονι· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα παράλληλός ἐστιν ἡ ΑΕ τῇ ΒΓ. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλη τις πλὴν τῆς ΑΔ· ἡ ΑΔ ἄρα τῇ ΒΓ ἐστι παράλληλος.
Τὰ ἄρα ἴσα τρίγωνα τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐπὶ τὰ αὐτὰ μέρη καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις μ΄ 40 Βιβλίον I
Τὰ ἴσα τρίγωνα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐπὶ τὰ αὐτὰ μέρη καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν.
Ἔστω ἴσα τρίγωνα τὰ ΑΒΓ, ΓΔΕ ἐπὶ ἴσων βάσεων τῶν ΒΓ, ΓΕ καὶ ἐπὶ τὰ αὐτὰ μέρη. λέγω, ὅτι καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν.
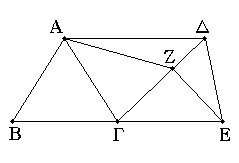
Ἐπεζεύχθω γὰρ ἡ ΑΔ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΔ τῇ ΒΕ.
Εἰ γὰρ μή, ἤχθω διὰ τοῦ Α τῇ ΒΕ παράλληλος ἡ ΑΖ, καὶ ἐπεζεύχθω ἡ ΖΕ. ἴσον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΖΓΕ τριγώνῳ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΒΓ, ΓΕ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΕ, ΑΖ. ἀλλὰ τὸ ΑΒΓ τρίγωνον ἴσον ἐστὶ τῷ ΔΓΕ [τριγώνῳ]· καὶ τὸ ΔΓΕ ἄρα [τρίγωνον] ἴσον ἐστὶ τῷ ΖΓΕ τριγώνῳ τὸ μεῖζον τῷ ἐλάσσονι· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα παράλληλος ἡ ΑΖ τῇ ΒΕ. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλη τις πλὴν τῆς ΑΔ· ἡ ΑΔ ἄρα τῇ ΒΕ ἐστι παράλληλος.
Τὰ ἄρα ἴσα τρίγωνα τὰ ἐπὶ ἴσων βάσεων ὄντα καὶ ἐπὶ τὰ αὐτὰ μέρη καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις μα΄ 41 Βιβλίον I
Ἐὰν παραλληλόγραμμον τριγώνῳ βάσιν τε ἔχῃ τὴν αὐτὴν καὶ ἐν ταῖς αὐταῖς παραλλήλοις ᾖ, διπλάσιόν ἐστι τὸ παραλληλόγραμμον τοῦ τριγώνου.
Παραλληλόγραμμον γὰρ τὸ ΑΒΓΔ τριγώνῳ τῷ ΕΒΓ βάσιν τε ἐχέτω τὴν αὐτὴν τὴν ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἔστω ταῖς ΒΓ, ΑΕ· λέγω, ὅτι διπλάσιόν ἐστι τὸ ΑΒΓΔ παραλληλόγραμμον τοῦ ΒΕΓ τριγώνου.
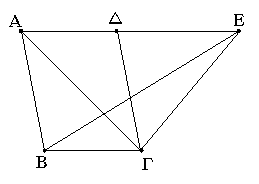
Ἐπεζεύχθω γὰρ ἡ ΑΓ. ἴσον δή ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΕΒΓ τριγώνῳ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς ἐστιν αὐτῷ τῆς ΒΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΓ, ΑΕ. ἀλλὰ τὸ ΑΒΓΔ παραλληλόγραμμον διπλάσιόν ἐστι τοῦ ΑΒΓ τριγώνου· ἡ γὰρ ΑΓ διάμετρος αὐτὸ δίχα τέμνει· ὥστε τὸ ΑΒΓΔ παραλληλόγραμμον καὶ τοῦ ΕΒΓ τριγώνου ἐστὶ διπλάσιον.
Ἐὰν ἄρα παραλληλόγραμμον τριγώνῳ βάσιν τε ἔχῃ τὴν αὐτὴν καὶ ἐν ταῖς αὐταῖς παραλλήλοις ᾖ, διπλάσιόν ἐστι τὸ παραλληλόγραμμον τοῦ τριγώνου· ὅπερ ἔδει δεῖξαι.
Πρότασις μβ΄ 42 Βιβλίον I
Τῷ δοθέντι τριγώνῳ ἴσον παραλληλόγραμμον συστήσασθαι ἐν τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ.
Ἔστω τὸ μὲν δοθὲν τρίγωνον τὸ ΑΒΓ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ Δ· δεῖ δὴ τῷ ΑΒΓ τριγώνῳ ἴσον παραλληλόγραμμον συστήσασθαι ἐν τῇ Δ γωνίᾳ εὐθυγράμμῳ.
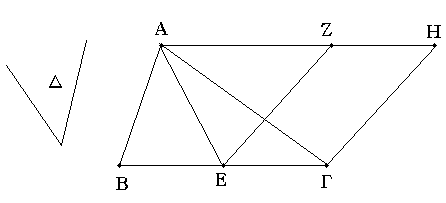
Τετμήσθω ἡ ΒΓ δίχα κατὰ τὸ Ε, καὶ ἐπεζεύχθω ἡ ΑΕ, καὶ συνεστάτω πρὸς τῇ ΕΓ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Ε τῇ Δ γωνίᾳ ἴση ἡ ὑπὸ ΓΕΖ, καὶ διὰ μὲν τοῦ Α τῇ ΕΓ παράλληλος ἤχθω ἡ ΑΗ, διὰ δὲ τοῦ Γ τῇ ΕΖ παράλληλος ἤχθω ἡ ΓΗ· παραλληλόγραμμον ἄρα ἐστὶ τὸ ΖΕΓΗ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΕΓ, ἴσον ἐστὶ καὶ τὸ ΑΒΕ τρίγωνον τῷ ΑΕΓ τριγώνῳ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΒΕ, ΕΓ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΒΓ, ΑΗ· διπλάσιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τοῦ ΑΕΓ τριγώνου. ἔστι δὲ καὶ τὸ ΖΕΓΗ παραλληλόγραμμον διπλάσιον τοῦ ΑΕΓ τριγώνου· βάσιν τε γὰρ αὐτῷ τὴν αὐτὴν ἔχει καὶ ἐν ταῖς αὐταῖς ἐστιν αὐτῷ παραλλήλοις· ἴσον ἄρα ἐστὶ τὸ ΖΕΓΗ παραλληλόγραμμον τῷ ΑΒΓ τριγώνῳ. καὶ ἔχει τὴν ὑπὸ ΓΕΖ γωνίαν ἴσην τῇ δοθείσῃ τῇ Δ.
Τῷ ἄρα δοθέντι τριγώνῳ τῷ ΑΒΓ ἴσον παραλληλόγραμμον συνέσταται τὸ ΖΕΓΗ ἐν γωνίᾳ τῇ ὑπὸ ΓΕΖ, ἥτις ἐστὶν ἴση τῇ Δ· ὅπερ ἔδει ποιῆσαι.
Πρότασις μγ΄ 43 Βιβλίον I
Παντὸς παραλληλογράμμου τῶν περὶ τὴν διάμετρον παραλληλογράμμων τὰ παραπληρώματα ἴσα ἀλλήλοις ἐστίν.
Ἔστω παραλληλόγραμμον τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ, περὶ δὲ τὴν ΑΓ παραλληλόγραμμα μὲν ἔστω τὰ ΖΘ, ΖΗ, τὰ δὲ λεγόμενα παραπληρώματα τὰ ΒΚ, ΚΔ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΒΚ παραπλήρωμα τῷ ΚΔ παραπληρώματι.
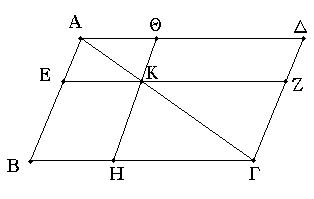
Ἐπεὶ γὰρ παραλληλόγραμμόν ἐστι τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ, ἴσον ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΑΓΔ τριγώνῳ. πάλιν, ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΕΘ, διάμετρος δὲ αὐτοῦ ἐστιν ἡ ΑΚ, ἴσον ἐστὶ τὸ ΑΕΚ τρίγωνον τῷ ΑΘΚ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΚΖΓ τρίγωνον τῷ ΚΗΓ ἐστιν ἴσον. ἐπεὶ οὖν τὸ μὲν ΑΕΚ τρίγωνον τῷ ΑΘΚ τριγώνῳ ἐστὶν ἴσον, τὸ δὲ ΚΖΓ τῷ ΚΗΓ, τὸ ΑΕΚ τρίγωνον μετὰ τοῦ ΚΗΓ ἴσον ἐστὶ τῷ ΑΘΚ τριγώνῳ μετὰ τοῦ ΚΖΓ· ἔστι δὲ καὶ ὅλον τὸ ΑΒΓ τρίγωνον ὅλῳ τῷ ΑΔΓ ἴσον· λοιπὸν ἄρα τὸ ΒΚ παραπλήρωμα λοιπῷ τῷ ΚΔ παραπληρώματί ἐστιν ἴσον.
Παντὸς ἄρα παραλληλογράμμου χωρίου τῶν περὶ τὴν διάμετρον παραλληλογράμμων τὰ παραπληρώματα ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις μδ΄ 44 Βιβλίον I
Παρὰ τὴν δοθεῖσαν εὐθεῖαν τῷ δοθέντι τριγώνῳ ἴσον παραλληλόγραμμον παραβαλεῖν ἐν τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν τρίγωνον τὸ Γ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ Δ· δεῖ δὴ παρὰ τὴν δοθεῖσαν εὐθεῖαν τὴν ΑΒ τῷ δοθέντι τριγώνῳ τῷ Γ ἴσον παραλληλόγραμμον παραβαλεῖν ἐν ἴσῃ τῇ Δ γωνίᾳ.
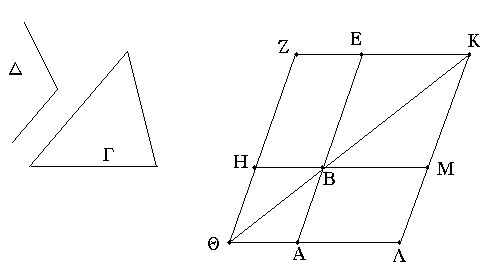
Συνεστάτω τῷ Γ τριγώνῳ ἴσον παραλληλόγραμμον τὸ ΒΕΖΗ ἐν γωνίᾳ τῇ ὑπὸ ΕΒΗ, ἥ ἐστιν ἴση τῇ Δ· καὶ κείσθω ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΒΕ τῇ ΑΒ, καὶ διήχθω ἡ ΖΗ ἐπὶ τὸ Θ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΒΗ, ΕΖ παράλληλος ἤχθω ἡ ΑΘ, καὶ ἐπεζεύχθω ἡ ΘΒ. καὶ ἐπεὶ εἰς παραλλήλους τὰς ΑΘ, ΕΖ εὐθεῖα ἐνέπεσεν ἡ ΘΖ, αἱ ἄρα ὑπὸ ΑΘΖ, ΘΖΕ γωνίαι δυσὶν ὀρθαῖς εἰσιν ἴσαι. αἱ ἄρα ὑπὸ ΒΘΗ, ΗΖΕ δύο ὀρθῶν ἐλάσσονές εἰσιν· αἱ δὲ ἀπὸ ἐλασσόνων ἢ δύο ὀρθῶν εἰς ἄπειρον ἐκβαλλόμεναι συμπίπτουσιν· αἱ ΘΒ, ΖΕ ἄρα ἐκβαλλόμεναι συμπεσοῦνται. ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν κατὰ τὸ Κ, καὶ διὰ τοῦ Κ σημείου ὁποτέρᾳ τῶν ΕΑ, ΖΘ παράλληλος ἤχθω ἡ ΚΛ, καὶ ἐκβεβλήσθωσαν αἱ ΘΑ, ΗΒ ἐπὶ τὰ Λ, Μ σημεῖα. παραλληλόγραμμον ἄρα ἐστὶ τὸ ΘΛΚΖ, διάμετρος δὲ αὐτοῦ ἡ ΘΚ, περὶ δὲ τὴν ΘΚ παραλληλόγραμμα μὲν τὰ ΑΗ, ΜΕ, τὰ δὲ λεγόμενα παραπληρώματα τὰ ΛΒ, ΒΖ· ἴσον ἄρα ἐστὶ τὸ ΛΒ τῷ ΒΖ. ἀλλὰ τὸ ΒΖ τῷ Γ τριγώνῳ ἐστὶν ἴσον· καὶ τὸ ΛΒ ἄρα τῷ Γ ἐστιν ἴσον. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΗΒΕ γωνία τῇ ὑπὸ ΑΒΜ, ἀλλὰ ἡ ὑπὸ ΗΒΕ τῇ Δ ἐστιν ἴση, καὶ ἡ ὑπὸ ΑΒΜ ἄρα τῇ Δ γωνίᾳ ἐστὶν ἴση.
Παρὰ τὴν δοθεῖσαν ἄρα εὐθεῖαν τὴν ΑΒ τῷ δοθέντι τριγώνῳ τῷ Γ ἴσον παραλληλόγραμμον παραβέβληται τὸ ΛΒ ἐν γωνίᾳ τῇ ὑπὸ ΑΒΜ, ἥ ἐστιν ἴση τῇ Δ· ὅπερ ἔδει ποιῆσαι.
Πρότασις με΄ 45 Βιβλίον I
Τῷ δοθέντι εὐθυγράμμῳ ἴσον παραλληλόγραμμον συστήσασθαι ἐν τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ.
Ἔστω τὸ μὲν δοθὲν εὐθύγραμμον τὸ ΑΒΓΔ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ Ε· δεῖ δὴ τῷ ΑΒΓΔ εὐθυγράμμῳ ἴσον παραλληλόγραμμον συστήσασθαι ἐν τῇ δοθείσῃ γωνίᾳ τῇ Ε.
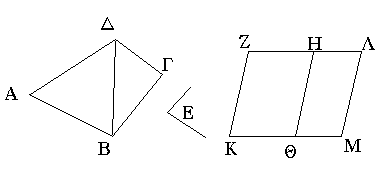
Ἐπεζεύχθω ἡ ΔΒ, καὶ συνεστάτω τῷ ΑΒΔ τριγώνῳ ἴσον παραλληλόγραμμον τὸ ΖΘ ἐν τῇ ὑπὸ ΘΚΖ γωνίᾳ, ἥ ἐστιν ἴση τῇ Ε· καὶ παραβεβλήσθω παρὰ τὴν ΗΘ εὐθεῖαν τῷ ΔΒΓ τριγώνῳ ἴσον παραλληλόγραμμον τὸ ΗΜ ἐν τῇ ὑπὸ ΗΘΜ γωνίᾳ, ἥ ἐστιν ἴση τῇ Ε. καὶ ἐπεὶ ἡ Ε γωνία ἑκατέρᾳ τῶν ὑπὸ ΘΚΖ, ΗΘΜ ἐστιν ἴση, καὶ ἡ ὑπὸ ΘΚΖ ἄρα τῇ ὑπὸ ΗΘΜ ἐστιν ἴση. κοινὴ προσκείσθω ἡ ὑπὸ ΚΘΗ· αἱ ἄρα ὑπὸ ΖΚΘ, ΚΘΗ ταῖς ὑπὸ ΚΘΗ, ΗΘΜ ἴσαι εἰσίν. ἀλλ' αἱ ὑπὸ ΖΚΘ, ΚΘΗ δυσὶν ὀρθαῖς ἴσαι εἰσίν· καὶ αἱ ὑπὸ ΚΘΗ, ΗΘΜ ἄρα δύο ὀρθαῖς ἴσαι εἰσίν. πρὸς δή τινι εὐθείᾳ τῇ ΗΘ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Θ δύο εὐθεῖαι αἱ ΚΘ, ΘΜ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δύο ὀρθαῖς ἴσας ποιοῦσιν· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΚΘ τῇ ΘΜ· καὶ ἐπεὶ εἰς παραλλήλους τὰς ΚΜ, ΖΗ εὐθεῖα ἐνέπεσεν ἡ ΘΗ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΜΘΗ, ΘΗΖ ἴσαι ἀλλήλαις εἰσίν. κοινὴ προσκείσθω ἡ ὑπὸ ΘΗΛ· αἱ ἄρα ὑπὸ ΜΘΗ, ΘΗΛ ταῖς ὑπὸ ΘΗΖ, ΘΗΛ ἴσαι εἰσίν. ἀλλ' αἱ ὑπὸ ΜΘΗ, ΘΗΛ δύο ὀρθαῖς ἴσαι εἰσίν· καὶ αἱ ὑπὸ ΘΗΖ, ΘΗΛ ἄρα δύο ὀρθαῖς ἴσαι εἰσίν· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΖΗ τῇ ΗΛ. καὶ ἐπεὶ ἡ ΖΚ τῇ ΘΗ ἴση τε καὶ παράλληλός ἐστιν, ἀλλὰ καὶ ἡ ΘΗ τῇ ΜΛ, καὶ ἡ ΚΖ ἄρα τῇ ΜΛ ἴση τε καὶ παράλληλός ἐστιν· καὶ ἐπιζευγνύουσιν αὐτὰς εὐθεῖαι αἱ ΚΜ, ΖΛ· καὶ αἱ ΚΜ, ΖΛ ἄρα ἴσαι τε καὶ παράλληλοί εἰσιν· παραλληλόγραμμον ἄρα ἐστὶ τὸ ΚΖΛΜ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ μὲν ΑΒΔ τρίγωνον τῷ ΖΘ παραλληλογράμμῳ, τὸ δὲ ΔΒΓ τῷ ΗΜ, ὅλον ἄρα τὸ ΑΒΓΔ εὐθύγραμμον ὅλῳ τῷ ΚΖΛΜ παραλληλογράμμῳ ἐστὶν ἴσον.
Τῷ ἄρα δοθέντι εὐθυγράμμῳ τῷ ΑΒΓΔ ἴσον παραλληλόγραμμον συνέσταται τὸ ΚΖΛΜ ἐν γωνίᾳ τῇ ὑπὸ ΖΚΜ, ἥ ἐστιν ἴση τῇ δοθείσῃ τῇ Ε· ὅπερ ἔδει ποιῆσαι.
Πρότασις μς΄ 46 Βιβλίον I
Ἀπὸ τῆς δοθείσης εὐθείας τετράγωνον ἀναγράψαι.
Ἔστω ἡ δοθεῖσα εὐθεῖα ἡ ΑΒ· δεῖ δὴ ἀπὸ τῆς ΑΒ εὐθείας τετράγωνον ἀναγράψαι.
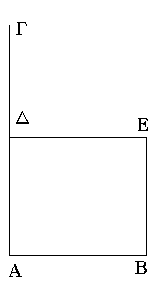
Ἤχθω τῇ ΑΒ εὐθείᾳ ἀπὸ τοῦ πρὸς αὐτῇ σημείου τοῦ Α πρὸς ὀρθὰς ἡ ΑΓ, καὶ κείσθω τῇ ΑΒ ἴση ἡ ΑΔ· καὶ διὰ μὲν τοῦ Δ σημείου τῇ ΑΒ παράλληλος ἤχθω ἡ ΔΕ, διὰ δὲ τοῦ Β σημείου τῇ ΑΔ παράλληλος ἤχθω ἡ ΒΕ. Παραλληλόγραμμον ἄρα ἐστὶ τὸ ΑΔΕΒ· ἴση ἄρα ἐστὶν ἡ μὲν ΑΒ τῇ ΔΕ, ἡ δὲ ΑΔ τῇ ΒΕ. ἀλλὰ ἡ ΑΒ τῇ ΑΔ ἐστιν ἴση· αἱ τέσσαρες ἄρα αἱ ΒΑ, ΑΔ, ΔΕ, ΕΒ ἴσαι ἀλλήλαις εἰσίν· ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΔΕΒ παραλληλόγραμμον. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ εἰς παραλλήλους τὰς ΑΒ, ΔΕ εὐθεῖα ἐνέπεσεν ἡ ΑΔ, αἱ ἄρα ὑπὸ ΒΑΔ, ΑΔΕ γωνίαι δύο ὀρθαῖς ἴσαι εἰσίν. ὀρθὴ δὲ ἡ ὑπὸ ΒΑΔ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΑΔΕ. τῶν δὲ παραλληλογράμμων χωρίων αἱ ἀπεναντίον πλευραί τε καὶ γωνίαι ἴσαι ἀλλήλαις εἰσίν· ὀρθὴ ἄρα καὶ ἑκατέρα τῶν ἀπεναντίον τῶν ὑπὸ ΑΒΕ, ΒΕΔ γωνιῶν· ὀρθογώνιον ἄρα ἐστὶ τὸ ΑΔΕΒ. ἐδείχθη δὲ καὶ ἰσόπλευρον.
Τετράγωνον ἄρα ἐστίν· καί ἐστιν ἀπὸ τῆς ΑΒ εὐθείας ἀναγεγραμμένον· ὅπερ ἔδει ποιῆσαι.
Πρότασις μζ΄ 47 Βιβλίον I
Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.
Ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν ὑπὸ ΒΑΓ γωνίαν· λέγω, ὅτι τὸ ἀπὸ τῆς ΒΓ τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ τετραγώνοις.
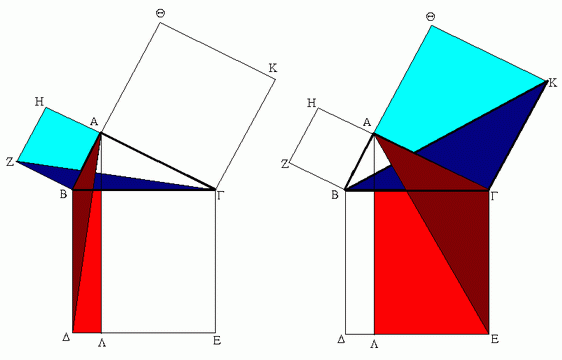
Ἀναγεγράφθω γὰρ ἀπὸ μὲν τῆς ΒΓ τετράγωνον τὸ ΒΔΕΓ, ἀπὸ δὲ τῶν ΒΑ, ΑΓ τὰ ΗΒ, ΘΓ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΒΔ, ΓΕ παράλληλος ἤχθω ἡ ΑΛ· καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΖΓ. καὶ ἐπεὶ ὀρθή ἐστιν ἑκατέρα τῶν ὑπὸ ΒΑΓ, ΒΑΗ γωνιῶν, πρὸς δή τινι εὐθείᾳ τῇ ΒΑ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α δύο εὐθεῖαι αἱ ΑΓ, ΑΗ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιοῦσιν· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΓΑ τῇ ΑΗ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΒΑ τῇ ΑΘ ἐστιν ἐπ᾿ εὐθείας. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΒΓ γωνία τῇ ὑπὸ ΖΒΑ· ὀρθὴ γὰρ ἑκατέρα· κοινὴ προσκείσθω ἡ ὑπὸ ΑΒΓ· ὅλη ἄρα ἡ ὑπὸ ΔΒΑ ὅλῃ τῇ ὑπὸ ΖΒΓ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΔΒ τῇ ΒΓ, ἡ δὲ ΖΒ τῇ ΒΑ, δύο δὴ αἱ ΔΒ, ΒΑ δύο ταῖς ΖΒ, ΒΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΔΒΑ γωνίᾳ τῇ ὑπὸ ΖΒΓ ἴση· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΖΓ [ἐστιν] ἴση, καὶ τὸ ΑΒΔ τρίγωνον τῷ ΖΒΓ τριγώνῳ ἐστὶν ἴσον· καὶ [ἐστὶ] τοῦ μὲν ΑΒΔ τριγώνου διπλάσιον τὸ ΒΛ παραλληλόγραμμον· βάσιν τε γὰρ τὴν αὐτὴν ἔχουσι τὴν ΒΔ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΒΔ, ΑΛ· τοῦ δὲ ΖΒΓ τριγώνου διπλάσιον τὸ ΗΒ τετράγωνον· βάσιν τε γὰρ πάλιν τὴν αὐτὴν ἔχουσι τὴν ΖΒ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΖΒ, ΗΓ. [τὰ δὲ τῶν ἴσων διπλάσια ἴσα ἀλλήλοις ἐστίν·] ἴσον ἄρα ἐστὶ καὶ τὸ ΒΛ παραλληλόγραμμον τῷ ΗΒ τετραγώνῳ. ὁμοίως δὴ ἐπιζευγνυμένων τῶν ΑΕ, ΒΚ δειχθήσεται καὶ τὸ ΓΛ παραλληλόγραμμον ἴσον τῷ ΘΓ τετραγώνῳ· ὅλον ἄρα τὸ ΒΔΕΓ τετράγωνον δυσὶ τοῖς ΗΒ, ΘΓ τετραγώνοις ἴσον ἐστίν. καί ἐστι τὸ μὲν ΒΔΕΓ τετράγωνον ἀπὸ τῆς ΒΓ ἀναγραφέν, τὰ δὲ ΗΒ, ΘΓ ἀπὸ τῶν ΒΑ, ΑΓ. τὸ ἄρα ἀπὸ τῆς ΒΓ πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ πλευρῶν τετραγώνοις.
Ἐν ἄρα τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν [γωνίαν] περιεχουσῶν πλευρῶν τετραγώνοις· ὅπερ ἔδει δεῖξαι.
Πρότασις μη΄ 48 Βιβλίον I
Ἐὰν τριγώνου τὸ ἀπὸ μιᾶς τῶν πλευρῶν τετράγωνον ἴσον ᾖ τοῖς ἀπὸ τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν τετραγώνοις, ἡ περιεχομένη γωνία ὑπὸ τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν ὀρθή ἐστιν.
Τριγώνου γὰρ τοῦ ΑΒΓ τὸ ἀπὸ μιᾶς τῆς ΒΓ πλευρᾶς τετράγωνον ἴσον ἔστω τοῖς ἀπὸ τῶν ΒΑ, ΑΓ πλευρῶν τετραγώνοις· λέγω, ὅτι ὀρθή ἐστιν ἡ ὑπὸ ΒΑΓ γωνία.
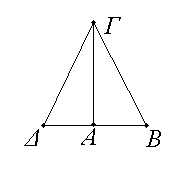
Ἤχθω γὰρ ἀπὸ τοῦ Α σημείου τῇ ΑΓ εὐθείᾳ πρὸς ὀρθὰς ἡ ΑΔ καὶ κείσθω τῇ ΒΑ ἴση ἡ ΑΔ, καὶ ἐπεζεύχθω ἡ ΔΓ. ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΑΒ, ἴσον ἐστὶ καὶ τὸ ἀπὸ τῆς ΔΑ τετράγωνον τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ. κοινὸν προσκείσθω τὸ ἀπὸ τῆς ΑΓ τετράγωνον· τὰ ἄρα ἀπὸ τῶν ΔΑ, ΑΓ τετράγωνα ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ τετραγώνοις. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΔΑ, ΑΓ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΔΓ· ὀρθὴ γάρ ἐστιν ἡ ὑπὸ ΔΑΓ γωνία· τοῖς δὲ ἀπὸ τῶν ΒΑ, ΑΓ ἴσον ἐστὶ τὸ ἀπὸ ΒΓ· ὑπόκειται γάρ· τὸ ἄρα ἀπὸ τῆς ΔΓ τετράγωνον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΒΓ τετραγώνῳ· ὥστε καὶ πλευρὰ ἡ ΔΓ τῇ ΒΓ ἐστιν ἴση· καὶ ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΑΒ, κοινὴ δὲ ἡ ΑΓ, δύο δὴ αἱ ΔΑ, ΑΓ δύο ταῖς ΒΑ, ΑΓ ἴσαι εἰσίν· καὶ βάσις ἡ ΔΓ βάσει τῇ ΒΓ ἴση· γωνία ἄρα ἡ ὑπὸ ΔΑΓ γωνίᾳ τῇ ὑπὸ ΒΑΓ [ἐστιν] ἴση. ὀρθὴ δὲ ἡ ὑπὸ ΔΑΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΒΑΓ.
Ἐὰν ἄρα τριγώνου τὸ ἀπὸ μιᾶς τῶν πλευρῶν τετράγωνον ἴσον ᾖ τοῖς ἀπὸ τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν τετραγώνοις, ἡ περιεχομένη γωνία ὑπὸ τῶν λοιπῶν τοῦ τριγώνου δύο πλευρῶν ὀρθή ἐστιν· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου β΄
Βιβλίον II
Ὅροι b΄ 2.
α΄ 1. Πᾶν παραλληλόγραμμον ὀρθογώνιον περιέχεσθαι λέγεται ὑπὸ δύο τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν εὐθειῶν.
β΄ 2. Παντὸς δὲ παραλληλογράμμου χωρίου τῶν περὶ τὴν διάμετρον αὐτοῦ παραλληλογράμμων ἓν ὁποιονοῦν σὺν τοῖς δυσὶ παραπληρώμασι γνώμων καλείσθω.
Προτάσεις ιδ΄ 14 Βιβλίον II
Πρότασις α΄ 1 Βιβλίον II
Ἐὰν ὦσι δύο εὐθεῖαι, τμηθῇ δὲ ἡ ἑτέρα αὐτῶν εἰς ὁσαδηποτοῦν τμήματα, τὸ περιεχόμενον ὀρθογώνιον ὑπὸ τῶν δύο εὐθειῶν ἴσον ἐστὶ τοῖς ὑπό τε τῆς ἀτμήτου καὶ ἑκάστου τῶν τμημάτων περιεχομένοις ὀρθογωνίοις.
Ἔστωσαν δύο εὐθεῖαι αἱ Α, ΒΓ, καὶ τετμήσθω ἡ ΒΓ, ὡς ἔτυχεν, κατὰ τὰ Δ, Ε σημεῖα· λέγω, ὅτι τὸ ὑπὸ τῶν Α, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν Α, ΒΔ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ὑπὸ τῶν Α, ΔΕ καὶ ἔτι τῷ ὑπὸ τῶν Α, ΕΓ.
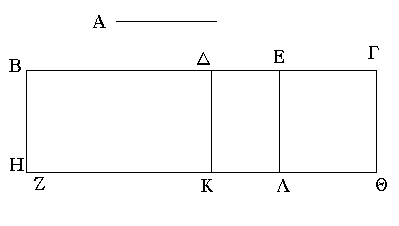
Ἤχθω γὰρ ἀπὸ τοῦ Β τῇ ΒΓ πρὸς ὀρθὰς ἡ ΒΖ, καὶ κείσθω τῇ Α ἴση ἡ ΒΗ, καὶ διὰ μὲν τοῦ Η τῇ ΒΓ παράλληλος ἤχθω ἡ ΗΘ, διὰ δὲ τῶν Δ, Ε, Γ τῇ ΒΗ παράλληλοι ἤχθωσαν αἱ ΔΚ, ΕΛ, ΓΘ.
Ἴσον δή ἐστι τὸ ΒΘ τοῖς ΒΚ, ΔΛ, ΕΘ. καί ἐστι τὸ μὲν ΒΘ τὸ ὑπὸ τῶν Α, ΒΓ· περιέχεται μὲν γὰρ ὑπὸ τῶν ΗΒ, ΒΓ, ἴση δὲ ἡ ΒΗ τῇ Α· τὸ δὲ ΒΚ τὸ ὑπὸ τῶν Α, ΒΔ· περιέχεται μὲν γὰρ ὑπὸ τῶν ΗΒ, ΒΔ, ἴση δὲ ἡ ΒΗ τῇ Α. τὸ δὲ ΔΛ τὸ ὑπὸ τῶν Α, ΔΕ· ἴση γὰρ ἡ ΔΚ, τουτέστιν ἡ ΒΗ, τῇ Α. καὶ ἔτι ὁμοίως τὸ ΕΘ τὸ ὑπὸ τῶν Α, ΕΓ· τὸ ἄρα ὑπὸ τῶν Α, ΒΓ ἴσον ἐστὶ τῷ τε ὑπὸ Α, ΒΔ καὶ τῷ ὑπὸ Α, ΔΕ καὶ ἔτι τῷ ὑπὸ Α, ΕΓ.
Ἐὰν ἄρα ὦσι δύο εὐθεῖαι, τμηθῇ δὲ ἡ ἑτέρα αὐτῶν εἰς ὁσαδηποτοῦν τμήματα, τὸ περιεχόμενον ὀρθογώνιον ὑπὸ τῶν δύο εὐθειῶν ἴσον ἐστὶ τοῖς ὑπό τε τῆς ἀτμήτου καὶ ἑκάστου τῶν τμημάτων περιεχομένοις ὀρθογωνίοις· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑκατέρου τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς ὅλης τετραγώνῳ.
Εὐθεῖα γὰρ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ σημεῖον· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ὑπὸ ΒΑ, ΑΓ περιεχομένου ὀρθογωνίου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ.
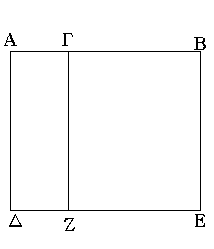
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ, καὶ ἤχθω διὰ τοῦ Γ ὁποτέρᾳ τῶν ΑΔ, ΒΕ παράλληλος ἡ ΓΖ.
Ἴσον δή ἐστι τὸ ΑΕ τοῖς ΑΖ, ΓΕ. καί ἐστι τὸ μὲν ΑΕ τὸ ἀπὸ τῆς ΑΒ τετράγωνον, τὸ δὲ ΑΖ τὸ ὑπὸ τῶν ΒΑ, ΑΓ περιεχόμενον ὀρθογώνιον· περιέχεται μὲν γὰρ ὑπὸ τῶν ΔΑ, ΑΓ, ἴση δὲ ἡ ΑΔ τῇ ΑΒ· τὸ δὲ ΓΕ τὸ ὑπὸ τῶν ΑΒ, ΒΓ· ἴση γὰρ ἡ ΒΕ τῇ ΑΒ. τὸ ἄρα ὑπὸ τῶν ΒΑ, ΑΓ μετὰ τοῦ ὑπὸ τῶν ΑΒ, ΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑκατέρου τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς ὅλης τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ προειρημένου τμήματος τετραγώνῳ.
Εὐθεῖα γὰρ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΒΓ τετραγώνου.
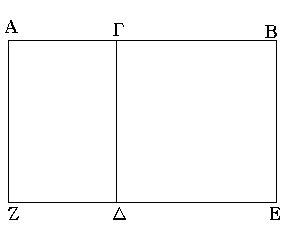
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΒ τετράγωνον τὸ ΓΔΕΒ, καὶ διήχθω ἡ ΕΔ ἐπὶ τὸ Ζ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΔ, ΒΕ παράλληλος ἤχθω ἡ ΑΖ. ἴσον δή ἐστι τὸ ΑΕ τοῖς ΑΔ, ΓΕ· καί ἐστι τὸ μὲν ΑΕ τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον· περιέχεται μὲν γὰρ ὑπὸ τῶν ΑΒ, ΒΕ, ἴση δὲ ἡ ΒΕ τῇ ΒΓ· τὸ δὲ ΑΔ τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴση γὰρ ἡ ΔΓ τῇ ΓΒ· τὸ δὲ ΔΒ τὸ ἀπὸ τῆς ΓΒ τετράγωνον· τὸ ἄρα ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΒΓ τετραγώνου.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ προειρημένου τμήματος τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ.
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ. λέγω, ὅτι τὸ ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ.
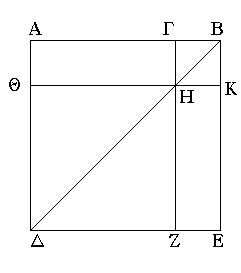
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ, καὶ ἐπεζεύχθω ἡ ΒΔ, καὶ διὰ μὲν τοῦ Γ ὁποτέρᾳ τῶν ΑΔ, ΕΒ παράλληλος ἤχθω ἡ ΓΖ, διὰ δὲ τοῦ Η ὁποτέρᾳ τῶν ΑΒ, ΔΕ παράλληλος ἤχθω ἡ ΘΚ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΓΖ τῇ ΑΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΒΔ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΓΗΒ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΑΔΒ. ἀλλ' ἡ ὑπὸ ΑΔΒ τῇ ὑπὸ ΑΒΔ ἐστιν ἴση, ἐπεὶ καὶ πλευρὰ ἡ ΒΑ τῇ ΑΔ ἐστιν ἴση· καὶ ἡ ὑπὸ ΓΗΒ ἄρα γωνία τῇ ὑπὸ ΗΒΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΒΓ πλευρᾷ τῇ ΓΗ ἐστιν ἴση· ἀλλ' ἡ μὲν ΓΒ τῇ ΗΚ ἐστιν ἴση, ἡ δὲ ΓΗ τῇ ΚΒ· καὶ ἡ ΗΚ ἄρα τῇ ΚΒ ἐστιν ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΓΗΚΒ. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ παράλληλός ἐστιν ἡ ΓΗ τῇ ΒΚ [καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΓΒ], αἱ ἄρα ὑπὸ ΚΒΓ, ΗΓΒ γωνίαι δύο ὀρθαῖς εἰσιν ἴσαι. ὀρθὴ δὲ ἡ ὑπὸ ΚΒΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΒΓΗ· ὥστε καὶ αἱ ἀπεναντίον αἱ ὑπὸ ΓΗΚ, ΗΚΒ ὀρθαί εἰσιν. ὀρθογώνιον ἄρα ἐστὶ τὸ ΓΗΚΒ· ἐδείχθη δὲ καὶ ἰσόπλευρον· τετράγωνον ἄρα ἐστίν· καί ἐστιν ἀπὸ τῆς ΓΒ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΘΖ τετράγωνόν ἐστιν· καί ἐστιν ἀπὸ τῆς ΘΗ, τουτέστιν [ἀπὸ] τῆς ΑΓ· τὰ ἄρα ΘΖ, ΚΓ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ εἰσιν. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, καί ἐστι τὸ ΑΗ τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴση γὰρ ἡ ΗΓ τῇ ΓΒ· καὶ τὸ ΗΕ ἄρα ἴσον ἐστὶ τῷ ὑπὸ ΑΓ, ΓΒ· τὰ ἄρα ΑΗ, ΗΕ ἴσα ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. ἔστι δὲ καὶ τὰ ΘΖ, ΓΚ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ· τὰ ἄρα τέσσαρα τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ἴσα ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ. ἀλλὰ τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ὅλον ἐστὶ τὸ ΑΔΕΒ, ὅ ἐστιν ἀπὸ τῆς ΑΒ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω εἰς μὲν ἴσα κατὰ τὸ Γ, εἰς δὲ ἄνισα κατὰ τὸ Δ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ.
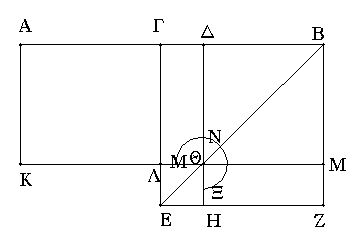
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΒ τετράγωνον τὸ ΓΕΖΒ, καὶ ἐπεζεύχθω ἡ ΒΕ, καὶ διὰ μὲν τοῦ Δ ὁποτέρᾳ τῶν ΓΕ, ΒΖ παράλληλος ἤχθω ἡ ΔΗ, διὰ δὲ τοῦ Θ ὁποτέρᾳ τῶν ΑΒ, ΕΖ παράλληλος πάλιν ἤχθω ἡ ΚΜ, καὶ πάλιν διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΛ, ΒΜ παράλληλος ἤχθω ἡ ΑΚ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΓΘ παραπλήρωμα τῷ ΘΖ παραπληρώματι, κοινὸν προσκείσθω τὸ ΔΜ· ὅλον ἄρα τὸ ΓΜ ὅλῳ τῷ ΔΖ ἴσον ἐστίν. ἀλλὰ τὸ ΓΜ τῷ ΑΛ ἴσον ἐστίν, ἐπεὶ καὶ ἡ ΑΓ τῇ ΓΒ ἐστιν ἴση· καὶ τὸ ΑΛ ἄρα τῷ ΔΖ ἴσον ἐστίν. κοινὸν προσκείσθω τὸ ΓΘ· ὅλον ἄρα τὸ ΑΘ τῷ ΜΝΞ γνώμονι ἴσον ἐστίν. ἀλλὰ τὸ ΑΘ τὸ ὑπὸ τῶν ΑΔ, ΔΒ ἐστιν· ἴση γὰρ ἡ ΔΘ τῇ ΔΒ· καὶ ὁ ΜΝΞ ἄρα γνώμων ἴσος ἐστὶ τῷ ὑπὸ ΑΔ, ΔΒ. κοινὸν προσκείσθω τὸ ΛΗ, ὅ ἐστιν ἴσον τῷ ἀπὸ τῆς ΓΔ· ὁ ἄρα ΜΝΞ γνώμων καὶ τὸ ΛΗ ἴσα ἐστὶ τῷ ὑπὸ τῶν ΑΔ, ΔΒ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΔ τετραγώνῳ. ἀλλὰ ὁ ΜΝΞ γνώμων καὶ τὸ ΛΗ ὅλον ἐστὶ τὸ ΓΕΖΒ τετράγωνον, ὅ ἐστιν ἀπὸ τῆς ΓΒ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ δίχα, προστεθῇ δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας, τὸ ὑπὸ τῆς ὅλης σὺν τῇ προσκειμένῃ καὶ τῆς προσκειμένης περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ἡμισείας τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς συγκειμένης ἔκ τε τῆς ἡμισείας καὶ τῆς προσκειμένης τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω δίχα κατὰ τὸ Γ σημεῖον, προσκείσθω δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας ἡ ΒΔ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΒ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΔ τετραγώνῳ.
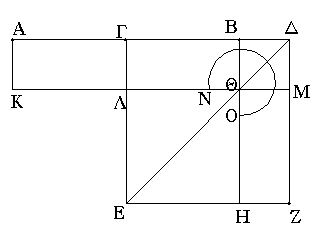
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΔ τετράγωνον τὸ ΓΕΖΔ, καὶ ἐπεζεύχθω ἡ ΔΕ, καὶ διὰ μὲν τοῦ Β σημείου ὁποτέρᾳ τῶν ΕΓ, ΔΖ παράλληλος ἤχθω ἡ ΒΗ, διὰ δὲ τοῦ Θ σημείου ὁποτέρᾳ τῶν ΑΒ, ΕΖ παράλληλος ἤχθω ἡ ΚΜ, καὶ ἔτι διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΛ, ΔΜ παράλληλος ἤχθω ἡ ΑΚ.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, ἴσον ἐστὶ καὶ τὸ ΑΛ τῷ ΓΘ. ἀλλὰ τὸ ΓΘ τῷ ΘΖ ἴσον ἐστίν. καὶ τὸ ΑΛ ἄρα τῷ ΘΖ ἐστιν ἴσον. κοινὸν προσκείσθω τὸ ΓΜ· ὅλον ἄρα τὸ ΑΜ τῷ ΝΞΟ γνώμονί ἐστιν ἴσον. ἀλλὰ τὸ ΑΜ ἐστι τὸ ὑπὸ τῶν ΑΔ, ΔΒ· ἴση γάρ ἐστιν ἡ ΔΜ τῇ ΔΒ· καὶ ὁ ΝΞΟ ἄρα γνώμων ἴσος ἐστὶ τῷ ὑπὸ τῶν ΑΔ, ΔΒ [περιεχομένῳ ὀρθογωνίῳ]. κοινὸν προσκείσθω τὸ ΛΗ, ὅ ἐστιν ἴσον τῷ ἀπὸ τῆς ΒΓ τετραγώνῳ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΒ τετραγώνου ἴσον ἐστὶ τῷ ΝΞΟ γνώμονι καὶ τῷ ΛΗ. ἀλλὰ ὁ ΝΞΟ γνώμων καὶ τὸ ΛΗ ὅλον ἐστὶ τὸ ΓΕΖΔ τετράγωνον, ὅ ἐστιν ἀπὸ τῆς ΓΔ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΒ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΔ τετραγώνῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ δίχα, προστεθῇ δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας, τὸ ὑπὸ τῆς ὅλης σὺν τῇ προσκειμένῃ καὶ τῆς προσκειμένης περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ἡμισείας τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς συγκειμένης ἔκ τε τῆς ἡμισείας καὶ τῆς προσκειμένης τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ' ἑνὸς τῶν τμημάτων τὰ συναμφότερα τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ σημεῖον· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΑ τετραγώνῳ.
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ· καὶ καταγεγράφθω τὸ σχῆμα.
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, κοινὸν προσκείσθω τὸ ΓΖ· ὅλον ἄρα τὸ ΑΖ ὅλῳ τῷ ΓΕ ἴσον ἐστίν· τὰ ἄρα ΑΖ, ΓΕ διπλάσιά ἐστι τοῦ ΑΖ. ἀλλὰ τὰ ΑΖ, ΓΕ ὁ ΚΛΜ ἐστι γνώμων καὶ τὸ ΓΖ τετράγωνον· ὁ ΚΛΜ ἄρα γνώμων καὶ τὸ ΓΖ διπλάσιά ἐστι τοῦ ΑΖ. ἔστι δὲ τοῦ ΑΖ διπλάσιον καὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἴση γὰρ ἡ ΒΖ τῇ ΒΓ· ὁ ἄρα ΚΛΜ γνώμων καὶ τὸ ΓΖ τετράγωνον ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. κοινὸν προσκείσθω τὸ ΔΗ, ὅ ἐστιν ἀπὸ τῆς ΑΓ τετράγωνον· ὁ ἄρα ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΑΓ τετραγώνῳ. ἀλλὰ ὁ ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ὅλον ἐστὶ τὸ ΑΔΕΒ καὶ τὸ ΓΖ, ἅ ἐστιν ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα· τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ [τε] δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΑΓ τετραγώνου.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ' ἑνὸς τῶν τμημάτων τὰ συναμφότερα τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον II
Ἐὰν εὐθεῖα γραμμή τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ' ἑνὸς τῶν τμημάτων τὰ συναμφότερα τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ σημεῖον· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενα ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΑ τετραγώνῳ. Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ· καὶ καταγεγράφθω τὸ σχῆμα.
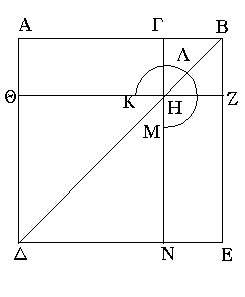
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, κοινὸν προσκείσθω τὸ ΓΖ· ὅλον ἄρα τὸ ΑΖ ὅλῳ τῷ ΓΕ ἴσον ἐστίν· τὰ ἄρα ΑΖ, ΓΕ διπλάσιά ἐστι τοῦ ΑΖ. ἀλλὰ τὰ ΑΖ, ΓΕ ὁ ΚΛΜ ἐστι γνώμων καὶ τὸ ΓΖ τετράγωνον· ὁ ΚΛΜ ἄρα γνώμων καὶ τὸ ΓΖ διπλάσιά ἐστι τοῦ ΑΖ. ἔστι δὲ τοῦ ΑΖ διπλάσιον καὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἴση γὰρ ἡ ΒΖ τῇ ΒΓ· ὁ ἄρα ΚΛΜ γνώμων καὶ τὸ ΓΖ τετράγωνον ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. κοινὸν προσκείσθω τὸ ΔΗ, ὅ ἐστιν ἀπὸ τῆς ΑΓ τετράγωνον· ὁ ἄρα ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΑΓ τετραγώνῳ. ἀλλὰ ὁ ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ὅλον ἐστὶ τὸ ΑΔΕΒ καὶ τὸ ΓΖ, ἅ ἐστιν ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα· τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ [τε] δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΑΓ τετραγώνου.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ’ ἑνὸς τῶν τμημάτων τὰ συναμφότερα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένω ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῷ· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ τετράκις ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνου ἴσον ἐστὶ τῷ ἀπό τε τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος ὡς ἀπὸ μιᾶς ἀναγραφέντι τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ σημεῖον· λέγω, ὅτι τὸ τετράκις ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΑΓ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ, ΒΓ ὡς ἀπὸ μιᾶς ἀναγραφέντι τετραγώνῳ.
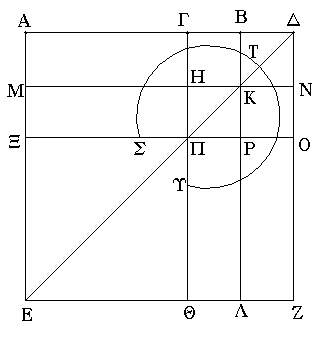
Ἐκβεβλήσθω γὰρ ἐπ᾿ εὐθείας [τῇ ΑΒ εὐθεῖα] ἡ ΒΔ, καὶ κείσθω τῇ ΓΒ ἴση ἡ ΒΔ, καὶ ἀναγεγράφθω ἀπὸ τῆς ΑΔ τετράγωνον τὸ ΑΕΖΔ, καὶ καταγεγράφθω διπλοῦν τὸ σχῆμα.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΓΒ τῇ ΒΔ, ἀλλὰ ἡ μὲν ΓΒ τῇ ΗΚ ἐστιν ἴση, ἡ δὲ ΒΔ τῇ ΚΝ, καὶ ἡ ΗΚ ἄρα τῇ ΚΝ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΠΡ τῇ ΡΟ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΓ τῇ ΒΔ, ἡ δὲ ΗΚ τῇ ΚΝ, ἴσον ἄρα ἐστὶ καὶ τὸ μὲν ΓΚ τῷ ΚΔ, τὸ δὲ ΗΡ τῷ ΡΝ. ἀλλὰ τὸ ΓΚ τῷ ΡΝ ἐστιν ἴσον· παραπληρώματα γὰρ τοῦ ΓΟ παραλληλογράμμου· καὶ τὸ ΚΔ ἄρα τῷ ΗΡ ἴσον ἐστίν· τὰ τέσσαρα ἄρα τὰ ΔΚ, ΓΚ, ΗΡ, ΡΝ ἴσα ἀλλήλοις ἐστίν. τὰ τέσσαρα ἄρα τετραπλάσιά ἐστι τοῦ ΓΚ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΓΒ τῇ ΒΔ, ἀλλὰ ἡ μὲν ΒΔ τῇ ΒΚ, τουτέστι τῇ ΓΗ ἴση, ἡ δὲ ΓΒ τῇ ΗΚ, τουτέστι τῇ ΗΠ, ἐστιν ἴση, καὶ ἡ ΓΗ ἄρα τῇ ΗΠ ἴση ἐστίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΓΗ τῇ ΗΠ, ἡ δὲ ΠΡ τῇ ΡΟ, ἴσον ἐστὶ καὶ τὸ μὲν ΑΗ τῷ ΜΠ, τὸ δὲ ΠΛ τῷ ΡΖ. ἀλλὰ τὸ ΜΠ τῷ ΠΛ ἐστιν ἴσον· παραπληρώματα γὰρ τοῦ ΜΛ παραλληλογράμμου· καὶ τὸ ΑΗ ἄρα τῷ ΡΖ ἴσον ἐστίν· τὰ τέσσαρα ἄρα τὰ ΑΗ, ΜΠ, ΠΛ, ΡΖ ἴσα ἀλλήλοις ἐστίν· τὰ τέσσαρα ἄρα τοῦ ΑΗ ἐστι τετραπλάσια. ἐδείχθη δὲ καὶ τὰ τέσσαρα τὰ ΓΚ, ΚΔ, ΗΡ, ΡΝ τοῦ ΓΚ τετραπλάσια· τὰ ἄρα ὀκτώ, ἃ περιέχει τὸν ΣΤΥ γνώμονα, τετραπλάσιά ἐστι τοῦ ΑΚ. καὶ ἐπεὶ τὸ ΑΚ τὸ ὑπὸ τῶν ΑΒ, ΒΔ ἐστιν· ἴση γὰρ ἡ ΒΚ τῇ ΒΔ· τὸ ἄρα τετράκις ὑπὸ τῶν ΑΒ, ΒΔ τετραπλάσιόν ἐστι τοῦ ΑΚ. ἐδείχθη δὲ τοῦ ΑΚ τετραπλάσιος καὶ ὁ ΣΤΥ γνώμων· τὸ ἄρα τετράκις ὑπὸ τῶν ΑΒ, ΒΔ ἴσον ἐστὶ τῷ ΣΤΥ γνώμονι. κοινὸν προσκείσθω τὸ ΞΘ, ὅ ἐστιν ἴσον τῷ ἀπὸ τῆς ΑΓ τετραγώνῳ· τὸ ἄρα τετράκις ὑπὸ τῶν ΑΒ, ΒΔ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ ΑΓ τετραγώνου ἴσον ἐστὶ τῷ ΣΤΥ γνώμονι καὶ τῷ ΞΘ. ἀλλὰ ὁ ΣΤΥ γνώμων καὶ τὸ ΞΘ ὅλον ἐστὶ τὸ ΑΕΖΔ τετράγωνον, ὅ ἐστιν ἀπὸ τῆς ΑΔ· τὸ ἄρα τετράκις ὑπὸ τῶν ΑΒ, ΒΔ μετὰ τοῦ ἀπὸ ΑΓ ἴσον ἐστὶ τῷ ἀπὸ ΑΔ τετραγώνῳ· ἴση δὲ ἡ ΒΔ τῇ ΒΓ. τὸ ἄρα τετράκις ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ ΑΓ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΔ, τουτέστι τῷ ἀπὸ τῆς ΑΒ καὶ ΒΓ ὡς ἀπὸ μιᾶς ἀναγραφέντι τετραγώνῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ τετράκις ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνου ἴσον ἐστὶ τῷ ἀπό τε τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος ὡς ἀπὸ μιᾶς ἀναγραφέντι τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὰ ἀπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω εἰς μὲν ἴσα κατὰ τὸ Γ, εἰς δὲ ἄνισα κατὰ τὸ Δ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
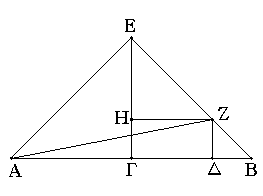
Ἤχθω γὰρ ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΕ, καὶ κείσθω ἴση ἑκατέρᾳ τῶν ΑΓ, ΓΒ, καὶ ἐπεζεύχθωσαν αἱ ΕΑ, ΕΒ, καὶ διὰ μὲν τοῦ Δ τῇ ΕΓ παράλληλος ἤχθω ἡ ΔΖ, διὰ δὲ τοῦ Ζ τῇ ΑΒ ἡ ΖΗ, καὶ ἐπεζεύχθω ἡ ΑΖ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΕ, ἴση ἐστὶ καὶ ἡ ὑπὸ ΕΑΓ γωνία τῇ ὑπὸ ΑΕΓ. καὶ ἐπεὶ ὀρθή ἐστιν ἡ πρὸς τῷ Γ, λοιπαὶ ἄρα αἱ ὑπὸ ΕΑΓ, ΑΕΓ μιᾷ ὀρθῇ ἴσαι εἰσίν· καί εἰσιν ἴσαι· ἡμίσεια ἄρα ὀρθῆς ἐστιν ἑκατέρα τῶν ὑπὸ ΓΕΑ, ΓΑΕ. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ὑπὸ ΓΕΒ, ΕΒΓ ἡμίσειά ἐστιν ὀρθῆς· ὅλη ἄρα ἡ ὑπὸ ΑΕΒ ὀρθή ἐστιν. καὶ ἐπεὶ ἡ ὑπὸ ΗΕΖ ἡμίσειά ἐστιν ὀρθῆς, ὀρθὴ δὲ ἡ ὑπὸ ΕΗΖ· ἴση γάρ ἐστι τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΕΓΒ· λοιπὴ ἄρα ἡ ὑπὸ ΕΖΗ ἡμίσειά ἐστιν ὀρθῆς· ἴση ἄρα [ἐστὶν] ἡ ὑπὸ ΗΕΖ γωνία τῇ ὑπὸ ΕΖΗ· ὥστε καὶ πλευρὰ ἡ ΕΗ τῇ ΗΖ ἐστιν ἴση. πάλιν ἐπεὶ ἡ πρὸς τῷ Β γωνία ἡμίσειά ἐστιν ὀρθῆς, ὀρθὴ δὲ ἡ ὑπὸ ΖΔΒ· ἴση γὰρ πάλιν ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΕΓΒ· λοιπὴ ἄρα ἡ ὑπὸ ΒΖΔ ἡμίσειά ἐστιν ὀρθῆς· ἴση ἄρα ἡ πρὸς τῷ Β γωνία τῇ ὑπὸ ΔΖΒ· ὥστε καὶ πλευρὰ ἡ ΖΔ πλευρᾷ τῇ ΔΒ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΕ, ἴσον ἐστὶ καὶ τὸ ἀπὸ ΑΓ τῷ ἀπὸ ΓΕ· τὰ ἄρα ἀπὸ τῶν ΑΓ, ΓΕ τετράγωνα διπλάσιά ἐστι τοῦ ἀπὸ ΑΓ. τοῖς δὲ ἀπὸ τῶν ΑΓ, ΓΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΑ τετράγωνον· ὀρθὴ γὰρ ἡ ὑπὸ ΑΓΕ γωνία· τὸ ἄρα ἀπὸ τῆς ΕΑ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΑΓ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΕΗ τῇ ΗΖ, ἴσον καὶ τὸ ἀπὸ τῆς ΕΗ τῷ ἀπὸ τῆς ΗΖ· τὰ ἄρα ἀπὸ τῶν ΕΗ, ΗΖ τετράγωνα διπλάσιά ἐστι τοῦ ἀπὸ τῆς ΗΖ τετραγώνου. τοῖς δὲ ἀπὸ τῶν ΕΗ, ΗΖ τετραγώνοις ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΖ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΕΖ τετράγωνον διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΗΖ. ἴση δὲ ἡ ΗΖ τῇ ΓΔ· τὸ ἄρα ἀπὸ τῆς ΕΖ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΓΔ. ἔστι δὲ καὶ τὸ ἀπὸ τῆς ΕΑ διπλάσιον τοῦ ἀπὸ τῆς ΑΓ· τὰ ἄρα ἀπὸ τῶν ΑΕ, ΕΖ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων. τοῖς δὲ ἀπὸ τῶν ΑΕ, ΕΖ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΑΖ τετράγωνον· ὀρθὴ γάρ ἐστιν ἡ ὑπὸ ΑΕΖ γωνία· τὸ ἄρα ἀπὸ τῆς ΑΖ τετράγωνον διπλάσιόν ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ. τῷ δὲ ἀπὸ τῆς ΑΖ ἴσα τὰ ἀπὸ τῶν ΑΔ, ΔΖ· ὀρθὴ γὰρ ἡ πρὸς τῷ Δ γωνία· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΖ διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων. ἴση δὲ ἡ ΔΖ τῇ ΔΒ· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὰ ἀπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον II
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ δίχα, προστεθῇ δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας, τὸ ἀπὸ τῆς ὅλης σὺν τῇ προσκειμένῃ καὶ τὸ ἀπὸ τῆς προσκειμένης τὰ συναμφότερα τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς συγκειμένης ἔκ τε τῆς ἡμισείας καὶ τῆς προσκειμένης ὡς ἀπὸ μιᾶς ἀναγραφέντος τετραγώνου.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω δίχα κατὰ τὸ Γ, προσκείσθω δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας ἡ ΒΔ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
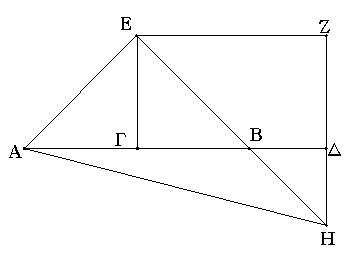
Ἤχθω γὰρ ἀπὸ τοῦ Γ σημείου τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΕ, καὶ κείσθω ἴση ἑκατέρᾳ, τῶν ΑΓ, ΓΒ, καὶ ἐπεζεύχθωσαν αἱ ΕΑ, ΕΒ· καὶ διὰ μὲν τοῦ Ε τῇ ΑΔ παράλληλος ἤχθω ἡ ΕΖ, διὰ δὲ τοῦ Δ τῇ ΓΕ παράλληλος ἤχθω ἡ ΖΔ. καὶ ἐπεὶ εἰς παραλλήλους εὐθείας τὰς ΕΓ, ΖΔ εὐθεῖά τις ἐνέπεσεν ἡ ΕΖ, αἱ ὑπὸ ΓΕΖ, ΕΖΔ ἄρα δυσὶν ὀρθαῖς ἴσαι εἰσίν· αἱ ἄρα ὑπὸ ΖΕΒ, ΕΖΔ δύο ὀρθῶν ἐλάσσονές εἰσιν· αἱ δὲ ἀπ' ἐλασσόνων ἢ δύο ὀρθῶν ἐκβαλλόμεναι συμπίπτουσιν· αἱ ἄρα ΕΒ, ΖΔ ἐκβαλλόμεναι ἐπὶ τὰ Β, Δ μέρη συμπεσοῦνται. ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν κατὰ τὸ Η, καὶ ἐπεζεύχθω ἡ ΑΗ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΕ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΕΑΓ τῇ ὑπὸ ΑΕΓ· καὶ ὀρθὴ ἡ πρὸς τῷ Γ· ἡμίσεια ἄρα ὀρθῆς [ἐστιν] ἑκατέρα τῶν ὑπὸ ΕΑΓ, ΑΕΓ. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ὑπὸ ΓΕΒ, ΕΒΓ ἡμίσειά ἐστιν ὀρθῆς· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΑΕΒ. καὶ ἐπεὶ ἡμίσεια ὀρθῆς ἐστιν ἡ ὑπὸ ΕΒΓ, ἡμίσεια ἄρα ὀρθῆς καὶ ἡ ὑπὸ ΔΒΗ. ἔστι δὲ καὶ ἡ ὑπὸ ΒΔΗ ὀρθή· ἴση γάρ ἐστι τῇ ὑπὸ ΔΓΕ· ἐναλλὰξ γάρ· λοιπὴ ἄρα ἡ ὑπὸ ΔΗΒ ἡμίσειά ἐστιν ὀρθῆς· ἡ ἄρα ὑπὸ ΔΗΒ τῇ ὑπὸ ΔΒΗ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΒΔ πλευρᾷ τῇ ΗΔ ἐστιν ἴση. πάλιν, ἐπεὶ ἡ ὑπὸ ΕΗΖ ἡμίσειά ἐστιν ὀρθῆς, ὀρθὴ δὲ ἡ πρὸς τῷ Ζ· ἴση γάρ ἐστι τῇ ἀπεναντίον τῇ πρὸς τῷ Γ· λοιπὴ ἄρα ἡ ὑπὸ ΖΕΗ ἡμίσειά ἐστιν ὀρθῆς· ἴση ἄρα ἡ ὑπὸ ΕΗΖ γωνία τῇ ὑπὸ ΖΕΗ· ὥστε καὶ πλευρὰ ἡ ΗΖ πλευρᾷ τῇ ΕΖ ἐστιν ἴση. καὶ ἐπεὶ [ἴση ἐστὶν ἡ ΕΓ τῇ ΓΑ,] ἴσον ἐστὶ [καὶ] τὸ ἀπὸ τῆς ΕΓ τετράγωνον τῷ ἀπὸ τῆς ΓΑ τετραγώνῳ· τὰ ἄρα ἀπὸ τῶν ΕΓ, ΓΑ τετράγωνα διπλάσιά ἐστι τοῦ ἀπὸ τῆς ΓΑ τετραγώνου. τοῖς δὲ ἀπὸ τῶν ΕΓ, ΓΑ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΑ· τὸ ἄρα ἀπὸ τῆς ΕΑ τετράγωνον διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΑΓ τετραγώνου. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΖΗ τῇ ΕΖ, ἴσον ἐστὶ καὶ τὸ ἀπὸ τῆς ΖΗ τῷ ἀπὸ τῆς ΖΕ· τὰ ἄρα ἀπὸ τῶν ΗΖ, ΖΕ διπλάσιά ἐστι τοῦ ἀπὸ τῆς ΕΖ. τοῖς δὲ ἀπὸ τῶν ΗΖ, ΖΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΗ· τὸ ἄρα ἀπὸ τῆς ΕΗ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΖ. ἴση δὲ ἡ ΕΖ τῇ ΓΔ· τὸ ἄρα ἀπὸ τῆς ΕΗ τετράγωνον διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΓΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΕΑ διπλάσιον τοῦ ἀπὸ τῆς ΑΓ· τὰ ἄρα ἀπὸ τῶν ΑΕ, ΕΗ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων. τοῖς δὲ ἀπὸ τῶν ΑΕ, ΕΗ τετραγώνοις ἴσον ἐστὶ τὸ ἀπὸ τῆς ΑΗ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΑΗ διπλάσιόν ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ. τῷ δὲ ἀπὸ τῆς ΑΗ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΑΔ, ΔΗ· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΗ [τετράγωνα] διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ [τετραγώνων]. ἴση δὲ ἡ ΔΗ τῇ ΔΒ· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΒ [τετράγωνα] διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ δίχα, προστεθῇ δέ τις αὐτῇ εὐθεῖα ἐπ᾿ εὐθείας, τὸ ἀπὸ τῆς ὅλης σὺν τῇ προσκειμένῃ καὶ τὸ ἀπὸ τῆς προσκειμένης τὰ συναμφότερα τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς συγκειμένης ἔκ τε τῆς ἡμισείας καὶ τῆς προσκειμένης ὡς ἀπὸ μιᾶς ἀναγραφέντος τετραγώνου· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον II
Τὴν δοθεῖσαν εὐθεῖαν τεμεῖν ὥστε τὸ ὑπὸ τῆς ὅλης καὶ τοῦ ἑτέρου τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον εἶναι τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ.
Ἔστω ἡ δοθεῖσα εὐθεῖα ἡ ΑΒ· δεῖ δὴ τὴν ΑΒ τεμεῖν ὥστε τὸ ὑπὸ τῆς ὅλης καὶ τοῦ ἑτέρου τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον εἶναι τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ.
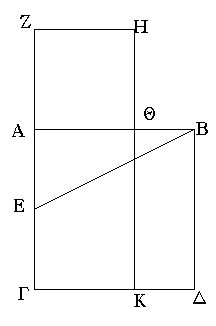
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΒΔΓ, καὶ τετμήσθω ἡ ΑΓ δίχα κατὰ τὸ Ε σημεῖον, καὶ ἐπεζεύχθω ἡ ΒΕ, καὶ διήχθω ἡ ΓΑ ἐπὶ τὸ Ζ, καὶ κείσθω τῇ ΒΕ ἴση ἡ ΕΖ, καὶ ἀναγεγράφθω ἀπὸ τῆς ΑΖ τετράγωνον τὸ ΖΘ, καὶ διήχθω ἡ ΗΘ ἐπὶ τὸ Κ· λέγω, ὅτι ἡ ΑΒ τέτμηται κατὰ τὸ Θ, ὥστε τὸ ὑπὸ τῶν ΑΒ, ΒΘ περιεχόμενον ὀρθογώνιον ἴσον ποιεῖν τῷ ἀπὸ τῆς ΑΘ τετραγώνῳ.
Ἐπεὶ γὰρ εὐθεῖα ἡ ΑΓ τέτμηται δίχα κατὰ τὸ Ε, πρόσκειται δὲ αὐτῇ ἡ ΖΑ, τὸ ἄρα ὑπὸ τῶν ΓΖ, ΖΑ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΑΕ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΖ τετραγώνῳ. ἴση δὲ ἡ ΕΖ τῇ ΕΒ· τὸ ἄρα ὑπὸ τῶν ΓΖ, ΖΑ μετὰ τοῦ ἀπὸ τῆς ΑΕ ἴσον ἐστὶ τῷ ἀπὸ ΕΒ. ἀλλὰ τῷ ἀπὸ ΕΒ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΒΑ, ΑΕ· ὀρθὴ γὰρ ἡ πρὸς τῷ Α γωνία· τὸ ἄρα ὑπὸ τῶν ΓΖ, ΖΑ μετὰ τοῦ ἀπὸ τῆς ΑΕ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΕ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΑΕ· λοιπὸν ἄρα τὸ ὑπὸ τῶν ΓΖ, ΖΑ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ. καί ἐστι τὸ μὲν ὑπὸ τῶν ΓΖ, ΖΑ τὸ ΖΚ· ἴση γὰρ ἡ ΑΖ τῇ ΖΗ· τὸ δὲ ἀπὸ τῆς ΑΒ τὸ ΑΔ· τὸ ἄρα ΖΚ ἴσον ἐστὶ τῷ ΑΔ. κοινὸν ἀφῃρήσθω τὸ ΑΚ· λοιπὸν ἄρα τὸ ΖΘ τῷ ΘΔ ἴσον ἐστίν. καί ἐστι τὸ μὲν ΘΔ τὸ ὑπὸ τῶν ΑΒ, ΒΘ· ἴση γὰρ ἡ ΑΒ τῇ ΒΔ· τὸ δὲ ΖΘ τὸ ἀπὸ τῆς ΑΘ· τὸ ἄρα ὑπὸ τῶν ΑΒ, ΒΘ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ ΘΑ τετραγώνῳ.
Ἡ ἄρα δοθεῖσα εὐθεῖα ἡ ΑΒ τέτμηται κατὰ τὸ Θ ὥστε τὸ ὑπὸ τῶν ΑΒ, ΒΘ περιεχόμενον ὀρθογώνιον ἴσον ποιεῖν τῷ ἀπὸ τῆς ΘΑ τετραγώνῳ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιβ΄ 12 Βιβλίον II
Ἐν τοῖς ἀμβλυγωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ἀμβλεῖαν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον μεῖζόν ἐστι τῶν ἀπὸ τῶν τὴν ἀμβλεῖαν γωνίαν περιεχουσῶν πλευρῶν τετραγώνων τῷ περιεχομένῳ δὶς ὑπό τε μιᾶς τῶν περὶ τὴν ἀμβλεῖαν γωνίαν, ἐφ' ἣν ἡ κάθετος πίπτει, καὶ τῆς ἀπολαμβανομένης ἐκτὸς ὑπὸ τῆς καθέτου πρὸς τῇ ἀμβλείᾳ γωνίᾳ.
Ἔστω ἀμβλυγώνιον τρίγωνον τὸ ΑΒΓ ἀμβλεῖαν ἔχον τὴν ὑπὸ ΒΑΓ, καὶ ἤχθω ἀπὸ τοῦ Β σημείου ἐπὶ τὴν ΓΑ ἐκβληθεῖσαν κάθετος ἡ ΒΔ. λέγω, ὅτι τὸ ἀπὸ τῆς ΒΓ τετράγωνον μεῖζόν ἐστι τῶν ἀπὸ τῶν ΒΑ, ΑΓ τετραγώνων τῷ δὶς ὑπὸ τῶν ΓΑ, ΑΔ περιεχομένῳ ὀρθογωνίῳ.
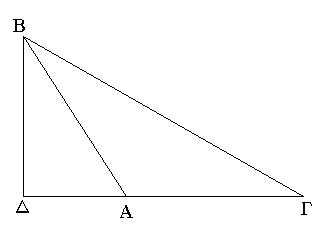
Ἐπεὶ γὰρ εὐθεῖα ἡ ΓΑ τέτμηται, ὡς ἔτυχεν, κατὰ τὸ Α σημεῖον, τὸ ἄρα ἀπὸ τῆς ΔΓ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΓΑ, ΑΔ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΓΑ, ΑΔ περιεχομένῳ ὀρθογωνίῳ. κοινὸν προσκείσθω τὸ ἀπὸ τῆς ΔΒ· τὰ ἄρα ἀπὸ τῶν ΓΔ, ΔΒ ἴσα ἐστὶ τοῖς τε ἀπὸ τῶν ΓΑ, ΑΔ, ΔΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΓΑ, ΑΔ [περιεχομένῳ ὀρθογωνίῳ]. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΓΔ, ΔΒ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΓΒ· ὀρθὴ γὰρ ἡ πρὸς τῷ Δ γωνία· τοῖς δὲ ἀπὸ τῶν ΑΔ, ΔΒ ἴσον τὸ ἀπὸ τῆς ΑΒ· τὸ ἄρα ἀπὸ τῆς ΓΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΓΑ, ΑΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΓΑ, ΑΔ περιεχομένῳ ὀρθογωνίῳ· ὥστε τὸ ἀπὸ τῆς ΓΒ τετράγωνον τῶν ἀπὸ τῶν ΓΑ, ΑΒ τετραγώνων μεῖζόν ἐστι τῷ δὶς ὑπὸ τῶν ΓΑ, ΑΔ περιεχομένῳ ὀρθογωνίῳ.
Ἐν ἄρα τοῖς ἀμβλυγωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ἀμβλεῖαν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον μεῖζόν ἐστι τῶν ἀπὸ τῶν τὴν ἀμβλεῖαν γωνίαν περιεχουσῶν πλευρῶν τετραγώνων τῷ περιεχομένῳ δὶς ὑπό τε μιᾶς τῶν περὶ τὴν ἀμβλεῖαν γωνίαν, ἐφ' ἣν ἡ κάθετος πίπτει, καὶ τῆς ἀπολαμβανομένης ἐκτὸς ὑπὸ τῆς καθέτου πρὸς τῇ ἀμβλείᾳ γωνίᾳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον II
Ἐν τοῖς ὀξυγωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀξεῖαν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἔλαττόν ἐστι τῶν ἀπὸ τῶν τὴν ὀξεῖαν γωνίαν περιεχουσῶν πλευρῶν τετραγώνων τῷ περιεχομένῳ δὶς ὑπό τε μιᾶς τῶν περὶ τὴν ὀξεῖαν γωνίαν, ἐφ' ἣν ἡ κάθετος πίπτει, καὶ τῆς ἀπολαμβανομένης ἐντὸς ὑπὸ τῆς καθέτου πρὸς τῇ ὀξείᾳ γωνίᾳ.
Ἔστω ὀξυγώνιον τρίγωνον τὸ ΑΒΓ ὀξεῖαν ἔχον τὴν πρὸς τῷ Β γωνίαν, καὶ ἤχθω ἀπὸ τοῦ Α σημείου ἐπὶ τὴν ΒΓ κάθετος ἡ ΑΔ· λέγω, ὅτι τὸ ἀπὸ τῆς ΑΓ τετράγωνον ἔλαττόν ἐστι τῶν ἀπὸ τῶν ΓΒ, ΒΑ τετραγώνων τῷ δὶς ὑπὸ τῶν ΓΒ, ΒΔ περιεχομένῳ ὀρθογωνίῳ.
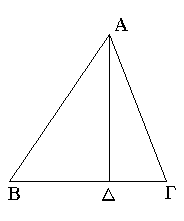
Ἐπεὶ γὰρ εὐθεῖα ἡ ΓΒ τέτμηται, ὡς ἔτυχεν, κατὰ τὸ Δ, τὰ ἄρα ἀπὸ τῶν ΓΒ, ΒΔ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΓΒ, ΒΔ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΔΓ τετραγώνῳ. κοινὸν προσκείσθω τὸ ἀπὸ τῆς ΔΑ τετράγωνον· τὰ ἄρα ἀπὸ τῶν ΓΒ, ΒΔ, ΔΑ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΓΒ, ΒΔ περιεχομένῳ ὀρθογωνίῳ καὶ τοῖς ἀπὸ τῶν ΑΔ, ΔΓ τετραγώνοις. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΒΔ, ΔΑ ἴσον τὸ ἀπὸ τῆς ΑΒ· ὀρθὴ γὰρ ἡ πρὸς τῷ Δ γωνίᾳ· τοῖς δὲ ἀπὸ τῶν ΑΔ, ΔΓ ἴσον τὸ ἀπὸ τῆς ΑΓ· τὰ ἄρα ἀπὸ τῶν ΓΒ, ΒΑ ἴσα ἐστὶ τῷ τε ἀπὸ τῆς ΑΓ καὶ τῷ δὶς ὑπὸ τῶν ΓΒ, ΒΔ· ὥστε μόνον τὸ ἀπὸ τῆς ΑΓ ἔλαττόν ἐστι τῶν ἀπὸ τῶν ΓΒ, ΒΑ τετραγώνων τῷ δὶς ὑπὸ τῶν ΓΒ, ΒΔ περιεχομένῳ ὀρθογωνίῳ.
Ἐν ἄρα τοῖς ὀξυγωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀξεῖαν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἔλαττόν ἐστι τῶν ἀπὸ τῶν τὴν ὀξεῖαν γωνίαν περιεχουσῶν πλευρῶν τετραγώνων τῷ περιεχομένῳ δὶς ὑπό τε μιᾶς τῶν περὶ τὴν ὀξεῖαν γωνίαν, ἐφ' ἣν ἡ κάθετος πίπτει, καὶ τῆς ἀπολαμβανομένης ἐντὸς ὑπὸ τῆς καθέτου πρὸς τῇ ὀξείᾳ γωνίᾳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον II
Τῷ δοθέντι εὐθυγράμμῳ ἴσον τετράγωνον συστήσασθαι.
Ἔστω τὸ δοθὲν εὐθύγραμμον τὸ Α· δεῖ δὴ τῷ Α εὐθυγράμμῳ ἴσον τετράγωνον συστήσασθαι.
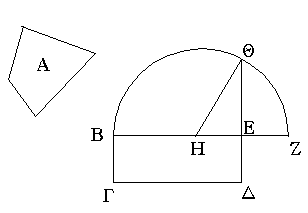
Συνεστάτω γὰρ τῷ Α εὐθυγράμμῳ ἴσον παραλληλόγραμμον ὀρθογώνιον τὸ ΒΔ· εἰ μὲν οὖν ἴση ἐστὶν ἡ ΒΕ τῇ ΕΔ, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. συνέσταται γὰρ τῷ Α εὐθυγράμμῳ ἴσον τετράγωνον τὸ ΒΔ· εἰ δὲ οὔ, μία τῶν ΒΕ, ΕΔ μείζων ἐστίν. ἔστω μείζων ἡ ΒΕ, καὶ ἐκβεβλήσθω ἐπὶ τὸ Ζ, καὶ κείσθω τῇ ΕΔ ἴση ἡ ΕΖ, καὶ τετμήσθω ἡ ΒΖ δίχα κατὰ τὸ Η, καὶ κέντρῳ τῷ Η, διαστήματι δὲ ἑνὶ τῶν ΗΒ, ΗΖ ἡμικύκλιον γεγράφθω τὸ ΒΘΖ, καὶ ἐκβεβλήσθω ἡ ΔΕ ἐπὶ τὸ Θ, καὶ ἐπεζεύχθω ἡ ΗΘ.
Ἐπεὶ οὖν εὐθεῖα ἡ ΒΖ τέτμηται εἰς μὲν ἴσα κατὰ τὸ Η, εἰς δὲ ἄνισα κατὰ τὸ Ε, τὸ ἄρα ὑπὸ τῶν ΒΕ, ΕΖ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΕΗ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΗΖ τετραγώνῳ. ἴση δὲ ἡ ΗΖ τῇ ΗΘ· τὸ ἄρα ὑπὸ τῶν ΒΕ, ΕΖ μετὰ τοῦ ἀπὸ τῆς ΗΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΗΘ. τῷ δὲ ἀπὸ τῆς ΗΘ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΘΕ, ΕΗ τετράγωνα· τὸ ἄρα ὑπὸ τῶν ΒΕ, ΕΖ μετὰ τοῦ ἀπὸ ΗΕ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΘΕ, ΕΗ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΗΕ τετράγωνον· λοιπὸν ἄρα τὸ ὑπὸ τῶν ΒΕ, ΕΖ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΘ τετραγώνῳ. ἀλλὰ τὸ ὑπὸ τῶν ΒΕ, ΕΖ τὸ ΒΔ ἐστιν· ἴση γὰρ ἡ ΕΖ τῇ ΕΔ· τὸ ἄρα ΒΔ παραλληλόγραμμον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΘΕ τετραγώνῳ. ἴσον δὲ τὸ ΒΔ τῷ Α εὐθυγράμμῳ. καὶ τὸ Α ἄρα εὐθύγραμμον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΘ ἀναγραφησομένῳ τετραγώνῳ.
Τῷ ἄρα δοθέντι εὐθυγράμμῳ τῷ Α ἴσον τετράγωνον συνέσταται τὸ ἀπὸ τῆς ΕΘ ἀναγραφησόμενον· ὅπερ ἔδει ποιῆσαι.
Στοιχεῖα Εὐκλείδου γ΄
Βιβλίον III
Ὅροι ια΄ 11.
α΄ 1. Ἴσοι κύκλοι εἰσίν, ὧν αἱ διάμετροι ἴσαι εἰσίν, ἢ ὧν αἱ ἐκ τῶν κέντρων ἴσαι εἰσίν.
β΄ 2. Εὐθεῖα κύκλου ἐφάπτεσθαι λέγεται, ἥτις ἁπτομένη τοῦ κύκλου καὶ ἐκβαλλομένη οὐ τέμνει τὸν κύκλον.
γ΄ 3. Κύκλοι ἐφάπτεσθαι ἀλλήλων λέγονται οἵτινες ἁπτόμενοι ἀλλήλων οὐ τέμνουσιν ἀλλήλους.
δ΄ 4. Ἐν κύκλῳ ἴσον ἀπέχειν ἀπὸ τοῦ κέντρου εὐθεῖαι λέγονται, ὅταν αἱ ἀπὸ τοῦ κέντρου ἐπ᾿ αὐτὰς κάθετοι ἀγόμεναι ἴσαι ὦσιν.
ε΄ 5. Μεῖζον δὲ ἀπέχειν λέγεται, ἐφ' ἣν ἡ μείζων κάθετος πίπτει.
ς΄ 6. Τμῆμα κύκλου ἐστὶ τὸ περιεχόμενον σχῆμα ὑπό τε εὐθείας καὶ κύκλου περιφερείας.
ζ΄ 7. Τμήματος δὲ γωνία ἐστὶν ἡ περιεχομένη ὑπό τε εὐθείας καὶ κύκλου περιφερείας.
η΄ 8. Ἐν τμήματι δὲ γωνία ἐστίν, ὅταν ἐπὶ τῆς περιφερείας τοῦ τμήματος ληφθῇ τι σημεῖον καὶ ἀπ' αὐτοῦ ἐπὶ τὰ πέρατα τῆς εὐθείας, ἥ ἐστι βάσις τοῦ τμήματος, ἐπιζευχθῶσιν εὐθεῖαι, ἡ περιεχομένη γωνία ὑπὸ τῶν ἐπιζευχθεισῶν εὐθειῶν.
θ΄ 9. Ὅταν δὲ αἱ περιέχουσαι τὴν γωνίαν εὐθεῖαι ἀπολαμβάνωσί τινα περιφέρειαν, ἐπ᾿ ἐκείνης λέγεται βεβηκέναι ἡ γωνία.
ι΄ 10. Τομεὺς δὲ κύκλου ἐστίν, ὅταν πρὸς τῷ κέντρῳ τοῦ κύκλου συσταθῇ γωνία, τὸ περιεχόμενον σχῆμα ὑπό τε τῶν τὴν γωνίαν περιεχουσῶν εὐθειῶν καὶ τῆς ἀπολαμβανομένης ὑπ' αὐτῶν περιφερείας.
ια΄ 11. Ὅμοια τμήματα κύκλων ἐστὶ τὰ δεχόμενα γωνίας ἴσας, ἢ ἐν οἷς αἱ γωνίαι ἴσαι ἀλλήλαις εἰσίν.
Στοιχεῖα Εὐκλείδου γ΄
Βιβλίον III
Προτάσεις λζ΄ 37
Πρότασις α΄ 1 Βιβλίον III
Τοῦ δοθέντος κύκλου τὸ κέντρον εὑρεῖν.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ· δεῖ δὴ τοῦ ΑΒΓ κύκλου τὸ κέντρον εὑρεῖν.
Διήχθω τις εἰς αὐτόν, ὡς ἔτυχεν, εὐθεῖα ἡ ΑΒ, καὶ τετμήσθω δίχα κατὰ τὸ Δ σημεῖον, καὶ ἀπὸ τοῦ Δ τῇ ΑΒ πρὸς ὀρθὰς ἤχθω ἡ ΔΓ καὶ διήχθω ἐπὶ τὸ Ε, καὶ τετμήσθω ἡ ΓΕ δίχα κατὰ τὸ Ζ· λέγω, ὅτι τὸ Ζ κέντρον ἐστὶ τοῦ ΑΒΓ [κύκλου].
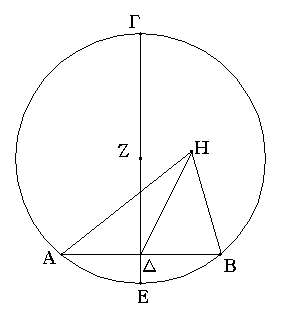
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἔστω τὸ Η, καὶ ἐπεζεύχθωσαν αἱ ΗΑ, ΗΔ, ΗΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΔΒ, κοινὴ δὲ ἡ ΔΗ, δύο δὴ αἱ ΑΔ, ΔΗ δύο ταῖς ΗΔ, ΔΒ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΗΑ βάσει τῇ ΗΒ ἐστιν ἴση· ἐκ κέντρου γάρ· γωνία ἄρα ἡ ὑπὸ ΑΔΗ γωνίᾳ τῇ ὑπὸ ΗΔΒ ἴση ἐστίν. ὅταν δὲ εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα τὰς ἐφεξῆς γωνίας ἴσας ἀλλήλαις ποιῇ, ὀρθὴ ἑκατέρα τῶν ἴσων γωνιῶν ἐστιν· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΗΔΒ. ἐστὶ δὲ καὶ ἡ ὑπὸ ΖΔΒ ὀρθή· ἴση ἄρα ἡ ὑπὸ ΖΔΒ τῇ ὑπὸ ΗΔΒ, ἡ μείζων τῇ ἐλάττονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὸ Η κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλο τι πλὴν τοῦ Ζ.
Τὸ Ζ ἄρα σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ [κύκλου].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν ἐν κύκλῳ εὐθεῖά τις εὐθεῖάν τινα δίχα καὶ πρὸς ὀρθὰς τέμνῃ, ἐπὶ τῆς τεμνούσης ἐστὶ τὸ κέντρον τοῦ κύκλου· ὅπερ ἔδει ποιῆσαι.
Πρότασις β΄ 2 Βιβλίον III
Ἐὰν κύκλου ἐπὶ τῆς περιφερείας ληφθῇ δύο τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐντὸς πεσεῖται τοῦ κύκλου.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ ἐπὶ τῆς περιφερείας αὐτοῦ εἰλήφθω δύο τυχόντα σημεῖα τὰ Α, Β· λέγω, ὅτι ἡ ἀπὸ τοῦ Α ἐπὶ τὸ Β ἐπιζευγνυμένη εὐθεῖα ἐντὸς πεσεῖται τοῦ κύκλου.
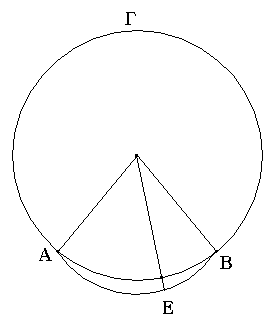
Μὴ γάρ, ἀλλ' εἰ δυνατόν, πιπτέτω ἐκτὸς ὡς ἡ ΑΕΒ, καὶ εἰλήφθω τὸ κέντρον τοῦ ΑΒΓ κύκλου, καὶ ἔστω τὸ Δ, καὶ ἐπεζεύχθωσαν αἱ ΔΑ, ΔΒ, καὶ διήχθω ἡ ΔΖΕ.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΔΑ τῇ ΔΒ, ἴση ἄρα καὶ γωνία ἡ ὑπὸ ΔΑΕ τῇ ὑπὸ ΔΒΕ· καὶ ἐπεὶ τριγώνου τοῦ ΔΑΕ μία πλευρὰ προσεκβέβληται ἡ ΑΕΒ, μείζων ἄρα ἡ ὑπὸ ΔΕΒ γωνία τῆς ὑπὸ ΔΑΕ. ἴση δὲ ἡ ὑπὸ ΔΑΕ τῇ ὑπὸ ΔΒΕ· μείζων ἄρα ἡ ὑπὸ ΔΕΒ τῆς ὑπὸ ΔΒΕ. ὑπὸ δὲ τὴν μείζονα γωνίαν ἡ μείζων πλευρὰ ὑποτείνει· μείζων ἄρα ἡ ΔΒ τῆς ΔΕ. ἴση δὲ ἡ ΔΒ τῇ ΔΖ. μείζων ἄρα ἡ ΔΖ τῆς ΔΕ ἡ ἐλάττων τῆς μείζονος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ἀπὸ τοῦ Α ἐπὶ τὸ Β ἐπιζευγνυμένη εὐθεῖα ἐκτὸς πεσεῖται τοῦ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἐπ᾿ αὐτῆς τῆς περιφερείας· ἐντὸς ἄρα.
Ἐὰν ἄρα κύκλου ἐπὶ τῆς περιφερείας ληφθῇ δύο τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐντὸς πεσεῖται τοῦ κύκλου· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον III
Ἐὰν ἐν κύκλῳ εὐθεῖά τις διὰ τοῦ κέντρου εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου δίχα τέμνῃ, καὶ πρὸς ὀρθὰς αὐτὴν τέμνει· καὶ ἐὰν πρὸς ὀρθὰς αὐτὴν τέμνῃ, καὶ δίχα αὐτὴν τέμνει.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ ἐν αὐτῷ εὐθεῖά τις διὰ τοῦ κέντρου ἡ ΓΔ εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου τὴν ΑΒ δίχα τεμνέτω κατὰ τὸ Ζ σημεῖον· λέγω, ὅτι καὶ πρὸς ὀρθὰς αὐτὴν τέμνει.
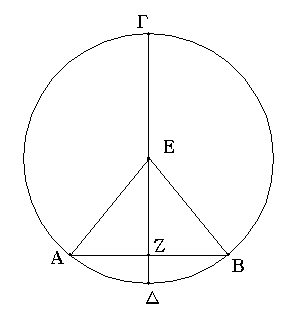
Εἰλήφθω γὰρ τὸ κέντρον τοῦ ΑΒΓ κύκλου, καὶ ἔστω τὸ Ε, καὶ ἐπεζεύχθωσαν αἱ ΕΑ, ΕΒ.
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΖ τῇ ΖΒ, κοινὴ δὲ ἡ ΖΕ, δύο δυσὶν ἴσαι [εἰσίν]. καὶ βάσις ἡ ΕΑ βάσει τῇ ΕΒ ἴση· γωνία ἄρα ἡ ὑπὸ ΑΖΕ γωνίᾳ τῇ ὑπὸ ΒΖΕ ἴση ἐστίν. ὅταν δὲ εὐθεῖα ἐπ᾿ εὐθεῖαν σταθεῖσα τὰς ἐφεξῆς γωνίας ἴσας ἀλλήλαις ποιῇ, ὀρθὴ ἑκατέρα τῶν ἴσων γωνιῶν ἐστιν· ἑκατέρα ἄρα τῶν ὑπὸ ΑΖΕ, ΒΖΕ ὀρθή ἐστιν. ἡ ΓΔ ἄρα διὰ τοῦ κέντρου οὖσα τὴν ΑΒ μὴ διὰ τοῦ κέντρου οὖσαν δίχα τέμνουσα καὶ πρὸς ὀρθὰς τέμνει.
Ἀλλὰ δὴ ἡ ΓΔ τὴν ΑΒ πρὸς ὀρθὰς τεμνέτω· λέγω, ὅτι καὶ δίχα αὐτὴν τέμνει, τουτέστιν, ὅτι ἴση ἐστὶν ἡ ΑΖ τῇ ΖΒ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεὶ ἴση ἐστὶν ἡ ΕΑ τῇ ΕΒ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΕΑΖ τῇ ὑπὸ ΕΒΖ. ἐστὶ δὲ καὶ ὀρθὴ ἡ ὑπὸ ΑΖΕ ὀρθῇ τῇ ὑπὸ ΒΖΕ ἴση· δύο ἄρα τρίγωνά ἐστι τὰ ΕΑΖ, ΕΖΒ τὰς δύο γωνίας δυσὶ γωνίαις ἴσας ἔχοντα καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην κοινὴν αὐτῶν τὴν ΕΖ ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει· ἴση ἄρα ἡ ΑΖ τῇ ΖΒ.
Ἐὰν ἄρα ἐν κύκλῳ εὐθεῖά τις διὰ τοῦ κέντρου εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου δίχα τέμνῃ, καὶ πρὸς ὀρθὰς αὐτὴν τέμνει· καὶ ἐὰν πρὸς ὀρθὰς αὐτὴν τέμνῃ, καὶ δίχα αὐτὴν τέμνει· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον III
Ἔστω κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ δύο εὐθεῖαι αἱ ΑΓ, ΒΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε μὴ διὰ τοῦ κέντρου οὖσαι· λέγω, ὅτι οὐ τέμνουσιν ἀλλήλας δίχα.
Εἰ γὰρ δυνατόν, τεμνέτωσαν ἀλλήλας δίχα ὥστε ἴσην εἶναι τὴν μὲν ΑΕ τῇ ΕΓ, τὴν δὲ ΒΕ τῇ ΕΔ· καὶ εἰλήφθω τὸ κέντρον τοῦ ΑΒΓΔ κύκλου, καὶ ἔστω τὸ Ζ, καὶ ἐπεζεύχθω ἡ ΖΕ.
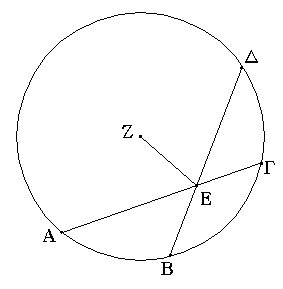
Ἐπεὶ οὖν εὐθεῖά τις διὰ τοῦ κέντρου ἡ ΖΕ εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου τὴν ΑΓ δίχα τέμνει, καὶ πρὸς ὀρθὰς αὐτὴν τέμνει· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΖΕΑ· πάλιν, ἐπεὶ εὐθεῖά τις ἡ ΖΕ εὐθεῖάν τινα τὴν ΒΔ δίχα τέμνει, καὶ πρὸς ὀρθὰς αὐτὴν τέμνει· ὀρθὴ ἄρα ἡ ὑπὸ ΖΕΒ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΖΕΑ ὀρθή· ἴση ἄρα ἡ ὑπὸ ΖΕΑ τῇ ὑπὸ ΖΕΒ ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα αἱ ΑΓ, ΒΔ τέμνουσιν ἀλλήλας δίχα.
Ἐὰν ἄρα ἐν κύκλῳ δύο εὐθεῖαι τέμνωσιν ἀλλήλας μὴ διὰ τοῦ κέντρου οὖσαι, οὐ τέμνουσιν ἀλλήλας δίχα· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον III
Ἐὰν δύο κύκλοι τέμνωσιν ἀλλήλους, οὐκ ἔσται αὐτῶν τὸ αὐτὸ κέντρον.
Δύο γὰρ κύκλοι οἱ ΑΒΓ, ΓΔΗ τεμνέτωσαν ἀλλήλους κατὰ τὰ Β, Γ σημεῖα. λέγω, ὅτι οὐκ ἔσται αὐτῶν τὸ αὐτὸ κέντρον.
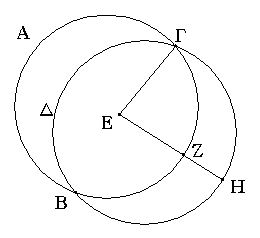
Εἰ γὰρ δυνατόν, ἔστω τὸ Ε, καὶ ἐπεζεύχθω ἡ ΕΓ, καὶ διήχθω ἡ ΕΖΗ, ὡς ἔτυχεν. καὶ ἐπεὶ τὸ Ε σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου, ἴση ἐστὶν ἡ ΕΓ τῇ ΕΖ. πάλιν, ἐπεὶ τὸ Ε σημεῖον κέντρον ἐστὶ τοῦ ΓΔΗ κύκλου, ἴση ἐστὶν ἡ ΕΓ τῇ ΕΗ· ἐδείχθη δὲ ἡ ΕΓ καὶ τῇ ΕΖ ἴση· καὶ ἡ ΕΖ ἄρα τῇ ΕΗ ἐστιν ἴση ἡ ἐλάσσων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὸ Ε σημεῖον κέντρον ἐστὶ τῶν ΑΒΓ, ΓΔΗ κύκλων.
Ἐὰν ἄρα δύο κύκλοι τέμνωσιν ἀλλήλους, οὐκ ἔστιν αὐτῶν τὸ αὐτὸ κέντρον· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον III
Ἐὰν δύο κύκλοι ἐφάπτωνται ἀλλήλων, οὐκ ἔσται αὐτῶν τὸ αὐτὸ κέντρον.
Δύο γὰρ κύκλοι οἱ ΑΒΓ, ΓΔΕ ἐφαπτέσθωσαν ἀλλήλων κατὰ τὸ Γ σημεῖον· λέγω, ὅτι οὐκ ἔσται αὐτῶν τὸ αὐτὸ κέντρον.
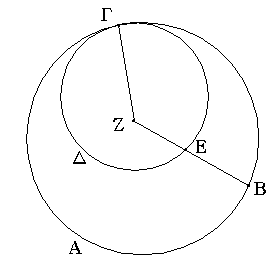
Εἰ γὰρ δυνατόν, ἔστω τὸ Ζ, καὶ ἐπεζεύχθω ἡ ΖΓ, καὶ διήχθω, ὡς ἔτυχεν, ἡ ΖΕΒ.
Ἐπεὶ οὖν τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου, ἴση ἐστὶν ἡ ΖΓ τῇ ΖΒ. πάλιν, ἐπεὶ τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ ΓΔΕ κύκλου, ἴση ἐστὶν ἡ ΖΓ τῇ ΖΕ. ἐδείχθη δὲ ἡ ΖΓ τῇ ΖΒ ἴση· καὶ ἡ ΖΕ ἄρα τῇ ΖΒ ἐστιν ἴση, ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὸ Ζ σημεῖον κέντρον ἐστὶ τῶν ΑΒΓ, ΓΔΕ κύκλων.
Ἐὰν ἄρα δύο κύκλοι ἐφάπτωνται ἀλλήλων, οὐκ ἔσται αὐτῶν τὸ αὐτὸ κέντρον· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον III
Ἐὰν κύκλου ἐπὶ τῆς διαμέτρου ληφθῇ τι σημεῖον, ὃ μή ἐστι κέντρον τοῦ κύκλου, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσιν εὐθεῖαί τινες, μεγίστη μὲν ἔσται, ἐφ' ἧς τὸ κέντρον, ἐλαχίστη δὲ ἡ λοιπή, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης.
Ἔστω κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἔστω ἡ ΑΔ, καὶ ἐπὶ τῆς ΑΔ εἰλήφθω τι σημεῖον τὸ Ζ, ὃ μή ἐστι κέντρον τοῦ κύκλου, κέντρον δὲ τοῦ κύκλου ἔστω τὸ Ε, καὶ ἀπὸ τοῦ Ζ πρὸς τὸν ΑΒΓΔ κύκλον προσπιπτέτωσαν εὐθεῖαί τινες αἱ ΖΒ, ΖΓ, ΖΗ· λέγω, ὅτι μεγίστη μέν ἐστιν ἡ ΖΑ, ἐλαχίστη δὲ ἡ ΖΔ, τῶν δὲ ἄλλων ἡ μὲν ΖΒ τῆς ΖΓ μείζων, ἡ δὲ ΖΓ τῆς ΖΗ.
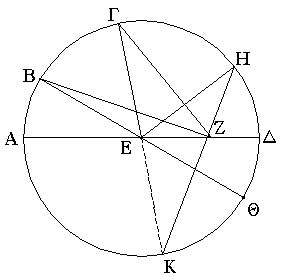
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΓΕ, ΗΕ. καὶ ἐπεὶ παντὸς τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσιν, αἱ ἄρα ΕΒ, ΕΖ τῆς ΒΖ μείζονές εἰσιν. ἴση δὲ ἡ ΑΕ τῇ ΒΕ [αἱ ἄρα ΒΕ, ΕΖ ἴσαι εἰσὶ τῇ ΑΖ]· μείζων ἄρα ἡ ΑΖ τῆς ΒΖ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΓΕ, κοινὴ δὲ ἡ ΖΕ, δύο δὴ αἱ ΒΕ, ΕΖ δυσὶ ταῖς ΓΕ, ΕΖ ἴσαι εἰσίν. ἀλλὰ καὶ γωνία ἡ ὑπὸ ΒΕΖ γωνίας τῆς ὑπὸ ΓΕΖ μείζων. βάσις ἄρα ἡ ΒΖ βάσεως τῆς ΓΖ μείζων ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΓΖ τῆς ΖΗ μείζων ἐστίν.
Πάλιν, ἐπεὶ αἱ ΗΖ, ΖΕ τῆς ΕΗ μείζονές εἰσιν, ἴση δὲ ἡ ΕΗ τῇ ΕΔ, αἱ ἄρα ΗΖ, ΖΕ τῆς ΕΔ μείζονές εἰσιν. κοινὴ ἀφῃρήσθω ἡ ΕΖ· λοιπὴ ἄρα ἡ ΗΖ λοιπῆς τῆς ΖΔ μείζων ἐστίν. μεγίστη μὲν ἄρα ἡ ΖΑ, ἐλαχίστη δὲ ἡ ΖΔ, μείζων δὲ ἡ μὲν ΖΒ τῆς ΖΓ, ἡ δὲ ΖΓ τῆς ΖΗ.
Λέγω, ὅτι καὶ ἀπὸ τοῦ Ζ σημείου δύο μόνον ἴσαι προσπεσοῦνται πρὸς τὸν ΑΒΓΔ κύκλον ἐφ' ἑκάτερα τῆς ΖΔ ἐλαχίστης. συνεστάτω γὰρ πρὸς τῇ ΕΖ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Ε τῇ ὑπὸ ΗΕΖ γωνίᾳ ἴση ἡ ὑπὸ ΖΕΘ, καὶ ἐπεζεύχθω ἡ ΖΘ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ΗΕ τῇ ΕΘ, κοινὴ δὲ ἡ ΕΖ, δύο δὴ αἱ ΗΕ, ΕΖ δυσὶ ταῖς ΘΕ, ΕΖ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΗΕΖ γωνίᾳ τῇ ὑπὸ ΘΕΖ ἴση· βάσις ἄρα ἡ ΖΗ βάσει τῇ ΖΘ ἴση ἐστίν. λέγω δή, ὅτι τῇ ΖΗ ἄλλη ἴση οὐ προσπεσεῖται πρὸς τὸν κύκλον ἀπὸ τοῦ Ζ σημείου. εἰ γὰρ δυνατόν, προσπιπτέτω ἡ ΖΚ. καὶ ἐπεὶ ἡ ΖΚ τῇ ΖΗ ἴση ἐστίν, ἀλλὰ ἡ ΖΘ τῇ ΖΗ [ἴση ἐστίν], καὶ ἡ ΖΚ ἄρα τῇ ΖΘ ἐστιν ἴση, ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῇ ἀπώτερον ἴση· ὅπερ ἀδύνατον. οὐκ ἄρα ἀπὸ τοῦ Ζ σημείου ἑτέρα τις προσπεσεῖται πρὸς τὸν κύκλον ἴση τῇ ΗΖ· μία ἄρα μόνη.
Ἐὰν ἄρα κύκλου ἐπὶ τῆς διαμέτρου ληφθῇ τι σημεῖον, ὃ μή ἐστι κέντρον τοῦ κύκλου, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσιν εὐθεῖαί τινες, μεγίστη μὲν ἔσται, ἐφ' ἧς τὸ κέντρον, ἐλαχίστη δὲ ἡ λοιπή, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ αὐτοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον III
Ἐὰν κύκλου ληφθῇ τι σημεῖον ἐκτός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον διαχθῶσιν εὐθεῖαί τινες, ὧν μία μὲν διὰ τοῦ κέντρου, αἱ δὲ λοιπαί, ὡς ἔτυχεν, τῶν μὲν πρὸς τὴν κοίλην περιφέρειαν προσπιπτουσῶν εὐθειῶν μεγίστη μέν ἐστιν ἡ διὰ τοῦ κέντρου, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, τῶν δὲ πρὸς τὴν κυρτὴν περιφέρειαν προσπιπτουσῶν εὐθειῶν ἐλαχίστη μέν ἐστιν ἡ μεταξὺ τοῦ τε σημείου καὶ τῆς διαμέτρου, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς ἐλαχίστης τῆς ἀπώτερόν ἐστιν ἐλάττων, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ τοῦ ΑΒΓ εἰλήφθω τι σημεῖον ἐκτὸς τὸ Δ, καὶ ἀπ' αὐτοῦ διήχθωσαν εὐθεῖαί τινες αἱ ΔΑ, ΔΕ, ΔΖ, ΔΓ, ἔστω δὲ ἡ ΔΑ διὰ τοῦ κέντρου. λέγω, ὅτι τῶν μὲν πρὸς τὴν ΑΕΖΓ κοίλην περιφέρειαν προσπιπτουσῶν εὐθειῶν μεγίστη μέν ἐστιν ἡ διὰ τοῦ κέντρου ἡ ΔΑ, μείζων δὲ ἡ μὲν ΔΕ τῆς ΔΖ ἡ δὲ ΔΖ τῆς ΔΓ, τῶν δὲ πρὸς τὴν ΘΛΚΗ κυρτὴν περιφέρειαν προσπιπτουσῶν εὐθειῶν ἐλαχίστη μέν ἐστιν ἡ ΔΗ ἡ μεταξὺ τοῦ σημείου καὶ τῆς διαμέτρου τῆς ΑΗ, ἀεὶ δὲ ἡ ἔγγιον τῆς ΔΗ ἐλαχίστης ἐλάττων ἐστὶ τῆς ἀπώτερον, ἡ μὲν ΔΚ τῆς ΔΛ, ἡ δὲ ΔΛ τῆς ΔΘ.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ ΑΒΓ κύκλου καὶ ἔστω τὸ Μ· καὶ ἐπεζεύχθωσαν αἱ ΜΕ, ΜΖ, ΜΓ, ΜΚ, ΜΛ, ΜΘ.
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΜ τῇ ΕΜ, κοινὴ προσκείσθω ἡ ΜΔ· ἡ ἄρα ΑΔ ἴση ἐστὶ ταῖς ΕΜ, ΜΔ. ἀλλ' αἱ ΕΜ, ΜΔ τῆς ΕΔ μείζονές εἰσιν· καὶ ἡ ΑΔ ἄρα τῆς ΕΔ μείζων ἐστίν. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΜΕ τῇ ΜΖ, κοινὴ δὲ ἡ ΜΔ, αἱ ΕΜ, ΜΔ ἄρα ταῖς ΖΜ, ΜΔ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΕΜΔ γωνίας τῆς ὑπὸ ΖΜΔ μείζων ἐστίν. βάσις ἄρα ἡ ΕΔ βάσεως τῆς ΖΔ μείζων ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΖΔ τῆς ΓΔ μείζων ἐστίν· μεγίστη μὲν ἄρα ἡ ΔΑ, μείζων δὲ ἡ μὲν ΔΕ τῆς ΔΖ, ἡ δὲ ΔΖ τῆς ΔΓ.
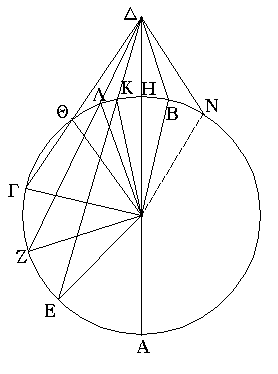
Καὶ ἐπεὶ αἱ ΜΚ, ΚΔ τῆς ΜΔ μείζονές εἰσιν, ἴση δὲ ἡ ΜΗ τῇ ΜΚ, λοιπὴ ἄρα ἡ ΚΔ λοιπῆς τῆς ΗΔ μείζων ἐστίν· ὥστε ἡ ΗΔ τῆς ΚΔ ἐλάττων ἐστίν· καὶ ἐπεὶ τριγώνου τοῦ ΜΛΔ ἐπὶ μιᾶς τῶν πλευρῶν τῆς ΜΔ δύο εὐθεῖαι ἐντὸς συνεστάθησαν αἱ ΜΚ, ΚΔ, αἱ ἄρα ΜΚ, ΚΔ τῶν ΜΛ, ΛΔ ἐλάττονές εἰσιν· ἴση δὲ ἡ ΜΚ τῇ ΜΛ· λοιπὴ ἄρα ἡ ΔΚ λοιπῆς τῆς ΔΛ ἐλάττων ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΔΛ τῆς ΔΘ ἐλάττων ἐστίν· ἐλαχίστη μὲν ἄρα ἡ ΔΗ, ἐλάττων δὲ ἡ μὲν ΔΚ τῆς ΔΛ ἡ δὲ ΔΛ τῆς ΔΘ.
Λέγω, ὅτι καὶ δύο μόνον ἴσαι ἀπὸ τοῦ Δ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ΔΗ ἐλαχίστης· συνεστάτω πρὸς τῇ ΜΔ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Μ τῇ ὑπὸ ΚΜΔ γωνίᾳ ἴση γωνία ἡ ὑπὸ ΔΜΒ καὶ ἐπεζεύχθω ἡ ΔΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΜΚ τῇ ΜΒ, κοινὴ δὲ ἡ ΜΔ, δύο δὴ αἱ ΚΜ, ΜΔ δύο ταῖς ΒΜ, ΜΔ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΚΜΔ γωνίᾳ τῇ ὑπὸ ΒΜΔ ἴση· βάσις ἄρα ἡ ΔΚ βάσει τῇ ΔΒ ἴση ἐστίν. λέγω [δή], ὅτι τῇ ΔΚ εὐθείᾳ ἄλλη ἴση οὐ προσπεσεῖται πρὸς τὸν κύκλον ἀπὸ τοῦ Δ σημείου. εἰ γὰρ δυνατόν, προσπιπτέτω καὶ ἔστω ἡ ΔΝ. ἐπεὶ οὖν ἡ ΔΚ τῇ ΔΝ ἐστιν ἴση, ἀλλ' ἡ ΔΚ τῇ ΔΒ ἐστιν ἴση, καὶ ἡ ΔΒ ἄρα τῇ ΔΝ ἐστιν ἴση, ἡ ἔγγιον τῆς ΔΗ ἐλαχίστης τῇ ἀπώτερον [ἐστιν] ἴση· ὅπερ ἀδύνατον ἐδείχθη. οὐκ ἄρα πλείους ἢ δύο ἴσαι πρὸς τὸν ΑΒΓ κύκλον ἀπὸ τοῦ Δ σημείου ἐφ' ἑκάτερα τῆς ΔΗ ἐλαχίστης προσπεσοῦνται.
Ἐὰν ἄρα κύκλου ληφθῇ τι σημεῖον ἐκτός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον διαχθῶσιν εὐθεῖαί τινες, ὧν μία μὲν διὰ τοῦ κέντρου αἱ δὲ λοιπαί, ὡς ἔτυχεν, τῶν μὲν πρὸς τὴν κοίλην περιφέρειαν προσπιπτουσῶν εὐθειῶν μεγίστη μέν ἐστιν ἡ διὰ τοῦ κέντρου, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, τῶν δὲ πρὸς τὴν κυρτὴν περιφέρειαν προσπιπτουσῶν εὐθειῶν ἐλαχίστη μέν ἐστιν ἡ μεταξὺ τοῦ τε σημείου καὶ τῆς διαμέτρου, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς ἐλαχίστης τῆς ἀπώτερόν ἐστιν ἐλάττων, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον III
Ἐὰν κύκλου ληφθῇ τι σημεῖον ἐντός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσι πλείους ἢ δύο ἴσαι εὐθεῖαι, τὸ ληφθὲν σημεῖον κέντρον ἐστὶ τοῦ κύκλου.
Ἔστω κύκλος ὁ ΑΒΓ, ἐντὸς δὲ αὐτοῦ σημεῖον τὸ Δ, καὶ ἀπὸ τοῦ Δ πρὸς τὸν ΑΒΓ κύκλον προσπιπτέτωσαν πλείους ἢ δύο ἴσαι εὐθεῖαι αἱ ΔΑ, ΔΒ, ΔΓ· λέγω, ὅτι τὸ Δ σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου.
Ἐπεζεύχθωσαν γὰρ αἱ ΑΒ, ΒΓ καὶ τετμήσθωσαν δίχα κατὰ τὰ Ε, Ζ σημεῖα, καὶ ἐπιζευχθεῖσαι αἱ ΕΔ, ΖΔ διήχθωσαν ἐπὶ τὰ Η, Κ, Θ, Λ σημεῖα.
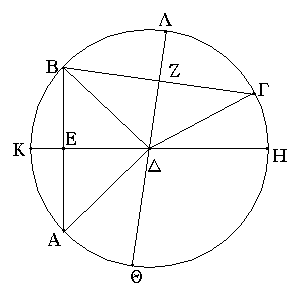
Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΑΕ τῇ ΕΒ, κοινὴ δὲ ἡ ΕΔ, δύο δὴ αἱ ΑΕ, ΕΔ δύο ταῖς ΒΕ, ΕΔ ἴσαι εἰσίν· καὶ βάσις ἡ ΔΑ βάσει τῇ ΔΒ ἴση· γωνία ἄρα ἡ ὑπὸ ΑΕΔ γωνίᾳ τῇ ὑπὸ ΒΕΔ ἴση ἐστίν· ὀρθὴ ἄρα ἑκατέρα τῶν ὑπὸ ΑΕΔ, ΒΕΔ γωνιῶν· ἡ ΗΚ ἄρα τὴν ΑΒ τέμνει δίχα καὶ πρὸς ὀρθάς. καὶ ἐπεί, ἐὰν ἐν κύκλῳ εὐθεῖά τις εὐθεῖάν τινα δίχα τε καὶ πρὸς ὀρθὰς τέμνῃ, ἐπὶ τῆς τεμνούσης ἐστὶ τὸ κέντρον τοῦ κύκλου, ἐπὶ τῆς ΗΚ ἄρα ἐστὶ τὸ κέντρον τοῦ κύκλου. διὰ τὰ αὐτὰ δὴ καὶ ἐπὶ τῆς ΘΛ ἐστι τὸ κέντρον τοῦ ΑΒΓ κύκλου. καὶ οὐδὲν ἕτερον κοινὸν ἔχουσιν αἱ ΗΚ, ΘΛ εὐθεῖαι ἢ τὸ Δ σημεῖον· τὸ Δ ἄρα σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου.
Ἐὰν ἄρα κύκλου ληφθῇ τι σημεῖον ἐντός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσι πλείους ἢ δύο ἴσαι εὐθεῖαι, τὸ ληφθὲν σημεῖον κέντρον ἐστὶ τοῦ κύκλου· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον III
Κύκλος κύκλον οὐ τέμνει κατὰ πλείονα σημεῖα ἢ δύο.
Εἰ γὰρ δυνατόν, κύκλος ὁ ΑΒΓ κύκλον τὸν ΔΕΖ τεμνέτω κατὰ πλείονα σημεῖα ἢ δύο τὰ Β, Η, Ζ, Θ, καὶ ἐπιζευχθεῖσαι αἱ ΒΘ, ΒΗ δίχα τεμνέσθωσαν κατὰ τὰ Κ, Λ σημεῖα· καὶ ἀπὸ τῶν Κ, Λ ταῖς ΒΘ, ΒΗ πρὸς ὀρθὰς ἀχθεῖσαι αἱ ΚΓ, ΛΜ διήχθωσαν ἐπὶ τὰ Α, Ε σημεῖα
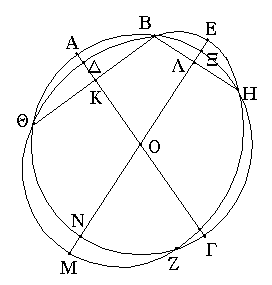
Ἐπεὶ οὖν ἐν κύκλῳ τῷ ΑΒΓ εὐθεῖά τις ἡ ΑΓ εὐθεῖάν τινα τὴν ΒΘ δίχα καὶ πρὸς ὀρθὰς τέμνει, ἐπὶ τῆς ΑΓ ἄρα ἐστὶ τὸ κέντρον τοῦ ΑΒΓ κύκλου. πάλιν, ἐπεὶ ἐν κύκλῳ τῷ αὐτῷ τῷ ΑΒΓ εὐθεῖά τις ἡ ΝΞ εὐθεῖάν τινα τὴν ΒΗ δίχα καὶ πρὸς ὀρθὰς τέμνει, ἐπὶ τῆς ΝΞ ἄρα ἐστὶ τὸ κέντρον τοῦ ΑΒΓ κύκλου. ἐδείχθη δὲ καὶ ἐπὶ τῆς ΑΓ, καὶ κατ' οὐδὲν συμβάλλουσιν αἱ ΑΓ, ΝΞ εὐθεῖαι ἢ κατὰ τὸ Ο· τὸ Ο ἄρα σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι καὶ τοῦ ΔΕΖ κύκλου κέντρον ἐστὶ τὸ Ο· δύο ἄρα κύκλων τεμνόντων ἀλλήλους τῶν ΑΒΓ, ΔΕΖ τὸ αὐτό ἐστι κέντρον τὸ Ο· ὅπερ ἐστὶν ἀδύνατον.
Οὐκ ἄρα κύκλος κύκλον τέμνει κατὰ πλείονα σημεῖα ἢ δύο· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον III
Ἐὰν δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐντός, καὶ ληφθῇ αὐτῶν τὰ κέντρα, ἡ ἐπὶ τὰ κέντρα αὐτῶν ἐπιζευγνυμένη εὐθεῖα καὶ ἐκβαλλομένη ἐπὶ τὴν συναφὴν πεσεῖται τῶν κύκλων.
Δύο γὰρ κύκλοι οἱ ΑΒΓ, ΑΔΕ ἐφαπτέσθωσαν ἀλλήλων ἐντὸς κατὰ τὸ Α σημεῖον, καὶ εἰλήφθω τοῦ μὲν ΑΒΓ κύκλου κέντρον τὸ Ζ, τοῦ δὲ ΑΔΕ τὸ Η· λέγω, ὅτι ἡ ἀπὸ τοῦ Η ἐπὶ τὸ Ζ ἐπιζευγνυμένη εὐθεῖα ἐκβαλλομένη ἐπὶ τὸ Α πεσεῖται.
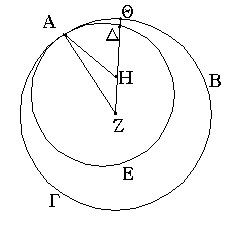
Μὴ γάρ, ἀλλ' εἰ δυνατόν, πιπτέτω ὡς ἡ ΖΗΘ, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΑΗ.
Ἐπεὶ οὖν αἱ ΑΗ, ΗΖ τῆς ΖΑ, τουτέστι τῆς ΖΘ, μείζονές εἰσιν, κοινὴ ἀφῃρήσθω ἡ ΖΗ· λοιπὴ ἄρα ἡ ΑΗ λοιπῆς τῆς ΗΘ μείζων ἐστίν. ἴση δὲ ἡ ΑΗ τῇ ΗΔ· καὶ ἡ ΗΔ ἄρα τῆς ΗΘ μείζων ἐστὶν ἡ ἐλάττων τῆς μείζονος· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα ἡ ἀπὸ τοῦ Ζ ἐπὶ τὸ Η ἐπιζευγνυμένη εὐθεῖα ἐκτὸς πεσεῖται· κατὰ τὸ Α ἄρα ἐπὶ τῆς συναφῆς πεσεῖται.
Ἐὰν ἄρα δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐντός, [καὶ ληφθῇ αὐτῶν τὰ κέντρα], ἡ ἐπὶ τὰ κέντρα αὐτῶν ἐπιζευγνυμένη εὐθεῖα [καὶ ἐκβαλλομένη] ἐπὶ τὴν συναφὴν πεσεῖται τῶν κύκλων· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον III
Ἐὰν δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐκτός, ἡ ἐπὶ τὰ κέντρα αὐτῶν ἐπιζευγνυμένη διὰ τῆς ἐπαφῆς ἐλεύσεται.
Δύο γὰρ κύκλοι οἱ ΑΒΓ, ΑΔΕ ἐφαπτέσθωσαν ἀλλήλων ἐκτὸς κατὰ τὸ Α σημεῖον, καὶ εἰλήφθω τοῦ μὲν ΑΒΓ κέντρον τὸ Ζ, τοῦ δὲ ΑΔΕ τὸ Η· λέγω, ὅτι ἡ ἀπὸ τοῦ Ζ ἐπὶ τὸ Η ἐπιζευγνυμένη εὐθεῖα διὰ τῆς κατὰ τὸ Α ἐπαφῆς ἐλεύσεται.
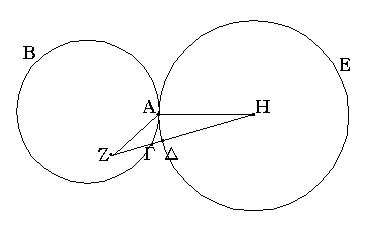
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἐρχέσθω ὡς ἡ ΖΓΔΗ, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΑΗ.
Ἐπεὶ οὖν τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου, ἴση ἐστὶν ἡ ΖΑ τῇ ΖΓ. πάλιν, ἐπεὶ τὸ Η σημεῖον κέντρον ἐστὶ τοῦ ΑΔΕ κύκλου, ἴση ἐστὶν ἡ ΗΑ τῇ ΗΔ. ἐδείχθη δὲ καὶ ἡ ΖΑ τῇ ΖΓ ἴση· αἱ ἄρα ΖΑ, ΑΗ ταῖς ΖΓ, ΗΔ ἴσαι εἰσίν· ὥστε ὅλη ἡ ΖΗ τῶν ΖΑ, ΑΗ μείζων ἐστίν· ἀλλὰ καὶ ἐλάττων· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ἀπὸ τοῦ Ζ ἐπὶ τὸ Η ἐπιζευγνυμένη εὐθεῖα διὰ τῆς κατὰ τὸ Α ἐπαφῆς οὐκ ἐλεύσεται· δι' αὐτῆς ἄρα.
Ἐὰν ἄρα δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐκτός, ἡ ἐπὶ τὰ κέντρα αὐτῶν ἐπιζευγνυμένη [εὐθεῖα] διὰ τῆς ἐπαφῆς ἐλεύσεται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον III
Κύκλος κύκλου οὐκ ἐφάπτεται κατὰ πλείονα σημεῖα ἢ καθ᾿ ἕν, ἐάν τε ἐντὸς ἐάν τε ἐκτὸς ἐφάπτηται.
Εἰ γὰρ δυνατόν, κύκλος ὁ ΑΒΓΔ κύκλου τοῦ ΕΒΖΔ ἐφαπτέσθω πρότερον ἐντὸς κατὰ πλείονα σημεῖα ἢ ἓν τὰ Δ, Β.
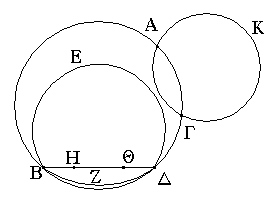
Καὶ εἰλήφθω τοῦ μὲν ΑΒΓΔ κύκλου κέντρον τὸ Η, τοῦ δὲ ΕΒΖΔ τὸ Θ.
Ἡ ἄρα ἀπὸ τοῦ Η ἐπὶ τὸ Θ ἐπιζευγνυμένη ἐπὶ τὰ Β, Δ πεσεῖται. πιπτέτω ὡς ἡ ΒΗΘΔ. καὶ ἐπεὶ τὸ Η σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓΔ κύκλου, ἴση ἐστὶν ἡ ΒΗ τῇ ΗΔ· μείζων ἄρα ἡ ΒΗ τῆς ΘΔ· πολλῷ ἄρα μείζων ἡ ΒΘ τῆς ΘΔ. πάλιν, ἐπεὶ τὸ Θ σημεῖον κέντρον ἐστὶ τοῦ ΕΒΖΔ κύκλου, ἴση ἐστὶν ἡ ΒΘ τῇ ΘΔ· ἐδείχθη δὲ αὐτῆς καὶ πολλῷ μείζων· ὅπερ ἀδύνατον· οὐκ ἄρα κύκλος κύκλου ἐφάπτεται ἐντὸς κατὰ πλείονα σημεῖα ἢ ἕν.
Λέγω δή, ὅτι οὐδὲ ἐκτός.
Εἰ γὰρ δυνατόν, κύκλος ὁ ΑΓΚ κύκλου τοῦ ΑΒΓΔ ἐφαπτέσθω ἐκτὸς κατὰ πλείονα σημεῖα ἢ ἓν τὰ Α, Γ, καὶ ἐπεζεύχθω ἡ ΑΓ.
Ἐπεὶ οὖν κύκλων τῶν ΑΒΓΔ, ΑΓΚ εἴληπται ἐπὶ τῆς περιφερείας ἑκατέρου δύο τυχόντα σημεῖα τὰ Α, Γ, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐντὸς ἑκατέρου πεσεῖται· ἀλλὰ τοῦ μὲν ΑΒΓΔ ἐντὸς ἔπεσεν, τοῦ δὲ ΑΓΚ ἐκτός· ὅπερ ἄτοπον· οὐκ ἄρα κύκλος κύκλου ἐφάπτεται ἐκτὸς κατὰ πλείονα σημεῖα ἢ ἕν. ἐδείχθη δέ, ὅτι οὐδὲ ἐντός.
Κύκλος ἄρα κύκλου οὐκ ἐφάπτεται κατὰ πλείονα σημεῖα ἢ [καθ᾿] ἕν, ἐάν τε ἐντὸς ἐάν τε ἐκτὸς ἐφάπτηται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον III
Ἐν κύκλῳ αἱ ἴσαι εὐθεῖαι ἴσον ἀπέχουσιν ἀπὸ τοῦ κέντρου, καὶ αἱ ἴσον ἀπέχουσαι ἀπὸ τοῦ κέντρου ἴσαι ἀλλήλαις εἰσίν.
Ἔστω κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ ἴσαι εὐθεῖαι ἔστωσαν αἱ ΑΒ, ΓΔ· λέγω, ὅτι αἱ ΑΒ, ΓΔ ἴσον ἀπέχουσιν ἀπὸ τοῦ κέντρου.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ ΑΒΓΔ κύκλου καὶ ἔστω τὸ Ε, καὶ ἀπὸ τοῦ Ε ἐπὶ τὰς ΑΒ, ΓΔ κάθετοι ἤχθωσαν αἱ ΕΖ, ΕΗ, καὶ ἐπεζεύχθωσαν αἱ ΑΕ, ΕΓ.
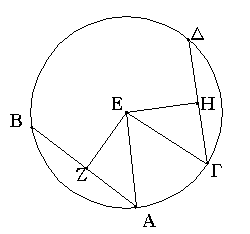
Ἐπεὶ οὖν εὐθεῖά τις διὰ τοῦ κέντρου ἡ ΕΖ εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου τὴν ΑΒ πρὸς ὀρθὰς τέμνει, καὶ δίχα αὐτὴν τέμνει. ἴση ἄρα ἡ ΑΖ τῇ ΖΒ· διπλῆ ἄρα ἡ ΑΒ τῆς ΑΖ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΓΔ τῆς ΓΗ ἐστι διπλῆ· καί ἐστιν ἴση ἡ ΑΒ τῇ ΓΔ· ἴση ἄρα καὶ ἡ ΑΖ τῇ ΓΗ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΕ τῇ ΕΓ, ἴσον καὶ τὸ ἀπὸ τῆς ΑΕ τῷ ἀπὸ τῆς ΕΓ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΕ ἴσα τὰ ἀπὸ τῶν ΑΖ, ΕΖ· ὀρθὴ γὰρ ἡ πρὸς τῷ Ζ γωνία· τῷ δὲ ἀπὸ τῆς ΕΓ ἴσα τὰ ἀπὸ τῶν ΕΗ, ΗΓ· ὀρθὴ γὰρ ἡ πρὸς τῷ Η γωνία· τὰ ἄρα ἀπὸ τῶν ΑΖ, ΖΕ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΓΗ, ΗΕ, ὧν τὸ ἀπὸ τῆς ΑΖ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΗ· ἴση γάρ ἐστιν ἡ ΑΖ τῇ ΓΗ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΖΕ τῷ ἀπὸ τῆς ΕΗ ἴσον ἐστίν· ἴση ἄρα ἡ ΕΖ τῇ ΕΗ. ἐν δὲ κύκλῳ ἴσον ἀπέχειν ἀπὸ τοῦ κέντρου εὐθεῖαι λέγονται, ὅταν αἱ ἀπὸ τοῦ κέντρου ἐπ᾿ αὐτὰς κάθετοι ἀγόμεναι ἴσαι ὦσιν· αἱ ἄρα ΑΒ, ΓΔ ἴσον ἀπέχουσιν ἀπὸ τοῦ κέντρου.
Ἀλλὰ δὴ αἱ ΑΒ, ΓΔ εὐθεῖαι ἴσον ἀπεχέτωσαν ἀπὸ τοῦ κέντρου, τουτέστιν ἴση ἔστω ἡ ΕΖ τῇ ΕΗ. λέγω, ὅτι ἴση ἐστὶ καὶ ἡ ΑΒ τῇ ΓΔ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι διπλῆ ἐστιν ἡ μὲν ΑΒ τῆς ΑΖ, ἡ δὲ ΓΔ τῆς ΓΗ· καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΕ τῇ ΓΕ, ἴσον ἐστὶ τὸ ἀπὸ τῆς ΑΕ τῷ ἀπὸ τῆς ΓΕ· ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΕ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΕΖ, ΖΑ, τῷ δὲ ἀπὸ τῆς ΓΕ ἴσα τὰ ἀπὸ τῶν ΕΗ, ΗΓ. τὰ ἄρα ἀπὸ τῶν ΕΖ, ΖΑ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΕΗ, ΗΓ· ὧν τὸ ἀπὸ τῆς ΕΖ τῷ ἀπὸ τῆς ΕΗ ἐστιν ἴσον· ἴση γὰρ ἡ ΕΖ τῇ ΕΗ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΑΖ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΗ· ἴση ἄρα ἡ ΑΖ τῇ ΓΗ· καί ἐστι τῆς μὲν ΑΖ διπλῆ ἡ ΑΒ, τῆς δὲ ΓΗ διπλῆ ἡ ΓΔ· ἴση ἄρα ἡ ΑΒ τῇ ΓΔ.
Ἐν κύκλῳ ἄρα αἱ ἴσαι εὐθεῖαι ἴσον ἀπέχουσιν ἀπὸ τοῦ κέντρου, καὶ αἱ ἴσον ἀπέχουσαι ἀπὸ τοῦ κέντρου ἴσαι ἀλλήλαις εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον III
Ἐν κύκλῳ μεγίστη μὲν ἡ διάμετρος τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν.
Ἔστω κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἔστω ἡ ΑΔ, κέντρον δὲ τὸ Ε, καὶ ἔγγιον μὲν τῆς ΑΔ διαμέτρου ἔστω ἡ ΒΓ, ἀπώτερον δὲ ἡ ΖΗ· λέγω, ὅτι μεγίστη μέν ἐστιν ἡ ΑΔ, μείζων δὲ ἡ ΒΓ τῆς ΖΗ.
Ἤχθωσαν γὰρ ἀπὸ τοῦ Ε κέντρου ἐπὶ τὰς ΒΓ, ΖΗ κάθετοι αἱ ΕΘ, ΕΚ. καὶ ἐπεὶ ἔγγιον μὲν τοῦ κέντρου ἐστὶν ἡ ΒΓ, ἀπώτερον δὲ ἡ ΖΗ, μείζων ἄρα ἡ ΕΚ τῆς ΕΘ. κείσθω τῇ ΕΘ ἴση ἡ ΕΛ, καὶ διὰ τοῦ Λ τῇ ΕΚ πρὸς ὀρθὰς ἀχθεῖσα ἡ ΛΜ διήχθω ἐπὶ τὸ Ν, καὶ ἐπεζεύχθωσαν αἱ ΜΕ, ΕΝ, ΖΕ, ΕΗ.
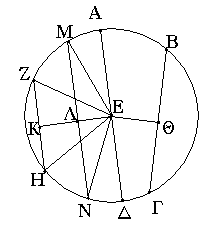
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΕΘ τῇ ΕΛ, ἴση ἐστὶ καὶ ἡ ΒΓ τῇ ΜΝ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ μὲν ΑΕ τῇ ΕΜ, ἡ δὲ ΕΔ τῇ ΕΝ, ἡ ἄρα ΑΔ ταῖς ΜΕ, ΕΝ ἴση ἐστίν. ἀλλ' αἱ μὲν ΜΕ, ΕΝ τῆς ΜΝ μείζονές εἰσιν [καὶ ἡ ΑΔ τῆς ΜΝ μείζων ἐστίν, ἴση δὲ ἡ ΜΝ τῇ ΒΓ· ἡ ΑΔ ἄρα τῆς ΒΓ μείζων ἐστίν. καὶ ἐπεὶ δύο αἱ ΜΕ, ΕΝ δύο ταῖς ΖΕ, ΕΗ ἴσαι εἰσίν, καὶ γωνία ἡ ὑπὸ ΜΕΝ γωνίας τῆς ὑπὸ ΖΕΗ μείζων [ἐστίν], βάσις ἄρα ἡ ΜΝ βάσεως τῆς ΖΗ μείζων ἐστίν. ἀλλὰ ἡ ΜΝ τῇ ΒΓ ἐδείχθη ἴση [καὶ ἡ ΒΓ τῆς ΖΗ μείζων ἐστίν]. μεγίστη μὲν ἄρα ἡ ΑΔ διάμετρος, μείζων δὲ ἡ ΒΓ τῆς ΖΗ.
Ἐν κύκλῳ ἄρα μεγίστη μέν ἐστιν ἡ διάμετρος, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον III
Ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐκτὸς πεσεῖται τοῦ κύκλου, καὶ εἰς τὸν μεταξὺ τόπον τῆς τε εὐθείας καὶ τῆς περιφερείας ἑτέρα εὐθεῖα οὐ παρεμπεσεῖται, καὶ ἡ μὲν τοῦ ἡμικυκλίου γωνία ἁπάσης γωνίας ὀξείας εὐθυγράμμου μείζων ἐστίν, ἡ δὲ λοιπὴ ἐλάττων.
Ἔστω κύκλος ὁ ΑΒΓ περὶ κέντρον τὸ Δ καὶ διάμετρον τὴν ΑΒ· λέγω, ὅτι ἡ ἀπὸ τοῦ Α τῇ ΑΒ πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐκτὸς πεσεῖται τοῦ κύκλου.
Μὴ γάρ, ἀλλ' εἰ δυνατόν, πιπτέτω ἐντὸς ὡς ἡ ΓΑ, καὶ ἐπεζεύχθω ἡ ΔΓ.
Ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΔΓ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΔΑΓ γωνίᾳ τῇ ὑπὸ ΑΓΔ. ὀρθὴ δὲ ἡ ὑπὸ ΔΑΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΑΓΔ· τριγώνου δὴ τοῦ ΑΓΔ αἱ δύο γωνίαι αἱ ὑπὸ ΔΑΓ, ΑΓΔ δύο ὀρθαῖς ἴσαι εἰσίν· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ἀπὸ τοῦ Α σημείου τῇ ΒΑ πρὸς ὀρθὰς ἀγομένη ἐντὸς πεσεῖται τοῦ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἐπὶ τῆς περιφερείας· ἐκτὸς ἄρα.
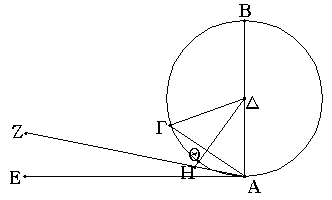
Πιπτέτω ὡς ἡ ΑΕ· λέγω δή, ὅτι εἰς τὸν μεταξὺ τόπον τῆς τε ΑΕ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἑτέρα εὐθεῖα οὐ παρεμπεσεῖται.
Εἰ γὰρ δυνατόν, παρεμπιπτέτω ὡς ἡ ΖΑ, καὶ ἤχθω ἀπὸ τοῦ Δ σημείου ἐπὶ τὴν ΖΑ κάθετος ἡ ΔΗ. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΑΗΔ, ἐλάττων δὲ ὀρθῆς ἡ ὑπὸ ΔΑΗ, μείζων ἄρα ἡ ΑΔ τῆς ΔΗ. ἴση δὲ ἡ ΔΑ τῇ ΔΘ· μείζων ἄρα ἡ ΔΘ τῆς ΔΗ, ἡ ἐλάττων τῆς μείζονος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα εἰς τὸν μεταξὺ τόπον τῆς τε εὐθείας καὶ τῆς περιφερείας ἑτέρα εὐθεῖα παρεμπεσεῖται.
Λέγω, ὅτι καὶ ἡ μὲν τοῦ ἡμικυκλίου γωνία ἡ περιεχομένη ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἁπάσης γωνίας ὀξείας εὐθυγράμμου μείζων ἐστίν, ἡ δὲ λοιπὴ ἡ περιεχομένη ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας ἁπάσης γωνίας ὀξείας εὐθυγράμμου ἐλάττων ἐστίν.
Εἰ γὰρ ἐστί τις γωνία εὐθύγραμμος μείζων μὲν τῆς περιεχομένης ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας, ἐλάττων δὲ τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας, εἰς τὸν μεταξὺ τόπον τῆς τε ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας εὐθεῖα περεμπεσεῖται, ἥτις ποιήσει μείζονα μὲν τῆς περιεχομένης ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ὑπὸ εὐθειῶν περιεχομένην, ἐλάττονα δὲ τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας. οὐ παρεμπίπτει δέ· οὐκ ἄρα τῆς περιεχομένης γωνίας ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἔσται μείζων ὀξεῖα ὑπὸ εὐθειῶν περιεχομένη, οὐδὲ μὴν ἐλάττων τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐφάπτεται τοῦ κύκλου [καὶ ὅτι εὐθεῖα κύκλου καθ᾿ ἓν μόνον ἐφάπτεται σημεῖον, ἐπειδήπερ καὶ ἡ κατὰ δύο αὐτῷ συμβάλλουσα ἐντὸς αὐτοῦ πίπτουσα ἐδείχθη]. ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον III
Ἀπὸ τοῦ δοθέντος σημείου τοῦ δοθέντος κύκλου ἐφαπτομένην εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω τὸ μὲν δοθὲν σημεῖον τὸ Α, ὁ δὲ δοθεὶς κύκλος ὁ ΒΓΔ· δεῖ δὴ ἀπὸ τοῦ Α σημείου τοῦ ΒΓΔ κύκλου ἐφαπτομένην εὐθεῖαν γραμμὴν ἀγαγεῖν.
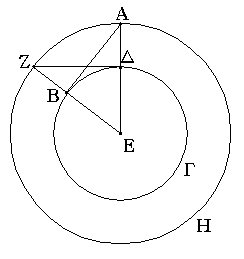
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ε, καὶ ἐπεζεύχθω ἡ ΑΕ, καὶ κέντρῳ μὲν τῷ Ε διαστήματι δὲ τῷ ΕΑ κύκλος γεγράφθω ὁ ΑΖΗ, καὶ ἀπὸ τοῦ Δ τῇ ΕΑ πρὸς ὀρθὰς ἤχθω ἡ ΔΖ, καὶ ἐπεζεύχθωσαν αἱ ΕΖ, ΑΒ· λέγω, ὅτι ἀπὸ τοῦ Α σημείου τοῦ ΒΓΔ κύκλου ἐφαπτομένη ἦκται ἡ ΑΒ.
Ἐπεὶ γὰρ τὸ Ε κέντρον ἐστὶ τῶν ΒΓΔ, ΑΖΗ κύκλων, ἴση ἄρα ἐστὶν ἡ μὲν ΕΑ τῇ ΕΖ, ἡ δὲ ΕΔ τῇ ΕΒ· δύο δὴ αἱ ΑΕ, ΕΒ δύο ταῖς ΖΕ, ΕΔ ἴσαι εἰσίν· καὶ γωνίαν κοινὴν περιέχουσι τὴν πρὸς τῷ Ε· βάσις ἄρα ἡ ΔΖ βάσει τῇ ΑΒ ἴση ἐστίν, καὶ τὸ ΔΕΖ τρίγωνον τῷ ΕΒΑ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις· ἴση ἄρα ἡ ὑπὸ ΕΔΖ τῇ ὑπὸ ΕΒΑ. ὀρθὴ δὲ ἡ ὑπὸ ΕΔΖ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΕΒΑ. καί ἐστιν ἡ ΕΒ ἐκ τοῦ κέντρου· ἡ δὲ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐφάπτεται τοῦ κύκλου· ἡ ΑΒ ἄρα ἐφάπτεται τοῦ ΒΓΔ κύκλου.
Ἀπὸ τοῦ ἄρα δοθέντος σημείου τοῦ Α τοῦ δοθέντος κύκλου τοῦ ΒΓΔ ἐφαπτομένη εὐθεῖα γραμμὴ ἦκται ἡ ΑΒ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιη΄ 18 Βιβλίον III
Ἐὰν κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τοῦ κέντρου ἐπὶ τὴν ἁφὴν ἐπιζευχθῇ τις εὐθεῖα, ἡ ἐπιζευχθεῖσα κάθετος ἔσται ἐπὶ τὴν ἐφαπτομένην.
Κύκλου γὰρ τοῦ ΑΒΓ ἐφαπτέσθω τις εὐθεῖα ἡ ΔΕ κατὰ τὸ Γ σημεῖον, καὶ εἰλήφθω τὸ κέντρον τοῦ ΑΒΓ κύκλου τὸ Ζ, καὶ ἀπὸ τοῦ Ζ ἐπὶ τὸ Γ ἐπεζεύχθω ἡ ΖΓ· λέγω, ὅτι ἡ ΖΓ κάθετός ἐστιν ἐπὶ τὴν ΔΕ.
Εἰ γὰρ μή, ἤχθω ἀπὸ τοῦ Ζ ἐπὶ τὴν ΔΕ κάθετος ἡ ΖΗ.
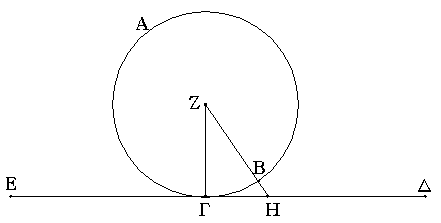
Ἐπεὶ οὖν ἡ ὑπὸ ΖΗΓ γωνία ὀρθή ἐστιν, ὀξεῖα ἄρα ἐστὶν ἡ ὑπὸ ΖΓΗ· ὑπὸ δὲ τὴν μείζονα γωνίαν ἡ μείζων πλευρὰ ὑποτείνει· μείζων ἄρα ἡ ΖΓ τῆς ΖΗ· ἴση δὲ ἡ ΖΓ τῇ ΖΒ· μείζων ἄρα καὶ ἡ ΖΒ τῆς ΖΗ ἡ ἐλάττων τῆς μείζονος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ΖΗ κάθετός ἐστιν ἐπὶ τὴν ΔΕ. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλη τις πλὴν τῆς ΖΓ· ἡ ΖΓ ἄρα κάθετός ἐστιν ἐπὶ τὴν ΔΕ.
Ἐὰν ἄρα κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τοῦ κέντρου ἐπὶ τὴν ἁφὴν ἐπιζευχθῇ τις εὐθεῖα, ἡ ἐπιζευχθεῖσα κάθετος ἔσται ἐπὶ τὴν ἐφαπτομένην· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον III
Ἐὰν κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τῆς ἁφῆς τῇ ἐφαπτομένῃ πρὸς ὀρθὰς [γωνίας] εὐθεῖα γραμμὴ ἀχθῇ, ἐπὶ τῆς ἀχθείσης ἔσται τὸ κέντρον τοῦ κύκλου.
Κύκλου γὰρ τοῦ ΑΒΓ ἐφαπτέσθω τις εὐθεῖα ἡ ΔΕ κατὰ τὸ Γ σημεῖον, καὶ ἀπὸ τοῦ Γ τῇ ΔΕ πρὸς ὀρθὰς ἤχθω ἡ ΓΑ· λέγω, ὅτι ἐπὶ τῆς ΑΓ ἐστι τὸ κέντρον τοῦ κύκλου.
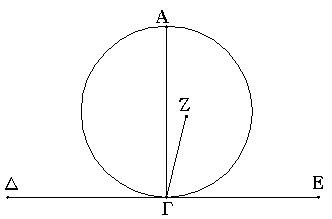
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἔστω τὸ Ζ, καὶ ἐπεζεύχθω ἡ ΓΖ
Ἐπεὶ [οὖν] κύκλου τοῦ ΑΒΓ ἐφάπτεταί τις εὐθεῖα ἡ ΔΕ, ἀπὸ δὲ τοῦ κέντρου ἐπὶ τὴν ἁφὴν ἐπέζευκται ἡ ΖΓ, ἡ ΖΓ ἄρα κάθετός ἐστιν ἐπὶ τὴν ΔΕ· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΖΓΕ. ἐστὶ δὲ καὶ ἡ ὑπὸ ΑΓΕ ὀρθή· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΖΓΕ τῇ ὑπὸ ΑΓΕ ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὸ Ζ κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλο τι πλὴν ἐπὶ τῆς ΑΓ.
Ἐὰν ἄρα κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τῆς ἁφῆς τῇ ἐφαπτομένῃ πρὸς ὀρθὰς εὐθεῖα γραμμὴ ἀχθῇ, ἐπὶ τῆς ἀχθείσης ἔσται τὸ κέντρον τοῦ κύκλου· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον III
Ἐν κύκλῳ ἡ πρὸς τῷ κέντρῳ γωνία διπλασίων ἐστὶ τῆς πρὸς τῇ περιφερείᾳ, ὅταν τὴν αὐτὴν περιφέρειαν βάσιν ἔχωσιν αἱ γωνίαι.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ πρὸς μὲν τῷ κέντρῳ αὐτοῦ γωνία ἔστω ἡ ὑπὸ ΒΕΓ, πρὸς δὲ τῇ περιφερείᾳ ἡ ὑπὸ ΒΑΓ, ἐχέτωσαν δὲ τὴν αὐτὴν περιφέρειαν βάσιν τὴν ΒΓ· λέγω, ὅτι διπλασίων ἐστὶν ἡ ὑπὸ ΒΕΓ γωνία τῆς ὑπὸ ΒΑΓ.
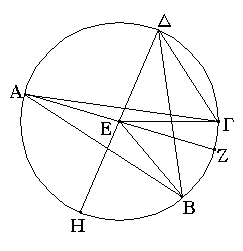
Ἐπιζευχθεῖσα γὰρ ἡ ΑΕ διήχθω ἐπὶ τὸ Ζ.
Ἐπεὶ οὖν ἴση ἐστὶν ἡ ΕΑ τῇ ΕΒ, ἴση καὶ γωνία ἡ ὑπὸ ΕΑΒ τῇ ὑπὸ ΕΒΑ· αἱ ἄρα ὑπὸ ΕΑΒ, ΕΒΑ γωνίαι τῆς ὑπὸ ΕΑΒ διπλασίους εἰσίν. ἴση δὲ ἡ ὑπὸ ΒΕΖ ταῖς ὑπὸ ΕΑΒ, ΕΒΑ· καὶ ἡ ὑπὸ ΒΕΖ ἄρα τῆς ὑπὸ ΕΑΒ ἐστι διπλῆ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΖΕΓ τῆς ὑπὸ ΕΑΓ ἐστι διπλῆ. ὅλη ἄρα ἡ ὑπὸ ΒΕΓ ὅλης τῆς ὑπὸ ΒΑΓ ἐστι διπλῆ.
Κεκλάσθω δὴ πάλιν, καὶ ἔστω ἑτέρα γωνία ἡ ὑπὸ ΒΔΓ, καὶ ἐπιζευχθεῖσα ἡ ΔΕ ἐκβεβλήσθω ἐπὶ τὸ Η. ὁμοίως δὴ δείξομεν, ὅτι διπλῆ ἐστιν ἡ ὑπὸ ΗΕΓ γωνία τῆς ὑπὸ ΕΔΓ, ὧν ἡ ὑπὸ ΗΕΒ διπλῆ ἐστι τῆς ὑπὸ ΕΔΒ· λοιπὴ ἄρα ἡ ὑπὸ ΒΕΓ διπλῆ ἐστι τῆς ὑπὸ ΒΔΓ.
Ἐν κύκλῳ ἄρα ἡ πρὸς τῷ κέντρῳ γωνία διπλασίων ἐστὶ τῆς πρὸς τῇ περιφερείᾳ, ὅταν τὴν αὐτὴν περιφέρειαν βάσιν ἔχωσιν [αἱ γωνίαι]· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 21 Βιβλίον III
Ἐν κύκλῳ αἱ ἐν τῷ αὐτῷ τμήματι γωνίαι ἴσαι ἀλλήλαις εἰσίν.
Ἔστω κύκλος ὁ ΑΒΓΔ, καὶ ἐν τῷ αὐτῷ τμήματι τῷ ΒΑΕΔ γωνίαι ἔστωσαν αἱ ὑπὸ ΒΑΔ, ΒΕΔ· λέγω, ὅτι αἱ ὑπὸ ΒΑΔ, ΒΕΔ γωνίαι ἴσαι ἀλλήλαις εἰσίν.
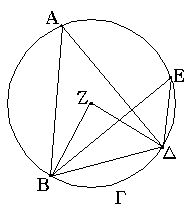
Εἰλήφθω γὰρ τοῦ ΑΒΓΔ κύκλου τὸ κέντρον, καὶ ἔστω τὸ Ζ, καὶ ἐπεζεύχθωσαν αἱ ΒΖ, ΖΔ.
Καὶ ἐπεὶ ἡ μὲν ὑπὸ ΒΖΔ γωνία πρὸς τῷ κέντρῳ ἐστίν, ἡ δὲ ὑπὸ ΒΑΔ πρὸς τῇ περιφερείᾳ, καὶ ἔχουσι τὴν αὐτὴν περιφέρειαν βάσιν τὴν ΒΓΔ, ἡ ἄρα ὑπὸ ΒΖΔ γωνία διπλασίων ἐστὶ τῆς ὑπὸ ΒΑΔ. διὰ τὰ αὐτὰ δὴ ἡ ὑπὸ ΒΖΔ καὶ τῆς ὑπὸ ΒΕΔ ἐστι διπλασίων· ἴση ἄρα ἡ ὑπὸ ΒΑΔ τῇ ὑπὸ ΒΕΔ.
Ἐν κύκλῳ ἄρα αἱ ἐν τῷ αὐτῷ τμήματι γωνίαι ἴσαι ἀλλήλαις εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον III
Τῶν ἐν τοῖς κύκλοις τετραπλεύρων αἱ ἀπεναντίον γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν.
Ἔστω κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ τετράπλευρον ἔστω τὸ ΑΒΓΔ· λέγω, ὅτι αἱ ἀπεναντίον γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν.
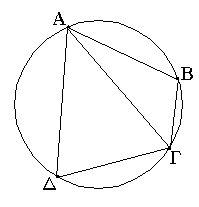
Ἐπεζεύχθωσαν αἱ ΑΓ, ΒΔ.
Ἐπεὶ οὖν παντὸς τριγώνου αἱ τρεῖς γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν, τοῦ ΑΒΓ ἄρα τριγώνου αἱ τρεῖς γωνίαι αἱ ὑπὸ ΓΑΒ, ΑΒΓ, ΒΓΑ δυσὶν ὀρθαῖς ἴσαι εἰσίν. ἴση δὲ ἡ μὲν ὑπὸ ΓΑΒ τῇ ὑπὸ ΒΔΓ· ἐν γὰρ τῷ αὐτῷ τμήματί εἰσι τῷ ΒΑΔΓ· ἡ δὲ ὑπὸ ΑΓΒ τῇ ὑπὸ ΑΔΒ· ἐν γὰρ τῷ αὐτῷ τμήματί εἰσι τῷ ΑΔΓΒ· ὅλη ἄρα ἡ ὑπὸ ΑΔΓ ταῖς ὑπὸ ΒΑΓ, ΑΓΒ ἴση ἐστίν. κοινὴ προσκείσθω ἡ ὑπὸ ΑΒΓ· αἱ ἄρα ὑπὸ ΑΒΓ, ΒΑΓ, ΑΓΒ ταῖς ὑπὸ ΑΒΓ, ΑΔΓ ἴσαι εἰσίν. ἀλλ' αἱ ὑπὸ ΑΒΓ, ΒΑΓ, ΑΓΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν. καὶ αἱ ὑπὸ ΑΒΓ, ΑΔΓ ἄρα δυσὶν ὀρθαῖς ἴσαι εἰσίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ὑπὸ ΒΑΔ, ΔΓΒ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν.
Τῶν ἄρα ἐν τοῖς κύκλοις τετραπλεύρων αἱ ἀπεναντίον γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον III
Ἐπὶ τῆς αὐτῆς εὐθείας δύο τμήματα κύκλων ὅμοια καὶ ἄνισα οὐ συσταθήσεται ἐπὶ τὰ αὐτὰ μέρη.
Εἰ γὰρ δυνατόν, ἐπὶ τῆς αὐτῆς εὐθείας τῆς ΑΒ δύο τμήματα κύκλων ὅμοια καὶ ἄνισα συνεστάτω ἐπὶ τὰ αὐτὰ μέρη τὰ ΑΓΒ, ΑΔΒ, καὶ διήχθω ἡ ΑΓΔ, καὶ ἐπεζεύχθωσαν αἱ ΓΒ, ΔΒ.
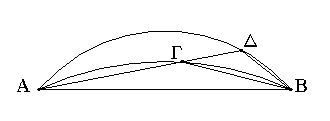
Ἐπεὶ οὖν ὅμοιόν ἐστι τὸ ΑΓΒ τμῆμα τῷ ΑΔΒ τμήματι, ὅμοια δὲ τμήματα κύκλων ἐστὶ τὰ δεχόμενα γωνίας ἴσας, ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΓΒ γωνία τῇ ὑπὸ ΑΔΒ ἡ ἐκτὸς τῇ ἐντός· ὅπερ ἐστὶν ἀδύνατον.
Οὐκ ἄρα ἐπὶ τῆς αὐτῆς εὐθείας δύο τμήματα κύκλων ὅμοια καὶ ἄνισα συσταθήσεται ἐπὶ τὰ αὐτὰ μέρη· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον III
Τὰ ἐπὶ ἴσων εὐθειῶν ὅμοια τμήματα κύκλων ἴσα ἀλλήλοις ἐστίν.
Ἔστωσαν γὰρ ἐπὶ ἴσων εὐθειῶν τῶν ΑΒ, ΓΔ ὅμοια τμήματα κύκλων τὰ ΑΕΒ, ΓΖΔ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΕΒ τμῆμα τῷ ΓΖΔ τμήματι.
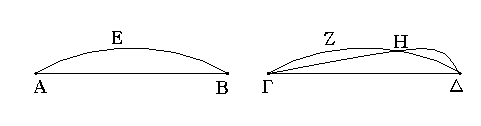
Ἐφαρμοζομένου γὰρ τοῦ ΑΕΒ τμήματος ἐπὶ τὸ ΓΖΔ καὶ τιθεμένου τοῦ μὲν Α σημείου ἐπὶ τὸ Γ τῆς δὲ ΑΒ εὐθείας ἐπὶ τὴν ΓΔ, ἐφαρμόσει καὶ τὸ Β σημεῖον ἐπὶ τὸ Δ σημεῖον διὰ τὸ ἴσην εἶναι τὴν ΑΒ τῇ ΓΔ· τῆς δὲ ΑΒ ἐπὶ τὴν ΓΔ ἐφαρμοσάσης ἐφαρμόσει καὶ τὸ ΑΕΒ τμῆμα ἐπὶ τὸ ΓΖΔ. εἰ γὰρ ἡ ΑΒ εὐθεῖα ἐπὶ τὴν ΓΔ ἐφαρμόσει, τὸ δὲ ΑΕΒ τμῆμα ἐπὶ τὸ ΓΖΔ μὴ ἐφαρμόσει, ἤτοι ἐντὸς αὐτοῦ πεσεῖται ἢ ἐκτὸς ἢ παραλλάξει ὡς τὸ ΓΗΔ, καὶ κύκλος κύκλον τέμνει κατὰ πλείονα σημεῖα ἢ δύο· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐφαρμοζομένης τῆς ΑΒ εὐθείας ἐπὶ τὴν ΓΔ οὐκ ἐφαρμόσει καὶ τὸ ΑΕΒ τμῆμα ἐπὶ τὸ ΓΖΔ· ἐφαρμόσει ἄρα, καὶ ἴσον αὐτῷ ἔσται.
Τὰ ἄρα ἐπὶ ἴσων εὐθειῶν ὅμοια τμήματα κύκλων ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον III
Κύκλου τμήματος δοθέντος προσαναγράψαι τὸν κύκλον, οὗπέρ ἐστι τμῆμα.
Ἔστω τὸ δοθὲν τμῆμα κύκλου τὸ ΑΒΓ· δεῖ δὴ τοῦ ΑΒΓ τμήματος προσαναγράψαι τὸν κύκλον, οὗπέρ ἐστι τμῆμα.
Τετμήσθω γὰρ ἡ ΑΓ δίχα κατὰ τὸ Δ, καὶ ἤχθω ἀπὸ τοῦ Δ σημείου τῇ ΑΓ πρὸς ὀρθὰς ἡ ΔΒ, καὶ ἐπεζεύχθω ἡ ΑΒ· ἡ ὑπὸ ΑΒΔ γωνία ἄρα τῆς ὑπὸ ΒΑΔ ἤτοι μείζων ἐστὶν ἢ ἴση ἢ ἐλάττων.
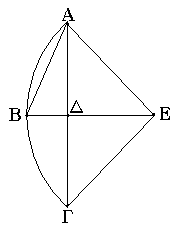
Ἔστω πρότερον μείζων, καὶ συνεστάτω πρὸς τῇ ΒΑ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΑΒΔ γωνίᾳ ἴση ἡ ὑπὸ ΒΑΕ, καὶ διήχθω ἡ ΔΒ ἐπὶ τὸ Ε, καὶ ἐπεζεύχθω ἡ ΕΓ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΑΒΕ γωνία τῇ ὑπὸ ΒΑΕ, ἴση ἄρα ἐστὶ καὶ ἡ ΕΒ εὐθεῖα τῇ ΕΑ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΔΓ, κοινὴ δὲ ἡ ΔΕ, δύο δὴ αἱ ΑΔ, ΔΕ δύο ταῖς ΓΔ, ΔΕ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΔΕ γωνίᾳ τῇ ὑπὸ ΓΔΕ ἐστιν ἴση· ὀρθὴ γὰρ ἑκατέρα· βάσις ἄρα ἡ ΑΕ βάσει τῇ ΓΕ ἐστιν ἴση. ἀλλὰ ἡ ΑΕ τῇ ΒΕ ἐδείχθη ἴση· καὶ ἡ ΒΕ ἄρα τῇ ΓΕ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΑΕ, ΕΒ, ΕΓ ἴσαι ἀλλήλαις εἰσίν· ὁ ἄρα κέντρῳ τῷ Ε διαστήματι δὲ ἑνὶ τῶν ΑΕ, ΕΒ, ΕΓ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἔσται προσαναγεγραμμένος. κύκλου ἄρα τμήματος δοθέντος προσαναγέγραπται ὁ κύκλος. καὶ δῆλον, ὡς τὸ ΑΒΓ τμῆμα ἔλαττόν ἐστιν ἡμικυκλίου διὰ τὸ τὸ Ε κέντρον ἐκτὸς αὐτοῦ τυγχάνειν.
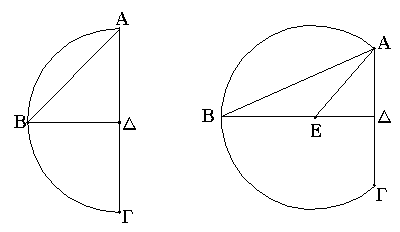
Ὁμοίως [δὲ] κἂν ᾖ ἡ ὑπὸ ΑΒΔ γωνία ἴση τῇ ὑπὸ ΒΑΔ, τῆς ΑΔ ἴσης γενομένης ἑκατέρᾳ τῶν ΒΔ, ΔΓ αἱ τρεῖς αἱ ΔΑ, ΔΒ, ΔΓ ἴσαι ἀλλήλαις ἔσονται, καὶ ἔσται τὸ Δ κέντρον τοῦ προσαναπεπληρωμένου κύκλου, καὶ δηλαδὴ ἔσται τὸ ΑΒΓ ἡμικύκλιον.
Ἐὰν δὲ ἡ ὑπὸ ΑΒΔ ἐλάττων ᾖ τῆς ὑπὸ ΒΑΔ, καὶ συστησώμεθα πρὸς τῇ ΒΑ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΑΒΔ γωνίᾳ ἴσην, ἐντὸς τοῦ ΑΒΓ τμήματος πεσεῖται τὸ κέντρον ἐπὶ τῆς ΔΒ, καὶ ἔσται δηλαδὴ τὸ ΑΒΓ τμῆμα μεῖζον ἡμικυκλίου.
Κύκλου ἄρα τμήματος δοθέντος προσαναγέγραπται ὁ κύκλος· ὅπερ ἔδει ποιῆσαι.
Πρότασις κς΄ 26 Βιβλίον III
Ἐν τοῖς ἴσοις κύκλοις αἱ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι.
Ἔστωσαν ἴσοι κύκλοι οἱ ΑΒΓ, ΔΕΖ καὶ ἐν αὐτοῖς ἴσαι γωνίαι ἔστωσαν πρὸς μὲν τοῖς κέντροις αἱ ὑπὸ ΒΗΓ, ΕΘΖ, πρὸς δὲ ταῖς περιφερείαις αἱ ὑπὸ ΒΑΓ, ΕΔΖ· λέγω, ὅτι ἴση ἐστὶν ἡ ΒΚΓ περιφέρεια τῇ ΕΛΖ περιφερείᾳ.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΓ, ΕΖ.
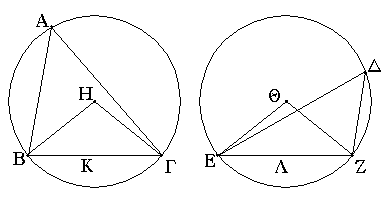
Καὶ ἐπεὶ ἴσοι εἰσὶν οἱ ΑΒΓ, ΔΕΖ κύκλοι, ἴσαι εἰσὶν αἱ ἐκ τῶν κέντρων· δύο δὴ αἱ ΒΗ, ΗΓ δύο ταῖς ΕΘ, ΘΖ ἴσαι· καὶ γωνία ἡ πρὸς τῷ
Η γωνίᾳ τῇ πρὸς τῷ Θ ἴση· βάσις ἄρα ἡ ΒΓ βάσει τῇ ΕΖ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ πρὸς τῷ Α γωνία τῇ πρὸς τῷ Δ, ὅμοιον ἄρα ἐστὶ τὸ ΒΑΓ τμῆμα τῷ ΕΔΖ τμήματι· καί εἰσιν ἐπὶ ἴσων εὐθειῶν [τῶν ΒΓ, ΕΖ]· τὰ δὲ ἐπὶ ἴσων εὐθειῶν ὅμοια τμήματα κύκλων ἴσα ἀλλήλοις ἐστίν· ἴσον ἄρα τὸ ΒΑΓ τμῆμα τῷ ΕΔΖ. ἔστι δὲ καὶ ὅλος ὁ ΑΒΓ κύκλος ὅλῳ τῷ ΔΕΖ κύκλῳ ἴσος· λοιπὴ ἄρα ἡ ΒΚΓ περιφέρεια τῇ ΕΛΖ περιφερείᾳ ἐστὶν ἴση.
Ἐν ἄρα τοῖς ἴσοις κύκλοις αἱ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον III
Ἐν τοῖς ἴσοις κύκλοις αἱ ἐπὶ ἴσων περιφερειῶν βεβηκυῖαι γωνίαι ἴσαι ἀλλήλαις εἰσίν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι.
Ἐν γὰρ ἴσοις κύκλοις τοῖς ΑΒΓ, ΔΕΖ ἐπὶ ἴσων περιφερειῶν τῶν ΒΓ, ΕΖ πρὸς μὲν τοῖς Η, Θ κέντροις γωνίαι βεβηκέτωσαν αἱ ὑπὸ ΒΗΓ, ΕΘΖ, πρὸς δὲ ταῖς περιφερείαις αἱ ὑπὸ ΒΑΓ, ΕΔΖ· λέγω, ὅτι ἡ μὲν ὑπὸ ΒΗΓ γωνία τῇ ὑπὸ ΕΘΖ ἐστιν ἴση, ἡ δὲ ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ ἐστιν ἴση.
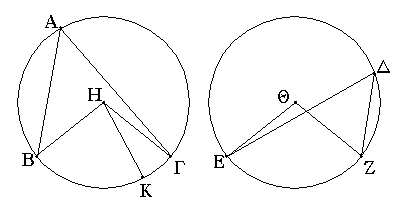
Εἰ γὰρ ἄνισός ἐστιν ἡ ὑπὸ ΒΗΓ τῇ ὑπὸ ΕΘΖ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ὑπὸ ΒΗΓ, καὶ συνεστάτω πρὸς τῇ ΒΗ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Η τῇ ὑπὸ ΕΘΖ γωνίᾳ ἴση ἡ ὑπὸ ΒΗΚ· αἱ δὲ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ὅταν πρὸς τοῖς κέντροις ὦσιν· ἴση ἄρα ἡ ΒΚ περιφέρεια τῇ ΕΖ περιφερείᾳ. ἀλλὰ ἡ ΕΖ τῇ ΒΓ ἐστιν ἴση· καὶ ἡ ΒΚ ἄρα τῇ ΒΓ ἐστιν ἴση ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἄνισός ἐστιν ἡ ὑπὸ ΒΗΓ γωνία τῇ ὑπὸ ΕΘΖ· ἴση ἄρα. καί ἐστι τῆς μὲν ὑπὸ ΒΗΓ ἡμίσεια ἡ πρὸς τῷ Α, τῆς δὲ ὑπὸ ΕΘΖ ἡμίσεια ἡ πρὸς τῷ Δ· ἴση ἄρα καὶ ἡ πρὸς τῷ Α γωνία τῇ πρὸς τῷ Δ.
Ἐν ἄρα τοῖς ἴσοις κύκλοις αἱ ἐπὶ ἴσων περιφερειῶν βεβηκυῖαι γωνίαι ἴσαι ἀλλήλαις εἰσίν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον III
Ἐν τοῖς ἴσοις κύκλοις αἱ ἴσαι εὐθεῖαι ἴσας περιφερείας ἀφαιροῦσι τὴν μὲν μείζονα τῇ μείζονι τὴν δὲ ἐλάττονα τῇ ἐλάττονι.
Ἔστωσαν ἴσοι κύκλοι οἱ ΑΒΓ, ΔΕΖ, καὶ ἐν τοῖς κύκλοις ἴσαι εὐθεῖαι ἔστωσαν αἱ ΑΒ, ΔΕ τὰς μὲν ΑΓΒ, ΔΖΕ περιφερείας μείζονας ἀφαιροῦσαι τὰς δὲ ΑΗΒ, ΔΘΕ ἐλάττονας· λέγω, ὅτι ἡ μὲν ΑΓΒ μείζων περιφέρεια ἴση ἐστὶ τῇ ΔΖΕ μείζονι περιφερείᾳ, ἡ δὲ ΑΗΒ ἐλάττων περιφέρεια τῇ ΔΘΕ.
Εἰλήφθω γὰρ τὰ κέντρα τῶν κύκλων τὰ Κ, Λ, καὶ ἐπεζεύχθωσαν αἱ ΑΚ, ΚΒ, ΔΛ, ΛΕ.
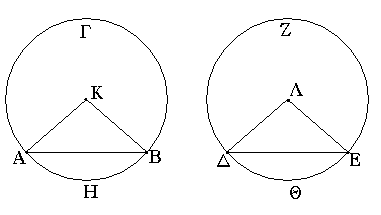
Καὶ ἐπεὶ ἴσοι κύκλοι εἰσίν, ἴσαι εἰσὶ καὶ αἱ ἐκ τῶν κέντρων· δύο δὴ αἱ ΑΚ, ΚΒ δυσὶ ταῖς ΔΛ, ΛΕ ἴσαι εἰσίν· καὶ βάσις ἡ ΑΒ βάσει τῇ ΔΕ ἴση· γωνία ἄρα ἡ ὑπὸ ΑΚΒ γωνίᾳ τῇ ὑπὸ ΔΛΕ ἴση ἐστίν. αἱ δὲ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ὅταν πρὸς τοῖς κέντροις ὦσιν· ἴση ἄρα ἡ ΑΗΒ περιφέρεια τῇ ΔΘΕ. ἐστὶ δὲ καὶ ὅλος ὁ ΑΒΓ κύκλος ὅλῳ τῷ ΔΕΖ κύκλῳ ἴσος· καὶ λοιπὴ ἄρα ἡ ΑΓΒ περιφέρεια λοιπῇ τῇ ΔΖΕ περιφερείᾳ ἴση ἐστίν.
Ἐν ἄρα τοῖς ἴσοις κύκλοις αἱ ἴσαι εὐθεῖαι ἴσας περιφερείας ἀφαιροῦσι τὴν μὲν μείζονα τῇ μείζονι τὴν δὲ ἐλάττονα τῇ ἐλάττονι· ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον III
Ἐν τοῖς ἴσοις κύκλοις τὰς ἴσας περιφερείας ἴσαι εὐθεῖαι ὑποτείνουσιν.
Ἔστωσαν ἴσοι κύκλοι οἱ ΑΒΓ, ΔΕΖ, καὶ ἐν αὐτοῖς ἴσαι περιφέρειαι ἀπειλήφθωσαν αἱ ΒΗΓ, ΕΘΖ, καὶ ἐπεζεύχθωσαν αἱ ΒΓ, ΕΖ εὐθεῖαι· λέγω, ὅτι ἴση ἐστὶν ἡ ΒΓ τῇ ΕΖ.
Εἰλήφθω γὰρ τὰ κέντρα τῶν κύκλων, καὶ ἔστω τὰ Κ, Λ, καὶ ἐπεζεύχθωσαν αἱ ΒΚ, ΚΓ, ΕΛ, ΛΖ.
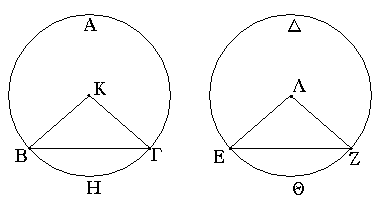
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΗΓ περιφέρεια τῇ ΕΘΖ περιφερείᾳ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΒΚΓ τῇ ὑπὸ ΕΛΖ. καὶ ἐπεὶ ἴσοι εἰσὶν οἱ ΑΒΓ, ΔΕΖ κύκλοι, ἴσαι εἰσὶ καὶ αἱ ἐκ τῶν κέντρων· δύο δὴ αἱ ΒΚ, ΚΓ δυσὶ ταῖς ΕΛ, ΛΖ ἴσαι εἰσίν· καὶ γωνίας ἴσας περιέχουσιν· βάσις ἄρα ἡ ΒΓ βάσει τῇ ΕΖ ἴση ἐστίν.
Ἐν ἄρα τοῖς ἴσοις κύκλοις τὰς ἴσας περιφερείας ἴσαι εὐθεῖαι ὑποτείνουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον III
Ἐν τοῖς ἴσοις κύκλοις τὰς ἴσας περιφερείας ἴσαι εὐθεῖαι ὑποτείνουσιν.
Ἔστω ἡ δοθεῖσα περιφέρεια ἡ ΑΔΒ· δεῖ δὴ τὴν ΑΔΒ περιφέρειαν δίχα τεμεῖν.
Ἐπεζεύχθω ἡ ΑΒ, καὶ τετμήσθω δίχα κατὰ τὸ Γ, καὶ ἀπὸ τοῦ Γ σημείου τῇ ΑΒ εὐθείᾳ πρὸς ὀρθὰς ἤχθω ἡ ΓΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΒ.
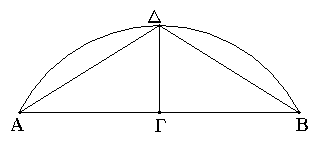
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, κοινὴ δὲ ἡ ΓΔ, δύο δὴ αἱ ΑΓ, ΓΔ δυσὶ ταῖς ΒΓ, ΓΔ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΑΓΔ γωνίᾳ τῇ ὑπὸ ΒΓΔ ἴση· ὀρθὴ γὰρ ἑκατέρα· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΔΒ ἴση ἐστίν. αἱ δὲ ἴσαι εὐθεῖαι ἴσας περιφερείας ἀφαιροῦσι τὴν μὲν μείζονα τῇ μείζονι τὴν δὲ ἐλάττονα τῇ ἐλάττονι· καί ἐστιν ἑκατέρα τῶν ΑΔ, ΔΒ περιφερειῶν ἐλάττων ἡμικυκλίου· ἴση ἄρα ἡ ΑΔ περιφέρεια τῇ ΔΒ περιφερείᾳ.
Ἡ ἄρα δοθεῖσα περιφέρεια δίχα τέτμηται κατὰ τὸ Δ σημεῖον· ὅπερ ἔδει ποιῆσαι.
Πρότασις λα΄ 31 Βιβλίον III
Ἐν κύκλῳ ἡ μὲν ἐν τῷ ἡμικυκλίῳ γωνία ὀρθή ἐστιν, ἡ δὲ ἐν τῷ μείζονι τμήματι ἐλάττων ὀρθῆς, ἡ δὲ ἐν τῷ ἐλάττονι τμήματι μείζων ὀρθῆς· καὶ ἔτι ἡ μὲν τοῦ μείζονος τμήματος γωνία μείζων ἐστὶν ὀρθῆς, ἡ δὲ τοῦ ἐλάττονος τμήματος γωνία ἐλάττων ὀρθῆς.
Ἔστω κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἔστω ἡ ΒΓ, κέντρον δὲ τὸ Ε, καὶ ἐπεζεύχθωσαν αἱ ΒΑ, ΑΓ, ΑΔ, ΔΓ· λέγω, ὅτι ἡ μὲν ἐν τῷ ΒΑΓ ἡμικυκλίῳ γωνία ἡ ὑπὸ ΒΑΓ ὀρθή ἐστιν, ἡ δὲ ἐν τῷ ΑΒΓ μείζονι τοῦ ἡμικυκλίου τμήματι γωνία ἡ ὑπὸ ΑΒΓ ἐλάττων ἐστὶν ὀρθῆς, ἡ δὲ ἐν τῷ ΑΔΓ ἐλάττονι τοῦ ἡμικυκλίου τμήματι γωνία ἡ ὑπὸ ΑΔΓ μείζων ἐστὶν ὀρθῆς.
Ἐπεζεύχθω ἡ ΑΕ, καὶ διήχθω ἡ ΒΑ ἐπὶ τὸ Ζ.
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΕΑ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΑΒΕ τῇ ὑπὸ ΒΑΕ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΓΕ τῇ ΕΑ, ἴση ἐστὶ καὶ ἡ ὑπὸ ΑΓΕ τῇ ὑπὸ ΓΑΕ· ὅλη ἄρα ἡ ὑπὸ ΒΑΓ δυσὶ ταῖς ὑπὸ ΑΒΓ, ΑΓΒ ἴση ἐστίν. ἐστὶ δὲ καὶ ἡ ὑπὸ ΖΑΓ ἐκτὸς τοῦ ΑΒΓ τριγώνου δυσὶ ταῖς ὑπὸ ΑΒΓ, ΑΓΒ γωνίαις ἴση· ἴση ἄρα καὶ ἡ ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΖΑΓ· ὀρθὴ ἄρα ἑκατέρα· ἡ ἄρα ἐν τῷ ΒΑΓ ἡμικυκλίῳ γωνία ἡ ὑπὸ ΒΑΓ ὀρθή ἐστιν.
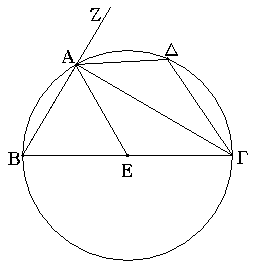
Καὶ ἐπεὶ τοῦ ΑΒΓ τριγώνου δύο γωνίαι αἱ ὑπὸ ΑΒΓ, ΒΑΓ δύο ὀρθῶν ἐλάττονές εἰσιν, ὀρθὴ δὲ ἡ ὑπὸ ΒΑΓ, ἐλάττων ἄρα ὀρθῆς ἐστιν ἡ ὑπὸ ΑΒΓ γωνία· καί ἐστιν ἐν τῷ ΑΒΓ μείζονι τοῦ ἡμικυκλίου τμήματι.
Καὶ ἐπεὶ ἐν κύκλῳ τετράπλευρόν ἐστι τὸ ΑΒΓΔ, τῶν δὲ ἐν τοῖς κύκλοις τετραπλεύρων αἱ ἀπεναντίον γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν [αἱ ἄρα ὑπὸ ΑΒΓ, ΑΔΓ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν], καί ἐστιν ἡ ὑπὸ ΑΒΓ ἐλάττων ὀρθῆς· λοιπὴ ἄρα ἡ ὑπὸ ΑΔΓ γωνία μείζων ὀρθῆς ἐστιν· καί ἐστιν ἐν τῷ ΑΔΓ ἐλάττονι τοῦ ἡμικυκλίου τμήματι.
Λέγω, ὅτι καὶ ἡ μὲν τοῦ μείζονος τμήματος γωνία ἡ περιεχομένη ὑπό [τε] τῆς ΑΒΓ περιφερείας καὶ τῆς ΑΓ εὐθείας μείζων ἐστὶν ὀρθῆς, ἡ δὲ τοῦ ἐλάττονος τμήματος γωνία ἡ περιεχομένη ὑπό [τε] τῆς ΑΔ[Γ] περιφερείας καὶ τῆς ΑΓ εὐθείας ἐλάττων ἐστὶν ὀρθῆς. καί ἐστιν αὐτόθεν φανερόν. ἐπεὶ γὰρ ἡ ὑπὸ τῶν ΒΑ, ΑΓ εὐθειῶν ὀρθή ἐστιν, ἡ ἄρα ὑπὸ τῆς ΑΒΓ περιφερείας καὶ τῆς ΑΓ εὐθείας περιεχομένη μείζων ἐστὶν ὀρθῆς. πάλιν, ἐπεὶ ἡ ὑπὸ τῶν ΑΓ, ΑΖ εὐθειῶν ὀρθή ἐστιν, ἡ ἄρα ὑπὸ τῆς ΓΑ εὐθείας καὶ τῆς ΑΔ[Γ] περιφερείας περιεχομένη ἐλάττων ἐστὶν ὀρθῆς.
Ἐν κύκλῳ ἄρα ἡ μὲν ἐν τῷ ἡμικυκλίῳ γωνία ὀρθή ἐστιν, ἡ δὲ ἐν τῷ μείζονι τμήματι ἐλάττων ὀρθῆς, ἡ δὲ ἐν τῷ ἐλάττονι [τμήματι] μείζων ὀρθῆς, καὶ ἔτι ἡ μὲν τοῦ μείζονος τμήματος [γωνία] μείζων [ἐστὶν] ὀρθῆς, ἡ δὲ τοῦ ἐλάττονος τμήματος [γωνία] ἐλάττων ὀρθῆς· ὅπερ ἔδει δεῖξαι.
[Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν [ἡ] μία γωνία τριγώνου ταῖς δυσὶν ἴση ᾖ, ὀρθή ἐστιν ἡ γωνία διὰ τὸ καὶ τὴν ἐκείνης ἐκτὸς ταῖς αὐταῖς ἴσην εἶναι· ἐὰν δὲ αἱ ἐφεξῆς ἴσαι ὦσιν, ὀρθαί εἰσιν.]
Πρότασις λβ΄ 32 Βιβλίον III
Ἐὰν κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τῆς ἁφῆς εἰς τὸν κύκλον διαχθῇ τις εὐθεῖα τέμνουσα τὸν κύκλον, ἃς ποιεῖ γωνίας πρὸς τῇ ἐφαπτομένῃ, ἴσαι ἔσονται ταῖς ἐν τοῖς ἐναλλὰξ τοῦ κύκλου τμήμασι γωνίαις.
Κύκλου γὰρ τοῦ ΑΒΓΔ ἐφαπτέσθω τις εὐθεῖα ἡ ΕΖ κατὰ τὸ Β σημεῖον, καὶ ἀπὸ τοῦ Β σημείου διήχθω τις εὐθεῖα εἰς τὸν ΑΒΓΔ κύκλον τέμνουσα αὐτὸν ἡ ΒΔ. λέγω, ὅτι ἃς ποιεῖ γωνίας ἡ ΒΔ μετὰ τῆς ΕΖ ἐφαπτομένης, ἴσαι ἔσονται ταῖς ἐν τοῖς ἐναλλὰξ τμήμασι τοῦ κύκλου γωνίαις, τουτέστιν, ὅτι ἡ μὲν ὑπὸ ΖΒΔ γωνία ἴση ἐστὶ τῇ ἐν τῷ ΒΑΔ τμήματι συνισταμένῃ γωνίᾳ, ἡ δὲ ὑπὸ ΕΒΔ γωνία ἴση ἐστὶ τῇ ἐν τῷ ΔΓΒ τμήματι συνισταμένῃ γωνίᾳ.
Ἤχθω γὰρ ἀπὸ τοῦ Β τῇ ΕΖ πρὸς ὀρθὰς ἡ ΒΑ, καὶ εἰλήφθω ἐπὶ τῆς ΒΔ περιφερείας τυχὸν σημεῖον τὸ Γ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΓ, ΓΒ.
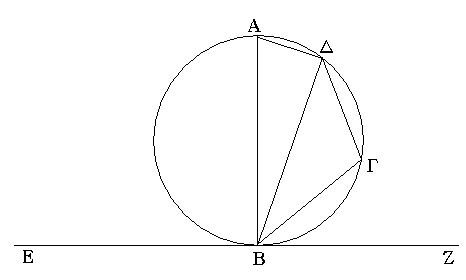
Καὶ ἐπεὶ κύκλου τοῦ ΑΒΓΔ ἐφάπτεταί τις εὐθεῖα ἡ ΕΖ κατὰ τὸ Β, καὶ ἀπὸ τῆς ἁφῆς ἦκται τῇ ἐφαπτομένῃ πρὸς ὀρθὰς ἡ ΒΑ, ἐπὶ τῆς ΒΑ ἄρα τὸ κέντρον ἐστὶ τοῦ ΑΒΓΔ κύκλου. ἡ ΒΑ ἄρα διάμετρός ἐστι τοῦ ΑΒΓΔ κύκλου· ἡ ἄρα ὑπὸ ΑΔΒ γωνία ἐν ἡμικυκλίῳ οὖσα ὀρθή ἐστιν. λοιπαὶ ἄρα αἱ ὑπὸ ΒΑΔ, ΑΒΔ μιᾷ ὀρθῇ ἴσαι εἰσίν. ἐστὶ δὲ καὶ ἡ ὑπὸ ΑΒΖ ὀρθή· ἡ ἄρα ὑπὸ ΑΒΖ ἴση ἐστὶ ταῖς ὑπὸ ΒΑΔ, ΑΒΔ. κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΑΒΔ· λοιπὴ ἄρα ἡ ὑπὸ ΔΒΖ γωνία ἴση ἐστὶ τῇ ἐν τῷ ἐναλλὰξ τμήματι τοῦ κύκλου γωνίᾳ τῇ ὑπὸ ΒΑΔ. καὶ ἐπεὶ ἐν κύκλῳ τετράπλευρόν ἐστι τὸ ΑΒΓΔ, αἱ ἀπεναντίον αὐτοῦ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. εἰσὶ δὲ καὶ αἱ ὑπὸ ΔΒΖ, ΔΒΕ δυσὶν ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΔΒΖ, ΔΒΕ ταῖς ὑπὸ ΒΑΔ, ΒΓΔ ἴσαι εἰσίν, ὧν ἡ ὑπὸ ΒΑΔ τῇ ὑπὸ ΔΒΖ ἐδείχθη ἴση· λοιπὴ ἄρα ἡ ὑπὸ ΔΒΕ τῇ ἐν τῷ ἐναλλὰξ τοῦ κύκλου τμήματι τῷ ΔΓΒ τῇ ὑπὸ ΔΓΒ γωνίᾳ ἐστὶν ἴση.
Ἐὰν ἄρα κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τῆς ἁφῆς εἰς τὸν κύκλον διαχθῇ τις εὐθεῖα τέμνουσα τὸν κύκλον, ἃς ποιεῖ γωνίας πρὸς τῇ ἐφαπτομένῃ, ἴσαι ἔσονται ταῖς ἐν τοῖς ἐναλλὰξ τοῦ κύκλου τμήμασι γωνίαις· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον III
Ἐπὶ τῆς δοθείσης εὐθείας γράψαι τμῆμα κύκλου δεχόμενον γωνίαν ἴσην τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ.
Ἔστω ἡ δοθεῖσα εὐθεῖα ἡ ΑΒ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ πρὸς τῷ Γ· δεῖ δὴ ἐπὶ τῆς δοθείσης εὐθείας τῆς ΑΒ γράψαι τμῆμα κύκλου δεχόμενον γωνίαν ἴσην τῇ πρὸς τῷ Γ.
Ἡ δὴ πρὸς τῷ Γ [γωνία] ἤτοι ὀξεῖά ἐστιν ἢ ὀρθὴ ἢ ἀμβλεῖα· ἔστω πρότερον ὀξεῖα, καὶ ὡς ἐπὶ τῆς πρώτης καταγραφῆς συνεστάτω πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ Α σημείῳ τῇ πρὸς τῷ Γ γωνίᾳ ἴση ἡ ὑπὸ ΒΑΔ· ὀξεῖα ἄρα ἐστὶ καὶ ἡ ὑπὸ ΒΑΔ. ἤχθω τῇ ΔΑ πρὸς ὀρθὰς ἡ ΑΕ, καὶ τετμήσθω ἡ ΑΒ δίχα κατὰ τὸ Ζ, καὶ ἤχθω ἀπὸ τοῦ Ζ σημείου τῇ ΑΒ πρὸς ὀρθὰς ἡ ΖΗ, καὶ ἐπεζεύχθω ἡ ΗΒ.
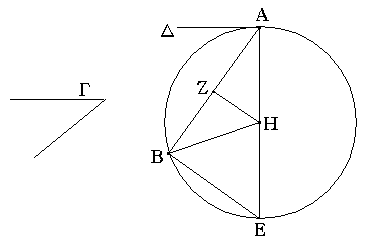
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΖ τῇ ΖΒ, κοινὴ δὲ ἡ ΖΗ, δύο δὴ αἱ ΑΖ, ΖΗ δύο ταῖς ΒΖ, ΖΗ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΑΖΗ [γωνίᾳ] τῇ ὑπὸ ΒΖΗ ἴση· βάσις ἄρα ἡ ΑΗ βάσει τῇ ΒΗ ἴση ἐστίν. ὁ ἄρα κέντρῳ μὲν τῷ Η διαστήματι δὲ τῷ ΗΑ κύκλος γραφόμενος ἥξει καὶ διὰ τοῦ Β. γεγράφθω καὶ ἔστω ὁ ΑΒΕ, καὶ ἐπεζεύχθω ἡ ΕΒ. ἐπεὶ οὖν ἀπ' ἄκρας τῆς ΑΕ διαμέτρου ἀπὸ τοῦ Α τῇ ΑΕ πρὸς ὀρθάς ἐστιν ἡ ΑΔ, ἡ ΑΔ ἄρα ἐφάπτεται τοῦ ΑΒΕ κύκλου· ἐπεὶ οὖν κύκλου τοῦ ΑΒΕ ἐφάπτεταί τις εὐθεῖα ἡ ΑΔ, καὶ ἀπὸ τῆς κατὰ τὸ Α ἁφῆς εἰς τὸν ΑΒΕ κύκλον διῆκταί τις εὐθεῖα ἡ ΑΒ, ἡ ἄρα ὑπὸ ΔΑΒ γωνία ἴση ἐστὶ τῇ ἐν τῷ ἐναλλὰξ τοῦ κύκλου τμήματι γωνίᾳ τῇ ὑπὸ ΑΕΒ. ἀλλ' ἡ ὑπὸ ΔΑΒ τῇ πρὸς τῷ Γ ἐστιν ἴση· καὶ ἡ πρὸς τῷ Γ ἄρα γωνία ἴση ἐστὶ τῇ ὑπὸ ΑΕΒ.
Ἐπὶ τῆς δοθείσης ἄρα εὐθείας τῆς ΑΒ τμῆμα κύκλου γέγραπται τὸ ΑΕΒ δεχόμενον γωνίαν τὴν ὑπὸ ΑΕΒ ἴσην τῇ δοθείσῃ τῇ πρὸς τῷ Γ.
Ἀλλὰ δὴ ὀρθὴ ἔστω ἡ πρὸς τῷ Γ· καὶ δέον πάλιν ἔστω ἐπὶ τῆς ΑΒ γράψαι τμῆμα κύκλου δεχόμενον γωνίαν ἴσην τῇ πρὸς τῷ Γ ὀρθῇ [γωνίᾳ]. συνεστάτω [πάλιν] τῇ πρὸς τῷ Γ ὀρθῇ γωνίᾳ ἴση ἡ ὑπὸ ΒΑΔ, ὡς ἔχει ἐπὶ τῆς δευτέρας καταγραφῆς, καὶ τετμήσθω ἡ ΑΒ δίχα κατὰ τὸ Ζ, καὶ κέντρῳ τῷ Ζ, διαστήματι δὲ ὁποτέρῳ τῶν ΖΑ, ΖΒ, κύκλος γεγράφθω ὁ ΑΕΒ.
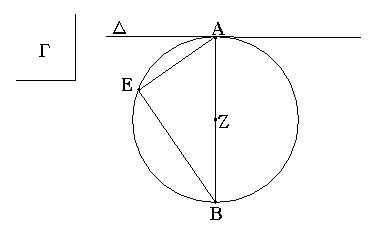
Ἐφάπτεται ἄρα ἡ ΑΔ εὐθεῖα τοῦ ΑΒΕ κύκλου διὰ τὸ ὀρθὴν εἶναι τὴν πρὸς τῷ Α γωνίαν. καὶ ἴση ἐστὶν ἡ ὑπὸ ΒΑΔ γωνία τῇ ἐν τῷ ΑΕΒ τμήματι· ὀρθὴ γὰρ καὶ αὐτὴ ἐν ἡμικυκλίῳ οὖσα. ἀλλὰ καὶ ἡ ὑπὸ ΒΑΔ τῇ πρὸς τῷ Γ ἴση ἐστίν. καὶ ἡ ἐν τῷ ΑΕΒ ἄρα ἴση ἐστὶ τῇ πρὸς τῷ Γ. γέγραπται ἄρα πάλιν ἐπὶ τῆς ΑΒ τμῆμα κύκλου τὸ ΑΕΒ δεχόμενον γωνίαν ἴσην τῇ πρὸς τῷ Γ.
Ἀλλὰ δὴ ἡ πρὸς τῷ Γ ἀμβλεῖα ἔστω· καὶ συνεστάτω αὐτῇ ἴση πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ Α σημείῳ ἡ ὑπὸ ΒΑΔ, ὡς ἔχει ἐπὶ τῆς τρίτης καταγραφῆς, καὶ τῇ ΑΔ πρὸς ὀρθὰς ἤχθω ἡ ΑΕ, καὶ τετμήσθω πάλιν ἡ ΑΒ δίχα κατὰ τὸ Ζ, καὶ τῇ ΑΒ πρὸς ὀρθὰς ἤχθω ἡ ΖΗ, καὶ ἐπεζεύχθω ἡ ΗΒ.
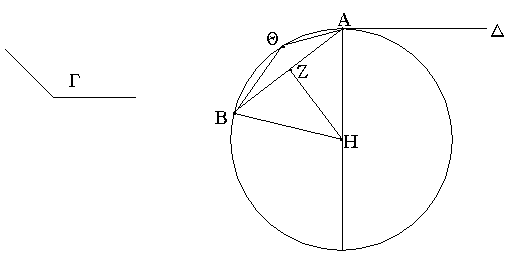
Καὶ ἐπεὶ πάλιν ἴση ἐστὶν ἡ ΑΖ τῇ ΖΒ, καὶ κοινὴ ἡ ΖΗ, δύο δὴ αἱ ΑΖ, ΖΗ δύο ταῖς ΒΖ, ΖΗ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΑΖΗ γωνίᾳ τῇ ὑπὸ ΒΖΗ ἴση· βάσις ἄρα ἡ ΑΗ βάσει τῇ ΒΗ ἴση ἐστίν· ὁ ἄρα κέντρῳ μὲν τῷ Η διαστήματι δὲ τῷ ΗΑ κύκλος γραφόμενος ἥξει καὶ διὰ τοῦ Β. ἐρχέσθω ὡς ὁ ΑΕΒ. καὶ ἐπεὶ τῇ ΑΕ διαμέτρῳ ἀπ' ἄκρας πρὸς ὀρθάς ἐστιν ἡ ΑΔ, ἡ ΑΔ ἄρα ἐφάπτεται τοῦ ΑΕΒ κύκλου. καὶ ἀπὸ τῆς κατὰ τὸ Α ἐπαφῆς διῆκται ἡ ΑΒ· ἡ ἄρα ὑπὸ ΒΑΔ γωνία ἴση ἐστὶ τῇ ἐν τῷ ἐναλλὰξ τοῦ κύκλου τμήματι τῷ ΑΘΒ συνισταμένῃ γωνίᾳ. ἀλλ' ἡ ὑπὸ ΒΑΔ γωνία τῇ πρὸς τῷ Γ ἴση ἐστίν. καὶ ἡ ἐν τῷ ΑΘΒ ἄρα τμήματι γωνία ἴση ἐστὶ τῇ πρὸς τῷ Γ.
Ἐπὶ τῆς ἄρα δοθείσης εὐθείας τῆς ΑΒ γέγραπται τμῆμα κύκλου τὸ ΑΘΒ δεχόμενον γωνίαν ἴσην τῇ πρὸς τῷ Γ· ὅπερ ἔδει ποιῆσαι.
Πρότασις λδ΄ 34 Βιβλίον III
Ἀπὸ τοῦ δοθέντος κύκλου τμῆμα ἀφελεῖν δεχόμενον γωνίαν ἴσην τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ πρὸς τῷ Δ· δεῖ δὴ ἀπὸ τοῦ ΑΒΓ κύκλου τμῆμα ἀφελεῖν δεχόμενον γωνίαν ἴσην τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ πρὸς τῷ Δ.
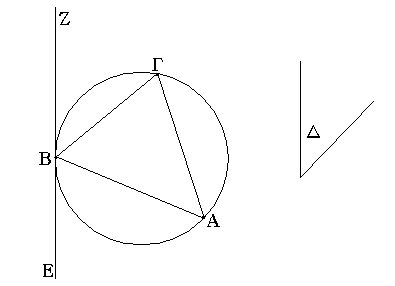
Ἤχθω τοῦ ΑΒΓ ἐφαπτομένη ἡ ΕΖ κατὰ τὸ Β σημεῖον, καὶ συνεστάτω πρὸς τῇ ΖΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Β τῇ πρὸς τῷ Δ γωνίᾳ ἴση ἡ ὑπὸ ΖΒΓ.
Ἐπεὶ οὖν κύκλου τοῦ ΑΒΓ ἐφάπτεταί τις εὐθεῖα ἡ ΕΖ, καὶ ἀπὸ τῆς κατὰ τὸ Β ἐπαφῆς διῆκται ἡ ΒΓ, ἡ ὑπὸ ΖΒΓ ἄρα γωνία ἴση ἐστὶ τῇ ἐν τῷ ΒΑΓ ἐναλλὰξ τμήματι συνισταμένῃ γωνίᾳ. ἀλλ' ἡ ὑπὸ ΖΒΓ τῇ πρὸς τῷ Δ ἐστιν ἴση· καὶ ἡ ἐν τῷ ΒΑΓ ἄρα τμήματι ἴση ἐστὶ τῇ πρὸς τῷ Δ [γωνίᾳ].
Ἀπὸ τοῦ δοθέντος ἄρα κύκλου τοῦ ΑΒΓ τμῆμα ἀφῄρηται τὸ ΒΑΓ δεχόμενον γωνίαν ἴσην τῇ δοθείσῃ γωνίᾳ εὐθυγράμμῳ τῇ πρὸς τῷ Δ· ὅπερ ἔδει ποιῆσαι.
Πρότασις λε΄ 35 Βιβλίον III
Ἐὰν ἐν κύκλῳ δύο εὐθεῖαι τέμνωσιν ἀλλήλας, τὸ ὑπὸ τῶν τῆς μιᾶς τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν τῆς ἑτέρας τμημάτων περιεχομένῳ ὀρθογωνίῳ.
Ἐν γὰρ κύκλῳ τῷ ΑΒΓΔ δύο εὐθεῖαι αἱ ΑΓ, ΒΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε σημεῖον· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΕ, ΕΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΔΕ, ΕΒ περιεχομένῳ ὀρθογωνίῳ.
Εἰ μὲν οὖν αἱ ΑΓ, ΒΔ διὰ τοῦ κέντρου εἰσὶν ὥστε τὸ Ε κέντρον εἶναι τοῦ ΑΒΓΔ κύκλου, φανερόν, ὅτι ἴσων οὐσῶν τῶν ΑΕ, ΕΓ, ΔΕ, ΕΒ καὶ τὸ ὑπὸ τῶν ΑΕ, ΕΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΔΕ, ΕΒ περιεχομένῳ ὀρθογωνίῳ.
Μὴ ἔστωσαν δὴ αἱ ΑΓ, ΔΒ διὰ τοῦ κέντρου, καὶ εἰλήφθω τὸ κέντρον τοῦ ΑΒΓΔ, καὶ ἔστω τὸ Ζ, καὶ ἀπὸ τοῦ Ζ ἐπὶ τὰς ΑΓ, ΔΒ εὐθείας κάθετοι ἤχθωσαν αἱ ΖΗ, ΖΘ, καὶ ἐπεζεύχθωσαν αἱ ΖΒ, ΖΓ, ΖΕ.
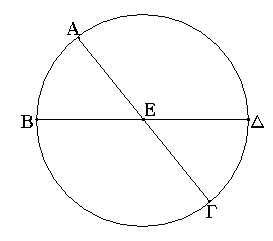
Καὶ ἐπεὶ εὐθεῖά τις διὰ τοῦ κέντρου ἡ ΗΖ εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου τὴν ΑΓ πρὸς ὀρθὰς τέμνει, καὶ δίχα αὐτὴν τέμνει· ἴση ἄρα ἡ ΑΗ τῇ ΗΓ. ἐπεὶ οὖν εὐθεῖα ἡ ΑΓ τέτμηται εἰς μὲν ἴσα κατὰ τὸ Η, εἰς δὲ ἄνισα κατὰ τὸ Ε, τὸ ἄρα ὑπὸ τῶν ΑΕ, ΕΓ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΕΗ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΗΓ· [κοινὸν] προσκείσθω τὸ ἀπὸ τῆς ΗΖ· τὸ ἄρα ὑπὸ τῶν ΑΕ, ΕΓ μετὰ τῶν ἀπὸ τῶν ΗΕ, ΗΖ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΓΗ, ΗΖ. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΕΗ, ΗΖ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΖΕ, τοῖς δὲ ἀπὸ τῶν ΓΗ, ΗΖ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΖΓ· τὸ ἄρα ὑπὸ τῶν ΑΕ, ΕΓ μετὰ τοῦ ἀπὸ τῆς ΖΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΓ. ἴση δὲ ἡ ΖΓ τῇ ΖΒ· τὸ ἄρα ὑπὸ τῶν ΑΕ, ΕΓ μετὰ τοῦ ἀπὸ τῆς ΕΖ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΒ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ὑπὸ τῶν ΔΕ, ΕΒ μετὰ τοῦ ἀπὸ τῆς ΖΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΒ. ἐδείχθη δὲ καὶ τὸ ὑπὸ τῶν ΑΕ, ΕΓ μετὰ τοῦ ἀπὸ τῆς ΖΕ ἴσον τῷ ἀπὸ τῆς ΖΒ· τὸ ἄρα ὑπὸ τῶν ΑΕ, ΕΓ μετὰ τοῦ ἀπὸ τῆς ΖΕ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΔΕ, ΕΒ μετὰ τοῦ ἀπὸ τῆς ΖΕ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΖΕ· λοιπὸν ἄρα τὸ ὑπὸ τῶν ΑΕ, ΕΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΔΕ, ΕΒ περιεχομένῳ ὀρθογωνίῳ.
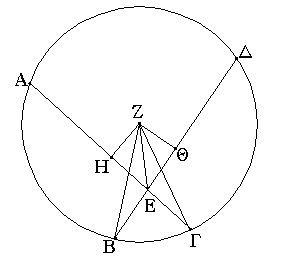
Ἐὰν ἄρα ἐν κύκλῳ εὐθεῖαι δύο τέμνωσιν ἀλλήλας, τὸ ὑπὸ τῶν τῆς μιᾶς τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν τῆς ἑτέρας τμημάτων περιεχομένῳ ὀρθογωνίῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον III
Ἐὰν κύκλου ληφθῇ τι σημεῖον ἐκτός, καὶ ἀπ' αὐτοῦ πρὸς τὸν κύκλον προσπίπτωσι δύο εὐθεῖαι, καὶ ἡ μὲν αὐτῶν τέμνῃ τὸν κύκλον, ἡ δὲ ἐφάπτηται, ἔσται τὸ ὑπὸ ὅλης τῆς τεμνούσης καὶ τῆς ἐκτὸς ἀπολαμβανομένης μεταξὺ τοῦ τε σημείου καὶ τῆς κυρτῆς περιφερείας ἴσον τῷ ἀπὸ τῆς ἐφαπτομένης τετραγώνῳ.
Κύκλου γὰρ τοῦ ΑΒΓ εἰλήφθω τι σημεῖον ἐκτὸς τὸ Δ, καὶ ἀπὸ τοῦ Δ πρὸς τὸν ΑΒΓ κύκλον προσπιπτέτωσαν δύο εὐθεῖαι αἱ ΔΓ[Α], ΔΒ· καὶ ἡ μὲν ΔΓΑ τεμνέτω τὸν ΑΒΓ κύκλον, ἡ δὲ ΒΔ ἐφαπτέσθω· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΔ, ΔΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΒ τετραγώνῳ.
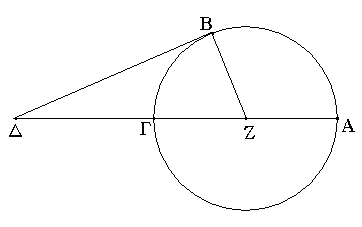
Ἡ ἄρα [Δ]ΓΑ ἤτοι διὰ τοῦ κέντρου ἐστὶν ἢ οὔ. ἔστω πρότερον διὰ τοῦ κέντρου, καὶ ἔστω τὸ Ζ κέντρον τοῦ ΑΒΓ κύκλου, καὶ ἐπεζεύχθω ἡ ΖΒ· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΖΒΔ. καὶ ἐπεὶ εὐθεῖα ἡ ΑΓ δίχα τέτμηται κατὰ τὸ Ζ, πρόσκειται δὲ αὐτῇ ἡ ΓΔ, τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΖΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΔ. ἴση δὲ ἡ ΖΓ τῇ ΖΒ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΖΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΔ. τῷ δὲ ἀπὸ τῆς ΖΔ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΖΒ, ΒΔ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΖΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΖΒ, ΒΔ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΖΒ· λοιπὸν ἄρα τὸ ὑπὸ τῶν ΑΔ, ΔΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΒ ἐφαπτομένης. ἀλλὰ δὴ ἡ ΔΓΑ μὴ ἔστω διὰ τοῦ κέντρου τοῦ ΑΒΓ κύκλου, καὶ εἰλήφθω τὸ κέντρον τὸ Ε, καὶ ἀπὸ τοῦ Ε ἐπὶ τὴν ΑΓ κάθετος ἤχθω ἡ ΕΖ, καὶ ἐπεζεύχθωσαν αἱ ΕΒ, ΕΓ, ΕΔ· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΕΒΔ. καὶ ἐπεὶ εὐθεῖά τις διὰ τοῦ κέντρου ἡ ΕΖ εὐθεῖάν τινα μὴ διὰ τοῦ κέντρου τὴν ΑΓ πρὸς ὀρθὰς τέμνει, καὶ δίχα αὐτὴν τέμνει· ἡ ΑΖ ἄρα τῇ ΖΓ ἐστιν ἴση. καὶ ἐπεὶ εὐθεῖα ἡ ΑΓ τέτμηται δίχα κατὰ τὸ Ζ σημεῖον, πρόσκειται δὲ αὐτῇ ἡ ΓΔ, τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΖΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΖΔ. κοινὸν προσκείσθω τὸ ἀπὸ τῆς ΖΕ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τῶν ἀπὸ τῶν ΓΖ, ΖΕ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΖΔ, ΖΕ. τοῖς δὲ ἀπὸ τῶν ΓΖ, ΖΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΓ· ὀρθὴ γὰρ [ἐστιν] ἡ ὑπὸ ΕΖΓ [γωνία]· τοῖς δὲ ἀπὸ τῶν ΔΖ, ΖΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΔ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΕΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΔ. ἴση δὲ ἡ ΕΓ τῇ ΕΒ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΕΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΔ. τῷ δὲ ἀπὸ τῆς ΕΔ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΕΒ, ΒΔ· ὀρθὴ γὰρ ἡ ὑπὸ ΕΒΔ γωνία· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ μετὰ τοῦ ἀπὸ τῆς ΕΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΕΒ, ΒΔ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΕΒ· λοιπὸν ἄρα τὸ ὑπὸ τῶν ΑΔ, ΔΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΒ.
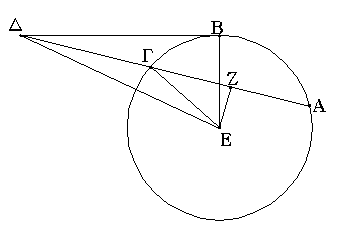
Ἐὰν ἄρα κύκλου ληφθῇ τι σημεῖον ἐκτός, καὶ ἀπ' αὐτοῦ πρὸς τὸν κύκλον προσπίπτωσι δύο εὐθεῖαι, καὶ ἡ μὲν αὐτῶν τέμνῃ τὸν κύκλον, ἡ δὲ ἐφάπτηται, ἔσται τὸ ὑπὸ ὅλης τῆς τεμνούσης καὶ τῆς ἐκτὸς ἀπολαμβανομένης μεταξὺ τοῦ τε σημείου καὶ τῆς κυρτῆς περιφερείας ἴσον τῷ ἀπὸ τῆς ἐφαπτομένης τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις λζ΄ 37 Βιβλίον III
Ἐὰν κύκλου ληφθῇ τι σημεῖον ἐκτός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσι δύο εὐθεῖαι, καὶ ἡ μὲν αὐτῶν τέμνῃ τὸν κύκλον, ἡ δὲ προσπίπτῃ, ᾖ δὲ τὸ ὑπὸ [τῆς] ὅλης τῆς τεμνούσης καὶ τῆς ἐκτὸς ἀπολαμβανομένης μεταξὺ τοῦ τε σημείου καὶ τῆς κυρτῆς περιφερείας ἴσον τῷ ἀπὸ τῆς προσπιπτούσης, ἡ προσπίπτουσα ἐφάψεται τοῦ κύκλου.
κύκλου γὰρ τοῦ ΑΒΓ εἰλήφθω τι σημεῖον ἐκτὸς τὸ Δ, καὶ ἀπὸ τοῦ Δ πρὸς τὸν ΑΒΓ κύκλον προσπιπτέτωσαν δύο εὐθεῖαι αἱ ΔΓΑ, ΔΒ, καὶ ἡ μὲν ΔΓΑ τεμνέτω τὸν κύκλον, ἡ δὲ ΔΒ προσπιπτέτω, ἔστω δὲ τὸ ὑπὸ τῶν ΑΔ, ΔΓ ἴσον τῷ ἀπὸ τῆς ΔΒ. λέγω, ὅτι ἡ ΔΒ ἐφάπτεται τοῦ ΑΒΓ κύκλου.
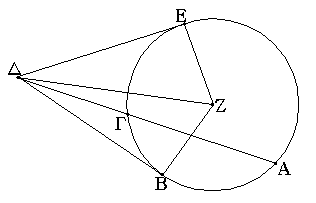
Ἤχθω γὰρ τοῦ ΑΒΓ ἐφαπτομένη ἡ ΔΕ, καὶ εἰλήφθω τὸ κέντρον τοῦ ΑΒΓ κύκλου, καὶ ἔστω τὸ Ζ, καὶ ἐπεζεύχθωσαν αἱ ΖΕ, ΖΒ, ΖΔ. ἡ ἄρα ὑπὸ ΖΕΔ ὀρθή ἐστιν. καὶ ἐπεὶ ἡ ΔΕ ἐφάπτεται τοῦ ΑΒΓ κύκλου, τέμνει δὲ ἡ ΔΓΑ, τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΕ. ἦν δὲ καὶ τὸ ὑπὸ τῶν ΑΔ, ΔΓ ἴσον τῷ ἀπὸ τῆς ΔΒ· τὸ ἄρα ἀπὸ τῆς ΔΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΒ· ἴση ἄρα ἡ ΔΕ τῇ ΔΒ. ἐστὶ δὲ καὶ ἡ ΖΕ τῇ ΖΒ ἴση· δύο δὴ αἱ ΔΕ, ΕΖ δύο ταῖς ΔΒ, ΒΖ ἴσαι εἰσίν· καὶ βάσις αὐτῶν κοινὴ ἡ ΖΔ· γωνία ἄρα ἡ ὑπὸ ΔΕΖ γωνίᾳ τῇ ὑπὸ ΔΒΖ ἐστιν ἴση. ὀρθὴ δὲ ἡ ὑπὸ ΔΕΖ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΔΒΖ. καί ἐστιν ἡ ΖΒ ἐκβαλλομένη διάμετρος· ἡ δὲ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐφάπτεται τοῦ κύκλου· ἡ ΔΒ ἄρα ἐφάπτεται τοῦ ΑΒΓ κύκλου. ὁμοίως δὴ δειχθήσεται, κἂν τὸ κέντρον ἐπὶ τῆς ΑΓ τυγχάνῃ.
Ἐὰν ἄρα κύκλου ληφθῇ τι σημεῖον ἐκτός, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσι δύο εὐθεῖαι, καὶ ἡ μὲν αὐτῶν τέμνῃ τὸν κύκλον, ἡ δὲ προσπίπτῃ, ᾖ δὲ τὸ ὑπὸ ὅλης τῆς τεμνούσης καὶ τῆς ἐκτὸς ἀπολαμβανομένης μεταξὺ τοῦ τε σημείου καὶ τῆς κυρτῆς περιφερείας ἴσον τῷ ἀπὸ τῆς προσπιπτούσης, ἡ προσπίπτουσα ἐφάψεται τοῦ κύκλου· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου δ΄
Βιβλίον IV
Ὅροι ζ΄ 7.
α΄ 1. Σχῆμα εὐθύγραμμον εἰς σχῆμα εὐθύγραμμον ἐγγράφεσθαι λέγεται, ὅταν ἑκάστη τῶν τοῦ ἐγγραφομένου σχήματος γωνιῶν ἑκάστης πλευρᾶς τοῦ, εἰς ὃ ἐγγράφεται, ἅπτηται.
β΄ 2.Σχῆμα δὲ ὁμοίως περὶ σχῆμα περιγράφεσθαι λέγεται, ὅταν ἑκάστη πλευρὰ τοῦ περιγραφομένου ἑκάστης γωνίας τοῦ, περὶ ὃ περιγράφεται, ἅπτηται.
γ΄ 3. Σχῆμα εὐθύγραμμον εἰς κύκλον ἐγγράφεσθαι λέγεται, ὅταν ἑκάστη γωνία τοῦ ἐγγραφομένου ἅπτηται τῆς τοῦ κύκλου περιφερείας.
δ΄ 4. Σχῆμα δὲ εὐθύγραμμον περὶ κύκλον περιγράφεσθαι λέγεται, ὅταν ἑκάστη πλευρὰ τοῦ περιγραφομένου ἐφάπτηται τῆς τοῦ κύκλου περιφερείας.
ε΄ 5. Κύκλος δὲ εἰς σχῆμα ὁμοίως ἐγγράφεσθαι λέγεται, ὅταν ἡ τοῦ κύκλου περιφέρεια ἑκάστης πλευρᾶς τοῦ, εἰς ὃ ἐγγράφεται, ἅπτηται.
ς΄ 6. Κύκλος δὲ περὶ σχῆμα περιγράφεσθαι λέγεται, ὅταν ἡ τοῦ κύκλου περιφέρεια ἑκάστης γωνίας τοῦ, περὶ ὃ περιγράφεται, ἅπτηται.
ζ΄ 7. Εὐθεῖα εἰς κύκλον ἐναρμόζεσθαι λέγεται, ὅταν τὰ πέρατα αὐτῆς ἐπὶ τῆς περιφερείας ᾖ τοῦ κύκλου.
Στοιχεῖα Εὐκλείδου δ΄
Βιβλίον IV
Προτάσεις ιζ΄ 16
Πρότασις α΄ 1 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον τῇ δοθείσῃ εὐθείᾳ μὴ μείζονι οὔσῃ τῆς τοῦ κύκλου διαμέτρου ἴσην εὐθεῖαν ἐναρμόσαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ, ἡ δὲ δοθεῖσα εὐθεῖα μὴ μείζων τῆς τοῦ κύκλου διαμέτρου ἡ Δ. δεῖ δὴ εἰς τὸν ΑΒΓ κύκλον τῇ Δ εὐθείᾳ ἴσην εὐθεῖαν ἐναρμόσαι.
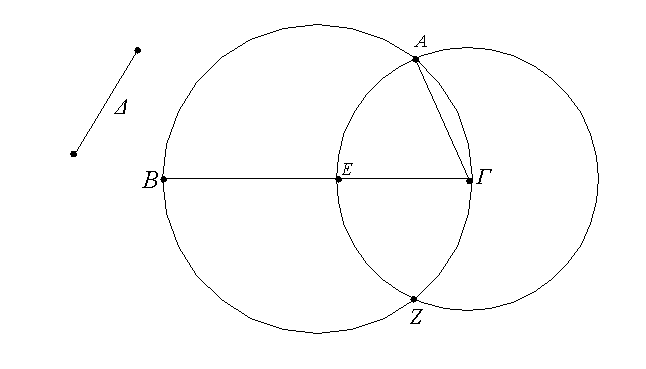
Ἤχθω τοῦ ΑΒΓ κύκλου διάμετρος ἡ ΒΓ. εἰ μὲν οὖν ἴση ἐστὶν ἡ ΒΓ τῇ Δ, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν· ἐνήρμοσται γὰρ εἰς τὸν ΑΒΓ κύκλον τῇ Δ εὐθείᾳ ἴση ἡ ΒΓ. εἰ δὲ μείζων ἐστὶν ἡ ΒΓ τῆς Δ, κείσθω τῇ Δ ἴση ἡ ΓΕ, καὶ κέντρῳ τῷ Γ διαστήματι δὲ τῷ ΓΕ κύκλος γεγράφθω ὁ ΕΑΖ, καὶ ἐπεζεύχθω ἡ ΓΑ.
Ἐπεὶ οὖν τὸ Γ σημεῖον κέντρον ἐστὶ τοῦ ΕΑΖ κύκλου, ἴση ἐστὶν ἡ ΓΑ τῇ ΓΕ. ἀλλὰ τῇ Δ ἡ ΓΕ ἐστιν ἴση· καὶ ἡ Δ ἄρα τῇ ΓΑ ἐστιν ἴση.
Εἰς ἄρα τὸν δοθέντα κύκλον τὸν ΑΒΓ τῇ δοθείσῃ εὐθείᾳ τῇ Δ ἴση ἐνήρμοσται ἡ ΓΑ· ὅπερ ἔδει ποιῆσαι.
Πρότασις β΄ 2 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον ἐγγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ, τὸ δὲ δοθὲν τρίγωνον τὸ ΔΕΖ· δεῖ δὴ εἰς τὸν ΑΒΓ κύκλον τῷ ΔΕΖ τριγώνῳ ἰσογώνιον τρίγωνον ἐγγράψαι.
Ἤχθω τοῦ ΑΒΓ κύκλου ἐφαπτομένη ἡ ΗΘ κατὰ τὸ Α, καὶ συνεστάτω πρὸς τῇ ΑΘ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΔΕΖ γωνίᾳ ἴση ἡ ὑπὸ ΘΑΓ, πρὸς δὲ τῇ ΑΗ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΔΖΕ [γωνίᾳ] ἴση ἡ ὑπὸ ΗΑΒ, καὶ ἐπεζεύχθω ἡ ΒΓ.
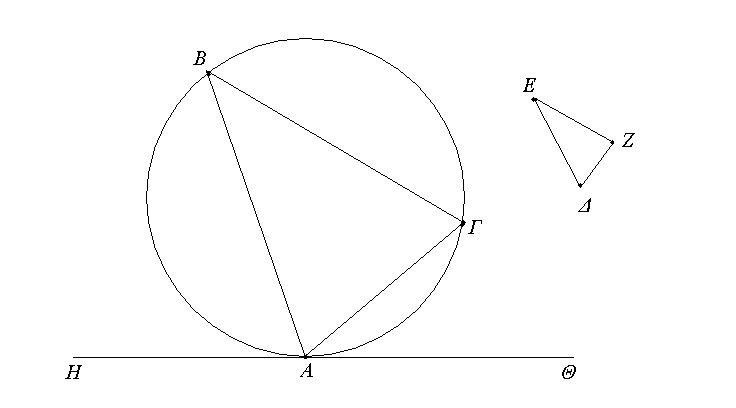
Ἐπεὶ οὖν κύκλου τοῦ ΑΒΓ ἐφάπτεταί τις εὐθεῖα ἡ ΑΘ, καὶ ἀπὸ τῆς κατὰ τὸ Α ἐπαφῆς εἰς τὸν κύκλον διῆκται εὐθεῖα ἡ ΑΓ, ἡ ἄρα ὑπὸ ΘΑΓ ἴση ἐστὶ τῇ ἐν τῷ ἐναλλὰξ τοῦ κύκλου τμήματι γωνίᾳ τῇ ὑπὸ ΑΒΓ. ἀλλ' ἡ ὑπὸ ΘΑΓ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση· καὶ ἡ ὑπὸ ΑΒΓ ἄρα γωνία τῇ ὑπὸ ΔΕΖ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΖΕ ἐστιν ἴση· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΒΑΓ λοιπῇ τῇ ὑπὸ ΕΔΖ ἐστιν ἴση· [ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ, καὶ ἐγγέγραπται εἰς τὸν ΑΒΓ κύκλον].
Εἰς τὸν δοθέντα ἄρα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον ἐγγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις γ΄ 3 Βιβλίον IV
Περὶ τὸν δοθέντα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον περιγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ, τὸ δὲ δοθὲν τρίγωνον τὸ ΔΕΖ· δεῖ δὴ περὶ τὸν ΑΒΓ κύκλον τῷ ΔΕΖ τριγώνῳ ἰσογώνιον τρίγωνον περιγράψαι.
Ἐκβεβλήσθω ἡ ΕΖ ἐφ' ἑκάτερα τὰ μέρη κατὰ τὰ Η, Θ σημεῖα, καὶ εἰλήφθω τοῦ ΑΒΓ κύκλου κέντρον τὸ Κ, καὶ διήχθω, ὡς ἔτυχεν, εὐθεῖα ἡ ΚΒ, καὶ συνεστάτω πρὸς τῇ ΚΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Κ τῇ μὲν ὑπὸ ΔΕΗ γωνίᾳ ἴση ἡ ὑπὸ ΒΚΑ, τῇ δὲ ὑπὸ ΔΖΘ ἴση ἡ ὑπὸ ΒΚΓ, καὶ διὰ τῶν Α, Β, Γ σημείων ἤχθωσαν ἐφαπτόμεναι τοῦ ΑΒΓ κύκλου αἱ ΛΑΜ, ΜΒΝ, ΝΓΛ.
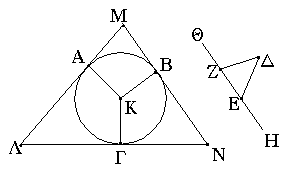
Καὶ ἐπεὶ ἐφάπτονται τοῦ ΑΒΓ κύκλου αἱ ΛΜ, ΜΝ, ΝΛ κατὰ τὰ Α, Β, Γ σημεῖα, ἀπὸ δὲ τοῦ Κ κέντρου ἐπὶ τὰ Α, Β, Γ σημεῖα ἐπεζευγμέναι εἰσὶν αἱ ΚΑ, ΚΒ, ΚΓ, ὀρθαὶ ἄρα εἰσὶν αἱ πρὸς τοῖς Α, Β, Γ σημείοις γωνίαι. καὶ ἐπεὶ τοῦ ΑΜΒΚ τετραπλεύρου αἱ τέσσαρες γωνίαι τέτρασιν ὀρθαῖς ἴσαι εἰσίν, ἐπειδήπερ καὶ εἰς δύο τρίγωνα διαιρεῖται τὸ ΑΜΒΚ, καί εἰσιν ὀρθαὶ αἱ ὑπὸ ΚΑΜ, ΚΒΜ γωνίαι, λοιπαὶ ἄρα αἱ ὑπὸ ΑΚΒ, ΑΜΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν. εἰσὶ δὲ καὶ αἱ ὑπὸ ΔΕΗ, ΔΕΖ δυσὶν ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΑΚΒ, ΑΜΒ ταῖς ὑπὸ ΔΕΗ, ΔΕΖ ἴσαι εἰσίν, ὧν ἡ ὑπὸ ΑΚΒ τῇ ὑπὸ ΔΕΗ ἐστιν ἴση· λοιπὴ ἄρα ἡ ὑπὸ ΑΜΒ λοιπῇ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἡ ὑπὸ ΛΝΒ τῇ ὑπὸ ΔΖΕ ἐστιν ἴση· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΜΛΝ [λοιπῇ] τῇ ὑπὸ ΕΔΖ ἐστιν ἴση. ἰσογώνιον ἄρα ἐστὶ τὸ ΛΜΝ τρίγωνον τῷ ΔΕΖ τριγώνῳ· καὶ περιγέγραπται περὶ τὸν ΑΒΓ κύκλον.
Περὶ τὸν δοθέντα ἄρα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις δ΄ 4 Βιβλίον IV
Εἰς τὸ δοθὲν τρίγωνον κύκλον ἐγγράψαι.
Ἔστω τὸ δοθὲν τρίγωνον τὸ ΑΒΓ· δεῖ δὴ εἰς τὸ ΑΒΓ τρίγωνον κύκλον ἐγγράψαι.
Τετμήσθωσαν αἱ ὑπὸ ΑΒΓ, ΑΓΒ γωνίαι δίχα ταῖς ΒΔ, ΓΔ εὐθείαις, καὶ συμβαλλέτωσαν ἀλλήλαις κατὰ τὸ Δ σημεῖον, καὶ ἤχθωσαν ἀπὸ τοῦ Δ ἐπὶ τὰς ΑΒ, ΒΓ, ΓΑ εὐθείας κάθετοι αἱ ΔΕ, ΔΖ, ΔΗ.
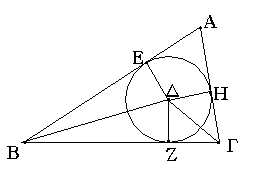
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΑΒΔ γωνία τῇ ὑπὸ ΓΒΔ, ἐστὶ δὲ καὶ ὀρθὴ ἡ ὑπὸ ΒΕΔ ὀρθῇ τῇ ὑπὸ ΒΖΔ ἴση, δύο δὴ τρίγωνά ἐστι τὰ ΕΒΔ, ΖΒΔ τὰς δύο γωνίας ταῖς δυσὶ γωνίαις ἴσας ἔχοντα καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν κοινὴν αὐτῶν τὴν ΒΔ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξουσιν· ἴση ἄρα ἡ ΔΕ τῇ ΔΖ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΔΗ τῇ ΔΖ ἐστιν ἴση. αἱ τρεῖς ἄρα εὐθεῖαι αἱ ΔΕ, ΔΖ, ΔΗ ἴσαι ἀλλήλαις εἰσίν· ὁ ἄρα κέντρῳ τῷ Δ καὶ διαστήματι ἑνὶ τῶν Ε, Ζ, Η κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἐφάψεται τῶν ΑΒ, ΒΓ, ΓΑ εὐθειῶν διὰ τὸ ὀρθὰς εἶναι τὰς πρὸς τοῖς Ε, Ζ, Η σημείοις γωνίας. εἰ γὰρ τεμεῖ αὐτάς, ἔσται ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐντὸς πίπτουσα τοῦ κύκλου· ὅπερ ἄτοπον ἐδείχθη· οὐκ ἄρα ὁ κέντρῳ τῷ Δ διαστήματι δὲ ἑνὶ τῶν Ε, Ζ, Η γραφόμενος κύκλος τεμεῖ τὰς ΑΒ, ΒΓ, ΓΑ εὐθείας· ἐφάψεται ἄρα αὐτῶν, καὶ ἔσται ὁ κύκλος ἐγγεγραμμένος εἰς τὸ ΑΒΓ τρίγωνον. ἐγγεγράφθω ὡς ὁ ΖΗΕ.
Εἰς ἄρα τὸ δοθὲν τρίγωνον τὸ ΑΒΓ κύκλος ἐγγέγραπται ὁ ΕΖΗ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ε΄ 5 Βιβλίον IV
Περὶ τὸ δοθὲν τρίγωνον κύκλον περιγράψαι.
Ἔστω τὸ δοθὲν τρίγωνον τὸ ΑΒΓ· δεῖ δὴ περὶ τὸ δοθὲν τρίγωνον τὸ ΑΒΓ κύκλον περιγράψαι.
Τετμήσθωσαν αἱ ΑΒ, ΑΓ εὐθεῖαι δίχα κατὰ τὰ Δ, Ε σημεῖα, καὶ ἀπὸ τῶν Δ, Ε σημείων ταῖς ΑΒ, ΑΓ πρὸς ὁρθὰς ἤχθωσαν αἱ ΔΖ, ΕΖ· συμπεσοῦνται δὴ ἤτοι ἐντὸς τοῦ ΑΒΓ τριγώνου ἢ ἐπὶ τῆς ΒΓ εὐθείας ἢ ἐκτὸς τῆς ΒΓ.
Συμπιπτέτωσαν πρότερον ἐντὸς κατὰ τὸ Ζ, καὶ ἐπεζεύχθωσαν αἱ ΖΒ, ΖΓ, ΖΑ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΔΒ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΔΖ, βάσις ἄρα ἡ ΑΖ βάσει τῇ ΖΒ ἐστιν ἴση. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΓΖ τῇ ΑΖ ἐστιν ἴση· ὥστε καὶ ἡ ΖΒ τῇ ΖΓ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΖΑ, ΖΒ, ΖΓ ἴσαι ἀλλήλαις εἰσίν. ὁ ἄρα κέντρῳ τῷ Ζ διαστήματι δὲ ἑνὶ τῶν Α, Β, Γ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων, καὶ ἔσται περιγεγραμμένος ὁ κύκλος περὶ τὸ ΑΒΓ τρίγωνον. περιγεγράφθω ὡς ὁ ΑΒΓ.
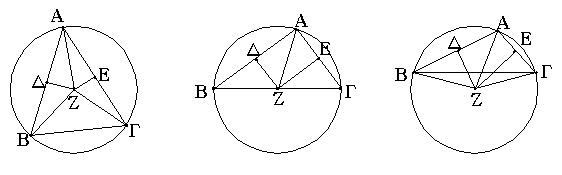
Ἀλλὰ δὴ αἱ ΔΖ, ΕΖ συμπιπτέτωσαν ἐπὶ τῆς ΒΓ εὐθείας κατὰ τὸ Ζ, ὡς ἔχει ἐπὶ τῆς δευτέρας καταγραφῆς, καὶ ἐπεζεύχθω ἡ ΑΖ. ὁμοίως δὴ δείξομεν, ὅτι τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ περὶ τὸ ΑΒΓ τρίγωνον περιγραφομένου κύκλου.
Ἀλλὰ δὴ αἱ ΔΖ, ΕΖ συμπιπτέτωσαν ἐκτὸς τοῦ ΑΒΓ τριγώνου κατὰ τὸ Ζ πάλιν, ὡς ἔχει ἐπὶ τῆς τρίτης καταγραφῆς, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΒΖ, ΓΖ. καὶ ἐπεὶ πάλιν ἴση ἐστὶν ἡ ΑΔ τῇ ΔΒ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΔΖ, βάσις ἄρα ἡ ΑΖ βάσει τῇ ΒΖ ἐστιν ἴση. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΓΖ τῇ ΑΖ ἐστιν ἴση· ὥστε καὶ ἡ ΒΖ τῇ ΖΓ ἐστιν ἴση· ὁ ἄρα [πάλιν] κέντρῳ τῷ Ζ διαστήματι δὲ ἑνὶ τῶν ΖΑ, ΖΒ, ΖΓ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων, καὶ ἔσται περιγεγραμμένος περὶ τὸ ΑΒΓ τρίγωνον.
Περὶ τὸ δοθὲν ἄρα τρίγωνον κύκλος περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
[Πόρισμα]
Καὶ φανερόν, ὅτι, ὅτε μὲν ἐντὸς τοῦ τριγώνου πίπτει τὸ κέντρον τοῦ κύκλου, ἡ ὑπὸ ΒΑΓ γωνία ἐν μείζονι τμήματι τοῦ ἡμικυκλίου τυγχάνουσα ἐλάττων ἐστὶν ὀρθῆς· ὅτε δὲ ἐπὶ τῆς ΒΓ εὐθείας τὸ κέντρον πίπτει, ἡ ὑπὸ ΒΑΓ γωνία ἐν ἡμικυκλίῳ τυγχάνουσα ὀρθή ἐστιν· ὅτε δὲ τὸ κέντρον τοῦ κύκλου ἐκτὸς τοῦ τριγώνου πίπτει, ἡ ὑπὸ ΒΑΓ ἐν ἐλάττονι τμήματι τοῦ ἡμικυκλίου τυγχάνουσα μείζων ἐστὶν ὀρθῆς. [ὥστε καὶ ὅταν ἐλάττων ὀρθῆς τυγχάνῃ ἡ διδομένη γωνία, ἐντὸς τοῦ τριγώνου πεσοῦνται αἱ ΔΖ, ΕΖ, ὅταν δὲ ὀρθή, ἐπὶ τῆς ΒΓ, ὅταν δὲ μείζων ὀρθῆς, ἐκτὸς τῆς ΒΓ· ὅπερ ἔδει ποιῆσαι.]
Πρότασις ς΄ 6 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον τετράγωνον ἐγγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔ· δεῖ δὴ εἰς τὸν ΑΒΓΔ κύκλον τετράγωνον ἐγγράψαι.
Ἤχθωσαν τοῦ ΑΒΓΔ κύκλου δύο διάμετροι πρὸς ὀρθὰς ἀλλήλαις αἱ ΑΓ, ΒΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΒ, ΒΓ, ΓΔ, ΔΑ.
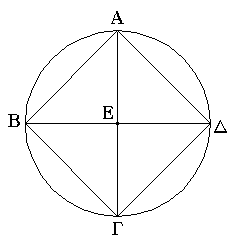
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΕΔ· κέντρον γὰρ τὸ Ε· κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΕΑ, βάσις ἄρα ἡ ΑΒ βάσει τῇ ΑΔ ἴση ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ΒΓ, ΓΔ ἑκατέρᾳ τῶν ΑΒ, ΑΔ ἴση ἐστίν· ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓΔ τετράπλευρον. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ ἡ ΒΔ εὐθεῖα διάμετρός ἐστι τοῦ ΑΒΓΔ κύκλου, ἡμικύκλιον ἄρα ἐστὶ τὸ ΒΑΔ· ὀρθὴ ἄρα ἡ ὑπὸ ΒΑΔ γωνία. διὰ τὰ αὐτὰ δὴ καὶ ἑκάστη τῶν ὑπὸ ΑΒΓ, ΒΓΔ, ΓΔΑ ὀρθή ἐστιν· ὀρθογώνιον ἄρα ἐστὶ τὸ ΑΒΓΔ τετράπλευρον. ἐδείχθη δὲ καὶ ἰσόπλευρον· τετράγωνον ἄρα ἐστίν. καὶ ἐγγέγραπται εἰς τὸν ΑΒΓΔ κύκλον.
Εἰς ἄρα τὸν δοθέντα κύκλον τετράγωνον ἐγγέγραπται τὸ ΑΒΓΔ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ζ΄ 7 Βιβλίον IV
Περὶ τὸν δοθέντα κύκλον τετράγωνον περιγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔ· δεῖ δὴ περὶ τὸν ΑΒΓΔ κύκλον τετράγωνον περιγράψαι.
Ἤχθωσαν τοῦ ΑΒΓΔ κύκλου δύο διάμετροι πρὸς ὀρθὰς ἀλλήλαις αἱ ΑΓ, ΒΔ, καὶ διὰ τῶν Α, Β, Γ, Δ σημείων ἤχθωσαν ἐφαπτόμεναι τοῦ ΑΒΓΔ κύκλου αἱ ΖΗ, ΗΘ, ΘΚ, ΚΖ.
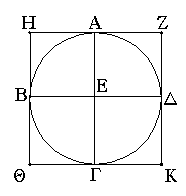
Ἐπεὶ οὖν ἐφάπτεται ἡ ΖΗ τοῦ ΑΒΓΔ κύκλου, ἀπὸ δὲ τοῦ Ε κέντρου ἐπὶ τὴν κατὰ τὸ Α ἐπαφὴν ἐπέζευκται ἡ ΕΑ, αἱ ἄρα πρὸς τῷ Α γωνίαι ὀρθαί εἰσιν. διὰ τὰ αὐτὰ δὴ καὶ αἱ πρὸς τοῖς Β, Γ, Δ σημείοις γωνίαι ὀρθαί εἰσιν. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΑΕΒ γωνία, ἐστὶ δὲ ὀρθὴ καὶ ἡ ὑπὸ ΕΒΗ, παράλληλος ἄρα ἐστὶν ἡ ΗΘ τῇ ΑΓ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΑΓ τῇ ΖΚ ἐστι παράλληλος. ὥστε καὶ ἡ ΗΘ τῇ ΖΚ ἐστι παράλληλος. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἑκατέρα τῶν ΗΖ, ΘΚ τῇ ΒΕΔ ἐστι παράλληλος. παραλληλόγραμμα ἄρα ἐστὶ τὰ ΗΚ, ΗΓ, ΑΚ, ΖΒ, ΒΚ· ἴση ἄρα ἐστὶν ἡ μὲν ΗΖ τῇ ΘΚ, ἡ δὲ ΗΘ τῇ ΖΚ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΒΔ, ἀλλὰ καὶ ἡ μὲν ΑΓ ἑκατέρᾳ τῶν ΗΘ, ΖΚ, ἡ δὲ ΒΔ ἑκατέρᾳ τῶν ΗΖ, ΘΚ ἐστιν ἴση [καὶ ἑκατέρα ἄρα τῶν ΗΘ, ΖΚ ἑκατέρᾳ τῶν ΗΖ, ΘΚ ἐστιν ἴση], ἰσόπλευρον ἄρα ἐστὶ τὸ ΖΗΘΚ τετράπλευρον. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ παραλληλόγραμμόν ἐστι τὸ ΗΒΕΑ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΑΕΒ, ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΑΗΒ. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ πρὸς τοῖς Θ, Κ, Ζ γωνίαι ὀρθαί εἰσιν. ὀρθογώνιον ἄρα ἐστὶ τὸ ΖΗΘΚ. ἐδείχθη δὲ καὶ ἰσόπλευρον· τετράγωνον ἄρα ἐστίν. καὶ περιγέγραπται περὶ τὸν ΑΒΓΔ κύκλον.
Περὶ τὸν δοθέντα ἄρα κύκλον τετράγωνον περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις η΄ 8 Βιβλίον IV
Εἰς τὸ δοθὲν τετράγωνον κύκλον ἐγγράψαι.
Ἔστω τὸ δοθὲν τετράγωνον τὸ ΑΒΓΔ· δεῖ δὴ εἰς τὸ ΑΒΓΔ τετράγωνον κύκλον ἐγγράψαι.
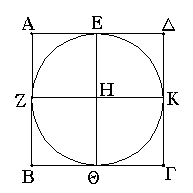
Τετμήσθω ἑκατέρα τῶν ΑΔ, ΑΒ δίχα κατὰ τὰ Ε, Ζ σημεῖα, καὶ διὰ μὲν τοῦ Ε ὁποτέρᾳ τῶν ΑΒ, ΓΔ παράλληλος ἤχθω ἡ ΕΘ, διὰ δὲ τοῦ Ζ ὁποτέρᾳ τῶν ΑΔ, ΒΓ παράλληλος ἤχθω ἡ ΖΚ· παραλληλόγραμμον ἄρα ἐστὶν ἕκαστον τῶν ΑΚ, ΚΒ, ΑΘ, ΘΔ, ΑΗ, ΗΓ, ΒΗ, ΗΔ, καὶ αἱ ἀπεναντίον αὐτῶν πλευραὶ δηλονότι ἴσαι [εἰσίν]. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΑΒ, καί ἐστι τῆς μὲν ΑΔ ἡμίσεια ἡ ΑΕ, τῆς δὲ ΑΒ ἡμίσεια ἡ ΑΖ, ἴση ἄρα καὶ ἡ ΑΕ τῇ ΑΖ· ὥστε καὶ αἱ ἀπεναντίον· ἴση ἄρα καὶ ἡ ΖΗ τῇ ΗΕ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἑκατέρα τῶν ΗΘ, ΗΚ ἑκατέρᾳ τῶν ΖΗ, ΗΕ ἐστιν ἴση· αἱ τέσσαρες ἄρα αἱ ΗΕ, ΗΖ, ΗΘ, ΗΚ ἴσαι ἀλλήλαις [εἰσίν]. ὁ ἄρα κέντρῳ μὲν τῷ Η διαστήματι δὲ ἑνὶ τῶν Ε, Ζ, Θ, Κ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων· καὶ ἐφάψεται τῶν ΑΒ, ΒΓ, ΓΔ, ΔΑ εὐθειῶν διὰ τὸ ὀρθὰς εἶναι τὰς πρὸς τοῖς Ε, Ζ, Θ, Κ γωνίας· εἰ γὰρ τεμεῖ ὁ κύκλος τὰς ΑΒ, ΒΓ, ΓΔ, ΔΑ, ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐντὸς πεσεῖται τοῦ κύκλου· ὅπερ ἄτοπον ἐδείχθη. οὐκ ἄρα ὁ κέντρῳ τῷ Η διαστήματι δὲ ἑνὶ τῶν Ε, Ζ, Θ, Κ κύκλος γραφόμενος τεμεῖ τὰς ΑΒ, ΒΓ, ΓΔ, ΔΑ εὐθείας. ἐφάψεται ἄρα αὐτῶν καὶ ἔσται ἐγγεγραμμένος εἰς τὸ ΑΒΓΔ τετράγωνον.
Εἰς ἄρα τὸ δοθὲν τετράγωνον κύκλος ἐγγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις θ΄ 9 Βιβλίον IV
Περὶ τὸ δοθὲν τετράγωνον κύκλον περιγράψαι.
Ἔστω τὸ δοθὲν τετράγωνον τὸ ΑΒΓΔ· δεῖ δὴ περὶ τὸ ΑΒΓΔ τετράγωνον κύκλον περιγράψαι.
Ἐπιζευχθεῖσαι γὰρ αἱ ΑΓ, ΒΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε.
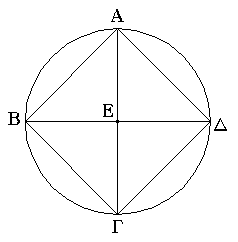
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΑΒ, κοινὴ δὲ ἡ ΑΓ, δύο δὴ αἱ ΔΑ, ΑΓ δυσὶ ταῖς ΒΑ, ΑΓ ἴσαι εἰσίν· καὶ βάσις ἡ ΔΓ βάσει τῇ ΒΓ ἴση· γωνία ἄρα ἡ ὑπὸ ΔΑΓ γωνίᾳ τῇ ὑπὸ ΒΑΓ ἴση ἐστίν· ἡ ἄρα ὑπὸ ΔΑΒ γωνία δίχα τέτμηται ὑπὸ τῆς ΑΓ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἑκάστη τῶν ὑπὸ ΑΒΓ, ΒΓΔ, ΓΔΑ δίχα τέτμηται ὑπὸ τῶν ΑΓ, ΔΒ εὐθειῶν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΑΒ γωνία τῇ ὑπὸ ΑΒΓ, καί ἐστι τῆς μὲν ὑπὸ ΔΑΒ ἡμίσεια ἡ ὑπὸ ΕΑΒ, τῆς δὲ ὑπὸ ΑΒΓ ἡμίσεια ἡ ὑπὸ ΕΒΑ, καὶ ἡ ὑπὸ ΕΑΒ ἄρα τῇ ὑπὸ ΕΒΑ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΕΑ τῇ ΕΒ ἐστιν ἴση. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἑκατέρα τῶν ΕΑ, ΕΒ [εὐθειῶν] ἑκατέρᾳ τῶν ΕΓ, ΕΔ ἴση ἐστίν. αἱ τέσσαρες ἄρα αἱ ΕΑ, ΕΒ, ΕΓ, ΕΔ ἴσαι ἀλλήλαις εἰσίν. ὁ ἄρα κέντρῳ τῷ Ε καὶ διαστήματι ἑνὶ τῶν Α, Β, Γ, Δ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἔσται περιγεγραμμένος περὶ τὸ ΑΒΓΔ τετράγωνον. περιγεγράφθω ὡς ὁ ΑΒΓΔ.
Περὶ τὸ δοθὲν ἄρα τετράγωνον κύκλος περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις ι΄ 10 Βιβλίον IV
Ἰσοσκελὲς τρίγωνον συστήσασθαι ἔχον ἑκατέραν τῶν πρὸς τῇ βάσει γωνιῶν διπλασίονα τῆς λοιπῆς.
Ἐκκείσθω τις εὐθεῖα ἡ ΑΒ, καὶ τετμήσθω κατὰ τὸ Γ σημεῖον, ὥστε τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον εἶναι τῷ ἀπὸ τῆς ΓΑ τετραγώνῳ· καὶ κέντρῳ τῷ Α καὶ διαστήματι τῷ ΑΒ κύκλος γεγράφθω ὁ ΒΔΕ, καὶ ἐνηρμόσθω εἰς τὸν ΒΔΕ κύκλον τῇ ΑΓ εὐθείᾳ μὴ μείζονι οὔσῃ τῆς τοῦ ΒΔΕ κύκλου διαμέτρου ἴση εὐθεῖα ἡ ΒΔ· καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΓ, καὶ περιγεγράφθω περὶ τὸ ΑΓΔ τρίγωνον κύκλος ὁ ΑΓΔ.
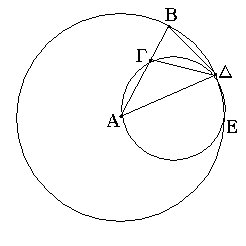
Καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ, ἴση δὲ ἡ ΑΓ τῇ ΒΔ, τὸ ἄρα ὑπὸ τῶν ΑΒ, ΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΒΔ. καὶ ἐπεὶ κύκλου τοῦ ΑΓΔ εἴληπταί τι σημεῖον ἐκτὸς τὸ Β, καὶ ἀπὸ τοῦ Β πρὸς τὸν ΑΓΔ κύκλον προσπεπτώκασι δύο εὐθεῖαι αἱ ΒΑ, ΒΔ, καὶ ἡ μὲν αὐτῶν τέμνει, ἡ δὲ προσπίπτει, καί ἐστι τὸ ὑπὸ τῶν ΑΒ, ΒΓ ἴσον τῷ ἀπὸ τῆς ΒΔ, ἡ ΒΔ ἄρα ἐφάπτεται τοῦ ΑΓΔ κύκλου. ἐπεὶ οὖν ἐφάπτεται μὲν ἡ ΒΔ, ἀπὸ δὲ τῆς κατὰ τὸ Δ ἐπαφῆς διῆκται ἡ ΔΓ, ἡ ἄρα ὑπὸ ΒΔΓ γωνία ἴση ἐστὶ τῇ ἐν τῷ ἐναλλὰξ τοῦ κύκλου τμήματι γωνίᾳ τῇ ὑπὸ ΔΑΓ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΒΔΓ τῇ ὑπὸ ΔΑΓ, κοινὴ προσκείσθω ἡ ὑπὸ ΓΔΑ· ὅλη ἄρα ἡ ὑπὸ ΒΔΑ ἴση ἐστὶ δυσὶ ταῖς ὑπὸ ΓΔΑ, ΔΑΓ. ἀλλὰ ταῖς ὑπὸ ΓΔΑ, ΔΑΓ ἴση ἐστὶν ἡ ἐκτὸς ἡ ὑπὸ ΒΓΔ· καὶ ἡ ὑπὸ ΒΔΑ ἄρα ἴση ἐστὶ τῇ ὑπὸ ΒΓΔ. ἀλλὰ ἡ ὑπὸ ΒΔΑ τῇ ὑπὸ ΓΒΔ ἐστιν ἴση, ἐπεὶ καὶ πλευρὰ ἡ ΑΔ τῇ ΑΒ ἐστιν ἴση· ὥστε καὶ ἡ ὑπὸ ΔΒΑ τῇ ὑπὸ ΒΓΔ ἐστιν ἴση. αἱ τρεῖς ἄρα αἱ ὑπὸ ΒΔΑ, ΔΒΑ, ΒΓΔ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΒΓ γωνία τῇ ὑπὸ ΒΓΔ, ἴση ἐστὶ καὶ πλευρὰ ἡ ΒΔ πλευρᾷ τῇ ΔΓ. ἀλλὰ ἡ ΒΔ τῇ ΓΑ ὑπόκειται ἴση· καὶ ἡ ΓΑ ἄρα τῇ ΓΔ ἐστιν ἴση· ὥστε καὶ γωνία ἡ ὑπὸ ΓΔΑ γωνίᾳ τῇ ὑπὸ ΔΑΓ ἐστιν ἴση· αἱ ἄρα ὑπὸ ΓΔΑ, ΔΑΓ τῆς ὑπὸ ΔΑΓ εἰσι διπλασίους. ἴση δὲ ἡ ὑπὸ ΒΓΔ ταῖς ὑπὸ ΓΔΑ, ΔΑΓ· καὶ ἡ ὑπὸ ΒΓΔ ἄρα τῆς ὑπὸ ΓΑΔ ἐστι διπλῆ. ἴση δὲ ἡ ὑπὸ ΒΓΔ ἑκατέρᾳ τῶν ὑπὸ ΒΔΑ, ΔΒΑ· καὶ ἑκατέρα ἄρα τῶν ὑπὸ ΒΔΑ, ΔΒΑ τῆς ὑπὸ ΔΑΒ ἐστι διπλῆ.
Ἰσοσκελὲς ἄρα τρίγωνον συνέσταται τὸ ΑΒΔ ἔχον ἑκατέραν τῶν πρὸς τῇ ΔΒ βάσει γωνιῶν διπλασίονα τῆς λοιπῆς· ὅπερ ἔδει ποιῆσαι.
Πρότασις ια΄ 11 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔΕ· δεῖ δὴ εἰς τὸν ΑΒΓΔΕ κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἐκκείσθω τρίγωνον ἰσοσκελὲς τὸ ΖΗΘ διπλασίονα ἔχον ἑκατέραν τῶν πρὸς τοῖς Η, Θ γωνιῶν τῆς πρὸς τῷ Ζ, καὶ ἐγγεγράφθω εἰς τὸν ΑΒΓΔΕ κύκλον τῷ ΖΗΘ τριγώνῳ ἰσογώνιον τρίγωνον τὸ ΑΓΔ, ὥστε τῇ μὲν πρὸς τῷ Ζ γωνίᾳ ἴσην εἶναι τὴν ὑπὸ ΓΑΔ, ἑκατέραν δὲ τῶν πρὸς τοῖς Η, Θ ἴσην ἑκατέρᾳ τῶν ὑπὸ ΑΓΔ, ΓΔΑ· καὶ ἑκατέρα ἄρα τῶν ὑπὸ ΑΓΔ, ΓΔΑ τῆς ὑπὸ ΓΑΔ ἐστι διπλῆ. τετμήσθω δὴ ἑκατέρα τῶν ὑπὸ ΑΓΔ, ΓΔΑ δίχα ὑπὸ ἑκατέρας τῶν ΓΕ, ΔΒ εὐθειῶν, καὶ ἐπεζεύχθωσαν αἱ ΑΒ, ΒΓ, [ΓΔ], ΔΕ, ΕΑ.
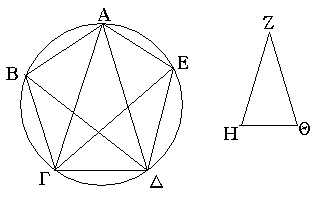
Ἐπεὶ οὖν ἑκατέρα τῶν ὑπὸ ΑΓΔ, ΓΔΑ γωνιῶν διπλασίων ἐστὶ τῆς ὑπὸ ΓΑΔ, καὶ τετμημέναι εἰσὶ δίχα ὑπὸ τῶν ΓΕ, ΔΒ εὐθειῶν, αἱ πέντε ἄρα γωνίαι αἱ ὑπὸ ΔΑΓ, ΑΓΕ, ΕΓΔ, ΓΔΒ, ΒΔΑ ἴσαι ἀλλήλαις εἰσίν. αἱ δὲ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν· αἱ πέντε ἄρα περιφέρειαι αἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ ἴσαι ἀλλήλαις εἰσίν. ὑπὸ δὲ τὰς ἴσας περιφερείας ἴσαι εὐθεῖαι ὑποτείνουσιν· αἱ πέντε ἄρα εὐθεῖαι αἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ ἴσαι ἀλλήλαις εἰσίν· ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓΔΕ πεντάγωνον. λέγω δή, ὅτι καὶ ἰσογώνιον. ἐπεὶ γὰρ ἡ ΑΒ περιφέρεια τῇ ΔΕ περιφερείᾳ ἐστὶν ἴση, κοινὴ προσκείσθω ἡ ΒΓΔ· ὅλη ἄρα ἡ ΑΒΓΔ περιφέρεια ὅλῃ τῇ ΕΔΓΒ περιφερείᾳ ἐστὶν ἴση. καὶ βέβηκεν ἐπὶ μὲν τῆς ΑΒΓΔ περιφερείας γωνία ἡ ὑπὸ ΑΕΔ, ἐπὶ δὲ τῆς ΕΔΓΒ περιφερείας γωνία ἡ ὑπὸ ΒΑΕ· καὶ ἡ ὑπὸ ΒΑΕ ἄρα γωνία τῇ ὑπὸ ΑΕΔ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἑκάστη τῶν ὑπὸ ΑΒΓ, ΒΓΔ, ΓΔΕ γωνιῶν ἑκατέρᾳ τῶν ὑπὸ ΒΑΕ, ΑΕΔ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓΔΕ πεντάγωνον. ἐδείχθη δὲ καὶ ἰσόπλευρον.
Εἰς ἄρα τὸν δοθέντα κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιβ΄ 12 Βιβλίον IV
Περὶ τὸν δοθέντα κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον περιγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔΕ· δεῖ δὴ περὶ τὸν ΑΒΓΔΕ κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον περιγράψαι.
Νενοήσθω τοῦ ἐγγεγραμμένου πενταγώνου τῶν γωνιῶν σημεῖα τὰ Α, Β, Γ, Δ, Ε, ὥστε ἴσας εἶναι τὰς ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ περιφερείας· καὶ διὰ τῶν Α, Β, Γ, Δ, Ε ἤχθωσαν τοῦ κύκλου ἐφαπτόμεναι αἱ ΗΘ, ΘΚ, ΚΛ, ΛΜ, ΜΗ, καὶ εἰλήφθω τοῦ ΑΒΓΔΕ κύκλου κέντρον τὸ Ζ, καὶ ἐπεζεύχθωσαν αἱ ΖΒ, ΖΚ, ΖΓ, ΖΛ, ΖΔ.
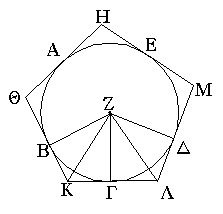
Καὶ ἐπεὶ ἡ μὲν ΚΛ εὐθεῖα ἐφάπτεται τοῦ ΑΒΓΔΕ κατὰ τὸ Γ, ἀπὸ δὲ τοῦ Ζ κέντρου ἐπὶ τὴν κατὰ τὸ Γ ἐπαφὴν ἐπέζευκται ἡ ΖΓ, ἡ ΖΓ ἄρα κάθετός ἐστιν ἐπὶ τὴν ΚΛ· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν πρὸς τῷ Γ γωνιῶν. διὰ τὰ αὐτὰ δὴ καὶ αἱ πρὸς τοῖς Β, Δ σημείοις γωνίαι ὀρθαί εἰσιν. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΖΓΚ γωνία, τὸ ἄρα ἀπὸ τῆς ΖΚ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΖΓ, ΓΚ. διὰ τὰ αὐτὰ δὴ καὶ τοῖς ἀπὸ τῶν ΖΒ, ΒΚ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΖΚ· ὥστε τὰ ἀπὸ τῶν ΖΓ, ΓΚ τοῖς ἀπὸ τῶν ΖΒ, ΒΚ ἐστιν ἴσα, ὧν τὸ ἀπὸ τῆς ΖΓ τῷ ἀπὸ τῆς ΖΒ ἐστιν ἴσον· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΓΚ τῷ ἀπὸ τῆς ΒΚ ἐστιν ἴσον. ἴση ἄρα ἡ ΒΚ τῇ ΓΚ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΖΒ τῇ ΖΓ, καὶ κοινὴ ἡ ΖΚ, δύο δὴ αἱ ΒΖ, ΖΚ δυσὶ ταῖς ΓΖ, ΖΚ ἴσαι εἰσίν· καὶ βάσις ἡ ΒΚ βάσει τῇ ΓΚ [ἐστιν] ἴση· γωνία ἄρα ἡ μὲν ὑπὸ ΒΖΚ [γωνίᾳ] τῇ ὑπὸ ΚΖΓ ἐστιν ἴση· ἡ δὲ ὑπὸ ΒΚΖ τῇ ὑπὸ ΖΚΓ· διπλῆ ἄρα ἡ μὲν ὑπὸ ΒΖΓ τῆς ὑπὸ ΚΖΓ, ἡ δὲ ὑπὸ ΒΚΓ τῆς ὑπὸ ΖΚΓ. διὰ τὰ αὐτὰ δὴ καὶ ἡ μὲν ὑπὸ ΓΖΔ τῆς ὑπὸ ΓΖΛ ἐστι διπλῆ, ἡ δὲ ὑπὸ ΔΛΓ τῆς ὑπὸ ΖΛΓ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΓ περιφέρεια τῇ ΓΔ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΒΖΓ τῇ ὑπὸ ΓΖΔ. καί ἐστιν ἡ μὲν ὑπὸ ΒΖΓ τῆς ὑπὸ ΚΖΓ διπλῆ, ἡ δὲ ὑπὸ ΔΖΓ τῆς ὑπὸ ΛΖΓ· ἴση ἄρα καὶ ἡ ὑπὸ ΚΖΓ τῇ ὑπὸ ΛΖΓ· ἐστὶ δὲ καὶ ἡ ὑπὸ ΖΓΚ γωνία τῇ ὑπὸ ΖΓΛ ἴση. δύο δὴ τρίγωνά ἐστι τὰ ΖΚΓ, ΖΛΓ τὰς δύο γωνίας ταῖς δυσὶ γωνίαις ἴσας ἔχοντα καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην κοινὴν αὐτῶν τὴν ΖΓ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει καὶ τὴν λοιπὴν γωνίαν τῇ λοιπῇ γωνίᾳ· ἴση ἄρα ἡ μὲν ΚΓ εὐθεῖα τῇ ΓΛ, ἡ δὲ ὑπὸ ΖΚΓ γωνία τῇ ὑπὸ ΖΛΓ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΚΓ τῇ ΓΛ, διπλῆ ἄρα ἡ ΚΛ τῆς ΚΓ. διὰ τὰ αὐτὰ δὴ δειχθήσεται καὶ ἡ ΘΚ τῆς ΒΚ διπλῆ. καί ἐστιν ἡ ΒΚ τῇ ΚΓ ἴση· καὶ ἡ ΘΚ ἄρα τῇ ΚΛ ἐστιν ἴση. ὁμοίως δὴ δειχθήσεται καὶ ἑκάστη τῶν ΘΗ, ΗΜ, ΜΛ ἑκατέρᾳ τῶν ΘΚ, ΚΛ ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΗΘΚΛΜ πεντάγωνον. λέγω δή, ὅτι καὶ ἰσογώνιον. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ὑπὸ ΖΚΓ γωνία τῇ ὑπὸ ΖΛΓ, καὶ ἐδείχθη τῆς μὲν ὑπὸ ΖΚΓ διπλῆ ἡ ὑπὸ ΘΚΛ, τῆς δὲ ὑπὸ ΖΛΓ διπλῆ ἡ ὑπὸ ΚΛΜ, καὶ ἡ ὑπὸ ΘΚΛ ἄρα τῇ ὑπὸ ΚΛΜ ἐστιν ἴση. ὁμοίως δὴ δειχθήσεται καὶ ἑκάστη τῶν ὑπὸ ΚΘΗ, ΘΗΜ, ΗΜΛ ἑκατέρᾳ τῶν ὑπὸ ΘΚΛ, ΚΛΜ ἴση· αἱ πέντε ἄρα γωνίαι αἱ ὑπὸ ΗΘΚ, ΘΚΛ, ΚΛΜ, ΛΜΗ, ΜΗΘ ἴσαι ἀλλήλαις εἰσίν. ἰσογώνιον ἄρα ἐστὶ τὸ ΗΘΚΛΜ πεντάγωνον. ἐδείχθη δὲ καὶ ἰσόπλευρον, καὶ περιγέγραπται περὶ τὸν ΑΒΓΔΕ κύκλον.
[Περὶ τὸν δοθέντα ἄρα κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον περιγέγραπται]· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιγ΄ 13 Βιβλίον IV
Εἰς τὸ δοθὲν πεντάγωνον, ὅ ἐστιν ἰσόπλευρόν τε καὶ ἰσογώνιον, κύκλον ἐγγράψαι.
Ἔστω τὸ δοθὲν πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον τὸ ΑΒΓΔΕ· δεῖ δὴ εἰς τὸ ΑΒΓΔΕ πεντάγωνον κύκλον ἐγγράψαι.
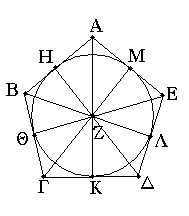
Τετμήσθω γὰρ ἑκατέρα τῶν ὑπὸ ΒΓΔ, ΓΔΕ γωνιῶν δίχα ὑπὸ ἑκατέρας τῶν ΓΖ, ΔΖ εὐθειῶν· καὶ ἀπὸ τοῦ Ζ σημείου, καθ᾿ ὃ συμβάλλουσιν ἀλλήλαις αἱ ΓΖ, ΔΖ εὐθεῖαι, ἐπεζεύχθωσαν αἱ ΖΒ, ΖΑ, ΖΕ εὐθεῖαι. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΓ τῇ ΓΔ, κοινὴ δὲ ἡ ΓΖ, δύο δὴ αἱ ΒΓ, ΓΖ δυσὶ ταῖς ΔΓ, ΓΖ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΒΓΖ γωνίᾳ τῇ ὑπὸ ΔΓΖ [ἐστιν] ἴση· βάσις ἄρα ἡ ΒΖ βάσει τῇ ΔΖ ἐστιν ἴση, καὶ τὸ ΒΓΖ τρίγωνον τῷ ΔΓΖ τριγώνῳ ἐστιν ἴσον, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἡ ὑπὸ ΓΒΖ γωνία τῇ ὑπὸ ΓΔΖ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ὑπὸ ΓΔΕ τῆς ὑπὸ ΓΔΖ, ἴση δὲ ἡ μὲν ὑπὸ ΓΔΕ τῇ ὑπὸ ΑΒΓ, ἡ δὲ ὑπὸ ΓΔΖ τῇ ὑπὸ ΓΒΖ, καὶ ἡ ὑπὸ ΓΒΑ ἄρα τῆς ὑπὸ ΓΒΖ ἐστι διπλῆ· ἴση ἄρα ἡ ὑπὸ ΑΒΖ γωνία τῇ ὑπὸ ΖΒΓ· ἡ ἄρα ὑπὸ ΑΒΓ γωνία δίχα τέτμηται ὑπὸ τῆς ΒΖ εὐθείας. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἑκατέρα τῶν ὑπὸ ΒΑΕ, ΑΕΔ δίχα τέτμηται ὑπὸ ἑκατέρας τῶν ΖΑ, ΖΕ εὐθειῶν. ἤχθωσαν δὴ ἀπὸ τοῦ Ζ σημείου ἐπὶ τὰς ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ εὐθείας κάθετοι αἱ ΖΗ, ΖΘ, ΖΚ, ΖΛ, ΖΜ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΘΓΖ γωνία τῇ ὑπὸ ΚΓΖ, ἐστὶ δὲ καὶ ὀρθὴ ἡ ὑπὸ ΖΘΓ [ὀρθῇ] τῇ ὑπὸ ΖΚΓ ἴση, δύο δὴ τρίγωνά ἐστι τὰ ΖΘΓ, ΖΚΓ τὰς δύο γωνίας δυσὶ γωνίαις ἴσας ἔχοντα καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην κοινὴν αὐτῶν τὴν ΖΓ ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει· ἴση ἄρα ἡ ΖΘ κάθετος τῇ ΖΚ καθέτῳ. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἑκάστη τῶν ΖΛ, ΖΜ, ΖΗ ἑκατέρᾳ τῶν ΖΘ, ΖΚ ἴση ἐστίν· αἱ πέντε ἄρα εὐθεῖαι αἱ ΖΗ, ΖΘ, ΖΚ, ΖΛ, ΖΜ ἴσαι ἀλλήλαις εἰσίν. ὁ ἄρα κέντρῳ τῷ Ζ διαστήματι δὲ ἑνὶ τῶν Η, Θ, Κ, Λ, Μ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἐφάψεται τῶν ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ εὐθειῶν διὰ τὸ ὀρθὰς εἶναι τὰς πρὸς τοῖς Η, Θ, Κ, Λ, Μ σημείοις γωνίας. εἰ γὰρ οὐκ ἐφάψεται αὐτῶν, ἀλλὰ τεμεῖ αὐτάς, συμβήσεται τὴν τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένην ἐντὸς πίπτειν τοῦ κύκλου· ὅπερ ἄτοπον ἐδείχθη. οὐκ ἄρα ὁ κέντρῳ τῷ Ζ διαστήματι δὲ ἑνὶ τῶν Η, Θ, Κ, Λ, Μ σημείων γραφόμενος κύκλος τεμεῖ τὰς ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΑ εὐθείας· ἐφάψεται ἄρα αὐτῶν. γεγράφθω ὡς ὁ ΗΘΚΛΜ.
Εἰς ἄρα τὸ δοθὲν πεντάγωνον, ὅ ἐστιν ἰσόπλευρόν τε καὶ ἰσογώνιον, κύκλος ἐγγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιδ΄ 14 Βιβλίον IV
Περὶ τὸ δοθὲν πεντάγωνον, ὅ ἐστιν ἰσόπλευρόν τε καὶ ἰσογώνιον, κύκλον περιγράψαι.
Ἔστω τὸ δοθὲν πεντάγωνον, ὅ ἐστιν ἰσόπλευρόν τε καὶ ἰσογώνιον, τὸ ΑΒΓΔΕ· δεῖ δὴ περὶ τὸ ΑΒΓΔΕ πεντάγωνον κύκλον περιγράψαι.
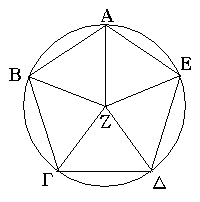
Τετμήσθω δὴ ἑκατέρα τῶν ὑπὸ ΒΓΔ, ΓΔΕ γωνιῶν δίχα ὑπὸ ἑκατέρας τῶν ΓΖ, ΔΖ, καὶ ἀπὸ τοῦ Ζ σημείου, καθ᾿ ὃ συμβάλλουσιν αἱ εὐθεῖαι, ἐπὶ τὰ Β, Α, Ε σημεῖα ἐπεζεύχθωσαν εὐθεῖαι αἱ ΖΒ, ΖΑ, ΖΕ. ὁμοίως δὴ τῷ πρὸ τούτου δειχθήσεται, ὅτι καὶ ἑκάστη τῶν ὑπὸ ΓΒΑ, ΒΑΕ, ΑΕΔ γωνιῶν δίχα τέτμηται ὑπὸ ἑκάστης τῶν ΖΒ, ΖΑ, ΖΕ εὐθειῶν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΒΓΔ γωνία τῇ ὑπὸ ΓΔΕ, καί ἐστι τῆς μὲν ὑπὸ ΒΓΔ ἡμίσεια ἡ ὑπὸ ΖΓΔ, τῆς δὲ ὑπὸ ΓΔΕ ἡμίσεια ἡ ὑπὸ ΓΔΖ, καὶ ἡ ὑπὸ ΖΓΔ ἄρα τῇ ὑπὸ ΖΔΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΖΓ πλευρᾷ τῇ ΖΔ ἐστιν ἴση. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἑκάστη τῶν ΖΒ, ΖΑ, ΖΕ ἑκατέρᾳ τῶν ΖΓ, ΖΔ ἐστιν ἴση· αἱ πέντε ἄρα εὐθεῖαι αἱ ΖΑ, ΖΒ, ΖΓ, ΖΔ, ΖΕ ἴσαι ἀλλήλαις εἰσίν. ὁ ἄρα κέντρῳ τῷ Ζ καὶ διαστήματι ἑνὶ τῶν ΖΑ, ΖΒ, ΖΓ, ΖΔ, ΖΕ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἔσται περιγεγραμμένος. περιγεγράφθω καὶ ἔστω ὁ ΑΒΓΔΕ.
Περὶ ἄρα τὸ δοθὲν πεντάγωνον, ὅ ἐστιν ἰσόπλευρόν τε καὶ ἰσογώνιον, κύκλος περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιε΄ 15 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον ἑξάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔΕΖ· δεῖ δὴ εἰς τὸν ΑΒΓΔΕΖ κύκλον ἑξάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἤχθω τοῦ ΑΒΓΔΕΖ κύκλου διάμετρος ἡ ΑΔ, καὶ εἰλήφθω τὸ κέντρον τοῦ κύκλου τὸ Η, καὶ κέντρῳ μὲν τῷ Δ διαστήματι δὲ τῷ ΔΗ κύκλος γεγράφθω ὁ ΕΗΓΘ, καὶ ἐπιζευχθεῖσαι αἱ ΕΗ, ΓΗ διήχθωσαν ἐπὶ τὰ Β, Ζ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΖ, ΖΑ· λέγω, ὅτι τὸ ΑΒΓΔΕΖ ἑξάγωνον ἰσόπλευρόν τέ ἐστι καὶ ἰσογώνιον.
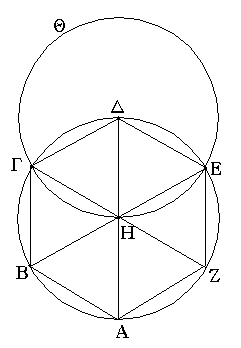
Ἐπεὶ γὰρ τὸ Η σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓΔΕΖ κύκλου, ἴση ἐστὶν ἡ ΗΕ τῇ ΗΔ. πάλιν, ἐπεὶ τὸ Δ σημεῖον κέντρον ἐστὶ τοῦ ΗΓΘ κύκλου, ἴση ἐστὶν ἡ ΔΕ τῇ ΔΗ. ἀλλ' ἡ ΗΕ τῇ ΗΔ ἐδείχθη ἴση· καὶ ἡ ΗΕ ἄρα τῇ ΕΔ ἴση ἐστίν· ἰσόπλευρον ἄρα ἐστὶ τὸ ΕΗΔ τρίγωνον· καὶ αἱ τρεῖς ἄρα αὐτοῦ γωνίαι αἱ ὑπὸ ΕΗΔ, ΗΔΕ, ΔΕΗ ἴσαι ἀλλήλαις εἰσίν, ἐπειδήπερ τῶν ἰσοσκελῶν τριγώνων αἱ πρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν· καί εἰσιν αἱ τρεῖς τοῦ τριγώνου γωνίαι δυσὶν ὀρθαῖς ἴσαι· ἡ ἄρα ὑπὸ ΕΗΔ γωνία τρίτον ἐστὶ δύο ὀρθῶν. ὁμοίως δὴ δειχθήσεται καὶ ἡ ὑπὸ ΔΗΓ τρίτον δύο ὀρθῶν. καὶ ἐπεὶ ἡ ΓΗ εὐθεῖα ἐπὶ τὴν ΕΒ σταθεῖσα τὰς ἐφεξῆς γωνίας τὰς ὑπὸ ΕΗΓ, ΓΗΒ δυσὶν ὀρθαῖς ἴσας ποιεῖ, καὶ λοιπὴ ἄρα ἡ ὑπὸ ΓΗΒ τρίτον ἐστὶ δύο ὀρθῶν· αἱ ἄρα ὑπὸ ΕΗΔ, ΔΗΓ, ΓΗΒ γωνίαι ἴσαι ἀλλήλαις εἰσίν· ὥστε καὶ αἱ κατὰ κορυφὴν αὐταῖς αἱ ὑπὸ ΒΗΑ, ΑΗΖ, ΖΗΕ ἴσαι εἰσίν [ταῖς ὑπὸ ΕΗΔ, ΔΗΓ, ΓΗΒ]. αἱ ἓξ ἄρα γωνίαι αἱ ὑπὸ ΕΗΔ, ΔΗΓ, ΓΗΒ, ΒΗΑ, ΑΗΖ, ΖΗΕ ἴσαι ἀλλήλαις εἰσίν. αἱ δὲ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν· αἱ ἓξ ἄρα περιφέρειαι αἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ, ΕΖ, ΖΑ ἴσαι ἀλλήλαις εἰσίν. ὑπὸ δὲ τὰς ἴσας περιφερείας αἱ ἴσαι εὐθεῖαι ὑποτείνουσιν· αἱ ἓξ ἄρα εὐθεῖαι ἴσαι ἀλλήλαις εἰσίν· ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓΔΕΖ ἑξάγωνον. λέγω δή, ὅτι καὶ ἰσογώνιον. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΖΑ περιφέρεια τῇ ΕΔ περιφερείᾳ, κοινὴ προσκείσθω ἡ ΑΒΓΔ περιφέρεια· ὅλη ἄρα ἡ ΖΑΒΓΔ ὅλῃ τῇ ΕΔΓΒΑ ἐστιν ἴση· καὶ βέβηκεν ἐπὶ μὲν τῆς ΖΑΒΓΔ περιφερείας ἡ ὑπὸ ΖΕΔ γωνία, ἐπὶ δὲ τῆς ΕΔΓΒΑ περιφερείας ἡ ὑπὸ ΑΖΕ γωνία· ἴση ἄρα ἡ ὑπὸ ΑΖΕ γωνία τῇ ὑπὸ ΔΕΖ. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ αἱ λοιπαὶ γωνίαι τοῦ ΑΒΓΔΕΖ ἑξαγώνου κατὰ μίαν ἴσαι εἰσὶν ἑκατέρᾳ τῶν ὑπὸ ΑΖΕ, ΖΕΔ γωνιῶν· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓΔΕΖ ἑξάγωνον. ἐδείχθη δὲ καὶ ἰσόπλευρον· καὶ ἐγγέγραπται εἰς τὸν ΑΒΓΔΕΖ κύκλον.
Εἰς ἄρα τὸν δοθέντα κύκλον ἑξάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγέγραπται· ὅπερ ἔδει ποιῆσαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἡ τοῦ ἑξαγώνου πλευρὰ ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου τοῦ κύκλου.
Ὁμοίως δὲ τοῖς ἐπὶ τοῦ πενταγώνου ἐὰν διὰ τῶν κατὰ τὸν κύκλον διαιρέσεων ἐφαπτομένας τοῦ κύκλου ἀγάγωμεν, περιγραφήσεται περὶ τὸν κύκλον ἑξάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἀκολούθως τοῖς ἐπὶ τοῦ πενταγώνου εἰρημένοις. καὶ ἔτι διὰ τῶν ὁμοίων τοῖς ἐπὶ τοῦ πενταγώνου εἰρημένοις εἰς τὸ δοθὲν ἑξάγωνον κύκλον ἐγγράψομέν τε καὶ περιγράψομεν· ὅπερ ἔδει ποιῆσαι.
Πρότασις ις΄ 16 Βιβλίον IV
Εἰς τὸν δοθέντα κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔ· δεῖ δὴ εἰς τὸν ΑΒΓΔ κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἐγγεγράφθω εἰς τὸν ΑΒΓΔ κύκλον τριγώνου μὲν ἰσοπλεύρου τοῦ εἰς αὐτὸν ἐγγραφομένου πλευρὰ ἡ ΑΓ, πενταγώνου δὲ ἰσοπλεύρου ἡ ΑΒ· οἵων ἄρα ἐστὶν ὁ ΑΒΓΔ κύκλος ἴσων τμημάτων δεκαπέντε, τοιούτων ἡ μὲν ΑΒΓ περιφέρεια τρίτον οὖσα τοῦ κύκλου ἔσται πέντε, ἡ δὲ ΑΒ περιφέρεια πέμπτον οὖσα τοῦ κύκλου ἔσται τριῶν· λοιπὴ ἄρα ἡ ΒΓ τῶν ἴσων δύο. τετμήσθω ἡ ΒΓ δίχα κατὰ τὸ Ε· ἑκατέρα ἄρα τῶν ΒΕ, ΕΓ περιφερειῶν πεντεκαιδέκατόν ἐστι τοῦ ΑΒΓΔ κύκλου.
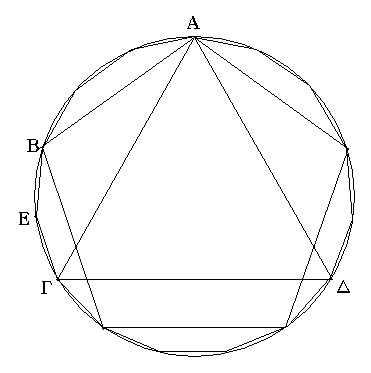
Ἐὰν ἄρα ἐπιζεύξαντες τὰς ΒΕ, ΕΓ ἴσας αὐταῖς κατὰ τὸ συνεχὲς εὐθείας ἐναρμόσωμεν εἰς τὸν ΑΒΓΔ[Ε] κύκλον, ἔσται εἰς αὐτὸν ἐγγεγραμμένον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον· ὅπερ ἔδει ποιῆσαι.
Ὁμοίως δὲ τοῖς ἐπὶ τοῦ πενταγώνου ἐὰν διὰ τῶν κατὰ τὸν κύκλον διαιρέσεων ἐφαπτομένας τοῦ κύκλου ἀγάγωμεν, περιγραφήσεται περὶ τὸν κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον. ἔτι δὲ διὰ τῶν ὁμοίων τοῖς ἐπὶ τοῦ πενταγώνου δείξεων καὶ εἰς τὸ δοθὲν πεντεκαιδεκάγωνον κύκλον ἐγγράψομέν τε καὶ περιγράψομεν· ὅπερ ἔδει ποιῆσαι.
Στοιχεῖα Εὐκλείδου ε΄
Βιβλίον V
Ὅροι ιη΄ 18.
α΄ 1. Μέρος ἐστὶ μέγεθος μεγέθους τὸ ἔλασσον τοῦ μείζονος, ὅταν καταμετρῇ τὸ μεῖζον.
β΄ 2. Πολλαπλάσιον δὲ τὸ μεῖζον τοῦ ἐλάττονος, ὅταν καταμετρῆται ὑπὸ τοῦ ἐλάττονος.
γ΄ 3. Λόγος ἐστὶ δύο μεγεθῶν ὁμογενῶν ἡ κατὰ πηλικότητά ποια σχέσις.
δ΄ 4. Λόγον ἔχειν πρὸς ἄλληλα μεγέθη λέγεται, ἃ δύναται πολλαπλασιαζόμενα ἀλλήλων ὑπερέχειν.
ε΄ 5. Ἐν τῷ αὐτῷ λόγῳ μεγέθη λέγεται εἶναι πρῶτον πρὸς δεύτερον καὶ τρίτον πρὸς τέταρτον, ὅταν τὰ τοῦ πρώτου καὶ τρίτου ἰσάκις πολλαπλάσια τῶν τοῦ δευτέρου καὶ τετάρτου ἰσάκις πολλαπλασίων καθ᾿ ὁποιονοῦν πολλαπλασιασμὸν ἑκάτερον ἑκατέρου ἢ ἅμα ὑπερέχῃ ἢ ἅμα ἴσα ᾖ ἢ ἅμα ἐλλείπῃ ληφθέντα κατάλληλα.
ς΄ 6. Τὰ δὲ τὸν αὐτὸν ἔχοντα λόγον μεγέθη ἀνάλογον καλείσθω.
ζ΄ 7. Ὅταν δὲ τῶν ἰσάκις πολλαπλασίων τὸ μὲν τοῦ πρώτου πολλαπλάσιον ὑπερέχῃ τοῦ τοῦ δευτέρου πολλαπλασίου, τὸ δὲ τοῦ τρίτου πολλαπλάσιον μὴ ὑπερέχῃ τοῦ τοῦ τετάρτου πολλαπλασίου, τότε τὸ πρῶτον πρὸς τὸ δεύτερον μείζονα λόγον ἔχειν λέγεται, ἤπερ τὸ τρίτον πρὸς τὸ τέταρτον.
η΄ 8. Ἀναλογία δὲ ἐν τρισὶν ὅροις ἐλαχίστη ἐστίν.
θ΄ 9. Ὅταν δὲ τρία μεγέθη ἀνάλογον ᾖ, τὸ πρῶτον πρὸς τὸ τρίτον διπλασίονα λόγον ἔχειν λέγεται ἤπερ πρὸς τὸ δεύτερον.
ι΄ 10. Ὅταν δὲ τέσσαρα μεγέθη ἀνάλογον ᾖ, τὸ πρῶτον πρὸς τὸ τέταρτον τριπλασίονα λόγον ἔχειν λέγεται ἤπερ πρὸς τὸ δεύτερον, καὶ ἀεὶ ἑξῆς ὁμοίως, ὡς ἂν ἡ ἀναλογία ὑπάρχῃ.
ια΄ 11. Ὁμόλογα μεγέθη λέγεται τὰ μὲν ἡγούμενα τοῖς ἡγουμένοις τὰ δὲ ἑπόμενα τοῖς ἑπομένοις.
ιβ΄ 12. Ἐναλλὰξ λόγος ἐστὶ λῆψις τοῦ ἡγουμένου πρὸς τὸ ἡγούμενον καὶ τοῦ ἑπομένου πρὸς τὸ ἑπόμενον.
ιγ΄ 13. Ἀνάπαλιν λόγος ἐστὶ λῆψις τοῦ ἑπομένου ὡς ἡγουμένου πρὸς τὸ ἡγούμενον ὡς ἑπόμενον.
ιδ΄ 14. Σύνθεσις λόγου ἐστὶ λῆψις τοῦ ἡγουμένου μετὰ τοῦ ἑπομένου ὡς ἑνὸς πρὸς αὐτὸ τὸ ἑπόμενον.
ιε΄ 15. Διαίρεσις λόγου ἐστὶ λῆψις τῆς ὑπεροχῆς, ᾗ ὑπερέχει τὸ ἡγούμενον τοῦ ἑπομένου, πρὸς αὐτὸ τὸ ἑπόμενον.
ις΄ 16. Ἀναστροφὴ λόγου ἐστὶ λῆψις τοῦ ἡγουμένου πρὸς τὴν ὑπεροχήν, ᾗ ὑπερέχει τὸ ἡγούμενον τοῦ ἑπομένου.
ιζ΄ 17. Δι' ἴσου λόγος ἐστὶ πλειόνων ὄντων μεγεθῶν καὶ ἄλλων αὐτοῖς ἴσων τὸ πλῆθος σύνδυο λαμβανομένων καὶ ἐν τῷ αὐτῷ λόγῳ, ὅταν ᾖ ὡς ἐν τοῖς πρώτοις μεγέθεσι τὸ πρῶτον πρὸς τὸ ἔσχατον, οὕτως ἐν τοῖς δευτέροις μεγέθεσι τὸ πρῶτον πρὸς τὸ ἔσχατον· ἢ ἄλλως· Λῆψις τῶν ἄκρων καθ᾿ ὑπεξαίρεσιν τῶν μέσων.
ιη΄ 18. Τεταραγμένη δὲ ἀναλογία ἐστίν, ὅταν τριῶν ὄντων μεγεθῶν καὶ ἄλλων αὐτοῖς ἴσων τὸ πλῆθος γίνηται ὡς μὲν ἐν τοῖς πρώτοις μεγέθεσιν ἡγούμενον πρὸς ἑπόμενον, οὕτως ἐν τοῖς δευτέροις μεγέθεσιν ἡγούμενον πρὸς ἑπόμενον, ὡς δὲ ἐν τοῖς πρώτοις μεγέθεσιν ἑπόμενον πρὸς ἄλλο τι, οὕτως ἐν τοῖς δευτέροις ἄλλο τι πρὸς ἡγούμενον.
Στοιχεῖα Εὐκλείδου ε΄
Προτάσεις κε΄ 25
Πρότασις α΄ 1 Βιβλίον V
Ἐὰν ᾖ ὁποσαοῦν μεγέθη ὁποσωνοῦν μεγεθῶν ἴσων τὸ πλῆθος ἕκαστον ἑκάστου ἰσάκις πολλαπλάσιον, ὁσαπλάσιόν ἐστιν ἓν τῶν μεγεθῶν ἑνός, τοσαυταπλάσια ἔσται καὶ τὰ πάντα τῶν πάντων.
Ἔστω ὁποσαοῦν μεγέθη τὰ ΑΒ, ΓΔ ὁποσωνοῦν μεγεθῶν τῶν Ε, Ζ ἴσων τὸ πλῆθος ἕκαστον ἑκάστου ἰσάκις πολλαπλάσιον· λέγω, ὅτι ὁσαπλάσιόν ἐστι τὸ ΑΒ τοῦ Ε, τοσαυταπλάσια ἔσται καὶ τὰ ΑΒ, ΓΔ τῶν Ε, Ζ.
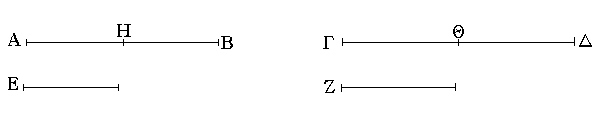
Ἐπεὶ γὰρ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΒ τοῦ Ε καὶ τὸ ΓΔ τοῦ Ζ, ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ μεγέθη ἴσα τῷ Ε, τοσαῦτα καὶ ἐν τῷ ΓΔ ἴσα τῷ Ζ. διῃρήσθω τὸ μὲν ΑΒ εἰς τὰ τῷ Ε μεγέθη ἴσα τὰ ΑΗ, ΗΒ, τὸ δὲ ΓΔ εἰς τὰ τῷ Ζ ἴσα τὰ ΓΘ, ΘΔ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΑΗ, ΗΒ τῷ πλήθει τῶν ΓΘ, ΘΔ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ μὲν ΑΗ τῷ Ε, τὸ δὲ ΓΘ τῷ Ζ, ἴσον ἄρα τὸ ΑΗ τῷ Ε, καὶ τὰ ΑΗ, ΓΘ τοῖς Ε, Ζ. διὰ τὰ αὐτὰ δὴ ἴσον ἐστὶ τὸ ΗΒ τῷ Ε, καὶ τὰ ΗΒ, ΘΔ τοῖς Ε, Ζ· ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ ἴσα τῷ Ε, τοσαῦτα καὶ ἐν τοῖς ΑΒ, ΓΔ ἴσα τοῖς Ε, Ζ· ὁσαπλάσιον ἄρα ἐστὶ τὸ ΑΒ τοῦ Ε, τοσαυταπλάσια ἔσται καὶ τὰ ΑΒ, ΓΔ τῶν Ε, Ζ.
Ἐὰν ἄρα ᾖ ὁποσαοῦν μεγέθη ὁποσωνοῦν μεγεθῶν ἴσων τὸ πλῆθος ἕκαστον ἑκάστου ἰσάκις πολλαπλάσιον, ὁσαπλάσιόν ἐστιν ἓν τῶν μεγεθῶν ἑνός, τοσαυταπλάσια ἔσται καὶ τὰ πάντα τῶν πάντων· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον V
Ἐὰν πρῶτον δευτέρου ἰσάκις ᾖ πολλαπλάσιον καὶ τρίτον τετάρτου, ᾖ δὲ καὶ πέμπτον δευτέρου ἰσάκις πολλαπλάσιον καὶ ἕκτον τετάρτου, καὶ συντεθὲν πρῶτον καὶ πέμπτον δευτέρου ἰσάκις ἔσται πολλαπλάσιον καὶ τρίτον καὶ ἕκτον τετάρτου.
Πρῶτον γὰρ τὸ ΑΒ δευτέρου τοῦ Γ ἰσάκις ἔστω πολλαπλάσιον καὶ τρίτον τὸ ΔΕ τετάρτου τοῦ Ζ, ἔστω δὲ καὶ πέμπτον τὸ ΒΗ δευτέρου τοῦ Γ ἰσάκις πολλαπλάσιον καὶ ἕκτον τὸ ΕΘ τετάρτου τοῦ Ζ· λέγω, ὅτι καὶ συντεθὲν πρῶτον καὶ πέμπτον τὸ ΑΗ δευτέρου τοῦ Γ ἰσάκις ἔσται πολλαπλάσιον καὶ τρίτον καὶ ἕκτον τὸ ΔΘ τετάρτου τοῦ Ζ.
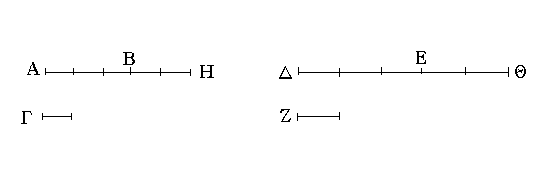
Ἐπεὶ γὰρ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΒ τοῦ Γ καὶ τὸ ΔΕ τοῦ Ζ, ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ ἴσα τῷ Γ, τοσαῦτα καὶ ἐν τῷ ΔΕ ἴσα τῷ Ζ. διὰ τὰ αὐτὰ δὴ καὶ ὅσα ἐστὶν ἐν τῷ ΒΗ ἴσα τῷ Γ, τοσαῦτα καὶ ἐν τῷ ΕΘ ἴσα τῷ Ζ· ὅσα ἄρα ἐστὶν ἐν ὅλῳ τῷ ΑΗ ἴσα τῷ Γ, τοσαῦτα καὶ ἐν ὅλῳ τῷ ΔΘ ἴσα τῷ Ζ· ὁσαπλάσιον ἄρα ἐστὶ τὸ ΑΗ τοῦ Γ, τοσαυταπλάσιον ἔσται καὶ τὸ ΔΘ τοῦ Ζ. καὶ συντεθὲν ἄρα πρῶτον καὶ πέμπτον τὸ ΑΗ δευτέρου τοῦ Γ ἰσάκις ἔσται πολλαπλάσιον καὶ τρίτον καὶ ἕκτον τὸ ΔΘ τετάρτου τοῦ Ζ.
Ἐὰν ἄρα πρῶτον δευτέρου ἰσάκις ᾖ πολλαπλάσιον καὶ τρίτον τετάρτου, ᾖ δὲ καὶ πέμπτον δευτέρου ἰσάκις πολλαπλάσιον καὶ ἕκτον τετάρτου, καὶ συντεθὲν πρῶτον καὶ πέμπτον δευτέρου ἰσάκις ἔσται πολλαπλάσιον καὶ τρίτον καὶ ἕκτον τετάρτου· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον V
Ἐὰν πρῶτον δευτέρου ἰσάκις ᾖ πολλαπλάσιον καὶ τρίτον τετάρτου, ληφθῇ δὲ ἰσάκις πολλαπλάσια τοῦ τε πρώτου καὶ τρίτου, καὶ δι' ἴσου τῶν ληφθέντων ἑκάτερον ἑκατέρου ἰσάκις ἔσται πολλαπλάσιον τὸ μὲν τοῦ δευτέρου τὸ δὲ τοῦ τετάρτου.
Πρῶτον γὰρ τὸ Α δευτέρου τοῦ Β ἰσάκις ἔστω πολλαπλάσιον καὶ τρίτον τὸ Γ τετάρτου τοῦ Δ, καὶ εἰλήφθω τῶν Α, Γ ἰσάκις πολλαπλάσια τὰ ΕΖ, ΗΘ· λέγω, ὅτι ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΕΖ τοῦ Β καὶ τὸ ΗΘ τοῦ Δ.
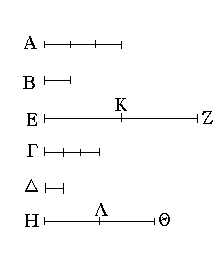
Ἐπεὶ γὰρ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΕΖ τοῦ Α καὶ τὸ ΗΘ τοῦ Γ, ὅσα ἄρα ἐστὶν ἐν τῷ ΕΖ ἴσα τῷ Α, τοσαῦτα καὶ ἐν τῷ ΗΘ ἴσα τῷ Γ. διῃρήσθω τὸ μὲν ΕΖ εἰς τὰ τῷ Α μεγέθη ἴσα τὰ ΕΚ, ΚΖ, τὸ δὲ ΗΘ εἰς τὰ τῷ Γ ἴσα τὰ ΗΛ, ΛΘ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΕΚ, ΚΖ τῷ πλήθει τῶν ΗΛ, ΛΘ. καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ Α τοῦ Β καὶ τὸ Γ τοῦ Δ, ἴσον δὲ τὸ μὲν ΕΚ τῷ Α, τὸ δὲ ΗΛ τῷ Γ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΕΚ τοῦ Β καὶ τὸ ΗΛ τοῦ Δ. διὰ τὰ αὐτὰ δὴ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΚΖ τοῦ Β καὶ τὸ ΛΘ τοῦ Δ. ἐπεὶ οὖν πρῶτον τὸ ΕΚ δευτέρου τοῦ Β ἰσάκις ἐστὶ πολλαπλάσιον καὶ τρίτον τὸ ΗΛ τετάρτου τοῦ Δ, ἔστι δὲ καὶ πέμπτον τὸ ΚΖ δευτέρου τοῦ Β ἰσάκις πολλαπλάσιον καὶ ἕκτον τὸ ΛΘ τετάρτου τοῦ Δ, καὶ συντεθὲν ἄρα πρῶτον καὶ πέμπτον τὸ ΕΖ δευτέρου τοῦ Β ἰσάκις ἐστὶ πολλαπλάσιον καὶ τρίτον καὶ ἕκτον τὸ ΗΘ τετάρτου τοῦ Δ.
Ἐὰν ἄρα πρῶτον δευτέρου ἰσάκις ᾖ πολλαπλάσιον καὶ τρίτον τετάρτου, ληφθῇ δὲ τοῦ πρώτου καὶ τρίτου ἰσάκις πολλαπλάσια, καὶ δι' ἴσου τῶν ληφθέντων ἑκάτερον ἑκατέρου ἰσάκις ἔσται πολλαπλάσιον τὸ μὲν τοῦ δευτέρου τὸ δὲ τοῦ τετάρτου· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον V
Ἐὰν πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, καὶ τὰ ἰσάκις πολλαπλάσια τοῦ τε πρώτου καὶ τρίτου πρὸς τὰ ἰσάκις πολλαπλάσια τοῦ δευτέρου καὶ τετάρτου καθ᾿ ὁποιονοῦν πολλαπλασιασμὸν τὸν αὐτὸν ἕξει λόγον ληφθέντα κατάλληλα.
Πρῶτον γὰρ τὸ Α πρὸς δεύτερον τὸ Β τὸν αὐτὸν ἐχέτω λόγον καὶ τρίτον τὸ Γ πρὸς τέταρτον τὸ Δ, καὶ εἰλήφθω τῶν μὲν Α, Γ ἰσάκις πολλαπλάσια τὰ Ε, Ζ, τῶν δὲ Β, Δ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Η, Θ· λέγω, ὅτι ἐστὶν ὡς τὸ Ε πρὸς τὸ Η, οὕτως τὸ Ζ πρὸς τὸ Θ.
Εἰλήφθω γὰρ τῶν μὲν Ε, Ζ ἰσάκις πολλαπλάσια τὰ Κ, Λ, τῶν δὲ Η, Θ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Μ, Ν.
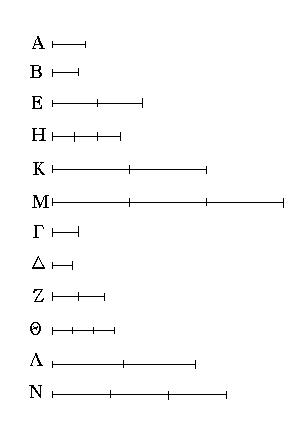
[Καὶ] ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ μὲν Ε τοῦ Α, τὸ δὲ Ζ τοῦ Γ, καὶ εἴληπται τῶν Ε, Ζ ἰσάκις πολλαπλάσια τὰ Κ, Λ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ Κ τοῦ Α καὶ τὸ Λ τοῦ Γ. διὰ τὰ αὐτὰ δὴ ἰσάκις ἐστὶ πολλαπλάσιον τὸ Μ τοῦ Β καὶ τὸ Ν τοῦ Λ. καὶ ἐπεί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, καὶ εἴληπται τῶν μὲν Α, Γ ἰσάκις πολλαπλάσια τὰ Κ, Λ, τῶν δὲ Β, Δ ἄλλα ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Μ, Ν, εἰ ἄρα ὑπερέχει τὸ Κ τοῦ Μ, ὑπερέχει καὶ τὸ Λ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Κ, Λ τῶν Ε, Ζ ἰσάκις πολλαπλάσια, τὰ δὲ Μ, Ν τῶν Η, Θ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· ἔστιν ἄρα ὡς τὸ Ε πρὸς τὸ Η, οὕτως τὸ Ζ πρὸς τὸ Θ.
Ἐὰν ἄρα πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, καὶ τὰ ἰσάκις πολλαπλάσια τοῦ τε πρώτου καὶ τρίτου πρὸς τὰ ἰσάκις πολλαπλάσια τοῦ δευτέρου καὶ τετάρτου τὸν αὐτὸν ἕξει λόγον καθ᾿ ὁποιονοῦν πολλαπλασιασμὸν ληφθέντα κατάλληλα· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον V
Ἐὰν μέγεθος μεγέθους ἰσάκις ᾖ πολλαπλάσιον, ὅπερ ἀφαιρεθὲν ἀφαιρεθέντος, καὶ τὸ λοιπὸν τοῦ λοιποῦ ἰσάκις ἔσται πολλαπλάσιον, ὁσαπλάσιόν ἐστι τὸ ὅλον τοῦ ὅλου.
Μέγεθος γὰρ τὸ ΑΒ μεγέθους τοῦ ΓΔ ἰσάκις ἔστω πολλαπλάσιον, ὅπερ ἀφαιρεθὲν τὸ ΑΕ ἀφαιρεθέντος τοῦ ΓΖ· λέγω, ὅτι καὶ λοιπὸν τὸ ΕΒ λοιποῦ τοῦ ΖΔ ἰσάκις ἔσται πολλαπλάσιον, ὁσαπλάσιόν ἐστιν ὅλον τὸ ΑΒ ὅλου τοῦ ΓΔ.
Ὁσαπλάσιον γάρ ἐστι τὸ ΑΕ τοῦ ΓΖ, τοσαυταπλάσιον γεγονέτω καὶ τὸ ΕΒ τοῦ ΓΗ.
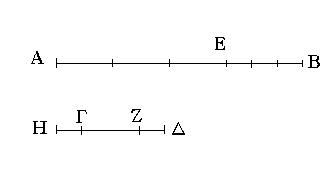
Καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΕΒ τοῦ ΗΓ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΑΒ τοῦ ΗΖ. κεῖται δὲ ἰσάκις πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΑΒ τοῦ ΓΔ. ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΑΒ ἑκατέρου τῶν ΗΖ, ΓΔ· ἴσον ἄρα τὸ ΗΖ τῷ ΓΔ. κοινὸν ἀφῃρήσθω τὸ ΓΖ· λοιπὸν ἄρα τὸ ΗΓ λοιπῷ τῷ ΖΔ ἴσον ἐστίν. καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΕΒ τοῦ ΗΓ, ἴσον δὲ τὸ ΗΓ τῷ ΔΖ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΕΒ τοῦ ΖΔ. ἰσάκις δὲ ὑπόκειται πολλαπλάσιον τὸ ΑΕ τοῦ ΓΖ καὶ τὸ ΑΒ τοῦ ΓΔ· ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΕΒ τοῦ ΖΔ καὶ τὸ ΑΒ τοῦ ΓΔ. καὶ λοιπὸν ἄρα τὸ ΕΒ λοιποῦ τοῦ ΖΔ ἰσάκις ἔσται πολλαπλάσιον, ὁσαπλάσιόν ἐστιν ὅλον τὸ ΑΒ ὅλου τοῦ ΓΔ.
Ἐὰν ἄρα μέγεθος μεγέθους ἰσάκις ᾖ πολλαπλάσιον, ὅπερ ἀφαιρεθὲν ἀφαιρεθέντος, καὶ τὸ λοιπὸν τοῦ λοιποῦ ἰσάκις ἔσται πολλαπλάσιον, ὁσαπλάσιόν ἐστι καὶ τὸ ὅλον τοῦ ὅλου· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον V
Ἐὰν δύο μεγέθη δύο μεγεθῶν ἰσάκις ᾖ πολλαπλάσια, καὶ ἀφαιρεθέντα τινὰ τῶν αὐτῶν ἰσάκις ᾖ πολλαπλάσια, καὶ τὰ λοιπὰ τοῖς αὐτοῖς ἤτοι ἴσα ἐστὶν ἢ ἰσάκις αὐτῶν πολλαπλάσια.
Δύο γὰρ μεγέθη τὰ ΑΒ, ΓΔ δύο μεγεθῶν τῶν Ε, Ζ ἰσάκις ἔστω πολλαπλάσια, καὶ ἀφαιρεθέντα τὰ ΑΗ, ΓΘ τῶν αὐτῶν τῶν Ε, Ζ ἰσάκις ἔστω πολλαπλάσια· λέγω, ὅτι καὶ λοιπὰ τὰ ΗΒ, ΘΔ τοῖς Ε, Ζ ἤτοι ἴσα ἐστὶν ἢ ἰσάκις αὐτῶν πολλαπλάσια.
Ἔστω γὰρ πρότερον τὸ ΗΒ τῷ Ε ἴσον. λέγω, ὅτι καὶ τὸ ΘΔ τῷ Ζ ἴσον ἐστίν.
Κείσθω γὰρ τῷ Ζ ἴσον τὸ ΓΚ. ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΗ τοῦ Ε καὶ τὸ ΓΘ τοῦ Ζ, ἴσον δὲ τὸ μὲν ΗΒ τῷ Ε, τὸ δὲ ΚΓ τῷ Ζ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΑΒ τοῦ Ε καὶ τὸ ΚΘ τοῦ Ζ. ἰσάκις δὲ ὑπόκειται πολλαπλάσιον τὸ ΑΒ τοῦ Ε καὶ τὸ ΓΔ τοῦ Ζ· ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΚΘ τοῦ Ζ καὶ τὸ ΓΔ τοῦ Ζ. ἐπεὶ οὖν ἑκάτερον τῶν ΚΘ, ΓΔ τοῦ Ζ ἰσάκις ἐστὶ πολλαπλάσιον, ἴσον ἄρα ἐστὶ τὸ ΚΘ τῷ ΓΔ. κοινὸν ἀφῃρήσθω τὸ ΓΘ· λοιπὸν ἄρα τὸ ΚΓ λοιπῷ τῷ ΘΔ ἴσον ἐστίν. ἀλλὰ τὸ Ζ τῷ ΚΓ ἐστιν ἴσον· καὶ τὸ ΘΔ ἄρα τῷ Ζ ἴσον ἐστίν. ὥστε εἰ τὸ ΗΒ τῷ Ε ἴσον ἐστίν, καὶ τὸ ΘΔ ἴσον ἔσται τῷ Ζ.
Ὁμοίως δὴ δείξομεν, ὅτι, κἂν πολλαπλάσιον ᾖ τὸ ΗΒ τοῦ Ε, τοσαυταπλάσιον ἔσται καὶ τὸ ΘΔ τοῦ Ζ.
Ἐὰν ἄρα δύο μεγέθη δύο μεγεθῶν ἰσάκις ᾖ πολλαπλάσια, καὶ ἀφαιρεθέντα τινὰ τῶν αὐτῶν ἰσάκις ᾖ πολλαπλάσια, καὶ τὰ λοιπὰ τοῖς αὐτοῖς ἤτοι ἴσα ἐστὶν ἢ ἰσάκις αὐτῶν πολλαπλάσια· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον V
Τὰ ἴσα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον καὶ τὸ αὐτὸ πρὸς τὰ ἴσα.
Ἔστω ἴσα μεγέθη τὰ Α, Β, ἄλλο δέ τι, ὃ ἔτυχεν, μέγεθος τὸ Γ· λέγω, ὅτι ἑκάτερον τῶν Α, Β πρὸς τὸ Γ τὸν αὐτὸν ἔχει λόγον, καὶ τὸ Γ πρὸς ἑκάτερον τῶν Α, Β.
Εἰλήφθω γὰρ τῶν μὲν Α, Β ἰσάκις πολλαπλάσια τὰ Δ, Ε, τοῦ δὲ Γ ἄλλο, ὃ ἔτυχεν, πολλαπλάσιον τὸ Ζ.
Ἐπεὶ οὖν ἰσάκις ἐστὶ πολλαπλάσιον τὸ Δ τοῦ Α καὶ τὸ Ε τοῦ Β, ἴσον δὲ τὸ Α τῷ Β, ἴσον ἄρα καὶ τὸ Δ τῷ Ε. ἄλλο δέ, ὃ ἔτυχεν, τὸ Ζ. Εἰ ἄρα ὑπερέχει τὸ Δ τοῦ Ζ, ὑπερέχει καὶ τὸ Ε τοῦ Ζ, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Δ, Ε τῶν Α, Β ἰσάκις πολλαπλάσια, τὸ δὲ Ζ τοῦ Γ ἄλλο, ὃ ἔτυχεν, πολλαπλάσιον· ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Β πρὸς τὸ Γ.
Λέγω [δή], ὅτι καὶ τὸ Γ πρὸς ἑκάτερον τῶν Α, Β τὸν αὐτὸν ἔχει λόγον.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι ἴσον ἐστὶ τὸ Δ τῷ Ε· ἄλλο δέ τι τὸ Ζ· εἰ ἄρα ὑπερέχει τὸ Ζ τοῦ Δ, ὑπερέχει καὶ τοῦ Ε, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὸ μὲν Ζ τοῦ Γ πολλαπλάσιον, τὰ δὲ Δ, Ε τῶν Α, Β ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Α, οὕτως τὸ Γ πρὸς τὸ Β.
Τὰ ἴσα ἄρα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον καὶ τὸ αὐτὸ πρὸς τὰ ἴσα.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν μεγέθη τινὰ ἀνάλογον ᾖ, καὶ ἀνάπαλιν ἀνάλογον ἔσται. ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον V
Τῶν ἀνίσων μεγεθῶν τὸ μεῖζον πρὸς τὸ αὐτὸ μείζονα λόγον ἔχει ἤπερ τὸ ἔλαττον. καὶ τὸ αὐτὸ πρὸς τὸ ἔλαττον μείζονα λόγον ἔχει ἤπερ πρὸς τὸ μεῖζον.
Ἔστω ἄνισα μεγέθη τὰ ΑΒ, Γ, καὶ ἔστω μεῖζον τὸ ΑΒ, ἄλλο δέ, ὃ ἔτυχεν, τὸ Δ· λέγω, ὅτι τὸ ΑΒ πρὸς τὸ Δ μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Δ, καὶ τὸ Δ πρὸς τὸ Γ μείζονα λόγον ἔχει ἤπερ πρὸς τὸ ΑΒ.
Ἐπεὶ γὰρ μεῖζόν ἐστι τὸ ΑΒ τοῦ Γ, κείσθω τῷ Γ ἴσον τὸ ΒΕ· τὸ δὴ ἔλασσον τῶν ΑΕ, ΕΒ πολλαπλασιαζόμενον ἔσται ποτὲ τοῦ Δ μεῖζον. ἔστω πρότερον τὸ ΑΕ ἔλαττον τοῦ ΕΒ, καὶ πεπολλαπλασιάσθω τὸ ΑΕ, καὶ ἔστω αὐτοῦ πολλαπλάσιον τὸ ΖΗ μεῖζον ὂν τοῦ Δ, καὶ ὁσαπλάσιόν ἐστι τὸ ΖΗ τοῦ ΑΕ, τοσαυταπλάσιον γεγονέτω καὶ τὸ μὲν ΗΘ τοῦ ΕΒ τὸ δὲ Κ τοῦ Γ· καὶ εἰλήφθω τοῦ Δ διπλάσιον μὲν τὸ Λ, τριπλάσιον δὲ τὸ Μ, καὶ ἑξῆς ἑνὶ πλεῖον, ἕως ἂν τὸ λαμβανόμενον πολλαπλάσιον μὲν γένηται τοῦ Δ, πρώτως δὲ μεῖζον τοῦ Κ. εἰλήφθω, καὶ ἔστω τὸ Ν τετραπλάσιον μὲν τοῦ Δ, πρώτως δὲ μεῖζον τοῦ Κ.
Ἐπεὶ οὖν τὸ Κ τοῦ Ν πρώτως ἐστὶν ἔλαττον, τὸ Κ ἄρα τοῦ Μ οὔκ ἐστιν ἔλαττον. καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΖΗ τοῦ ΑΕ καὶ τὸ ΗΘ τοῦ ΕΒ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΖΗ τοῦ ΑΕ καὶ τὸ ΖΘ τοῦ ΑΒ. ἰσάκις δέ ἐστι πολλαπλάσιον τὸ ΖΗ τοῦ ΑΕ καὶ τὸ Κ τοῦ Γ· ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΖΘ τοῦ ΑΒ καὶ τὸ Κ τοῦ Γ. τὰ ΖΘ, Κ ἄρα τῶν ΑΒ, Γ ἰσάκις ἐστὶ πολλαπλάσια. πάλιν, ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΗΘ τοῦ ΕΒ καὶ τὸ Κ τοῦ Γ, ἴσον δὲ τὸ ΕΒ τῷ Γ, ἴσον ἄρα καὶ τὸ ΗΘ τῷ Κ· τὸ δὲ Κ τοῦ Μ οὔκ ἐστιν ἔλαττον· οὐδ' ἄρα τὸ ΗΘ τοῦ Μ ἔλαττόν ἐστιν. μεῖζον δὲ τὸ ΖΗ τοῦ Δ· ὅλον ἄρα τὸ ΖΘ συναμφοτέρων τῶν Δ, Μ μεῖζόν ἐστιν. ἀλλὰ συναμφότερα τὰ Δ, Μ τῷ Ν ἐστιν ἴσα, ἐπειδήπερ τὸ Μ τοῦ Δ τριπλάσιόν ἐστιν, συναμφότερα δὲ τὰ Μ, Δ τοῦ Δ ἐστι τετραπλάσια, ἔστι δὲ καὶ τὸ Ν τοῦ Δ τετραπλάσιον· συναμφότερα ἄρα τὰ Μ, Δ τῷ Ν ἴσα ἐστίν. ἀλλὰ τὸ ΖΘ τῶν Μ, Δ μεῖζόν ἐστιν· τὸ ΖΘ ἄρα τοῦ Ν ὑπερέχει· τὸ δὲ Κ τοῦ Ν οὐχ ὑπερέχει. καί ἐστι τὰ μὲν ΖΘ, Κ τῶν ΑΒ, Γ ἰσάκις πολλαπλάσια, τὸ δὲ Ν τοῦ Δ ἄλλο, ὃ ἔτυχεν, πολλαπλάσιον· τὸ ΑΒ ἄρα πρὸς τὸ Δ μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Δ.
Λέγω δή, ὅτι καὶ τὸ Δ πρὸς τὸ Γ μείζονα λόγον ἔχει ἤπερ τὸ Δ πρὸς τὸ ΑΒ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι τὸ μὲν Ν τοῦ Κ ὑπερέχει, τὸ δὲ Ν τοῦ ΖΘ οὐχ ὑπερέχει. καί ἐστι τὸ μὲν Ν τοῦ Δ πολλαπλάσιον, τὰ δὲ ΖΘ, Κ τῶν ΑΒ, Γ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· τὸ Δ ἄρα πρὸς τὸ Γ μείζονα λόγον ἔχει ἤπερ τὸ Δ πρὸς τὸ ΑΒ.
Ἀλλὰ δὴ τὸ ΑΕ τοῦ ΕΒ μεῖζον ἔστω. τὸ δὴ ἔλαττον τὸ ΕΒ πολλαπλασιαζόμενον ἔσται ποτὲ τοῦ Δ μεῖζον. πεπολλαπλασιάσθω, καὶ ἔστω τὸ ΗΘ πολλαπλάσιον μὲν τοῦ ΕΒ, μεῖζον δὲ τοῦ Δ· καὶ ὁσαπλάσιόν ἐστι τὸ ΗΘ τοῦ ΕΒ, τοσαυταπλάσιον γεγονέτω καὶ τὸ μὲν ΖΗ τοῦ ΑΕ, τὸ δὲ Κ τοῦ Γ. ὁμοίως δὴ δείξομεν, ὅτι τὰ ΖΘ, Κ τῶν ΑΒ, Γ ἰσάκις ἐστὶ πολλαπλάσια· καὶ εἰλήφθω ὁμοίως τὸ Ν πολλαπλάσιον μὲν τοῦ Δ, πρώτως δὲ μεῖζον τοῦ ΖΗ· ὥστε πάλιν τὸ ΖΗ τοῦ Μ οὔκ ἐστιν ἔλασσον. μεῖζον δὲ τὸ ΗΘ τοῦ Δ· ὅλον ἄρα τὸ ΖΘ τῶν Δ, Μ, τουτέστι τοῦ Ν, ὑπερέχει. τὸ δὲ Κ τοῦ Ν οὐχ ὑπερέχει, ἐπειδήπερ καὶ τὸ ΖΗ μεῖζον ὂν τοῦ ΗΘ, τουτέστι τοῦ Κ, τοῦ Ν οὐχ ὑπερέχει. καὶ ὡσαύτως κατακολουθοῦντες τοῖς ἐπάνω περαίνομεν τὴν ἀπόδειξιν.
Τῶν ἄρα ἀνίσων μεγεθῶν τὸ μεῖζον πρὸς τὸ αὐτὸ μείζονα λόγον ἔχει ἤπερ τὸ ἔλαττον· καὶ τὸ αὐτὸ πρὸς τὸ ἔλαττον μείζονα λόγον ἔχει ἤπερ πρὸς τὸ μεῖζον· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον V
Τὰ πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχοντα λόγον ἴσα ἀλλήλοις ἐστίν· καὶ πρὸς ἃ τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον, ἐκεῖνα ἴσα ἐστίν.
Ἐχέτω γὰρ ἑκάτερον τῶν Α, Β πρὸς τὸ Γ τὸν αὐτὸν λόγον· λέγω, ὅτι ἴσον ἐστὶ τὸ Α τῷ Β.
Εἰ γὰρ μή, οὐκ ἂν ἑκάτερον τῶν Α, Β πρὸς τὸ Γ τὸν αὐτὸν εἶχε λόγον· ἔχει δέ· ἴσον ἄρα ἐστὶ τὸ Α τῷ Β.
Ἐχέτω δὴ πάλιν τὸ Γ πρὸς ἑκάτερον τῶν Α, Β τὸν αὐτὸν λόγον· λέγω, ὅτι ἴσον ἐστὶ τὸ Α τῷ Β.
Εἰ γὰρ μή, οὐκ ἂν τὸ Γ πρὸς ἑκάτερον τῶν Α, Β τὸν αὐτὸν εἶχε λόγον· ἔχει δέ· ἴσον ἄρα ἐστὶ τὸ Α τῷ Β.
Τὰ ἄρα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχοντα λόγον ἴσα ἀλλήλοις ἐστίν· καὶ πρὸς ἃ τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον, ἐκεῖνα ἴσα ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον V
Τῶν πρὸς τὸ αὐτὸ λόγον ἐχόντων τὸ μείζονα λόγον ἔχον ἐκεῖνο μεῖζόν ἐστιν· πρὸς ὃ δὲ τὸ αὐτὸ μείζονα λόγον ἔχει, ἐκεῖνο ἔλαττόν ἐστιν.
Ἐχέτω γὰρ τὸ Α πρὸς τὸ Γ μείζονα λόγον ἤπερ τὸ Β πρὸς τὸ Γ· λέγω, ὅτι μεῖζόν ἐστι τὸ Α τοῦ Β.
Εἰ γὰρ μή, ἤτοι ἴσον ἐστὶ τὸ Α τῷ Β ἢ ἔλασσον. ἴσον μὲν οὖν οὔκ ἐστι τὸ Α τῷ Β· ἑκάτερον γὰρ ἂν τῶν Α, Β πρὸς τὸ Γ τὸν αὐτὸν εἶχε λόγον. οὐκ ἔχει δέ· οὐκ ἄρα ἴσον ἐστὶ τὸ Α τῷ Β. οὐδὲ μὴν ἔλασσόν ἐστι τὸ Α τοῦ Β· τὸ Α γὰρ ἂν πρὸς τὸ Γ ἐλάσσονα λόγον εἶχεν ἤπερ τὸ Β πρὸς τὸ Γ. οὐκ ἔχει δέ· οὐκ ἄρα ἔλασσόν ἐστι τὸ Α τοῦ Β. ἐδείχθη δὲ οὐδὲ ἴσον· μεῖζον ἄρα ἐστὶ τὸ Α τοῦ Β.
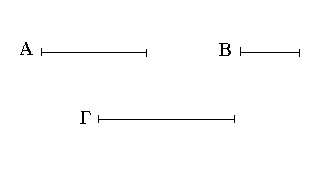
Ἐχέτω δὴ πάλιν τὸ Γ πρὸς τὸ Β μείζονα λόγον ἤπερ τὸ Γ πρὸς τὸ Α· λέγω, ὅτι ἔλασσόν ἐστι τὸ Β τοῦ Α.
Εἰ γὰρ μή, ἤτοι ἴσον ἐστὶν ἢ μεῖζον. ἴσον μὲν οὖν οὔκ ἐστι τὸ Β τῷ Α· τὸ Γ γὰρ ἂν πρὸς ἑκάτερον τῶν Α, Β τὸν αὐτὸν εἶχε λόγον. οὐκ ἔχει δέ· οὐκ ἄρα ἴσον ἐστὶ τὸ Α τῷ Β. οὐδὲ μὴν μεῖζόν ἐστι τὸ Β τοῦ Α· τὸ Γ γὰρ ἂν πρὸς τὸ Β ἐλάσσονα λόγον εἶχεν ἤπερ πρὸς τὸ Α. οὐκ ἔχει δέ· οὐκ ἄρα μεῖζόν ἐστι τὸ Β τοῦ Α. ἐδείχθη δέ, ὅτι οὐδὲ ἴσον· ἔλαττον ἄρα ἐστὶ τὸ Β τοῦ Α.
Τῶν ἄρα πρὸς τὸ αὐτὸ λόγον ἐχόντων τὸ μείζονα λόγον ἔχον μεῖζόν ἐστιν· καὶ πρὸς ὃ τὸ αὐτὸ μείζονα λόγον ἔχει, ἐκεῖνο ἔλαττόν ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον V
Οἱ τῷ αὐτῷ λόγῳ οἱ αὐτοὶ καὶ ἀλλήλοις εἰσὶν οἱ αὐτοί.
Ἔστωσαν γὰρ ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, ὡς δὲ τὸ Γ πρὸς τὸ Δ, οὕτως τὸ Ε πρὸς τὸ Ζ· λέγω, ὅτι ἐστὶν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ.
Εἰλήφθω γὰρ τῶν Α, Γ, Ε ἰσάκις πολλαπλάσια τὰ Η, Θ, Κ, τῶν δὲ Β, Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Λ, Μ, Ν.
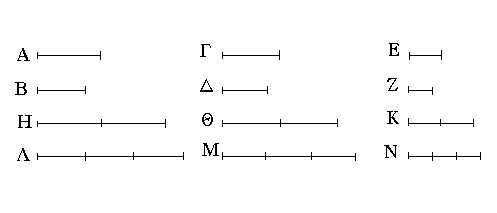
Καὶ ἐπεί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, καὶ εἴληπται τῶν μὲν Α, Γ ἰσάκις πολλαπλάσια τὰ Η, Θ, τῶν δὲ Β, Δ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Λ, Μ, εἰ ἄρα ὑπερέχει τὸ Η τοῦ Λ, ὑπερέχει καὶ τὸ Θ τοῦ Μ, καὶ εἰ ἴσον ἐστίν, ἴσον, καὶ εἰ ἐλλείπει, ἐλλείπει. πάλιν, ἐπεί ἐστιν ὡς τὸ Γ πρὸς τὸ Δ, οὕτως τὸ Ε πρὸς τὸ Ζ, καὶ εἴληπται τῶν Γ, Ε ἰσάκις πολλαπλάσια τὰ Θ, Κ, τῶν δὲ Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Μ, Ν, εἰ ἄρα ὑπερέχει τὸ Θ τοῦ Μ, ὑπερέχει καὶ τὸ Κ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. ἀλλὰ εἰ ὑπερεῖχε τὸ Θ τοῦ Μ, ὑπερεῖχε καὶ τὸ Η τοῦ Λ, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον· ὥστε καὶ εἰ ὑπερέχει τὸ Η τοῦ Λ, ὑπερέχει καὶ τὸ Κ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Η, Κ τῶν Α, Ε ἰσάκις πολλαπλάσια, τὰ δὲ Λ, Ν τῶν Β, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ.
Οἱ ἄρα τῷ αὐτῷ λόγῳ οἱ αὐτοὶ καὶ ἀλλήλοις εἰσὶν οἱ αὐτοί· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον V
Ἐὰν ᾖ ὁποσαοῦν μεγέθη ἀνάλογον, ἔσται ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα.
Ἔστωσαν ὁποσαοῦν μεγέθη ἀνάλογον τὰ Α, Β, Γ, Δ, Ε, Ζ, ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, καὶ τὸ Ε πρὸς τὸ Ζ· λέγω, ὅτι ἐστὶν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὰ Α, Γ, Ε πρὸς τὰ Β, Δ, Ζ.
Εἰλήφθω γὰρ τῶν μὲν Α, Γ, Ε ἰσάκις πολλαπλάσια τὰ Η, Θ, Κ, τῶν δὲ Β, Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Λ, Μ, Ν.
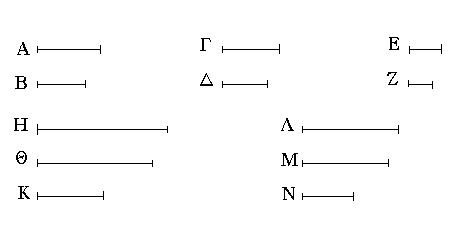
Καὶ ἐπεί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, καὶ τὸ Ε πρὸς τὸ Ζ, καὶ εἴληπται τῶν μὲν Α, Γ, Ε ἰσάκις πολλαπλάσια τὰ Η, Θ, Κ τῶν δὲ Β, Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Λ, Μ, Ν, εἰ ἄρα ὑπερέχει τὸ Η τοῦ Λ, ὑπερέχει καὶ τὸ Θ τοῦ Μ, καὶ τὸ Κ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. ὥστε καὶ εἰ ὑπερέχει τὸ Η τοῦ Λ, ὑπερέχει καὶ τὰ Η, Θ, Κ τῶν Λ, Μ, Ν, καὶ εἰ ἴσον, ἴσα, καὶ εἰ ἔλαττον, ἐλάττονα. καί ἐστι τὸ μὲν Η καὶ τὰ Η, Θ, Κ τοῦ Α καὶ τῶν Α, Γ, Ε ἰσάκις πολλαπλάσια, ἐπειδήπερ ἐὰν ᾖ ὁποσαοῦν μεγέθη ὁποσωνοῦν μεγεθῶν ἴσων τὸ πλῆθος ἕκαστον ἑκάστου ἰσάκις πολλαπλάσιον, ὁσαπλάσιόν ἐστιν ἓν τῶν μεγεθῶν ἑνός, τοσαυταπλάσια ἔσται καὶ τὰ πάντα τῶν πάντων. διὰ τὰ αὐτὰ δὴ καὶ τὸ Λ καὶ τὰ Λ, Μ, Ν τοῦ Β καὶ τῶν Β, Δ, Ζ ἰσάκις ἐστὶ πολλαπλάσια· ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Β, οὕτως τὰ Α, Γ, Ε πρὸς τὰ Β, Δ, Ζ.
Ἐὰν ἄρα ᾖ ὁποσαοῦν μεγέθη ἀνάλογον, ἔσται ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον V
Ἐὰν πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, τρίτον δὲ πρὸς τέταρτον μείζονα λόγον ἔχῃ ἢ πέμπτον πρὸς ἕκτον, καὶ πρῶτον πρὸς δεύτερον μείζονα λόγον ἕξει ἢ πέμπτον πρὸς ἕκτον.
Πρῶτον γὰρ τὸ Α πρὸς δεύτερον τὸ Β τὸν αὐτὸν ἐχέτω λόγον καὶ τρίτον τὸ Γ πρὸς τέταρτον τὸ Δ, τρίτον δὲ τὸ Γ πρὸς τέταρτον τὸ Δ μείζονα λόγον ἐχέτω ἢ πέμπτον τὸ Ε πρὸς ἕκτον τὸ Ζ. λέγω, ὅτι καὶ πρῶτον τὸ Α πρὸς δεύτερον τὸ Β μείζονα λόγον ἕξει ἤπερ πέμπτον τὸ Ε πρὸς ἕκτον τὸ Ζ.
Ἐπεὶ γὰρ ἔστι τινὰ τῶν μὲν Γ, Ε ἰσάκις πολλαπλάσια, τῶν δὲ Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια, καὶ τὸ μὲν τοῦ Γ πολλαπλάσιον τοῦ τοῦ Δ πολλαπλασίου ὑπερέχει, τὸ δὲ τοῦ Ε πολλαπλάσιον τοῦ τοῦ Ζ πολλαπλασίου οὐχ ὑπερέχει, εἰλήφθω, καὶ ἔστω τῶν μὲν Γ, Ε ἰσάκις πολλαπλάσια τὰ Η, Θ, τῶν δὲ Δ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Κ, Λ, ὥστε τὸ μὲν Η τοῦ Κ ὑπερέχειν, τὸ δὲ Θ τοῦ Λ μὴ ὑπερέχειν· καὶ ὁσαπλάσιον μέν ἐστι τὸ Η τοῦ Γ, τοσαυταπλάσιον ἔστω καὶ τὸ Μ τοῦ Α, ὁσαπλάσιον δὲ τὸ Κ τοῦ Δ, τοσαυταπλάσιον ἔστω καὶ τὸ Ν τοῦ Β.
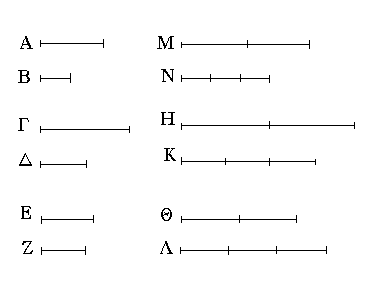
Καὶ ἐπεί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, καὶ εἴληπται τῶν μὲν Α, Γ ἰσάκις πολλαπλάσια τὰ Μ, Η, τῶν δὲ Β, Δ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Ν, Κ, εἰ ἄρα ὑπερέχει τὸ Μ τοῦ Ν, ὑπερέχει καὶ τὸ Η τοῦ Κ, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. ὑπερέχει δὲ τὸ Η τοῦ Κ· ὑπερέχει ἄρα καὶ τὸ Μ τοῦ Ν. τὸ δὲ Θ τοῦ Λ οὐχ ὑπερέχει· καί ἐστι τὰ μὲν Μ, Θ τῶν Α, Ε ἰσάκις πολλαπλάσια, τὰ δὲ Ν, Λ τῶν Β, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· τὸ ἄρα Α πρὸς τὸ Β μείζονα λόγον ἔχει ἤπερ τὸ Ε πρὸς τὸ Ζ.
Ἐὰν ἄρα πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, τρίτον δὲ πρὸς τέταρτον μείζονα λόγον ἔχῃ ἢ πέμπτον πρὸς ἕκτον, καὶ πρῶτον πρὸς δεύτερον μείζονα λόγον ἕξει ἢ πέμπτον πρὸς ἕκτον· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον V
Ἐὰν πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, τὸ δὲ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ δεύτερον τοῦ τετάρτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον.
Πρῶτον γὰρ τὸ Α πρὸς δεύτερον τὸ Β τὸν αὐτὸν ἐχέτω λόγον καὶ τρίτον τὸ Γ πρὸς τέταρτον τὸ Δ, μεῖζον δὲ ἔστω τὸ Α τοῦ Γ· λέγω, ὅτι καὶ τὸ Β τοῦ Δ μεῖζόν ἐστιν.
Ἐπεὶ γὰρ τὸ Α τοῦ Γ μεῖζόν ἐστιν, ἄλλο δέ, ὃ ἔτυχεν, [μέγεθος] τὸ Β, τὸ Α ἄρα πρὸς τὸ Β μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Β. ὡς δὲ τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ· καὶ τὸ Γ ἄρα πρὸς τὸ Δ μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Β. πρὸς ὃ δὲ τὸ αὐτὸ μείζονα λόγον ἔχει, ἐκεῖνο ἔλασσόν ἐστιν· ἔλασσον ἄρα τὸ Δ τοῦ Β· ὥστε μεῖζόν ἐστι τὸ Β τοῦ Δ.
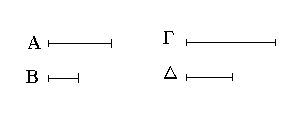
Ὁμοίως δὴ δείξομεν, ὅτι κἂν ἴσον ᾖ τὸ Α τῷ Γ, ἴσον ἔσται καὶ τὸ Β τῷ Δ, κἂν ἔλασσον ᾖ τὸ Α τοῦ Γ, ἔλασσον ἔσται καὶ τὸ Β τοῦ Δ.
Ἐὰν ἄρα πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, τὸ δὲ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ δεύτερον τοῦ τετάρτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον V
Τὰ μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον ληφθέντα κατάλληλα.
Ἔστω γὰρ ἰσάκις πολλαπλάσιον τὸ ΑΒ τοῦ Γ καὶ τὸ ΔΕ τοῦ Ζ· λέγω, ὅτι ἐστὶν ὡς τὸ Γ πρὸς τὸ Ζ, οὕτως τὸ ΑΒ πρὸς τὸ ΔΕ.
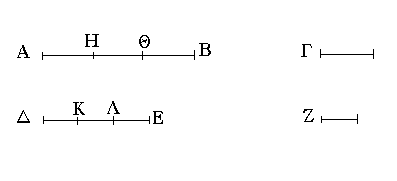
Ἐπεὶ γὰρ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΑΒ τοῦ Γ καὶ τὸ ΔΕ τοῦ Ζ, ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ μεγέθη ἴσα τῷ Γ, τοσαῦτα καὶ ἐν τῷ ΔΕ ἴσα τῷ Ζ. διῃρήσθω τὸ μὲν ΑΒ εἰς τὰ τῷ Γ ἴσα τὰ ΑΗ, ΗΘ, ΘΒ, τὸ δὲ ΔΕ εἰς τὰ τῷ Ζ ἴσα τὰ ΔΚ, ΚΛ, ΛΕ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΑΗ, ΗΘ, ΘΒ τῷ πλήθει τῶν ΔΚ, ΚΛ, ΛΕ. καὶ ἐπεὶ ἴσα ἐστὶ τὰ ΑΗ, ΗΘ, ΘΒ ἀλλήλοις, ἔστι δὲ καὶ τὰ ΔΚ, ΚΛ, ΛΕ ἴσα ἀλλήλοις, ἔστιν ἄρα ὡς τὸ ΑΗ πρὸς τὸ ΔΚ, οὕτως τὸ ΗΘ πρὸς τὸ ΚΛ, καὶ τὸ ΘΒ πρὸς τὸ ΛΕ. ἔσται ἄρα καὶ ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ἔστιν ἄρα ὡς τὸ ΑΗ πρὸς τὸ ΔΚ, οὕτως τὸ ΑΒ πρὸς τὸ ΔΕ. ἴσον δὲ τὸ μὲν ΑΗ τῷ Γ, τὸ δὲ ΔΚ τῷ Ζ· ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Ζ οὕτως τὸ ΑΒ πρὸς τὸ ΔΕ.
Τὰ ἄρα μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον ληφθέντα κατάλληλα· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον V
Ἐὰν τέσσαρα μεγέθη ἀνάλογον ᾖ, καὶ ἐναλλὰξ ἀνάλογον ἔσται.
Ἔστω τέσσαρα μεγέθη ἀνάλογον τὰ Α, Β, Γ, Δ, ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ· λέγω, ὅτι καὶ ἐναλλὰξ [ἀνάλογον] ἔσται, ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Β πρὸς τὸ Δ.
Εἰλήφθω γὰρ τῶν μὲν Α, Β ἰσάκις πολλαπλάσια τὰ Ε, Ζ, τῶν δὲ Γ, Δ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Η, Θ.
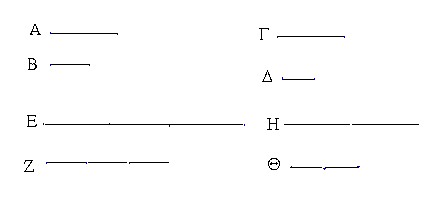
Καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ Ε τοῦ Α καὶ τὸ Ζ τοῦ Β, τὰ δὲ μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ. ὡς δὲ τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ· καὶ ὡς ἄρα τὸ Γ πρὸς τὸ Δ, οὕτως τὸ Ε πρὸς τὸ Ζ. πάλιν, ἐπεὶ τὰ Η, Θ τῶν Γ, Δ ἰσάκις ἐστὶ πολλαπλάσια, ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Δ, οὕτως τὸ Η πρὸς τὸ Θ. ὡς δὲ τὸ Γ πρὸς τὸ Δ, [οὕτως] τὸ Ε πρὸς τὸ Ζ· καὶ ὡς ἄρα τὸ Ε πρὸς τὸ Ζ, οὕτως τὸ Η πρὸς τὸ Θ. ἐὰν δὲ τέσσαρα μεγέθη ἀνάλογον ᾖ, τὸ δὲ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ δεύτερον τοῦ τετάρτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον. εἰ ἄρα ὑπερέχει τὸ Ε τοῦ Η, ὑπερέχει καὶ τὸ Ζ τοῦ Θ, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Ε, Ζ τῶν Α, Β ἰσάκις πολλαπλάσια, τὰ δὲ Η, Θ τῶν Γ, Δ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Β πρὸς τὸ Δ.
Ἐὰν ἄρα τέσσαρα μεγέθη ἀνάλογον ᾖ, καὶ ἐναλλὰξ ἀνάλογον ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον V
Ἐὰν συγκείμενα μεγέθη ἀνάλογον ᾖ, καὶ διαιρεθέντα ἀνάλογον ἔσται.
Ἔστω συγκείμενα μεγέθη ἀνάλογον τὰ ΑΒ, ΒΕ, ΓΔ, ΔΖ, ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς τὸ ΔΖ· λέγω, ὅτι καὶ διαιρεθέντα ἀνάλογον ἔσται, ὡς τὸ ΑΕ πρὸς τὸ ΕΒ, οὕτως τὸ ΓΖ πρὸς τὸ ΔΖ.
Εἰλήφθω γὰρ τῶν μὲν ΑΕ, ΕΒ, ΓΖ, ΖΔ ἰσάκις πολλαπλάσια τὰ ΗΘ, ΘΚ, ΛΜ, ΜΝ, τῶν δὲ ΕΒ, ΖΔ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ ΚΞ, ΝΠ.
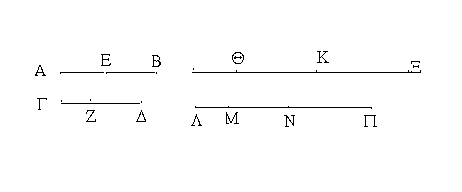
Καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΗΘ τοῦ ΑΕ καὶ τὸ ΘΚ τοῦ ΕΒ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΗΘ τοῦ ΑΕ καὶ τὸ ΗΚ τοῦ ΑΒ. ἰσάκις δέ ἐστι πολλαπλάσιον τὸ ΗΘ τοῦ ΑΕ καὶ τὸ ΛΜ τοῦ ΓΖ· ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΗΚ τοῦ ΑΒ καὶ τὸ ΛΜ τοῦ ΓΖ. πάλιν, ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΛΜ τοῦ ΓΖ καὶ τὸ ΜΝ τοῦ ΖΔ, ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΛΜ τοῦ ΓΖ καὶ τὸ ΛΝ τοῦ ΓΔ. ἰσάκις δὲ ἦν πολλαπλάσιον τὸ ΛΜ τοῦ ΓΖ καὶ τὸ ΗΚ τοῦ ΑΒ· ἰσάκις ἄρα ἐστὶ πολλαπλάσιον τὸ ΗΚ τοῦ ΑΒ καὶ τὸ ΛΝ τοῦ ΓΔ. τὰ ΗΚ, ΛΝ ἄρα τῶν ΑΒ, ΓΔ ἰσάκις ἐστὶ πολλαπλάσια. πάλιν, ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσιον τὸ ΘΚ τοῦ ΕΒ καὶ τὸ ΜΝ τοῦ ΖΔ, ἔστι δὲ καὶ τὸ ΚΞ τοῦ ΕΒ ἰσάκις πολλαπλάσιον καὶ τὸ ΝΠ τοῦ ΖΔ, καὶ συντεθὲν τὸ ΘΞ τοῦ ΕΒ ἰσάκις ἐστὶ πολλαπλάσιον καὶ τὸ ΜΠ τοῦ ΖΔ. Καὶ ἐπεί ἐστιν ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς τὸ ΔΖ, καὶ εἴληπται τῶν μὲν ΑΒ, ΓΔ ἰσάκις πολλαπλάσια τὰ ΗΚ, ΛΝ, τῶν δὲ ΕΒ, ΖΔ ἰσάκις πολλαπλάσια τὰ ΘΞ, ΜΠ, εἰ ἄρα ὑπερέχει τὸ ΗΚ τοῦ ΘΞ, ὑπερέχει καὶ τὸ ΛΝ τοῦ ΜΠ, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. ὑπερεχέτω δὴ τὸ ΗΚ τοῦ ΘΞ, καὶ κοινοῦ ἀφαιρεθέντος τοῦ ΘΚ ὑπερέχει ἄρα καὶ τὸ ΗΘ τοῦ ΚΞ. ἀλλὰ εἰ ὑπερεῖχε τὸ ΗΚ τοῦ ΘΞ, ὑπερεῖχε καὶ τὸ ΛΝ τοῦ ΜΠ· ὑπερέχει ἄρα καὶ τὸ ΛΝ τοῦ ΜΠ, καὶ κοινοῦ ἀφαιρεθέντος τοῦ ΜΝ ὑπερέχει καὶ τὸ ΛΜ τοῦ ΝΠ· ὥστε εἰ ὑπερέχει τὸ ΗΘ τοῦ ΚΞ, ὑπερέχει καὶ τὸ ΛΜ τοῦ ΝΠ. ὁμοίως δὴ δείξομεν, ὅτι κἂν ἴσον ᾖ τὸ ΗΘ τῷ ΚΞ, ἴσον ἔσται καὶ τὸ ΛΜ τῷ ΝΠ, κἂν ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν ΗΘ, ΛΜ τῶν ΑΕ, ΓΖ ἰσάκις πολλαπλάσια, τὰ δὲ ΚΞ, ΝΠ τῶν ΕΒ, ΖΔ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια· ἔστιν ἄρα ὡς τὸ ΑΕ πρὸς τὸ ΕΒ, οὕτως τὸ ΓΖ πρὸς τὸ ΖΔ.
Ἐὰν ἄρα συγκείμενα μεγέθη ἀνάλογον ᾖ, καὶ διαιρεθέντα ἀνάλογον ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον V
Ἐὰν διῃρημένα μεγέθη ἀνάλογον ᾖ, καὶ συντεθέντα ἀνάλογον ἔσται.
Ἔστω διῃρημένα μεγέθη ἀνάλογον τὰ ΑΕ, ΕΒ, ΓΖ, ΖΔ, ὡς τὸ ΑΕ πρὸς τὸ ΕΒ, οὕτως τὸ ΓΖ πρὸς τὸ ΖΔ· λέγω, ὅτι καὶ συντεθέντα ἀνάλογον ἔσται, ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς τὸ ΖΔ.
Εἰ γὰρ μή ἐστιν ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς τὸ ΔΖ, ἔσται ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ ἤτοι πρὸς ἔλασσόν τι τοῦ ΔΖ ἢ πρὸς μεῖζον.
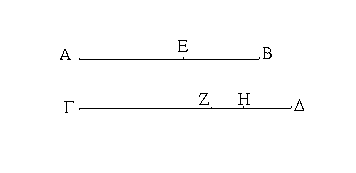
Ἔστω πρότερον πρὸς ἔλασσον τὸ ΔΗ. καὶ ἐπεί ἐστιν ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς τὸ ΔΗ, συγκείμενα μεγέθη ἀνάλογόν ἐστιν· ὥστε καὶ διαιρεθέντα ἀνάλογον ἔσται. ἔστιν ἄρα ὡς τὸ ΑΕ πρὸς τὸ ΕΒ, οὕτως τὸ ΓΗ πρὸς τὸ ΗΔ. ὑπόκειται δὲ καὶ ὡς τὸ ΑΕ πρὸς τὸ ΕΒ, οὕτως τὸ ΓΖ πρὸς τὸ ΖΔ. καὶ ὡς ἄρα τὸ ΓΗ πρὸς τὸ ΗΔ, οὕτως τὸ ΓΖ πρὸς τὸ ΖΔ. μεῖζον δὲ τὸ πρῶτον τὸ ΓΗ τοῦ τρίτου τοῦ ΓΖ· μεῖζον ἄρα καὶ τὸ δεύτερον τὸ ΗΔ τοῦ τετάρτου τοῦ ΖΔ. ἀλλὰ καὶ ἔλαττον· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα ἐστὶν ὡς τὸ ΑΒ πρὸς τὸ ΒΕ, οὕτως τὸ ΓΔ πρὸς ἔλασσον τοῦ ΖΔ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ πρὸς μεῖζον· πρὸς αὐτὸ ἄρα.
Ἐὰν ἄρα διῃρημένα μεγέθη ἀνάλογον ᾖ, καὶ συντεθέντα ἀνάλογον ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον V
Ἐὰν ᾖ ὡς ὅλον πρὸς ὅλον, οὕτως ἀφαιρεθὲν πρὸς ἀφαιρεθέν, καὶ τὸ λοιπὸν πρὸς τὸ λοιπὸν ἔσται ὡς ὅλον πρὸς ὅλον.
Ἔστω γὰρ ὡς ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ, οὕτως ἀφαιρεθὲν τὸ ΑΕ πρὸς ἀφαιρεθὲν τὸ ΓΖ· λέγω, ὅτι καὶ λοιπὸν τὸ ΕΒ πρὸς λοιπὸν τὸ ΖΔ ἔσται ὡς ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ.
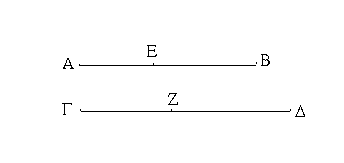
Ἐπεὶ γάρ ἐστιν ὡς τὸ ΑΒ πρὸς τὸ ΓΔ, οὕτως τὸ ΑΕ πρὸς τὸ ΓΖ, καὶ ἐναλλὰξ ὡς τὸ ΒΑ πρὸς τὸ ΑΕ, οὕτως τὸ ΔΓ πρὸς τὸ ΓΖ. καὶ ἐπεὶ συγκείμενα μεγέθη ἀνάλογόν ἐστιν, καὶ διαιρεθέντα ἀνάλογον ἔσται, ὡς τὸ ΒΕ πρὸς τὸ ΕΑ, οὕτως τὸ ΔΖ πρὸς τὸ ΓΖ· καὶ ἐναλλάξ, ὡς τὸ ΒΕ πρὸς τὸ ΔΖ, οὕτως τὸ ΕΑ πρὸς τὸ ΖΓ. ὡς δὲ τὸ ΑΕ πρὸς τὸ ΓΖ, οὕτως ὑπόκειται ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ. καὶ λοιπὸν ἄρα τὸ ΕΒ πρὸς λοιπὸν τὸ ΖΔ ἔσται ὡς ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ.
Ἐὰν ἄρα ᾖ ὡς ὅλον πρὸς ὅλον, οὕτως ἀφαιρεθὲν πρὸς ἀφαιρεθέν, καὶ τὸ λοιπὸν πρὸς τὸ λοιπὸν ἔσται ὡς ὅλον πρὸς ὅλον [ὅπερ ἔδει δεῖξαι].
[Καὶ ἐπεὶ ἐδείχθη ὡς τὸ ΑΒ πρὸς τὸ ΓΔ, οὕτως τὸ ΕΒ πρὸς τὸ ΖΔ, καὶ ἐναλλὰξ ὡς τὸ ΑΒ πρὸς τὸ ΒΕ οὕτως τὸ ΓΔ πρὸς τὸ ΖΔ, συγκείμενα ἄρα μεγέθη ἀνάλογόν ἐστιν· ἐδείχθη δὲ ὡς τὸ ΒΑ πρὸς τὸ ΑΕ, οὕτως τὸ ΔΓ πρὸς τὸ ΓΖ· καί ἐστιν ἀναστρέψαντι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν συγκείμενα μεγέθη ἀνάλογον ᾖ, καὶ ἀναστρέψαντι ἀνάλογον ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον V
Ἐὰν ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, δι' ἴσου δὲ τὸ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ τέταρτον τοῦ ἕκτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον.
Ἔστω τρία μεγέθη τὰ Α, Β, Γ, καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος τὰ Δ, Ε, Ζ, σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Δ πρὸς τὸ Ε, ὡς δὲ τὸ Β πρὸς τὸ Γ, οὕτως τὸ Ε πρὸς τὸ Ζ, δι' ἴσου δὲ μεῖζον ἔστω τὸ Α τοῦ Γ· λέγω, ὅτι καὶ τὸ Δ τοῦ Ζ μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον.
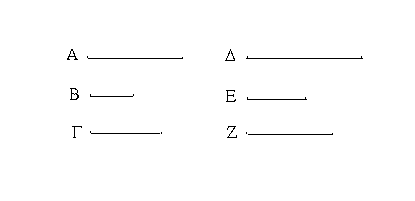
Ἐπεὶ γὰρ μεῖζόν ἐστι τὸ Α τοῦ Γ, ἄλλο δέ τι τὸ Β, τὸ δὲ μεῖζον πρὸς τὸ αὐτὸ μείζονα λόγον ἔχει ἤπερ τὸ ἔλαττον, τὸ Α ἄρα πρὸς τὸ Β μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Β. ἀλλ' ὡς μὲν τὸ Α πρὸς τὸ Β, [οὕτως] τὸ Δ πρὸς τὸ Ε, ὡς δὲ τὸ Γ πρὸς τὸ Β, ἀνάπαλιν οὕτως τὸ Ζ πρὸς τὸ Ε· καὶ τὸ Δ ἄρα πρὸς τὸ Ε μείζονα λόγον ἔχει ἤπερ τὸ Ζ πρὸς τὸ Ε. τῶν δὲ πρὸς τὸ αὐτὸ λόγον ἐχόντων τὸ μείζονα λόγον ἔχον μεῖζόν ἐστιν. μεῖζον ἄρα τὸ Δ τοῦ Ζ. ὁμοίως δὴ δείξομεν, ὅτι κἂν ἴσον ᾖ τὸ Α τῷ Γ, ἴσον ἔσται καὶ τὸ Δ τῷ Ζ, κἂν ἔλαττον, ἔλαττον.
Ἐὰν ἄρα ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, δι' ἴσου δὲ τὸ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ τέταρτον τοῦ ἕκτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον· ὅπερ ἔδει δεῖξαι.
Πρότασις κα΄ 21 Βιβλίον V
Ἐὰν ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, ᾖ δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, δι' ἴσου δὲ τὸ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ τέταρτον τοῦ ἕκτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον.
Ἔστω τρία μεγέθη τὰ Α, Β, Γ καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος τὰ Δ, Ε, Ζ, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, ἔστω δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ, ὡς δὲ τὸ Β πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ε, δι' ἴσου δὲ τὸ Α τοῦ Γ μεῖζον ἔστω· λέγω, ὅτι καὶ τὸ Δ τοῦ Ζ μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον.
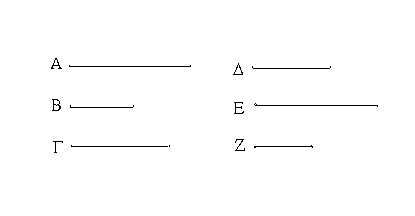
Ἐπεὶ γὰρ μεῖζόν ἐστι τὸ Α τοῦ Γ, ἄλλο δέ τι τὸ Β, τὸ Α ἄρα πρὸς τὸ Β μείζονα λόγον ἔχει ἤπερ τὸ Γ πρὸς τὸ Β. ἀλλ' ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ, ὡς δὲ τὸ Γ πρὸς τὸ Β, ἀνάπαλιν οὕτως τὸ Ε πρὸς τὸ Δ. καὶ τὸ Ε ἄρα πρὸς τὸ Ζ μείζονα λόγον ἔχει ἤπερ τὸ Ε πρὸς τὸ Δ. πρὸς ὃ δὲ τὸ αὐτὸ μείζονα λόγον ἔχει, ἐκεῖνο ἔλασσόν ἐστιν· ἔλασσον ἄρα ἐστὶ τὸ Ζ τοῦ Δ· μεῖζον ἄρα ἐστὶ τὸ Δ τοῦ Ζ. ὁμοίως δὴ δείξομεν, ὅτι κἂν ἴσον ᾖ τὸ Α τῷ Γ, ἴσον ἔσται καὶ τὸ Δ τῷ Ζ, κἂν ἔλαττον, ἔλαττον.
Ἐὰν ἄρα ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, ᾖ δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, δι' ἴσου δὲ τὸ πρῶτον τοῦ τρίτου μεῖζον ᾖ, καὶ τὸ τέταρτον τοῦ ἕκτου μεῖζον ἔσται, κἂν ἴσον, ἴσον, κἂν ἔλαττον, ἔλαττον· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον V
Ἐὰν ᾖ ὁποσαοῦν μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσται.
Ἔστω ὁποσαοῦν μεγέθη τὰ Α, Β, Γ καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος τὰ Δ, Ε, Ζ, σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Δ πρὸς τὸ Ε, ὡς δὲ τὸ Β πρὸς τὸ Γ, οὕτως τὸ Ε πρὸς τὸ Ζ· λέγω, ὅτι καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσται.
Εἰλήφθω γὰρ τῶν μὲν Α, Δ ἰσάκις πολλαπλάσια τὰ Η, Θ, τῶν δὲ Β, Ε ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Κ, Λ, καὶ ἔτι τῶν Γ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Μ, Ν.
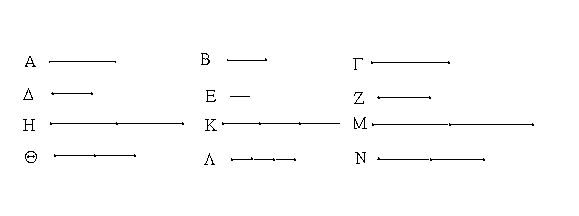
Καὶ ἐπεί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Δ πρὸς τὸ Ε, καὶ εἴληπται τῶν μὲν Α, Δ ἰσάκις πολλαπλάσια τὰ Η, Θ, τῶν δὲ Β, Ε ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Κ, Λ, ἔστιν ἄρα ὡς τὸ Η πρὸς τὸ Κ, οὕτως τὸ Θ πρὸς τὸ Λ. διὰ τὰ αὐτὰ δὴ καὶ ὡς τὸ Κ πρὸς τὸ Μ, οὕτως τὸ Λ πρὸς τὸ Ν. ἐπεὶ οὖν τρία μεγέθη ἐστὶ τὰ Η, Κ, Μ, καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος τὰ Θ, Λ, Ν, σύνδυο λαμβανόμενα καὶ ἐν τῷ αὐτῷ λόγῳ, δι' ἴσου ἄρα, εἰ ὑπερέχει τὸ Η τοῦ Μ, ὑπερέχει καὶ τὸ Θ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Η, Θ τῶν Α, Δ ἰσάκις πολλαπλάσια, τὰ δὲ Μ, Ν τῶν Γ, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια. ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ζ.
Ἐὰν ἄρα ᾖ ὁποσαοῦν μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος, σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον V
Ἐὰν ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, ᾖ δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσται.
Ἔστω τρία μεγέθη τὰ Α, Β, Γ καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ τὰ Δ, Ε, Ζ, ἔστω δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, ὡς μὲν τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ, ὡς δὲ τὸ Β πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ε· λέγω, ὅτι ἐστὶν ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ζ.
Εἰλήφθω τῶν μὲν Α, Β, Δ ἰσάκις πολλαπλάσια τὰ Η, Θ, Κ, τῶν δὲ Γ, Ε, Ζ ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια τὰ Λ, Μ, Ν.
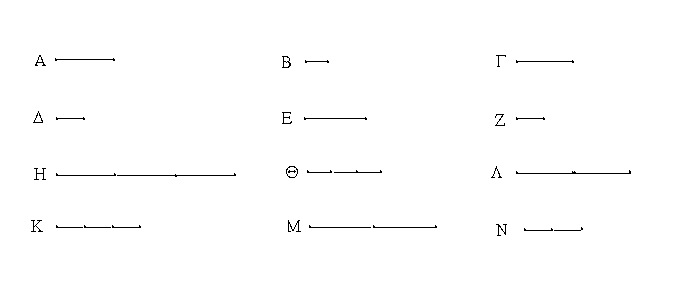
Καὶ ἐπεὶ ἰσάκις ἐστὶ πολλαπλάσια τὰ Η, Θ τῶν Α, Β, τὰ δὲ μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Η πρὸς τὸ Θ. διὰ τὰ αὐτὰ δὴ καὶ ὡς τὸ Ε πρὸς τὸ Ζ, οὕτως τὸ Μ πρὸς τὸ Ν· καί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Ε πρὸς τὸ Ζ· καὶ ὡς ἄρα τὸ Η πρὸς τὸ Θ, οὕτως τὸ Μ πρὸς τὸ Ν. καὶ ἐπεί ἐστιν ὡς τὸ Β πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ε, καὶ ἐναλλὰξ ὡς τὸ Β πρὸς τὸ Δ, οὕτως τὸ Γ πρὸς τὸ Ε. καὶ ἐπεὶ τὰ Θ, Κ τῶν Β, Δ ἰσάκις ἐστὶ πολλαπλάσια, τὰ δὲ μέρη τοῖς ἰσάκις πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ Β πρὸς τὸ Δ, οὕτως τὸ Θ πρὸς τὸ Κ. ἀλλ' ὡς τὸ Β πρὸς τὸ Δ, οὕτως τὸ Γ πρὸς τὸ Ε· καὶ ὡς ἄρα τὸ Θ πρὸς τὸ Κ, οὕτως τὸ Γ πρὸς τὸ Ε. πάλιν, ἐπεὶ τὰ Λ, Μ τῶν Γ, Ε ἰσάκις ἐστι πολλαπλάσια, ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Ε, οὕτως τὸ Λ πρὸς τὸ Μ. ἀλλ' ὡς τὸ Γ πρὸς τὸ Ε, οὕτως τὸ Θ πρὸς τὸ Κ· καὶ ὡς ἄρα τὸ Θ πρὸς τὸ Κ, οὕτως τὸ Λ πρὸς τὸ Μ, καὶ ἐναλλὰξ ὡς τὸ Θ πρὸς τὸ Λ, τὸ Κ πρὸς τὸ Μ. ἐδείχθη δὲ καὶ ὡς τὸ Η πρὸς τὸ Θ, οὕτως τὸ Μ πρὸς τὸ Ν. ἐπεὶ οὖν τρία μεγέθη ἐστὶ τὰ Η, Θ, Λ, καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος τὰ Κ, Μ, Ν σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, καί ἐστιν αὐτῶν τεταραγμένη ἡ ἀναλογία, δι' ἴσου ἄρα, εἰ ὑπερέχει τὸ Η τοῦ Λ, ὑπερέχει καὶ τὸ Κ τοῦ Ν, καὶ εἰ ἴσον, ἴσον, καὶ εἰ ἔλαττον, ἔλαττον. καί ἐστι τὰ μὲν Η, Κ τῶν Α, Δ ἰσάκις πολλαπλάσια, τὰ δὲ Λ, Ν τῶν Γ, Ζ. ἔστιν ἄρα ὡς τὸ Α πρὸς τὸ Γ, οὕτως τὸ Δ πρὸς τὸ Ζ.
Ἐὰν ἄρα ᾖ τρία μεγέθη καὶ ἄλλα αὐτοῖς ἴσα τὸ πλῆθος σύνδυο λαμβανόμενα ἐν τῷ αὐτῷ λόγῳ, ᾖ δὲ τεταραγμένη αὐτῶν ἡ ἀναλογία, καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον V
Ἐὰν πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, ἔχῃ δὲ καὶ πέμπτον πρὸς δεύτερον τὸν αὐτὸν λόγον καὶ ἕκτον πρὸς τέταρτον, καὶ συντεθὲν πρῶτον καὶ πέμπτον πρὸς δεύτερον τὸν αὐτὸν ἕξει λόγον καὶ τρίτον καὶ ἕκτον πρὸς τέταρτον.
Πρῶτον γὰρ τὸ ΑΒ πρὸς δεύτερον τὸ Γ τὸν αὐτὸν ἐχέτω λόγον καὶ τρίτον τὸ ΔΕ πρὸς τέταρτον τὸ Ζ, ἐχέτω δὲ καὶ πέμπτον τὸ ΒΗ πρὸς δεύτερον τὸ Γ τὸν αὐτὸν λόγον καὶ ἕκτον τὸ ΕΘ πρὸς τέταρτον τὸ Ζ· λέγω, ὅτι καὶ συντεθὲν πρῶτον καὶ πέμπτον τὸ ΑΗ πρὸς δεύτερον τὸ Γ τὸν αὐτὸν ἕξει λόγον, καὶ τρίτον καὶ ἕκτον τὸ ΔΘ πρὸς τέταρτον τὸ Ζ.
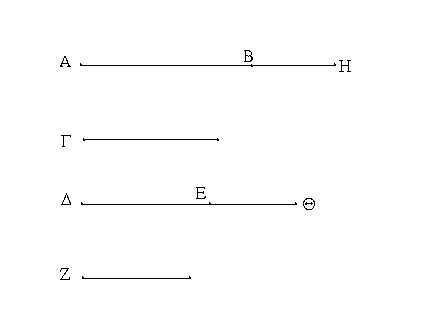
Ἐπεὶ γάρ ἐστιν ὡς τὸ ΒΗ πρὸς τὸ Γ, οὕτως τὸ ΕΘ πρὸς τὸ Ζ, ἀνάπαλιν ἄρα ὡς τὸ Γ πρὸς τὸ ΒΗ, οὕτως τὸ Ζ πρὸς τὸ ΕΘ. ἐπεὶ οὖν ἐστιν ὡς τὸ ΑΒ πρὸς τὸ Γ, οὕτως τὸ ΔΕ πρὸς τὸ Ζ, ὡς δὲ τὸ Γ πρὸς τὸ ΒΗ, οὕτως τὸ Ζ πρὸς τὸ ΕΘ, δι' ἴσου ἄρα ἐστὶν ὡς τὸ ΑΒ πρὸς τὸ ΒΗ, οὕτως τὸ ΔΕ πρὸς τὸ ΕΘ. καὶ ἐπεὶ διῃρημένα μεγέθη ἀνάλογόν ἐστιν, καὶ συντεθέντα ἀνάλογον ἔσται· ἔστιν ἄρα ὡς τὸ ΑΗ πρὸς τὸ ΗΒ, οὕτως τὸ ΔΘ πρὸς τὸ ΘΕ. ἔστι δὲ καὶ ὡς τὸ ΒΗ πρὸς τὸ Γ, οὕτως τὸ ΕΘ πρὸς τὸ Ζ· δι' ἴσου ἄρα ἐστὶν ὡς τὸ ΑΗ πρὸς τὸ Γ, οὕτως τὸ ΔΘ πρὸς τὸ Ζ.
Ἐὰν ἄρα πρῶτον πρὸς δεύτερον τὸν αὐτὸν ἔχῃ λόγον καὶ τρίτον πρὸς τέταρτον, ἔχῃ δὲ καὶ πέμπτον πρὸς δεύτερον τὸν αὐτὸν λόγον καὶ ἕκτον πρὸς τέταρτον, καὶ συντεθὲν πρῶτον καὶ πέμπτον πρὸς δεύτερον τὸν αὐτὸν ἕξει λόγον καὶ τρίτον καὶ ἕκτον πρὸς τέταρτον· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον V
Ἐὰν τέσσαρα μεγέθη ἀνάλογον ᾖ, τὸ μέγιστον [αὐτῶν] καὶ τὸ ἐλάχιστον δύο τῶν λοιπῶν μείζονά ἐστιν.
Ἔστω τέσσαρα μεγέθη ἀνάλογον τὰ ΑΒ, ΓΔ, Ε, Ζ, ὡς τὸ ΑΒ πρὸς τὸ ΓΔ, οὕτως τὸ Ε πρὸς τὸ Ζ, ἔστω δὲ μέγιστον μὲν αὐτῶν τὸ ΑΒ, ἐλάχιστον δὲ τὸ Ζ· λέγω, ὅτι τὰ ΑΒ, Ζ τῶν ΓΔ, Ε μείζονά ἐστιν.
Κείσθω γὰρ τῷ μὲν Ε ἴσον τὸ ΑΗ, τῷ δὲ Ζ ἴσον τὸ ΓΘ.
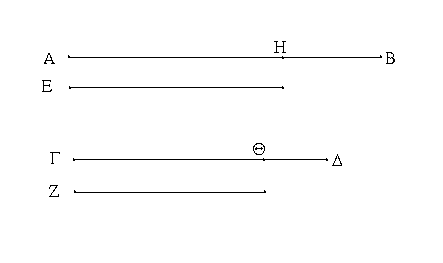
Ἐπεὶ [οὖν] ἐστιν ὡς τὸ ΑΒ πρὸς τὸ ΓΔ, οὕτως τὸ Ε πρὸς τὸ Ζ, ἴσον δὲ τὸ μὲν Ε τῷ ΑΗ, τὸ δὲ Ζ τῷ ΓΘ, ἔστιν ἄρα ὡς τὸ ΑΒ πρὸς τὸ ΓΔ, οὕτως τὸ ΑΗ πρὸς τὸ ΓΘ. καὶ ἐπεί ἐστιν ὡς ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ, οὕτως ἀφαιρεθὲν τὸ ΑΗ πρὸς ἀφαιρεθὲν τὸ ΓΘ, καὶ λοιπὸν ἄρα τὸ ΗΒ πρὸς λοιπὸν τὸ ΘΔ ἔσται ὡς ὅλον τὸ ΑΒ πρὸς ὅλον τὸ ΓΔ. μεῖζον δὲ τὸ ΑΒ τοῦ ΓΔ· μεῖζον ἄρα καὶ τὸ ΗΒ τοῦ ΘΔ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ μὲν ΑΗ τῷ Ε, τὸ δὲ ΓΘ τῷ Ζ, τὰ ἄρα ΑΗ, Ζ ἴσα ἐστὶ τοῖς ΓΘ, Ε. Καὶ [ἐπεὶ] ἐὰν [ἀνίσοις ἴσα προστεθῇ, τὰ ὅλα ἄνισά ἐστιν, ἐὰν ἄρα] τῶν ΗΒ, ΘΔ ἀνίσων ὄντων καὶ μείζονος τοῦ ΗΒ τῷ μὲν ΗΒ προστεθῇ τὰ ΑΗ, Ζ, τῷ δὲ ΘΔ προστεθῇ τὰ ΓΘ, Ε, συνάγεται τὰ ΑΒ, Ζ μείζονα τῶν ΓΔ, Ε.
Ἐὰν ἄρα τέσσαρα μεγέθη ἀνάλογον ᾖ, τὸ μέγιστον αὐτῶν καὶ τὸ ἐλάχιστον δύο τῶν λοιπῶν μείζονά ἐστιν· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου ς΄
Βιβλίον VI
Ὅροι ε΄ 5.
α΄ 1. Ὅμοια σχήματα εὐθύγραμμά ἐστιν, ὅσα τάς τε γωνίας ἴσας ἔχει κατὰ μίαν καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον.
β΄ 2. [Ἀντιπεπονθότα δὲ σχήματά ἐστιν, ὅταν ἐν ἑκατέρῳ τῶν σχημάτων ἡγούμενοί τε καὶ ἑπόμενοι λόγοι ὦσιν.]
γ΄ 3. Ἄκρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττον.
δ΄ 4.Ὕψος ἐστὶ παντὸς σχήματος ἡ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν βάσιν κάθετος ἀγομένη.
ε΄ 5. [Λόγος ἐκ λόγων συγκεῖσθαι λέγεται, ὅταν αἱ τῶν λόγων πηλικότητες ἐφ' ἑαυτὰς πολλαπλασιασθεῖσαι ποιῶσί τινα.]
Στοιχεῖα Εὐκλείδου ς΄
Προτάσεις λγ΄ 33
Πρότασις α΄ 1 Βιβλίον VI
Τὰ τρίγωνα καὶ τὰ παραλληλόγραμμα, τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις.
Ἔστω τρίγωνα μὲν τὰ ΑΒΓ, ΑΓΔ, παραλληλόγραμμα δὲ τὰ ΕΓ, ΓΖ ὑπὸ τὸ αὐτὸ ὕψος τὸ ΑΓ· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, καὶ τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον.
Ἐκβεβλήσθω γὰρ ἡ ΒΔ ἐφ' ἑκάτερα τὰ μέρη ἐπὶ τὰ Θ, Λ σημεῖα, καὶ κείσθωσαν τῇ μὲν ΒΓ βάσει ἴσαι [ὁσαιδηποτοῦν] αἱ ΒΗ, ΗΘ, τῇ δὲ ΓΔ βάσει ἴσαι ὁσαιδηποτοῦν αἱ ΔΚ, ΚΛ, καὶ ἐπεζεύχθωσαν αἱ ΑΗ, ΑΘ, ΑΚ, ΑΛ.
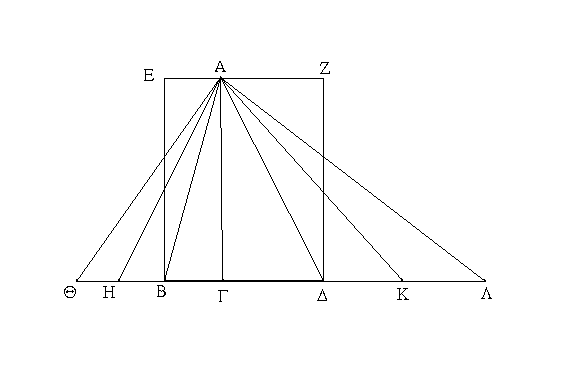
Καὶ ἐπεὶ ἴσαι εἰσὶν αἱ ΓΒ, ΒΗ, ΗΘ ἀλλήλαις, ἴσα ἐστὶ καὶ τὰ ΑΘΗ, ΑΗΒ, ΑΒΓ τρίγωνα ἀλλήλοις. ὁσαπλασίων ἄρα ἐστὶν ἡ ΘΓ βάσις τῆς ΒΓ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΒΓ τριγώνου. διὰ τὰ αὐτὰ δὴ ὁσαπλασίων ἐστὶν ἡ ΛΓ βάσις τῆς ΓΔ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΑΛΓ τρίγωνον τοῦ ΑΓΔ τριγώνου· καὶ εἰ ἴση ἐστὶν ἡ ΘΓ βάσις τῇ ΓΛ βάσει, ἴσον ἐστὶ καὶ τὸ ΑΘΓ τρίγωνον τῷ ΑΓΛ τριγώνῳ, καὶ εἰ ὑπερέχει ἡ ΘΓ βάσις τῆς ΓΛ βάσεως, ὑπερέχει καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΓΛ τριγώνου, καὶ εἰ ἐλάσσων, ἔλασσον. τεσσάρων δὴ ὄντων μεγεθῶν δύο μὲν βάσεων τῶν ΒΓ, ΓΔ, δύο δὲ τριγώνων τῶν ΑΒΓ, ΑΓΔ εἴληπται ἰσάκις πολλαπλάσια τῆς μὲν ΒΓ βάσεως καὶ τοῦ ΑΒΓ τριγώνου ἥ τε ΘΓ βάσις καὶ τὸ ΑΘΓ τρίγωνον, τῆς δὲ ΓΔ βάσεως καὶ τοῦ ΑΔΓ τριγώνου ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια ἥ τε ΛΓ βάσις καὶ τὸ ΑΛΓ τρίγωνον· καὶ δέδεικται, ὅτι, εἰ ὑπερέχει ἡ ΘΓ βάσις τῆς ΓΛ βάσεως, ὑπερέχει καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΛΓ τριγώνου, καὶ εἰ ἴση, ἴσον, καὶ εἰ ἐλάσσων, ἔλασσον· ἔστιν ἄρα ὡς ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον.
Καὶ ἐπεὶ τοῦ μὲν ΑΒΓ τριγώνου διπλάσιόν ἐστι τὸ ΕΓ παραλληλόγραμμον, τοῦ δὲ ΑΓΔ τριγώνου διπλάσιόν ἐστι τὸ ΖΓ παραλληλόγραμμον, τὰ δὲ μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΖΓ παραλληλόγραμμον. ἐπεὶ οὖν ἐδείχθη, ὡς μὲν ἡ ΒΓ βάσις πρὸς τὴν ΓΔ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, ὡς δὲ τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον, καὶ ὡς ἄρα ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΖΓ παραλληλόγραμμον.
Τὰ ἄρα τρίγωνα καὶ τὰ παραλληλόγραμμα τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον VI
Ἐὰν τριγώνου παρὰ μίαν τῶν πλευρῶν ἀχθῇ τις εὐθεῖα, ἀνάλογον τεμεῖ τὰς τοῦ τριγώνου πλευράς· καὶ ἐὰν αἱ τοῦ τριγώνου πλευραὶ ἀνάλογον τμηθῶσιν, ἡ ἐπὶ τὰς τομὰς ἐπιζευγνυμένη εὐθεῖα παρὰ τὴν λοιπὴν ἔσται τοῦ τριγώνου πλευράν.
Τριγώνου γὰρ τοῦ ΑΒΓ παράλληλος μιᾷ τῶν πλευρῶν τῇ ΒΓ ἤχθω ἡ ΔΕ· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΓΔ.
Ἴσον ἄρα ἐστὶ ΒΔΕ τρίγωνον τῷ ΓΔΕ τριγώνῳ· ἐπὶ γὰρ τῆς αὐτῆς βάσεώς ἐστι τῆς ΔΕ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΔΕ, ΒΓ· ἄλλο δέ τι τὸ ΑΔΕ τρίγωνον. τὰ δὲ ἴσα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον· ἔστιν ἄρα ὡς τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ [τρίγωνον], οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον. ἀλλ' ὡς μὲν τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ, οὕτως ἡ ΒΔ πρὸς τὴν ΔΑ· ὑπὸ γὰρ τὸ αὐτὸ ὕψος ὄντα τὴν ἀπὸ τοῦ Ε ἐπὶ τὴν ΑΒ κάθετον ἀγομένην πρὸς ἄλληλά εἰσιν ὡς αἱ βάσεις. διὰ τὰ αὐτὰ δὴ ὡς τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ· καὶ ὡς ἄρα ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ.
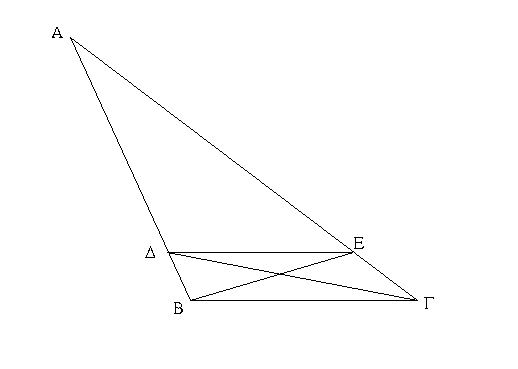
Ἀλλὰ δὴ αἱ τοῦ ΑΒΓ τριγώνου πλευραὶ αἱ ΑΒ, ΑΓ ἀνάλογον τετμήσθωσαν, ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ, καὶ ἐπεζεύχθω ἡ ΔΕ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΔΕ τῇ ΒΓ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ, ἀλλ' ὡς μὲν ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, ὡς δὲ ἡ ΓΕ πρὸς τὴν ΕΑ, οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, καὶ ὡς ἄρα τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον. ἑκάτερον ἄρα τῶν ΒΔΕ, ΓΔΕ τριγώνων πρὸς τὸ ΑΔΕ τὸν αὐτὸν ἔχει λόγον. ἴσον ἄρα ἐστὶ τὸ ΒΔΕ τρίγωνον τῷ ΓΔΕ τριγώνῳ· καί εἰσιν ἐπὶ τῆς αὐτῆς βάσεως τῆς ΔΕ. τὰ δὲ ἴσα τρίγωνα καὶ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν. παράλληλος ἄρα ἐστὶν ἡ ΔΕ τῇ ΒΓ.
Ἐὰν ἄρα τριγώνου παρὰ μίαν τῶν πλευρῶν ἀχθῇ τις εὐθεῖα, ἀνάλογον τεμεῖ τὰς τοῦ τριγώνου πλευράς· καὶ ἐὰν αἱ τοῦ τριγώνου πλευραὶ ἀνάλογον τμηθῶσιν, ἡ ἐπὶ τὰς τομὰς ἐπιζευγνυμένη εὐθεῖα παρὰ τὴν λοιπὴν ἔσται τοῦ τριγώνου πλευράν· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον VI
Ἐὰν τριγώνου ἡ γωνία δίχα τμηθῇ, ἡ δὲ τέμνουσα τὴν γωνίαν εὐθεῖα τέμνῃ καὶ τὴν βάσιν, τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἕξει λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς· καὶ ἐὰν τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἔχῃ λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς, ἡ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν τομὴν ἐπιζευγνυμένη εὐθεῖα δίχα τεμεῖ τὴν τοῦ τριγώνου γωνίαν.
Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ τετμήσθω ἡ ὑπὸ ΒΑΓ γωνία δίχα ὑπὸ τῆς ΑΔ εὐθείας· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΓΔ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ.
Ἤχθω γὰρ διὰ τοῦ Γ τῇ ΔΑ παράλληλος ἡ ΓΕ καὶ διαχθεῖσα ἡ ΒΑ συμπιπτέτω αὐτῇ κατὰ τὸ Ε.
Καὶ ἐπεὶ εἰς παραλλήλους τὰς ΑΔ, ΕΓ εὐθεῖα ἐνέπεσεν ἡ ΑΓ, ἡ ἄρα ὑπὸ ΑΓΕ γωνία ἴση ἐστὶ τῇ ὑπὸ ΓΑΔ. ἀλλ' ἡ ὑπὸ ΓΑΔ τῇ ὑπὸ ΒΑΔ ὑπόκειται ἴση· καὶ ἡ ὑπὸ ΒΑΔ ἄρα τῇ ὑπὸ ΑΓΕ ἐστιν ἴση. πάλιν, ἐπεὶ εἰς παραλλήλους τὰς ΑΔ, ΕΓ εὐθεῖα ἐνέπεσεν ἡ ΒΑΕ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΒΑΔ ἴση ἐστὶ τῇ ἐντὸς τῇ ὑπὸ ΑΕΓ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΑΓΕ τῇ ὑπὸ ΒΑΔ ἴση· καὶ ἡ ὑπὸ ΑΓΕ ἄρα γωνία τῇ ὑπὸ ΑΕΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΑΕ πλευρᾷ τῇ ΑΓ ἐστιν ἴση. καὶ ἐπεὶ τριγώνου τοῦ ΒΓΕ παρὰ μίαν τῶν πλευρῶν τὴν ΕΓ ἦκται ἡ ΑΔ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΕ. ἴση δὲ ἡ ΑΕ τῇ ΑΓ· ὡς ἄρα ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ.
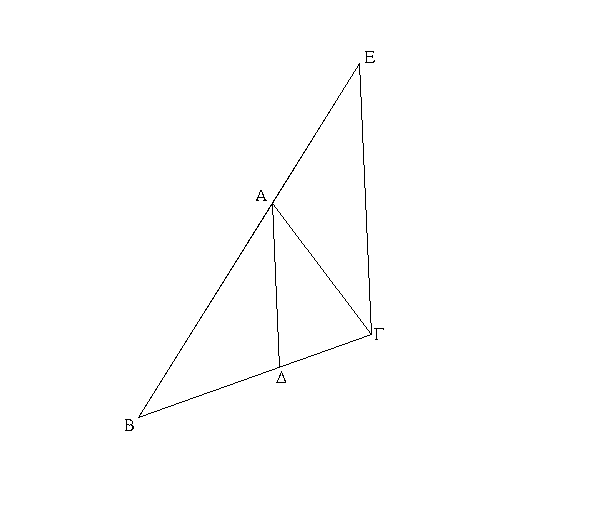
Ἀλλὰ δὴ ἔστω ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ, καὶ ἐπεζεύχθω ἡ ΑΔ· λέγω, ὅτι δίχα τέτμηται ἡ ὑπὸ ΒΑΓ γωνία ὑπὸ τῆς ΑΔ εὐθείας.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ, ἀλλὰ καὶ ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἐστὶν ἡ ΒΑ πρὸς τὴν ΑΕ· τριγώνου γὰρ τοῦ ΒΓΕ παρὰ μίαν τὴν ΕΓ ἦκται ἡ ΑΔ· καὶ ὡς ἄρα ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΕ. ἴση ἄρα ἡ ΑΓ τῇ ΑΕ· ὥστε καὶ γωνία ἡ ὑπὸ ΑΕΓ τῇ ὑπὸ ΑΓΕ ἐστιν ἴση. ἀλλ' ἡ μὲν ὑπὸ ΑΕΓ τῇ ἐκτὸς τῇ ὑπὸ ΒΑΔ [ἐστιν] ἴση, ἡ δὲ ὑπὸ ΑΓΕ τῇ ἐναλλὰξ τῇ ὑπὸ ΓΑΔ ἐστιν ἴση· καὶ ἡ ὑπὸ ΒΑΔ ἄρα τῇ ὑπὸ ΓΑΔ ἐστιν ἴση. ἡ ἄρα ὑπὸ ΒΑΓ γωνία δίχα τέτμηται ὑπὸ τῆς ΑΔ εὐθείας.
Ἐὰν ἄρα τριγώνου ἡ γωνία δίχα τμηθῇ, ἡ δὲ τέμνουσα τὴν γωνίαν εὐθεῖα τέμνῃ καὶ τὴν βάσιν, τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἕξει λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς· καὶ ἐὰν τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἔχῃ λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς, ἡ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν τομὴν ἐπιζευγνυμένη εὐθεῖα δίχα τέμνει τὴν τοῦ τριγώνου γωνίαν· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον VI
Τῶν ἰσογωνίων τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι.
Ἔστω ἰσογώνια τρίγωνα τὰ ΑΒΓ, ΔΓΕ ἴσην ἔχοντα τὴν μὲν ὑπὸ ΑΒΓ γωνίαν τῇ ὑπὸ ΔΓΕ, τὴν δὲ ὑπὸ ΒΑΓ τῇ ὑπὸ ΓΔΕ καὶ ἔτι τὴν ὑπὸ ΑΓΒ τῇ ὑπὸ ΓΕΔ· λέγω, ὅτι τῶν ΑΒΓ, ΔΓΕ τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι.
Κείσθω γὰρ ἐπ᾿ εὐθείας ἡ ΒΓ τῇ ΓΕ. καὶ ἐπεὶ αἱ ὑπὸ ΑΒΓ, ΑΓΒ γωνίαι δύο ὀρθῶν ἐλάττονές εἰσιν, ἴση δὲ ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΕΓ, αἱ ἄρα ὑπὸ ΑΒΓ, ΔΕΓ δύο ὀρθῶν ἐλάττονές εἰσιν· αἱ ΒΑ, ΕΔ ἄρα ἐκβαλλόμεναι συμπεσοῦνται. ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν κατὰ τὸ Ζ.
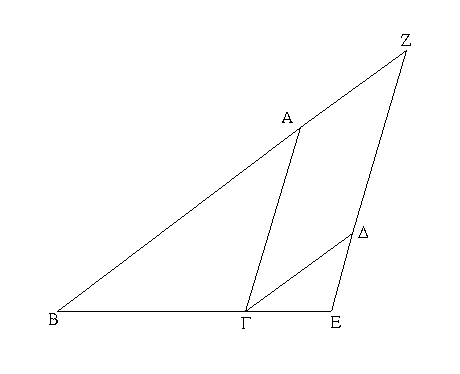
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΓΕ γωνία τῇ ὑπὸ ΑΒΓ, παράλληλός ἐστιν ἡ ΒΖ τῇ ΓΔ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΕΓ, παράλληλός ἐστιν ἡ ΑΓ τῇ ΖΕ. παραλληλόγραμμον ἄρα ἐστὶ τὸ ΖΑΓΔ· ἴση ἄρα ἡ μὲν ΖΑ τῇ ΔΓ, ἡ δὲ ΑΓ τῇ ΖΔ. καὶ ἐπεὶ τριγώνου τοῦ ΖΒΕ παρὰ μίαν τὴν ΖΕ ἦκται ἡ ΑΓ, ἔστιν ἄρα ὡς ἡ ΒΑ πρὸς τὴν ΑΖ, οὕτως ἡ ΒΓ πρὸς τὴν ΓΕ. ἴση δὲ ἡ ΑΖ τῇ ΓΔ· ὡς ἄρα ἡ ΒΑ πρὸς τὴν ΓΔ, οὕτως ἡ ΒΓ πρὸς τὴν ΓΕ, καὶ ἐναλλὰξ ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΕ. πάλιν, ἐπεὶ παράλληλός ἐστιν ἡ ΓΔ τῇ ΒΖ, ἔστιν ἄρα ὡς ἡ ΒΓ πρὸς τὴν ΓΕ, οὕτως ἡ ΖΔ πρὸς τὴν ΔΕ. ἴση δὲ ἡ ΖΔ τῇ ΑΓ· ὡς ἄρα ἡ ΒΓ πρὸς τὴν ΓΕ, οὕτως ἡ ΑΓ πρὸς τὴν ΔΕ, καὶ ἐναλλὰξ ὡς ἡ ΒΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΔ. ἐπεὶ οὖν ἐδείχθη ὡς μὲν ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΕ, ὡς δὲ ἡ ΒΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΔ, δι' ἴσου ἄρα ὡς ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΓΔ πρὸς τὴν ΔΕ.
Τῶν ἄρα ἰσογωνίων τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον VI
Ἐὰν δύο τρίγωνα τὰς πλευρὰς ἀνάλογον ἔχῃ, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, ὑφ᾿ ἃς αἱ ὁμόλογοι πλευραὶ ὑποτείνουσιν.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ τὰς πλευρὰς ἀνάλογον ἔχοντα, ὡς μὲν τὴν ΑΒ πρὸς τὴν ΒΓ, οὕτως τὴν ΔΕ πρὸς τὴν ΕΖ, ὡς δὲ τὴν ΒΓ πρὸς τὴν ΓΑ, οὕτως τὴν ΕΖ πρὸς τὴν ΖΔ, καὶ ἔτι ὡς τὴν ΒΑ πρὸς τὴν ΑΓ, οὕτως τὴν ΕΔ πρὸς τὴν ΔΖ. λέγω, ὅτι ἰσογώνιόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ καὶ ἴσας ἕξουσι τὰς γωνίας, ὑφ᾿ ἃς αἱ ὁμόλογοι πλευραὶ ὑποτείνουσιν, τὴν μὲν ὑπὸ ΑΒΓ τῇ ὑπὸ ΔΕΖ, τὴν δὲ ὑπὸ ΒΓΑ τῇ ὑπὸ ΕΖΔ καὶ ἔτι τὴν ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ.
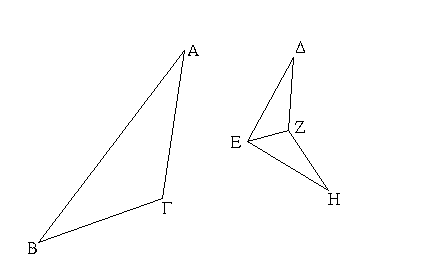
Συνεστάτω γὰρ πρὸς τῇ ΕΖ εὐθείᾳ καὶ τοῖς πρὸς αὐτῇ σημείοις τοῖς Ε, Ζ τῇ μὲν ὑπὸ ΑΒΓ γωνίᾳ ἴση ἡ ὑπὸ ΖΕΗ, τῇ δὲ ὑπὸ ΑΓΒ ἴση ἡ ὑπὸ ΕΖΗ· λοιπὴ ἄρα ἡ πρὸς τῷ Α λοιπῇ τῇ πρὸς τῷ Η ἐστιν ἴση. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΕΗΖ [τριγώνῳ]. τῶν ἄρα ΑΒΓ, ΕΗΖ τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι· ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, [οὕτως] ἡ ΗΕ πρὸς τὴν ΕΖ. ἀλλ' ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ὑπόκειται ἡ ΔΕ πρὸς τὴν ΕΖ· ὡς ἄρα ἡ ΔΕ πρὸς τὴν ΕΖ, οὕτως ἡ ΗΕ πρὸς τὴν ΕΖ. ἑκατέρα ἄρα τῶν ΔΕ, ΗΕ πρὸς τὴν ΕΖ τὸν αὐτὸν ἔχει λόγον· ἴση ἄρα ἐστὶν ἡ ΔΕ τῇ ΗΕ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΔΖ τῇ ΗΖ ἐστιν ἴση. ἐπεὶ οὖν ἴση ἐστὶν ἡ ΔΕ τῇ ΕΗ, κοινὴ δὲ ἡ ΕΖ, δύο δὴ αἱ ΔΕ, ΕΖ δυσὶ ταῖς ΗΕ, ΕΖ ἴσαι εἰσίν· καὶ βάσις ἡ ΔΖ βάσει τῇ ΖΗ [ἐστιν] ἴση· γωνία ἄρα ἡ ὑπὸ ΔΕΖ γωνίᾳ τῇ ὑπὸ ΗΕΖ ἐστιν ἴση, καὶ τὸ ΔΕΖ τρίγωνον τῷ ΗΕΖ τριγώνῳ ἴσον, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν. ἴση ἄρα ἐστὶ καὶ ἡ μὲν ὑπὸ ΔΖΕ γωνία τῇ ὑπὸ ΗΖΕ, ἡ δὲ ὑπὸ ΕΔΖ τῇ ὑπὸ ΕΗΖ. καὶ ἐπεὶ ἡ μὲν ὑπὸ ΖΕΔ τῇ ὑπὸ ΗΕΖ ἐστιν ἴση, ἀλλ' ἡ ὑπὸ ΗΕΖ τῇ ὑπὸ ΑΒΓ, καὶ ἡ ὑπὸ ΑΒΓ ἄρα γωνία τῇ ὑπὸ ΔΕΖ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΖΕ ἐστιν ἴση, καὶ ἔτι ἡ πρὸς τῷ Α τῇ πρὸς τῷ Δ· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
Ἐὰν ἄρα δύο τρίγωνα τὰς πλευρὰς ἀνάλογον ἔχῃ, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, ὑφ᾿ ἃς αἱ ὁμόλογοι πλευραὶ ὑποτείνουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον VI
Ἐὰν δύο τρίγωνα μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχῃ, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, ὑφ᾿ ἃς αἱ ὁμόλογοι πλευραὶ ὑποτείνουσιν.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ μίαν γωνίαν τὴν ὑπὸ ΒΑΓ μιᾷ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἴσην ἔχοντα, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον, ὡς τὴν ΒΑ πρὸς τὴν ΑΓ, οὕτως τὴν ΕΔ πρὸς τὴν ΔΖ· λέγω, ὅτι ἰσογώνιόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ καὶ ἴσην ἕξει τὴν ὑπὸ ΑΒΓ γωνίαν τῇ ὑπὸ ΔΕΖ, τὴν δὲ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΖΕ.
Συνεστάτω γὰρ πρὸς τῇ ΔΖ εὐθείᾳ καὶ τοῖς πρὸς αὐτῇ σημείοις τοῖς Δ, Ζ ὁποτέρᾳ μὲν τῶν ὑπὸ ΒΑΓ, ΕΔΖ ἴση ἡ ὑπὸ ΖΔΗ, τῇ δὲ ὑπὸ ΑΓΒ ἴση ἡ ὑπὸ ΔΖΗ· λοιπὴ ἄρα ἡ πρὸς τῷ Β γωνία λοιπῇ τῇ πρὸς τῷ Η ἴση ἐστίν.
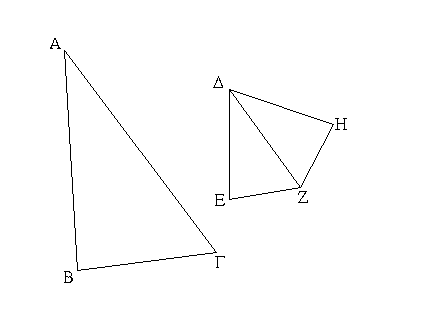
Ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΗΖ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΗΔ πρὸς τὴν ΔΖ. ὑπόκειται δὲ καὶ ὡς ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΕΔ πρὸς τὴν ΔΖ· καὶ ὡς ἄρα ἡ ΕΔ πρὸς τὴν ΔΖ, οὕτως ἡ ΗΔ πρὸς τὴν ΔΖ. ἴση ἄρα ἡ ΕΔ τῇ ΔΗ· καὶ κοινὴ ἡ ΔΖ· δύο δὴ αἱ ΕΔ, ΔΖ δυσὶ ταῖς ΗΔ, ΔΖ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΕΔΖ γωνίᾳ τῇ ὑπὸ ΗΔΖ [ἐστιν] ἴση· βάσις ἄρα ἡ ΕΖ βάσει τῇ ΗΖ ἐστιν ἴση, καὶ τὸ ΔΕΖ τρίγωνον τῷ ΗΔΖ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν. ἴση ἄρα ἐστὶν ἡ μὲν ὑπὸ ΔΖΗ τῇ ὑπὸ ΔΖΕ, ἡ δὲ ὑπὸ ΔΗΖ τῇ ὑπὸ ΔΕΖ. ἀλλ' ἡ ὑπὸ ΔΖΗ τῇ ὑπὸ ΑΓΒ ἐστιν ἴση· καὶ ἡ ὑπὸ ΑΓΒ ἄρα τῇ ὑπὸ ΔΖΕ ἐστιν ἴση. ὑπόκειται δὲ καὶ ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ ἴση· καὶ λοιπὴ ἄρα ἡ πρὸς τῷ Β λοιπῇ τῇ πρὸς τῷ Ε ἴση ἐστίν· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
Ἐὰν ἄρα δύο τρίγωνα μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχῃ, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, ὑφ᾿ ἃς αἱ ὁμόλογοι πλευραὶ ὑποτείνουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον VI
Ἐὰν δύο τρίγωνα μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχῃ, περὶ δὲ ἄλλας γωνίας τὰς πλευρὰς ἀνάλογον, τῶν δὲ λοιπῶν ἑκατέραν ἅμα ἤτοι ἐλάσσονα ἢ μὴ ἐλάσσονα ὀρθῆς, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, περὶ ἃς ἀνάλογόν εἰσιν αἱ πλευραί.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχοντα τὴν ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ, περὶ δὲ ἄλλας γωνίας τὰς ὑπὸ ΑΒΓ, ΔΕΖ τὰς πλευρὰς ἀνάλογον, ὡς τὴν ΑΒ πρὸς τὴν ΒΓ, οὕτως τὴν ΔΕ πρὸς τὴν ΕΖ, τῶν δὲ λοιπῶν τῶν πρὸς τοῖς Γ, Ζ πρότερον ἑκατέραν ἅμα ἐλάσσονα ὀρθῆς· λέγω, ὅτι ἰσογώνιόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ, καὶ ἴση ἔσται ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ, καὶ λοιπὴ δηλονότι ἡ πρὸς τῷ Γ λοιπῇ τῇ πρὸς τῷ Ζ ἴση.
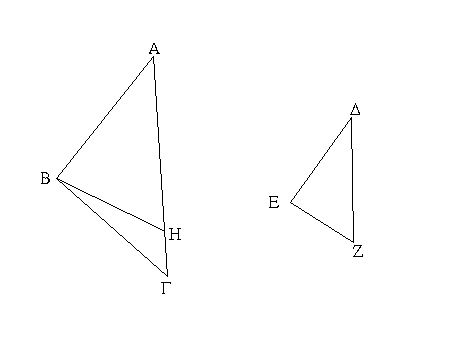
Εἰ γὰρ ἄνισός ἐστιν ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ὑπὸ ΑΒΓ. καὶ συνεστάτω πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Β τῇ ὑπὸ ΔΕΖ γωνίᾳ ἴση ἡ ὑπὸ ΑΒΗ.
Καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν Α γωνία τῇ Δ, ἡ δὲ ὑπὸ ΑΒΗ τῇ ὑπὸ ΔΕΖ, λοιπὴ ἄρα ἡ ὑπὸ ΑΗΒ λοιπῇ τῇ ὑπὸ ΔΖΕ ἐστιν ἴση. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΗ τρίγωνον τῷ ΔΕΖ τριγώνῳ. ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΒΗ, οὕτως ἡ ΔΕ πρὸς τὴν ΕΖ. ὡς δὲ ἡ ΔΕ πρὸς τὴν ΕΖ, [οὕτως] ὑπόκειται ἡ ΑΒ πρὸς τὴν ΒΓ· ἡ ΑΒ ἄρα πρὸς ἑκατέραν τῶν ΒΓ, ΒΗ τὸν αὐτὸν ἔχει λόγον· ἴση ἄρα ἡ ΒΓ τῇ ΒΗ. ὥστε καὶ γωνία ἡ πρὸς τῷ Γ γωνίᾳ τῇ ὑπὸ ΒΗΓ ἐστιν ἴση. ἐλάττων δὲ ὀρθῆς ὑπόκειται ἡ πρὸς τῷ Γ· ἐλάττων ἄρα ἐστὶν ὀρθῆς καὶ ἡ ὑπὸ ΒΗΓ· ὥστε ἡ ἐφεξῆς αὐτῇ γωνία ἡ ὑπὸ ΑΗΒ μείζων ἐστὶν ὀρθῆς. καὶ ἐδείχθη ἴση οὖσα τῇ πρὸς τῷ Ζ· καὶ ἡ πρὸς τῷ Ζ ἄρα μείζων ἐστὶν ὀρθῆς. ὑπόκειται δὲ ἐλάσσων ὀρθῆς· ὅπερ ἐστὶν ἄτοπον. οὐκ ἄρα ἄνισός ἐστιν ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ· ἴση ἄρα. ἔστι δὲ καὶ ἡ πρὸς τῷ Α ἴση τῇ πρὸς τῷ Δ· καὶ λοιπὴ ἄρα ἡ πρὸς τῷ Γ λοιπῇ τῇ πρὸς τῷ Ζ ἴση ἐστίν. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
Ἀλλὰ δὴ πάλιν ὑποκείσθω ἑκατέρα τῶν πρὸς τοῖς Γ, Ζ μὴ ἐλάσσων ὀρθῆς· λέγω πάλιν, ὅτι καὶ οὕτως ἐστὶν ἰσογώνιον τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι ἴση ἐστὶν ἡ ΒΓ τῇ ΒΗ· ὥστε καὶ γωνία ἡ πρὸς τῷ Γ τῇ ὑπὸ ΒΗΓ ἴση ἐστίν. οὐκ ἐλάττων δὲ ὀρθῆς ἡ πρὸς τῷ Γ· οὐκ ἐλάττων ἄρα ὀρθῆς οὐδὲ ἡ ὑπὸ ΒΗΓ. τριγώνου δὴ τοῦ ΒΗΓ αἱ δύο γωνίαι δύο ὀρθῶν οὔκ εἰσιν ἐλάττονες· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα πάλιν ἄνισός ἐστιν ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ· ἴση ἄρα. ἔστι δὲ καὶ ἡ πρὸς τῷ Α τῇ πρὸς τῷ Δ ἴση· λοιπὴ ἄρα ἡ πρὸς τῷ Γ λοιπῇ τῇ πρὸς τῷ Ζ ἴση ἐστίν. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ.
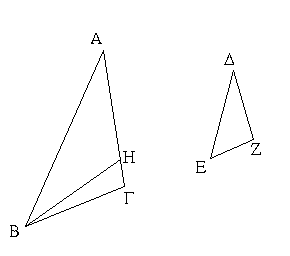
Ἐὰν ἄρα δύο τρίγωνα μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχῃ, περὶ δὲ ἄλλας γωνίας τὰς πλευρὰς ἀνάλογον, τῶν δὲ λοιπῶν ἑκατέραν ἅμα ἐλάττονα ἢ μὴ ἐλάττονα ὀρθῆς, ἰσογώνια ἔσται τὰ τρίγωνα καὶ ἴσας ἕξει τὰς γωνίας, περὶ ἃς ἀνάλογόν εἰσιν αἱ πλευραί· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον VI
Ἐὰν ἐν ὀρθογωνίῳ τριγώνῳ ἀπὸ τῆς ὀρθῆς γωνίας ἐπὶ τὴν βάσιν κάθετος ἀχθῇ, τὰ πρὸς τῇ καθέτῳ τρίγωνα ὅμοιά ἐστι τῷ τε ὅλῳ καὶ ἀλλήλοις.
Ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν ὑπὸ ΒΑΓ γωνίαν, καὶ ἤχθω ἀπὸ τοῦ Α ἐπὶ τὴν ΒΓ κάθετος ἡ ΑΔ· λέγω, ὅτι ὅμοιόν ἐστιν ἑκάτερον τῶν ΑΒΔ, ΑΔΓ τριγώνων ὅλῳ τῷ ΑΒΓ καὶ ἔτι ἀλλήλοις.
Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΑΔΒ· ὀρθὴ γὰρ ἑκατέρα· καὶ κοινὴ τῶν δύο τριγώνων τοῦ τε ΑΒΓ καὶ τοῦ ΑΒΔ ἡ πρὸς τῷ Β, λοιπὴ ἄρα ἡ ὑπὸ ΑΓΒ λοιπῇ τῇ ὑπὸ ΒΑΔ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΑΒΔ τριγώνῳ. ἔστιν ἄρα ὡς ἡ ΒΓ ὑποτείνουσα τὴν ὀρθὴν τοῦ ΑΒΓ τριγώνου πρὸς τὴν ΒΑ ὑποτείνουσαν τὴν ὀρθὴν τοῦ ΑΒΔ τριγώνου, οὕτως αὐτὴ ἡ ΑΒ ὑποτείνουσα τὴν πρὸς τῷ Γ γωνίαν τοῦ ΑΒΓ τριγώνου πρὸς τὴν ΒΔ ὑποτείνουσαν τὴν ἴσην τὴν ὑπὸ ΒΑΔ τοῦ ΑΒΔ τριγώνου, καὶ ἔτι ἡ ΑΓ πρὸς τὴν ΑΔ ὑποτείνουσαν τὴν πρὸς τῷ Β γωνίαν κοινὴν τῶν δύο τριγώνων. τὸ ΑΒΓ ἄρα τρίγωνον τῷ ΑΒΔ τριγώνῳ ἰσογώνιόν τέ ἐστι καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον ἔχει. ὅμοιον ἄρα [ἐστὶ] τὸ ΑΒΓ τρίγωνον τῷ ΑΒΔ τριγώνῳ. ὁμοίως δὴ δείξομεν, ὅτι καὶ τῷ ΑΔΓ τριγώνῳ ὅμοιόν ἐστι τὸ ΑΒΓ τρίγωνον· ἑκάτερον ἄρα τῶν ΑΒΔ, ΑΔΓ [τριγώνων] ὅμοιόν ἐστιν ὅλῳ τῷ ΑΒΓ.
Λέγω δή, ὅτι καὶ ἀλλήλοις ἐστὶν ὅμοια τὰ ΑΒΔ, ΑΔΓ τρίγωνα.
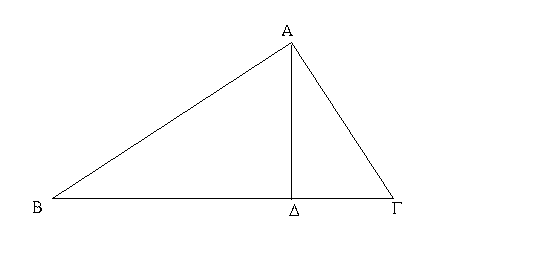
Ἐπεὶ γὰρ ὀρθὴ ἡ ὑπὸ ΒΔΑ ὀρθῇ τῇ ὑπὸ ΑΔΓ ἐστιν ἴση, ἀλλὰ μὴν καὶ ἡ ὑπὸ ΒΑΔ τῇ πρὸς τῷ Γ ἐδείχθη ἴση, καὶ λοιπὴ ἄρα ἡ πρὸς τῷ Β λοιπῇ τῇ ὑπὸ ΔΑΓ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΔ τρίγωνον τῷ ΑΔΓ τριγώνῳ. ἔστιν ἄρα ὡς ἡ ΒΔ τοῦ ΑΒΔ τριγώνου ὑποτείνουσα τὴν ὑπὸ ΒΑΔ πρὸς τὴν ΔΑ τοῦ ΑΔΓ τριγώνου ὑποτείνουσαν τὴν πρὸς τῷ Γ ἴσην τῇ ὑπὸ ΒΑΔ, οὕτως αὐτὴ ἡ ΑΔ τοῦ ΑΒΔ τριγώνου ὑποτείνουσα τὴν πρὸς τῷ Β γωνίαν πρὸς τὴν ΔΓ ὑποτείνουσαν τὴν ὑπὸ ΔΑΓ τοῦ ΑΔΓ τριγώνου ἴσην τῇ πρὸς τῷ Β, καὶ ἔτι ἡ ΒΑ πρὸς τὴν ΑΓ ὑποτείνουσαι τὰς ὀρθάς· ὅμοιον ἄρα ἐστὶ τὸ ΑΒΔ τρίγωνον τῷ ΑΔΓ τριγώνῳ.
Ἐὰν ἄρα ἐν ὀρθογωνίῳ τριγώνῳ ἀπὸ τῆς ὀρθῆς γωνίας ἐπὶ τὴν βάσιν κάθετος ἀχθῇ, τὰ πρὸς τῇ καθέτῳ τρίγωνα ὅμοιά ἐστι τῷ τε ὅλῳ καὶ ἀλλήλοις [ὅπερ ἔδει δεῖξαι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν ἐν ὀρθογωνίῳ τριγώνῳ ἀπὸ τῆς ὀρθῆς ἐπὶ τὴν βάσιν κάθετος ἀχθῇ, ἡ ἀχθεῖσα τῶν τῆς βάσεως τμημάτων μέση ἀνάλογόν ἐστιν· ὅπερ ἔδει δεῖξαι [καὶ ἔτι τῆς βάσεως καὶ ἑνὸς ὁποιουοῦν τῶν τμημάτων ἡ πρὸς τῷ τμήματι πλευρὰ μέση ἀνάλογόν ἐστιν].
Πρότασις θ΄ 9 Βιβλίον VI
Τῆς δοθείσης εὐθείας τὸ προσταχθὲν μέρος ἀφελεῖν.
Ἔστω ἡ δοθεῖσα εὐθεῖα ἡ ΑΒ· δεῖ δὴ τῆς ΑΒ τὸ προσταχθὲν μέρος ἀφελεῖν.
Ἐπιτετάχθω δὴ τὸ τρίτον. [καὶ] διήχθω τις ἀπὸ τοῦ Α εὐθεῖα ἡ ΑΓ γωνίαν περιέχουσα μετὰ τῆς ΑΒ τυχοῦσαν· καὶ εἰλήφθω τυχὸν σημεῖον ἐπὶ τῆς ΑΓ τὸ Δ, καὶ κείσθωσαν τῇ ΑΔ ἴσαι αἱ ΔΕ, ΕΓ. καὶ ἐπεζεύχθω ἡ ΒΓ, καὶ διὰ τοῦ Δ παράλληλος αὐτῇ ἤχθω ἡ ΔΖ.
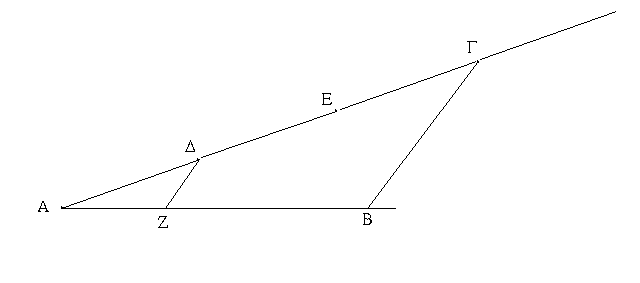
Ἐπεὶ οὖν τριγώνου τοῦ ΑΒΓ παρὰ μίαν τῶν πλευρῶν τὴν ΒΓ ἦκται ἡ ΖΔ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΓΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΒΖ πρὸς τὴν ΖΑ. διπλῆ δὲ ἡ ΓΔ τῆς ΔΑ· διπλῆ ἄρα καὶ ἡ ΒΖ τῆς ΖΑ· τριπλῆ ἄρα ἡ ΒΑ τῆς ΑΖ.
Τῆς ἄρα δοθείσης εὐθείας τῆς ΑΒ τὸ ἐπιταχθὲν τρίτον μέρος ἀφῄρηται τὸ ΑΖ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ι΄ 10 Βιβλίον VI
Τὴν δοθεῖσαν εὐθεῖαν ἄτμητον τῇ δοθείσῃ τετμημένῃ ὁμοίως τεμεῖν.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἄτμητος ἡ ΑΒ, ἡ δὲ τετμημένη ἡ ΑΓ κατὰ τὰ Δ, Ε σημεῖα, καὶ κείσθωσαν ὥστε γωνίαν τυχοῦσαν περιέχειν, καὶ ἐπεζεύχθω ἡ ΓΒ, καὶ διὰ τῶν Δ, Ε τῇ ΒΓ παράλληλοι ἤχθωσαν αἱ ΔΖ, ΕΗ, διὰ δὲ τοῦ Δ τῇ ΑΒ παράλληλος ἤχθω ἡ ΔΘΚ.
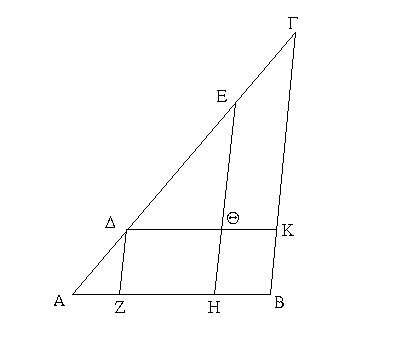
Παραλληλόγραμμον ἄρα ἐστὶν ἑκάτερον τῶν ΖΘ, ΘΒ· ἴση ἄρα ἡ μὲν ΔΘ τῇ ΖΗ, ἡ δὲ ΘΚ τῇ ΗΒ. καὶ ἐπεὶ τριγώνου τοῦ ΔΚΓ παρὰ μίαν τῶν πλευρῶν τὴν ΚΓ εὐθεῖα ἦκται ἡ ΘΕ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΓΕ πρὸς τὴν ΕΔ, οὕτως ἡ ΚΘ πρὸς τὴν ΘΔ. ἴση δὲ ἡ μὲν ΚΘ τῇ ΒΗ, ἡ δὲ ΘΔ τῇ ΗΖ. ἔστιν ἄρα ὡς ἡ ΓΕ πρὸς τὴν ΕΔ, οὕτως ἡ ΒΗ πρὸς τὴν ΗΖ. πάλιν, ἐπεὶ τριγώνου τοῦ ΑΗΕ παρὰ μίαν τῶν πλευρῶν τὴν ΗΕ ἦκται ἡ ΖΔ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΕΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΑ. ἐδείχθη δὲ καὶ ὡς ἡ ΓΕ πρὸς τὴν ΕΔ, οὕτως ἡ ΒΗ πρὸς τὴν ΗΖ· ἔστιν ἄρα ὡς μὲν ἡ ΓΕ πρὸς τὴν ΕΔ, οὕτως ἡ ΒΗ πρὸς τὴν ΗΖ, ὡς δὲ ἡ ΕΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΑ.
Ἡ ἄρα δοθεῖσα εὐθεῖα ἄτμητος ἡ ΑΒ τῇ δοθείσῃ εὐθείᾳ τετμημένῃ τῇ ΑΓ ὁμοίως τέτμηται· ὅπερ ἔδει ποιῆσαι.
Πρότασις ια΄ 11 Βιβλίον VI
Δύο δοθεισῶν εὐθειῶν τρίτην ἀνάλογον προσευρεῖν.
Ἔστωσαν αἱ δοθεῖσαι [δύο εὐθεῖαι] αἱ ΒΑ, ΑΓ καὶ κείσθωσαν γωνίαν περιέχουσαι τυχοῦσαν. δεῖ δὴ τῶν ΒΑ, ΑΓ τρίτην ἀνάλογον προσευρεῖν. ἐκβεβλήσθωσαν γὰρ ἐπὶ τὰ Δ, Ε σημεῖα, καὶ κείσθω τῇ ΑΓ ἴση ἡ ΒΔ, καὶ ἐπεζεύχθω ἡ ΒΓ, καὶ διὰ τοῦ Δ παράλληλος αὐτῇ ἤχθω ἡ ΔΕ.
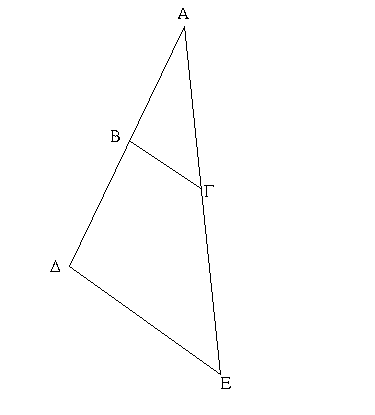
Ἐπεὶ οὖν τριγώνου τοῦ ΑΔΕ παρὰ μίαν τῶν πλευρῶν τὴν ΔΕ ἦκται ἡ ΒΓ, ἀνάλογόν ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΒΔ, οὕτως ἡ ΑΓ πρὸς τὴν ΓΕ. ἴση δὲ ἡ ΒΔ τῇ ΑΓ. ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΑΓ, οὕτως ἡ ΑΓ πρὸς τὴν ΓΕ.
Δύο ἄρα δοθεισῶν εὐθειῶν τῶν ΑΒ, ΑΓ τρίτη ἀνάλογον αὐταῖς προσεύρηται ἡ ΓΕ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιβ΄ 12 Βιβλίον VI
Τριῶν δοθεισῶν εὐθειῶν τετάρτην ἀνάλογον προσευρεῖν.
Ἔστωσαν αἱ δοθεῖσαι τρεῖς εὐθεῖαι αἱ Α, Β, Γ· δεῖ δὴ τῶν Α, Β, Γ τετάρτην ἀνάλογον προσευρεῖν.
Ἐκκείσθωσαν δύο εὐθεῖαι αἱ ΔΕ, ΔΖ γωνίαν περιέχουσαι [τυχοῦσαν] τὴν ὑπὸ ΕΔΖ· καὶ κείσθω τῇ μὲν Α ἴση ἡ ΔΗ, τῇ δὲ Β ἴση ἡ ΗΕ, καὶ ἔτι τῇ Γ ἴση ἡ ΔΘ· καὶ ἐπιζευχθείσης τῆς ΗΘ παράλληλος αὐτῇ ἤχθω διὰ τοῦ Ε ἡ ΕΖ.
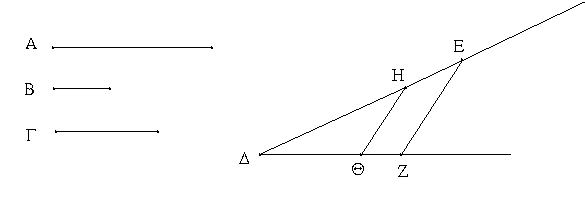
Ἐπεὶ οὖν τριγώνου τοῦ ΔΕΖ παρὰ μίαν τὴν ΕΖ ἦκται ἡ ΗΘ, ἔστιν ἄρα ὡς ἡ ΔΗ πρὸς τὴν ΗΕ, οὕτως ἡ ΔΘ πρὸς τὴν ΘΖ. ἴση δὲ ἡ μὲν ΔΗ τῇ Α, ἡ δὲ ΗΕ τῇ Β, ἡ δὲ ΔΘ τῇ Γ· ἔστιν ἄρα ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν ΘΖ.
Τριῶν ἄρα δοθεισῶν εὐθειῶν τῶν Α, Β, Γ τετάρτη ἀνάλογον προσεύρηται ἡ ΘΖ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιγ΄ 13 Βιβλίον VI
Δύο δοθεισῶν εὐθειῶν μέσην ἀνάλογον προσευρεῖν.
Ἔστωσαν αἱ δοθεῖσαι δύο εὐθεῖαι αἱ ΑΒ, ΒΓ· δεῖ δὴ τῶν ΑΒ, ΒΓ μέσην ἀνάλογον προσευρεῖν.
Κείσθωσαν ἐπ᾿ εὐθείας, καὶ γεγράφθω ἐπὶ τῆς ΑΓ ἡμικύκλιον τὸ ΑΔΓ, καὶ ἤχθω ἀπὸ τοῦ Β σημείου τῇ ΑΓ εὐθείᾳ πρὸς ὀρθὰς ἡ ΒΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΓ.
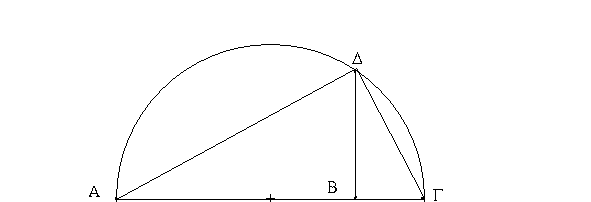
Ἐπεὶ ἐν ἡμικυκλίῳ γωνία ἐστὶν ἡ ὑπὸ ΑΔΓ, ὀρθή ἐστιν. καὶ ἐπεὶ ἐν ὀρθογωνίῳ τριγώνῳ τῷ ΑΔΓ ἀπὸ τῆς ὀρθῆς γωνίας ἐπὶ τὴν βάσιν κάθετος ἦκται ἡ ΔΒ, ἡ ΔΒ ἄρα τῶν τῆς βάσεως τμημάτων τῶν ΑΒ, ΒΓ μέση ἀνάλογόν ἐστιν.
Δύο ἄρα δοθεισῶν εὐθειῶν τῶν ΑΒ, ΒΓ μέση ἀνάλογον προσεύρηται ἡ ΔΒ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιδ΄ 14 Βιβλίον VI
Τῶν ἴσων τε καὶ ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· καὶ ὧν ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἴσα ἐστὶν ἐκεῖνα.
Ἔστω ἴσα τε καὶ ἰσογώνια παραλληλόγραμμα τὰ ΑΒ, ΒΓ ἴσας ἔχοντα τὰς πρὸς τῷ Β γωνίας, καὶ κείσθωσαν ἐπ᾿ εὐθείας αἱ ΔΒ, ΒΕ· ἐπ᾿ εὐθείας ἄρα εἰσὶ καὶ αἱ ΖΒ, ΒΗ. λέγω, ὅτι τῶν ΑΒ, ΒΓ ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, τουτέστιν, ὅτι ἐστὶν ὡς ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΗΒ πρὸς τὴν ΒΖ.
Συμπεπληρώσθω γὰρ τὸ ΖΕ παραλληλόγραμμον. ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΑΒ παραλληλόγραμμον τῷ ΒΓ παραλληλογράμμῳ, ἄλλο δέ τι τὸ ΖΕ, ἔστιν ἄρα ὡς τὸ ΑΒ πρὸς τὸ ΖΕ, οὕτως τὸ ΒΓ πρὸς τὸ ΖΕ. ἀλλ' ὡς μὲν τὸ ΑΒ πρὸς τὸ ΖΕ, οὕτως ἡ ΔΒ πρὸς τὴν ΒΕ, ὡς δὲ τὸ ΒΓ πρὸς τὸ ΖΕ, οὕτως ἡ ΗΒ πρὸς τὴν ΒΖ· καὶ ὡς ἄρα ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΗΒ πρὸς τὴν ΒΖ. τῶν ἄρα ΑΒ, ΒΓ παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας.
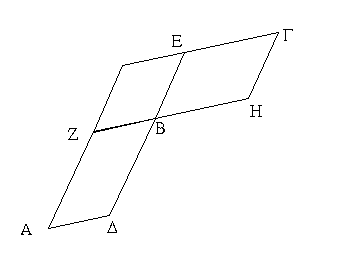
Ἀλλὰ δὴ ἔστω ὡς ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΗΒ πρὸς τὴν ΒΖ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒ παραλληλόγραμμον τῷ ΒΓ παραλληλογράμμῳ.
Ἐπεὶ γάρ ἐστιν ὡς ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΗΒ πρὸς τὴν ΒΖ, ἀλλ' ὡς μὲν ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως τὸ ΑΒ παραλληλόγραμμον πρὸς τὸ ΖΕ παραλληλόγραμμον, ὡς δὲ ἡ ΗΒ πρὸς τὴν ΒΖ, οὕτως τὸ ΒΓ παραλληλόγραμμον πρὸς τὸ ΖΕ παραλληλόγραμμον, καὶ ὡς ἄρα τὸ ΑΒ πρὸς τὸ ΖΕ, οὕτως τὸ ΒΓ πρὸς τὸ ΖΕ· ἴσον ἄρα ἐστὶ τὸ ΑΒ παραλληλόγραμμον τῷ ΒΓ παραλληλογράμμῳ.
Τῶν ἄρα ἴσων τε καὶ ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· καὶ ὧν ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἴσα ἐστὶν ἐκεῖνα· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον VI
Τῶν ἴσων καὶ μίαν μιᾷ ἴσην ἐχόντων γωνίαν τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· καὶ ὧν μίαν μιᾷ ἴσην ἐχόντων γωνίαν τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἴσα ἐστὶν ἐκεῖνα.
Ἔστω ἴσα τρίγωνα τὰ ΑΒΓ, ΑΔΕ μίαν μιᾷ ἴσην ἔχοντα γωνίαν τὴν ὑπὸ ΒΑΓ τῇ ὑπὸ ΔΑΕ· λέγω, ὅτι τῶν ΑΒΓ, ΑΔΕ τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, τουτέστιν, ὅτι ἐστὶν ὡς ἡ ΓΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΒ.
Κείσθω γὰρ ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΓΑ τῇ ΑΔ· ἐπ᾿ εὐθείας ἄρα ἐστὶ καὶ ἡ ΕΑ τῇ ΑΒ. καὶ ἐπεζεύχθω ἡ ΒΔ.
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΑΔΕ τριγώνῳ, ἄλλο δέ τι τὸ ΒΑΔ, ἔστιν ἄρα ὡς τὸ ΓΑΒ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον, οὕτως τὸ ΕΑΔ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον. ἀλλ' ὡς μὲν τὸ ΓΑΒ πρὸς τὸ ΒΑΔ, οὕτως ἡ ΓΑ πρὸς τὴν ΑΔ, ὡς δὲ τὸ ΕΑΔ πρὸς τὸ ΒΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΒ. καὶ ὡς ἄρα ἡ ΓΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΒ. τῶν ΑΒΓ, ΑΔΕ ἄρα τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας.
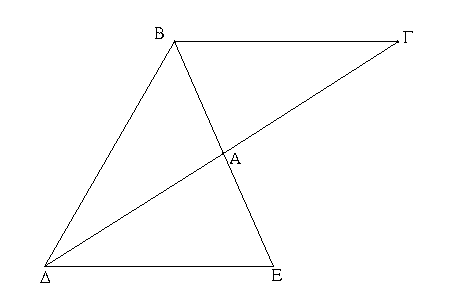
Ἀλλὰ δὴ ἀντιπεπονθέτωσαν αἱ πλευραὶ τῶν ΑΒΓ, ΑΔΕ τριγώνων, καὶ ἔστω ὡς ἡ ΓΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΒ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΑΔΕ τριγώνῳ.
Ἐπιζευχθείσης γὰρ πάλιν τῆς ΒΔ, ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΒ, ἀλλ' ὡς μὲν ἡ ΓΑ πρὸς τὴν ΑΔ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον, ὡς δὲ ἡ ΕΑ πρὸς τὴν ΑΒ, οὕτως τὸ ΕΑΔ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον, ὡς ἄρα τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον, οὕτως τὸ ΕΑΔ τρίγωνον πρὸς τὸ ΒΑΔ τρίγωνον. ἑκάτερον ἄρα τῶν ΑΒΓ, ΕΑΔ πρὸς τὸ ΒΑΔ τὸν αὐτὸν ἔχει λόγον. ἴσον ἄρα ἐστὶ τὸ ΑΒΓ [τρίγωνον] τῷ ΕΑΔ τριγώνῳ.
Τῶν ἄρα ἴσων καὶ μίαν μιᾷ ἴσην ἐχόντων γωνίαν τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· καὶ ὧν μίαν μιᾷ ἴσην ἐχόντων γωνίαν τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἐκεῖνα ἴσα ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον VI
Ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν μέσων περιεχομένῳ ὀρθογωνίῳ· κἂν τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ᾖ τῷ ὑπὸ τῶν μέσων περιεχομένῳ ὀρθογωνίῳ, αἱ τέσσαρες εὐθεῖαι ἀνάλογον ἔσονται.
Ἔστωσαν τέσσαρες εὐθεῖαι ἀνάλογον αἱ ΑΒ, ΓΔ, Ε, Ζ, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ Ε πρὸς τὴν Ζ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΒ, Ζ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΓΔ, Ε περιεχομένῳ ὀρθογωνίῳ.
Ἤχθωσαν [γὰρ] ἀπὸ τῶν Α, Γ σημείων ταῖς ΑΒ, ΓΔ εὐθείαις πρὸς ὀρθὰς αἱ ΑΗ, ΓΘ, καὶ κείσθω τῇ μὲν Ζ ἴση ἡ ΑΓ, τῇ δὲ Ε ἴση ἡ ΓΘ. καὶ συμπεπληρώσθω τὰ ΒΗ, ΔΘ παραλληλόγραμμα.
Καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ Ε πρὸς τὴν Ζ, ἴση δὲ ἡ μὲν Ε τῇ ΓΘ, ἡ δὲ Ζ τῇ ΑΗ, ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΓΘ πρὸς τὴν ΑΗ. τῶν ΒΗ, ΔΘ ἄρα παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας. ὧν δὲ ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἴσα ἐστὶν ἐκεῖνα· ἴσον ἄρα ἐστὶ τὸ ΒΗ παραλληλόγραμμον τῷ ΔΘ παραλληλογράμμῳ. καί ἐστι τὸ μὲν ΒΗ τὸ ὑπὸ τῶν ΑΒ, Ζ· ἴση γὰρ ἡ ΑΗ τῇ Ζ· τὸ δὲ ΔΘ τὸ ὑπὸ τῶν ΓΔ, Ε· ἴση γὰρ ἡ Ε τῇ ΓΘ· τὸ ἄρα ὑπὸ τῶν ΑΒ, Ζ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΓΔ, Ε περιεχομένῳ ὀρθογωνίῳ.
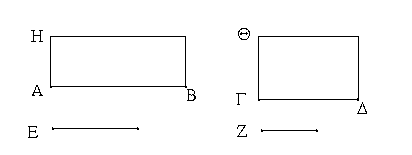
Ἀλλὰ δὴ τὸ ὑπὸ τῶν ΑΒ, Ζ περιεχόμενον ὀρθογώνιον ἴσον ἔστω τῷ ὑπὸ τῶν ΓΔ, Ε περιεχομένῳ ὀρθογωνίῳ· λέγω, ὅτι αἱ τέσσαρες εὐθεῖαι ἀνάλογον ἔσονται, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ Ε πρὸς τὴν Ζ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεὶ τὸ ὑπὸ τῶν ΑΒ, Ζ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΓΔ, Ε, καί ἐστι τὸ μὲν ὑπὸ τῶν ΑΒ, Ζ τὸ ΒΗ· ἴση γάρ ἐστιν ἡ ΑΗ τῇ Ζ· τὸ δὲ ὑπὸ τῶν ΓΔ, Ε τὸ ΔΘ· ἴση γὰρ ἡ ΓΘ τῇ Ε· τὸ ἄρα ΒΗ ἴσον ἐστὶ τῷ ΔΘ. καί ἐστιν ἰσογώνια. τῶν δὲ ἴσων καὶ ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας. ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΓΘ πρὸς τὴν ΑΗ. ἴση δὲ ἡ μὲν ΓΘ τῇ Ε, ἡ δὲ ΑΗ τῇ Ζ· ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ Ε πρὸς τὴν Ζ.
Ἐὰν ἄρα τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν μέσων περιεχομένῳ ὀρθογωνίῳ· κἂν τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ᾖ τῷ ὑπὸ τῶν μέσων περιεχομένῳ ὀρθογωνίῳ, αἱ τέσσαρες εὐθεῖαι ἀνάλογον ἔσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον VI
Ἐὰν τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς μέσης τετραγώνῳ· κἂν τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ᾖ τῷ ἀπὸ τῆς μέσης τετραγώνῳ, αἱ τρεῖς εὐθεῖαι ἀνάλογον ἔσονται.
Ἔστωσαν τρεῖς εὐθεῖαι ἀνάλογον αἱ Α, Β, Γ, ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ· λέγω, ὅτι τὸ ὑπὸ τῶν Α, Γ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς Β τετραγώνῳ.
Κείσθω τῇ Β ἴση ἡ Δ.
Καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ, ἴση δὲ ἡ Β τῇ Δ, ἔστιν ἄρα ὡς ἡ Α πρὸς τὴν Β, ἡ Δ πρὸς τὴν Γ. ἐὰν δὲ τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων περιεχόμενον [ὀρθογώνιον] ἴσον ἐστὶ τῷ ὑπὸ τῶν μέσων περιεχομένῳ ὀρθογωνίῳ. τὸ ἄρα ὑπὸ τῶν Α, Γ ἴσον ἐστὶ τῷ ὑπὸ τῶν Β, Δ. ἀλλὰ τὸ ὑπὸ τῶν Β, Δ τὸ ἀπὸ τῆς Β ἐστιν· ἴση γὰρ ἡ Β τῇ Δ· τὸ ἄρα ὑπὸ τῶν Α, Γ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς Β τετραγώνῳ.
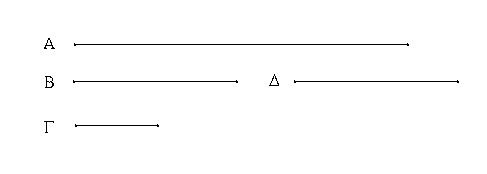
Ἀλλὰ δὴ τὸ ὑπὸ τῶν Α, Γ ἴσον ἔστω τῷ ἀπὸ τῆς Β· λέγω, ὅτι ἐστὶν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεὶ τὸ ὑπὸ τῶν Α, Γ ἴσον ἐστὶ τῷ ἀπὸ τῆς Β, ἀλλὰ τὸ ἀπὸ τῆς Β τὸ ὑπὸ τῶν Β, Δ ἐστιν· ἴση γὰρ ἡ Β τῇ Δ· τὸ ἄρα ὑπὸ τῶν Α, Γ ἴσον ἐστὶ τῷ ὑπὸ τῶν Β, Δ. ἐὰν δὲ τὸ ὑπὸ τῶν ἄκρων ἴσον ᾖ τῷ ὑπὸ τῶν μέσων, αἱ τέσσαρες εὐθεῖαι ἀνάλογόν εἰσιν. ἔστιν ἄρα ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Δ πρὸς τὴν Γ. ἴση δὲ ἡ Β τῇ Δ· ὡς ἄρα ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ.
Ἐὰν ἄρα τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ἀπὸ τῆς μέσης τετραγώνῳ· κἂν τὸ ὑπὸ τῶν ἄκρων περιεχόμενον ὀρθογώνιον ἴσον ᾖ τῷ ἀπὸ τῆς μέσης τετραγώνῳ, αἱ τρεῖς εὐθεῖαι ἀνάλογον ἔσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον VI
Ἀπὸ τῆς δοθείσης εὐθείας τῷ δοθέντι εὐθυγράμμῳ ὅμοιόν τε καὶ ὁμοίως κείμενον εὐθύγραμμον ἀναγράψαι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν εὐθύγραμμον τὸ ΓΕ· δεῖ δὴ ἀπὸ τῆς ΑΒ εὐθείας τῷ ΓΕ εὐθυγράμμῳ ὅμοιόν τε καὶ ὁμοίως κείμενον εὐθύγραμμον ἀναγράψαι.
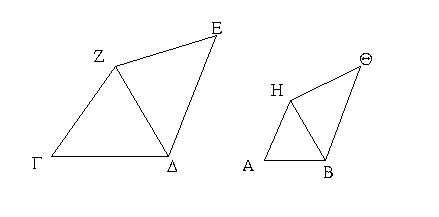
Ἐπεζεύχθω ἡ ΔΖ, καὶ συνεστάτω πρὸς τῇ ΑΒ εὐθείᾳ καὶ τοῖς πρὸς αὐτῇ σημείοις τοῖς Α, Β τῇ μὲν πρὸς τῷ Γ γωνίᾳ ἴση ἡ ὑπὸ ΗΑΒ, τῇ δὲ ὑπὸ ΓΔΖ ἴση ἡ ὑπὸ ΑΒΗ. λοιπὴ ἄρα ἡ ὑπὸ ΓΖΔ τῇ ὑπὸ ΑΗΒ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΖΓΔ τρίγωνον τῷ ΗΑΒ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΖΔ πρὸς τὴν ΗΒ, οὕτως ἡ ΖΓ πρὸς τὴν ΗΑ, καὶ ἡ ΓΔ πρὸς τὴν ΑΒ. πάλιν συνεστάτω πρὸς τῇ ΒΗ εὐθείᾳ καὶ τοῖς πρὸς αὐτῇ σημείοις τοῖς Β, Η τῇ μὲν ὑπὸ ΔΖΕ γωνίᾳ ἴση ἡ ὑπὸ ΒΗΘ, τῇ δὲ ὑπὸ ΖΔΕ ἴση ἡ ὑπὸ ΗΒΘ. λοιπὴ ἄρα ἡ πρὸς τῷ Ε λοιπῇ τῇ πρὸς τῷ Θ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΖΔΕ τρίγωνον τῷ ΗΘΒ τριγώνῳ· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΖΔ πρὸς τὴν ΗΒ, οὕτως ἡ ΖΕ πρὸς τὴν ΗΘ καὶ ἡ ΕΔ πρὸς τὴν ΘΒ. ἐδείχθη δὲ καὶ ὡς ἡ ΖΔ πρὸς τὴν ΗΒ, οὕτως ἡ ΖΓ πρὸς τὴν ΗΑ καὶ ἡ ΓΔ πρὸς τὴν ΑΒ· καὶ ὡς ἄρα ἡ ΖΓ πρὸς τὴν ΑΗ, οὕτως ἥ τε ΓΔ πρὸς τὴν ΑΒ καὶ ἡ ΖΕ πρὸς τὴν ΗΘ καὶ ἔτι ἡ ΕΔ πρὸς τὴν ΘΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ὑπὸ ΓΖΔ γωνία τῇ ὑπὸ ΑΗΒ, ἡ δὲ ὑπὸ ΔΖΕ τῇ ὑπὸ ΒΗΘ, ὅλη ἄρα ἡ ὑπὸ ΓΖΕ ὅλῃ τῇ ὑπὸ ΑΗΘ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΓΔΕ τῇ ὑπὸ ΑΒΘ ἐστιν ἴση. ἔστι δὲ καὶ ἡ μὲν πρὸς τῷ Γ τῇ πρὸς τῷ Α ἴση, ἡ δὲ πρὸς τῷ Ε τῇ πρὸς τῷ Θ. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΘ τῷ ΓΕ· καὶ τὰς περὶ τὰς ἴσας γωνίας αὐτῶν πλευρὰς ἀνάλογον ἔχει· ὅμοιον ἄρα ἐστὶ τὸ ΑΘ εὐθύγραμμον τῷ ΓΕ εὐθυγράμμῳ.
Ἀπὸ τῆς δοθείσης ἄρα εὐθείας τῆς ΑΒ τῷ δοθέντι εὐθυγράμμῳ τῷ ΓΕ ὅμοιόν τε καὶ ὁμοίως κείμενον εὐθύγραμμον ἀναγέγραπται τὸ ΑΘ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιθ΄ 19 Βιβλίον VI
Τὰ ὅμοια τρίγωνα πρὸς ἄλληλα ἐν διπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν.
Ἔστω ὅμοια τρίγωνα τὰ ΑΒΓ, ΔΕΖ ἴσην ἔχοντα τὴν πρὸς τῷ Β γωνίαν τῇ πρὸς τῷ Ε, ὡς δὲ τὴν ΑΒ πρὸς τὴν ΒΓ, οὕτως τὴν ΔΕ πρὸς τὴν ΕΖ, ὥστε ὁμόλογον εἶναι τὴν ΒΓ τῇ ΕΖ· λέγω, ὅτι τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΔΕΖ τρίγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Εἰλήφθω γὰρ τῶν ΒΓ, ΕΖ τρίτη ἀνάλογον ἡ ΒΗ, ὥστε εἶναι ὡς τὴν ΒΓ πρὸς τὴν ΕΖ, οὕτως τὴν ΕΖ πρὸς τὴν ΒΗ· καὶ ἐπεζεύχθω ἡ ΑΗ.
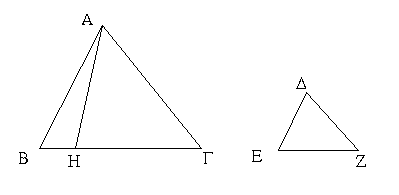
Ἐπεὶ οὖν ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΔΕ πρὸς τὴν ΕΖ, ἐναλλὰξ ἄρα ἐστὶν ὡς ἡ ΑΒ πρὸς τὴν ΔΕ, οὕτως ἡ ΒΓ πρὸς τὴν ΕΖ. ἀλλ' ὡς ἡ ΒΓ πρὸς ΕΖ, οὕτως ἐστὶν ἡ ΕΖ πρὸς ΒΗ. καὶ ὡς ἄρα ἡ ΑΒ πρὸς ΔΕ, οὕτως ἡ ΕΖ πρὸς ΒΗ· τῶν ΑΒΗ, ΔΕΖ ἄρα τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας. ὧν δὲ μίαν μιᾷ ἴσην ἐχόντων γωνίαν τριγώνων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας, ἴσα ἐστὶν ἐκεῖνα. ἴσον ἄρα ἐστὶ τὸ ΑΒΗ τρίγωνον τῷ ΔΕΖ τριγώνῳ. καὶ ἐπεί ἐστιν ὡς ἡ ΒΓ πρὸς τὴν ΕΖ, οὕτως ἡ ΕΖ πρὸς τὴν ΒΗ, ἐὰν δὲ τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, ἡ πρώτη πρὸς τὴν τρίτην διπλασίονα λόγον ἔχει ἤπερ πρὸς τὴν δευτέραν, ἡ ΒΓ ἄρα πρὸς τὴν ΒΗ διπλασίονα λόγον ἔχει ἤπερ ἡ ΓΒ πρὸς τὴν ΕΖ. ὡς δὲ ἡ ΓΒ πρὸς τὴν ΒΗ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΒΗ τρίγωνον· καὶ τὸ ΑΒΓ ἄρα τρίγωνον πρὸς τὸ ΑΒΗ διπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ. ἴσον δὲ τὸ ΑΒΗ τρίγωνον τῷ ΔΕΖ τριγώνῳ· καὶ τὸ ΑΒΓ ἄρα τρίγωνον πρὸς τὸ ΔΕΖ τρίγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Τὰ ἄρα ὅμοια τρίγωνα πρὸς ἄλληλα ἐν διπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· [ὅπερ ἔδει δεῖξαι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι, ἐὰν τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, ἔστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης εἶδος πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον [ἐπείπερ ἐδείχθη, ὡς ἡ ΓΒ πρὸς ΒΗ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΒΗ τρίγωνον, τουτέστι τὸ ΔΕΖ]· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον VI
Τὰ ὅμοια πολύγωνα εἴς τε ὅμοια τρίγωνα διαιρεῖται καὶ εἰς ἴσα τὸ πλῆθος καὶ ὁμόλογα τοῖς ὅλοις, καὶ τὸ πολύγωνον πρὸς τὸ πολύγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν.
Ἔστω ὅμοια πολύγωνα τὰ ΑΒΓΔΕ, ΖΗΘΚΛ, ὁμόλογος δὲ ἔστω ἡ ΑΒ τῇ ΖΗ· λέγω, ὅτι τὰ ΑΒΓΔΕ, ΖΗΘΚΛ πολύγωνα εἴς τε ὅμοια τρίγωνα διαιρεῖται καὶ εἰς ἴσα τὸ πλῆθος καὶ ὁμόλογα τοῖς ὅλοις, καὶ τὸ ΑΒΓΔΕ πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ πρὸς τὴν ΖΗ.
Ἐπεζεύχθωσαν αἱ ΒΕ, ΕΓ, ΗΛ, ΛΘ.
Καὶ ἐπεὶ ὅμοιόν ἐστι τὸ ΑΒΓΔΕ πολύγωνον τῷ ΖΗΘΚΛ πολυγώνῳ, ἴση ἐστὶν ἡ ὑπὸ ΒΑΕ γωνία τῇ ὑπὸ ΗΖΛ. καί ἐστιν ὡς ἡ ΒΑ πρὸς ΑΕ, οὕτως ἡ ΗΖ πρὸς ΖΛ. ἐπεὶ οὖν δύο τρίγωνά ἐστι τὰ ΑΒΕ, ΖΗΛ μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχοντα, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον, ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΕ τρίγωνον τῷ ΖΗΛ τριγώνῳ· ὥστε καὶ ὅμοιον· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΒΕ γωνία τῇ ὑπὸ ΖΗΛ. ἔστι δὲ καὶ ὅλη ἡ ὑπὸ ΑΒΓ ὅλῃ τῇ ὑπὸ ΖΗΘ ἴση διὰ τὴν ὁμοιότητα τῶν πολυγώνων· λοιπὴ ἄρα ἡ ὑπὸ ΕΒΓ γωνία τῇ ὑπὸ ΛΗΘ ἐστιν ἴση. καὶ ἐπεὶ διὰ τὴν ὁμοιότητα τῶν ΑΒΕ, ΖΗΛ τριγώνων ἐστὶν ὡς ἡ ΕΒ πρὸς ΒΑ, οὕτως ἡ ΛΗ πρὸς ΗΖ, ἀλλὰ μὴν καὶ διὰ τὴν ὁμοιότητα τῶν πολυγώνων ἐστὶν ὡς ἡ ΑΒ πρὸς ΒΓ, οὕτως ἡ ΖΗ πρὸς ΗΘ, δι' ἴσου ἄρα ἐστὶν ὡς ἡ ΕΒ πρὸς ΒΓ, οὕτως ἡ ΛΗ πρὸς ΗΘ, καὶ περὶ τὰς ἴσας γωνίας τὰς ὑπὸ ΕΒΓ, ΛΗΘ αἱ πλευραὶ ἀνάλογόν εἰσιν· ἰσογώνιον ἄρα ἐστὶ τὸ ΕΒΓ τρίγωνον τῷ ΛΗΘ τριγώνῳ· ὥστε καὶ ὅμοιόν ἐστι τὸ ΕΒΓ τρίγωνον τῷ ΛΗΘ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΕΓΔ τρίγωνον ὅμοιόν ἐστι τῷ ΛΘΚ τριγώνῳ. τὰ ἄρα ὅμοια πολύγωνα τὰ ΑΒΓΔΕ, ΖΗΘΚΛ εἴς τε ὅμοια τρίγωνα διῄρηται καὶ εἰς ἴσα τὸ πλῆθος.
Λέγω, ὅτι καὶ ὁμόλογα τοῖς ὅλοις, τουτέστιν ὥστε ἀνάλογον εἶναι τὰ τρίγωνα, καὶ ἡγούμενα μὲν εἶναι τὰ ΑΒΕ, ΕΒΓ, ΕΓΔ, ἑπόμενα δὲ αὐτῶν τὰ ΖΗΛ, ΛΗΘ, ΛΘΚ, καὶ ὅτι τὸ ΑΒΓΔΕ πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἡ ΑΒ πρὸς τὴν ΖΗ.
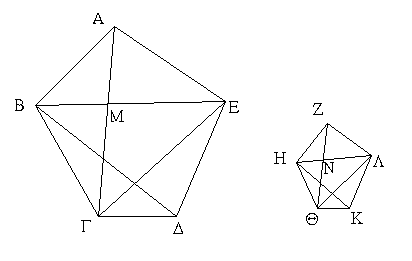
Ἐπεζεύχθωσαν γὰρ αἱ ΑΓ, ΖΘ. καὶ ἐπεὶ διὰ τὴν ὁμοιότητα τῶν πολυγώνων ἴση ἐστὶν ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΖΗΘ, καί ἐστιν ὡς ἡ ΑΒ πρὸς ΒΓ, οὕτως ἡ ΖΗ πρὸς ΗΘ, ἰσογώνιόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΖΗΘ τριγώνῳ· ἴση ἄρα ἐστὶν ἡ μὲν ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΗΖΘ, ἡ δὲ ὑπὸ ΒΓΑ τῇ ὑπὸ ΗΘΖ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΒΑΜ γωνία τῇ ὑπὸ ΗΖΝ, ἔστι δὲ καὶ ἡ ὑπὸ ΑΒΜ τῇ ὑπὸ ΖΗΝ ἴση, καὶ λοιπὴ ἄρα ἡ ὑπὸ ΑΜΒ λοιπῇ τῇ ὑπὸ ΖΝΗ ἴση ἐστίν· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΜ τρίγωνον τῷ ΖΗΝ τριγώνῳ. ὁμοίως δὴ δείξομεν, ὅτι καὶ τὸ ΒΜΓ τρίγωνον ἰσογώνιόν ἐστι τῷ ΗΝΘ τριγώνῳ. ἀνάλογον ἄρα ἐστίν, ὡς μὲν ἡ ΑΜ πρὸς ΜΒ, οὕτως ἡ ΖΝ πρὸς ΝΗ, ὡς δὲ ἡ ΒΜ πρὸς ΜΓ, οὕτως ἡ ΗΝ πρὸς ΝΘ· ὥστε καὶ δι' ἴσου, ὡς ἡ ΑΜ πρὸς ΜΓ, οὕτως ἡ ΖΝ πρὸς ΝΘ. ἀλλ' ὡς ἡ ΑΜ πρὸς ΜΓ, οὕτως τὸ ΑΒΜ [τρίγωνον] πρὸς τὸ ΜΒΓ, καὶ τὸ ΑΜΕ πρὸς τὸ ΕΜΓ· πρὸς ἄλληλα γάρ εἰσιν ὡς αἱ βάσεις. καὶ ὡς ἄρα ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ὡς ἄρα τὸ ΑΜΒ τρίγωνον πρὸς τὸ ΒΜΓ, οὕτως τὸ ΑΒΕ πρὸς τὸ ΓΒΕ.ἀλλ' ὡς τὸ ΑΜΒ πρὸς τὸ ΒΜΓ, οὕτως ἡ ΑΜ πρὸς ΜΓ· καὶ ὡς ἄρα ἡ ΑΜ πρὸς ΜΓ, οὕτως τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΕΒΓ τρίγωνον. διὰ τὰ αὐτὰ δὴ καὶ ὡς ἡ ΖΝ πρὸς ΝΘ, οὕτως τὸ ΖΗΛ τρίγωνον πρὸς τὸ ΗΛΘ τρίγωνον. καί ἐστιν ὡς ἡ ΑΜ πρὸς ΜΓ, οὕτως ἡ ΖΝ πρὸς ΝΘ· καὶ ὡς ἄρα τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΒΕΓ τρίγωνον, οὕτως τὸ ΖΗΛ τρίγωνον πρὸς τὸ ΗΛΘ τρίγωνον, καὶ ἐναλλὰξ, ὡς τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΖΗΛ τρίγωνον, οὕτως τὸ ΒΕΓ τρίγωνον πρὸς τὸ ΗΛΘ τρίγωνον. ὁμοίως δὴ δείξομεν ἐπιζευχθεισῶν τῶν ΒΔ, ΗΚ, ὅτι καὶ ὡς τὸ ΒΕΓ τρίγωνον πρὸς τὸ ΛΗΘ τρίγωνον, οὕτως τὸ ΕΓΔ τρίγωνον πρὸς τὸ ΛΘΚ τρίγωνον. καὶ ἐπεί ἐστιν ὡς τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΖΗΛ τρίγωνον, οὕτως τὸ ΕΒΓ πρὸς τὸ ΛΗΘ, καὶ ἔτι τὸ ΕΓΔ πρὸς τὸ ΛΘΚ, καὶ ὡς ἄρα ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ἔστιν ἄρα ὡς τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΖΗΛ τρίγωνον, οὕτως τὸ ΑΒΓΔΕ πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον. ἀλλὰ τὸ ΑΒΕ τρίγωνον πρὸς τὸ ΖΗΛ τρίγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ ὁμόλογος πλευρὰ πρὸς τὴν ΖΗ ὁμόλογον πλευράν· τὰ γὰρ ὅμοια τρίγωνα ἐν διπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν. καὶ τὸ ΑΒΓΔΕ ἄρα πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ ὁμόλογος πλευρὰ πρὸς τὴν ΖΗ ὁμόλογον πλευράν.
Τὰ ἄρα ὅμοια πολύγωνα εἴς τε ὅμοια τρίγωνα διαιρεῖται καὶ εἰς ἴσα τὸ πλῆθος καὶ ὁμόλογα τοῖς ὅλοις, καὶ τὸ πολύγωνον πρὸς τὸ πολύγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν· [ὅπερ ἔδει δεῖξαι].
Πόρισμα α΄
Ὡσαύτως δὲ καὶ ἐπὶ τῶν [ὁμοίων] τετραπλεύρων δειχθήσεται, ὅτι ἐν διπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν. ἐδείχθη δὲ καὶ ἐπὶ τῶν τριγώνων· ὥστε καὶ καθόλου τὰ ὅμοια εὐθύγραμμα σχήματα πρὸς ἄλληλα ἐν διπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν. ὅπερ ἔδει δεῖξαι.
[Πόρισμα β΄
Καὶ ἐὰν τῶν ΑΒ, ΖΗ τρίτην ἀνάλογον λάβωμεν τὴν Ξ, ἡ ΒΑ πρὸς τὴν Ξ διπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ πρὸς τὴν ΖΗ. ἔχει δὲ καὶ τὸ πολύγωνον πρὸς τὸ πολύγωνον ἢ τὸ τετράπλευρον πρὸς τὸ τετράπλευρον διπλασίονα λόγον ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἡ ΑΒ πρὸς τὴν ΖΗ· ἐδείχθη δὲ τοῦτο καὶ ἐπὶ τῶν τριγώνων· ὥστε καὶ καθόλου φανερόν, ὅτι, ἐὰν τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, ἔσται ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης εἶδος πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον].
Πρότασις κα΄ 21 Βιβλίον VI
Τὰ τῷ αὐτῷ εὐθυγράμμῳ ὅμοια καὶ ἀλλήλοις ἐστὶν ὅμοια.
Ἔστω γὰρ ἑκάτερον τῶν Α, Β εὐθυγράμμων τῷ Γ ὅμοιον· λέγω, ὅτι καὶ τὸ Α τῷ Β ἐστιν ὅμοιον.
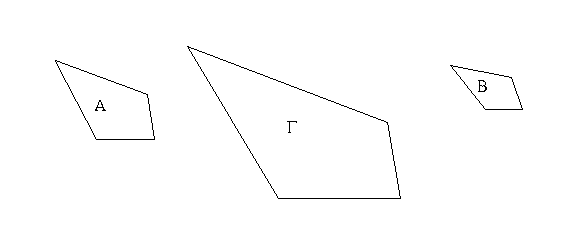
Ἐπεὶ γὰρ ὅμοιόν ἐστι τὸ Α τῷ Γ, ἰσογώνιόν τέ ἐστιν αὐτῷ καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον ἔχει. πάλιν, ἐπεὶ ὅμοιόν ἐστι τὸ Β τῷ Γ, ἰσογώνιόν τέ ἐστιν αὐτῷ καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον ἔχει. ἑκάτερον ἄρα τῶν Α, Β τῷ Γ ἰσογώνιόν τέ ἐστι καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον ἔχει [ὥστε καὶ τὸ Α τῷ Β ἰσογώνιόν τέ ἐστι καὶ τὰς περὶ τὰς ἴσας γωνίας πλευρὰς ἀνάλογον ἔχει]. ὅμοιον ἄρα ἐστὶ τὸ Α τῷ Β· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον VI
Ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, καὶ τὰ ἀπ' αὐτῶν εὐθύγραμμα ὅμοιά τε καὶ ὁμοίως ἀναγεγραμμένα ἀνάλογον ἔσται· κἂν τὰ ἀπ' αὐτῶν εὐθύγραμμα ὅμοιά τε καὶ ὁμοίως ἀναγεγραμμένα ἀνάλογον ᾖ, καὶ αὐταὶ αἱ εὐθεῖαι ἀνάλογον ἔσονται.
Ἔστωσαν τέσσαρες εὐθεῖαι ἀνάλογον αἱ ΑΒ, ΓΔ, ΕΖ, ΗΘ, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ, καὶ ἀναγεγράφθωσαν ἀπὸ μὲν τῶν ΑΒ, ΓΔ ὅμοιά τε καὶ ὁμοίως κείμενα εὐθύγραμμα τὰ ΚΑΒ, ΛΓΔ, ἀπὸ δὲ τῶν ΕΖ, ΗΘ ὅμοιά τε καὶ ὁμοίως κείμενα εὐθύγραμμα τὰ ΜΖ, ΝΘ· λέγω, ὅτι ἐστὶν ὡς τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ.
Εἰλήφθω γὰρ τῶν μὲν ΑΒ, ΓΔ τρίτη ἀνάλογον ἡ Ξ, τῶν δὲ ΕΖ, ΗΘ τρίτη ἀνάλογον ἡ Ο. καὶ ἐπεί ἐστιν ὡς μὲν ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ, ὡς δὲ ἡ ΓΔ πρὸς τὴν Ξ, οὕτως ἡ ΗΘ πρὸς τὴν Ο, δι' ἴσου ἄρα ἐστὶν ὡς ἡ ΑΒ πρὸς τὴν Ξ, οὕτως ἡ ΕΖ πρὸς τὴν Ο. ἀλλ' ὡς μὲν ἡ ΑΒ πρὸς τὴν Ξ, οὕτως [καὶ] τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, ὡς δὲ ἡ ΕΖ πρὸς τὴν Ο, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ· καὶ ὡς ἄρα τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ.
Ἀλλὰ δὴ ἔστω ὡς τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ· λέγω, ὅτι ἐστὶ καὶ ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ. εἰ γὰρ μή ἐστιν, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ, ἔστω ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΠΡ, καὶ ἀναγεγράφθω ἀπὸ τῆς ΠΡ ὁποτέρῳ τῶν ΜΖ, ΝΘ ὅμοιόν τε καὶ ὁμοίως κείμενον εὐθύγραμμον τὸ ΣΡ.
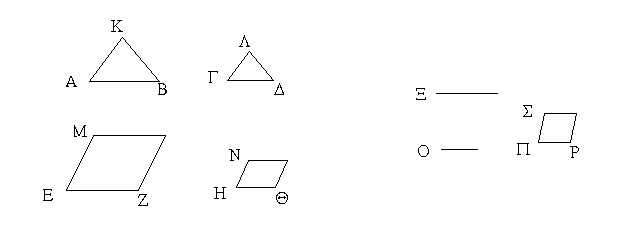
Ἐπεὶ οὖν ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΠΡ, καὶ ἀναγέγραπται ἀπὸ μὲν τῶν ΑΒ, ΓΔ ὅμοιά τε καὶ ὁμοίως κείμενα τὰ ΚΑΒ, ΛΓΔ, ἀπὸ δὲ τῶν ΕΖ, ΠΡ ὅμοιά τε καὶ ὁμοίως κείμενα τὰ ΜΖ, ΣΡ, ἔστιν ἄρα ὡς τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, οὕτως τὸ ΜΖ πρὸς τὸ ΣΡ. ὑπόκειται δὲ καὶ ὡς τὸ ΚΑΒ πρὸς τὸ ΛΓΔ, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ· καὶ ὡς ἄρα τὸ ΜΖ πρὸς τὸ ΣΡ, οὕτως τὸ ΜΖ πρὸς τὸ ΝΘ. τὸ ΜΖ ἄρα πρὸς ἑκάτερον τῶν ΝΘ, ΣΡ τὸν αὐτὸν ἔχει λόγον· ἴσον ἄρα ἐστὶ τὸ ΝΘ τῷ ΣΡ. ἔστι δὲ αὐτῷ καὶ ὅμοιον καὶ ὁμοίως κείμενον· ἴση ἄρα ἡ ΗΘ τῇ ΠΡ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΠΡ, ἴση δὲ ἡ ΠΡ τῇ ΗΘ, ἔστιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ.
Ἐὰν ἄρα τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, καὶ τὰ ἀπ' αὐτῶν εὐθύγραμμα ὅμοιά τε καὶ ὁμοίως ἀναγεγραμμένα ἀνάλογον ἔσται· κἂν τὰ ἀπ' αὐτῶν εὐθύγραμμα ὅμοιά τε καὶ ὁμοίως ἀναγεγραμμένα ἀνάλογον ᾖ, καὶ αὐταὶ αἱ εὐθεῖαι ἀνάλογον ἔσονται· ὅπερ ἔδει δεῖξαι.
Λῆμμα
[Ὅτι δέ, ἐὰν εὐθύγραμμα ἴσα ᾖ καὶ ὅμοια, αἱ ὁμόλογοι αὐτῶν πλευραὶ ἴσαι ἀλλήλαις εἰσίν, δείξομεν οὕτως.
Ἔστω ἴσα καὶ ὅμοια εὐθύγραμμα τὰ ΝΘ, ΣΡ, καὶ ἔστω ὡς ἡ ΘΗ πρὸς τὴν ΗΝ, οὕτως ἡ ΡΠ πρὸς τὴν ΠΣ· λέγω, ὅτι ἴση ἐστὶν ἡ ΡΠ τῇ ΘΗ.
Εἰ γὰρ ἄνισοί εἰσιν, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ΡΠ τῆς ΘΗ. καὶ ἐπεί ἐστιν ὡς ἡ ΡΠ πρὸς ΠΣ, οὕτως ἡ ΘΗ πρὸς τὴν ΗΝ, καὶ ἐναλλάξ, ὡς ἡ ΡΠ πρὸς τὴν ΘΗ, οὕτως ἡ ΠΣ πρὸς τὴν ΗΝ, μείζων δὲ ἡ ΠΡ τῆς ΘΗ, μείζων ἄρα καὶ ἡ ΠΣ τῆς ΗΝ· ὥστε καὶ τὸ ΡΣ μεῖζόν ἐστι τοῦ ΘΝ. ἀλλὰ καὶ ἴσον· ὅπερ ἀδύνατον. οὐκ ἄρα ἄνισός ἐστιν ἡ ΠΡ τῇ ΗΘ· ἴση ἄρα· ὅπερ ἔδει δεῖξαι.]
Πρότασις κγ΄ 23 Βιβλίον VI
Τὰ ἰσογώνια παραλληλόγραμμα πρὸς ἄλληλα λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν.
Ἔστω ἰσογώνια παραλληλόγραμμα τὰ ΑΓ, ΓΖ ἴσην ἔχοντα τὴν ὑπὸ ΒΓΔ γωνίαν τῇ ὑπὸ ΕΓΗ· λέγω, ὅτι τὸ ΑΓ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν.
Κείσθω γὰρ ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΒΓ τῇ ΓΗ· ἐπ᾿ εὐθείας ἄρα ἐστὶ καὶ ἡ ΔΓ τῇ ΓΕ. καὶ συμπεπληρώσθω τὸ ΔΗ παραλληλόγραμμον, καὶ ἐκκείσθω τις εὐθεῖα ἡ Κ, καὶ γεγονέτω ὡς μὲν ἡ ΒΓ πρὸς τὴν ΓΗ, οὕτως ἡ Κ πρὸς τὴν Λ, ὡς δὲ ἡ ΔΓ πρὸς τὴν ΓΕ, οὕτως ἡ Λ πρὸς τὴν Μ.

Οἱ ἄρα λόγοι τῆς τε Κ πρὸς τὴν Λ καὶ τῆς Λ πρὸς τὴν Μ οἱ αὐτοί εἰσι τοῖς λόγοις τῶν πλευρῶν, τῆς τε ΒΓ πρὸς τὴν ΓΗ καὶ τῆς ΔΓ πρὸς τὴν ΓΕ. ἀλλ' ὁ τῆς Κ πρὸς Μ λόγος σύγκειται ἔκ τε τοῦ τῆς Κ πρὸς Λ λόγου καὶ τοῦ τῆς Λ πρὸς Μ· ὥστε καὶ ἡ Κ πρὸς τὴν Μ λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν. καὶ ἐπεί ἐστιν ὡς ἡ ΒΓ πρὸς τὴν ΓΗ, οὕτως τὸ ΑΓ παραλληλόγραμμον πρὸς τὸ ΓΘ, ἀλλ' ὡς ἡ ΒΓ πρὸς τὴν ΓΗ, οὕτως ἡ Κ πρὸς τὴν Λ, καὶ ὡς ἄρα ἡ Κ πρὸς τὴν Λ, οὕτως τὸ ΑΓ πρὸς τὸ ΓΘ. πάλιν, ἐπεί ἐστιν ὡς ἡ ΔΓ πρὸς τὴν ΓΕ, οὕτως τὸ ΓΘ παραλληλόγραμμον πρὸς τὸ ΓΖ, ἀλλ' ὡς ἡ ΔΓ πρὸς τὴν ΓΕ, οὕτως ἡ Λ πρὸς τὴν Μ, καὶ ὡς ἄρα ἡ Λ πρὸς τὴν Μ, οὕτως τὸ ΓΘ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον. ἐπεὶ οὖν ἐδείχθη, ὡς μὲν ἡ Κ πρὸς τὴν Λ, οὕτως τὸ ΑΓ παραλληλόγραμμον πρὸς τὸ ΓΘ παραλληλόγραμμον, ὡς δὲ ἡ Λ πρὸς τὴν Μ, οὕτως τὸ ΓΘ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον, δι' ἴσου ἄρα ἐστὶν ὡς ἡ Κ πρὸς τὴν Μ, οὕτως τὸ ΑΓ πρὸς τὸ ΓΖ παραλληλόγραμμον. ἡ δὲ Κ πρὸς τὴν Μ λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν· καὶ τὸ ΑΓ ἄρα πρὸς τὸ ΓΖ λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν.
Τὰ ἄρα ἰσογώνια παραλληλόγραμμα πρὸς ἄλληλα λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον VI
Παντὸς παραλληλογράμμου τὰ περὶ τὴν διάμετρον παραλληλόγραμμα ὅμοιά ἐστι τῷ τε ὅλῳ καὶ ἀλλήλοις.
Ἔστω παραλληλόγραμμον τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ, περὶ δὲ τὴν ΑΓ παραλληλόγραμμα ἔστω τὰ ΕΗ, ΘΚ· λέγω, ὅτι ἑκάτερον τῶν ΕΗ, ΘΚ παραλληλογράμμων ὅμοιόν ἐστι ὅλῳ τῷ ΑΒΓΔ καὶ ἀλλήλοις.
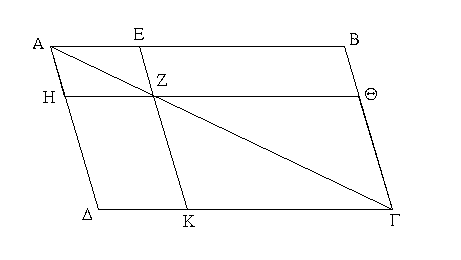
Ἐπεὶ γὰρ τριγώνου τοῦ ΑΒΓ παρὰ μίαν τῶν πλευρῶν τὴν ΒΓ ἦκται ἡ ΕΖ, ἀνάλογόν ἐστιν ὡς ἡ ΒΕ πρὸς τὴν ΕΑ, οὕτως, ἡ ΓΖ πρὸς τὴν ΖΑ. πάλιν, ἐπεὶ τριγώνου τοῦ ΑΓΔ παρὰ μίαν τὴν ΓΔ ἦκται ἡ ΖΗ, ἀνάλογόν ἐστιν ὡς ἡ ΓΖ πρὸς τὴν ΖΑ, οὕτως ἡ ΔΗ πρὸς τὴν ΗΑ. ἀλλ' ὡς ἡ ΓΖ πρὸς τὴν ΖΑ, οὕτως ἐδείχθη καὶ ἡ ΒΕ πρὸς τὴν ΕΑ· καὶ ὡς ἄρα ἡ ΒΕ πρὸς τὴν ΕΑ, οὕτως ἡ ΔΗ πρὸς τὴν ΗΑ, καὶ συνθέντι ἄρα ὡς ἡ ΒΑ πρὸς ΑΕ, οὕτως ἡ ΔΑ πρὸς ΑΗ, καὶ ἐναλλὰξ ὡς ἡ ΒΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΕΑ πρὸς τὴν ΑΗ. τῶν ἄρα ΑΒΓΔ, ΕΗ παραλληλογράμμων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὴν κοινὴν γωνίαν τὴν ὑπὸ ΒΑΔ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΗΖ τῇ ΔΓ, ἴση ἐστὶν ἡ μὲν ὑπὸ ΑΖΗ γωνία τῇ ὑπὸ ΔΓΑ· καὶ κοινὴ τῶν δύο τριγώνων τῶν ΑΔΓ, ΑΗΖ ἡ ὑπὸ ΔΑΓ γωνία· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΔΓ τρίγωνον τῷ ΑΗΖ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΑΓΒ τρίγωνον ἰσογώνιόν ἐστι τῷ ΑΖΕ τριγώνῳ, καὶ ὅλον τὸ ΑΒΓΔ παραλληλόγραμμον τῷ ΕΗ παραλληλογράμμῳ ἰσογώνιόν ἐστιν. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΑΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΑΗ πρὸς τὴν ΗΖ, ὡς δὲ ἡ ΔΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΑ, ὡς δὲ ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως ἡ ΑΖ πρὸς τὴν ΖΕ, καὶ ἔτι ὡς ἡ ΓΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΖΕ πρὸς τὴν ΕΑ. καὶ ἐπεὶ ἐδείχθη ὡς μὲν ἡ ΔΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΑ, ὡς δὲ ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως ἡ ΑΖ πρὸς τὴν ΖΕ, δι' ἴσου ἄρα ἐστὶν ὡς ἡ ΔΓ πρὸς τὴν ΓΒ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΕ. τῶν ἄρα ΑΒΓΔ, ΕΗ παραλληλογράμμων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· ὅμοιον ἄρα ἐστὶ τὸ ΑΒΓΔ παραλληλόγραμμον τῷ ΕΗ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ τὸ ΑΒΓΔ παραλληλόγραμμον καὶ τῷ ΚΘ παραλληλογράμμῳ ὅμοιόν ἐστιν· ἑκάτερον ἄρα τῶν ΕΗ, ΘΚ παραλληλογράμμων τῷ ΑΒΓΔ [παραλληλογράμμῳ] ὅμοιόν ἐστιν. τὰ δὲ τῷ αὐτῷ εὐθυγράμμῳ ὅμοια καὶ ἀλλήλοις ἐστὶν ὅμοια· καὶ τὸ ΕΗ ἄρα παραλληλόγραμμον τῷ ΘΚ παραλληλογράμμῳ ὅμοιόν ἐστιν.
Παντὸς ἄρα παραλληλογράμμου τὰ περὶ τὴν διάμετρον παραλληλόγραμμα ὅμοιά ἐστι τῷ τε ὅλῳ καὶ ἀλλήλοις· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον VI
Τῷ δοθέντι εὐθυγράμμῳ ὅμοιον καὶ ἄλλῳ τῷ δοθέντι ἴσον τὸ αὐτὸ συστήσασθαι.
Ἔστω τὸ μὲν δοθὲν εὐθύγραμμον, ᾧ δεῖ ὅμοιον συστήσασθαι, τὸ ΑΒΓ, ᾧ δὲ δεῖ ἴσον, τὸ Δ· δεῖ δὴ τῷ μὲν ΑΒΓ ὅμοιον, τῷ δὲ Δ ἴσον τὸ αὐτὸ συστήσασθαι.
Παραβεβλήσθω γὰρ παρὰ μὲν τὴν ΒΓ τῷ ΑΒΓ τριγώνῳ ἴσον παραλληλόγραμμον τὸ ΒΕ, παρὰ δὲ τὴν ΓΕ τῷ Δ ἴσον παραλληλόγραμμον τὸ ΓΜ ἐν γωνίᾳ τῇ ὑπὸ ΖΓΕ, ἥ ἐστιν ἴση τῇ ὑπὸ ΓΒΛ. ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ μὲν ΒΓ τῇ ΓΖ, ἡ δὲ ΛΕ τῇ ΕΜ. καὶ εἰλήφθω τῶν ΒΓ, ΓΖ μέση ἀνάλογον ἡ ΗΘ, καὶ ἀναγεγράφθω ἀπὸ τῆς ΗΘ τῷ ΑΒΓ ὅμοιόν τε καὶ ὁμοίως κείμενον τὸ ΚΗΘ.
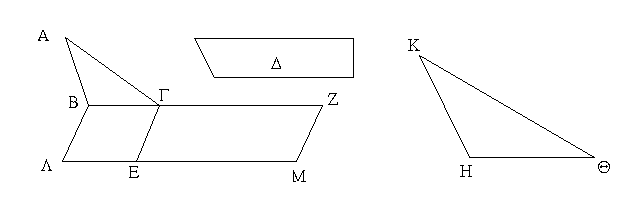
Καὶ ἐπεί ἐστιν ὡς ἡ ΒΓ πρὸς τὴν ΗΘ, οὕτως ἡ ΗΘ πρὸς τὴν ΓΖ, ἐὰν δὲ τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, ἔστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης εἶδος πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον, ἔστιν ἄρα ὡς ἡ ΒΓ πρὸς τὴν ΓΖ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΚΗΘ τρίγωνον. ἀλλὰ καὶ ὡς ἡ ΒΓ πρὸς τὴν ΓΖ, οὕτως τὸ ΒΕ παραλληλόγραμμον πρὸς τὸ ΕΖ παραλληλόγραμμον. καὶ ὡς ἄρα τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΚΗΘ τρίγωνον, οὕτως τὸ ΒΕ παραλληλόγραμμον πρὸς τὸ ΕΖ παραλληλόγραμμον· ἐναλλὰξ ἄρα ὡς τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΒΕ παραλληλόγραμμον, οὕτως τὸ ΚΗΘ τρίγωνον πρὸς τὸ ΕΖ παραλληλόγραμμον. ἴσον δὲ τὸ ΑΒΓ τρίγωνον τῷ ΒΕ παραλληλογράμμῳ· ἴσον ἄρα καὶ τὸ ΚΗΘ τρίγωνον τῷ ΕΖ παραλληλογράμμῳ. ἀλλὰ τὸ ΕΖ παραλληλόγραμμον τῷ Δ ἐστιν ἴσον· καὶ τὸ ΚΗΘ ἄρα τῷ Δ ἐστιν ἴσον. ἔστι δὲ τὸ ΚΗΘ καὶ τῷ ΑΒΓ ὅμοιον.
Τῷ ἄρα δοθέντι εὐθυγράμμῳ τῷ ΑΒΓ ὅμοιον καὶ ἄλλῳ τῷ δοθέντι τῷ Δ ἴσον τὸ αὐτὸ συνέσταται τὸ ΚΗΘ· ὅπερ ἔδει ποιῆσαι.
Πρότασις κς΄ 26 Βιβλίον VI
Ἐὰν ἀπὸ παραλληλογράμμου παραλληλόγραμμον ἀφαιρεθῇ ὅμοιόν τε τῷ ὅλῳ καὶ ὁμοίως κείμενον κοινὴν γωνίαν ἔχον αὐτῷ, περὶ τὴν αὐτὴν διάμετρόν ἐστι τῷ ὅλῳ.
Ἀπὸ γὰρ παραλληλογράμμου τοῦ ΑΒΓΔ παραλληλόγραμμον ἀφῃρήσθω τὸ ΑΖ ὅμοιον τῷ ΑΒΓΔ καὶ ὁμοίως κείμενον κοινὴν γωνίαν ἔχον αὐτῷ τὴν ὑπὸ ΔΑΒ· λέγω, ὅτι περὶ τὴν αὐτὴν διάμετρόν ἐστι τὸ ΑΒΓΔ τῷ ΑΖ.
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἔστω [αὐτῶν] διάμετρος ἡ ΑΘΓ, καὶ ἐκβληθεῖσα ἡ ΗΖ διήχθω ἐπὶ τὸ Θ, καὶ ἤχθω διὰ τοῦ Θ ὁποτέρᾳ τῶν ΑΔ, ΒΓ παράλληλος ἡ ΘΚ.
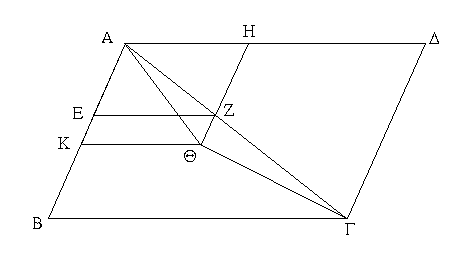
Ἐπεὶ οὖν περὶ τὴν αὐτὴν διάμετρόν ἐστι τὸ ΑΒΓΔ τῷ ΚΗ, ἔστιν ἄρα ὡς ἡ ΔΑ πρὸς τὴν ΑΒ, οὕτως ἡ ΗΑ πρὸς τὴν ΑΚ. ἔστι δὲ καὶ διὰ τὴν ὁμοιότητα τῶν ΑΒΓΔ, ΕΗ καὶ ὡς ἡ ΔΑ πρὸς τὴν ΑΒ, οὕτως ἡ ΗΑ πρὸς τὴν ΑΕ· καὶ ὡς ἄρα ἡ ΗΑ πρὸς τὴν ΑΚ, οὕτως ἡ ΗΑ πρὸς τὴν ΑΕ. ἡ ΗΑ ἄρα πρὸς ἑκατέραν τῶν ΑΚ, ΑΕ τὸν αὐτὸν ἔχει λόγον. ἴση ἄρα ἐστὶν ἡ ΑΕ τῇ ΑΚ ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οὔκ ἐστι περὶ τὴν αὐτὴν διάμετρον τὸ ΑΒΓΔ τῷ ΑΖ· περὶ τὴν αὐτὴν ἄρα ἐστὶ διάμετρον τὸ ΑΒΓΔ παραλληλόγραμμον τῷ ΑΖ παραλληλογράμμῳ.
Ἐὰν ἄρα ἀπὸ παραλληλογράμμου παραλληλόγραμμον ἀφαιρεθῇ ὅμοιόν τε τῷ ὅλῳ καὶ ὁμοίως κείμενον κοινὴν γωνίαν ἔχον αὐτῷ, περὶ τὴν αὐτὴν διάμετρόν ἐστι τῷ ὅλῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον VI
Πάντων τῶν παρὰ τὴν αὐτὴν εὐθεῖαν παραβαλλομένων παραλληλογράμμων καὶ ἐλλειπόντων εἴδεσι παραλληλογράμμοις ὁμοίοις τε καὶ ὁμοίως κειμένοις τῷ ἀπὸ τῆς ἡμισείας ἀναγραφομένῳ μέγιστόν ἐστι τὸ ἀπὸ τῆς ἡμισείας παραβαλλόμενον [παραλληλόγραμμον] ὅμοιον ὂν τῷ ἐλλείμματι.
Ἔστω εὐθεῖα ἡ ΑΒ καὶ τετμήσθω δίχα κατὰ τὸ Γ, καὶ παραβεβλήσθω παρὰ τὴν ΑΒ εὐθεῖαν τὸ ΑΔ παραλληλόγραμμον ἐλλεῖπον εἴδει παραλληλογράμμῳ τῷ ΔΒ ἀναγραφέντι ἀπὸ τῆς ἡμισείας τῆς ΑΒ, τουτέστι τῆς ΓΒ· λέγω, ὅτι πάντων τῶν παρὰ τὴν ΑΒ παραβαλλομένων παραλληλογράμμων καὶ ἐλλειπόντων εἴδεσι [παραλληλογράμμοις] ὁμοίοις τε καὶ ὁμοίως κειμένοις τῷ ΔΒ μέγιστόν ἐστι τὸ ΑΔ. παραβεβλήσθω γὰρ παρὰ τὴν ΑΒ εὐθεῖαν τὸ ΑΖ παραλληλόγραμμον ἐλλεῖπον εἴδει παραλληλογράμμῳ τῷ ΖΒ ὁμοίῳ τε καὶ ὁμοίως κειμένῳ τῷ ΔΒ· λέγω, ὅτι μεῖζόν ἐστι τὸ ΑΔ τοῦ ΑΖ.
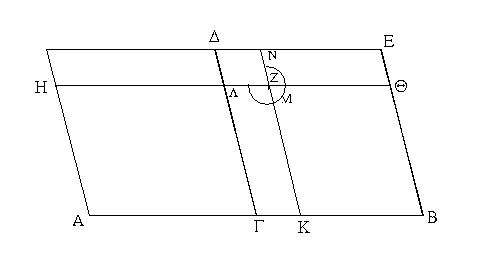
Ἐπεὶ γὰρ ὅμοιόν ἐστι τὸ ΔΒ παραλληλόγραμμον τῷ ΖΒ παραλληλογράμμῳ, περὶ τὴν αὐτήν εἰσι διάμετρον. ἤχθω αὐτῶν διάμετρος ἡ ΔΒ, καὶ καταγεγράφθω τὸ σχῆμα.
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΓΖ τῷ ΖΕ, κοινὸν δὲ τὸ ΖΒ, ὅλον ἄρα τὸ ΓΘ ὅλῳ τῷ ΚΕ ἐστιν ἴσον. ἀλλὰ τὸ ΓΘ τῷ ΓΗ ἐστιν ἴσον, ἐπεὶ καὶ ἡ ΑΓ τῇ ΓΒ. καὶ τὸ ΗΓ ἄρα τῷ ΕΚ ἐστιν ἴσον. κοινὸν προσκείσθω τὸ ΓΖ· ὅλον ἄρα τὸ ΑΖ τῷ ΛΜΝ γνώμονί ἐστιν ἴσον· ὥστε τὸ ΔΒ παραλληλόγραμμον, τουτέστι τὸ ΑΔ, τοῦ ΑΖ παραλληλογράμμου μεῖζόν ἐστιν.
Πάντων ἄρα τῶν παρὰ τὴν αὐτὴν εὐθεῖαν παραβαλλομένων παραλληλογράμμων καὶ ἐλλειπόντων εἴδεσι παραλληλογράμμοις ὁμοίοις τε καὶ ὁμοίως κειμένοις τῷ ἀπὸ τῆς ἡμισείας ἀναγραφομένῳ μέγιστόν ἐστι τὸ ἀπὸ τῆς ἡμισείας παραβληθέν· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον VI
Παρὰ τὴν δοθεῖσαν εὐθεῖαν τῷ δοθέντι εὐθυγράμμῳ ἴσον παραλληλόγραμμον παραβαλεῖν ἐλλεῖπον εἴδει παραλληλογράμμῳ ὁμοίῳ τῷ δοθέντι· δεῖ δὲ τὸ διδόμενον εὐθύγραμμον [ᾧ δεῖ ἴσον παραβαλεῖν] μὴ μεῖζον εἶναι τοῦ ἀπὸ τῆς ἡμισείας ἀναγραφομένου ὁμοίου τῷ ἐλλείμματι [τοῦ τε ἀπὸ τῆς ἡμισείας καὶ ᾧ δεῖ ὅμοιον ἐλλείπειν].
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν εὐθύγραμμον, ᾧ δεῖ ἴσον παρὰ τὴν ΑΒ παραβαλεῖν, τὸ Γ μὴ μεῖζον [ὂν] τοῦ ἀπὸ τῆς ἡμισείας τῆς ΑΒ ἀναγραφομένου ὁμοίου τῷ ἐλλείμματι, ᾧ δὲ δεῖ ὅμοιον ἐλλείπειν, τὸ Δ· δεῖ δὴ παρὰ τὴν δοθεῖσαν εὐθεῖαν τὴν ΑΒ τῷ δοθέντι εὐθυγράμμῳ τῷ Γ ἴσον παραλληλόγραμμον παραβαλεῖν ἐλλεῖπον εἴδει παραλληλογράμμῳ ὁμοίῳ ὄντι τῷ Δ.
Τετμήσθω ἡ ΑΒ δίχα κατὰ τὸ Ε σημεῖον, καὶ ἀναγεγράφθω ἀπὸ τῆς ΕΒ τῷ Δ ὅμοιον καὶ ὁμοίως κείμενον τὸ ΕΒΖΗ, καὶ συμπεπληρώσθω τὸ ΑΗ παραλληλόγραμμον.
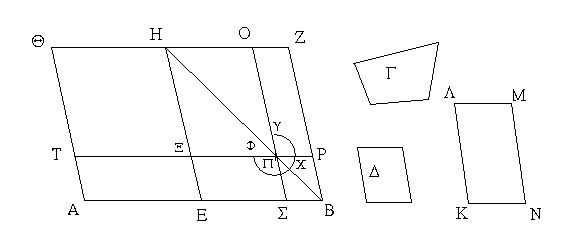
Εἰ μὲν οὖν ἴσον ἐστὶ τὸ ΑΗ τῷ Γ, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν· παραβέβληται γὰρ παρὰ τὴν δοθεῖσαν εὐθεῖαν τὴν ΑΒ τῷ δοθέντι εὐθυγράμμῳ τῷ Γ ἴσον παραλληλόγραμμον τὸ ΑΗ ἐλλεῖπον εἴδει παραλληλογράμμῳ τῷ ΗΒ ὁμοίῳ ὄντι τῷ Δ. εἰ δὲ οὔ, μεῖζον ἔστω τὸ ΘΕ τοῦ Γ. ἴσον δὲ τὸ ΘΕ τῷ ΗΒ· μεῖζον ἄρα καὶ τὸ ΗΒ τοῦ Γ. ᾧ δὴ μεῖζόν ἐστι τὸ ΗΒ τοῦ Γ, ταύτῃ τῇ ὑπεροχῇ ἴσον, τῷ δὲ Δ ὅμοιον καὶ ὁμοίως κείμενον τὸ αὐτὸ συνεστάτω τὸ ΚΛΜΝ. ἀλλὰ τὸ Δ τῷ ΗΒ [ἐστιν] ὅμοιον· καὶ τὸ ΚΜ ἄρα τῷ ΗΒ ἐστιν ὅμοιον. ἔστω οὖν ὁμόλογος ἡ μὲν ΚΛ τῇ ΗΕ, ἡ δὲ ΛΜ τῇ ΗΖ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΗΒ τοῖς Γ, ΚΜ, μεῖζον ἄρα ἐστὶ τὸ ΗΒ τοῦ ΚΜ· μείζων ἄρα ἐστὶ καὶ ἡ μὲν ΗΕ τῆς ΚΛ, ἡ δὲ ΗΖ τῆς ΛΜ. κείσθω τῇ μὲν ΚΛ ἴση ἡ ΗΞ, τῇ δὲ ΛΜ ἴση ἡ ΗΟ, καὶ συμπεπληρώσθω τὸ ΞΗΟΠ παραλληλόγραμμον· ἴσον ἄρα καὶ ὅμοιόν ἐστι [τὸ ΗΠ] τῷ ΚΜ [ἀλλὰ τὸ ΚΜ τῷ ΗΒ ὅμοιόν ἐστιν]. καὶ τὸ ΗΠ ἄρα τῷ ΗΒ ὅμοιόν ἐστιν· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὸ ΗΠ τῷ ΗΒ. ἔστω αὐτῶν διάμετρος ἡ ΗΠΒ, καὶ καταγεγράφθω τὸ σχῆμα.
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΒΗ τοῖς Γ, ΚΜ, ὧν τὸ ΗΠ τῷ ΚΜ ἐστιν ἴσον, λοιπὸς ἄρα ὁ ΥΧΦ γνώμων λοιπῷ τῷ Γ ἴσος ἐστίν. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΟΡ τῷ ΞΣ, κοινὸν προσκείσθω τὸ ΠΒ· ὅλον ἄρα τὸ ΟΒ ὅλῳ τῷ ΞΒ ἴσον ἐστίν. ἀλλὰ τὸ ΞΒ τῷ ΤΕ ἐστιν ἴσον, ἐπεὶ καὶ πλευρὰ ἡ ΑΕ πλευρᾷ τῇ ΕΒ ἐστιν ἴση· καὶ τὸ ΤΕ ἄρα τῷ ΟΒ ἐστιν ἴσον. κοινὸν προσκείσθω τὸ ΞΣ· ὅλον ἄρα τὸ ΤΣ ὅλῳ τῷ ΦΧΥ γνώμονί ἐστιν ἴσον. ἀλλ' ὁ ΦΧΥ γνώμων τῷ Γ ἐδείχθη ἴσος· καὶ τὸ ΤΣ ἄρα τῷ Γ ἐστιν ἴσον.
Παρὰ τὴν δοθεῖσαν ἄρα εὐθεῖαν τὴν ΑΒ τῷ δοθέντι εὐθυγράμμῳ τῷ Γ ἴσον παραλληλόγραμμον παραβέβληται τὸ ΣΤ ἐλλεῖπον εἴδει παραλληλογράμμῳ τῷ ΠΒ ὁμοίῳ ὄντι τῷ Δ [ἐπειδήπερ τὸ ΠΒ τῷ ΗΠ ὅμοιόν ἐστιν]· ὅπερ ἔδει ποιῆσαι.
Πρότασις κθ΄ 29 Βιβλίον VI
Παρὰ τὴν δοθεῖσαν εὐθεῖαν τῷ δοθέντι εὐθυγράμμῳ ἴσον παραλληλόγραμμον παραβαλεῖν ὑπερβάλλον εἴδει παραλληλογράμμῳ ὁμοίῳ τῷ δοθέντι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν εὐθύγραμμον, ᾧ δεῖ ἴσον παρὰ τὴν ΑΒ παραβαλεῖν, τὸ Γ, ᾧ δὲ δεῖ ὅμοιον ὑπερβάλλειν, τὸ Δ· δεῖ δὴ παρὰ τὴν ΑΒ εὐθεῖαν τῷ Γ εὐθυγράμμῳ ἴσον παραλληλόγραμμον παραβαλεῖν ὑπερβάλλον εἴδει παραλληλογράμμῳ ὁμοίῳ τῷ Δ.
Τετμήσθω ἡ ΑΒ δίχα κατὰ τὸ Ε, καὶ ἀναγεγράφθω ἀπὸ τῆς ΕΒ τῷ Δ ὅμοιον καὶ ὁμοίως κείμενον παραλληλόγραμμον τὸ ΒΖ, καὶ συναμφοτέροις μὲν τοῖς ΒΖ, Γ ἴσον, τῷ δὲ Δ ὅμοιον καὶ ὁμοίως κείμενον τὸ αὐτὸ συνεστάτω τὸ ΗΘ. ὁμόλογος δὲ ἔστω ἡ μὲν ΚΘ τῇ ΖΛ, ἡ δὲ ΚΗ τῇ ΖΕ. καὶ ἐπεὶ μεῖζόν ἐστι τὸ ΗΘ τοῦ ΖΒ, μείζων ἄρα ἐστὶ καὶ ἡ μὲν ΚΘ τῆς ΖΛ, ἡ δὲ ΚΗ τῆς ΖΕ. ἐκβεβλήσθωσαν αἱ ΖΛ, ΖΕ, καὶ τῇ μὲν ΚΘ ἴση ἔστω ἡ ΖΛΜ, τῇ δὲ ΚΗ ἴση ἡ ΖΕΝ, καὶ συμπεπληρώσθω τὸ ΜΝ· τὸ ΜΝ ἄρα τῷ ΗΘ ἴσον τέ ἐστι καὶ ὅμοιον. ἀλλὰ τὸ ΗΘ τῷ ΕΛ ἐστιν ὅμοιον· καὶ τὸ ΜΝ ἄρα τῷ ΕΛ ὅμοιόν ἐστιν· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὸ ΕΛ τῷ ΜΝ. ἤχθω αὐτῶν διάμετρος ἡ ΖΞ, καὶ καταγεγράφθω τὸ σχῆμα.
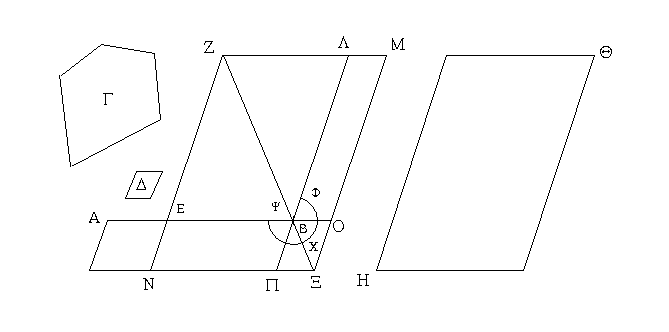
Ἐπεὶ ἴσον ἐστὶ τὸ ΗΘ τοῖς ΕΛ, Γ, ἀλλὰ τὸ ΗΘ τῷ ΜΝ ἴσον ἐστίν, καὶ τὸ ΜΝ ἄρα τοῖς ΕΛ, Γ ἴσον ἐστίν. κοινὸν ἀφῃρήσθω τὸ ΕΛ· λοιπὸς ἄρα ὁ ΨΧΦ γνώμων τῷ Γ ἐστιν ἴσος. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΕ τῇ ΕΒ, ἴσον ἐστὶ καὶ τὸ ΑΝ τῷ ΝΒ, τουτέστι τῷ ΛΟ. κοινὸν προσκείσθω τὸ ΕΞ· ὅλον ἄρα τὸ ΑΞ ἴσον ἐστὶ τῷ ΦΧΨ γνώμονι. ἀλλὰ ὁ ΦΧΨ γνώμων τῷ Γ ἴσος ἐστίν· καὶ τὸ ΑΞ ἄρα τῷ Γ ἴσον ἐστίν.
Παρὰ τὴν δοθεῖσαν ἄρα εὐθεῖαν τὴν ΑΒ τῷ δοθέντι εὐθυγράμμῳ τῷ Γ ἴσον παραλληλόγραμμον παραβέβληται τὸ ΑΞ ὑπερβάλλον εἴδει παραλληλογράμμῳ τῷ ΠΟ ὁμοίῳ ὄντι τῷ Δ, ἐπεὶ καὶ τῷ ΕΛ ἐστιν ὅμοιον τὸ ΟΠ· ὅπερ ἔδει ποιῆσαι.
Πρότασις λ΄ 30 Βιβλίον VI
Τὴν δοθεῖσαν εὐθεῖαν πεπερασμένην ἄκρον καὶ μέσον λόγον τεμεῖν.
Ἔστω ἡ δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ· δεῖ δὴ τὴν ΑΒ εὐθεῖαν ἄκρον καὶ μέσον λόγον τεμεῖν.
Ἀναγεγράφθω ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΒΓ, καὶ παραβεβλήσθω παρὰ τὴν ΑΓ τῇ ΒΓ ἴσον παραλληλόγραμμον τὸ ΓΔ ὑπερβάλλον εἴδει τῷ ΑΔ ὁμοίῳ τῷ ΒΓ.
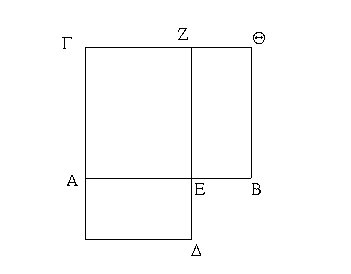
Τετράγωνον δέ ἐστι τὸ ΒΓ· τετράγωνον ἄρα ἐστὶ καὶ τὸ ΑΔ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΒΓ τῷ ΓΔ, κοινὸν ἀφῃρήσθω τὸ ΓΕ· λοιπὸν ἄρα τὸ ΒΖ λοιπῷ τῷ ΑΔ ἐστιν ἴσον. ἔστι δὲ αὐτῷ καὶ ἰσογώνιον· τῶν ΒΖ, ΑΔ ἄρα ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· ἔστιν ἄρα ὡς ἡ ΖΕ πρὸς τὴν ΕΔ, οὕτως ἡ ΑΕ πρὸς τὴν ΕΒ. ἴση δὲ ἡ μὲν ΖΕ τῇ ΑΒ, ἡ δὲ ΕΔ τῇ ΑΕ. ἔστιν ἄρα ὡς ἡ ΒΑ πρὸς τὴν ΑΕ, οὕτως ἡ ΑΕ πρὸς τὴν ΕΒ. μείζων δὲ ἡ ΑΒ τῆς ΑΕ· μείζων ἄρα καὶ ἡ ΑΕ τῆς ΕΒ.
Ἡ ἄρα ΑΒ εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Ε, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστι τὸ ΑΕ· ὅπερ ἔδει ποιῆσαι.
Πρότασις λα΄ 31 Βιβλίον VI
Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς εἶδος ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν εἴδεσι τοῖς ὁμοίοις τε καὶ ὁμοίως ἀναγραφομένοις.
Ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν ὑπὸ ΒΑΓ γωνίαν· λέγω, ὅτι τὸ ἀπὸ τῆς ΒΓ εἶδος ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ εἴδεσι τοῖς ὁμοίοις τε καὶ ὁμοίως ἀναγραφομένοις.
Ἤχθω κάθετος ἡ ΑΔ.
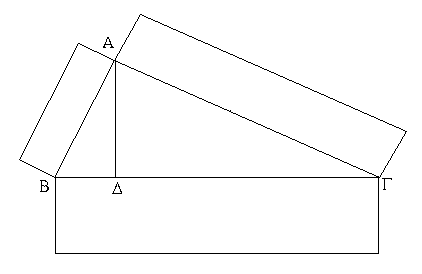
Ἐπεὶ οὖν ἐν ὀρθογωνίῳ τριγώνῳ τῷ ΑΒΓ ἀπὸ τῆς πρὸς τῷ Α ὀρθῆς γωνίας ἐπὶ τὴν ΒΓ βάσιν κάθετος ἦκται ἡ ΑΔ, τὰ ΑΒΔ, ΑΔΓ πρὸς τῇ καθέτῳ τρίγωνα ὅμοιά ἐστι τῷ τε ὅλῳ τῷ ΑΒΓ καὶ ἀλλήλοις. καὶ ἐπεὶ ὅμοιόν ἐστι τὸ ΑΒΓ τῷ ΑΒΔ, ἔστιν ἄρα ὡς ἡ ΓΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΑΒ πρὸς τὴν ΒΔ. καὶ ἐπεὶ τρεῖς εὐθεῖαι ἀνάλογόν εἰσιν, ἔστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης εἶδος πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον. ὡς ἄρα ἡ ΓΒ πρὸς τὴν ΒΔ, οὕτως τὸ ἀπὸ τῆς ΓΒ εἶδος πρὸς τὸ ἀπὸ τῆς ΒΑ τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον. διὰ τὰ αὐτὰ δὴ καὶ ὡς ἡ ΒΓ πρὸς τὴν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΒΓ εἶδος πρὸς τὸ ἀπὸ τῆς ΓΑ. ὥστε καὶ ὡς ἡ ΒΓ πρὸς τὰς ΒΔ, ΔΓ, οὕτως τὸ ἀπὸ τῆς ΒΓ εἶδος πρὸς τὰ ἀπὸ τῶν ΒΑ, ΑΓ τὰ ὅμοια καὶ ὁμοίως ἀναγραφόμενα. ἴση δὲ ἡ ΒΓ ταῖς ΒΔ, ΔΓ· ἴσον ἄρα καὶ τὸ ἀπὸ τῆς ΒΓ εἶδος τοῖς ἀπὸ τῶν ΒΑ, ΑΓ εἴδεσι τοῖς ὁμοίοις τε καὶ ὁμοίως ἀναγραφομένοις.
Ἐν ἄρα τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς εἶδος ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν εἴδεσι τοῖς ὁμοίοις τε καὶ ὁμοίως ἀναγραφομένοις· ὅπερ ἔδει δεῖξαι.
Πρότασις λβ΄ 32 Βιβλίον VI
Ἐὰν δύο τρίγωνα συντεθῇ κατὰ μίαν γωνίαν τὰς δύο πλευρὰς ταῖς δυσὶ πλευραῖς ἀνάλογον ἔχοντα ὥστε τὰς ὁμολόγους αὐτῶν πλευρὰς καὶ παραλλήλους εἶναι, αἱ λοιπαὶ τῶν τριγώνων πλευραὶ ἐπ᾿ εὐθείας ἔσονται.
Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΓΕ τὰς δύο πλευρὰς τὰς ΒΑ, ΑΓ ταῖς δυσὶ πλευραῖς ταῖς ΔΓ, ΔΕ ἀνάλογον ἔχοντα, ὡς μὲν τὴν ΑΒ πρὸς τὴν ΑΓ, οὕτως τὴν ΔΓ πρὸς τὴν ΔΕ, παράλληλον δὲ τὴν μὲν ΑΒ τῇ ΔΓ, τὴν δὲ ΑΓ τῇ ΔΕ· λέγω, ὅτι ἐπ᾿ εὐθείας ἐστὶν ἡ ΒΓ τῇ ΓΕ.
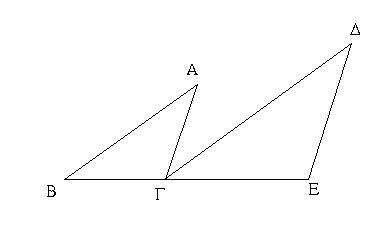
Ἐπεὶ γὰρ παράλληλός ἐστιν ἡ ΑΒ τῇ ΔΓ, καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΑΓ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΒΑΓ, ΑΓΔ ἴσαι ἀλλήλαις εἰσίν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΓΔΕ τῇ ὑπὸ ΑΓΔ ἴση ἐστίν. ὥστε καὶ ἡ ὑπὸ ΒΑΓ τῇ ὑπὸ ΓΔΕ ἐστιν ἴση. καὶ ἐπεὶ δύο τρίγωνά ἐστι τὰ ΑΒΓ, ΔΓΕ μίαν γωνίαν τὴν πρὸς τῷ Α μιᾷ γωνίᾳ τῇ πρὸς τῷ Δ ἴσην ἔχοντα, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον, ὡς τὴν ΒΑ πρὸς τὴν ΑΓ, οὕτως τὴν ΓΔ πρὸς τὴν ΔΕ, ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΔΓΕ τριγώνῳ· ἴση ἄρα ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΓΕ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΑΓΔ τῇ ὑπὸ ΒΑΓ ἴση· ὅλη ἄρα ἡ ὑπὸ ΑΓΕ δυσὶ ταῖς ὑπὸ ΑΒΓ, ΒΑΓ ἴση ἐστίν. κοινὴ προσκείσθω ἡ ὑπὸ ΑΓΒ· αἱ ἄρα ὑπὸ ΑΓΕ, ΑΓΒ ταῖς ὑπὸ ΒΑΓ, ΑΓΒ, ΓΒΑ ἴσαι εἰσίν. ἀλλ' αἱ ὑπὸ ΒΑΓ, ΑΒΓ, ΑΓΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν· καὶ αἱ ὑπὸ ΑΓΕ, ΑΓΒ ἄρα δυσὶν ὀρθαῖς ἴσαι εἰσίν. πρὸς δή τινι εὐθείᾳ τῇ ΑΓ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Γ δύο εὐθεῖαι αἱ ΒΓ, ΓΕ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας τὰς ὑπὸ ΑΓΕ, ΑΓΒ δυσὶν ὀρθαῖς ἴσας ποιοῦσιν· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΒΓ τῇ ΓΕ.
Ἐὰν ἄρα δύο τρίγωνα συντεθῇ κατὰ μίαν γωνίαν τὰς δύο πλευρὰς ταῖς δυσὶ πλευραῖς ἀνάλογον ἔχοντα ὥστε τὰς ὁμολόγους αὐτῶν πλευρὰς καὶ παραλλήλους εἶναι, αἱ λοιπαὶ τῶν τριγώνων πλευραὶ ἐπ᾿ εὐθείας ἔσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον VI
Ἐν τοῖς ἴσοις κύκλοις αἱ γωνίαι τὸν αὐτὸν ἔχουσι λόγον ταῖς περιφερείαις, ἐφ' ὧν βεβήκασιν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι.
Ἔστωσαν ἴσοι κύκλοι οἱ ΑΒΓ, ΔΕΖ, καὶ πρὸς μὲν τοῖς κέντροις αὐτῶν τοῖς Η, Θ γωνίαι ἔστωσαν αἱ ὑπὸ ΒΗΓ, ΕΘΖ, πρὸς δὲ ταῖς περιφερείαις αἱ ὑπὸ ΒΑΓ, ΕΔΖ· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΓ περιφέρεια πρὸς τὴν ΕΖ περιφέρειαν, οὕτως ἥ τε ὑπὸ ΒΗΓ γωνία πρὸς τὴν ὑπὸ ΕΘΖ καὶ ἡ ὑπὸ ΒΑΓ πρὸς τὴν ὑπὸ ΕΔΖ.
Κείσθωσαν γὰρ τῇ μὲν ΒΓ περιφερείᾳ ἴσαι κατὰ τὸ ἑξῆς ὁσαιδηποτοῦν αἱ ΓΚ, ΚΛ, τῇ δὲ ΕΖ περιφερείᾳ ἴσαι ὁσαιδηποτοῦν αἱ ΖΜ, ΜΝ, καὶ ἐπεζεύχθωσαν αἱ ΗΚ, ΗΛ, ΘΜ, ΘΝ.
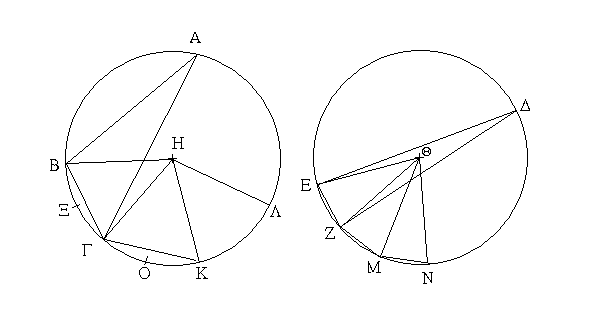
Ἐπεὶ οὖν ἴσαι εἰσὶν αἱ ΒΓ, ΓΚ, ΚΛ περιφέρειαι ἀλλήλαις, ἴσαι εἰσὶ καὶ αἱ ὑπὸ ΒΗΓ, ΓΗΚ, ΚΗΛ γωνίαι ἀλλήλαις· ὁσαπλασίων ἄρα ἐστὶν ἡ ΒΛ περιφέρεια τῆς ΒΓ, τοσαυταπλασίων ἐστὶ καὶ ἡ ὑπὸ ΒΗΛ γωνία τῆς ὑπὸ ΒΗΓ. διὰ τὰ αὐτὰ δὴ καὶ ὁσαπλασίων ἐστὶν ἡ ΝΕ περιφέρεια τῆς ΕΖ, τοσαυταπλασίων ἐστὶ καὶ ἡ ὑπὸ ΝΘΕ γωνία τῆς ὑπὸ ΕΘΖ. εἰ ἄρα ἴση ἐστὶν ἡ ΒΛ περιφέρεια τῇ ΕΝ περιφερείᾳ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΒΗΛ τῇ ὑπὸ ΕΘΝ, καὶ εἰ μείζων ἐστὶν ἡ ΒΛ περιφέρεια τῆς ΕΝ περιφερείας, μείζων ἐστὶ καὶ ἡ ὑπὸ ΒΗΛ γωνία τῆς ὑπὸ ΕΘΝ, καὶ εἰ ἐλάσσων, ἐλάσσων. τεσσάρων δὴ ὄντων μεγεθῶν, δύο μὲν περιφερειῶν τῶν ΒΓ, ΕΖ, δύο δὲ γωνιῶν τῶν ὑπὸ ΒΗΓ, ΕΘΖ, εἴληπται τῆς μὲν ΒΓ περιφερείας καὶ τῆς ὑπὸ ΒΗΓ γωνίας ἰσάκις πολλαπλασίων ἥ τε ΒΛ περιφέρεια καὶ ἡ ὑπὸ ΒΗΛ γωνία, τῆς δὲ ΕΖ περιφερείας καὶ τῆς ὑπὸ ΕΘΖ γωνίας ἥ τε ΕΝ περιφέρεια καὶ ἡ ὑπὸ ΕΘΝ γωνία. καὶ δέδεικται, ὅτι εἰ ὑπερέχει ἡ ΒΛ περιφέρεια τῆς ΕΝ περιφερείας, ὑπερέχει καὶ ἡ ὑπὸ ΒΗΛ γωνία τῆς ὑπὸ ΕΘΝ γωνίας, καὶ εἰ ἴση, ἴση, καὶ εἰ ἐλάσσων, ἐλάσσων. ἔστιν ἄρα, ὡς ἡ ΒΓ περιφέρεια πρὸς τὴν ΕΖ, οὕτως ἡ ὑπὸ ΒΗΓ γωνία πρὸς τὴν ὑπὸ ΕΘΖ. ἀλλ' ὡς ἡ ὑπὸ ΒΗΓ γωνία πρὸς τὴν ὑπὸ ΕΘΖ, οὕτως ἡ ὑπὸ ΒΑΓ πρὸς τὴν ὑπὸ ΕΔΖ· διπλασία γὰρ ἑκατέρα ἑκατέρας. καὶ ὡς ἄρα ἡ ΒΓ περιφέρεια πρὸς τὴν ΕΖ περιφέρειαν, οὕτως ἥ τε ὑπὸ ΒΗΓ γωνία πρὸς τὴν ὑπὸ ΕΘΖ καὶ ἡ ὑπὸ ΒΑΓ πρὸς τὴν ὑπὸ ΕΔΖ.
Ἐν ἄρα τοῖς ἴσοις κύκλοις αἱ γωνίαι τὸν αὐτὸν ἔχουσι λόγον ταῖς περιφερείαις, ἐφ' ὧν βεβήκασιν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου ζ΄
Βιβλίον VII
Ὅροι κγ΄ 23.
α΄ 1. Μονάς ἐστιν, καθ᾿ ἣν ἕκαστον τῶν ὄντων ἓν λέγεται.
β΄ 2. Ἀριθμὸς δὲ τὸ ἐκ μονάδων συγκείμενον πλῆθος.
γ΄ 3. Μέρος ἐστὶν ἀριθμὸς ἀριθμοῦ ὁ ἐλάσσων τοῦ μείζονος, ὅταν καταμετρῇ τὸν μείζονα.
δ΄ 4. Μέρη δέ, ὅταν μὴ καταμετρῇ.
ε΄ 5. Πολλαπλάσιος δὲ ὁ μείζων τοῦ ἐλάσσονος, ὅταν καταμετρῆται ὑπὸ τοῦ ἐλάσσονος.
ς΄ 6. Ἄρτιος ἀριθμός ἐστιν ὁ δίχα διαιρούμενος.
ζ΄ 7. Περισσὸς δὲ ὁ μὴ διαιρούμενος δίχα ἢ [ὁ] μονάδι διαφέρων ἀρτίου ἀριθμοῦ.
η΄ 8. Ἀρτιάκις ἄρτιος ἀριθμός ἐστιν ὁ ὑπὸ ἀρτίου ἀριθμοῦ μετρούμενος κατὰ ἄρτιον ἀριθμόν.
θ΄ 9. Ἀρτιάκις δὲ περισσός ἐστιν ὁ ὑπὸ ἀρτίου ἀριθμοῦ μετρούμενος κατὰ περισσὸν ἀριθμόν.
ι΄ 10. Περισσάκις ἄρτιός ἐστιν ὁ ὑπὸ περισσοῦ ἀριθμοῦ μετρούμενος κατὰ ἄρτιον ἀριθμόν.
ια΄ 11. Περισσάκις δὲ περισσὸς ἀριθμός ἐστιν ὁ ὑπὸ περισσοῦ ἀριθμοῦ μετρούμενος κατὰ περισσὸν ἀριθμόν.
ιβ΄ 12. Πρῶτος ἀριθμός ἐστιν ὁ μονάδι μόνῃ μετρούμενος.
ιγ΄ 13. Πρῶτοι πρὸς ἀλλήλους ἀριθμοί εἰσιν οἱ μονάδι μόνῃ μετρούμενοι κοινῷ μέτρῳ.
ιδ΄ 14. Σύνθετος ἀριθμός ἐστιν ὁ ἀριθμῷ τινι μετρούμενος.
ιε΄ 15. Σύνθετοι δὲ πρὸς ἀλλήλους ἀριθμοί εἰσιν οἱ ἀριθμῷ τινι μετρούμενοι κοινῷ μέτρῳ.
ις΄ 16. Ἀριθμὸς ἀριθμὸν πολλαπλασιάζειν λέγεται, ὅταν, ὅσαι εἰσὶν ἐν αὐτῷ μονάδες, τοσαυτάκις συντεθῇ ὁ πολλαπλασιαζόμενος, καὶ γένηταί τις.
ιζ΄ 17. Ὅταν δὲ δύο ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, ὁ γενόμενος ἐπίπεδος καλεῖται, πλευραὶ δὲ αὐτοῦ οἱ πολλαπλασιάσαντες ἀλλήλους ἀριθμοί.
ιη΄ 18. Ὅταν δὲ τρεῖς ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, ὁ γενόμενος στερεός ἐστιν, πλευραὶ δὲ αὐτοῦ οἱ πολλαπλασιάσαντες ἀλλήλους ἀριθμοί.
ιθ΄ 19. Τετράγωνος ἀριθμός ἐστιν ὁ ἰσάκις ἴσος ἢ [ὁ] ὑπὸ δύο ἴσων ἀριθμῶν περιεχόμενος.
κ΄ 20. Κύβος δὲ ὁ ἰσάκις ἴσος ἰσάκις ἢ [ὁ] ὑπὸ τριῶν ἴσων ἀριθμῶν περιεχόμενος.
κα΄ 21. Ἀριθμοὶ ἀνάλογόν εἰσιν, ὅταν ὁ πρῶτος τοῦ δευτέρου καὶ ὁ τρίτος τοῦ τετάρτου ἰσάκις ᾖ πολλαπλάσιος ἢ τὸ αὐτὸ μέρος ἢ τὰ αὐτὰ μέρη ὦσιν.
κβ΄ 22. Ὅμοιοι ἐπίπεδοι καὶ στερεοὶ ἀριθμοί εἰσιν οἱ ἀνάλογον ἔχοντες τὰς πλευράς.
κγ΄ 23. Τέλειος ἀριθμός ἐστιν ὁ τοῖς ἑαυτοῦ μέρεσιν ἴσος ὤν.
Στοιχεῖα Εὐκλείδου ζ΄
Προτάσεις λθ΄ 39
Πρότασις α΄ 1 Βιβλίον VII
Δύο ἀριθμῶν ἀνίσων ἐκκειμένων, ἀνθυφαιρουμένου δὲ ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος, ἐὰν ὁ λειπόμενος μηδέποτε καταμετρῇ τὸν πρὸ ἑαυτοῦ, ἕως οὗ λειφθῇ μονάς, οἱ ἐξ ἀρχῆς ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ἔσονται.
Δύο γὰρ [ἀνίσων] ἀριθμῶν τῶν ΑΒ, ΓΔ ἀνθυφαιρουμένου ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος ὁ λειπόμενος μηδέποτε καταμετρείτω τὸν πρὸ ἑαυτοῦ, ἕως οὗ λειφθῇ μονάς· λέγω, ὅτι οἱ ΑΒ, ΓΔ πρῶτοι πρὸς ἀλλήλους εἰσίν, τουτέστιν ὅτι τοὺς ΑΒ, ΓΔ μονὰς μόνη μετρεῖ.
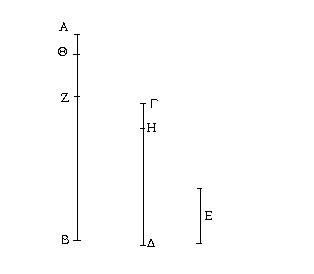
Εἰ γὰρ μή εἰσιν οἱ ΑΒ, ΓΔ πρῶτοι πρὸς ἀλλήλους, μετρήσει τις αὐτοὺς ἀριθμός. μετρείτω, καὶ ἔστω ὁ Ε· καὶ ὁ μὲν ΓΔ τὸν ΒΖ μετρῶν λειπέτω ἑαυτοῦ ἐλάσσονα τὸν ΖΑ, ὁ δὲ ΑΖ τὸν ΔΗ μετρῶν λειπέτω ἑαυτοῦ ἐλάσσονα τὸν ΗΓ, ὁ δὲ ΗΓ τὸν ΖΘ μετρῶν λειπέτω μονάδα τὴν ΘΑ.
Ἐπεὶ οὖν ὁ Ε τὸν ΓΔ μετρεῖ, ὁ δὲ ΓΔ τὸν ΒΖ μετρεῖ καὶ ὁ Ε ἄρα τὸν ΒΖ μετρεῖ· μετρεῖ δὲ καὶ ὅλον τὸν ΒΑ· καὶ λοιπὸν ἄρα τὸν ΑΖ μετρήσει. ὁ δὲ ΑΖ τὸν ΔΗ μετρεῖ· καὶ ὁ Ε ἄρα τὸν ΔΗ μετρεῖ· μετρεῖ δὲ καὶ ὅλον τὸν ΔΓ· καὶ λοιπὸν ἄρα τὸν ΓΗ μετρήσει. ὁ δὲ ΓΗ τὸν ΖΘ μετρεῖ· καὶ ὁ Ε ἄρα τὸν ΖΘ μετρεῖ· μετρεῖ δὲ καὶ ὅλον τὸν ΖΑ· καὶ λοιπὴν ἄρα τὴν ΑΘ μονάδα μετρήσει ἀριθμὸς ὤν· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς ΑΒ, ΓΔ ἀριθμοὺς μετρήσει τις ἀριθμός· οἱ ΑΒ, ΓΔ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον VII
Δύο ἀριθμῶν δοθέντων μὴ πρώτων πρὸς ἀλλήλους τὸ μέγιστον αὐτῶν κοινὸν μέτρον εὑρεῖν.
Ἔστωσαν οἱ δοθέντες δύο ἀριθμοὶ μὴ πρῶτοι πρὸς ἀλλήλους οἱ ΑΒ, ΓΔ. δεῖ δὴ τῶν ΑΒ, ΓΔ τὸ μέγιστον κοινὸν μέτρον εὑρεῖν.
Εἰ μὲν οὖν ὁ ΓΔ τὸν ΑΒ μετρεῖ, μετρεῖ δὲ καὶ ἑαυτόν, ὁ ΓΔ ἄρα τῶν ΓΔ, ΑΒ κοινὸν μέτρον ἐστίν. καὶ φανερόν, ὅτι καὶ μέγιστον· οὐδεὶς γὰρ μείζων τοῦ ΓΔ τὸν ΓΔ μετρήσει.
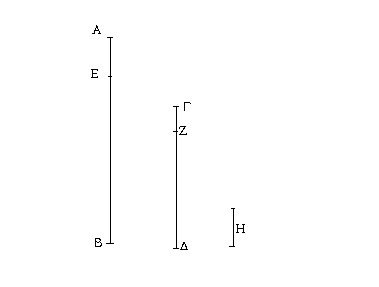
Εἰ δὲ οὐ μετρεῖ ὁ ΓΔ τὸν ΑΒ, τῶν ΑΒ, ΓΔ ἀνθυφαιρουμένου ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος λειφθήσεταί τις ἀριθμός, ὃς μετρήσει τὸν πρὸ ἑαυτοῦ. μονὰς μὲν γὰρ οὐ λειφθήσεται· εἰ δὲ μή, ἔσονται οἱ ΑΒ, ΓΔ πρῶτοι πρὸς ἀλλήλους· ὅπερ οὐχ ὑπόκειται. λειφθήσεταί τις ἄρα ἀριθμός, ὃς μετρήσει τὸν πρὸ ἑαυτοῦ. καὶ ὁ μὲν ΓΔ τὸν ΒΕ μετρῶν λειπέτω ἑαυτοῦ ἐλάσσονα τὸν ΕΑ, ὁ δὲ ΕΑ τὸν ΔΖ μετρῶν λειπέτω ἑαυτοῦ ἐλάσσονα τὸν ΖΓ, ὁ δὲ ΓΖ τὸν ΑΕ μετρείτω. ἐπεὶ οὖν ὁ ΓΖ τὸν ΑΕ μετρεῖ, ὁ δὲ ΑΕ τὸν ΔΖ μετρεῖ, καὶ ὁ ΓΖ ἄρα τὸν ΔΖ μετρήσει· μετρεῖ δὲ καὶ ἑαυτόν· καὶ ὅλον ἄρα τὸν ΓΔ μετρήσει. ὁ δὲ ΓΔ τὸν ΒΕ μετρεῖ· καὶ ὁ ΓΖ ἄρα τὸν ΒΕ μετρεῖ· μετρεῖ δὲ καὶ τὸν ΕΑ· καὶ ὅλον ἄρα τὸν ΒΑ μετρήσει· μετρεῖ δὲ καὶ τὸν ΓΔ· ὁ ΓΖ ἄρα τοὺς ΑΒ, ΓΔ μετρεῖ. ὁ ΓΖ ἄρα τῶν ΑΒ, ΓΔ κοινὸν μέτρον ἐστίν. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή ἐστιν ὁ ΓΖ τῶν ΑΒ, ΓΔ μέγιστον κοινὸν μέτρον, μετρήσει τις τοὺς ΑΒ, ΓΔ ἀριθμοὺς ἀριθμὸς μείζων ὢν τοῦ ΓΖ. μετρείτω, καὶ ἔστω ὁ Η. καὶ ἐπεὶ ὁ Η τὸν ΓΔ μετρεῖ, ὁ δὲ ΓΔ τὸν ΒΕ μετρεῖ, καὶ ὁ Η ἄρα τὸν ΒΕ μετρεῖ· μετρεῖ δὲ καὶ ὅλον τὸν ΒΑ· καὶ λοιπὸν ἄρα τὸν ΑΕ μετρήσει. ὁ δὲ ΑΕ τὸν ΔΖ μετρεῖ· καὶ ὁ Η ἄρα τὸν ΔΖ μετρήσει· μετρεῖ δὲ καὶ ὅλον τὸν ΔΓ· καὶ λοιπὸν ἄρα τὸν ΓΖ μετρήσει ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα τοὺς ΑΒ, ΓΔ ἀριθμοὺς ἀριθμός τις μετρήσει μείζων ὢν τοῦ ΓΖ· ὁ ΓΖ ἄρα τῶν ΑΒ, ΓΔ μέγιστόν ἐστι κοινὸν μέτρον· [ὅπερ ἔδει δεῖξαι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν ἀριθμὸς δύο ἀριθμοὺς μετρῇ, καὶ τὸ μέγιστον αὐτῶν κοινὸν μέτρον μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον VII
Τριῶν ἀριθμῶν δοθέντων μὴ πρώτων πρὸς ἀλλήλους τὸ μέγιστον αὐτῶν κοινὸν μέτρον εὑρεῖν.
Ἔστωσαν οἱ δοθέντες τρεῖς ἀριθμοὶ μὴ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β, Γ· δεῖ δὴ τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον εὑρεῖν.
Εἰλήφθω γὰρ δύο τῶν Α, Β τὸ μέγιστον κοινὸν μέτρον ὁ Δ· ὁ δὴ Δ τὸν Γ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω πρότερον· μετρεῖ δὲ καὶ τοὺς Α, Β· ὁ Δ ἄρα τοὺς Α, Β, Γ μετρεῖ· ὁ Δ ἄρα τῶν Α, Β, Γ κοινὸν μέτρον ἐστίν. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή ἐστιν ὁ Δ τῶν Α, Β, Γ μέγιστον κοινὸν μέτρον, μετρήσει τις τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμὸς μείζων ὢν τοῦ Δ. μετρείτω, καὶ ἔστω ὁ Ε. ἐπεὶ οὖν ὁ Ε τοὺς Α, Β, Γ μετρεῖ, καὶ τοὺς Α, Β ἄρα μετρήσει· καὶ τὸ τῶν Α, Β ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Α, Β μέγιστον κοινὸν μέτρον ἐστὶν ὁ Δ· ὁ Ε ἄρα τὸν Δ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμός τις μετρήσει μείζων ὢν τοῦ Δ· ὁ Δ ἄρα τῶν Α, Β, Γ μέγιστόν ἐστι κοινὸν μέτρον.
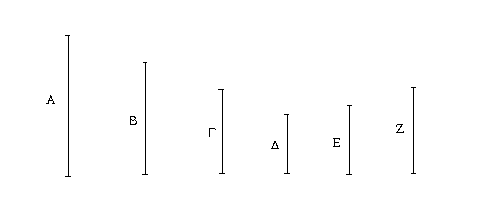
Μὴ μετρείτω δὴ ὁ Δ τὸν Γ· λέγω πρῶτον, ὅτι οἱ Γ, Δ οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους. ἐπεὶ γὰρ οἱ Α, Β, Γ οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους, μετρήσει τις αὐτοὺς ἀριθμός. ὁ δὴ τοὺς Α, Β, Γ μετρῶν καὶ τοὺς Α, Β μετρήσει, καὶ τὸ τῶν Α, Β μέγιστον κοινὸν μέτρον τὸν Δ μετρήσει· μετρεῖ δὲ καὶ τὸν Γ· τοὺς Δ, Γ ἄρα ἀριθμοὺς ἀριθμός τις μετρήσει· οἱ Δ, Γ ἄρα οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους. εἰλήφθω οὖν αὐτῶν τὸ μέγιστον κοινὸν μέτρον ὁ Ε. καὶ ἐπεὶ ὁ Ε τὸν Δ μετρεῖ, ὁ δὲ Δ τοὺς Α, Β μετρεῖ, καὶ ὁ Ε ἄρα τοὺς Α, Β μετρεῖ· μετρεῖ δὲ καὶ τὸν Γ· ὁ Ε ἄρα τοὺς Α, Β, Γ μετρεῖ· ὁ Ε ἄρα τῶν Α, Β, Γ κοινόν ἐστι μέτρον. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή ἐστιν ὁ Ε τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον, μετρήσει τις τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμὸς μείζων ὢν τοῦ Ε. μετρείτω, καὶ ἔστω ὁ Ζ. καὶ ἐπεὶ ὁ Ζ τοὺς Α, Β, Γ μετρεῖ, καὶ τοὺς Α, Β μετρεῖ· καὶ τὸ τῶν Α, Β ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Α, Β μέγιστον κοινὸν μέτρον ἐστὶν ὁ Δ· ὁ Ζ ἄρα τὸν Δ μετρεῖ· μετρεῖ δὲ καὶ τὸν Γ· ὁ Ζ ἄρα τοὺς Δ, Γ μετρεῖ· καὶ τὸ τῶν Δ, Γ ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Δ, Γ μέγιστον κοινὸν μέτρον ἐστὶν ὁ Ε· ὁ Ζ ἄρα τὸν Ε μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμός τις μετρήσει μείζων ὢν τοῦ Ε· ὁ Ε ἄρα τῶν Α, Β, Γ μέγιστόν ἐστι κοινὸν μέτρον· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον VII
Ἅπας ἀριθμὸς παντὸς ἀριθμοῦ ὁ ἐλάσσων τοῦ μείζονος ἤτοι μέρος ἐστὶν ἢ μέρη.
Ἔστωσαν δύο ἀριθμοὶ οἱ Α, ΒΓ, καὶ ἔστω ἐλάσσων ὁ ΒΓ· λέγω, ὅτι ὁ ΒΓ τοῦ Α ἤτοι μέρος ἐστὶν ἢ μέρη.
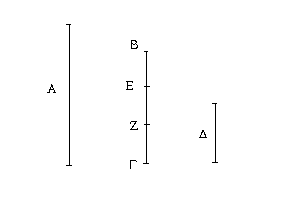
Οἱ Α, ΒΓ γὰρ ἤτοι πρῶτοι πρὸς ἀλλήλους εἰσὶν ἢ οὔ. ἔστωσαν πρότερον οἱ Α, ΒΓ πρῶτοι πρὸς ἀλλήλους. διαιρεθέντος δὴ τοῦ ΒΓ εἰς τὰς ἐν αὐτῷ μονάδας ἔσται ἑκάστη μονὰς τῶν ἐν τῷ ΒΓ μέρος τι τοῦ Α· ὥστε μέρη ἐστὶν ὁ ΒΓ τοῦ Α.
Μὴ ἔστωσαν δὴ οἱ Α, ΒΓ πρῶτοι πρὸς ἀλλήλους· ὁ δὴ ΒΓ τὸν Α ἤτοι μετρεῖ ἢ οὐ μετρεῖ. εἰ μὲν οὖν ὁ ΒΓ τὸν Α μετρεῖ, μέρος ἐστὶν ὁ ΒΓ τοῦ Α. εἰ δὲ οὔ, εἰλήφθω τῶν Α, ΒΓ μέγιστον κοινὸν μέτρον ὁ Δ, καὶ διῃρήσθω ὁ ΒΓ εἰς τοὺς τῷ Δ ἴσους τοὺς ΒΕ, ΕΖ, ΖΓ. καὶ ἐπεὶ ὁ Δ τὸν Α μετρεῖ, μέρος ἐστὶν ὁ Δ τοῦ Α· ἴσος δὲ ὁ Δ ἑκάστῳ τῶν ΒΕ, ΕΖ, ΖΓ· καὶ ἕκαστος ἄρα τῶν ΒΕ, ΕΖ, ΖΓ τοῦ Α μέρος ἐστίν· ὥστε μέρη ἐστὶν ὁ ΒΓ τοῦ Α.
Ἅπας ἄρα ἀριθμὸς παντὸς ἀριθμοῦ ὁ ἐλάσσων τοῦ μείζονος ἤτοι μέρος ἐστὶν ἢ μέρη· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον VII
Ἐὰν ἀριθμός ἀριθμοῦ μέρος ᾖ, καὶ ἕτερος ἑτέρου τὸ αὐτὸ μέρος ᾖ, καὶ συναμφότερος συναμφοτέρου τὸ αὐτὸ μέρος ἔσται, ὅπερ ὁ εἷς τοῦ ἑνός.
Ἀριθμὸς γὰρ ὁ Α [ἀριθμοῦ] τοῦ ΒΓ μέρος ἔστω, καὶ ἕτερος ὁ Δ ἑτέρου τοῦ ΕΖ τὸ αὐτὸ μέρος, ὅπερ ὁ Α τοῦ ΒΓ· λέγω, ὅτι καὶ συναμφότερος ὁ Α, Δ συναμφοτέρου τοῦ ΒΓ, ΕΖ τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὁ Α τοῦ ΒΓ.
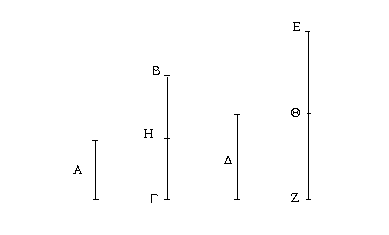
Ἐπεὶ γάρ, ὃ μέρος ἐστὶν ὁ Α τοῦ ΒΓ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Δ τοῦ ΕΖ, ὅσοι ἄρα εἰσὶν ἐν τῷ ΒΓ ἀριθμοὶ ἴσοι τῷ Α, τοσοῦτοί εἰσι καὶ ἐν τῷ ΕΖ ἀριθμοὶ ἴσοι τῷ Δ. διῃρήσθω ὁ μὲν ΒΓ εἰς τοὺς τῷ Α ἴσους τοὺς ΒΗ, ΗΓ, ὁ δὲ ΕΖ εἰς τοὺς τῷ Δ ἴσους τοὺς ΕΘ, ΘΖ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΒΗ, ΗΓ τῷ πλήθει τῶν ΕΘ, ΘΖ. καὶ ἐπεὶ ἴσος ἐστὶν ὁ μὲν ΒΗ τῷ Α, ὁ δὲ ΕΘ τῷ Δ, καὶ οἱ ΒΗ, ΕΘ ἄρα τοῖς Α, Δ ἴσοι. διὰ τὰ αὐτὰ δὴ καὶ οἱ ΗΓ, ΘΖ τοῖς Α, Δ. ὅσοι ἄρα [εἰσὶν] ἐν τῷ ΒΓ ἀριθμοὶ ἴσοι τῷ Α, τοσοῦτοί εἰσι καὶ ἐν τοῖς ΒΓ, ΕΖ ἴσοι τοῖς Α, Δ. ὁσαπλασίων ἄρα ἐστὶν ὁ ΒΓ τοῦ Α, τοσαυταπλασίων ἐστὶ καὶ συναμφότερος ὁ ΒΓ, ΕΖ συναμφοτέρου τοῦ Α, Δ. ὃ ἄρα μέρος ἐστὶν ὁ Α τοῦ ΒΓ, τὸ αὐτὸ μέρος ἐστὶ καὶ συναμφότερος ὁ Α, Δ συναμφοτέρου τοῦ ΒΓ, ΕΖ· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον VII
Ἐὰν ἀριθμὸς ἀριθμοῦ μέρη ᾖ, καὶ ἕτερος ἑτέρου τὰ αὐτὰ μέρη ᾖ, καὶ συναμφότερος συναμφοτέρου τὰ αὐτὰ μέρη ἔσται, ὅπερ ὁ εἷς τοῦ ἑνός.
Ἀριθμὸς γὰρ ὁ ΑΒ ἀριθμοῦ τοῦ Γ μέρη ἔστω, καὶ ἕτερος ὁ ΔΕ ἑτέρου τοῦ Ζ τὰ αὐτὰ μέρη, ἅπερ ὁ ΑΒ τοῦ Γ· λέγω, ὅτι καὶ συναμφότερος ὁ ΑΒ, ΔΕ συναμφοτέρου τοῦ Γ, Ζ τὰ αὐτὰ μέρη ἐστίν, ἅπερ ὁ ΑΒ τοῦ Γ.
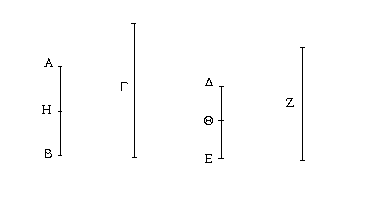
Ἐπεὶ γάρ, ἃ μέρη ἐστὶν ὁ ΑΒ τοῦ Γ, τὰ αὐτὰ μέρη καὶ ὁ ΔΕ τοῦ Ζ, ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ μέρη τοῦ Γ, τοσαῦτά ἐστι καὶ ἐν τῷ ΔΕ μέρη τοῦ Ζ. διῃρήσθω ὁ μὲν ΑΒ εἰς τὰ τοῦ Γ μέρη τὰ ΑΗ, ΗΒ, ὁ δὲ ΔΕ εἰς τὰ τοῦ Ζ μέρη τὰ ΔΘ, ΘΕ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΑΗ, ΗΒ τῷ πλήθει τῶν ΔΘ, ΘΕ. καὶ ἐπεί, ὃ μέρος ἐστὶν ὁ ΑΗ τοῦ Γ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΔΘ τοῦ Ζ, ὃ ἄρα μέρος ἐστὶν ὁ ΑΗ τοῦ Γ, τὸ αὐτὸ μέρος ἐστὶ καὶ συναμφότερος ὁ ΑΗ, ΔΘ συναμφοτέρου τοῦ Γ, Ζ. διὰ τὰ αὐτὰ δὴ καὶ ὃ μέρος ἐστὶν ὁ ΗΒ τοῦ Γ, τὸ αὐτὸ μέρος ἐστὶ καὶ συναμφότερος ὁ ΗΒ, ΘΕ συναμφοτέρου τοῦ Γ, Ζ. ἃ ἄρα μέρη ἐστὶν ὁ ΑΒ τοῦ Γ, τὰ αὐτὰ μέρη ἐστὶ καὶ συναμφότερος ὁ ΑΒ, ΔΕ συναμφοτέρου τοῦ Γ, Ζ· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον VII
Ἐὰν ἀριθμὸς ἀριθμοῦ μέρος ᾖ, ὅπερ ἀφαιρεθεὶς ἀφαιρεθέντος, καὶ ὁ λοιπὸς τοῦ λοιποῦ τὸ αὐτὸ μέρος ἔσται, ὅπερ ὁ ὅλος τοῦ ὅλου.
Ἀριθμὸς γὰρ ὁ ΑΒ ἀριθμοῦ τοῦ ΓΔ μέρος ἔστω, ὅπερ ἀφαιρεθεὶς ὁ ΑΕ ἀφαιρεθέντος τοῦ ΓΖ· λέγω, ὅτι καὶ λοιπὸς ὁ ΕΒ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὅλος ὁ ΑΒ ὅλου τοῦ ΓΔ.
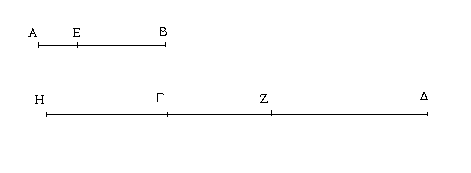
Ὃ γὰρ μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ἔστω καὶ ὁ ΕΒ τοῦ ΓΗ. καὶ ἐπεί, ὃ μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΕΒ τοῦ ΓΗ, ὃ ἄρα μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΑΒ τοῦ ΗΖ. ὃ δὲ μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ὑπόκειται καὶ ὁ ΑΒ τοῦ ΓΔ· ὃ ἄρα μέρος ἐστὶ καὶ ὁ ΑΒ τοῦ ΗΖ, τὸ αὐτὸ μέρος ἐστὶ καὶ τοῦ ΓΔ· ἴσος ἄρα ἐστὶν ὁ ΗΖ τῷ ΓΔ. κοινὸς ἀφῃρήσθω ὁ ΓΖ· λοιπὸς ἄρα ὁ ΗΓ λοιπῷ τῷ ΖΔ ἐστιν ἴσος. καὶ ἐπεί, ὃ μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος [ἐστὶ] καὶ ὁ ΕΒ τοῦ ΗΓ, ἴσος δὲ ὁ ΗΓ τῷ ΖΔ, ὃ ἄρα μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΕΒ τοῦ ΖΔ. ἀλλὰ ὃ μέρος ἐστὶν ὁ ΑΕ τοῦ ΓΖ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΑΒ τοῦ ΓΔ· καὶ λοιπὸς ἄρα ὁ ΕΒ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὅλος ὁ ΑΒ ὅλου τοῦ ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον VII
Ἐὰν ἀριθμὸς ἀριθμοῦ μέρη ᾖ, ἅπερ ἀφαιρεθεὶς ἀφαιρεθέντος, καὶ ὁ λοιπὸς τοῦ λοιποῦ τὰ αὐτὰ μέρη ἔσται, ἅπερ ὁ ὅλος τοῦ ὅλου.
Ἀριθμὸς γὰρ ὁ ΑΒ ἀριθμοῦ τοῦ ΓΔ μέρη ἔστω, ἅπερ ἀφαιρεθεὶς ὁ ΑΕ ἀφαιρεθέντος τοῦ ΓΖ· λέγω, ὅτι καὶ λοιπὸς ὁ ΕΒ λοιποῦ τοῦ ΖΔ τὰ αὐτὰ μέρη ἐστίν, ἅπερ ὅλος ὁ ΑΒ ὅλου τοῦ ΓΔ.
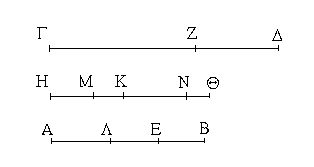
Κείσθω γὰρ τῷ ΑΒ ἴσος ὁ ΗΘ. ἃ ἄρα μέρη ἐστὶν ὁ ΗΘ τοῦ ΓΔ, τὰ αὐτὰ μέρη ἐστὶ καὶ ὁ ΑΕ τοῦ ΓΖ. διῃρήσθω ὁ μὲν ΗΘ εἰς τὰ τοῦ ΓΔ μέρη τὰ ΗΚ, ΚΘ, ὁ δὲ ΑΕ εἰς τὰ τοῦ ΓΖ μέρη τὰ ΑΛ, ΛΕ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΗΚ, ΚΘ τῷ πλήθει τῶν ΑΛ, ΛΕ. καὶ ἐπεί, ὃ μέρος ἐστὶν ὁ ΗΚ τοῦ ΓΔ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΑΛ τοῦ ΓΖ, μείζων δὲ ὁ ΓΔ τοῦ ΓΖ, μείζων ἄρα καὶ ὁ ΗΚ τοῦ ΑΛ. κείσθω τῷ ΑΛ ἴσος ὁ ΗΜ. ὃ ἄρα μέρος ἐστὶν ὁ ΗΚ τοῦ ΓΔ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΗΜ τοῦ ΓΖ· καὶ λοιπὸς ἄρα ὁ ΜΚ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὅλος ὁ ΗΚ ὅλου τοῦ ΓΔ. πάλιν ἐπεί, ὃ μέρος ἐστὶν ὁ ΚΘ τοῦ ΓΔ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΕΛ τοῦ ΓΖ, μείζων δὲ ὁ ΓΔ τοῦ ΓΖ, μείζων ἄρα καὶ ὁ ΘΚ τοῦ ΕΛ. κείσθω τῷ ΕΛ ἴσος ὁ ΚΝ. ὃ ἄρα μέρος ἐστὶν ὁ ΚΘ τοῦ ΓΔ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΚΝ τοῦ ΓΖ· καὶ λοιπὸς ἄρα ὁ ΝΘ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὅλος ὁ ΚΘ ὅλου τοῦ ΓΔ. ἐδείχθη δὲ καὶ λοιπὸς ὁ ΜΚ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ὤν, ὅπερ ὅλος ὁ ΗΚ ὅλου τοῦ ΓΔ· καὶ συναμφότερος ἄρα ὁ ΜΚ, ΝΘ τοῦ ΔΖ τὰ αὐτὰ μέρη ἐστίν, ἅπερ ὅλος ὁ ΘΗ ὅλου τοῦ ΓΔ. ἴσος δὲ συναμφότερος μὲν ὁ ΜΚ, ΝΘ τῷ ΕΒ, ὁ δὲ ΘΗ τῷ ΒΑ· καὶ λοιπὸς ἄρα ὁ ΕΒ λοιποῦ τοῦ ΖΔ τὰ αὐτὰ μέρη ἐστίν, ἅπερ ὅλος ὁ ΑΒ ὅλου τοῦ ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον VII
Ἐὰν ἀριθμὸς ἀριθμοῦ μέρος ᾖ, καὶ ἕτερος ἑτέρου τὸ αὐτὸ μέρος ᾖ, καὶ ἐναλλάξ, ὃ μέρος ἐστὶν ἢ μέρη ὁ πρῶτος τοῦ τρίτου, τὸ αὐτὸ μέρος ἔσται ἢ τὰ αὐτὰ μέρη καὶ ὁ δεύτερος τοῦ τετάρτου.
Ἀριθμὸς γὰρ ὁ Α ἀριθμοῦ τοῦ ΒΓ μέρος ἔστω, καὶ ἕτερος ὁ Δ ἑτέρου τοῦ ΕΖ τὸ αὐτὸ μέρος, ὅπερ ὁ Α τοῦ ΒΓ· λέγω, ὅτι καὶ ἐναλλάξ, ὃ μέρος ἐστὶν ὁ Α τοῦ Δ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΒΓ τοῦ ΕΖ ἢ μέρη.
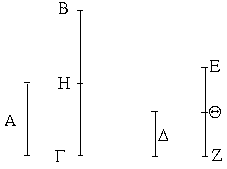
Ἐπεὶ γὰρ ὃ μέρος ἐστὶν ὁ Α τοῦ ΒΓ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Δ τοῦ ΕΖ, ὅσοι ἄρα εἰσὶν ἐν τῷ ΒΓ ἀριθμοὶ ἴσοι τῷ Α, τοσοῦτοί εἰσι καὶ ἐν τῷ ΕΖ ἴσοι τῷ Δ. διῃρήσθω ὁ μὲν ΒΓ εἰς τοὺς τῷ Α ἴσους τοὺς ΒΗ, ΗΓ, ὁ δὲ ΕΖ εἰς τοὺς τῷ Δ ἴσους τοὺς ΕΘ, ΘΖ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΒΗ, ΗΓ τῷ πλήθει τῶν ΕΘ, ΘΖ.
Καὶ ἐπεὶ ἴσοι εἰσὶν οἱ ΒΗ, ΗΓ ἀριθμοὶ ἀλλήλοις, εἰσὶ δὲ καὶ οἱ ΕΘ, ΘΖ ἀριθμοὶ ἴσοι ἀλλήλοις, καί ἐστιν ἴσον τὸ πλῆθος τῶν ΒΗ, ΗΓ τῷ πλήθει τῶν ΕΘ, ΘΖ, ὃ ἄρα μέρος ἐστὶν ὁ ΒΗ τοῦ ΕΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΗΓ τοῦ ΘΖ ἢ τὰ αὐτὰ μέρη· ὥστε καὶ ὃ μέρος ἐστὶν ὁ ΒΗ τοῦ ΕΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ συναμφότερος ὁ ΒΓ συναμφοτέρου τοῦ ΕΖ ἢ τὰ αὐτὰ μέρη. ἴσος δὲ ὁ μὲν ΒΗ τῷ Α, ὁ δὲ ΕΘ τῷ Δ· ὃ ἄρα μέρος ἐστὶν ὁ Α τοῦ Δ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΒΓ τοῦ ΕΖ ἢ τὰ αὐτὰ μέρη· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον VII
Ἐὰν ἀριθμὸς ἀριθμοῦ μέρη ᾖ, καὶ ἕτερος ἑτέρου τὰ αὐτὰ μέρη ᾖ, καὶ ἐναλλάξ, ἃ μέρη ἐστὶν ὁ πρῶτος τοῦ τρίτου ἢ μέρος, τὰ αὐτὰ μέρη ἔσται καὶ ὁ δεύτερος τοῦ τετάρτου ἢ τὸ αὐτὸ μέρος.
Ἀριθμὸς γὰρ ὁ ΑΒ ἀριθμοῦ τοῦ Γ μέρη ἔστω, καὶ ἕτερος ὁ ΔΕ ἑτέρου τοῦ Ζ τὰ αὐτὰ μέρη· λέγω, ὅτι καὶ ἐναλλάξ, ἃ μέρη ἐστὶν ὁ ΑΒ τοῦ ΔΕ ἢ μέρος, τὰ αὐτὰ μέρη ἐστὶ καὶ ὁ Γ τοῦ Ζ ἢ τὸ αὐτὸ μέρος.
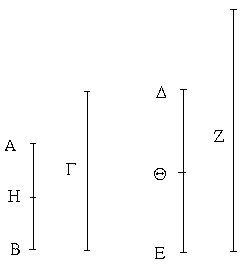
Ἐπεὶ γάρ, ἃ μέρη ἐστὶν ὁ ΑΒ τοῦ Γ, τὰ αὐτὰ μέρη ἐστὶ καὶ ὁ ΔΕ τοῦ Ζ, ὅσα ἄρα ἐστὶν ἐν τῷ ΑΒ μέρη τοῦ Γ, τοσαῦτα καὶ ἐν τῷ ΔΕ μέρη τοῦ Ζ. διῃρήσθω ὁ μὲν ΑΒ εἰς τὰ τοῦ Γ μέρη τὰ ΑΗ, ΗΒ, ὁ δὲ ΔΕ εἰς τὰ τοῦ Ζ μέρη τὰ ΔΘ, ΘΕ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΑΗ, ΗΒ τῷ πλήθει τῶν ΔΘ, ΘΕ. καὶ ἐπεί, ὃ μέρος ἐστὶν ὁ ΑΗ τοῦ Γ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΔΘ τοῦ Ζ, καὶ ἐναλλάξ, ὃ μέρος ἐστὶν ὁ ΑΗ τοῦ ΔΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Γ τοῦ Ζ ἢ τὰ αὐτὰ μέρη. διὰ τὰ αὐτὰ δὴ καί, ὃ μέρος ἐστὶν ὁ ΗΒ τοῦ ΘΕ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Γ τοῦ Ζ ἢ τὰ αὐτὰ μέρη· ὥστε καί [ὃ μέρος ἐστὶν ὁ ΑΗ τοῦ ΔΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΗΒ τοῦ ΘΕ ἢ τὰ αὐτὰ μέρη· καὶ ὃ ἄρα μέρος ἐστὶν ὁ ΑΗ τοῦ ΔΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΑΒ τοῦ ΔΕ ἢ τὰ αὐτὰ μέρη· ἀλλ' ὃ μέρος ἐστὶν ὁ ΑΗ τοῦ ΔΘ ἢ μέρη, τὸ αὐτὸ μέρος ἐδείχθη καὶ ὁ Γ τοῦ Ζ ἢ τὰ αὐτὰ μέρη, καὶ] ἃ [ἄρα] μέρη ἐστὶν ὁ ΑΒ τοῦ ΔΕ ἢ μέρος, τὰ αὐτὰ μέρη ἐστὶ καὶ ὁ Γ τοῦ Ζ ἢ τὸ αὐτὸ μέρος· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον VII
Ἐὰν ᾖ ὡς ὅλος πρὸς ὅλον, οὕτως ἀφαιρεθεὶς πρὸς ἀφαιρεθέντα, καὶ ὁ λοιπὸς πρὸς τὸν λοιπὸν ἔσται, ὡς ὅλος πρὸς ὅλον.
Ἔστω ὡς ὅλος ὁ ΑΒ πρὸς ὅλον τὸν ΓΔ, οὕτως ἀφαιρεθεὶς ὁ ΑΕ πρὸς ἀφαιρεθέντα τὸν ΓΖ· λέγω, ὅτι καὶ λοιπὸς ὁ ΕΒ πρὸς λοιπὸν τὸν ΖΔ ἐστιν, ὡς ὅλος ὁ ΑΒ πρὸς ὅλον τὸν ΓΔ.
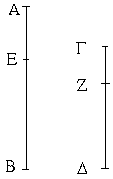
Ἐπεί ἐστιν ὡς ὁ ΑΒ πρὸς τὸν ΓΔ, οὕτως ὁ ΑΕ πρὸς τὸν ΓΖ, ὃ ἄρα μέρος ἐστὶν ὁ ΑΒ τοῦ ΓΔ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ ΑΕ τοῦ ΓΖ ἢ τὰ αὐτὰ μέρη. καὶ λοιπὸς ἄρα ὁ ΕΒ λοιποῦ τοῦ ΖΔ τὸ αὐτὸ μέρος ἐστὶν ἢ μέρη, ἅπερ ὁ ΑΒ τοῦ ΓΔ. ἔστιν ἄρα ὡς ὁ ΕΒ πρὸς τὸν ΖΔ, οὕτως ὁ ΑΒ πρὸς τὸν ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον VII
Ἐὰν ὦσιν ὁποσοιοῦν ἀριθμοὶ ἀνάλογον, ἔσται ὡς εἷς τῶν ἡγουμένων πρὸς ἕνα τῶν ἑπομένων, οὕτως ἅπαντες οἱ ἡγούμενοι πρὸς ἅπαντας τοὺς ἑπομένους.
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἀνάλογον οἱ Α, Β, Γ, Δ, ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ· λέγω, ὅτι ἐστὶν ὡς ὁ Α πρὸς τὸν Β, οὕτως οἱ Α, Γ πρὸς τοὺς Β, Δ.
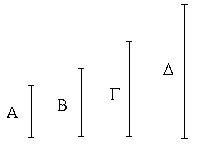
Ἐπεὶ γάρ ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ, ὃ ἄρα μέρος ἐστὶν ὁ Α τοῦ Β ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Γ τοῦ Δ ἢ μέρη. καὶ συναμφότερος ἄρα ὁ Α, Γ συναμφοτέρου τοῦ Β, Δ τὸ αὐτὸ μέρος ἐστὶν ἢ τὰ αὐτὰ μέρη, ἅπερ ὁ Α τοῦ Β. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως οἱ Α, Γ πρὸς τοὺς Β, Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον VII
Ἐὰν τέσσαρες ἀριθμοὶ ἀνάλογον ὦσιν, καὶ ἐναλλὰξ ἀνάλογον ἔσονται.
Ἔστωσαν τέσσαρες ἀριθμοὶ ἀνάλογον οἱ Α, Β, Γ, Δ, ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ· λέγω, ὅτι καὶ ἐναλλὰξ ἀνάλογον ἔσονται, ὡς ὁ Α πρὸς τὸν Γ, οὕτως ὁ Β πρὸς τὸν Δ.
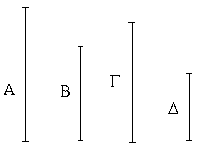
Ἐπεὶ γάρ ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ, ὃ ἄρα μέρος ἐστὶν ὁ Α τοῦ Β ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Γ τοῦ Δ ἢ τὰ αὐτὰ μέρη. ἐναλλὰξ ἄρα, ὃ μέρος ἐστὶν ὁ Α τοῦ Γ ἢ μέρη, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Β τοῦ Δ ἢ τὰ αὐτὰ μέρη. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Γ, οὕτως ὁ Β πρὸς τὸν Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον VII
Ἐὰν ὦσιν ὁποσοιοῦν ἀριθμοὶ καὶ ἄλλοι αὐτοῖς ἴσοι τὸ πλῆθος σύνδυο λαμβανόμενοι καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ δι' ἴσου ἐν τῷ αὐτῷ λόγῳ ἔσονται.
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ οἱ Α, Β, Γ καὶ ἄλλοι αὐτοῖς ἴσοι τὸ πλῆθος σύνδυο λαμβανόμενοι ἐν τῷ αὐτῷ λόγῳ οἱ Δ, Ε, Ζ, ὡς μὲν ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε, ὡς δὲ ὁ Β πρὸς τὸν Γ, οὕτως ὁ Ε πρὸς τὸν Ζ· λέγω, ὅτι καὶ δι' ἴσου ἐστὶν ὡς ὁ Α πρὸς τὸν Γ, οὕτως ὁ Δ πρὸς τὸν Ζ.
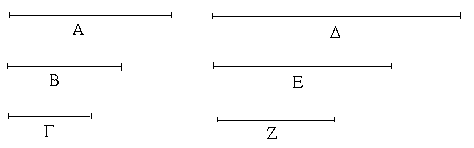
Ἐπεὶ γάρ ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε, ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Δ, οὕτως ὁ Β πρὸς τὸν Ε. πάλιν, ἐπεί ἐστιν ὡς ὁ Β πρὸς τὸν Γ, οὕτως ὁ Ε πρὸς τὸν Ζ, ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Β πρὸς τὸν Ε, οὕτως ὁ Γ πρὸς τὸν Ζ. ὡς δὲ ὁ Β πρὸς τὸν Ε, οὕτως ὁ Α πρὸς τὸν Δ· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Δ, οὕτως ὁ Γ πρὸς τὸν Ζ· ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Γ, οὕτως ὁ Δ πρὸς τὸν Ζ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον VII
Ἐὰν μονὰς ἀριθμόν τινα μετρῇ, ἰσάκις δὲ ἕτερος ἀριθμὸς ἄλλον τινὰ ἀριθμὸν μετρῇ, καὶ ἐναλλὰξ ἰσάκις ἡ μονὰς τὸν τρίτον ἀριθμὸν μετρήσει καὶ ὁ δεύτερος τὸν τέταρτον.
Μονὰς γὰρ ἡ Α ἀριθμόν τινα τὸν ΒΓ μετρείτω, ἰσάκις δὲ ἕτερος ἀριθμὸς ὁ Δ ἄλλον τινὰ ἀριθμὸν τὸν ΕΖ μετρείτω· λέγω, ὅτι καὶ ἐναλλὰξ ἰσάκις ἡ Α μονὰς τὸν Δ ἀριθμὸν μετρεῖ καὶ ὁ ΒΓ τὸν ΕΖ.
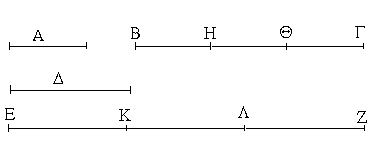
Ἐπεὶ γὰρ ἰσάκις ἡ Α μονὰς τὸν ΒΓ ἀριθμὸν μετρεῖ καὶ ὁ Δ τὸν ΕΖ, ὅσαι ἄρα εἰσὶν ἐν τῷ ΒΓ μονάδες, τοσοῦτοί εἰσι καὶ ἐν τῷ ΕΖ ἀριθμοὶ ἴσοι τῷ Δ. διῃρήσθω ὁ μὲν ΒΓ εἰς τὰς ἐν ἑαυτῷ μονάδας τὰς ΒΗ, ΗΘ, ΘΓ, ὁ δὲ ΕΖ εἰς τοὺς τῷ Δ ἴσους τοὺς ΕΚ, ΚΛ, ΛΖ. ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΒΗ, ΗΘ, ΘΓ τῷ πλήθει τῶν ΕΚ, ΚΛ, ΛΖ. καὶ ἐπεὶ ἴσαι εἰσὶν αἱ ΒΗ, ΗΘ, ΘΓ μονάδες ἀλλήλαις, εἰσὶ δὲ καὶ οἱ ΕΚ, ΚΛ, ΛΖ ἀριθμοὶ ἴσοι ἀλλήλοις, καί ἐστιν ἴσον τὸ πλῆθος τῶν ΒΗ, ΗΘ, ΘΓ μονάδων τῷ πλήθει τῶν ΕΚ, ΚΛ, ΛΖ ἀριθμῶν, ἔσται ἄρα ὡς ἡ ΒΗ μονὰς πρὸς τὸν ΕΚ ἀριθμόν, οὕτως ἡ ΗΘ μονὰς πρὸς τὸν ΚΛ ἀριθμὸν καὶ ἡ ΘΓ μονὰς πρὸς τὸν ΛΖ ἀριθμόν. ἔσται ἄρα καὶ ὡς εἷς τῶν ἡγουμένων πρὸς ἕνα τῶν ἑπομένων, οὕτως ἅπαντες οἱ ἡγούμενοι πρὸς ἅπαντας τοὺς ἑπομένους· ἔστιν ἄρα ὡς ἡ ΒΗ μονὰς πρὸς τὸν ΕΚ ἀριθμόν, οὕτως ὁ ΒΓ πρὸς τὸν ΕΖ. ἴση δὲ ἡ ΒΗ μονὰς τῇ Α μονάδι, ὁ δὲ ΕΚ ἀριθμὸς τῷ Δ ἀριθμῷ. ἔστιν ἄρα ὡς ἡ Α μονὰς πρὸς τὸν Δ ἀριθμόν, οὕτως ὁ ΒΓ πρὸς τὸν ΕΖ. ἰσάκις ἄρα ἡ Α μονὰς τὸν Δ ἀριθμὸν μετρεῖ καὶ ὁ ΒΓ τὸν ΕΖ· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινας, οἱ γενόμενοι ἐξ αὐτῶν ἴσοι ἀλλήλοις ἔσονται.
Ἔστωσαν δύο ἀριθμοὶ οἱ Α, Β, καὶ ὁ μὲν Α τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω, ὁ δὲ Β τὸν Α πολλαπλασιάσας τὸν Δ ποιείτω· λέγω, ὅτι ἴσος ἐστὶν ὁ Γ τῷ Δ.
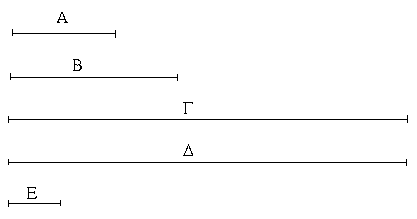
Ἐπεὶ γὰρ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ Β ἄρα τὸν Γ μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας. μετρεῖ δὲ καὶ ἡ Ε μονὰς τὸν Α ἀριθμὸν κατὰ τὰς ἐν αὐτῷ μονάδας· ἰσάκις ἄρα ἡ Ε μονὰς τὸν Α ἀριθμὸν μετρεῖ καὶ ὁ Β τὸν Γ. ἐναλλὰξ ἄρα ἰσάκις ἡ Ε μονὰς τὸν Β ἀριθμὸν μετρεῖ καὶ ὁ Α τὸν Γ. πάλιν, ἐπεὶ ὁ Β τὸν Α πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ Α ἄρα τὸν Δ μετρεῖ κατὰ τὰς ἐν τῷ Β μονάδας. μετρεῖ δὲ καὶ ἡ Ε μονὰς τὸν Β κατὰ τὰς ἐν αὐτῷ μονάδας· ἰσάκις ἄρα ἡ Ε μονὰς τὸν Β ἀριθμὸν μετρεῖ καὶ ὁ Α τὸν Δ. ἰσάκις δὲ ἡ Ε μονὰς τὸν Β ἀριθμὸν ἐμέτρει καὶ ὁ Α τὸν Γ· ἰσάκις ἄρα ὁ Α ἑκάτερον τῶν Γ, Δ μετρεῖ. ἴσος ἄρα ἐστὶν ὁ Γ τῷ Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον VII
Ἐὰν ἀριθμὸς δύο ἀριθμοὺς πολλαπλασιάσας ποιῇ τινας, οἱ γενόμενοι ἐξ αὐτῶν τὸν αὐτὸν ἕξουσι λόγον τοῖς πολλαπλασιασθεῖσιν.
Ἀριθμὸς γὰρ ὁ Α δύο ἀριθμοὺς τοὺς Β, Γ πολλαπλασιάσας τοὺς Δ, Ε ποιείτω· λέγω, ὅτι ἐστὶν ὡς ὁ Β πρὸς τὸν Γ, οὕτως ὁ Δ πρὸς τὸν Ε.
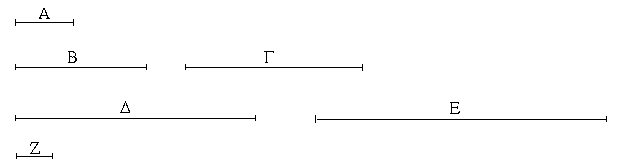
Ἐπεὶ γὰρ ὁ Α τὸν Β πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ Β ἄρα τὸν Δ μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας. μετρεῖ δὲ καὶ ἡ Ζ μονὰς τὸν Α ἀριθμὸν κατὰ τὰς ἐν αὐτῷ μονάδας· ἰσάκις ἄρα ἡ Ζ μονὰς τὸν Α ἀριθμὸν μετρεῖ καὶ ὁ Β τὸν Δ. ἔστιν ἄρα ὡς ἡ Ζ μονὰς πρὸς τὸν Α ἀριθμόν, οὕτως ὁ Β πρὸς τὸν Δ. διὰ τὰ αὐτὰ δὴ καὶ ὡς ἡ Ζ μονὰς πρὸς τὸν Α ἀριθμόν, οὕτως ὁ Γ πρὸς τὸν Ε· καὶ ὡς ἄρα ὁ Β πρὸς τὸν Δ, οὕτως ὁ Γ πρὸς τὸν Ε. ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Β πρὸς τὸν Γ, οὕτως ὁ Δ πρὸς τὸν Ε· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ ἀριθμόν τινα πολλαπλασιάσαντες ποιῶσί τινας, οἱ γενόμενοι ἐξ αὐτῶν τὸν αὐτὸν ἕξουσι λόγον τοῖς πολλαπλασιάσασιν.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β ἀριθμόν τινα τὸν Γ πολλαπλασιάσαντες τοὺς Δ, Ε ποιείτωσαν· λέγω, ὅτι ἐστὶν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε.
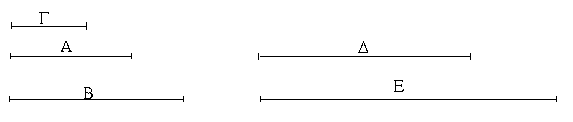
Ἐπεὶ γὰρ ὁ Α τὸν Γ πολλαπλασιάσας τὸν Δ πεποίηκεν, καὶ ὁ Γ ἄρα τὸν Α πολλαπλασιάσας τὸν Δ πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Γ τὸν Β πολλαπλασιάσας τὸν Ε πεποίηκεν. ἀριθμὸς δὴ ὁ Γ δύο ἀριθμοὺς τοὺς Α, Β πολλαπλασιάσας τοὺς Δ, Ε πεποίηκεν. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον VII
Ἐὰν τέσσαρες ἀριθμοὶ ἀνάλογον ὦσιν, ὁ ἐκ πρώτου καὶ τετάρτου γενόμενος ἀριθμὸς ἴσος ἔσται τῷ ἐκ δευτέρου καὶ τρίτου γενομένῳ ἀριθμῷ· καὶ ἐὰν ὁ ἐκ πρώτου καὶ τετάρτου γενόμενος ἀριθμὸς ἴσος ᾖ τῷ ἐκ δευτέρου καὶ τρίτου, οἱ τέσσαρες ἀριθμοὶ ἀνάλογον ἔσονται.
Ἔστωσαν τέσσαρες ἀριθμοὶ ἀνάλογον οἱ Α, Β, Γ, Δ, ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ, καὶ ὁ μὲν Α τὸν Δ πολλαπλασιάσας τὸν Ε ποιείτω, ὁ δὲ Β τὸν Γ πολλαπλασιάσας τὸν Ζ ποιείτω· λέγω, ὅτι ἴσος ἐστὶν ὁ Ε τῷ Ζ.
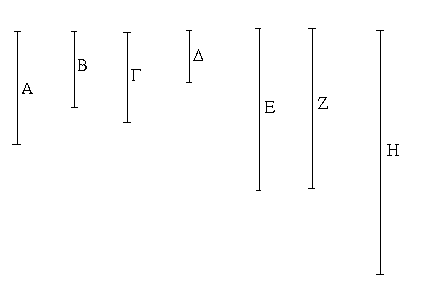
Ὁ γὰρ Α τὸν Γ πολλαπλασιάσας τὸν Η ποιείτω. ἐπεὶ οὖν ὁ Α τὸν Γ πολλαπλασιάσας τὸν Η πεποίηκεν, τὸν δὲ Δ πολλαπλασιάσας τὸν Ε πεποίηκεν, ἀριθμὸς δὴ ὁ Α δύο ἀριθμοὺς τοὺς Γ, Δ πολλαπλασιάσας τοὺς Η, Ε πεποίηκεν. ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Η πρὸς τὸν Ε. ἀλλ' ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Α πρὸς τὸν Β· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, οὕτως ὁ Η πρὸς τὸν Ε. πάλιν, ἐπεὶ ὁ Α τὸν Γ πολλαπλασιάσας τὸν Η πεποίηκεν, ἀλλὰ μὴν καὶ ὁ Β τὸν Γ πολλαπλασιάσας τὸν Ζ πεποίηκεν, δύο δὴ ἀριθμοὶ οἱ Α, Β ἀριθμόν τινα τὸν Γ πολλαπλασιάσαντες τοὺς Η, Ζ πεποιήκασιν. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Η πρὸς τὸν Ζ. ἀλλὰ μὴν καὶ ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Η πρὸς τὸν Ε· καὶ ὡς ἄρα ὁ Η πρὸς τὸν Ε, οὕτως ὁ Η πρὸς τὸν Ζ. ὁ Η ἄρα πρὸς ἑκάτερον τῶν Ε, Ζ τὸν αὐτὸν ἔχει λόγον· ἴσος ἄρα ἐστὶν ὁ Ε τῷ Ζ.
Ἔστω δὴ πάλιν ἴσος ὁ Ε τῷ Ζ· λέγω, ὅτι ἐστὶν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεὶ ἴσος ἐστὶν ὁ Ε τῷ Ζ, ἔστιν ἄρα ὡς ὁ Η πρὸς τὸν Ε, οὕτως ὁ Η πρὸς τὸν Ζ. ἀλλ' ὡς μὲν ὁ Η πρὸς τὸν Ε, οὕτως ὁ Γ πρὸς τὸν Δ, ὡς δὲ ὁ Η πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Β. καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, οὕτως ὁ Γ πρὸς τὸν Δ· ὅπερ ἔδει δεῖξαι
Πρότασις κ΄ 20 Βιβλίον VII
Οἱ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα.
Ἔστωσαν γὰρ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β οἱ ΓΔ, ΕΖ· λέγω, ὅτι ἰσάκις ὁ ΓΔ τὸν Α μετρεῖ καὶ ὁ ΕΖ τὸν Β.
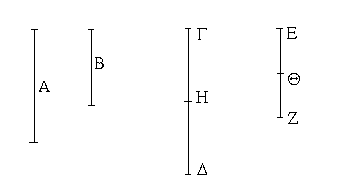
Ὁ ΓΔ γὰρ τοῦ Α οὔκ ἐστι μέρη. εἰ γὰρ δυνατόν, ἔστω· καὶ ὁ ΕΖ ἄρα τοῦ Β τὰ αὐτὰ μέρη ἐστίν, ἅπερ ὁ ΓΔ τοῦ Α. ὅσα ἄρα ἐστὶν ἐν τῷ ΓΔ μέρη τοῦ Α, τοσαῦτά ἐστι καὶ ἐν τῷ ΕΖ μέρη τοῦ Β. διῃρήσθω ὁ μὲν ΓΔ εἰς τὰ τοῦ Α μέρη τὰ ΓΗ, ΗΔ, ὁ δὲ ΕΖ εἰς τὰ τοῦ Β μέρη τὰ ΕΘ, ΘΖ· ἔσται δὴ ἴσον τὸ πλῆθος τῶν ΓΗ, ΗΔ τῷ πλήθει τῶν ΕΘ, ΘΖ. καὶ ἐπεὶ ἴσοι εἰσὶν οἱ ΓΗ, ΗΔ ἀριθμοὶ ἀλλήλοις, εἰσὶ δὲ καὶ οἱ ΕΘ, ΘΖ ἀριθμοὶ ἴσοι ἀλλήλοις, καί ἐστιν ἴσον τὸ πλῆθος τῶν ΓΗ, ΗΔ τῷ πλήθει τῶν ΕΘ, ΘΖ, ἔστιν ἄρα ὡς ὁ ΓΗ πρὸς τὸν ΕΘ, οὕτως ὁ ΗΔ πρὸς τὸν ΘΖ. ἔσται ἄρα καὶ ὡς εἷς τῶν ἡγουμένων πρὸς ἕνα τῶν ἑπομένων, οὕτως ἅπαντες οἱ ἡγούμενοι πρὸς ἅπαντας τοὺς ἑπομένους. ἔστιν ἄρα ὡς ὁ ΓΗ πρὸς τὸν ΕΘ, οὕτως ὁ ΓΔ πρὸς τὸν ΕΖ· οἱ ΓΗ, ΕΘ ἄρα τοῖς ΓΔ, ΕΖ ἐν τῷ αὐτῷ λόγῳ εἰσὶν ἐλάσσονες ὄντες αὐτῶν· ὅπερ ἐστὶν ἀδύνατον· ὑπόκεινται γὰρ οἱ ΓΔ, ΕΖ ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς. οὐκ ἄρα μέρη ἐστὶν ὁ ΓΔ τοῦ Α· μέρος ἄρα. καὶ ὁ ΕΖ τοῦ Β τὸ αὐτὸ μέρος ἐστίν, ὅπερ ὁ ΓΔ τοῦ Α· ἰσάκις ἄρα ὁ ΓΔ τὸν Α μετρεῖ καὶ ὁ ΕΖ τὸν Β· ὅπερ ἔδει δεῖξαι.
Πρότασις κα΄ 21 Βιβλίον VII
Οἱ πρῶτοι πρὸς ἀλλήλους ἀριθμοὶ ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
Ἔστωσαν πρῶτοι πρὸς ἀλλήλους ἀριθμοὶ οἱ Α, Β· λέγω, ὅτι οἱ Α, Β ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
Εἰ γὰρ μή, ἔσονταί τινες τῶν Α, Β ἐλάσσονες ἀριθμοὶ ἐν τῷ αὐτῷ λόγῳ ὄντες τοῖς Α, Β. ἔστωσαν οἱ Γ, Δ.
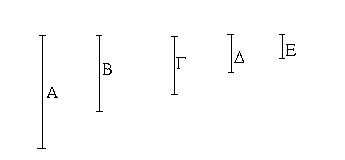
Ἐπεὶ οὖν οἱ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάττων τὸν ἐλάττονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον, ἰσάκις ἄρα ὁ Γ τὸν Α μετρεῖ καὶ ὁ Δ τὸν Β. ὁσάκις δὴ ὁ Γ τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε. καὶ ὁ Δ ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας. καὶ ἐπεὶ ὁ Γ τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας, καὶ ὁ Ε ἄρα τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Γ μονάδας. διὰ τὰ αὐτὰ δὴ ὁ Ε καὶ τὸν Β μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας. ὁ Ε ἄρα τοὺς Α, Β μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἔσονταί τινες τῶν Α, Β ἐλάσσονες ἀριθμοὶ ἐν τῷ αὐτῷ λόγῳ ὄντες τοῖς Α, Β. οἱ Α, Β ἄρα ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον VII
Οἱ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς πρῶτοι πρὸς ἀλλήλους εἰσίν.
Ἔστωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς οἱ Α, Β· λέγω, ὅτι οἱ Α, Β πρῶτοι πρὸς ἀλλήλους εἰσίν.
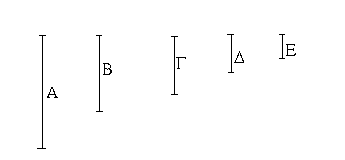
Εἰ γὰρ μή εἰσι πρῶτοι πρὸς ἀλλήλους, μετρήσει τις αὐτοὺς ἀριθμός. μετρείτω, καὶ ἔστω ὁ Γ. καὶ ὁσάκις μὲν ὁ Γ τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Δ, ὁσάκις δὲ ὁ Γ τὸν Β μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε.
Ἐπεὶ ὁ Γ τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας, ὁ Γ ἄρα τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Γ τὸν Ε πολλαπλασιάσας τὸν Β πεποίηκεν. ἀριθμὸς δὴ ὁ Γ δύο ἀριθμοὺς τοὺς Δ, Ε πολλαπλασιάσας τοὺς Α, Β πεποίηκεν· ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Α πρὸς τὸν Β· οἱ Δ, Ε ἄρα τοῖς Α, Β ἐν τῷ αὐτῷ λόγῳ εἰσὶν ἐλάσσονες ὄντες αὐτῶν· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Α, Β ἀριθμοὺς ἀριθμός τις μετρήσει. οἱ Α, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, ὁ τὸν ἕνα αὐτῶν μετρῶν ἀριθμὸς πρὸς τὸν λοιπὸν πρῶτος ἔσται.
Ἔστωσαν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β, τὸν δὲ Α μετρείτω τις ἀριθμὸς ὁ Γ· λέγω, ὅτι καὶ οἱ Γ, Β πρῶτοι πρὸς ἀλλήλους εἰσίν.
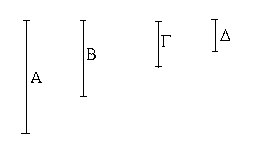
Εἰ γὰρ μή εἰσιν οἱ Γ, Β πρῶτοι πρὸς ἀλλήλους, μετρήσει [τις] τοὺς Γ, Β ἀριθμός. μετρείτω, καὶ ἔστω ὁ Δ. ἐπεὶ ὁ Δ τὸν Γ μετρεῖ, ὁ δὲ Γ τὸν Α μετρεῖ, καὶ ὁ Δ ἄρα τὸν Α μετρεῖ. μετρεῖ δὲ καὶ τὸν Β· ὁ Δ ἄρα τοὺς Α, Β μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Γ, Β ἀριθμοὺς ἀριθμός τις μετρήσει. οἱ Γ, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρός τινα ἀριθμὸν πρῶτοι ὦσιν, καὶ ὁ ἐξ αὐτῶν γενόμενος πρὸς τὸν αὐτὸν πρῶτος ἔσται.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρός τινα ἀριθμὸν τὸν Γ πρῶτοι ἔστωσαν, καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Δ ποιείτω· λέγω, ὅτι οἱ Γ, Δ πρῶτοι πρὸς ἀλλήλους εἰσίν.
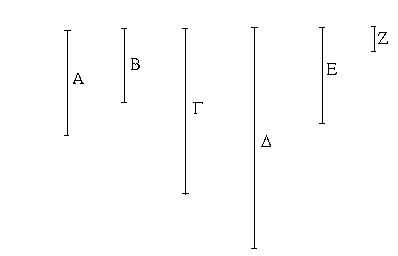
Εἰ γὰρ μή εἰσιν οἱ Γ, Δ πρῶτοι πρὸς ἀλλήλους, μετρήσει [τις] τοὺς Γ, Δ ἀριθμός. μετρείτω, καὶ ἔστω ὁ Ε. καὶ ἐπεὶ οἱ Γ, Α πρῶτοι πρὸς ἀλλήλους εἰσίν, τὸν δὲ Γ μετρεῖ τις ἀριθμὸς ὁ Ε, οἱ Α, Ε ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. ὁσάκις δὴ ὁ Ε τὸν Δ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ζ· καὶ ὁ Ζ ἄρα τὸν Δ μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας. ὁ Ε ἄρα τὸν Ζ πολλαπλασιάσας τὸν Δ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Δ πεποίηκεν· ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Ε, Ζ τῷ ἐκ τῶν Α, Β. ἐὰν δὲ ὁ ὑπὸ τῶν ἄκρων ἴσος ᾖ τῷ ὑπὸ τῶν μέσων, οἱ τέσσαρες ἀριθμοὶ ἀνάλογόν εἰσιν· ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Α, οὕτως ὁ Β πρὸς τὸν Ζ. οἱ δὲ Α, Ε πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· ὁ Ε ἄρα τὸν Β μετρεῖ. μετρεῖ δὲ καὶ τὸν Γ· ὁ Ε ἄρα τοὺς Β, Γ μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Γ, Δ ἀριθμοὺς ἀριθμός τις μετρήσει. οἱ Γ, Δ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, ὁ ἐκ τοῦ ἑνὸς αὐτῶν γενόμενος πρὸς τὸν λοιπὸν πρῶτος ἔσται.
Ἔστωσαν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β, καὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι οἱ Β, Γ πρῶτοι πρὸς ἀλλήλους εἰσίν.
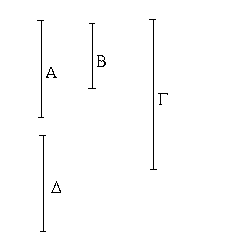
Κείσθω γὰρ τῷ Α ἴσος ὁ Δ. ἐπεὶ οἱ Α, Β πρῶτοι πρὸς ἀλλήλους εἰσίν, ἴσος δὲ ὁ Α τῷ Δ, καὶ οἱ Δ, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. ἑκάτερος ἄρα τῶν Δ, Α πρὸς τὸν Β πρῶτός ἐστιν· καὶ ὁ ἐκ τῶν Δ, Α ἄρα γενόμενος πρὸς τὸν Β πρῶτος ἔσται. ὁ δὲ ἐκ τῶν Δ, Α γενόμενος ἀριθμός ἐστιν ὁ Γ. οἱ Γ, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κς΄ 26 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρὸς δύο ἀριθμοὺς ἀμφότεροι πρὸς ἑκάτερον πρῶτοι ὦσιν, καὶ οἱ ἐξ αὐτῶν γενόμενοι πρῶτοι πρὸς ἀλλήλους ἔσονται.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρὸς δύο ἀριθμοὺς τοὺς Γ, Δ ἀμφότεροι πρὸς ἑκάτερον πρῶτοι ἔστωσαν, καὶ ὁ μὲν Α τὸν Β πολλαπλασιάσας τὸν Ε ποιείτω, ὁ δὲ Γ τὸν Δ πολλαπλασιάσας τὸν Ζ ποιείτω· λέγω, ὅτι οἱ Ε, Ζ πρῶτοι πρὸς ἀλλήλους εἰσίν.
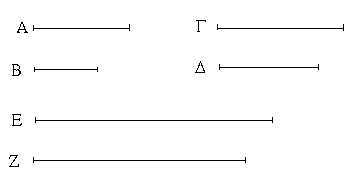
Ἐπεὶ γὰρ ἑκάτερος τῶν Α, Β πρὸς τὸν Γ πρῶτός ἐστιν, καὶ ὁ ἐκ τῶν Α, Β ἄρα γενόμενος πρὸς τὸν Γ πρῶτος ἔσται. ὁ δὲ ἐκ τῶν Α, Β γενόμενός ἐστιν ὁ Ε· οἱ Ε, Γ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. διὰ τὰ αὐτὰ δὴ καὶ οἱ Δ, Ε πρῶτοι πρὸς ἀλλήλους εἰσίν. ἑκάτερος ἄρα τῶν Γ, Δ πρὸς τὸν Ε πρῶτός ἐστιν. καὶ ὁ ἐκ τῶν Γ, Δ ἄρα γενόμενος πρὸς τὸν Ε πρῶτος ἔσται. ὁ δὲ ἐκ τῶν Γ, Δ γενόμενός ἐστιν ὁ Ζ. οἱ Ε, Ζ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, καὶ πολλαπλασιάσας ἑκάτερος ἑαυτὸν ποιῇ τινα, οἱ γενόμενοι ἐξ αὐτῶν πρῶτοι πρὸς ἀλλήλους ἔσονται, κἂν οἱ ἐξ ἀρχῆς τοὺς γενομένους πολλαπλασιάσαντες ποιῶσί τινας, κἀκεῖνοι πρῶτοι πρὸς ἀλλήλους ἔσονται [καὶ ἀεὶ περὶ τοὺς ἄκρους τοῦτο συμβαίνει].
Ἔστωσαν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β, καὶ ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Γ ποιείτω, τὸν δὲ Γ πολλαπλασιάσας τὸν Δ ποιείτω, ὁ δὲ Β ἑαυτὸν μὲν πολλαπλασιάσας τὸν Ε ποιείτω, τὸν δὲ Ε πολλαπλασιάσας τὸν Ζ ποιείτω· λέγω, ὅτι οἵ τε Γ, Ε καὶ οἱ Δ, Ζ πρῶτοι πρὸς ἀλλήλους εἰσίν.
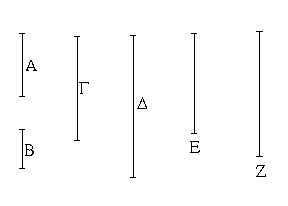
Ἐπεὶ γὰρ οἱ Α, Β πρῶτοι πρὸς ἀλλήλους εἰσίν, καὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Γ πεποίηκεν, οἱ Γ, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. ἐπεὶ οὖν οἱ Γ, Β πρῶτοι πρὸς ἀλλήλους εἰσίν, καὶ ὁ Β ἑαυτὸν πολλαπλασιάσας τὸν Ε πεποίηκεν, οἱ Γ, Ε ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. πάλιν, ἐπεὶ οἱ Α, Β πρῶτοι πρὸς ἀλλήλους εἰσίν, καὶ ὁ Β ἑαυτὸν πολλαπλασιάσας τὸν Ε πεποίηκεν, οἱ Α, Ε ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. ἐπεὶ οὖν δύο ἀριθμοὶ οἱ Α, Γ πρὸς δύο ἀριθμοὺς τοὺς Β, Ε ἀμφότεροι πρὸς ἑκάτερον πρῶτοί εἰσιν, καὶ ὁ ἐκ τῶν Α, Γ ἄρα γενόμενος πρὸς τὸν ἐκ τῶν Β, Ε πρῶτός ἐστιν. καί ἐστιν ὁ μὲν ἐκ τῶν Α, Γ ὁ Δ, ὁ δὲ ἐκ τῶν Β, Ε ὁ Ζ. οἱ Δ, Ζ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, καὶ συναμφότερος πρὸς ἑκάτερον αὐτῶν πρῶτος ἔσται· καὶ ἐὰν συναμφότερος πρὸς ἕνα τινὰ αὐτῶν πρῶτος ᾖ, καὶ οἱ ἐξ ἀρχῆς ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ἔσονται.
Συγκείσθωσαν γὰρ δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους οἱ ΑΒ, ΒΓ· λέγω, ὅτι καὶ συναμφότερος ὁ ΑΓ πρὸς ἑκάτερον τῶν ΑΒ, ΒΓ πρῶτός ἐστιν.
Εἰ γὰρ μή εἰσιν οἱ ΓΑ, ΑΒ πρῶτοι πρὸς ἀλλήλους, μετρήσει τις τοὺς ΓΑ, ΑΒ ἀριθμός. μετρείτω, καὶ ἔστω ὁ Δ. ἐπεὶ οὖν ὁ Δ τοὺς ΓΑ, ΑΒ μετρεῖ, καὶ λοιπὸν ἄρα τὸν ΒΓ μετρήσει. μετρεῖ δὲ καὶ τὸν ΒΑ· ὁ Δ ἄρα τοὺς ΑΒ, ΒΓ μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς ΓΑ, ΑΒ ἀριθμοὺς ἀριθμός τις μετρήσει· οἱ ΓΑ, ΑΒ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. διὰ τὰ αὐτὰ δὴ καὶ οἱ ΑΓ, ΓΒ πρῶτοι πρὸς ἀλλήλους εἰσίν. ὁ ΓΑ ἄρα πρὸς ἑκάτερον τῶν ΑΒ, ΒΓ πρῶτός ἐστιν.
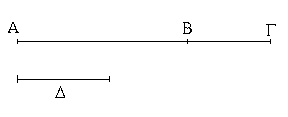
Ἔστωσαν δὴ πάλιν οἱ ΓΑ, ΑΒ πρῶτοι πρὸς ἀλλήλους· λέγω, ὅτι καὶ οἱ ΑΒ, ΒΓ πρῶτοι πρὸς ἀλλήλους εἰσίν.
Εἰ γὰρ μή εἰσιν οἱ ΑΒ, ΒΓ πρῶτοι πρὸς ἀλλήλους, μετρήσει τις τοὺς ΑΒ, ΒΓ ἀριθμός. μετρείτω, καὶ ἔστω ὁ Δ. καὶ ἐπεὶ ὁ Δ ἑκάτερον τῶν ΑΒ, ΒΓ μετρεῖ, καὶ ὅλον ἄρα τὸν ΓΑ μετρήσει. μετρεῖ δὲ καὶ τὸν ΑΒ· ὁ Δ ἄρα τοὺς ΓΑ, ΑΒ μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς ΑΒ, ΒΓ ἀριθμοὺς ἀριθμός τις μετρήσει. οἱ ΑΒ, ΒΓ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον VII
Ἅπας πρῶτος ἀριθμὸς πρὸς ἅπαντα ἀριθμόν, ὃν μὴ μετρεῖ, πρῶτός ἐστιν.
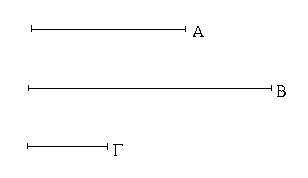
Ἔστω πρῶτος ἀριθμὸς ὁ Α καὶ τὸν Β μὴ μετρείτω· λέγω, ὅτι οἱ Β, Α πρῶτοι πρὸς ἀλλήλους εἰσίν. εἰ γὰρ μή εἰσιν οἱ Β, Α πρῶτοι πρὸς ἀλλήλους, μετρήσει τις αὐτοὺς ἀριθμός. μετρείτω ὁ Γ. ἐπεὶ ὁ Γ τὸν Β μετρεῖ, ὁ δὲ Α τὸν Β οὐ μετρεῖ, ὁ Γ ἄρα τῷ Α οὔκ ἐστιν ὁ αὐτός. καὶ ἐπεὶ ὁ Γ τοὺς Β, Α μετρεῖ, καὶ τὸν Α ἄρα μετρεῖ πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Β, Α μετρήσει τις ἀριθμός. οἱ Α, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, τὸν δὲ γενόμενον ἐξ αὐτῶν μετρῇ τις πρῶτος ἀριθμός, καὶ ἕνα τῶν ἐξ ἀρχῆς μετρήσει.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πολλαπλασιάσαντες ἀλλήλους τὸν Γ ποιείτωσαν, τὸν δὲ Γ μετρείτω τις πρῶτος ἀριθμὸς ὁ Δ· λέγω, ὅτι ὁ Δ ἕνα τῶν Α, Β μετρεῖ.
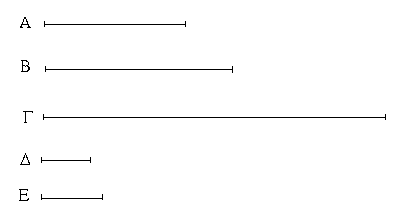
Τὸν γὰρ Α μὴ μετρείτω· καί ἐστι πρῶτος ὁ Δ· οἱ Α, Δ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ὁσάκις ὁ Δ τὸν Γ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε. ἐπεὶ οὖν ὁ Δ τὸν Γ μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας, ὁ Δ ἄρα τὸν Ε πολλαπλασιάσας τὸν Γ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν· ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Δ, Ε τῷ ἐκ τῶν Α, Β. ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Α, οὕτως ὁ Β πρὸς τὸν Ε. οἱ δὲ Δ, Α πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· ὁ Δ ἄρα τὸν Β μετρεῖ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἐὰν τὸν Β μὴ μετρῇ, τὸν Α μετρήσει. ὁ Δ ἄρα ἕνα τῶν Α, Β μετρεῖ· ὅπερ ἔδει δεῖξαι.
Πρότασις λα΄ 31 Βιβλίον VII
Ἅπας σύνθετος ἀριθμὸς ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται.
Ἔστω σύνθετος ἀριθμὸς ὁ Α· λέγω, ὅτι ὁ Α ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται.
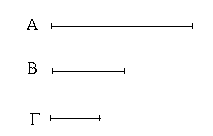
Ἐπεὶ γὰρ σύνθετός ἐστιν ὁ Α, μετρήσει τις αὐτὸν ἀριθμός. μετρείτω, καὶ ἔστω ὁ Β. καὶ εἰ μὲν πρῶτός ἐστιν ὁ Β, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. εἰ δὲ σύνθετος, μετρήσει τις αὐτὸν ἀριθμός. μετρείτω, καὶ ἔστω ὁ Γ. καὶ ἐπεὶ ὁ Γ τὸν Β μετρεῖ, ὁ δὲ Β τὸν Α μετρεῖ, καὶ ὁ Γ ἄρα τὸν Α μετρεῖ. καὶ εἰ μὲν πρῶτός ἐστιν ὁ Γ, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. εἰ δὲ σύνθετος, μετρήσει τις αὐτὸν ἀριθμός. τοιαύτης δὴ γινομένης ἐπισκέψεως ληφθήσεταί τις πρῶτος ἀριθμός, ὃς μετρήσει. εἰ γὰρ οὐ ληφθήσεται, μετρήσουσι τὸν Α ἀριθμὸν ἄπειροι ἀριθμοί, ὧν ἕτερος ἑτέρου ἐλάσσων ἐστίν· ὅπερ ἐστὶν ἀδύνατον ἐν ἀριθμοῖς. ληφθήσεταί τις ἄρα πρῶτος ἀριθμός, ὃς μετρήσει τὸν πρὸ ἑαυτοῦ, ὃς καὶ τὸν Α μετρήσει.
Ἅπας ἄρα σύνθετος ἀριθμὸς ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται· ὅπερ ἔδει δεῖξαι.
Πρότασις λβ΄ 32 Βιβλίον VII
Ἅπας ἀριθμὸς ἤτοι πρῶτός ἐστιν ἢ ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται.
Ἔστω ἀριθμὸς ὁ Α· λέγω, ὅτι ὁ Α ἤτοι πρῶτός ἐστιν ἢ ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται.
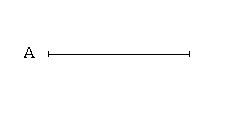
Εἰ μὲν οὖν πρῶτός ἐστιν ὁ Α, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. εἰ δὲ σύνθετος, μετρήσει τις αὐτὸν πρῶτος ἀριθμός.
Ἅπας ἄρα ἀριθμὸς ἤτοι πρῶτός ἐστιν ἢ ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον VII
Ἀριθμῶν δοθέντων ὁποσωνοῦν εὑρεῖν τοὺς ἐλαχίστους τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
Ἔστωσαν οἱ δοθέντες ὁποσοιοῦν ἀριθμοὶ οἱ Α, Β, Γ· δεῖ δὴ εὑρεῖν τοὺς ἐλαχίστους τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β, Γ.
Οἱ Α, Β, Γ γὰρ ἤτοι πρῶτοι πρὸς ἀλλήλους εἰσὶν ἢ οὔ. εἰ μὲν οὖν οἱ Α, Β, Γ πρῶτοι πρὸς ἀλλήλους εἰσίν, ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
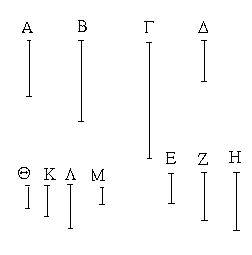
Εἰ δὲ οὔ, εἰλήφθω τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον ὁ Δ, καὶ ὁσάκις ὁ Δ ἕκαστον τῶν Α, Β, Γ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν ἑκάστῳ τῶν Ε, Ζ, Η. καὶ ἕκαστος ἄρα τῶν Ε, Ζ, Η ἕκαστον τῶν Α, Β, Γ μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας. οἱ Ε, Ζ, Η ἄρα τοὺς Α, Β, Γ ἰσάκις μετροῦσιν· οἱ Ε, Ζ, Η ἄρα τοῖς Α, Β, Γ ἐν τῷ αὐτῷ λόγῳ εἰσίν. λέγω δή, ὅτι καὶ ἐλάχιστοι. εἰ γὰρ μή εἰσιν οἱ Ε, Ζ, Η ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β, Γ, ἔσονται [τινες] τῶν Ε, Ζ, Η ἐλάσσονες ἀριθμοὶ ἐν τῷ αὐτῷ λόγῳ ὄντες τοῖς Α, Β, Γ. ἔστωσαν οἱ Θ, Κ, Λ· ἰσάκις ἄρα ὁ Θ τὸν Α μετρεῖ καὶ ἑκάτερος τῶν Κ, Λ ἑκάτερον τῶν Β, Γ. ὁσάκις δὲ ὁ Θ τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Μ· καὶ ἑκάτερος ἄρα τῶν Κ, Λ ἑκάτερον τῶν Β, Γ μετρεῖ κατὰ τὰς ἐν τῷ Μ μονάδας. καὶ ἐπεὶ ὁ Θ τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Μ μονάδας, καὶ ὁ Μ ἄρα τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Θ μονάδας. διὰ τὰ αὐτὰ δὴ ὁ Μ καὶ ἑκάτερον τῶν Β, Γ μετρεῖ κατὰ τὰς ἐν ἑκατέρῳ τῶν Κ, Λ μονάδας· ὁ Μ ἄρα τοὺς Α, Β, Γ μετρεῖ. καὶ ἐπεὶ ὁ Θ τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Μ μονάδας, ὁ Θ ἄρα τὸν Μ πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Ε τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν. ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Ε, Δ τῷ ἐκ τῶν Θ, Μ. ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Μ πρὸς τὸν Δ. μείζων δὲ ὁ Ε τοῦ Θ· μείζων ἄρα καὶ ὁ Μ τοῦ Δ. καὶ μετρεῖ τοὺς Α, Β, Γ· ὅπερ ἐστὶν ἀδύνατον· ὑπόκειται γὰρ ὁ Δ τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον. οὐκ ἄρα ἔσονταί τινες τῶν Ε, Ζ, Η ἐλάσσονες ἀριθμοὶ ἐν τῷ αὐτῷ λόγῳ ὄντες τοῖς Α, Β, Γ. οἱ Ε, Ζ, Η ἄρα ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β, Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις λδ΄ 34 Βιβλίον VII
Δύο ἀριθμῶν δοθέντων εὑρεῖν, ὃν ἐλάχιστον μετροῦσιν ἀριθμόν.
Ἔστωσαν οἱ δοθέντες δύο ἀριθμοὶ οἱ Α, Β· δεῖ δὴ εὑρεῖν, ὃν ἐλάχιστον μετροῦσιν ἀριθμόν.
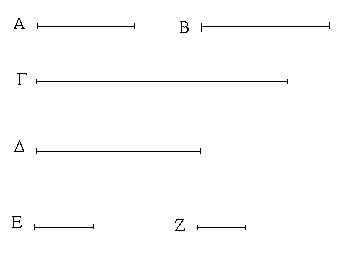
Οἱ Α, Β γὰρ ἤτοι πρῶτοι πρὸς ἀλλήλους εἰσὶν ἢ οὔ. ἔστωσαν πρότερον οἱ Α, Β πρῶτοι πρὸς ἀλλήλους, καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· καὶ ὁ Β ἄρα τὸν Α πολλαπλασιάσας τὸν Γ πεποίηκεν. οἱ Α, Β ἄρα τὸν Γ μετροῦσιν. λέγω δή, ὅτι καὶ ἐλάχιστον. εἰ γὰρ μή, μετρήσουσί τινα ἀριθμὸν οἱ Α, Β ἐλάσσονα ὄντα τοῦ Γ. μετρείτωσαν τὸν Δ. καὶ ὁσάκις ὁ Α τὸν Δ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε, ὁσάκις δὲ ὁ Β τὸν Δ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ζ· ὁ μὲν Α ἄρα τὸν Ε πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ δὲ Β τὸν Ζ πολλαπλασιάσας τὸν Δ πεποίηκεν· ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Α, Ε τῷ ἐκ τῶν Β, Ζ. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Ζ πρὸς τὸν Ε. οἱ δὲ Α, Β πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα· ὁ Β ἄρα τὸν Ε μετρεῖ, ὡς ἑπόμενος ἑπόμενον. καὶ ἐπεὶ ὁ Α τοὺς Β, Ε πολλαπλασιάσας τοὺς Γ, Δ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Β πρὸς τὸν Ε, οὕτως ὁ Γ πρὸς τὸν Δ. μετρεῖ δὲ ὁ Β τὸν Ε· μετρεῖ ἄρα καὶ ὁ Γ τὸν Δ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οἱ Α, Β μετροῦσί τινα ἀριθμὸν ἐλάσσονα ὄντα τοῦ Γ. ὁ Γ ἄρα ἐλάχιστος ὢν ὑπὸ τῶν Α, Β μετρεῖται.
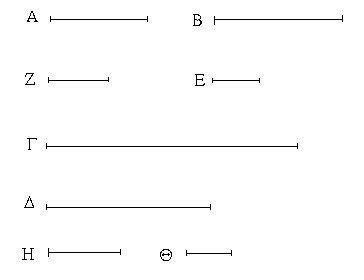
Μὴ ἔστωσαν δὴ οἱ Α, Β πρῶτοι πρὸς ἀλλήλους, καὶ εἰλήφθωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β οἱ Ζ, Ε· ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Α, Ε τῷ ἐκ τῶν Β, Ζ. καὶ ὁ Α τὸν Ε πολλαπλασιάσας τὸν Γ ποιείτω· καὶ ὁ Β ἄρα τὸν Ζ πολλαπλασιάσας τὸν Γ πεποίηκεν· οἱ Α, Β ἄρα τὸν Γ μετροῦσιν. λέγω δή, ὅτι καὶ ἐλάχιστον. εἰ γὰρ μή, μετρήσουσί τινα ἀριθμὸν οἱ Α, Β ἐλάσσονα ὄντα τοῦ Γ. μετρείτωσαν τὸν Δ. καὶ ὁσάκις μὲν ὁ Α τὸν Δ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Η, ὁσάκις δὲ ὁ Β τὸν Δ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Θ. ὁ μὲν Α ἄρα τὸν Η πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ δὲ Β τὸν Θ πολλαπλασιάσας τὸν Δ πεποίηκεν. ἴσος ἄρα ἐστὶν ὁ ἐκ τῶν Α, Η τῷ ἐκ τῶν Β, Θ· ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Θ πρὸς τὸν Η. ὡς δὲ ὁ Α πρὸς τὸν Β, οὕτως ὁ Ζ πρὸς τὸν Ε· καὶ ὡς ἄρα ὁ Ζ πρὸς τὸν Ε, οὕτως ὁ Θ πρὸς τὸν Η. οἱ δὲ Ζ, Ε ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα· ὁ Ε ἄρα τὸν Η μετρεῖ. καὶ ἐπεὶ ὁ Α τοὺς Ε, Η πολλαπλασιάσας τοὺς Γ, Δ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Η, οὕτως ὁ Γ πρὸς τὸν Δ. ὁ δὲ Ε τὸν Η μετρεῖ· καὶ ὁ Γ ἄρα τὸν Δ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οἱ Α, Β μετρήσουσί τινα ἀριθμὸν ἐλάσσονα ὄντα τοῦ Γ. ὁ Γ ἄρα ἐλάχιστος ὢν ὑπὸ τῶν Α, Β μετρεῖται· ὅπερ ἔδει δεῖξαι
Πρότασις λε΄ 35 Βιβλίον VII
Ἐὰν δύο ἀριθμοὶ ἀριθμόν τινα μετρῶσιν, καὶ ὁ ἐλάχιστος ὑπ' αὐτῶν μετρούμενος τὸν αὐτὸν μετρήσει.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β ἀριθμόν τινα τὸν ΓΔ μετρείτωσαν, ἐλάχιστον δὲ τὸν Ε· λέγω, ὅτι καὶ ὁ Ε τὸν ΓΔ μετρεῖ.
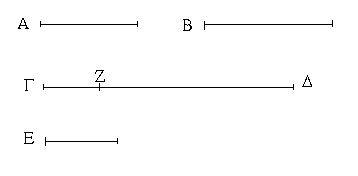
Εἰ γὰρ οὐ μετρεῖ ὁ Ε τὸν ΓΔ, ὁ Ε τὸν ΔΖ μετρῶν λειπέτω ἑαυτοῦ ἐλάσσονα τὸν ΓΖ. καὶ ἐπεὶ οἱ Α, Β τὸν Ε μετροῦσιν, ὁ δὲ Ε τὸν ΔΖ μετρεῖ, καὶ οἱ Α, Β ἄρα τὸν ΔΖ μετρήσουσιν. μετροῦσι δὲ καὶ ὅλον τὸν ΓΔ· καὶ λοιπὸν ἄρα τὸν ΓΖ μετρήσουσιν ἐλάσσονα ὄντα τοῦ Ε· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οὐ μετρεῖ ὁ Ε τὸν ΓΔ· μετρεῖ ἄρα· ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον VII
Τριῶν ἀριθμῶν δοθέντων εὑρεῖν, ὃν ἐλάχιστον μετροῦσιν ἀριθμόν.
Ἔστωσαν οἱ δοθέντες τρεῖς ἀριθμοὶ οἱ Α, Β, Γ· δεῖ δὴ εὑρεῖν, ὃν ἐλάχιστον μετροῦσιν ἀριθμόν.
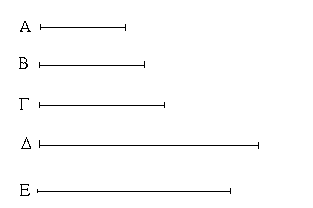
Εἰλήφθω γὰρ ὑπὸ δύο τῶν Α, Β ἐλάχιστος μετρούμενος ὁ Δ. ὁ δὴ Γ τὸν Δ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω πρότερον. μετροῦσι δὲ καὶ οἱ Α, Β τὸν Δ· οἱ Α, Β, Γ ἄρα τὸν Δ μετροῦσιν. λέγω δή, ὅτι καὶ ἐλάχιστον. εἰ γὰρ μή, μετρήσουσιν [τινα] ἀριθμὸν οἱ Α, Β, Γ ἐλάσσονα ὄντα τοῦ Δ. μετρείτωσαν τὸν Ε. ἐπεὶ οἱ Α, Β, Γ τὸν Ε μετροῦσιν, καὶ οἱ Α, Β ἄρα τὸν Ε μετροῦσιν. καὶ ὁ ἐλάχιστος ἄρα ὑπὸ τῶν Α, Β μετρούμενος [τὸν Ε] μετρήσει. ἐλάχιστος δὲ ὑπὸ τῶν Α, Β μετρούμενός ἐστιν ὁ Δ· ὁ Δ ἄρα τὸν Ε μετρήσει ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οἱ Α, Β, Γ μετρήσουσί τινα ἀριθμὸν ἐλάσσονα ὄντα τοῦ Δ· οἱ Α, Β, Γ ἄρα ἐλάχιστον τὸν Δ μετροῦσιν.
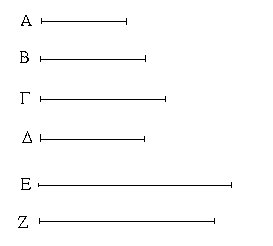
Μὴ μετρείτω δὴ πάλιν ὁ Γ τὸν Δ, καὶ εἰλήφθω ὑπὸ τῶν Γ, Δ ἐλάχιστος μετρούμενος ἀριθμὸς ὁ Ε. ἐπεὶ οἱ Α, Β τὸν Δ μετροῦσιν, ὁ δὲ Δ τὸν Ε μετρεῖ, καὶ οἱ Α, Β ἄρα τὸν Ε μετροῦσιν. μετρεῖ δὲ καὶ ὁ Γ [τὸν Ε· καὶ] οἱ Α, Β, Γ ἄρα τὸν Ε μετροῦσιν. λέγω δή, ὅτι καὶ ἐλάχιστον. εἰ γὰρ μή, μετρήσουσί τινα οἱ Α, Β, Γ ἐλάσσονα ὄντα τοῦ Ε. μετρείτωσαν τὸν Ζ. ἐπεὶ οἱ Α, Β, Γ τὸν Ζ μετροῦσιν, καὶ οἱ Α, Β ἄρα τὸν Ζ μετροῦσιν· καὶ ὁ ἐλάχιστος ἄρα ὑπὸ τῶν Α, Β μετρούμενος τὸν Ζ μετρήσει. ἐλάχιστος δὲ ὑπὸ τῶν Α, Β μετρούμενός ἐστιν ὁ Δ· ὁ Δ ἄρα τὸν Ζ μετρεῖ. μετρεῖ δὲ καὶ ὁ Γ τὸν Ζ· οἱ Δ, Γ ἄρα τὸν Ζ μετροῦσιν· ὥστε καὶ ὁ ἐλάχιστος ὑπὸ τῶν Δ, Γ μετρούμενος τὸν Ζ μετρήσει. ὁ δὲ ἐλάχιστος ὑπὸ τῶν Γ, Δ μετρούμενός ἐστιν ὁ Ε· ὁ Ε ἄρα τὸν Ζ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οἱ Α, Β, Γ μετρήσουσί τινα ἀριθμὸν ἐλάσσονα ὄντα τοῦ Ε. ὁ Ε ἄρα ἐλάχιστος ὢν ὑπὸ τῶν Α, Β, Γ μετρεῖται· ὅπερ ἔδει δεῖξαι.
Πρότασις λζ΄ 37 Βιβλίον VII
Ἐὰν ἀριθμὸς ὑπό τινος ἀριθμοῦ μετρῆται, ὁ μετρούμενος ὁμώνυμον μέρος ἕξει τῷ μετροῦντι.
Ἀριθμὸς γὰρ ὁ Α ὑπό τινος ἀριθμοῦ τοῦ Β μετρείσθω· λέγω, ὅτι ὁ Α ὁμώνυμον μέρος ἔχει τῷ Β.
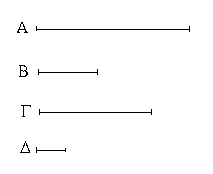
Ὁσάκις γὰρ ὁ Β τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Γ. ἐπεὶ ὁ Β τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Γ μονάδας, μετρεῖ δὲ καὶ ἡ Δ μονὰς τὸν Γ ἀριθμὸν κατὰ τὰς ἐν αὐτῷ μονάδας, ἰσάκις ἄρα ἡ Δ μονὰς τὸν Γ ἀριθμὸν μετρεῖ καὶ ὁ Β τὸν Α. ἐναλλὰξ ἄρα ἰσάκις ἡ Δ μονὰς τὸν Β ἀριθμὸν μετρεῖ καὶ ὁ Γ τὸν Α· ὃ ἄρα μέρος ἐστὶν ἡ Δ μονὰς τοῦ Β ἀριθμοῦ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Γ τοῦ Α. ἡ δὲ Δ μονὰς τοῦ Β ἀριθμοῦ μέρος ἐστὶν ὁμώνυμον αὐτῷ· καὶ ὁ Γ ἄρα τοῦ Α μέρος ἐστὶν ὁμώνυμον τῷ Β. ὥστε ὁ Α μέρος ἔχει τὸν Γ ὁμώνυμον ὄντα τῷ Β· ὅπερ ἔδει δεῖξαι.
Πρότασις λη΄ 38 Βιβλίον VII
Ἐὰν ἀριθμὸς μέρος ἔχῃ ὁτιοῦν, ὑπὸ ὁμωνύμου ἀριθμοῦ μετρηθήσεται τῷ μέρει.
Ἀριθμὸς γὰρ ὁ Α μέρος ἐχέτω ὁτιοῦν τὸν Β, καὶ τῷ Β μέρει ὁμώνυμος ἔστω [ἀριθμὸς] ὁ Γ· λέγω, ὅτι ὁ Γ τὸν Α μετρεῖ.
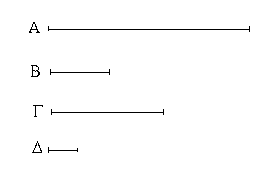
Ἐπεὶ γὰρ ὁ Β τοῦ Α μέρος ἐστὶν ὁμώνυμον τῷ Γ, ἔστι δὲ καὶ ἡ Δ μονὰς τοῦ Γ μέρος ὁμώνυμον αὐτῷ, ὃ ἄρα μέρος ἐστὶν ἡ Δ μονὰς τοῦ Γ ἀριθμοῦ, τὸ αὐτὸ μέρος ἐστὶ καὶ ὁ Β τοῦ Α· ἰσάκις ἄρα ἡ Δ μονὰς τὸν Γ ἀριθμὸν μετρεῖ καὶ ὁ Β τὸν Α. ἐναλλὰξ ἄρα ἰσάκις ἡ Δ μονὰς τὸν Β ἀριθμὸν μετρεῖ καὶ ὁ Γ τὸν Α. ὁ Γ ἄρα τὸν Α μετρεῖ· ὅπερ ἔδει δεῖξαι.
Πρότασις λθ΄ 39 Βιβλίον VII
Ἀριθμὸν εὑρεῖν, ὃς ἐλάχιστος ὢν ἕξει τὰ δοθέντα μέρη.
Ἔστω τὰ δοθέντα μέρη τὰ Α, Β, Γ· δεῖ δὴ ἀριθμὸν εὑρεῖν, ὃς ἐλάχιστος ὢν ἕξει τὰ Α, Β, Γ μέρη.
Ἔστωσαν γὰρ τοῖς Α, Β, Γ μέρεσιν ὁμώνυμοι ἀριθμοὶ οἱ Δ, Ε, Ζ, καὶ εἰλήφθω ὑπὸ τῶν Δ, Ε, Ζ ἐλάχιστος μετρούμενος ἀριθμὸς ὁ Η.
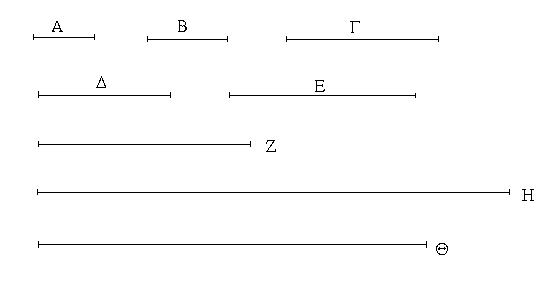
Ὁ Η ἄρα ὁμώνυμα μέρη ἔχει τοῖς Δ, Ε, Ζ. τοῖς δὲ Δ, Ε, Ζ ὁμώνυμα μέρη ἐστὶ τὰ Α, Β, Γ· ὁ Η ἄρα ἔχει τὰ Α, Β, Γ μέρη. λέγω δή, ὅτι καὶ ἐλάχιστος ὤν. εἰ γὰρ μή, ἔσται τις τοῦ Η ἐλάσσων ἀριθμός, ὃς ἕξει τὰ Α, Β, Γ μέρη. ἔστω ὁ Θ. ἐπεὶ ὁ Θ ἔχει τὰ Α, Β, Γ μέρη, ὁ Θ ἄρα ὑπὸ ὁμωνύμων ἀριθμῶν μετρηθήσεται τοῖς Α, Β, Γ μέρεσιν. τοῖς δὲ Α, Β, Γ μέρεσιν ὁμώνυμοι ἀριθμοί εἰσιν οἱ Δ, Ε, Ζ· ὁ Θ ἄρα ὑπὸ τῶν Δ, Ε, Ζ μετρεῖται. καί ἐστιν ἐλάσσων τοῦ Η· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἔσται τις τοῦ Η ἐλάσσων ἀριθμός, ὃς ἕξει τὰ Α, Β, Γ μέρη· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου η΄
Βιβλίον VIII
Προτάσεις κζ΄ 27
Πρότασις α΄ 1 Βιβλίον VIII
Ἐὰν ὦσιν ὁσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, οἱ δὲ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους ὦσιν, ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, οἱ δὲ ἄκροι αὐτῶν οἱ Α, Δ πρῶτοι πρὸς ἀλλήλους ἔστωσαν· λέγω, ὅτι οἱ Α, Β, Γ, Δ ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς.
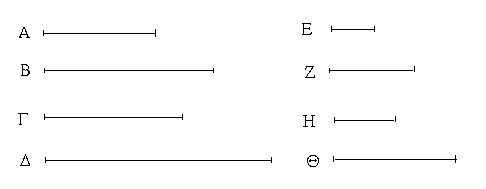
Εἰ γὰρ μή, ἔστωσαν ἐλάττονες τῶν Α, Β, Γ, Δ οἱ Ε, Ζ, Η, Θ ἐν τῷ αὐτῷ λόγῳ ὄντες αὐτοῖς. καὶ ἐπεὶ οἱ Α, Β, Γ, Δ ἐν τῷ αὐτῷ λόγῳ εἰσὶ τοῖς Ε, Ζ, Η, Θ, καί ἐστιν ἴσον τὸ πλῆθος [τῶν Α, Β, Γ, Δ] τῷ πλήθει [τῶν Ε, Ζ, Η, Θ], δι' ἴσου ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Δ, ὁ Ε πρὸς τὸν Θ. οἱ δὲ Α, Δ πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον. μετρεῖ ἄρα ὁ Α τὸν Ε ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα οἱ Ε, Ζ, Η, Θ ἐλάσσονες ὄντες τῶν Α, Β, Γ, Δ ἐν τῷ αὐτῷ λόγῳ εἰσὶν αὐτοῖς. οἱ Α, Β, Γ, Δ ἄρα ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον VIII
Ἀριθμοὺς εὑρεῖν ἑξῆς ἀνάλογον ἐλαχίστους, ὅσους ἂν ἐπιτάξῃ τις, ἐν τῷ δοθέντι λόγῳ.
Ἔστω ὁ δοθεὶς λόγος ἐν ἐλαχίστοις ἀριθμοῖς ὁ τοῦ Α πρὸς τὸν Β· δεῖ δὴ ἀριθμοὺς εὑρεῖν ἑξῆς ἀνάλογον ἐλαχίστους, ὅσους ἄν τις ἐπιτάξῃ, ἐν τῷ τοῦ Α πρὸς τὸν Β λόγῳ.
Ἐπιτετάχθωσαν δὴ τέσσαρες, καὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Γ ποιείτω, τὸν δὲ Β πολλαπλασιάσας τὸν Δ ποιείτω, καὶ ἔτι ὁ Β ἑαυτὸν πολλαπλασιάσας τὸν Ε ποιείτω, καὶ ἔτι ὁ Α τοὺς Γ, Δ, Ε πολλαπλασιάσας τοὺς Ζ, Η, Θ ποιείτω, ὁ δὲ Β τὸν Ε πολλαπλασιάσας τὸν Κ ποιείτω.
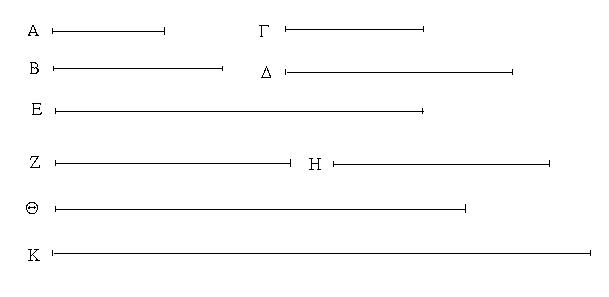
Καὶ ἐπεὶ ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Γ πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Δ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, [οὕτως] ὁ Γ πρὸς τὸν Δ. πάλιν, ἐπεὶ ὁ μὲν Α τὸν Β πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ δὲ Β ἑαυτὸν πολλαπλασιάσας τὸν Ε πεποίηκεν, ἑκάτερος ἄρα τῶν Α, Β τὸν Β πολλαπλασιάσας ἑκάτερον τῶν Δ, Ε πεποίηκεν. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε. ἀλλ' ὡς ὁ Α πρὸς τὸν Β, ὁ Γ πρὸς τὸν Δ· καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Δ, ὁ Δ πρὸς τὸν Ε. καὶ ἐπεὶ ὁ Α τοὺς Γ, Δ πολλαπλασιάσας τοὺς Ζ, Η πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, [οὕτως] ὁ Ζ πρὸς τὸν Η. ὡς δὲ ὁ Γ πρὸς τὸν Δ, οὕτως ἦν ὁ Α πρὸς τὸν Β· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, ὁ Ζ πρὸς τὸν Η. πάλιν, ἐπεὶ ὁ Α τοὺς Δ, Ε πολλαπλασιάσας τοὺς Η, Θ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ε, ὁ Η πρὸς τὸν Θ. ἀλλ' ὡς ὁ Δ πρὸς τὸν Ε, ὁ Α πρὸς τὸν Β. καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, οὕτως ὁ Η πρὸς τὸν Θ. καὶ ἐπεὶ οἱ Α, Β τὸν Ε πολλαπλασιάσαντες τοὺς Θ, Κ πεποιήκασιν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Θ πρὸς τὸν Κ. ἀλλ' ὡς ὁ Α πρὸς τὸν Β, οὕτως ὅ τε Ζ πρὸς τὸν Η καὶ ὁ Η πρὸς τὸν Θ. καὶ ὡς ἄρα ὁ Ζ πρὸς τὸν Η, οὕτως ὅ τε Η πρὸς τὸν Θ καὶ ὁ Θ πρὸς τὸν Κ· οἱ Γ, Δ, Ε ἄρα καὶ οἱ Ζ, Η, Θ, Κ ἀνάλογόν εἰσιν ἐν τῷ τοῦ Α πρὸς τὸν Β λόγῳ. λέγω δή, ὅτι καὶ ἐλάχιστοι. ἐπεὶ γὰρ οἱ Α, Β ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, οἱ δὲ ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων πρῶτοι πρὸς ἀλλήλους εἰσίν, οἱ Α, Β ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἑκάτερος μὲν τῶν Α, Β ἑαυτὸν πολλαπλασιάσας ἑκάτερον τῶν Γ, Ε πεποίηκεν, ἑκάτερον δὲ τῶν Γ, Ε πολλαπλασιάσας ἑκάτερον τῶν Ζ, Κ πεποίηκεν· οἱ Γ, Ε ἄρα καὶ οἱ Ζ, Κ πρῶτοι πρὸς ἀλλήλους εἰσίν. ἐὰν δὲ ὦσιν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, οἱ δὲ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους ὦσιν, ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς. οἱ Γ, Δ, Ε ἄρα καὶ οἱ Ζ, Η, Θ, Κ ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β· ὅπερ ἔδει δεῖξαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν τρεῖς ἀριθμοὶ ἑξῆς ἀνάλογον ἐλάχιστοι ὦσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, οἱ ἄκροι αὐτῶν τετράγωνοί εἰσιν, ἐὰν δὲ τέσσαρες, κύβοι.
Πρότασις γ΄ 3 Βιβλίον VIII
Ἐὰν ὦσιν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, οἱ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους εἰσίν.
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς οἱ Α, Β, Γ, Δ· λέγω, ὅτι οἱ ἄκροι αὐτῶν οἱ Α, Δ πρῶτοι πρὸς ἀλλήλους εἰσίν.
Εἰλήφθωσαν γὰρ δύο μὲν ἀριθμοὶ ἐλάχιστοι ἐν τῷ τῶν Α, Β, Γ, Δ λόγῳ οἱ Ε, Ζ, τρεῖς δὲ οἱ Η, Θ, Κ, καὶ ἑξῆς ἑνὶ πλείους, ἕως τὸ λαμβανόμενον πλῆθος ἴσον γένηται τῷ πλήθει τῶν Α, Β, Γ, Δ. εἰλήφθωσαν καὶ ἔστωσαν οἱ Λ, Μ, Ν, Ξ.
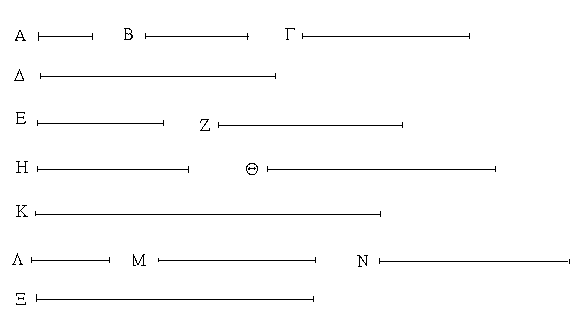
Καὶ ἐπεὶ οἱ Ε, Ζ ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἐπεὶ ἑκάτερος τῶν Ε, Ζ ἑαυτὸν μὲν πολλαπλασιάσας ἑκάτερον τῶν Η, Κ πεποίηκεν, ἑκάτερον δὲ τῶν Η, Κ πολλαπλασιάσας ἑκάτερον τῶν Λ, Ξ πεποίηκεν, καὶ οἱ Η, Κ ἄρα καὶ οἱ Λ, Ξ πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἐπεὶ οἱ Α, Β, Γ, Δ ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, εἰσὶ δὲ καὶ οἱ Λ, Μ, Ν, Ξ ἐλάχιστοι ἐν τῷ αὐτῷ λόγῳ ὄντες τοῖς Α, Β, Γ, Δ, καί ἐστιν ἴσον τὸ πλῆθος τῶν Α, Β, Γ, Δ τῷ πλήθει τῶν Λ, Μ, Ν, Ξ, ἕκαστος ἄρα τῶν Α, Β, Γ, Δ ἑκάστῳ τῶν Λ, Μ, Ν, Ξ ἴσος ἐστίν· ἴσος ἄρα ἐστὶν ὁ μὲν Α τῷ Λ, ὁ δὲ Δ τῷ Ξ. καί εἰσιν οἱ Λ, Ξ πρῶτοι πρὸς ἀλλήλους. καὶ οἱ Α, Δ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον VIII
Λόγων δοθέντων ὁποσωνοῦν ἐν ἐλαχίστοις ἀριθμοῖς ἀριθμοὺς εὑρεῖν ἑξῆς ἀνάλογον ἐλαχίστους ἐν τοῖς δοθεῖσι λόγοις.
Ἔστωσαν οἱ δοθέντες λόγοι ἐν ἐλαχίστοις ἀριθμοῖς ὅ τε τοῦ Α πρὸς τὸν Β καὶ ὁ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι ὁ τοῦ Ε πρὸς τὸν Ζ· δεῖ δὴ ἀριθμοὺς εὑρεῖν ἑξῆς ἀνάλογον ἐλαχίστους ἔν τε τῷ τοῦ Α πρὸς τὸν Β λόγῳ καὶ ἐν τῷ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι ἐν τῷ τοῦ Ε πρὸς τὸν Ζ.
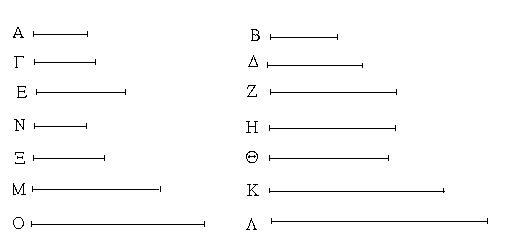
Εἰλήφθω γὰρ ὁ ὑπὸ τῶν Β, Γ ἐλάχιστος μετρούμενος ἀριθμὸς ὁ Η. καὶ ὁσάκις μὲν ὁ Β τὸν Η μετρεῖ, τοσαυτάκις καὶ ὁ Α τὸν Θ μετρείτω, ὁσάκις δὲ ὁ Γ τὸν Η μετρεῖ, τοσαυτάκις καὶ ὁ Δ τὸν Κ μετρείτω. ὁ δὲ Ε τὸν Κ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω πρότερον. καὶ ὁσάκις ὁ Ε τὸν Κ μετρεῖ, τοσαυτάκις καὶ ὁ Ζ τὸν Λ μετρείτω. καὶ ἐπεὶ ἰσάκις ὁ Α τὸν Θ μετρεῖ καὶ ὁ Β τὸν Η, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Θ πρὸς τὸν Η. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Η πρὸς τὸν Κ, καὶ ἔτι ὡς ὁ Ε πρὸς τὸν Ζ, οὕτως ὁ Κ πρὸς τὸν Λ· οἱ Θ, Η, Κ, Λ ἄρα ἑξῆς ἀνάλογόν εἰσιν ἔν τε τῷ τοῦ Α πρὸς τὸν Β καὶ ἐν τῷ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι ἐν τῷ τοῦ Ε πρὸς τὸν Ζ λόγῳ. λέγω δή, ὅτι καὶ ἐλάχιστοι. εἰ γὰρ μή εἰσιν οἱ Θ, Η, Κ, Λ ἑξῆς ἀνάλογον ἐλάχιστοι ἔν τε τοῖς τοῦ Α πρὸς τὸν Β καὶ τοῦ Γ πρὸς τὸν Δ καὶ ἐν τῷ τοῦ Ε πρὸς τὸν Ζ λόγοις, ἔστωσαν οἱ Ν, Ξ, Μ, Ο. καὶ ἐπεί ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Ν πρὸς τὸν Ξ, οἱ δὲ Α, Β ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον, ὁ Β ἄρα τὸν Ξ μετρεῖ. διὰ τὰ αὐτὰ δὴ καὶ ὁ Γ τὸν Ξ μετρεῖ· οἱ Β, Γ ἄρα τὸν Ξ μετροῦσιν· καὶ ὁ ἐλάχιστος ἄρα ὑπὸ τῶν Β, Γ μετρούμενος τὸν Ξ μετρήσει. ἐλάχιστος δὲ ὑπὸ τῶν Β, Γ μετρεῖται ὁ Η· ὁ Η ἄρα τὸν Ξ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἔσονταί τινες τῶν Θ, Η, Κ, Λ ἐλάσσονες ἀριθμοὶ ἑξῆς ἔν τε τῷ τοῦ Α πρὸς τὸν Β καὶ τῷ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι τῷ τοῦ Ε πρὸς τὸν Ζ λόγῳ.
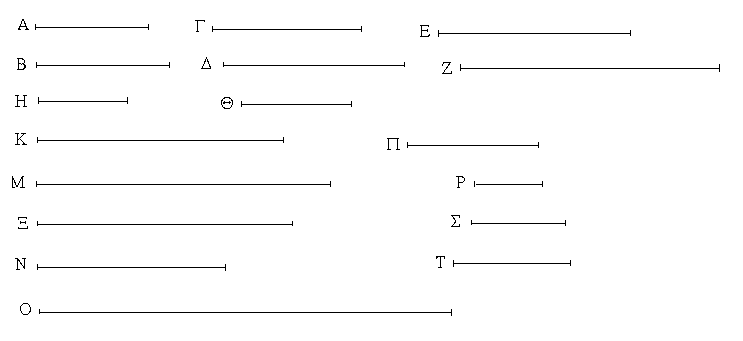
Μὴ μετρείτω δὴ ὁ Ε τὸν Κ. καὶ εἰλήφθω ὑπὸ τῶν Ε, Κ ἐλάχιστος μετρούμενος ἀριθμὸς ὁ Μ. καὶ ὁσάκις μὲν ὁ Κ τὸν Μ μετρεῖ, τοσαυτάκις καὶ ἑκάτερος τῶν Θ, Η ἑκάτερον τῶν Ν, Ξ μετρείτω, ὁσάκις δὲ ὁ Ε τὸν Μ μετρεῖ, τοσαυτάκις καὶ ὁ Ζ τὸν Ο μετρείτω. ἐπεὶ ἰσάκις ὁ Θ τὸν Ν μετρεῖ καὶ ὁ Η τὸν Ξ, ἔστιν ἄρα ὡς ὁ Θ πρὸς τὸν Η, οὕτως ὁ Ν πρὸς τὸν Ξ. ὡς δὲ ὁ Θ πρὸς τὸν Η, οὕτως ὁ Α πρὸς τὸν Β· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, οὕτως ὁ Ν πρὸς τὸν Ξ. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ξ πρὸς τὸν Μ. πάλιν, ἐπεὶ ἰσάκις ὁ Ε τὸν Μ μετρεῖ καὶ ὁ Ζ τὸν Ο, ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Ζ, οὕτως ὁ Μ πρὸς τὸν Ο· οἱ Ν, Ξ, Μ, Ο ἄρα ἑξῆς ἀνάλογόν εἰσιν ἐν τοῖς τοῦ τε Α πρὸς τὸν Β καὶ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι τοῦ Ε πρὸς τὸν Ζ λόγοις. λέγω δή, ὅτι καὶ ἐλάχιστοι ἐν τοῖς ΑΒ, ΓΔ, ΕΖ λόγοις. εἰ γὰρ μή, ἔσονταί τινες τῶν Ν, Ξ, Μ, Ο ἐλάσσονες ἀριθμοὶ ἑξῆς ἀνάλογον ἐν τοῖς ΑΒ, ΓΔ, ΕΖ λόγοις. ἔστωσαν οἱ Π, Ρ, Σ, Τ. καὶ ἐπεί ἐστιν ὡς ὁ Π πρὸς τὸν Ρ, οὕτως ὁ Α πρὸς τὸν Β, οἱ δὲ Α, Β ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας αὐτοῖς ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον, ὁ Β ἄρα τὸν Ρ μετρεῖ. διὰ τὰ αὐτὰ δὴ καὶ ὁ Γ τὸν Ρ μετρεῖ· οἱ Β, Γ ἄρα τὸν Ρ μετροῦσιν. καὶ ὁ ἐλάχιστος ἄρα ὑπὸ τῶν Β, Γ μετρούμενος τὸν Ρ μετρήσει. ἐλάχιστος δὲ ὑπὸ τῶν Β, Γ μετρούμενός ἐστιν ὁ Η· ὁ Η ἄρα τὸν Ρ μετρεῖ. καί ἐστιν ὡς ὁ Η πρὸς τὸν Ρ, οὕτως ὁ Κ πρὸς τὸν Σ· καὶ ὁ Κ ἄρα τὸν Σ μετρεῖ. μετρεῖ δὲ καὶ ὁ Ε τὸν Σ· οἱ Ε, Κ ἄρα τὸν Σ μετροῦσιν. καὶ ὁ ἐλάχιστος ἄρα ὑπὸ τῶν Ε, Κ μετρούμενος τὸν Σ μετρήσει. ἐλάχιστος δὲ ὑπὸ τῶν Ε, Κ μετρούμενός ἐστιν ὁ Μ· ὁ Μ ἄρα τὸν Σ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἔσονταί τινες τῶν Ν, Ξ, Μ, Ο ἐλάσσονες ἀριθμοὶ ἑξῆς ἀνάλογον ἔν τε τοῖς τοῦ Α πρὸς τὸν Β καὶ τοῦ Γ πρὸς τὸν Δ καὶ ἔτι τοῦ Ε πρὸς τὸν Ζ λόγοις· οἱ Ν, Ξ, Μ, Ο ἄρα ἑξῆς ἀνάλογον ἐλάχιστοί εἰσιν ἐν τοῖς ΑΒ, ΓΔ, ΕΖ λόγοις· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον VIII
Οἱ ἐπίπεδοι ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχουσι τὸν συγκείμενον ἐκ τῶν πλευρῶν.
Ἔστωσαν ἐπίπεδοι ἀριθμοὶ οἱ Α, Β, καὶ τοῦ μὲν Α πλευραὶ ἔστωσαν οἱ Γ, Δ ἀριθμοί, τοῦ δὲ Β οἱ Ε, Ζ· λέγω, ὅτι ὁ Α πρὸς τὸν Β λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν.
Λόγων γὰρ δοθέντων τοῦ τε ὃν ἔχει ὁ Γ πρὸς τὸν Ε καὶ ὁ Δ πρὸς τὸν Ζ εἰλήφθωσαν ἀριθμοὶ ἑξῆς ἐλάχιστοι ἐν τοῖς ΓΕ, ΔΖ λόγοις, οἱ Η, Θ, Κ, ὥστε εἶναι ὡς μὲν τὸν Γ πρὸς τὸν Ε, οὕτως τὸν Η πρὸς τὸν Θ, ὡς δὲ τὸν Δ πρὸς τὸν Ζ, οὕτως τὸν Θ πρὸς τὸν Κ. καὶ ὁ Δ τὸν Ε πολλαπλασιάσας τὸν Λ ποιείτω.
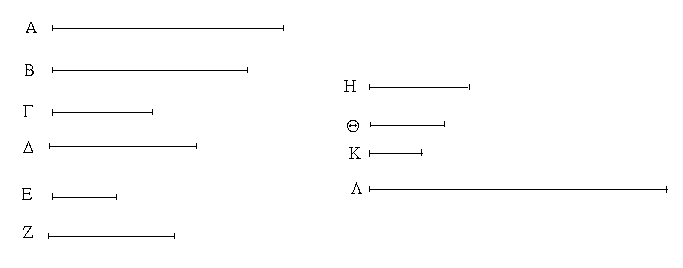
Καὶ ἐπεὶ ὁ Δ τὸν μὲν Γ πολλαπλασιάσας τὸν Α πεποίηκεν, τὸν δὲ Ε πολλαπλασιάσας τὸν Λ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Ε, οὕτως ὁ Α πρὸς τὸν Λ. ὡς δὲ ὁ Γ πρὸς τὸν Ε, οὕτως ὁ Η πρὸς τὸν Θ· καὶ ὡς ἄρα ὁ Η πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Λ. πάλιν, ἐπεὶ ὁ Ε τὸν Δ πολλαπλασιάσας τὸν Λ πεποίηκεν, ἀλλὰ μὴν καὶ τὸν Ζ πολλαπλασιάσας τὸν Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Λ πρὸς τὸν Β. ἀλλ' ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Θ πρὸς τὸν Κ· καὶ ὡς ἄρα ὁ Θ πρὸς τὸν Κ, οὕτως ὁ Λ πρὸς τὸν Β. ἐδείχθη δὲ καὶ ὡς ὁ Η πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Λ· δι' ἴσου ἄρα ἐστὶν ὡς ὁ Η πρὸς τὸν Κ, [οὕτως] ὁ Α πρὸς τὸν Β, ὁ δὲ Η πρὸς τὸν Κ λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν· καὶ ὁ Α ἄρα πρὸς τὸν Β λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν· ὅπερ ἔδει δεῖξαι
Πρότασις ς΄ 6 Βιβλίον VIII
Ἐὰν ὦσιν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, ὁ δὲ πρῶτος τὸν δεύτερον μὴ μετρῇ, οὐδὲ ἄλλος οὐδεὶς οὐδένα μετρήσει.
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, Ε, ὁ δὲ Α τὸν Β μὴ μετρείτω· λέγω, ὅτι οὐδὲ ἄλλος οὐδεὶς οὐδένα μετρήσει.
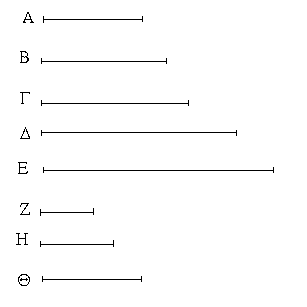
Ὅτι μὲν οὖν οἱ Α, Β, Γ, Δ, Ε ἑξῆς ἀλλήλους οὐ μετροῦσιν, φανερόν· οὐδὲ γὰρ ὁ Α τὸν Β μετρεῖ. λέγω δή, ὅτι οὐδὲ ἄλλος οὐδεὶς οὐδένα μετρήσει. εἰ γὰρ δυνατόν, μετρείτω ὁ Α τὸν Γ. καὶ ὅσοι εἰσὶν οἱ Α, Β, Γ, τοσοῦτοι εἰλήφθωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β, Γ οἱ Ζ, Η, Θ. καὶ ἐπεὶ οἱ Ζ, Η, Θ ἐν τῷ αὐτῷ λόγῳ εἰσὶ τοῖς Α, Β, Γ, καί ἐστιν ἴσον τὸ πλῆθος τῶν Α, Β, Γ τῷ πλήθει τῶν Ζ, Η, Θ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Γ, οὕτως ὁ Ζ πρὸς τὸν Θ. καὶ ἐπεί ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Ζ πρὸς τὸν Η, οὐ μετρεῖ δὲ ὁ Α τὸν Β, οὐ μετρεῖ ἄρα οὐδὲ ὁ Ζ τὸν Η· οὐκ ἄρα μονάς ἐστιν ὁ Ζ· ἡ γὰρ μονὰς πάντα ἀριθμὸν μετρεῖ. καί εἰσιν οἱ Ζ, Θ πρῶτοι πρὸς ἀλλήλους [οὐδὲ ὁ Ζ ἄρα τὸν Θ μετρεῖ]. καί ἐστιν ὡς ὁ Ζ πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Γ· οὐδὲ ὁ Α ἄρα τὸν Γ μετρεῖ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἄλλος οὐδεὶς οὐδένα μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον VIII
Ἐὰν ὦσιν ὁποσοιοῦν ἀριθμοὶ [ἑξῆς] ἀνάλογον, ὁ δὲ πρῶτος τὸν ἔσχατον μετρῇ, καὶ τὸν δεύτερον μετρήσει.
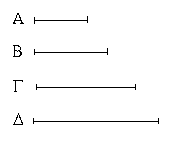
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, ὁ δὲ Α τὸν Δ μετρείτω· λέγω, ὅτι καὶ ὁ Α τὸν Β μετρεῖ. εἰ γὰρ οὐ μετρεῖ ὁ Α τὸν Β, οὐδὲ ἄλλος οὐδεὶς οὐδένα μετρήσει· μετρεῖ δὲ ὁ Α τὸν Δ. μετρεῖ ἄρα καὶ ὁ Α τὸν Β· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον VIII
Ἐὰν δύο ἀριθμῶν μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτωσιν ἀριθμοί, ὅσοι εἰς αὐτοὺς μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτουσιν ἀριθμοί, τοσοῦτοι καὶ εἰς τοὺς τὸν αὐτὸν λόγον ἔχοντας [αὐτοῖς] μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
Δύο γὰρ ἀριθμῶν τῶν Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπιπτέτωσαν ἀριθμοὶ οἱ Γ, Δ, καὶ πεποιήσθω ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Ε πρὸς τὸν Ζ· λέγω, ὅτι ὅσοι εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί, τοσοῦτοι καὶ εἰς τοὺς Ε, Ζ μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
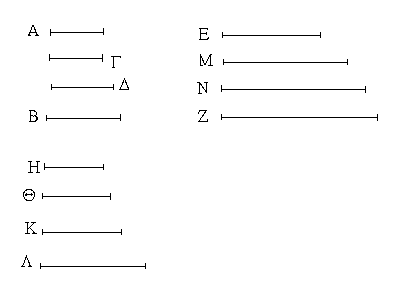
Ὅσοι γάρ εἰσι τῷ πλήθει οἱ Α, Β, Γ, Δ, τοσοῦτοι εἰλήφθωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ, Δ, Β οἱ Η, Θ, Κ, Λ· οἱ ἄρα ἄκροι αὐτῶν οἱ Η, Λ πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἐπεὶ οἱ Α, Γ, Δ, Β τοῖς Η, Θ, Κ, Λ ἐν τῷ αὐτῷ λόγῳ εἰσίν, καί ἐστιν ἴσον τὸ πλῆθος τῶν Α, Γ, Δ, Β τῷ πλήθει τῶν Η, Θ, Κ, Λ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Η πρὸς τὸν Λ. ὡς δὲ ὁ Α πρὸς τὸν Β, οὕτως ὁ Ε πρὸς τὸν Ζ· καὶ ὡς ἄρα ὁ Η πρὸς τὸν Λ, οὕτως ὁ Ε πρὸς τὸν Ζ. οἱ δὲ Η, Λ πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον. ἰσάκις ἄρα ὁ Η τὸν Ε μετρεῖ καὶ ὁ Λ τὸν Ζ. ὁσάκις δὴ ὁ Η τὸν Ε μετρεῖ, τοσαυτάκις καὶ ἑκάτερος τῶν Θ, Κ ἑκάτερον τῶν Μ, Ν μετρείτω· οἱ Η, Θ, Κ, Λ ἄρα τοὺς Ε, Μ, Ν, Ζ ἰσάκις μετροῦσιν. οἱ Η, Θ, Κ, Λ ἄρα τοῖς Ε, Μ, Ν, Ζ ἐν τῷ αὐτῷ λόγῳ εἰσίν. ἀλλὰ οἱ Η, Θ, Κ, Λ τοῖς Α, Γ, Δ, Β ἐν τῷ αὐτῷ λόγῳ εἰσίν· καὶ οἱ Α, Γ, Δ, Β ἄρα τοῖς Ε, Μ, Ν, Ζ ἐν τῷ αὐτῷ λόγῳ εἰσίν. οἱ δὲ Α, Γ, Δ, Β ἑξῆς ἀνάλογόν εἰσιν· καὶ οἱ Ε, Μ, Ν, Ζ ἄρα ἑξῆς ἀνάλογόν εἰσιν. ὅσοι ἄρα εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί, τοσοῦτοι καὶ εἰς τοὺς Ε, Ζ μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον VIII
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, καὶ εἰς αὐτοὺς μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτωσιν ἀριθμοί, ὅσοι εἰς αὐτοὺς μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτουσιν ἀριθμοί, τοσοῦτοι καὶ ἑκατέρου αὐτῶν καὶ μονάδος μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
Ἔστωσαν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β καὶ εἰς αὐτοὺς μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπιπτέτωσαν οἱ Γ, Δ, καὶ ἐκκείσθω ἡ Ε μονάς· λέγω, ὅτι ὅσοι εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί, τοσοῦτοι καὶ ἑκατέρου τῶν Α, Β καὶ τῆς μονάδος μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
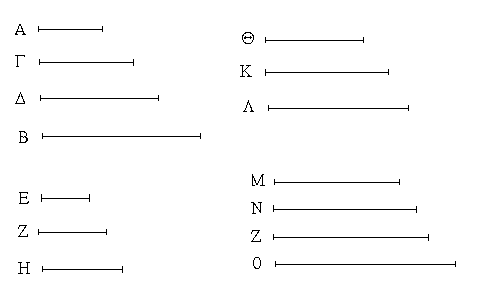
Εἰλήφθωσαν γὰρ δύο μὲν ἀριθμοὶ ἐλάχιστοι ἐν τῷ τῶν Α, Γ, Δ, Β λόγῳ ὄντες οἱ Ζ, Η, τρεῖς δὲ οἱ Θ, Κ, Λ, καὶ ἀεὶ ἑξῆς ἑνὶ πλείους, ἕως ἂν ἴσον γένηται τὸ πλῆθος αὐτῶν τῷ πλήθει τῶν Α, Γ, Δ, Β. εἰλήφθωσαν, καὶ ἔστωσαν οἱ Μ, Ν, Ξ, Ο. φανερὸν δή, ὅτι ὁ μὲν Ζ ἑαυτὸν πολλαπλασιάσας τὸν Θ πεποίηκεν, τὸν δὲ Θ πολλαπλασιάσας τὸν Μ πεποίηκεν, καὶ ὁ Η ἑαυτὸν μὲν πολλαπλασιάσας τὸν Λ πεποίηκεν, τὸν δὲ Λ πολλαπλασιάσας τὸν Ο πεποίηκεν. καὶ ἐπεὶ οἱ Μ, Ν, Ξ, Ο ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Ζ, Η, εἰσὶ δὲ καὶ οἱ Α, Γ, Δ, Β ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Ζ, Η, καί ἐστιν ἴσον τὸ πλῆθος τῶν Μ, Ν, Ξ, Ο τῷ πλήθει τῶν Α, Γ, Δ, Β, ἕκαστος ἄρα τῶν Μ, Ν, Ξ, Ο ἑκάστῳ τῶν Α, Γ, Δ, Β ἴσος ἐστίν· ἴσος ἄρα ἐστὶν ὁ μὲν Μ τῷ Α, ὁ δὲ Ο τῷ Β. καὶ ἐπεὶ ὁ Ζ ἑαυτὸν πολλαπλασιάσας τὸν Θ πεποίηκεν, ὁ Ζ ἄρα τὸν Θ μετρεῖ κατὰ τὰς ἐν τῷ Ζ μονάδας. μετρεῖ δὲ καὶ ἡ Ε μονὰς τὸν Ζ κατὰ τὰς ἐν αὐτῷ μονάδας· ἰσάκις ἄρα ἡ Ε μονὰς τὸν Ζ ἀριθμὸν μετρεῖ καὶ ὁ Ζ τὸν Θ. ἔστιν ἄρα ὡς ἡ Ε μονὰς πρὸς τὸν Ζ ἀριθμόν, οὕτως ὁ Ζ πρὸς τὸν Θ. πάλιν, ἐπεὶ ὁ Ζ τὸν Θ πολλαπλασιάσας τὸν Μ πεποίηκεν, ὁ Θ ἄρα τὸν Μ μετρεῖ κατὰ τὰς ἐν τῷ Ζ μονάδας. μετρεῖ δὲ καὶ ἡ Ε μονὰς τὸν Ζ ἀριθμὸν κατὰ τὰς ἐν αὐτῷ μονάδας· ἰσάκις ἄρα ἡ Ε μονὰς τὸν Ζ ἀριθμὸν μετρεῖ καὶ ὁ Θ τὸν Μ. ἔστιν ἄρα ὡς ἡ Ε μονὰς πρὸς τὸν Ζ ἀριθμόν, οὕτως ὁ Θ πρὸς τὸν Μ. ἐδείχθη δὲ καὶ ὡς ἡ Ε μονὰς πρὸς τὸν Ζ ἀριθμόν, οὕτως ὁ Ζ πρὸς τὸν Θ· καὶ ὡς ἄρα ἡ Ε μονὰς πρὸς τὸν Ζ ἀριθμόν, οὕτως ὁ Ζ πρὸς τὸν Θ καὶ ὁ Θ πρὸς τὸν Μ. ἴσος δὲ ὁ Μ τῷ Α· ἔστιν ἄρα ὡς ἡ Ε μονὰς πρὸς τὸν Ζ ἀριθμόν, οὕτως ὁ Ζ πρὸς τὸν Θ καὶ ὁ Θ πρὸς τὸν Α. διὰ τὰ αὐτὰ δὴ καὶ ὡς ἡ Ε μονὰς πρὸς τὸν Η ἀριθμόν, οὕτως ὁ Η πρὸς τὸν Λ καὶ ὁ Λ πρὸς τὸν Β. ὅσοι ἄρα εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί, τοσοῦτοι καὶ ἑκατέρου τῶν Α, Β καὶ μονάδος τῆς Ε μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον VIII
Ἐὰν δύο ἀριθμῶν ἑκατέρου καὶ μονάδος μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτωσιν ἀριθμοί, ὅσοι ἑκατέρου αὐτῶν καὶ μονάδος μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτουσιν ἀριθμοί, τοσοῦτοι καὶ εἰς αὐτοὺς μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
Δύο γὰρ ἀριθμῶν τῶν Α, Β καὶ μονάδος τῆς Γ μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπιπτέτωσαν ἀριθμοὶ οἵ τε Δ, Ε καὶ οἱ Ζ, Η· λέγω, ὅτι ὅσοι ἑκατέρου τῶν Α, Β καὶ μονάδος τῆς Γ μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεπτώκασιν ἀριθμοί, τοσοῦτοι καὶ εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπεσοῦνται.
Ὁ Δ γὰρ τὸν Ζ πολλαπλασιάσας τὸν Θ ποιείτω, ἑκάτερος δὲ τῶν Δ, Ζ τὸν Θ πολλαπλασιάσας ἑκάτερον τῶν Κ, Λ ποιείτω.
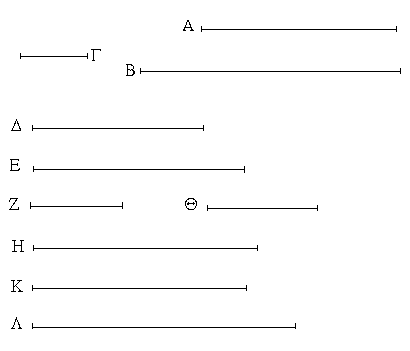
Καὶ ἐπεί ἐστιν ὡς ἡ Γ μονὰς πρὸς τὸν Δ ἀριθμόν, οὕτως ὁ Δ πρὸς τὸν Ε, ἰσάκις ἄρα ἡ Γ μονὰς τὸν Δ ἀριθμὸν μετρεῖ καὶ ὁ Δ τὸν Ε. ἡ δὲ Γ μονὰς τὸν Δ ἀριθμὸν μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας· καὶ ὁ Δ ἄρα ἀριθμὸς τὸν Ε μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας· ὁ Δ ἄρα ἑαυτὸν πολλαπλασιάσας τὸν Ε πεποίηκεν. πάλιν, ἐπεί ἐστιν ὡς ἡ Γ [μονὰς] πρὸς τὸν Δ ἀριθμὸν, οὕτως ὁ Ε πρὸς τὸν Α, ἰσάκις ἄρα ἡ Γ μονὰς τὸν Δ ἀριθμὸν μετρεῖ καὶ ὁ Ε τὸν Α. ἡ δὲ Γ μονὰς τὸν Δ ἀριθμὸν μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας· καὶ ὁ Ε ἄρα τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας· ὁ Δ ἄρα τὸν Ε πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ μὲν Ζ ἑαυτὸν πολλαπλασιάσας τὸν Η πεποίηκεν, τὸν δὲ Η πολλαπλασιάσας τὸν Β πεποίηκεν. καὶ ἐπεὶ ὁ Δ ἑαυτὸν μὲν πολλαπλασιάσας τὸν Ε πεποίηκεν, τὸν δὲ Ζ πολλαπλασιάσας τὸν Θ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Ε πρὸς τὸν Θ. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Θ πρὸς τὸν Η. καὶ ὡς ἄρα ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Θ πρὸς τὸν Η. πάλιν, ἐπεὶ ὁ Δ ἑκάτερον τῶν Ε, Θ πολλαπλασιάσας ἑκάτερον τῶν Α, Κ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Κ. ἀλλ' ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Δ πρὸς τὸν Ζ· καὶ ὡς ἄρα ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Κ. πάλιν, ἐπεὶ ἑκάτερος τῶν Δ, Ζ τὸν Θ πολλαπλασιάσας ἑκάτερον τῶν Κ, Λ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Κ πρὸς τὸν Λ. ἀλλ' ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Κ· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Κ, οὕτως ὁ Κ πρὸς τὸν Λ. ἔτι ἐπεὶ ὁ Ζ ἑκάτερον τῶν Θ, Η πολλαπλασιάσας ἑκάτερον τῶν Λ, Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Θ πρὸς τὸν Η, οὕτως ὁ Λ πρὸς τὸν Β. ὡς δὲ ὁ Θ πρὸς τὸν Η, οὕτως ὁ Δ πρὸς τὸν Ζ· καὶ ὡς ἄρα ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Λ πρὸς τὸν Β. ἐδείχθη δὲ καὶ ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὅ τε Α πρὸς τὸν Κ καὶ ὁ Κ πρὸς τὸν Λ· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Κ, οὕτως ὁ Κ πρὸς τὸν Λ καὶ ὁ Λ πρὸς τὸν Β. οἱ Α, Κ, Λ, Β ἄρα κατὰ τὸ συνεχὲς ἑξῆς εἰσιν ἀνάλογον. ὅσοι ἄρα ἑκατέρου τῶν Α, Β καὶ τῆς Γ μονάδος μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτουσιν ἀριθμοί, τοσοῦτοι καὶ εἰς τοὺς Α, Β μεταξὺ κατὰ τὸ συνεχὲς ἐμπεσοῦνται· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον VIII
Δύο τετραγώνων ἀριθμῶν εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός, καὶ ὁ τετράγωνος πρὸς τὸν τετράγωνον διπλασίονα λόγον ἔχει ἤπερ ἡ πλευρὰ πρὸς τὴν πλευράν.
Ἔστωσαν τετράγωνοι ἀριθμοὶ οἱ Α, Β, καὶ τοῦ μὲν Α πλευρὰ ἔστω ὁ Γ, τοῦ δὲ Β ὁ Δ· λέγω, ὅτι τῶν Α, Β εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός, καὶ ὁ Α πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Δ.
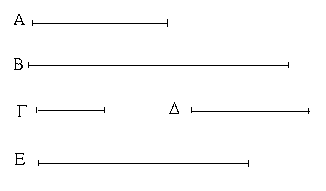
Ὁ Γ γὰρ τὸν Δ πολλαπλασιάσας τὸν Ε ποιείτω. καὶ ἐπεὶ τετράγωνός ἐστιν ὁ Α, πλευρὰ δὲ αὐτοῦ ἐστιν ὁ Γ, ὁ Γ ἄρα ἑαυτὸν πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Δ ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν. ἐπεὶ οὖν ὁ Γ ἑκάτερον τῶν Γ, Δ πολλαπλασιάσας ἑκάτερον τῶν Α, Ε πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Α πρὸς τὸν Ε. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ε πρὸς τὸν Β. καὶ ὡς ἄρα ὁ Α πρὸς τὸν Ε, οὕτως ὁ Ε πρὸς τὸν Β. τῶν Α, Β ἄρα εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός.
Λέγω δή, ὅτι καὶ ὁ Α πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Δ. ἐπεὶ γὰρ τρεῖς ἀριθμοὶ ἀνάλογόν εἰσιν οἱ Α, Ε, Β, ὁ Α ἄρα πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ὁ Α πρὸς τὸν Ε. ὡς δὲ ὁ Α πρὸς τὸν Ε, οὕτως ὁ Γ πρὸς τὸν Δ. ὁ Α ἄρα πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ἡ Γ πλευρὰ πρὸς τὴν Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον VIII
Δύο κύβων ἀριθμῶν δύο μέσοι ἀνάλογόν εἰσιν ἀριθμοί, καὶ ὁ κύβος πρὸς τὸν κύβον τριπλασίονα λόγον ἔχει ἤπερ ἡ πλευρὰ πρὸς τὴν πλευράν.
Ἔστωσαν κύβοι ἀριθμοὶ οἱ Α, Β καὶ τοῦ μὲν Α πλευρὰ ἔστω ὁ Γ, τοῦ δὲ Β ὁ Δ· λέγω, ὅτι τῶν Α, Β δύο μέσοι ἀνάλογόν εἰσιν ἀριθμοί, καὶ ὁ Α πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Δ.
Ὁ γὰρ Γ ἑαυτὸν μὲν πολλαπλασιάσας τὸν Ε ποιείτω, τὸν δὲ Δ πολλαπλασιάσας τὸν Ζ ποιείτω, ὁ δὲ Δ ἑαυτὸν πολλαπλασιάσας τὸν Η ποιείτω, ἑκάτερος δὲ τῶν Γ, Δ τὸν Ζ πολλαπλασιάσας ἑκάτερον τῶν Θ, Κ ποιείτω.
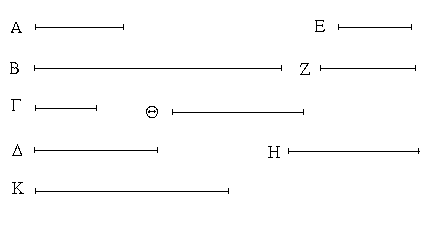
Καὶ ἐπεὶ κύβος ἐστὶν ὁ Α, πλευρὰ δὲ αὐτοῦ ὁ Γ, καὶ ὁ Γ ἑαυτὸν πολλαπλασιάσας τὸν Ε πεποίηκεν, ὁ Γ ἄρα ἑαυτὸν μὲν πολλαπλασιάσας τὸν Ε πεποίηκεν, τὸν δὲ Ε πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Δ ἑαυτὸν μὲν πολλαπλασιάσας τὸν Η πεποίηκεν, τὸν δὲ Η πολλαπλασιάσας τὸν Β πεποίηκεν. καὶ ἐπεὶ ὁ Γ ἑκάτερον τῶν Γ, Δ πολλαπλασιάσας ἑκάτερον τῶν Ε, Ζ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ε πρὸς τὸν Ζ. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ζ πρὸς τὸν Η. πάλιν, ἐπεὶ ὁ Γ ἑκάτερον τῶν Ε, Ζ πολλαπλασιάσας ἑκάτερον τῶν Α, Θ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Θ. ὡς δὲ ὁ Ε πρὸς τὸν Ζ, οὕτως ὁ Γ πρὸς τὸν Δ· καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Α πρὸς τὸν Θ. πάλιν, ἐπεὶ ἑκάτερος τῶν Γ, Δ τὸν Ζ πολλαπλασιάσας ἑκάτερον τῶν Θ, Κ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Θ πρὸς τὸν Κ. πάλιν, ἐπεὶ ὁ Δ ἑκάτερον τῶν Ζ, Η πολλαπλασιάσας ἑκάτερον τῶν Κ, Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ζ πρὸς τὸν Η, οὕτως ὁ Κ πρὸς τὸν Β. ὡς δὲ ὁ Ζ πρὸς τὸν Η, οὕτως ὁ Γ πρὸς τὸν Δ· καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Δ, οὕτως ὅ τε Α πρὸς τὸν Θ καὶ ὁ Θ πρὸς τὸν Κ καὶ ὁ Κ πρὸς τὸν Β. τῶν Α, Β ἄρα δύο μέσοι ἀνάλογόν εἰσιν οἱ Θ, Κ.
Λέγω δή, ὅτι καὶ ὁ Α πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Δ. ἐπεὶ γὰρ τέσσαρες ἀριθμοὶ ἀνάλογόν εἰσιν οἱ Α, Θ, Κ, Β, ὁ Α ἄρα πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Α πρὸς τὸν Θ. ὡς δὲ ὁ Α πρὸς τὸν Θ, οὕτως ὁ Γ πρὸς τὸν Δ· καὶ ὁ Α [ἄρα] πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Δ. ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον VIII
Ἐὰν ὦσιν ὁσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, καὶ πολλαπλασιάσας ἕκαστος ἑαυτὸν ποιῇ τινα, οἱ γενόμενοι ἐξ αὐτῶν ἀνάλογον ἔσονται· καὶ ἐὰν οἱ ἐξ ἀρχῆς τοὺς γενομένους πολλαπλασιάσαντες ποιῶσί τινας, καὶ αὐτοὶ ἀνάλογον ἔσονται [καὶ ἀεὶ περὶ τοὺς ἄκρους τοῦτο συμβαίνει].
Ἔστωσαν ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, οἱ Α, Β, Γ, ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Β πρὸς τὸν Γ, καὶ οἱ Α, Β, Γ ἑαυτοὺς μὲν πολλαπλασιάσαντες τοὺς Δ, Ε, Ζ ποιείτωσαν, τοὺς δὲ Δ, Ε, Ζ πολλαπλασιάσαντες τοὺς Η, Θ, Κ ποιείτωσαν· λέγω, ὅτι οἵ τε Δ, Ε, Ζ καὶ οἱ Η, Θ, Κ ἑξῆς ἀνάλογόν εἰσιν.
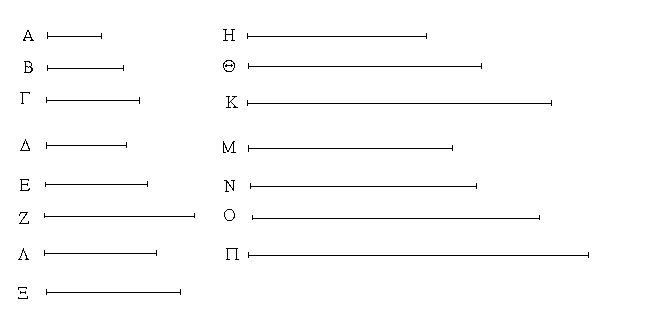
Ὁ μὲν γὰρ Α τὸν Β πολλαπλασιάσας τὸν Λ ποιείτω, ἑκάτερος δὲ τῶν Α, Β τὸν Λ πολλαπλασιάσας ἑκάτερον τῶν Μ, Ν ποιείτω. καὶ πάλιν ὁ μὲν Β τὸν Γ πολλαπλασιάσας τὸν Ξ ποιείτω, ἑκάτερος δὲ τῶν Β, Γ τὸν Ξ πολλαπλασιάσας ἑκάτερον τῶν Ο, Π ποιείτω.
Ὁμοίως δὴ τοῖς ἐπάνω δείξομεν, ὅτι οἱ Δ, Λ, Ε καὶ οἱ Η, Μ, Ν, Θ ἑξῆς εἰσιν ἀνάλογον ἐν τῷ τοῦ Α πρὸς τὸν Β λόγῳ, καὶ ἔτι οἱ Ε, Ξ, Ζ καὶ οἱ Θ, Ο, Π, Κ ἑξῆς εἰσιν ἀνάλογον ἐν τῷ τοῦ Β πρὸς τὸν Γ λόγῳ. καί ἐστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Β πρὸς τὸν Γ· καὶ οἱ Δ, Λ, Ε ἄρα τοῖς Ε, Ξ, Ζ ἐν τῷ αὐτῷ λόγῳ εἰσὶ καὶ ἔτι οἱ Η, Μ, Ν, Θ τοῖς Θ, Ο, Π, Κ. καί ἐστιν ἴσον τὸ μὲν τῶν Δ, Λ, Ε πλῆθος τῷ τῶν Ε, Ξ, Ζ πλήθει, τὸ δὲ τῶν Η, Μ, Ν, Θ τῷ τῶν Θ, Ο, Π, Κ· δι' ἴσου ἄρα ἐστὶν ὡς μὲν ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Ε πρὸς τὸν Ζ, ὡς δὲ ὁ Η πρὸς τὸν Θ, οὕτως ὁ Θ πρὸς τὸν Κ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον VIII
Ἐὰν τετράγωνος τετράγωνον μετρῇ, καὶ ἡ πλευρὰ τὴν πλευρὰν μετρήσει· καὶ ἐὰν ἡ πλευρὰ τὴν πλευρὰν μετρῇ, καὶ ὁ τετράγωνος τὸν τετράγωνον μετρήσει.
Ἔστωσαν τετράγωνοι ἀριθμοὶ οἱ Α, Β, πλευραὶ δὲ αὐτῶν ἔστωσαν οἱ Γ, Δ, ὁ δὲ Α τὸν Β μετρείτω· λέγω, ὅτι καὶ ὁ Γ τὸν Δ μετρεῖ.
Ὁ Γ γὰρ τὸν Δ πολλαπλασιάσας τὸν Ε ποιείτω· οἱ Α, Ε, Β ἄρα ἑξῆς ἀνάλογόν εἰσιν ἐν τῷ τοῦ Γ πρὸς τὸν Δ λόγῳ. καὶ ἐπεὶ οἱ Α, Ε, Β ἑξῆς ἀνάλογόν εἰσιν, καὶ μετρεῖ ὁ Α τὸν Β, μετρεῖ ἄρα καὶ ὁ Α τὸν Ε. καί ἐστιν ὡς ὁ Α πρὸς τὸν Ε, οὕτως ὁ Γ πρὸς τὸν Δ· μετρεῖ ἄρα καὶ ὁ Γ τὸν Δ.
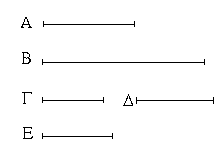
Πάλιν δὴ ὁ Γ τὸν Δ μετρείτω· λέγω, ὅτι καὶ ὁ Α τὸν Β μετρεῖ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι οἱ Α, Ε, Β ἑξῆς ἀνάλογόν εἰσιν ἐν τῷ τοῦ Γ πρὸς τὸν Δ λόγῳ. καὶ ἐπεί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Α πρὸς τὸν Ε, μετρεῖ δὲ ὁ Γ τὸν Δ, μετρεῖ ἄρα καὶ ὁ Α τὸν Ε. καί εἰσιν οἱ Α, Ε, Β ἑξῆς ἀνάλογον· μετρεῖ ἄρα καὶ ὁ Α τὸν Β.
Ἐὰν ἄρα τετράγωνος τετράγωνον μετρῇ, καὶ ἡ πλευρὰ τὴν πλευρὰν μετρήσει· καὶ ἐὰν ἡ πλευρὰ τὴν πλευρὰν μετρῇ, καὶ ὁ τετράγωνος τὸν τετράγωνον μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον VIII
Ἐὰν κύβος ἀριθμὸς κύβον ἀριθμὸν μετρῇ, καὶ ἡ πλευρὰ τὴν πλευρὰν μετρήσει· καὶ ἐὰν ἡ πλευρὰ τὴν πλευρὰν μετρῇ, καὶ ὁ κύβος τὸν κύβον μετρήσει.
Κύβος γὰρ ἀριθμὸς ὁ Α κύβον τὸν Β μετρείτω, καὶ τοῦ μὲν Α πλευρὰ ἔστω ὁ Γ, τοῦ δὲ Β ὁ Δ· λέγω, ὅτι ὁ Γ τὸν Δ μετρεῖ.
Ὁ Γ γὰρ ἑαυτὸν πολλαπλασιάσας τὸν Ε ποιείτω, ὁ δὲ Δ ἑαυτὸν πολλαπλασιάσας τὸν Η ποιείτω, καὶ ἔτι ὁ Γ τὸν Δ πολλαπλασιάσας τὸν Ζ [ποιείτω], ἑκάτερος δὲ τῶν Γ, Δ τὸν Ζ πολλαπλασιάσας ἑκάτερον τῶν Θ, Κ ποιείτω. φανερὸν δή, ὅτι οἱ Ε, Ζ,
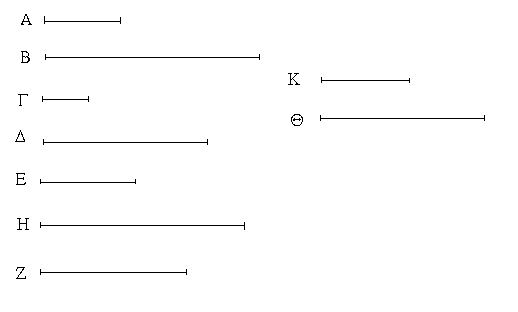
Η καὶ οἱ Α, Θ, Κ, Β ἑξῆς ἀνάλογόν εἰσιν ἐν τῷ τοῦ Γ πρὸς τὸν Δ λόγῳ. καὶ ἐπεὶ οἱ Α, Θ, Κ, Β ἑξῆς ἀνάλογόν εἰσιν, καὶ μετρεῖ ὁ Α τὸν Β, μετρεῖ ἄρα καὶ τὸν Θ. καί ἐστιν ὡς ὁ Α πρὸς τὸν Θ, οὕτως ὁ Γ πρὸς τὸν Δ· μετρεῖ ἄρα καὶ ὁ Γ τὸν Δ.
Ἀλλὰ δὴ μετρείτω ὁ Γ τὸν Δ· λέγω, ὅτι καὶ ὁ Α τὸν Β μετρήσει.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δὴ δείξομεν, ὅτι οἱ Α, Θ, Κ, Β ἑξῆς ἀνάλογόν εἰσιν ἐν τῷ τοῦ Γ πρὸς τὸν Δ λόγῳ. καὶ ἐπεὶ ὁ Γ τὸν Δ μετρεῖ, καί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Α πρὸς τὸν Θ, καὶ ὁ Α ἄρα τὸν Θ μετρεῖ· ὥστε καὶ τὸν Β μετρεῖ ὁ Α· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον VIII
Ἐὰν τετράγωνος ἀριθμὸς τετράγωνον ἀριθμὸν μὴ μετρῇ, οὐδὲ ἡ πλευρὰ τὴν πλευρὰν μετρήσει· κἂν ἡ πλευρὰ τὴν πλευρὰν μὴ μετρῇ, οὐδὲ ὁ τετράγωνος τὸν τετράγωνον μετρήσει.
Ἔστωσαν τετράγωνοι ἀριθμοὶ οἱ Α, Β, πλευραὶ δὲ αὐτῶν ἔστωσαν οἱ Γ, Δ, καὶ μὴ μετρείτω ὁ Α τὸν Β· λέγω, ὅτι οὐδὲ ὁ Γ τὸν Δ μετρεῖ.
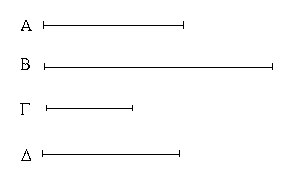
Εἰ γὰρ μετρεῖ ὁ Γ τὸν Δ, μετρήσει καὶ ὁ Α τὸν Β. οὐ μετρεῖ δὲ ὁ Α τὸν Β· οὐδὲ ἄρα ὁ Γ τὸν Δ μετρήσει.
Μὴ μετρείτω [δὴ] πάλιν ὁ Γ τὸν Δ· λέγω, ὅτι οὐδὲ ὁ Α τὸν Β μετρήσει.
Εἰ γὰρ μετρεῖ ὁ Α τὸν Β, μετρήσει καὶ ὁ Γ τὸν Δ. οὐ μετρεῖ δὲ ὁ Γ τὸν Δ· οὐδ' ἄρα ὁ Α τὸν Β μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον VIII
Ἐὰν κύβος ἀριθμὸς κύβον ἀριθμὸν μὴ μετρῇ, οὐδὲ ἡ πλευρὰ τὴν πλευρὰν μετρήσει· κἂν ἡ πλευρὰ τὴν πλευρὰν μὴ μετρῇ, οὐδὲ ὁ κύβος τὸν κύβον μετρήσει.
Κύβος γὰρ ἀριθμὸς ὁ Α κύβον ἀριθμὸν τὸν Β μὴ μετρείτω, καὶ τοῦ μὲν Α πλευρὰ ἔστω ὁ Γ, τοῦ δὲ Β ὁ Δ· λέγω, ὅτι ὁ Γ τὸν Δ οὐ μετρήσει.
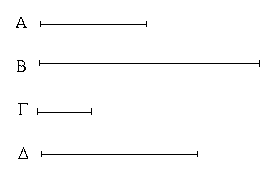
Εἰ γὰρ μετρεῖ ὁ Γ τὸν Δ, καὶ ὁ Α τὸν Β μετρήσει. οὐ μετρεῖ δὲ ὁ Α τὸν Β· οὐδ' ἄρα ὁ Γ τὸν Δ μετρεῖ.
Ἀλλὰ δὴ μὴ μετρείτω ὁ Γ τὸν Δ· λέγω, ὅτι οὐδὲ ὁ Α τὸν Β μετρήσει.
Εἰ γὰρ ὁ Α τὸν Β μετρεῖ, καὶ ὁ Γ τὸν Δ μετρήσει. οὐ μετρεῖ δὲ ὁ Γ τὸν Δ· οὐδ' ἄρα ὁ Α τὸν Β μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον VIII
Δύο ὁμοίων ἐπιπέδων ἀριθμῶν εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός· καὶ ὁ ἐπίπεδος πρὸς τὸν ἐπίπεδον διπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν.
Ἔστωσαν δύο ὅμοιοι ἐπίπεδοι ἀριθμοὶ οἱ Α, Β, καὶ τοῦ μὲν Α πλευραὶ ἔστωσαν οἱ Γ, Δ ἀριθμοί, τοῦ δὲ Β οἱ Ε, Ζ. καὶ ἐπεὶ ὅμοιοι ἐπίπεδοί εἰσιν οἱ ἀνάλογον ἔχοντες τὰς πλευράς, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ε πρὸς τὸν Ζ. λέγω οὖν, ὅτι τῶν Α, Β εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός, καὶ ὁ Α πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Ε ἢ ὁ Δ πρὸς τὸν Ζ, τουτέστιν ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον [πλευράν].
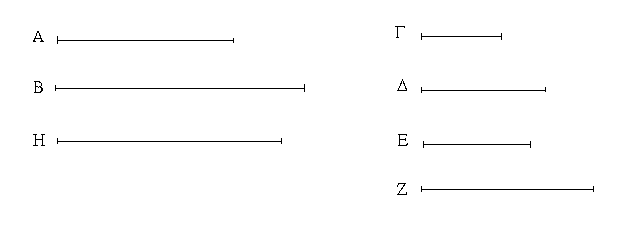
Καὶ ἐπεί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ε πρὸς τὸν Ζ, ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Γ πρὸς τὸν Ε, ὁ Δ πρὸς τὸν Ζ. καὶ ἐπεὶ ἐπίπεδός ἐστιν ὁ Α, πλευραὶ δὲ αὐτοῦ οἱ Γ, Δ, ὁ Δ ἄρα τὸν Γ πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Ε τὸν Ζ πολλαπλασιάσας τὸν Β πεποίηκεν. ὁ Δ δὴ τὸν Ε πολλαπλασιάσας τὸν Η ποιείτω. καὶ ἐπεὶ ὁ Δ τὸν μὲν Γ πολλαπλασιάσας τὸν Α πεποίηκεν, τὸν δὲ Ε πολλαπλασιάσας τὸν Η πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Ε, οὕτως ὁ Α πρὸς τὸν Η. ἀλλ' ὡς ὁ Γ πρὸς τὸν Ε, [οὕτως] ὁ Δ πρὸς τὸν Ζ· καὶ ὡς ἄρα ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Η. πάλιν, ἐπεὶ ὁ Ε τὸν μὲν Δ πολλαπλασιάσας τὸν Η πεποίηκεν, τὸν δὲ Ζ πολλαπλασιάσας τὸν Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Η πρὸς τὸν Β. ἐδείχθη δὲ καὶ ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Η· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Η, οὕτως ὁ Η πρὸς τὸν Β. οἱ Α, Η, Β ἄρα ἑξῆς ἀνάλογόν εἰσιν. τῶν Α, Β ἄρα εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός.
Λέγω δή, ὅτι καὶ ὁ Α πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἤπερ ὁ Γ πρὸς τὸν Ε ἢ ὁ Δ πρὸς τὸν Ζ. ἐπεὶ γὰρ οἱ Α, Η, Β ἑξῆς ἀνάλογόν εἰσιν, ὁ Α πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ πρὸς τὸν Η. καί ἐστιν ὡς ὁ Α πρὸς τὸν Η, οὕτως ὅ τε Γ πρὸς τὸν Ε καὶ ὁ Δ πρὸς τὸν Ζ. καὶ ὁ Α ἄρα πρὸς τὸν Β διπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Ε ἢ ὁ Δ πρὸς τὸν Ζ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον VIII
Δύο ὁμοίων στερεῶν ἀριθμῶν δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί· καὶ ὁ στερεὸς πρὸς τὸν ὅμοιον στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν.
Ἔστωσαν δύο ὅμοιοι στερεοὶ οἱ Α, Β, καὶ τοῦ μὲν Α πλευραὶ ἔστωσαν οἱ Γ, Δ, Ε, τοῦ δὲ Β οἱ Ζ, Η, Θ. καὶ ἐπεὶ ὅμοιοι στερεοί εἰσιν οἱ ἀνάλογον ἔχοντες τὰς πλευράς, ἔστιν ἄρα ὡς μὲν ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ζ πρὸς τὸν Η, ὡς δὲ ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Η πρὸς τὸν Θ. λέγω, ὅτι τῶν Α, Β δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί, καὶ ὁ Α πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ἔτι ὁ Ε πρὸς τὸν Θ.
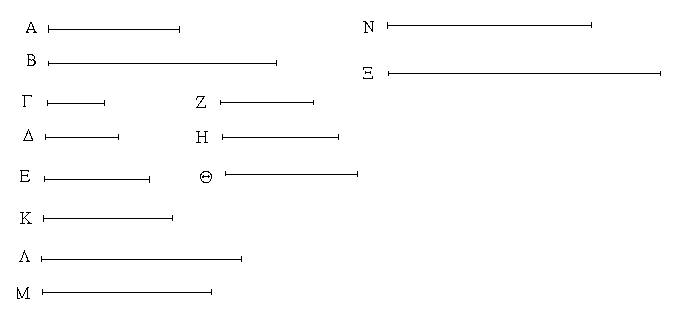
Ὁ Γ γὰρ τὸν Δ πολλαπλασιάσας τὸν Κ ποιείτω, ὁ δὲ Ζ τὸν Η πολλαπλασιάσας τὸν Λ ποιείτω. καὶ ἐπεὶ οἱ Γ, Δ τοῖς Ζ, Η ἐν τῷ αὐτῷ λόγῳ εἰσίν, καὶ ἐκ μὲν τῶν Γ, Δ ἐστιν ὁ Κ, ἐκ δὲ τῶν Ζ, Η ὁ Λ, οἱ Κ, Λ [ἄρα] ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί· τῶν Κ, Λ ἄρα εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός. ἔστω ὁ Μ. ὁ Μ ἄρα ἐστὶν ὁ ἐκ τῶν Δ, Ζ, ὡς ἐν τῷ πρὸ τούτου θεωρήματι ἐδείχθη. καὶ ἐπεὶ ὁ Δ τὸν μὲν Γ πολλαπλασιάσας τὸν Κ πεποίηκεν, τὸν δὲ Ζ πολλαπλασιάσας τὸν Μ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Γ πρὸς τὸν Ζ, οὕτως ὁ Κ πρὸς τὸν Μ. ἀλλ' ὡς ὁ Κ πρὸς τὸν Μ, ὁ Μ πρὸς τὸν Λ. οἱ Κ, Μ, Λ ἄρα ἑξῆς εἰσιν ἀνάλογον ἐν τῷ τοῦ Γ πρὸς τὸν Ζ λόγῳ. καὶ ἐπεί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, οὕτως ὁ Ζ πρὸς τὸν Η, ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Γ πρὸς τὸν Ζ, οὕτως ὁ Δ πρὸς τὸν Η. διὰ τὰ αὐτὰ δὴ καὶ ὡς ὁ Δ πρὸς τὸν Η, οὕτως ὁ Ε πρὸς τὸν Θ. οἱ Κ, Μ, Λ ἄρα ἑξῆς εἰσιν ἀνάλογον ἔν τε τῷ τοῦ Γ πρὸς τὸν Ζ λόγῳ καὶ τῷ τοῦ Δ πρὸς τὸν Η καὶ ἔτι τῷ τοῦ Ε πρὸς τὸν Θ. ἑκάτερος δὴ τῶν Ε, Θ τὸν Μ πολλαπλασιάσας ἑκάτερον τῶν Ν, Ξ ποιείτω. καὶ ἐπεὶ στερεός ἐστιν ὁ Α, πλευραὶ δὲ αὐτοῦ εἰσιν οἱ Γ, Δ, Ε, ὁ Ε ἄρα τὸν ἐκ τῶν Γ, Δ πολλαπλασιάσας τὸν Α πεποίηκεν. ὁ δὲ ἐκ τῶν Γ, Δ ἐστιν ὁ Κ· ὁ Ε ἄρα τὸν Κ πολλαπλασιάσας τὸν Α πεποίηκεν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Θ τὸν Λ πολλαπλασιάσας τὸν Β πεποίηκεν. καὶ ἐπεὶ ὁ Ε τὸν Κ πολλαπλασιάσας τὸν Α πεποίηκεν, ἀλλὰ μὴν καὶ τὸν Μ πολλαπλασιάσας τὸν Ν πεποίηκεν, ἔστιν ἄρα ὡς ὁ Κ πρὸς τὸν Μ, οὕτως ὁ Α πρὸς τὸν Ν. ὡς δὲ ὁ Κ πρὸς τὸν Μ, οὕτως ὅ τε Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ἔτι ὁ Ε πρὸς τὸν Θ· καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Ν. πάλιν, ἐπεὶ ἑκάτερος τῶν Ε, Θ τὸν Μ πολλαπλασιάσας ἑκάτερον τῶν Ν, Ξ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Ν πρὸς τὸν Ξ. ἀλλ' ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὅ τε Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η· καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ὁ Ε πρὸς τὸν Θ, οὕτως ὅ τε Α πρὸς τὸν Ν καὶ ὁ Ν πρὸς τὸν Ξ. πάλιν, ἐπεὶ ὁ Θ τὸν Μ πολλαπλασιάσας τὸν Ξ πεποίηκεν, ἀλλὰ μὴν καὶ τὸν Λ πολλαπλασιάσας τὸν Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Μ πρὸς τὸν Λ, οὕτως ὁ Ξ πρὸς τὸν Β. ἀλλ' ὡς ὁ Μ πρὸς τὸν Λ, οὕτως ὅ τε Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ὁ Ε πρὸς τὸν Θ. καὶ ὡς ἄρα ὁ Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ὁ Ε πρὸς τὸν Θ, οὕτως οὐ μόνον ὁ Ξ πρὸς τὸν Β, ἀλλὰ καὶ ὁ Α πρὸς τὸν Ν καὶ ὁ Ν πρὸς τὸν Ξ. οἱ Α, Ν, Ξ, Β ἄρα ἑξῆς εἰσιν ἀνάλογον ἐν τοῖς εἰρημένοις τῶν πλευρῶν λόγοις.
Λέγω, ὅτι καὶ ὁ Α πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἤπερ ὁ Γ ἀριθμὸς πρὸς τὸν Ζ ἢ ὁ Δ πρὸς τὸν Η καὶ ἔτι ὁ Ε πρὸς τὸν Θ. ἐπεὶ γὰρ τέσσαρες ἀριθμοὶ ἑξῆς ἀνάλογόν εἰσιν οἱ Α, Ν, Ξ, Β, ὁ Α ἄρα πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ὁ Α πρὸς τὸν Ν. ἀλλ' ὡς ὁ Α πρὸς τὸν Ν, οὕτως ἐδείχθη ὅ τε Γ πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ἔτι ὁ Ε πρὸς τὸν Θ. καὶ ὁ Α ἄρα πρὸς τὸν Β τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἤπερ ὁ Γ ἀριθμὸς πρὸς τὸν Ζ καὶ ὁ Δ πρὸς τὸν Η καὶ ἔτι ὁ Ε πρὸς τὸν Θ· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον VIII
Ἐὰν δύο ἀριθμῶν εἷς μέσος ἀνάλογον ἐμπίπτῃ ἀριθμός, ὅμοιοι ἐπίπεδοι ἔσονται οἱ ἀριθμοί.
Δύο γὰρ ἀριθμῶν τῶν Α, Β εἷς μέσος ἀνάλογον ἐμπιπτέτω ἀριθμὸς ὁ Γ· λέγω, ὅτι οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί.
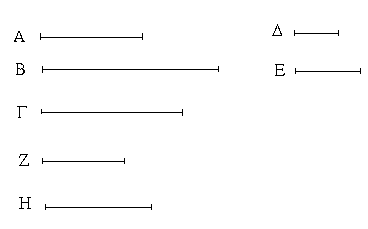
Εἰλήφθωσαν [γὰρ] ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ οἱ Δ, Ε· ἰσάκις ἄρα ὁ Δ τὸν Α μετρεῖ καὶ ὁ Ε τὸν Γ. ὁσάκις δὴ ὁ Δ τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ζ· ὁ Ζ ἄρα τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν. ὥστε ὁ Α ἐπίπεδός ἐστιν, πλευραὶ δὲ αὐτοῦ οἱ Δ, Ζ. πάλιν, ἐπεὶ οἱ Δ, Ε ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Γ, Β, ἰσάκις ἄρα ὁ Δ τὸν Γ μετρεῖ καὶ ὁ Ε τὸν Β. ὁσάκις δὴ ὁ Ε τὸν Β μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Η. ὁ Ε ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν τῷ Η μονάδας· ὁ Η ἄρα τὸν Ε πολλαπλασιάσας τὸν Β πεποίηκεν. ὁ Β ἄρα ἐπίπεδός ἐστι, πλευραὶ δὲ αὐτοῦ εἰσιν οἱ Ε, Η. οἱ Α, Β ἄρα ἐπίπεδοί εἰσιν ἀριθμοί. λέγω δή, ὅτι καὶ ὅμοιοι. ἐπεὶ γὰρ ὁ Ζ τὸν μὲν Δ πολλαπλασιάσας τὸν Α πεποίηκεν, τὸν δὲ Ε πολλαπλασιάσας τὸν Γ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Α πρὸς τὸν Γ, τουτέστιν ὁ Γ πρὸς τὸν Β. πάλιν, ἐπεὶ ὁ Ε ἑκάτερον τῶν Ζ, Η πολλαπλασιάσας τοὺς Γ, Β πεποίηκεν, ἔστιν ἄρα ὡς ὁ Ζ πρὸς τὸν Η, οὕτως ὁ Γ πρὸς τὸν Β. ὡς δὲ ὁ Γ πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε· καὶ ὡς ἄρα ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Ζ πρὸς τὸν Η. καὶ ἐναλλὰξ ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Ε πρὸς τὸν Η. οἱ Α, Β ἄρα ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί· αἱ γὰρ πλευραὶ αὐτῶν ἀνάλογόν εἰσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κα΄ 21 Βιβλίον VIII
Ἐὰν δύο ἀριθμῶν δύο μέσοι ἀνάλογον ἐμπίπτωσιν ἀριθμοί, ὅμοιοι στερεοί εἰσιν οἱ ἀριθμοί.
Δύο γὰρ ἀριθμῶν τῶν Α, Β δύο μέσοι ἀνάλογον ἐμπιπτέτωσαν ἀριθμοὶ οἱ Γ, Δ· λέγω, ὅτι οἱ Α, Β ὅμοιοι στερεοί εἰσιν.
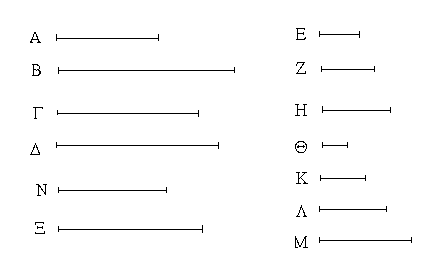
Εἰλήφθωσαν γὰρ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ, Δ τρεῖς οἱ Ε, Ζ, Η· οἱ ἄρα ἄκροι αὐτῶν οἱ Ε, Η πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἐπεὶ τῶν Ε, Η εἷς μέσος ἀνάλογον ἐμπέπτωκεν ἀριθμὸς ὁ Ζ, οἱ Ε, Η ἄρα ἀριθμοὶ ὅμοιοι ἐπίπεδοί εἰσιν. ἔστωσαν οὖν τοῦ μὲν Ε πλευραὶ οἱ Θ, Κ, τοῦ δὲ Η οἱ Λ, Μ. φανερὸν ἄρα ἐστὶν ἐκ τοῦ πρὸ τούτου, ὅτι οἱ Ε, Ζ, Η ἑξῆς εἰσιν ἀνάλογον ἔν τε τῷ τοῦ Θ πρὸς τὸν Λ λόγῳ καὶ τῷ τοῦ Κ πρὸς τὸν Μ. καὶ ἐπεὶ οἱ Ε, Ζ, Η ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ, Δ, καί ἐστιν ἴσον τὸ πλῆθος τῶν Ε, Ζ, Η τῷ πλήθει τῶν Α, Γ, Δ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Ε πρὸς τὸν Η, οὕτως ὁ Α πρὸς τὸν Δ. οἱ δὲ Ε, Η πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας αὐτοῖς ἰσάκις ὅ τε μείζων τὸν μείζονα καὶ ὁ ἐλάσσων τὸν ἐλάσσονα, τουτέστιν ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· ἰσάκις ἄρα ὁ Ε τὸν Α μετρεῖ καὶ ὁ Η τὸν Δ. ὁσάκις δὴ ὁ Ε τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ν. ὁ Ν ἄρα τὸν Ε πολλαπλασιάσας τὸν Α πεποίηκεν. ὁ δὲ Ε ἐστιν ὁ ἐκ τῶν Θ, Κ· ὁ Ν ἄρα τὸν ἐκ τῶν Θ, Κ πολλαπλασιάσας τὸν Α πεποίηκεν. στερεὸς ἄρα ἐστὶν ὁ Α, πλευραὶ δὲ αὐτοῦ εἰσιν οἱ Θ, Κ, Ν. πάλιν, ἐπεὶ οἱ Ε, Ζ, Η ἐλάχιστοί εἰσι τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Γ, Δ, Β, ἰσάκις ἄρα ὁ Ε τὸν Γ μετρεῖ καὶ ὁ Η τὸν Β. ὁσάκις δὴ ὁ Ε τὸν Γ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ξ. ὁ Η ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν τῷ Ξ μονάδας· ὁ Ξ ἄρα τὸν Η πολλαπλασιάσας τὸν Β πεποίηκεν. ὁ δὲ Η ἐστιν ὁ ἐκ τῶν Λ, Μ· ὁ Ξ ἄρα τὸν ἐκ τῶν Λ, Μ πολλαπλασιάσας τὸν Β πεποίηκεν. στερεὸς ἄρα ἐστὶν ὁ Β, πλευραὶ δὲ αὐτοῦ εἰσιν οἱ Λ, Μ, Ξ· οἱ Α, Β ἄρα στερεοί εἰσιν.
Λέγω [δή], ὅτι καὶ ὅμοιοι. ἐπεὶ γὰρ οἱ Ν, Ξ τὸν Ε πολλαπλασιάσαντες τοὺς Α, Γ πεποιήκασιν, ἔστιν ἄρα ὡς ὁ Ν πρὸς τὸν Ξ, ὁ Α πρὸς τὸν Γ, τουτέστιν ὁ Ε πρὸς τὸν Ζ. ἀλλ' ὡς ὁ Ε πρὸς τὸν Ζ, ὁ Θ πρὸς τὸν Λ καὶ ὁ Κ πρὸς τὸν Μ· καὶ ὡς ἄρα ὁ Θ πρὸς τὸν Λ, οὕτως ὁ Κ πρὸς τὸν Μ καὶ ὁ Ν πρὸς τὸν Ξ. καί εἰσιν οἱ μὲν Θ, Κ, Ν πλευραὶ τοῦ Α, οἱ δὲ Ξ, Λ, Μ πλευραὶ τοῦ Β. οἱ Α, Β ἄρα ἀριθμοὶ ὅμοιοι στερεοί εἰσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον VIII
Ἐὰν τρεῖς ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὁ δὲ πρῶτος τετράγωνος ᾖ, καὶ ὁ τρίτος τετράγωνος ἔσται.
Ἔστωσαν τρεῖς ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, ὁ δὲ πρῶτος ὁ Α τετράγωνος ἔστω· λέγω, ὅτι καὶ ὁ τρίτος ὁ Γ τετράγωνός ἐστιν.
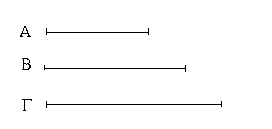
Ἐπεὶ γὰρ τῶν Α, Γ εἷς μέσος ἀνάλογόν ἐστιν ἀριθμὸς ὁ Β, οἱ Α, Γ ἄρα ὅμοιοι ἐπίπεδοί εἰσιν. τετράγωνος δὲ ὁ Α· τετράγωνος ἄρα καὶ ὁ Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον VIII
Ἐὰν τέσσαρες ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὁ δὲ πρῶτος κύβος ᾖ, καὶ ὁ τέταρτος κύβος ἔσται.
Ἔστωσαν τέσσαρες ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, ὁ δὲ Α κύβος ἔστω· λέγω, ὅτι καὶ ὁ Δ κύβος ἐστίν.
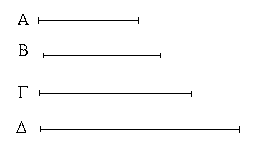
Ἐπεὶ γὰρ τῶν Α, Δ δύο μέσοι ἀνάλογόν εἰσιν ἀριθμοὶ οἱ Β, Γ, οἱ Α, Δ ἄρα ὅμοιοί εἰσι στερεοὶ ἀριθμοί. κύβος δὲ ὁ Α· κύβος ἄρα καὶ ὁ Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον VIII
Ἐὰν δύο ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχωσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ὁ δὲ πρῶτος τετράγωνος ᾖ, καὶ ὁ δεύτερος τετράγωνος ἔσται.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρὸς ἀλλήλους λόγον ἐχέτωσαν, ὃν τετράγωνος ἀριθμὸς ὁ Γ πρὸς τετράγωνον ἀριθμὸν τὸν Δ, ὁ δὲ Α τετράγωνος ἔστω· λέγω, ὅτι καὶ ὁ Β τετράγωνός ἐστιν.
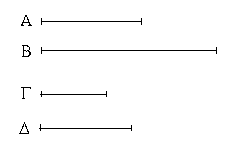
Ἐπεὶ γὰρ οἱ Γ, Δ τετράγωνοί εἰσιν, οἱ Γ, Δ ἄρα ὅμοιοι ἐπίπεδοί εἰσιν. τῶν Γ, Δ ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. καί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, ὁ Α πρὸς τὸν Β· καὶ τῶν Α, Β ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. καί ἐστιν ὁ Α τετράγωνος· καὶ ὁ Β ἄρα τετράγωνός ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον VIII
Ἐὰν δύο ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχωσιν, ὃν κύβος ἀριθμὸς πρὸς κύβον ἀριθμόν, ὁ δὲ πρῶτος κύβος ᾖ, καὶ ὁ δεύτερος κύβος ἔσται.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρὸς ἀλλήλους λόγον ἐχέτωσαν, ὃν κύβος ἀριθμὸς ὁ Γ πρὸς κύβον ἀριθμὸν τὸν Δ, κύβος δὲ ἔστω ὁ Α· λέγω [δή], ὅτι καὶ ὁ Β κύβος ἐστίν.
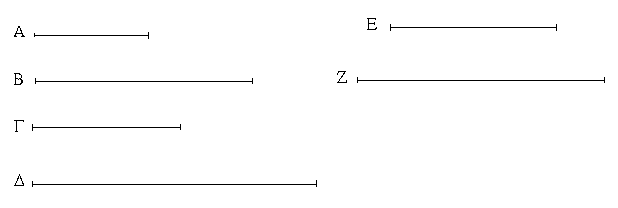
Ἐπεὶ γὰρ οἱ Γ, Δ κύβοι εἰσίν, οἱ Γ, Δ ὅμοιοι στερεοί εἰσιν· τῶν Γ, Δ ἄρα δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί. ὅσοι δὲ εἰς τοὺς Γ, Δ μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτουσιν, τοσοῦτοι καὶ εἰς τοὺς τὸν αὐτὸν λόγον ἔχοντας αὐτοῖς· ὥστε καὶ τῶν Α, Β δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί. ἐμπιπτέτωσαν οἱ Ε, Ζ. ἐπεὶ οὖν τέσσαρες ἀριθμοὶ οἱ Α, Ε, Ζ, Β ἑξῆς ἀνάλογόν εἰσιν, καί ἐστι κύβος ὁ Α, κύβος ἄρα καὶ ὁ Β· ὅπερ ἔδει δεῖξαι.
Πρότασις κς΄ 26 Βιβλίον VIII
Οἱ ὅμοιοι ἐπίπεδοι ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
Ἔστωσαν ὅμοιοι ἐπίπεδοι ἀριθμοὶ οἱ Α, Β· λέγω, ὅτι ὁ Α πρὸς τὸν Β λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
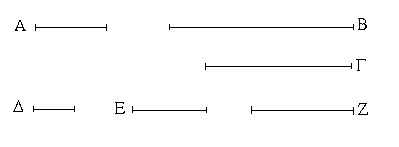
Ἐπεὶ γὰρ οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν, τῶν Α, Β ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. ἐμπιπτέτω καὶ ἔστω ὁ Γ, καὶ εἰλήφθωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ, Β οἱ Δ, Ε, Ζ· οἱ ἄρα ἄκροι αὐτῶν οἱ Δ, Ζ τετράγωνοί εἰσιν. καὶ ἐπεί ἐστιν ὡς ὁ Δ πρὸς τὸν Ζ, οὕτως ὁ Α πρὸς τὸν Β, καί εἰσιν οἱ Δ, Ζ τετράγωνοι, ὁ Α ἄρα πρὸς τὸν Β λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον VIII
Οἱ ὅμοιοι στερεοὶ ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν κύβος ἀριθμὸς πρὸς κύβον ἀριθμόν.
Ἔστωσαν ὅμοιοι στερεοὶ ἀριθμοὶ οἱ Α, Β· λέγω, ὅτι ὁ Α πρὸς τὸν Β λόγον ἔχει, ὃν κύβος ἀριθμὸς πρὸς κύβον ἀριθμόν.
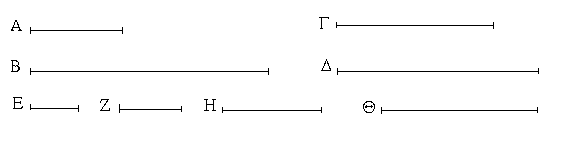
Ἐπεὶ γὰρ οἱ Α, Β ὅμοιοι στερεοί εἰσιν, τῶν Α, Β ἄρα δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί. ἐμπιπτέτωσαν οἱ Γ, Δ, καὶ εἰλήφθωσαν ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Γ, Δ, Β ἴσοι αὐτοῖς τὸ πλῆθος οἱ Ε, Ζ, Η, Θ· οἱ ἄρα ἄκροι αὐτῶν οἱ Ε, Θ κύβοι εἰσίν. καί ἐστιν ὡς ὁ Ε πρὸς τὸν Θ, οὕτως ὁ Α πρὸς τὸν Β· καὶ ὁ Α ἄρα πρὸς τὸν Β λόγον ἔχει, ὃν κύβος ἀριθμὸς πρὸς κύβον ἀριθμόν· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου θ΄
Βιβλίον IX
Προτάσεις λς΄ 36
Πρότασις α΄ 1 Βιβλίον IX
Ἐὰν δύο ὅμοιοι ἐπίπεδοι ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, ὁ γενόμενος τετράγωνος ἔσται.
Ἔστωσαν δύο ὅμοιοι ἐπίπεδοι ἀριθμοὶ οἱ Α, Β, καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι ὁ Γ τετράγωνός ἐστιν.
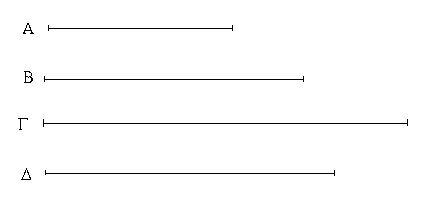
Ὁ γὰρ Α ἑαυτὸν πολλαπλασιάσας τὸν Δ ποιείτω. ὁ Δ ἄρα τετράγωνός ἐστιν. ἐπεὶ οὖν ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Δ πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Γ. καὶ ἐπεὶ οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί, τῶν Α, Β ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. ἐὰν δὲ δύο ἀριθμῶν μεταξὺ κατὰ τὸ συνεχὲς ἀνάλογον ἐμπίπτωσιν ἀριθμοί, ὅσοι εἰς αὐτοὺς ἐμπίπτουσι, τοσοῦτοι καὶ εἰς τοὺς τὸν αὐτὸν λόγον ἔχοντας· ὥστε καὶ τῶν Δ, Γ εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. καί ἐστι τετράγωνος ὁ Δ· τετράγωνος ἄρα καὶ ὁ Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον IX
Ἐὰν δύο ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσι τετράγωνον, ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί.
Ἔστωσαν δύο ἀριθμοὶ οἱ Α, Β, καὶ ὁ Α τὸν Β πολλαπλασιάσας τετράγωνον τὸν Γ ποιείτω· λέγω, ὅτι οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν ἀριθμοί.
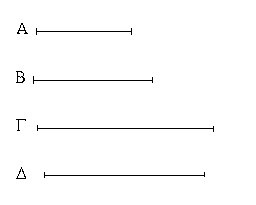
Ὁ γὰρ Α ἑαυτὸν πολλαπλασιάσας τὸν Δ ποιείτω· ὁ Δ ἄρα τετράγωνός ἐστιν. καὶ ἐπεὶ ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Δ πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, ὁ Δ πρὸς τὸν Γ. καὶ ἐπεὶ ὁ Δ τετράγωνός ἐστιν, ἀλλὰ καὶ ὁ Γ, οἱ Δ, Γ ἄρα ὅμοιοι ἐπίπεδοί εἰσιν. τῶν Δ, Γ ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει. καί ἐστιν ὡς ὁ Δ πρὸς τὸν Γ, οὕτως ὁ Α πρὸς τὸν Β· καὶ τῶν Α, Β ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει. ἐὰν δὲ δύο ἀριθμῶν εἷς μέσος ἀνάλογον ἐμπίπτῃ, ὅμοιοι ἐπίπεδοί εἰσιν [οἱ] ἀριθμοί· οἱ ἄρα Α, Β ὅμοιοί εἰσιν ἐπίπεδοι· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον IX
Ἐὰν κύβος ἀριθμὸς ἑαυτὸν πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος κύβος ἔσται.
Κύβος γὰρ ἀριθμὸς ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Β ποιείτω· λέγω, ὅτι ὁ Β κύβος ἐστίν.
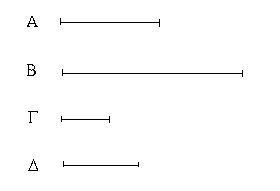
Εἰλήφθω γὰρ τοῦ Α πλευρὰ ὁ Γ, καὶ ὁ Γ ἑαυτὸν πολλαπλασιάσας τὸν Δ ποιείτω. φανερὸν δή ἐστιν, ὅτι ὁ Γ τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν. καὶ ἐπεὶ ὁ Γ ἑαυτὸν πολλαπλασιάσας τὸν Δ πεποίηκεν, ὁ Γ ἄρα τὸν Δ μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας. ἀλλὰ μὴν καὶ ἡ μονὰς τὸν Γ μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας· ἔστιν ἄρα ὡς ἡ μονὰς πρὸς τὸν Γ, ὁ Γ πρὸς τὸν Δ. πάλιν, ἐπεὶ ὁ Γ τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν, ὁ Δ ἄρα τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Γ μονάδας. μετρεῖ δὲ καὶ ἡ μονὰς τὸν Γ κατὰ τὰς ἐν αὐτῷ μονάδας· ἔστιν ἄρα ὡς ἡ μονὰς πρὸς τὸν Γ, ὁ Δ πρὸς τὸν Α. ἀλλ' ὡς ἡ μονὰς πρὸς τὸν Γ, ὁ Γ πρὸς τὸν Δ· καὶ ὡς ἄρα ἡ μονὰς πρὸς τὸν Γ, οὕτως ὁ Γ πρὸς τὸν Δ καὶ ὁ Δ πρὸς τὸν Α. τῆς ἄρα μονάδος καὶ τοῦ Α ἀριθμοῦ δύο μέσοι ἀνάλογον κατὰ τὸ συνεχὲς ἐμπεπτώκασιν ἀριθμοὶ οἱ Γ, Δ. πάλιν, ἐπεὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν, ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας. μετρεῖ δὲ καὶ ἡ μονὰς τὸν Α κατὰ τὰς ἐν αὐτῷ μονάδας· ἔστιν ἄρα ὡς ἡ μονὰς πρὸς τὸν Α, ὁ Α πρὸς τὸν Β. τῆς δὲ μονάδος καὶ τοῦ Α δύο μέσοι ἀνάλογον ἐμπεπτώκασιν ἀριθμοί· καὶ τῶν Α, Β ἄρα δύο μέσοι ἀνάλογον ἐμπεσοῦνται ἀριθμοί. ἐὰν δὲ δύο ἀριθμῶν δύο μέσοι ἀνάλογον ἐμπίπτωσιν, ὁ δὲ πρῶτος κύβος ᾖ, καὶ ὁ δεύτερος κύβος ἔσται. καί ἐστιν ὁ Α κύβος· καὶ ὁ Β ἄρα κύβος ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον IX
Ἐὰν κύβος ἀριθμὸς κύβον ἀριθμὸν πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος κύβος ἔσται.
Κύβος γὰρ ἀριθμὸς ὁ Α κύβον ἀριθμὸν τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι ὁ Γ κύβος ἐστίν.
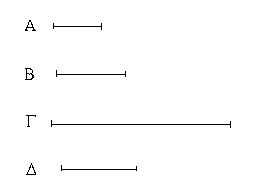
Ὁ γὰρ Α ἑαυτὸν πολλαπλασιάσας τὸν Δ ποιείτω· ὁ Δ ἄρα κύβος ἐστίν. καὶ ἐπεὶ ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Δ πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Γ. καὶ ἐπεὶ οἱ Α, Β κύβοι εἰσίν, ὅμοιοι στερεοί εἰσιν οἱ Α, Β. τῶν Α, Β ἄρα δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί· ὥστε καὶ τῶν Δ, Γ δύο μέσοι ἀνάλογον ἐμπεσοῦνται ἀριθμοί. καί ἐστι κύβος ὁ Δ· κύβος ἄρα καὶ ὁ Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον IX
Ἐὰν κύβος ἀριθμὸς ἀριθμόν τινα πολλαπλασιάσας κύβον ποιῇ, καὶ ὁ πολλαπλασιασθεὶς κύβος ἔσται.
Κύβος γὰρ ἀριθμὸς ὁ Α ἀριθμόν τινα τὸν Β πολλαπλασιάσας κύβον τὸν Γ ποιείτω· λέγω, ὅτι ὁ Β κύβος ἐστίν.
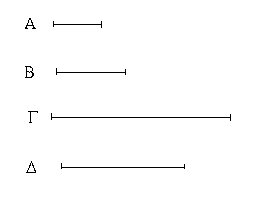
Ὁ γὰρ Α ἑαυτὸν πολλαπλασιάσας τὸν Δ ποιείτω· κύβος ἄρα ἐστίν ὁ Δ. καὶ ἐπεὶ ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Δ πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, ὁ Δ πρὸς τὸν Γ. καὶ ἐπεὶ οἱ Δ, Γ κύβοι εἰσίν, ὅμοιοι στερεοί εἰσιν. τῶν Δ, Γ ἄρα δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί. καί ἐστιν ὡς ὁ Δ πρὸς τὸν Γ, οὕτως ὁ Α πρὸς τὸν Β· καὶ τῶν Α, Β ἄρα δύο μέσοι ἀνάλογον ἐμπίπτουσιν ἀριθμοί. καί ἐστι κύβος ὁ Α· κύβος ἄρα ἐστὶ καὶ ὁ Β· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον IX
Ἐὰν ἀριθμὸς ἑαυτὸν πολλαπλασιάσας κύβον ποιῇ, καὶ αὐτὸς κύβος ἔσται.
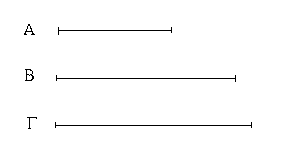
Ἀριθμὸς γὰρ ὁ Α ἑαυτὸν πολλαπλασιάσας κύβον τὸν Β ποιείτω· λέγω, ὅτι καὶ ὁ Α κύβος ἐστίν. ὁ γὰρ Α τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω. ἐπεὶ οὖν ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Β πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ Γ ἄρα κύβος ἐστίν. καὶ ἐπεὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν, ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας. μετρεῖ δὲ καὶ ἡ μονὰς τὸν Α κατὰ τὰς ἐν αὐτῷ μονάδας. ἔστιν ἄρα ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Α πρὸς τὸν Β. καὶ ἐπεὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ Β ἄρα τὸν Γ μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας. μετρεῖ δὲ καὶ ἡ μονὰς τὸν Α κατὰ τὰς ἐν αὐτῷ μονάδας. ἔστιν ἄρα ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Β πρὸς τὸν Γ. ἀλλ' ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Α πρὸς τὸν Β· καὶ ὡς ἄρα ὁ Α πρὸς τὸν Β, ὁ Β πρὸς τὸν Γ. καὶ ἐπεὶ οἱ Β, Γ κύβοι εἰσίν, ὅμοιοι στερεοί εἰσιν. τῶν Β, Γ ἄρα δύο μέσοι ἀνάλογόν εἰσιν ἀριθμοί. καί ἐστιν ὡς ὁ Β πρὸς τὸν Γ, ὁ Α πρὸς τὸν Β. καὶ τῶν Α, Β ἄρα δύο μέσοι ἀνάλογόν εἰσιν ἀριθμοί. καί ἐστι κύβος ὁ Β· κύβος ἄρα ἐστὶ καὶ ὁ Α· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον IX
Ἐὰν σύνθετος ἀριθμὸς ἀριθμόν τινα πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος στερεὸς ἔσται.
Σύνθετος γὰρ ἀριθμὸς ὁ Α ἀριθμόν τινα τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι ὁ Γ στερεός ἐστιν.
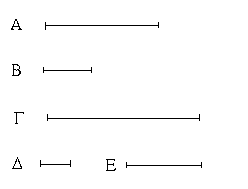
Ἐπεὶ γὰρ ὁ Α σύνθετός ἐστιν, ὑπὸ ἀριθμοῦ τινος μετρηθήσεται. μετρείσθω ὑπὸ τοῦ Δ, καὶ ὁσάκις ὁ Δ τὸν Α μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε. ἐπεὶ οὖν ὁ Δ τὸν Α μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας, ὁ Ε ἄρα τὸν Δ πολλαπλασιάσας τὸν Α πεποίηκεν. καὶ ἐπεὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ δὲ Α ἐστιν ὁ ἐκ τῶν Δ, Ε, ὁ ἄρα ἐκ τῶν Δ, Ε τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν. ὁ Γ ἄρα στερεός ἐστιν, πλευραὶ δὲ αὐτοῦ εἰσιν οἱ Δ, Ε, Β· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὁ μὲν τρίτος ἀπὸ τῆς μονάδος τετράγωνος ἔσται καὶ οἱ ἕνα διαλείποντες, ὁ δὲ τέταρτος κύβος καὶ οἱ δύο διαλείποντες πάντες, ὁ δὲ ἕβδομος κύβος ἅμα καὶ τετράγωνος καὶ οἱ πέντε διαλείποντες.
Ἔστωσαν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, Ε, Ζ· λέγω, ὅτι ὁ μὲν τρίτος ἀπὸ τῆς μονάδος ὁ Β τετράγωνός ἐστι καὶ οἱ ἕνα διαλείποντες πάντες, ὁ δὲ τέταρτος ὁ Γ κύβος καὶ οἱ δύο διαλείποντες πάντες, ὁ δὲ ἕβδομος ὁ Ζ κύβος ἅμα καὶ τετράγωνος καὶ οἱ πέντε διαλείποντες πάντες.
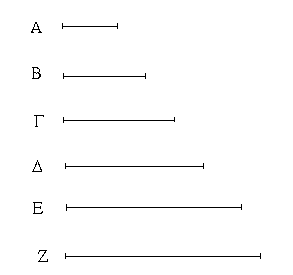
Ἐπεὶ γάρ ἐστιν ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Α πρὸς τὸν Β, ἰσάκις ἄρα ἡ μονὰς τὸν Α ἀριθμὸν μετρεῖ καὶ ὁ Α τὸν Β. ἡ δὲ μονὰς τὸν Α ἀριθμὸν μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας· καὶ ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας. ὁ Α ἄρα ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν· τετράγωνος ἄρα ἐστὶν ὁ Β. καὶ ἐπεὶ οἱ Β, Γ, Δ ἑξῆς ἀνάλογόν εἰσιν, ὁ δὲ Β τετράγωνός ἐστιν, καὶ ὁ Δ ἄρα τετράγωνός ἐστιν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Ζ τετράγωνός ἐστιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ οἱ ἕνα διαλείποντες πάντες τετράγωνοί εἰσιν. λέγω δή, ὅτι καὶ ὁ τέταρτος ἀπὸ τῆς μονάδος ὁ Γ κύβος ἐστὶ καὶ οἱ δύο διαλείποντες πάντες. ἐπεὶ γάρ ἐστιν ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Β πρὸς τὸν Γ, ἰσάκις ἄρα ἡ μονὰς τὸν Α ἀριθμὸν μετρεῖ καὶ ὁ Β τὸν Γ. ἡ δὲ μονὰς τὸν Α ἀριθμὸν μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας· καὶ ὁ Β ἄρα τὸν Γ μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας· ὁ Α ἄρα τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν. ἐπεὶ οὖν ὁ Α ἑαυτὸν μὲν πολλαπλασιάσας τὸν Β πεποίηκεν, τὸν δὲ Β πολλαπλασιάσας τὸν Γ πεποίηκεν, κύβος ἄρα ἐστὶν ὁ Γ. καὶ ἐπεὶ οἱ Γ, Δ, Ε, Ζ ἑξῆς ἀνάλογόν εἰσιν, ὁ δὲ Γ κύβος ἐστίν, καὶ ὁ Ζ ἄρα κύβος ἐστίν. ἐδείχθη δὲ καὶ τετράγωνος· ὁ ἄρα ἕβδομος ἀπὸ τῆς μονάδος κύβος τέ ἐστι καὶ τετράγωνος. ὁμοίως δὴ δείξομεν, ὅτι καὶ οἱ πέντε διαλείποντες πάντες κύβοι τέ εἰσι καὶ τετράγωνοι· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἑξῆς κατὰ τὸ συνεχὲς ἀριθμοὶ ἀνάλογον ὦσιν, ὁ δὲ μετὰ τὴν μονάδα τετράγωνος ᾖ, καὶ οἱ λοιποὶ πάντες τετράγωνοι ἔσονται. καὶ ἐὰν ὁ μετὰ τὴν μονάδα κύβος ᾖ, καὶ οἱ λοιποὶ πάντες κύβοι ἔσονται.
Ἔστωσαν ἀπὸ μονάδος ἑξῆς ἀνάλογον ὁσοιδηποτοῦν ἀριθμοὶ οἱ Α, Β, Γ, Δ, Ε, Ζ, ὁ δὲ μετὰ τὴν μονάδα ὁ Α τετράγωνος ἔστω· λέγω, ὅτι καὶ οἱ λοιποὶ πάντες τετράγωνοι ἔσονται.
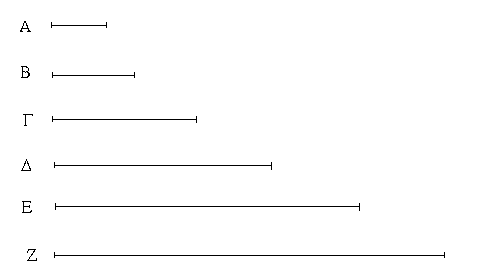
Ὅτι μὲν οὖν ὁ τρίτος ἀπὸ τῆς μονάδος ὁ Β τετράγωνός ἐστι καὶ οἱ ἕνα διαλείποντες πάντες, δέδεικται· λέγω [δή], ὅτι καὶ οἱ λοιποὶ πάντες τετράγωνοί εἰσιν. ἐπεὶ γὰρ οἱ Α, Β, Γ ἑξῆς ἀνάλογόν εἰσιν, καί ἐστιν ὁ Α τετράγωνος, καὶ ὁ Γ [ἄρα] τετράγωνός ἐστιν. πάλιν, ἐπεὶ [καὶ] οἱ Β, Γ, Δ ἑξῆς ἀνάλογόν εἰσιν, καί ἐστιν ὁ Β τετράγωνος, καὶ ὁ Δ [ἄρα] τετράγωνός ἐστιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ οἱ λοιποὶ πάντες τετράγωνοί εἰσιν.
Ἀλλὰ δὴ ἔστω ὁ Α κύβος· λέγω, ὅτι καὶ οἱ λοιποὶ πάντες κύβοι εἰσίν.
Ὅτι μὲν οὖν ὁ τέταρτος ἀπὸ τῆς μονάδος ὁ Γ κύβος ἐστὶ καὶ οἱ δύο διαλείποντες πάντες, δέδεικται· λέγω [δή], ὅτι καὶ οἱ λοιποὶ πάντες κύβοι εἰσίν. ἐπεὶ γάρ ἐστιν ὡς ἡ μονὰς πρὸς τὸν Α, οὕτως ὁ Α πρὸς τὸν Β, ἰσάκις ἄρα ἡ μονὰς τὸν Α μετρεῖ καὶ ὁ Α τὸν Β. ἡ δὲ μονὰς τὸν Α μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας· καὶ ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας· ὁ Α ἄρα ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν. καί ἐστιν ὁ Α κύβος. ἐὰν δὲ κύβος ἀριθμὸς ἑαυτὸν πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος κύβος ἐστίν· καὶ ὁ Β ἄρα κύβος ἐστίν. καὶ ἐπεὶ τέσσαρες ἀριθμοὶ οἱ Α, Β, Γ, Δ ἑξῆς ἀνάλογόν εἰσιν, καί ἐστιν ὁ Α κύβος, καὶ ὁ Δ ἄρα κύβος ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ ὁ Ε κύβος ἐστίν, καὶ ὁμοίως οἱ λοιποὶ πάντες κύβοι εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ [ἑξῆς] ἀνάλογον ὦσιν, ὁ δὲ μετὰ τὴν μονάδα μὴ ᾖ τετράγωνος, οὐδ' ἄλλος οὐδεὶς τετράγωνος ἔσται χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος καὶ τῶν ἕνα διαλειπόντων πάντων. καὶ ἐὰν ὁ μετὰ τὴν μονάδα κύβος μὴ ᾖ, οὐδὲ ἄλλος οὐδεὶς κύβος ἔσται χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων πάντων.
Ἔστωσαν ἀπὸ μονάδος ἑξῆς ἀνάλογον ὁσοιδηποτοῦν ἀριθμοὶ οἱ Α, Β, Γ, Δ, Ε, Ζ, ὁ δὲ μετὰ τὴν μονάδα ὁ Α μὴ ἔστω τετράγωνος· λέγω, ὅτι οὐδὲ ἄλλος οὐδεὶς τετράγωνος ἔσται χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος [καὶ τῶν ἕνα διαλειπόντων].
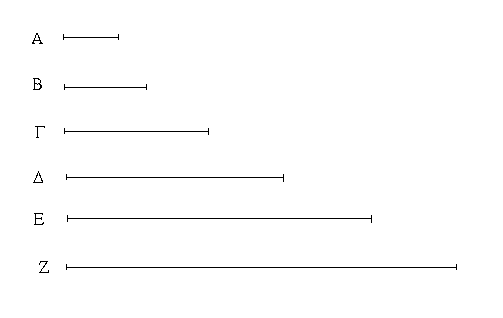
Εἰ γὰρ δυνατόν, ἔστω ὁ Γ τετράγωνος. ἔστι δὲ καὶ ὁ Β τετράγωνος· οἱ Β, Γ ἄρα πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. καί ἐστιν ὡς ὁ Β πρὸς τὸν Γ, ὁ Α πρὸς τὸν Β· οἱ Α, Β ἄρα πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ὥστε οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν. καί ἐστι τετράγωνος ὁ Β· τετράγωνος ἄρα ἐστὶ καὶ ὁ Α· ὅπερ οὐχ ὑπέκειτο. οὐκ ἄρα ὁ Γ τετράγωνός ἐστιν. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλος οὐδεὶς τετράγωνός ἐστι χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος καὶ τῶν ἕνα διαλειπόντων.
Ἀλλὰ δὴ μὴ ἔστω ὁ Α κύβος. λέγω, ὅτι οὐδ' ἄλλος οὐδεὶς κύβος ἔσται χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων.
Εἰ γὰρ δυνατόν, ἔστω ὁ Δ κύβος. ἔστι δὲ καὶ ὁ Γ κύβος· τέταρτος γάρ ἐστιν ἀπὸ τῆς μονάδος. καί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, ὁ Β πρὸς τὸν Γ· καὶ ὁ Β ἄρα πρὸς τὸν Γ λόγον ἔχει, ὃν κύβος πρὸς κύβον. καί ἐστιν ὁ Γ κύβος· καὶ ὁ Β ἄρα κύβος ἐστίν. καὶ ἐπεί ἐστιν ὡς ἡ μονὰς πρὸς τὸν Α, ὁ Α πρὸς τὸν Β, ἡ δὲ μονὰς τὸν Α μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας, καὶ ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας· ὁ Α ἄρα ἑαυτὸν πολλαπλασιάσας κύβον τὸν Β πεποίηκεν. ἐὰν δὲ ἀριθμὸς ἑαυτὸν πολλαπλασιάσας κύβον ποιῇ, καὶ αὐτὸς κύβος ἔσται. κύβος ἄρα καὶ ὁ Α· ὅπερ οὐχ ὑπόκειται. οὐκ ἄρα ὁ Δ κύβος ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλος οὐδεὶς κύβος ἐστὶ χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὁ ἐλάττων τὸν μείζονα μετρεῖ κατά τινα τῶν ὑπαρχόντων ἐν τοῖς ἀνάλογον ἀριθμοῖς.
Ἔστωσαν ἀπὸ μονάδος τῆς Α ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Β, Γ, Δ, Ε· λέγω, ὅτι τῶν Β, Γ, Δ, Ε ὁ ἐλάχιστος ὁ Β τὸν Ε μετρεῖ κατά τινα τῶν Γ, Δ.
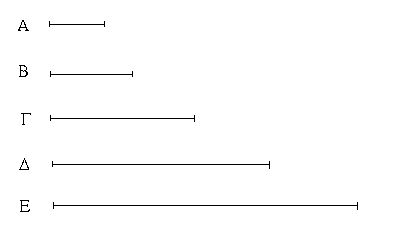
Ἐπεὶ γάρ ἐστιν ὡς ἡ Α μονὰς πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε, ἰσάκις ἄρα ἡ Α μονὰς τὸν Β ἀριθμὸν μετρεῖ καὶ ὁ Δ τὸν Ε· ἐναλλὰξ ἄρα ἰσάκις ἡ Α μονὰς τὸν Δ μετρεῖ καὶ ὁ Β τὸν Ε. ἡ δὲ Α μονὰς τὸν Δ μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας· καὶ ὁ Β ἄρα τὸν Ε μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας· ὥστε ὁ ἐλάσσων ὁ Β τὸν μείζονα τὸν Ε μετρεῖ κατά τινα ἀριθμὸν τῶν ὑπαρχόντων ἐν τοῖς ἀνάλογον ἀριθμοῖς.
Πόρισμα Καὶ φανερόν, ὅτι ἣν ἔχει τάξιν ὁ μετρῶν ἀπὸ μονάδος, τὴν αὐτὴν ἔχει καὶ ὁ καθ᾿ ὃν μετρεῖ ἀπὸ τοῦ μετρουμένου ἐπὶ τὸ πρὸ αὐτοῦ. ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὑφ᾿ ὅσων ἂν ὁ ἔσχατος πρώτων ἀριθμῶν μετρῆται, ὑπὸ τῶν αὐτῶν καὶ ὁ παρὰ τὴν μονάδα μετρηθήσεται.
Ἔστωσαν ἀπὸ μονάδος ὁποσοιδηποτοῦν ἀριθμοὶ ἀνάλογον οἱ Α, Β, Γ, Δ· λέγω, ὅτι ὑφ᾿ ὅσων ἂν ὁ Δ πρώτων ἀριθμῶν μετρῆται, ὑπὸ τῶν αὐτῶν καὶ ὁ Α μετρηθήσεται.
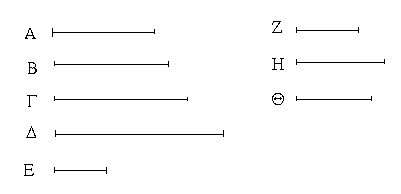
Μετρείσθω γὰρ ὁ Δ ὑπό τινος πρώτου ἀριθμοῦ τοῦ Ε· λέγω, ὅτι ὁ Ε τὸν Α μετρεῖ. μὴ γάρ· καί ἐστιν ὁ Ε πρῶτος, ἅπας δὲ πρῶτος ἀριθμὸς πρὸς ἅπαντα, ὃν μὴ μετρεῖ, πρῶτός ἐστιν· οἱ Ε, Α ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ἐπεὶ ὁ Ε τὸν Δ μετρεῖ, μετρείτω αὐτὸν κατὰ τὸν Ζ· ὁ Ε ἄρα τὸν Ζ πολλαπλασιάσας τὸν Δ πεποίηκεν. πάλιν, ἐπεὶ ὁ Α τὸν Δ μετρεῖ κατὰ τὰς ἐν τῷ Γ μονάδας, ὁ Α ἄρα τὸν Γ πολλαπλασιάσας τὸν Δ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Ε τὸν Ζ πολλαπλασιάσας τὸν Δ πεποίηκεν· ὁ ἄρα ἐκ τῶν Α, Γ ἴσος ἐστὶ τῷ ἐκ τῶν Ε, Ζ. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Ε, ὁ Ζ πρὸς τὸν Γ. οἱ δὲ Α, Ε πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· μετρεῖ ἄρα ὁ Ε τὸν Γ. μετρείτω αὐτὸν κατὰ τὸν Η· ὁ Ε ἄρα τὸν Η πολλαπλασιάσας τὸν Γ πεποίηκεν. ἀλλὰ μὴν διὰ τὸ πρὸ τούτου καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν. ὁ ἄρα ἐκ τῶν Α, Β ἴσος ἐστὶ τῷ ἐκ τῶν Ε, Η. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Ε, ὁ Η πρὸς τὸν Β. οἱ δὲ Α, Ε πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας αὐτοῖς ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· μετρεῖ ἄρα ὁ Ε τὸν Β. μετρείτω αὐτὸν κατὰ τὸν Θ· ὁ Ε ἄρα τὸν Θ πολλαπλασιάσας τὸν Β πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν· ὁ ἄρα ἐκ τῶν Ε, Θ ἴσος ἐστὶ τῷ ἀπὸ τοῦ Α. ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Α, ὁ Α πρὸς τὸν Θ. οἱ δὲ Α, Ε πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· μετρεῖ ἄρα ὁ Ε τὸν Α ὡς ἡγούμενος ἡγούμενον. ἀλλὰ μὴν καὶ οὐ μετρεῖ· ὅπερ ἀδύνατον. οὐκ ἄρα οἱ Ε, Α πρῶτοι πρὸς ἀλλήλους εἰσίν. σύνθετοι ἄρα. οἱ δὲ σύνθετοι ὑπὸ [πρώτου] ἀριθμοῦ τινος μετροῦνται. καὶ ἐπεὶ ὁ Ε πρῶτος ὑπόκειται, ὁ δὲ πρῶτος ὑπὸ ἑτέρου ἀριθμοῦ οὐ μετρεῖται ἢ ὑφ᾿ ἑαυτοῦ, ὁ Ε ἄρα τοὺς Α, Ε μετρεῖ· ὥστε ὁ Ε τὸν Α μετρεῖ. μετρεῖ δὲ καὶ τὸν Δ· ὁ Ε ἄρα τοὺς Α, Δ μετρεῖ. ὁμοίως δὴ δείξομεν, ὅτι ὑφ᾿ ὅσων ἂν ὁ Δ πρώτων ἀριθμῶν μετρῆται, ὑπὸ τῶν αὐτῶν καὶ ὁ Α μετρηθήσεται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν, ὁ δὲ μετὰ τὴν μονάδα πρῶτος ᾖ, ὁ μέγιστος ὑπ' οὐδενὸς [ἄλλου] μετρηθήσεται παρὲξ τῶν ὑπαρχόντων ἐν τοῖς ἀνάλογον ἀριθμοῖς.
Ἔστωσαν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, ὁ δὲ μετὰ τὴν μονάδα ὁ Α πρῶτος ἔστω· λέγω, ὅτι ὁ μέγιστος αὐτῶν ὁ Δ ὑπ' οὐδενὸς ἄλλου μετρηθήσεται παρὲξ τῶν Α, Β, Γ.
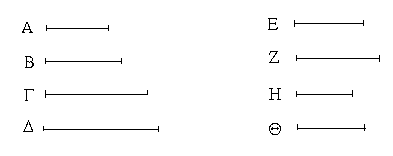
Εἰ γὰρ δυνατόν, μετρείσθω ὑπὸ τοῦ Ε, καὶ ὁ Ε μηδενὶ τῶν Α, Β, Γ ἔστω ὁ αὐτός. φανερὸν δή, ὅτι ὁ Ε πρῶτος οὔκ ἐστιν. εἰ γὰρ ὁ Ε πρῶτός ἐστι καὶ μετρεῖ τὸν Δ, καὶ τὸν Α μετρήσει πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ὁ Ε πρῶτός ἐστιν. σύνθετος ἄρα. πᾶς δὲ σύνθετος ἀριθμὸς ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται· ὁ Ε ἄρα ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται. λέγω δή, ὅτι ὑπ' οὐδενὸς ἄλλου πρώτου μετρηθήσεται πλὴν τοῦ Α. εἰ γὰρ ὑφ᾿ ἑτέρου μετρεῖται ὁ Ε, ὁ δὲ Ε τὸν Δ μετρεῖ, κἀκεῖνος ἄρα τὸν Δ μετρήσει· ὥστε καὶ τὸν Α μετρήσει πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἐστὶν ἀδύνατον. ὁ Α ἄρα τὸν Ε μετρεῖ. καὶ ἐπεὶ ὁ Ε τὸν Δ μετρεῖ, μετρείτω αὐτὸν κατὰ τὸν Ζ. λέγω, ὅτι ὁ Ζ οὐδενὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. εἰ γὰρ ὁ Ζ ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτὸς καὶ μετρεῖ τὸν Δ κατὰ τὸν Ε, καὶ εἷς ἄρα τῶν Α, Β, Γ τὸν Δ μετρεῖ κατὰ τὸν Ε. ἀλλὰ εἷς τῶν Α, Β, Γ τὸν Δ μετρεῖ κατά τινα τῶν Α, Β, Γ· καὶ ὁ Ε ἄρα ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός· ὅπερ οὐχ ὑπόκειται. οὐκ ἄρα ὁ Ζ ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. ὁμοίως δὴ δείξομεν, ὅτι μετρεῖται ὁ Ζ ὑπὸ τοῦ Α, δεικνύντες πάλιν, ὅτι ὁ Ζ οὔκ ἐστι πρῶτος. εἰ γάρ, καὶ μετρεῖ τὸν Δ, καὶ τὸν Α μετρήσει πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἐστὶν ἀδύνατον· οὐκ ἄρα πρῶτός ἐστιν ὁ Ζ· σύνθετος ἄρα. ἅπας δὲ σύνθετος ἀριθμὸς ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται· ὁ Ζ ἄρα ὑπὸ πρώτου τινὸς ἀριθμοῦ μετρεῖται. λέγω δή, ὅτι ὑφ᾿ ἑτέρου πρώτου οὐ μετρηθήσεται πλὴν τοῦ Α. εἰ γὰρ ἕτερός τις πρῶτος τὸν Ζ μετρεῖ, ὁ δὲ Ζ τὸν Δ μετρεῖ, κἀκεῖνος ἄρα τὸν Δ μετρήσει· ὥστε καὶ τὸν Α μετρήσει πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἐστὶν ἀδύνατον. ὁ Α ἄρα τὸν Ζ μετρεῖ. καὶ ἐπεὶ ὁ Ε τὸν Δ μετρεῖ κατὰ τὸν Ζ, ὁ Ε ἄρα τὸν Ζ πολλαπλασιάσας τὸν Δ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α τὸν Γ πολλαπλασιάσας τὸν Δ πεποίηκεν· ὁ ἄρα ἐκ τῶν Α, Γ ἴσος ἐστὶ τῷ ἐκ τῶν Ε, Ζ. ἀνάλογον ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Ε, οὕτως ὁ Ζ πρὸς τὸν Γ. ὁ δὲ Α τὸν Ε μετρεῖ· καὶ ὁ Ζ ἄρα τὸν Γ μετρεῖ. μετρείτω αὐτὸν κατὰ τὸν Η. ὁμοίως δὴ δείξομεν, ὅτι ὁ Η οὐδενὶ τῶν Α, Β ἐστιν ὁ αὐτός, καὶ ὅτι μετρεῖται ὑπὸ τοῦ Α. καὶ ἐπεὶ ὁ Ζ τὸν Γ μετρεῖ κατὰ τὸν Η, ὁ Ζ ἄρα τὸν Η πολλαπλασιάσας τὸν Γ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν· ὁ ἄρα ἐκ τῶν Α, Β ἴσος ἐστὶ τῷ ἐκ τῶν Ζ, Η. ἀνάλογον ἄρα ὡς ὁ Α πρὸς τὸν Ζ, ὁ Η πρὸς τὸν Β. μετρεῖ δὲ ὁ Α τὸν Ζ· μετρεῖ ἄρα καὶ ὁ Η τὸν Β. μετρείτω αὐτὸν κατὰ τὸν Θ. ὁμοίως δὴ δείξομεν, ὅτι ὁ Θ τῷ Α οὐκ ἔστιν ὁ αὐτός. καὶ ἐπεὶ ὁ Η τὸν Β μετρεῖ κατὰ τὸν Θ, ὁ Η ἄρα τὸν Θ πολλαπλασιάσας τὸν Β πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Α ἑαυτὸν πολλαπλασιάσας τὸν Β πεποίηκεν· ὁ ἄρα ὑπὸ Θ, Η ἴσος ἐστὶ τῷ ἀπὸ τοῦ Α τετραγώνῳ. ἔστιν ἄρα ὡς ὁ Θ πρὸς τὸν Α, ὁ Α πρὸς τὸν Η. μετρεῖ δὲ ὁ Α τὸν Η· μετρεῖ ἄρα καὶ ὁ Θ τὸν Α πρῶτον ὄντα μὴ ὢν αὐτῷ ὁ αὐτός· ὅπερ ἄτοπον. οὐκ ἄρα ὁ μέγιστος ὁ Δ ὑπὸ ἑτέρου ἀριθμοῦ μετρηθήσεται παρὲξ τῶν Α, Β, Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον IX
Ἐὰν ἐλάχιστος ἀριθμὸς ὑπὸ πρώτων ἀριθμῶν μετρῆται, ὑπ' οὐδενὸς ἄλλου πρώτου ἀριθμοῦ μετρηθήσεται παρὲξ τῶν ἐξ ἀρχῆς μετρούντων.
Ἐλάχιστος γὰρ ἀριθμὸς ὁ Α ὑπὸ πρώτων ἀριθμῶν τῶν Β, Γ, Δ μετρείσθω· λέγω, ὅτι ὁ Α ὑπ' οὐδενὸς ἄλλου πρώτου ἀριθμοῦ μετρηθήσεται παρὲξ τῶν Β, Γ, Δ.
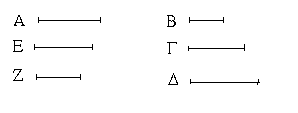
Εἰ γὰρ δυνατόν, μετρείσθω ὑπὸ πρώτου τοῦ Ε, καὶ ὁ Ε μηδενὶ τῶν Β, Γ, Δ ἔστω ὁ αὐτός. καὶ ἐπεὶ ὁ Ε τὸν Α μετρεῖ, μετρείτω αὐτὸν κατὰ τὸν Ζ· ὁ Ε ἄρα τὸν Ζ πολλαπλασιάσας τὸν Α πεποίηκεν. καὶ μετρεῖται ὁ Α ὑπὸ πρώτων ἀριθμῶν τῶν Β, Γ, Δ. ἐὰν δὲ δύο ἀριθμοὶ πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, τὸν δὲ γενόμενον ἐξ αὐτῶν μετρῇ τις πρῶτος ἀριθμός, καὶ ἕνα τῶν ἐξ ἀρχῆς μετρήσει· οἱ Β, Γ, Δ ἄρα ἕνα τῶν Ε, Ζ μετρήσουσιν. τὸν μὲν οὖν Ε οὐ μετρήσουσιν· ὁ γὰρ Ε πρῶτός ἐστι καὶ οὐδενὶ τῶν Β, Γ, Δ ὁ αὐτός. τὸν Ζ ἄρα μετροῦσιν ἐλάσσονα ὄντα τοῦ Α· ὅπερ ἀδύνατον. ὁ γὰρ Α ὑπόκειται ἐλάχιστος ὑπὸ τῶν Β, Γ, Δ μετρούμενος. οὐκ ἄρα τὸν Α μετρήσει πρῶτος ἀριθμὸς παρὲξ τῶν Β, Γ, Δ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον IX
Ἐὰν τρεῖς ἀριθμοὶ ἑξῆς ἀνάλογον ὦσιν ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς, δύο ὁποιοιοῦν συντεθέντες πρὸς τὸν λοιπὸν πρῶτοί εἰσιν.
Ἔστωσαν τρεῖς ἀριθμοὶ ἑξῆς ἀνάλογον ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς οἱ Α, Β, Γ· λέγω, ὅτι τῶν Α, Β, Γ δύο ὁποιοιοῦν συντεθέντες πρὸς τὸν λοιπὸν πρῶτοί εἰσιν, οἱ μὲν Α, Β πρὸς τὸν Γ, οἱ δὲ Β, Γ πρὸς τὸν Α καὶ ἔτι οἱ Α, Γ πρὸς τὸν Β.
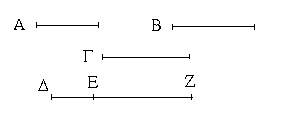
Εἰλήφθωσαν γὰρ ἐλάχιστοι ἀριθμοὶ τῶν τὸν αὐτὸν λόγον ἐχόντων τοῖς Α, Β, Γ δύο οἱ ΔΕ, ΕΖ. φανερὸν δή, ὅτι ὁ μὲν ΔΕ ἑαυτὸν πολλαπλασιάσας τὸν Α πεποίηκεν, τὸν δὲ ΕΖ πολλαπλασιάσας τὸν Β πεποίηκεν, καὶ ἔτι ὁ ΕΖ ἑαυτὸν πολλαπλασιάσας τὸν Γ πεποίηκεν. καὶ ἐπεὶ οἱ ΔΕ, ΕΖ ἐλάχιστοί εἰσιν, πρῶτοι πρὸς ἀλλήλους εἰσίν. ἐὰν δὲ δύο ἀριθμοί πρῶτοι πρὸς ἀλλήλους ὦσιν, καὶ συναμφότερος πρὸς ἑκάτερον πρῶτός ἐστιν· καὶ ὁ ΔΖ ἄρα πρὸς ἑκάτερον τῶν ΔΕ, ΕΖ πρῶτός ἐστιν. ἀλλὰ μὴν καὶ ὁ ΔΕ πρὸς τὸν ΕΖ πρῶτός ἐστιν· οἱ ΔΖ, ΔΕ ἄρα πρὸς τὸν ΕΖ πρῶτοί εἰσιν. ἐὰν δὲ δύο ἀριθμοὶ πρός τινα ἀριθμὸν πρῶτοι ὦσιν, καὶ ὁ ἐξ αὐτῶν γενόμενος πρὸς τὸν λοιπὸν πρῶτός ἐστιν· ὥστε ὁ ἐκ τῶν ΖΔ, ΔΕ πρὸς τὸν ΕΖ πρῶτός ἐστιν· ὥστε καὶ ὁ ἐκ τῶν ΖΔ, ΔΕ πρὸς τὸν ἀπὸ τοῦ ΕΖ πρῶτός ἐστιν. [ἐὰν γὰρ δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, ὁ ἐκ τοῦ ἑνὸς αὐτῶν γενόμενος πρὸς τὸν λοιπὸν πρῶτός ἐστιν]. ἀλλ' ὁ ἐκ τῶν ΖΔ, ΔΕ ὁ ἀπὸ τοῦ ΔΕ ἐστι μετὰ τοῦ ἐκ τῶν ΔΕ, ΕΖ· ὁ ἄρα ἀπὸ τοῦ ΔΕ μετὰ τοῦ ἐκ τῶν ΔΕ, ΕΖ πρὸς τὸν ἀπὸ τοῦ ΕΖ πρῶτός ἐστιν. καί ἐστιν ὁ μὲν ἀπὸ τοῦ ΔΕ ὁ Α, ὁ δὲ ἐκ τῶν ΔΕ, ΕΖ ὁ Β, ὁ δὲ ἀπὸ τοῦ ΕΖ ὁ Γ· οἱ Α, Β ἄρα συντεθέντες πρὸς τὸν Γ πρῶτοί εἰσιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ οἱ Β, Γ πρὸς τὸν Α πρῶτοί εἰσιν. λέγω δή, ὅτι καὶ οἱ Α, Γ πρὸς τὸν Β πρῶτοί εἰσιν. ἐπεὶ γὰρ ὁ ΔΖ πρὸς ἑκάτερον τῶν ΔΕ, ΕΖ πρῶτός ἐστιν, καὶ ὁ ἀπὸ τοῦ ΔΖ πρὸς τὸν ἐκ τῶν ΔΕ, ΕΖ πρῶτός ἐστιν. ἀλλὰ τῷ ἀπὸ τοῦ ΔΖ ἴσοι εἰσὶν οἱ ἀπὸ τῶν ΔΕ, ΕΖ μετὰ τοῦ δὶς ἐκ τῶν ΔΕ, ΕΖ· καὶ οἱ ἀπὸ τῶν ΔΕ, ΕΖ ἄρα μετὰ τοῦ δὶς ὑπὸ τῶν ΔΕ, ΕΖ πρὸς τὸν ὑπὸ τῶν ΔΕ, ΕΖ πρῶτοί [εἰσι]. διελόντι οἱ ἀπὸ τῶν ΔΕ, ΕΖ μετὰ τοῦ ἅπαξ ὑπὸ ΔΕ, ΕΖ πρὸς τὸν ὑπὸ ΔΕ, ΕΖ πρῶτοί εἰσιν. ἔτι διελόντι οἱ ἀπὸ τῶν ΔΕ, ΕΖ ἄρα πρὸς τὸν ὑπὸ ΔΕ, ΕΖ πρῶτοί εἰσιν. καί ἐστιν ὁ μὲν ἀπὸ τοῦ ΔΕ ὁ Α, ὁ δὲ ὑπὸ τῶν ΔΕ, ΕΖ ὁ Β, ὁ δὲ ἀπὸ τοῦ ΕΖ ὁ Γ. οἱ Α, Γ ἄρα συντεθέντες πρὸς τὸν Β πρῶτοί εἰσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον IX
Ἐὰν δύο ἀριθμοὶ πρῶτοι πρὸς ἀλλήλους ὦσιν, οὐκ ἔσται ὡς ὁ πρῶτος πρὸς τὸν δεύτερον, οὕτως ὁ δεύτερος πρὸς ἄλλον τινά.
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρῶτοι πρὸς ἀλλήλους ἔστωσαν· λέγω, ὅτι οὐκ ἔστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Β πρὸς ἄλλον τινά.
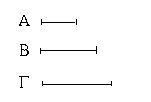
Εἰ γὰρ δυνατόν, ἔστω ὡς ὁ Α πρὸς τὸν Β, ὁ Β πρὸς τὸν Γ. οἱ δὲ Α, Β πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· μετρεῖ ἄρα ὁ Α τὸν Β ὡς ἡγούμενος ἡγούμενον. μετρεῖ δὲ καὶ ἑαυτόν· ὁ Α ἄρα τοὺς Α, Β μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἄτοπον. οὐκ ἄρα ἔσται ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Β πρὸς τὸν Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον IX
Ἐὰν ὦσιν ὁσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, οἱ δὲ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους ὦσιν, οὐκ ἔσται ὡς ὁ πρῶτος πρὸς τὸν δεύτερον, οὕτως ὁ ἔσχατος πρὸς ἄλλον τινά.
Ἔστωσαν ὁσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, Β, Γ, Δ, οἱ δὲ ἄκροι αὐτῶν οἱ Α, Δ πρῶτοι πρὸς ἀλλήλους ἔστωσαν· λέγω, ὅτι οὐκ ἔστιν ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς ἄλλον τινά.
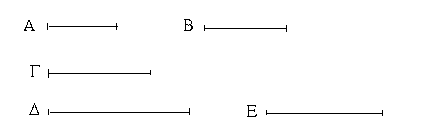
Εἰ γὰρ δυνατόν, ἔστω ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς τὸν Ε· ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Δ, ὁ Β πρὸς τὸν Ε. οἱ δὲ Α, Δ πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι ἀριθμοὶ μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον. μετρεῖ ἄρα ὁ Α τὸν Β. καί ἐστιν ὡς ὁ Α πρὸς τὸν Β, ὁ Β πρὸς τὸν Γ. καὶ ὁ Β ἄρα τὸν Γ μετρεῖ· ὥστε καὶ ὁ Α τὸν Γ μετρεῖ. καὶ ἐπεί ἐστιν ὡς ὁ Β πρὸς τὸν Γ, ὁ Γ πρὸς τὸν Δ, μετρεῖ δὲ ὁ Β τὸν Γ, μετρεῖ ἄρα καὶ ὁ Γ τὸν Δ. ἀλλ' ὁ Α τὸν Γ ἐμέτρει· ὥστε ὁ Α καὶ τὸν Δ μετρεῖ. μετρεῖ δὲ καὶ ἑαυτόν. ὁ Α ἄρα τοὺς Α, Δ μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἔσται ὡς ὁ Α πρὸς τὸν Β, οὕτως ὁ Δ πρὸς ἄλλον τινά· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον IX
Δύο ἀριθμῶν δοθέντων ἐπισκέψασθαι, εἰ δυνατόν ἐστιν αὐτοῖς τρίτον ἀνάλογον προσευρεῖν.
Ἔστωσαν οἱ δοθέντες δύο ἀριθμοὶ οἱ Α, Β, καὶ δέον ἔστω ἐπισκέψασθαι, εἰ δυνατόν ἐστιν αὐτοῖς τρίτον ἀνάλογον προσευρεῖν.
Οἱ δὴ Α, Β ἤτοι πρῶτοι πρὸς ἀλλήλους εἰσὶν ἢ οὔ. καὶ εἰ πρῶτοι πρὸς ἀλλήλους εἰσίν, δέδεικται, ὅτι ἀδύνατόν ἐστιν αὐτοῖς τρίτον ἀνάλογον προσευρεῖν.
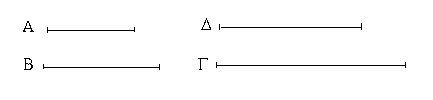
Ἀλλὰ δὴ μὴ ἔστωσαν οἱ Α, Β πρῶτοι πρὸς ἀλλήλους, καὶ ὁ Β ἑαυτὸν πολλαπλασιάσας τὸν Γ ποιείτω· ὁ Α δὴ τὸν Γ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω πρότερον κατὰ τὸν Δ· ὁ Α ἄρα τὸν Δ πολλαπλασιάσας τὸν Γ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Β ἑαυτὸν πολλαπλασιάσας τὸν Γ πεποίηκεν· ὁ ἄρα ἐκ τῶν Α, Δ ἴσος ἐστὶ τῷ ἀπὸ τοῦ Β. ἔστιν ἄρα ὡς ὁ Α πρὸς τὸν Β, ὁ Β πρὸς τὸν Δ· τοῖς Α, Β ἄρα τρίτος ἀριθμὸς ἀνάλογον προσηύρηται ὁ Δ.
Ἀλλὰ δὴ μὴ μετρείτω ὁ Α τὸν Γ· λέγω, ὅτι τοῖς Α, Β ἀδύνατόν ἐστι τρίτον ἀνάλογον προσευρεῖν ἀριθμόν. εἰ γὰρ δυνατόν, προσηυρήσθω ὁ Δ. ὁ ἄρα ἐκ τῶν Α, Δ ἴσος ἐστὶ τῷ ἀπὸ τοῦ Β. ὁ δὲ ἀπὸ τοῦ Β ἐστιν ὁ Γ· ὁ ἄρα ἐκ τῶν Α, Δ ἴσος ἐστὶ τῷ Γ. ὥστε ὁ Α τὸν Δ πολλαπλασιάσας τὸν Γ πεποίηκεν· ὁ Α ἄρα τὸν Γ μετρεῖ κατὰ τὸν Δ. ἀλλὰ μὴν ὑπόκειται καὶ μὴ μετρῶν· ὅπερ ἄτοπον. οὐκ ἄρα δυνατόν ἐστι τοῖς Α, Β τρίτον ἀνάλογον προσευρεῖν ἀριθμόν, ὅταν ὁ Α τὸν Γ μὴ μετρῇ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον IX
Τριῶν ἀριθμῶν δοθέντων ἐπισκέψασθαι, πότε δυνατόν ἐστιν αὐτοῖς τέταρτον ἀνάλογον προσευρεῖν.
Ἔστωσαν οἱ δοθέντες τρεῖς ἀριθμοὶ οἱ Α, Β, Γ, καὶ δέον ἔστω ἐπισκέψασθαι, πότε δυνατόν ἐστιν αὐτοῖς τέταρτον ἀνάλογον προσευρεῖν.
Ἤτοι οὖν οὔκ εἰσιν ἑξῆς ἀνάλογον, καὶ οἱ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους εἰσίν, ἢ ἑξῆς εἰσιν ἀνάλογον, καὶ οἱ ἄκροι αὐτῶν οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους, ἢ οὔτε ἑξῆς εἰσιν ἀνάλογον, οὔτε οἱ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους εἰσίν, ἢ καὶ ἑξῆς εἰσιν ἀνάλογον, καὶ οἱ ἄκροι αὐτῶν πρῶτοι πρὸς ἀλλήλους εἰσίν.
Εἰ μὲν οὖν οἱ Α, Β, Γ ἑξῆς εἰσιν ἀνάλογον, καὶ οἱ ἄκροι αὐτῶν οἱ Α, Γ πρῶτοι πρὸς ἀλλήλους εἰσίν, δέδεικται, ὅτι ἀδύνατόν ἐστιν αὐτοῖς τέταρτον ἀνάλογον προσευρεῖν ἀριθμόν. μὴ ἔστωσαν δὴ οἱ Α, Β, Γ ἑξῆς ἀνάλογον τῶν ἄκρων πάλιν ὄντων πρώτων πρὸς ἀλλήλους. λέγω, ὅτι καὶ οὕτως ἀδύνατόν ἐστιν αὐτοῖς τέταρτον ἀνάλογον προσευρεῖν. εἰ γὰρ δυνατόν, προσευρήσθω ὁ Δ, ὥστε εἶναι ὡς τὸν Α πρὸς τὸν Β, τὸν Γ πρὸς τὸν Δ, καὶ γεγονέτω ὡς ὁ Β πρὸς τὸν Γ, ὁ Δ πρὸς τὸν Ε. καὶ ἐπεί ἐστιν ὡς μὲν ὁ Α πρὸς τὸν Β, ὁ Γ πρὸς τὸν Δ, ὡς δὲ ὁ Β πρὸς τὸν Γ, ὁ Δ πρὸς τὸν Ε, δι' ἴσου ἄρα ὡς ὁ Α πρὸς τὸν Γ, ὁ Γ πρὸς τὸν Ε. οἱ δὲ Α, Γ πρῶτοι, οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον. μετρεῖ ἄρα ὁ Α τὸν Γ ὡς ἡγούμενος ἡγούμενον. μετρεῖ δὲ καὶ ἑαυτόν· ὁ Α ἄρα τοὺς Α, Γ μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοῖς Α, Β, Γ δυνατόν ἐστι τέταρτον ἀνάλογον προσευρεῖν.
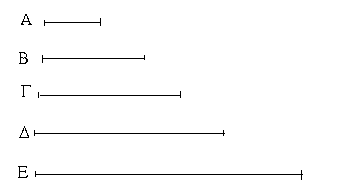
Ἀλλὰ δὴ πάλιν ἔστωσαν οἱ Α, Β, Γ ἑξῆς ἀνάλογον, οἱ δὲ Α, Γ μὴ ἔστωσαν πρῶτοι πρὸς ἀλλήλους. λέγω, ὅτι δυνατόν ἐστιν αὐτοῖς τέταρτον ἀνάλογον προσευρεῖν. ὁ γὰρ Β τὸν Γ πολλαπλασιάσας τὸν Δ ποιείτω· ὁ Α ἄρα τὸν Δ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω αὐτὸν πρότερον κατὰ τὸν Ε· ὁ Α ἄρα τὸν Ε πολλαπλασιάσας τὸν Δ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Β τὸν Γ πολλαπλασιάσας τὸν Δ πεποίηκεν· ὁ ἄρα ἐκ τῶν Α, Ε ἴσος ἐστὶ τῷ ἐκ τῶν Β, Γ. ἀνάλογον ἄρα [ἐστὶν] ὡς ὁ Α πρὸς τὸν Β, ὁ Γ πρὸς τὸν Ε· τοῖς Α, Β, Γ ἄρα τέταρτος ἀνάλογον προσηύρηται ὁ Ε.
Ἀλλὰ δὴ μὴ μετρείτω ὁ Α τὸν Δ· λέγω, ὅτι ἀδύνατόν ἐστι τοῖς Α, Β, Γ τέταρτον ἀνάλογον προσευρεῖν ἀριθμόν. εἰ γὰρ δυνατόν, προσευρήσθω ὁ Ε· ὁ ἄρα ἐκ τῶν Α, Ε ἴσος ἐστὶ τῷ ἐκ τῶν Β, Γ. ἀλλὰ ὁ ἐκ τῶν Β, Γ ἐστιν ὁ Δ· καὶ ὁ ἐκ τῶν Α, Ε ἄρα ἴσος ἐστὶ τῷ Δ. ὁ Α ἄρα τὸν Ε πολλαπλασιάσας τὸν Δ πεποίηκεν· ὁ Α ἄρα τὸν Δ μετρεῖ κατὰ τὸν Ε· ὥστε μετρεῖ ὁ Α τὸν Δ. ἀλλὰ καὶ οὐ μετρεῖ· ὅπερ ἄτοπον. οὐκ ἄρα δυνατόν ἐστι τοῖς Α, Β, Γ τέταρτον ἀνάλογον προσευρεῖν ἀριθμόν, ὅταν ὁ Α τὸν Δ μὴ μετρῇ. ἀλλὰ δὴ οἱ Α, Β, Γ μήτε ἑξῆς ἔστωσαν ἀνάλογον μήτε οἱ ἄκροι πρῶτοι πρὸς ἀλλήλους. καὶ ὁ Β τὸν Γ πολλαπλασιάσας τὸν Δ ποιείτω. ὁμοίως δὴ δειχθήσεται, ὅτι εἰ μὲν μετρεῖ ὁ Α τὸν Δ, δυνατόν ἐστιν αὐτοῖς ἀνάλογον προσευρεῖν, εἰ δὲ οὐ μετρεῖ, ἀδύνατον· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον IX
Οἱ πρῶτοι ἀριθμοὶ πλείους εἰσὶ παντὸς τοῦ προτεθέντος πλήθους πρώτων ἀριθμῶν.
Ἔστωσαν οἱ προτεθέντες πρῶτοι ἀριθμοὶ οἱ Α, Β, Γ· λέγω, ὅτι τῶν Α, Β, Γ πλείους εἰσὶ πρῶτοι ἀριθμοί.
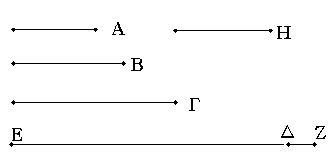
Εἰλήφθω γὰρ ὁ ὑπὸ τῶν Α, Β, Γ ἐλάχιστος μετρούμενος καὶ ἔστω ὁ ΔΕ, καὶ προσκείσθω τῷ ΔΕ μονὰς ἡ ΔΖ. ὁ δὴ ΕΖ ἤτοι πρῶτός ἐστιν ἢ οὔ. ἔστω πρότερον πρῶτος· εὑρημένοι ἄρα εἰσὶ πρῶτοι ἀριθμοὶ οἱ Α, Β, Γ, ΕΖ πλείους τῶν Α, Β, Γ.
Ἀλλὰ δὴ μὴ ἔστω ὁ ΕΖ πρῶτος· ὑπὸ πρώτου ἄρα τινὸς ἀριθμοῦ μετρεῖται. μετρείσθω ὑπὸ πρώτου τοῦ Η· λέγω, ὅτι ὁ Η οὐδενὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. εἰ γὰρ δυνατόν, ἔστω. οἱ δὲ Α, Β, Γ τὸν ΔΕ μετροῦσιν· καὶ ὁ Η ἄρα τὸν ΔΕ μετρήσει. μετρεῖ δὲ καὶ τὸν ΕΖ· καὶ λοιπὴν τὴν ΔΖ μονάδα μετρήσει ὁ Η ἀριθμὸς ὤν· ὅπερ ἄτοπον. οὐκ ἄρα ὁ Η ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. καὶ ὑπόκειται πρῶτος. εὑρημένοι ἄρα εἰσὶ πρῶτοι ἀριθμοὶ πλείους τοῦ προτεθέντος πλήθους τῶν Α, Β, Γ οἱ Α, Β, Γ, Η· ὅπερ ἔδει δεῖξαι.
Πρότασις κα΄ 21 Βιβλίον IX
Ἐὰν ἄρτιοι ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, ὁ ὅλος ἄρτιός ἐστιν.
Συγκείσθωσαν γὰρ ἄρτιοι ἀριθμοὶ ὁποσοιοῦν οἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ· λέγω, ὅτι ὅλος ὁ ΑΕ ἄρτιός ἐστιν.
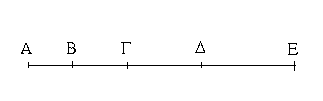
Ἐπεὶ γὰρ ἕκαστος τῶν ΑΒ, ΒΓ, ΓΔ, ΔΕ ἄρτιός ἐστιν, ἔχει μέρος ἥμισυ· ὥστε καὶ ὅλος ὁ ΑΕ ἔχει μέρος ἥμισυ. ἄρτιος δὲ ἀριθμός ἐστιν ὁ δίχα διαιρούμενος· ἄρτιος ἄρα ἐστὶν ὁ ΑΕ· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον IX
Ἐὰν περισσοὶ ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, τὸ δὲ πλῆθος αὐτῶν ἄρτιον ᾖ, ὁ ὅλος ἄρτιος ἔσται.
Συγκείσθωσαν γὰρ περισσοὶ ἀριθμοὶ ὁσοιδηποτοῦν ἄρτιοι τὸ πλῆθος οἱ ΑΒ, ΒΓ, ΓΔ, ΔΕ· λέγω, ὅτι ὅλος ὁ ΑΕ ἄρτιός ἐστιν.
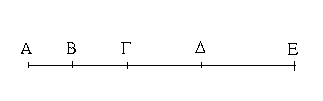
Ἐπεὶ γὰρ ἕκαστος τῶν ΑΒ, ΒΓ, ΓΔ, ΔΕ περιττός ἐστιν, ἀφαιρεθείσης μονάδος ἀφ' ἑκάστου ἕκαστος τῶν λοιπῶν ἄρτιος ἔσται· ὥστε καὶ ὁ συγκείμενος ἐξ αὐτῶν ἄρτιος ἔσται. ἔστι δὲ καὶ τὸ πλῆθος τῶν μονάδων ἄρτιον. καὶ ὅλος ἄρα ὁ ΑΕ ἄρτιός ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον IX
Ἐὰν περισσοὶ ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, τὸ δὲ πλῆθος αὐτῶν περισσὸν ᾖ, καὶ ὁ ὅλος περισσὸς ἔσται.
Συγκείσθωσαν γὰρ ὁποσοιοῦν περισσοὶ ἀριθμοί, ὧν τὸ πλῆθος περισσὸν ἔστω, οἱ ΑΒ, ΒΓ, ΓΔ· λέγω, ὅτι καὶ ὅλος ὁ ΑΔ περισσός ἐστιν.
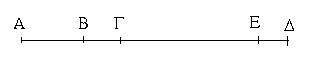
Ἀφῃρήσθω ἀπὸ τοῦ ΓΔ μονὰς ἡ ΔΕ· λοιπὸς ἄρα ὁ ΓΕ ἄρτιός ἐστιν. ἔστι δὲ καὶ ὁ ΓΑ ἄρτιος· καὶ ὅλος ἄρα ὁ ΑΕ ἄρτιός ἐστιν. καί ἐστι μονὰς ἡ ΔΕ. περισσὸς ἄρα ἐστὶν ὁ ΑΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις κδ΄ 24 Βιβλίον IX
Ἐὰν ἀπὸ ἀρτίου ἀριθμοῦ ἄρτιος ἀφαιρεθῇ, ὁ λοιπὸς ἄρτιος ἔσται.
Ἀπὸ γὰρ ἀρτίου τοῦ ΑΒ ἄρτιος ἀφῃρήσθω ὁ ΒΓ· λέγω, ὅτι ὁ λοιπὸς ὁ ΓΑ ἄρτιός ἐστιν.
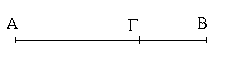
Ἐπεὶ γὰρ ὁ ΑΒ ἄρτιός ἐστιν, ἔχει μέρος ἥμισυ. διὰ τὰ αὐτὰ δὴ καὶ ὁ ΒΓ ἔχει μέρος ἥμισυ· ὥστε καὶ λοιπὸς [ὁ ΓΑ ἔχει μέρος ἥμισυ] ἄρτιος [ἄρα] ἐστὶν ὁ ΑΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον IX
Ἐὰν ἀπὸ ἀρτίου ἀριθμοῦ περισσὸς ἀφαιρεθῇ, ὁ λοιπὸς περισσὸς ἔσται.
Ἀπὸ γὰρ ἀρτίου τοῦ ΑΒ περισσὸς ἀφῃρήσθω ὁ ΒΓ· λέγω, ὅτι ὁ λοιπὸς ὁ ΓΑ περισσός ἐστιν.
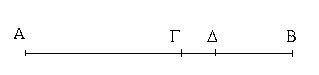
Ἀφῃρήσθω γὰρ ἀπὸ τοῦ ΒΓ μονὰς ἡ ΓΔ· ὁ ΔΒ ἄρα ἄρτιός ἐστιν. ἔστι δὲ καὶ ὁ ΑΒ ἄρτιος· καὶ λοιπὸς ἄρα ὁ ΑΔ ἄρτιός ἐστιν. καί ἐστι μονὰς ἡ ΓΔ· ὁ ΓΑ ἄρα περισσός ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κς΄ 26 Βιβλίον IX
Ἐὰν ἀπὸ περισσοῦ ἀριθμοῦ περισσὸς ἀφαιρεθῇ, ὁ λοιπὸς ἄρτιος ἔσται.
Ἀπὸ γὰρ περισσοῦ τοῦ ΑΒ περισσὸς ἀφῃρήσθω ὁ ΒΓ· λέγω, ὅτι ὁ λοιπὸς ὁ ΓΑ ἄρτιός ἐστιν.
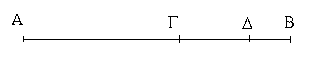
Ἐπεὶ γὰρ ὁ ΑΒ περισσός ἐστιν, ἀφῃρήσθω μονὰς ἡ ΒΔ· λοιπὸς ἄρα ὁ ΑΔ ἄρτιός ἐστιν. διὰ τὰ αὐτὰ δὴ καὶ ὁ ΓΔ ἄρτιός ἐστιν· ὥστε καὶ λοιπὸς ὁ ΓΑ ἄρτιός ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον IX
Ἐὰν ἀπὸ περισσοῦ ἀριθμοῦ ἄρτιος ἀφαιρεθῇ, ὁ λοιπὸς περισσὸς ἔσται.
Ἀπὸ γὰρ περισσοῦ τοῦ ΑΒ ἄρτιος ἀφῃρήσθω ὁ ΒΓ· λέγω, ὅτι ὁ λοιπὸς ὁ ΓΑ περισσός ἐστιν.
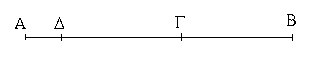
Ἀφῃρήσθω [γὰρ] μονὰς ἡ ΑΔ· ὁ ΔΒ ἄρα ἄρτιός ἐστιν. ἔστι δὲ καὶ ὁ ΒΓ ἄρτιος· καὶ λοιπὸς ἄρα ὁ ΓΔ ἄρτιός ἐστιν. περισσὸς ἄρα ὁ ΓΑ· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον IX
Ἐὰν περισσὸς ἀριθμὸς ἄρτιον πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος ἄρτιος ἔσται.
Περισσὸς γὰρ ἀριθμὸς ὁ Α ἄρτιον τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι ὁ Γ ἄρτιός ἐστιν.
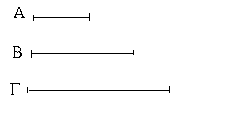
ἐπεὶ γὰρ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ Γ ἄρα σύγκειται ἐκ τοσούτων ἴσων τῷ Β, ὅσαι εἰσὶν ἐν τῷ Α μονάδες. καί ἐστιν ὁ Β ἄρτιος· ὁ Γ ἄρα σύγκειται ἐξ ἀρτίων. ἐὰν δὲ ἄρτιοι ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, ὁ ὅλος ἄρτιός ἐστιν. ἄρτιος ἄρα ἐστὶν ὁ Γ· ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον IX
Ἐὰν περισσὸς ἀριθμὸς περισσὸν ἀριθμὸν πολλαπλασιάσας ποιῇ τινα, ὁ γενόμενος περισσὸς ἔσται.
Περισσὸς γὰρ ἀριθμὸς ὁ Α περισσὸν τὸν Β πολλαπλασιάσας τὸν Γ ποιείτω· λέγω, ὅτι ὁ Γ περισσός ἐστιν.
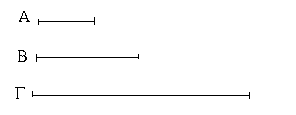
Ἐπεὶ γὰρ ὁ Α τὸν Β πολλαπλασιάσας τὸν Γ πεποίηκεν, ὁ Γ ἄρα σύγκειται ἐκ τοσούτων ἴσων τῷ Β, ὅσαι εἰσὶν ἐν τῷ Α μονάδες. καί ἐστιν ἑκάτερος τῶν Α, Β περισσός· ὁ Γ ἄρα σύγκειται ἐκ περισσῶν ἀριθμῶν, ὧν τὸ πλῆθος περισσόν ἐστιν. ὥστε ὁ Γ περισσός ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον IX
Ἐὰν περισσὸς ἀριθμὸς ἄρτιον ἀριθμὸν μετρῇ, καὶ τὸν ἥμισυν αὐτοῦ μετρήσει.
Περισσὸς γὰρ ἀριθμὸς ὁ Α ἄρτιον τὸν Β μετρείτω· λέγω, ὅτι καὶ τὸν ἥμισυν αὐτοῦ μετρήσει.
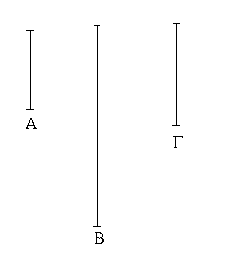
Ἐπεὶ γὰρ ὁ Α τὸν Β μετρεῖ, μετρείτω αὐτὸν κατὰ τὸν Γ· λέγω, ὅτι ὁ Γ οὐκ ἔστι περισσός. εἰ γὰρ δυνατόν, ἔστω. καὶ ἐπεὶ ὁ Α τὸν Β μετρεῖ κατὰ τὸν Γ, ὁ Α ἄρα τὸν Γ πολλαπλασιάσας τὸν Β πεποίηκεν. ὁ Β ἄρα σύγκειται ἐκ περισσῶν ἀριθμῶν, ὧν τὸ πλῆθος περισσόν ἐστιν. ὁ Β ἄρα περισσός ἐστιν· ὅπερ ἄτοπον· ὑπόκειται γὰρ ἄρτιος. οὐκ ἄρα ὁ Γ περισσός ἐστιν· ἄρτιος ἄρα ἐστὶν ὁ Γ. ὥστε ὁ Α τὸν Β μετρεῖ ἀρτιάκις. διὰ δὴ τοῦτο καὶ τὸν ἥμισυν αὐτοῦ μετρήσει· ὅπερ ἔδει δεῖξαι.
Πρότασις λα΄ 31 Βιβλίον IX
Ἐὰν περισσὸς ἀριθμὸς πρός τινα ἀριθμὸν πρῶτος ᾖ, καὶ πρὸς τὸν διπλασίονα αὐτοῦ πρῶτος ἔσται.
Περισσὸς γὰρ ἀριθμὸς ὁ Α πρός τινα ἀριθμὸν τὸν Β πρῶτος ἔστω, τοῦ δὲ Β διπλασίων ἔστω ὁ Γ· λέγω, ὅτι ὁ Α [καὶ] πρὸς τὸν Γ πρῶτός ἐστιν.
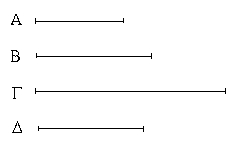
Εἰ γὰρ μή εἰσιν [οἱ Α, Γ] πρῶτοι, μετρήσει τις αὐτοὺς ἀριθμός. μετρείτω, καὶ ἔστω ὁ Δ. καί ἐστιν ὁ Α περισσός· περισσὸς ἄρα καὶ ὁ Δ. καὶ ἐπεὶ ὁ Δ περισσὸς ὢν τὸν Γ μετρεῖ, καί ἐστιν ὁ Γ ἄρτιος, καὶ τὸν ἥμισυν ἄρα τοῦ Γ μετρήσει [ὁ Δ]. τοῦ δὲ Γ ἥμισύ ἐστιν ὁ Β· ὁ Δ ἄρα τὸν Β μετρεῖ. μετρεῖ δὲ καὶ τὸν Α. ὁ Δ ἄρα τοὺς Α, Β μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ὁ Α πρὸς τὸν Γ πρῶτος οὔκ ἐστιν. οἱ Α, Γ ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λβ΄ 32 Βιβλίον IX
Τῶν ἀπὸ δυάδος διπλασιαζομένων ἀριθμῶν ἕκαστος ἀρτιάκις ἄρτιός ἐστι μόνον.
Ἀπὸ γὰρ δυάδος τῆς Α δεδιπλασιάσθωσαν ὁσοιδηποτοῦν ἀριθμοὶ οἱ Β, Γ, Δ· λέγω, ὅτι οἱ Β, Γ, Δ ἀρτιάκις ἄρτιοί εἰσι μόνον.
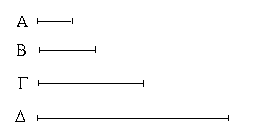
Ὅτι μὲν οὖν ἕκαστος [τῶν Β, Γ, Δ] ἀρτιάκις ἄρτιός ἐστιν, φανερόν· ἀπὸ γὰρ δυάδος ἐστὶ διπλασιασθείς. λέγω, ὅτι καὶ μόνον. ἐκκείσθω γὰρ μονάς. ἐπεὶ οὖν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἀνάλογόν εἰσιν, ὁ δὲ μετὰ τὴν μονάδα ὁ Α πρῶτός ἐστιν, ὁ μέγιστος τῶν Α, Β, Γ, Δ ὁ Δ ὑπ' οὐδενὸς ἄλλου μετρηθήσεται παρὲξ τῶν Α, Β, Γ. καί ἐστιν ἕκαστος τῶν Α, Β, Γ ἄρτιος· ὁ Δ ἄρα ἀρτιάκις ἄρτιός ἐστι μόνον. ὁμοίως δὴ δείξομεν, ὅτι [καὶ] ἑκάτερος τῶν Β, Γ ἀρτιάκις ἄρτιός ἐστι μόνον· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον IX
Ἐὰν ἀριθμὸς τὸν ἥμισυν ἔχῃ περισσόν, ἀρτιάκις περισσός ἐστι μόνον.
Ἀριθμὸς γὰρ ὁ Α τὸν ἥμισυν ἐχέτω περισσόν· λέγω, ὅτι ὁ Α ἀρτιάκις περισσός ἐστι μόνον.
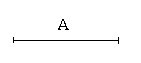
Ὅτι μὲν οὖν ἀρτιάκις περισσός ἐστιν, φανερόν· ὁ γὰρ ἥμισυς αὐτοῦ περισσὸς ὢν μετρεῖ αὐτὸν ἀρτιάκις. λέγω δή, ὅτι καὶ μόνον. εἰ γὰρ ἔσται ὁ Α καὶ ἀρτιάκις ἄρτιος, μετρηθήσεται ὑπὸ ἀρτίου κατὰ ἄρτιον ἀριθμόν· ὥστε καὶ ὁ ἥμισυς αὐτοῦ μετρηθήσεται ὑπὸ ἀρτίου ἀριθμοῦ περισσὸς ὤν· ὅπερ ἐστὶν ἄτοπον. ὁ Α ἄρα ἀρτιάκις περισσός ἐστι μόνον· ὅπερ ἔδει δεῖξαι.
Πρότασις λδ΄ 34 Βιβλίον IX
Ἐὰν ἀριθμὸς μήτε τῶν ἀπὸ δυάδος διπλασιαζομένων ᾖ μήτε τὸν ἥμισυν ἔχῃ περισσόν, ἀρτιάκις τε ἄρτιός ἐστι καὶ ἀρτιάκις περισσός.
Ἀριθμὸς γὰρ ὁ Α μήτε τῶν ἀπὸ δυάδος διπλασιαζομένων ἔστω μήτε τὸν ἥμισυν ἐχέτω περισσόν· λέγω, ὅτι ὁ Α ἀρτιάκις τέ ἐστιν ἄρτιος καὶ ἀρτιάκις περισσός.
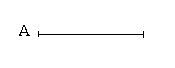
Ὅτι μὲν οὖν ὁ Α ἀρτιάκις ἐστὶν ἄρτιος, φανερόν· τὸν γὰρ ἥμισυν οὐκ ἔχει περισσόν. λέγω δή, ὅτι καὶ ἀρτιάκις περισσός ἐστιν. ἐὰν γὰρ τὸν Α τέμνωμεν δίχα καὶ τὸν ἥμισυν αὐτοῦ δίχα καὶ τοῦτο ἀεὶ ποιῶμεν, καταντήσομεν εἴς τινα ἀριθμὸν περισσόν, ὃς μετρήσει τὸν Α κατὰ ἄρτιον ἀριθμόν. εἰ γὰρ οὔ, καταντήσομεν εἰς δυάδα, καὶ ἔσται ὁ Α τῶν ἀπὸ δυάδος διπλασιαζομένων· ὅπερ οὐχ ὑπόκειται. ὥστε ὁ Α ἀρτιάκις περισσός ἐστιν. ἐδείχθη δὲ καὶ ἀρτιάκις ἄρτιος. ὁ Α ἄρα ἀρτιάκις τε ἄρτιός ἐστι καὶ ἀρτιάκις περισσός· ὅπερ ἔδει δεῖξαι.
Πρότασις λε΄ 35 Βιβλίον IX
Ἐὰν ὦσιν ὁσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον, ἀφαιρεθῶσι δὲ ἀπό τε τοῦ δευτέρου καὶ τοῦ ἐσχάτου ἴσοι τῷ πρώτῳ, ἔσται ὡς ἡ τοῦ δευτέρου ὑπεροχὴ πρὸς τὸν πρῶτον, οὕτως ἡ τοῦ ἐσχάτου ὑπεροχὴ πρὸς τοὺς πρὸ ἑαυτοῦ πάντας.
Ἔστωσαν ὁποσοιδηποτοῦν ἀριθμοὶ ἑξῆς ἀνάλογον οἱ Α, ΒΓ, Δ, ΕΖ ἀρχόμενοι ἀπὸ ἐλαχίστου τοῦ Α, καὶ ἀφῃρήσθω ἀπὸ τοῦ ΒΓ καὶ τοῦ ΕΖ τῷ Α ἴσος ἑκάτερος τῶν ΒΗ, ΖΘ· λέγω, ὅτι ἐστὶν ὡς ὁ ΗΓ πρὸς τὸν Α, οὕτως ὁ ΕΘ πρὸς τοὺς Α, ΒΓ, Δ.
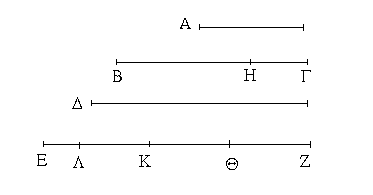
Κείσθω γὰρ τῷ μὲν ΒΓ ἴσος ὁ ΖΚ, τῷ δὲ Δ ἴσος ὁ ΖΛ. καὶ ἐπεὶ ὁ ΖΚ τῷ ΒΓ ἴσος ἐστίν, ὧν ὁ ΖΘ τῷ ΒΗ ἴσος ἐστίν, λοιπὸς ἄρα ὁ ΘΚ λοιπῷ τῷ ΗΓ ἐστιν ἴσος. καὶ ἐπεί ἐστιν ὡς ὁ ΕΖ πρὸς τὸν Δ, οὕτως ὁ Δ πρὸς τὸν ΒΓ καὶ ὁ ΒΓ πρὸς τὸν Α, ἴσος δὲ ὁ μὲν Δ τῷ ΖΛ, ὁ δὲ ΒΓ τῷ ΖΚ, ὁ δὲ Α τῷ ΖΘ, ἔστιν ἄρα ὡς ὁ ΕΖ πρὸς τὸν ΖΛ, οὕτως ὁ ΛΖ πρὸς τὸν ΖΚ καὶ ὁ ΖΚ πρὸς τὸν ΖΘ. διελόντι, ὡς ὁ ΕΛ πρὸς τὸν ΛΖ, οὕτως ὁ ΛΚ πρὸς τὸν ΖΚ καὶ ὁ ΚΘ πρὸς τὸν ΖΘ. ἔστιν ἄρα καὶ ὡς εἷς τῶν ἡγουμένων πρὸς ἕνα τῶν ἑπομένων, οὕτως ἅπαντες οἱ ἡγούμενοι πρὸς ἅπαντας τοὺς ἑπομένους· ἔστιν ἄρα ὡς ὁ ΚΘ πρὸς τὸν ΖΘ, οὕτως οἱ ΕΛ, ΛΚ, ΚΘ πρὸς τοὺς ΛΖ, ΖΚ, ΘΖ. ἴσος δὲ ὁ μὲν ΚΘ τῷ ΓΗ, ὁ δὲ ΖΘ τῷ Α, οἱ δὲ ΛΖ, ΖΚ, ΘΖ τοῖς Δ, ΒΓ, Α· ἔστιν ἄρα ὡς ὁ ΓΗ πρὸς τὸν Α, οὕτως ὁ ΕΘ πρὸς τοὺς Δ, ΒΓ, Α. ἔστιν ἄρα ὡς ἡ τοῦ δευτέρου ὑπεροχὴ πρὸς τὸν πρῶτον, οὕτως ἡ τοῦ ἐσχάτου ὑπεροχὴ πρὸς τοὺς πρὸ ἑαυτοῦ πάντας· ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον IX
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ ἑξῆς ἐκτεθῶσιν ἐν τῇ διπλασίονι ἀναλογίᾳ, ἕως οὗ ὁ σύμπας συντεθεὶς πρῶτος γένηται, καὶ ὁ σύμπας ἐπὶ τὸν ἔσχατον πολλαπλασιασθεὶς ποιῇ τινα, ὁ γενόμενος τέλειος ἔσται.
Ἀπὸ γὰρ μονάδος ἐκκείσθωσαν ὁσοιδηποτοῦν ἀριθμοὶ ἐν τῇ διπλασίονι ἀναλογίᾳ, ἕως οὗ ὁ σύμπας συντεθεὶς πρῶτος γένηται, οἱ Α, Β, Γ, Δ, καὶ τῷ σύμπαντι ἴσος ἔστω ὁ Ε, καὶ ὁ Ε τὸν Δ πολλαπλασιάσας τὸν ΖΗ ποιείτω. λέγω, ὅτι ὁ ΖΗ τέλειός ἐστιν.
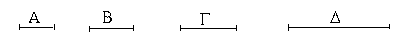
Ὅσοι γάρ εἰσιν οἱ Α, Β, Γ, Δ τῷ πλήθει, τοσοῦτοι ἀπὸ τοῦ Ε εἰλήφθωσαν ἐν τῇ διπλασίονι ἀναλογίᾳ οἱ Ε, ΘΚ, Λ, Μ· δι' ἴσου ἄρα ἐστὶν ὡς ὁ Α πρὸς τὸν Δ, οὕτως ὁ Ε πρὸς τὸν Μ. ὁ ἄρα ἐκ τῶν Ε, Δ ἴσος ἐστὶ τῷ ἐκ τῶν Α, Μ. καί ἐστιν ὁ ἐκ τῶν Ε, Δ ὁ ΖΗ· καὶ ὁ ἐκ τῶν Α, Μ ἄρα ἐστὶν ὁ ΖΗ. ὁ Α ἄρα τὸν Μ πολλαπλασιάσας τὸν ΖΗ πεποίηκεν· ὁ Μ ἄρα τὸν ΖΗ μετρεῖ κατὰ τὰς ἐν τῷ Α μονάδας. καί ἐστι δυὰς ὁ Α· διπλάσιος ἄρα ἐστὶν ὁ ΖΗ τοῦ Μ.
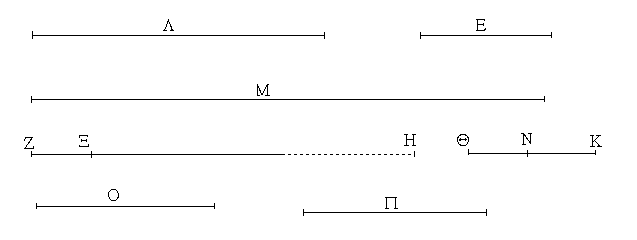
εἰσὶ δὲ καὶ οἱ Μ, Λ, ΘΚ, Ε ἑξῆς διπλάσιοι ἀλλήλων· οἱ Ε, ΘΚ, Λ, Μ, ΖΗ ἄρα ἑξῆς ἀνάλογόν εἰσιν ἐν τῇ διπλασίονι ἀναλογίᾳ. ἀφῃρήσθω δὴ ἀπὸ τοῦ δευτέρου τοῦ ΘΚ καὶ τοῦ ἐσχάτου τοῦ ΖΗ τῷ πρώτῳ τῷ Ε ἴσος ἑκάτερος τῶν ΘΝ, ΖΞ· ἔστιν ἄρα ὡς ἡ τοῦ δευτέρου ἀριθμοῦ ὑπεροχὴ πρὸς τὸν πρῶτον, οὕτως ἡ τοῦ ἐσχάτου ὑπεροχὴ πρὸς τοὺς πρὸ ἑαυτοῦ πάντας. ἔστιν ἄρα ὡς ὁ ΝΚ πρὸς τὸν Ε, οὕτως ὁ ΞΗ πρὸς τοὺς Μ, Λ, ΚΘ, Ε. καί ἐστιν ὁ ΝΚ ἴσος τῷ Ε· καὶ ὁ ΞΗ ἄρα ἴσος ἐστὶ τοῖς Μ, Λ, ΘΚ, Ε. ἔστι δὲ καὶ ὁ ΖΞ τῷ Ε ἴσος, ὁ δὲ Ε τοῖς Α, Β, Γ, Δ καὶ τῇ μονάδι. ὅλος ἄρα ὁ ΖΗ ἴσος ἐστὶ τοῖς τε Ε, ΘΚ, Λ, Μ καὶ τοῖς Α, Β, Γ, Δ καὶ τῇ μονάδι· καὶ μετρεῖται ὑπ' αὐτῶν. λέγω, ὅτι καὶ ὁ ΖΗ ὑπ' οὐδενὸς ἄλλου μετρηθήσεται παρὲξ τῶν Α, Β, Γ, Δ, Ε, ΘΚ, Λ, Μ καὶ τῆς μονάδος. εἰ γὰρ δυνατόν, μετρείτω τις τὸν ΖΗ ὁ Ο, καὶ ὁ Ο μηδενὶ τῶν Α, Β, Γ, Δ, Ε, ΘΚ, Λ, Μ ἔστω ὁ αὐτός. καὶ ὁσάκις ὁ Ο τὸν ΖΗ μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Π· ὁ Π ἄρα τὸν Ο πολλαπλασιάσας τὸν ΖΗ πεποίηκεν. ἀλλὰ μὴν καὶ ὁ Ε τὸν Δ πολλαπλασιάσας τὸν ΖΗ πεποίηκεν· ἔστιν ἄρα ὡς ὁ Ε πρὸς τὸν Π, ὁ Ο πρὸς τὸν Δ. καὶ ἐπεὶ ἀπὸ μονάδος ἑξῆς ἀνάλογόν εἰσιν οἱ Α, Β, Γ, Δ, ὁ Δ ἄρα ὑπ' οὐδενὸς ἄλλου ἀριθμοῦ μετρηθήσεται παρὲξ τῶν Α, Β, Γ. καὶ ὑπόκειται ὁ Ο οὐδενὶ τῶν Α, Β, Γ ὁ αὐτός· οὐκ ἄρα μετρήσει ὁ Ο τὸν Δ. ἀλλ' ὡς ὁ Ο πρὸς τὸν Δ, ὁ Ε πρὸς τὸν Π· οὐδὲ ὁ Ε ἄρα τὸν Π μετρεῖ. καί ἐστιν ὁ Ε πρῶτος· πᾶς δὲ πρῶτος ἀριθμὸς πρὸς ἅπαντα, ὃν μὴ μετρεῖ, πρῶτος [ἐστιν]. οἱ Ε, Π ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. οἱ δὲ πρῶτοι καὶ ἐλάχιστοι, οἱ δὲ ἐλάχιστοι μετροῦσι τοὺς τὸν αὐτὸν λόγον ἔχοντας ἰσάκις ὅ τε ἡγούμενος τὸν ἡγούμενον καὶ ὁ ἑπόμενος τὸν ἑπόμενον· καί ἐστιν ὡς ὁ Ε πρὸς τὸν Π, ὁ Ο πρὸς τὸν Δ· ἰσάκις ἄρα ὁ Ε τὸν Ο μετρεῖ καὶ ὁ Π τὸν Δ· ἰσάκις ἄρα ὁ Ε τὸν Ο μετρεῖ καὶ ὁ Π τὸν Δ. ὁ δὲ Δ ὑπ' οὐδενὸς ἄλλου μετρεῖται παρὲξ τῶν Α, Β, Γ· ὁ Π ἄρα ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. ἔστω τῷ Β ὁ αὐτός. καὶ ὅσοι εἰσὶν οἱ Β, Γ, Δ τῷ πλήθει τοσοῦτοι εἰλήφθωσαν ἀπὸ τοῦ Ε οἱ Ε, ΘΚ, Λ. καί εἰσιν οἱ Ε, ΘΚ, Λ τοῖς Β, Γ, Δ ἐν τῷ αὐτῷ λόγῳ· δι' ἴσου ἄρα ἐστὶν ὡς ὁ Β πρὸς τὸν Δ, ὁ Ε πρὸς τὸν Λ. ὁ ἄρα ἐκ τῶν Β, Λ ἴσος ἐστὶ τῷ ἐκ τῶν Δ, Ε· ἀλλ' ὁ ἐκ τῶν Δ, Ε ἴσος ἐστὶ τῷ ἐκ τῶν Π, Ο· καὶ ὁ ἐκ τῶν Π, Ο ἄρα ἴσος ἐστὶ τῷ ἐκ τῶν Β, Λ. ἔστιν ἄρα ὡς ὁ Π πρὸς τὸν Β, ὁ Λ πρὸς τὸν Ο. καί ἐστιν ὁ Π τῷ Β ὁ αὐτός· καὶ ὁ Λ ἄρα τῷ Ο ἐστιν ὁ αὐτός· ὅπερ ἀδύνατον· ὁ γὰρ Ο ὑπόκειται μηδενὶ τῶν ἐκκειμένων ὁ αὐτός. οὐκ ἄρα τὸν ΖΗ μετρήσει τις ἀριθμὸς παρὲξ τῶν Α, Β, Γ, Δ, Ε, ΘΚ, Λ, Μ καὶ τῆς μονάδος. καὶ ἐδείχθη ὁ ΖΗ τοῖς Α, Β, Γ, Δ, Ε, ΘΚ, Λ, Μ καὶ τῇ μονάδι ἴσος. τέλειος δὲ ἀριθμός ἐστιν ὁ τοῖς ἑαυτοῦ μέρεσιν ἴσος ὤν· τέλειος ἄρα ἐστὶν ὁ ΖΗ· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου ι΄
Βιβλίον X
Ὅροι δ΄ 4.
α΄ 1. Σύμμετρα μεγέθη λέγεται τὰ τῷ αὐτῷ μέτρῳ μετρούμενα, ἀσύμμετρα δέ, ὧν μηδὲν ἐνδέχεται κοινὸν μέτρον γενέσθαι.
β΄ 2. Εὐθεῖαι δυνάμει σύμμετροί εἰσιν, ὅταν τὰ ἀπ' αὐτῶν τετράγωνα τῷ αὐτῷ χωρίῳ μετρῆται, ἀσύμμετροι δέ, ὅταν τοῖς ἀπ' αὐτῶν τετραγώνοις μηδὲν ἐνδέχηται χωρίον κοινὸν μέτρον γενέσθαι.
γ΄ 3. Τούτων ὑποκειμένων δείκνυται, ὅτι τῇ προτεθείσῃ εὐθείᾳ ὑπάρχουσιν εὐθεῖαι πλήθει ἄπειροι σύμμετροί τε καὶ ἀσύμμετροι αἱ μὲν μήκει μόνον, αἱ δὲ καὶ δυνάμει. καλείσθω οὖν ἡ μὲν προτεθεῖσα εὐθεῖα ῥητή, καὶ αἱ ταύτῃ σύμμετροι εἴτε μήκει καὶ δυνάμει εἴτε δυνάμει μόνον ῥηταί, αἱ δὲ ταύτῃ ἀσύμμετροι ἄλογοι καλείσθωσαν.
δ΄ 4. Καὶ τὸ μὲν ἀπὸ τῆς προτεθείσης εὐθείας τετράγωνον ῥητόν, καὶ τὰ τούτῳ σύμμετρα ῥητά, τὰ δὲ τούτῳ ἀσύμμετρα ἄλογα καλείσθω, καὶ αἱ δυνάμεναι αὐτὰ ἄλογοι, εἰ μὲν τετράγωνα εἴη, αὐταὶ αἱ πλευραί, εἰ δὲ ἕτερά τινα εὐθύγραμμα, αἱ ἴσα αὐτοῖς τετράγωνα ἀναγράφουσαι.
Προτάσεις ριε΄ 115
Πρότασις α΄ 1 Βιβλίον X
Δύο μεγεθῶν ἀνίσων ἐκκειμένων, ἐὰν ἀπὸ τοῦ μείζονος ἀφαιρεθῇ μεῖζον ἢ τὸ ἥμισυ καὶ τοῦ καταλειπομένου μεῖζον ἢ τὸ ἥμισυ, καὶ τοῦτο ἀεὶ γίγνηται, λειφθήσεταί τι μέγεθος, ὃ ἔσται ἔλασσον τοῦ ἐκκειμένου ἐλάσσονος μεγέθους.
Ἔστω δύο μεγέθη ἄνισα τὰ ΑΒ, Γ, ὧν μεῖζον τὸ ΑΒ· λέγω, ὅτι, ἐὰν ἀπὸ τοῦ ΑΒ ἀφαιρεθῇ μεῖζον ἢ τὸ ἥμισυ καὶ τοῦ καταλειπομένου μεῖζον ἢ τὸ ἥμισυ, καὶ τοῦτο ἀεὶ γίγνηται, λειφθήσεταί τι μέγεθος, ὃ ἔσται ἔλασσον τοῦ Γ μεγέθους.
Τὸ Γ γὰρ πολλαπλασιαζόμενον ἔσται ποτὲ τοῦ ΑΒ μεῖζον. πεπολλαπλασιάσθω, καὶ ἔστω τὸ ΔΕ τοῦ μὲν Γ πολλαπλάσιον, τοῦ δὲ ΑΒ μεῖζον, καὶ διῃρήσθω τὸ ΔΕ εἰς τὰ τῷ Γ ἴσα τὰ ΔΖ, ΖΗ, ΗΕ, καὶ ἀφῃρήσθω ἀπὸ μὲν τοῦ ΑΒ μεῖζον ἢ τὸ ἥμισυ τὸ ΒΘ, ἀπὸ δὲ τοῦ ΑΘ μεῖζον ἢ τὸ ἥμισυ τὸ ΘΚ, καὶ τοῦτο ἀεὶ γιγνέσθω, ἕως ἂν αἱ ἐν τῷ ΑΒ διαιρέσεις ἰσοπληθεῖς γένωνται ταῖς ἐν τῷ ΔΕ διαιρέσεσιν.
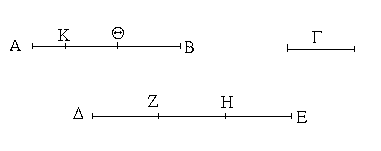
Ἔστωσαν οὖν αἱ ΑΚ, ΚΘ, ΘΒ διαιρέσεις ἰσοπληθεῖς οὖσαι ταῖς ΔΖ, ΖΗ, ΗΕ· καὶ ἐπεὶ μεῖζόν ἐστι τὸ ΔΕ τοῦ ΑΒ, καὶ ἀφῄρηται ἀπὸ μὲν τοῦ ΔΕ ἔλασσον τοῦ ἡμίσεος τὸ ΕΗ, ἀπὸ δὲ τοῦ ΑΒ μεῖζον ἢ τὸ ἥμισυ τὸ ΒΘ, λοιπὸν ἄρα τὸ ΗΔ λοιποῦ τοῦ ΘΑ μεῖζόν ἐστιν. καὶ ἐπεὶ μεῖζόν ἐστι τὸ ΗΔ τοῦ ΘΑ, καὶ ἀφῄρηται τοῦ μὲν ΗΔ ἥμισυ τὸ ΗΖ, τοῦ δὲ ΘΑ μεῖζον ἢ τὸ ἥμισυ τὸ ΘΚ, λοιπὸν ἄρα τὸ ΔΖ λοιποῦ τοῦ ΑΚ μεῖζόν ἐστιν. ἴσον δὲ τὸ ΔΖ τῷ Γ· καὶ τὸ Γ ἄρα τοῦ ΑΚ μεῖζόν ἐστιν. ἔλασσον ἄρα τὸ ΑΚ τοῦ Γ.
Καταλείπεται ἄρα ἀπὸ τοῦ ΑΒ μεγέθους τὸ ΑΚ μέγεθος ἔλασσον ὂν τοῦ ἐκκειμένου ἐλάσσονος μεγέθους τοῦ Γ· ὅπερ ἔδει δεῖξαι. ὁμοίως δὲ δειχθήσεται, κἂν ἡμίση ᾖ τὰ ἀφαιρούμενα.
Πρότασις β΄ 2 Βιβλίον X
Ἐὰν δύο μεγεθῶν [ἐκκειμένων] ἀνίσων ἀνθυφαιρουμένου ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος τὸ καταλειπόμενον μηδέποτε καταμετρῇ τὸ πρὸ ἑαυτοῦ, ἀσύμμετρα ἔσται τὰ μεγέθη.
Δύο γὰρ μεγεθῶν ὄντων ἀνίσων τῶν ΑΒ, ΓΔ καὶ ἐλάσσονος τοῦ ΑΒ ἀνθυφαιρουμένου ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος τὸ περιλειπόμενον μηδέποτε καταμετρείτω τὸ πρὸ ἑαυτοῦ· λέγω, ὅτι ἀσύμμετρά ἐστι τὰ ΑΒ, ΓΔ μεγέθη.
Εἰ γάρ ἐστι σύμμετρα, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, εἰ δυνατόν, καὶ ἔστω τὸ Ε· καὶ τὸ μὲν ΑΒ τὸ ΖΔ καταμετροῦν λειπέτω ἑαυτοῦ ἔλασσον τὸ ΓΖ, τὸ δὲ ΓΖ τὸ ΒΗ καταμετροῦν λειπέτω ἑαυτοῦ ἔλασσον τὸ ΑΗ, καὶ τοῦτο ἀεὶ γινέσθω, ἕως οὗ λειφθῇ τι μέγεθος, ὅ ἐστιν ἔλασσον τοῦ Ε. γεγονέτω,
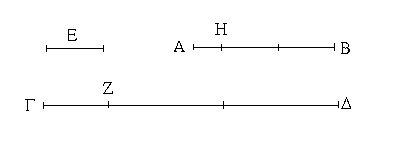
καὶ λελείφθω τὸ ΑΗ ἔλασσον τοῦ Ε. ἐπεὶ οὖν τὸ Ε τὸ ΑΒ μετρεῖ, ἀλλὰ τὸ ΑΒ τὸ ΔΖ μετρεῖ, καὶ τὸ Ε ἄρα τὸ ΖΔ μετρήσει. μετρεῖ δὲ καὶ ὅλον τὸ ΓΔ· καὶ λοιπὸν ἄρα τὸ ΓΖ μετρήσει. ἀλλὰ τὸ ΓΖ τὸ ΒΗ μετρεῖ· καὶ τὸ Ε ἄρα τὸ ΒΗ μετρεῖ. μετρεῖ δὲ καὶ ὅλον τὸ ΑΒ· καὶ λοιπὸν ἄρα τὸ ΑΗ μετρήσει, τὸ μεῖζον τὸ ἔλασσον. ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΑΒ, ΓΔ μεγέθη μετρήσει τι μέγεθος· ἀσύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΓΔ μεγέθη.
Ἐὰν ἄρα δύο μεγεθῶν ἀνίσων, καὶ τὰ ἑξῆς.
Πρότασις γ΄ 3 Βιβλίον X
Δύο μεγεθῶν συμμέτρων δοθέντων τὸ μέγιστον αὐτῶν κοινὸν μέτρον εὑρεῖν.
Ἔστω τὰ δοθέντα δύο μεγέθη σύμμετρα τὰ ΑΒ, ΓΔ, ὧν ἔλασσον τὸ ΑΒ· δεῖ δὴ τῶν ΑΒ, ΓΔ τὸ μέγιστον κοινὸν μέτρον εὑρεῖν.
Τὸ ΑΒ γὰρ μέγεθος ἤτοι μετρεῖ τὸ ΓΔ ἢ οὔ. εἰ μὲν οὖν μετρεῖ, μετρεῖ δὲ καὶ ἑαυτό, τὸ ΑΒ ἄρα τῶν ΑΒ, ΓΔ κοινὸν μέτρον ἐστίν· καὶ φανερόν, ὅτι καὶ μέγιστον. μεῖζον γὰρ τοῦ ΑΒ μεγέθους τὸ ΑΒ οὐ μετρήσει.
Μὴ μετρείτω δὴ τὸ ΑΒ τὸ ΓΔ. καὶ ἀνθυφαιρουμένου ἀεὶ τοῦ ἐλάσσονος ἀπὸ τοῦ μείζονος, τὸ περιλειπόμενον μετρήσει ποτὲ τὸ πρὸ ἑαυτοῦ διὰ τὸ μὴ εἶναι ἀσύμμετρα τὰ ΑΒ, ΓΔ· καὶ τὸ μὲν ΑΒ τὸ ΕΔ καταμετροῦν λειπέτω ἑαυτοῦ ἔλασσον τὸ ΕΓ, τὸ δὲ ΕΓ τὸ ΖΒ καταμετροῦν λειπέτω ἑαυτοῦ ἔλασσον τὸ ΑΖ, τὸ δὲ ΑΖ τὸ ΓΕ μετρείτω.
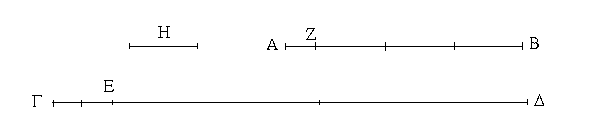
Ἐπεὶ οὖν τὸ ΑΖ τὸ ΓΕ μετρεῖ, ἀλλὰ τὸ ΓΕ τὸ ΖΒ μετρεῖ, καὶ τὸ ΑΖ ἄρα τὸ ΖΒ μετρήσει. μετρεῖ δὲ καὶ ἑαυτό· καὶ ὅλον ἄρα τὸ ΑΒ μετρήσει τὸ ΑΖ. ἀλλὰ τὸ ΑΒ τὸ ΔΕ μετρεῖ· καὶ τὸ ΑΖ ἄρα τὸ ΕΔ μετρήσει. μετρεῖ δὲ καὶ τὸ ΓΕ· καὶ ὅλον ἄρα τὸ ΓΔ μετρεῖ· τὸ ΑΖ ἄρα τῶν ΑΒ, ΓΔ κοινὸν μέτρον ἐστίν. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή, ἔσται τι μέγεθος μεῖζον τοῦ ΑΖ, ὃ μετρήσει τὰ ΑΒ, ΓΔ. ἔστω τὸ Η. ἐπεὶ οὖν τὸ Η τὸ ΑΒ μετρεῖ, ἀλλὰ τὸ ΑΒ τὸ ΕΔ μετρεῖ, καὶ τὸ Η ἄρα τὸ ΕΔ μετρήσει. μετρεῖ δὲ καὶ ὅλον τὸ ΓΔ· καὶ λοιπὸν ἄρα τὸ ΓΕ μετρήσει τὸ Η. ἀλλὰ τὸ ΓΕ τὸ ΖΒ μετρεῖ· καὶ τὸ Η ἄρα τὸ ΖΒ μετρήσει. μετρεῖ δὲ καὶ ὅλον τὸ ΑΒ, καὶ λοιπὸν τὸ ΑΖ μετρήσει, τὸ μεῖζον τὸ ἔλασσον· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα μεῖζόν τι μέγεθος τοῦ ΑΖ τὰ ΑΒ, ΓΔ μετρήσει· τὸ ΑΖ ἄρα τῶν ΑΒ, ΓΔ τὸ μέγιστον κοινὸν μέτρον ἐστίν.
Δύο ἄρα μεγεθῶν συμμέτρων δοθέντων τῶν ΑΒ, ΓΔ τὸ μέγιστον κοινὸν μέτρον ηὕρηται· ὅπερ ἔδει δεῖξαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι, ἐὰν μέγεθος δύο μεγέθη μετρῇ, καὶ τὸ μέγιστον αὐτῶν κοινὸν μέτρον μετρήσει.
Πρότασις δ΄ 4 Βιβλίον X
Τριῶν μεγεθῶν συμμέτρων δοθέντων τὸ μέγιστον αὐτῶν κοινὸν μέτρον εὑρεῖν.
Ἔστω τὰ δοθέντα τρία μεγέθη σύμμετρα τὰ Α, Β, Γ· δεῖ δὴ τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον εὑρεῖν.
Εἰλήφθω γὰρ δύο τῶν Α, Β τὸ μέγιστον κοινὸν μέτρον, καὶ ἔστω τὸ Δ· τὸ δὴ Δ τὸ Γ ἤτοι μετρεῖ ἢ οὔ [μετρεῖ]. μετρείτω πρότερον. ἐπεὶ οὖν τὸ Δ τὸ Γ μετρεῖ, μετρεῖ δὲ καὶ τὰ Α, Β, τὸ Δ ἄρα τὰ Α, Β, Γ μετρεῖ· τὸ Δ ἄρα τῶν Α, Β, Γ κοινὸν μέτρον ἐστίν. καὶ φανερόν, ὅτι καὶ μέγιστον· μεῖζον γὰρ τοῦ Δ μεγέθους τὰ Α, Β οὐ μετρεῖ.
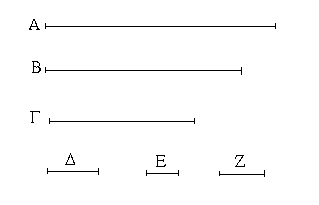
Μὴ μετρείτω δὴ τὸ Δ τὸ Γ. λέγω πρῶτον, ὅτι σύμμετρά ἐστι τὰ Γ, Δ. ἐπεὶ γὰρ σύμμετρά ἐστι τὰ Α, Β, Γ, μετρήσει τι αὐτὰ μέγεθος, ὃ δηλαδὴ καὶ τὰ Α, Β μετρήσει· ὥστε καὶ τὸ τῶν Α, Β μέγιστον κοινὸν μέτρον τὸ Δ μετρήσει. μετρεῖ δὲ καὶ τὸ Γ· ὥστε τὸ εἰρημένον μέγεθος μετρήσει τὰ Γ, Δ· σύμμετρα ἄρα ἐστὶ τὰ Γ, Δ. εἰλήφθω οὖν αὐτῶν τὸ μέγιστον κοινὸν μέτρον, καὶ ἔστω τὸ Ε. ἐπεὶ οὖν τὸ Ε τὸ Δ μετρεῖ, ἀλλὰ τὸ Δ τὰ Α, Β μετρεῖ, καὶ τὸ Ε ἄρα τὰ Α, Β μετρήσει. μετρεῖ δὲ καὶ τὸ Γ. τὸ Ε ἄρα τὰ Α, Β, Γ μετρεῖ· τὸ Ε ἄρα τῶν Α, Β, Γ κοινόν ἐστι μέτρον. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ δυνατόν, ἔστω τι τοῦ Ε μεῖζον μέγεθος τὸ Ζ, καὶ μετρείτω τὰ Α, Β, Γ. καὶ ἐπεὶ τὸ Ζ τὰ Α, Β, Γ μετρεῖ, καὶ τὰ Α, Β ἄρα μετρήσει καὶ τὸ τῶν Α, Β μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Α, Β μέγιστον κοινὸν μέτρον ἐστὶ τὸ Δ· τὸ Ζ ἄρα τὸ Δ μετρεῖ. μετρεῖ δὲ καὶ τὸ Γ· τὸ Ζ ἄρα τὰ Γ, Δ μετρεῖ· καὶ τὸ τῶν Γ, Δ ἄρα μέγιστον κοινὸν μέτρον μετρήσει τὸ Ζ. ἔστι δὲ τὸ Ε· τὸ Ζ ἄρα τὸ Ε μετρήσει, τὸ μεῖζον τὸ ἔλασσον· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα μεῖζόν τι τοῦ Ε μεγέθους [μέγεθος] τὰ Α, Β, Γ μετρεῖ· τὸ Ε ἄρα τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον ἐστίν, ἐὰν μὴ μετρῇ τὸ Δ τὸ Γ, ἐὰν δὲ μετρῇ, αὐτὸ τὸ Δ.
Τριῶν ἄρα μεγεθῶν συμμέτρων δοθέντων τὸ μέγιστον κοινὸν μέτρον ηὕρηται [ὅπερ ἔδει δεῖξαι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι, ἐὰν μέγεθος τρία μεγέθη μετρῇ, καὶ τὸ μέγιστον αὐτῶν κοινὸν μέτρον μετρήσει.
Ὁμοίως δὴ καὶ ἐπὶ πλειόνων τὸ μέγιστον κοινὸν μέτρον ληφθήσεται, καὶ τὸ πόρισμα προχωρήσει. ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον X
Τὰ σύμμετρα μεγέθη πρὸς ἄλληλα λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν.
Ἔστω σύμμετρα μεγέθη τὰ Α, Β· λέγω, ὅτι τὸ Α πρὸς τὸ Β λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν.
Ἐπεὶ γὰρ σύμμετρά ἐστι τὰ Α, Β, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, καὶ ἔστω τὸ Γ. καὶ ὁσάκις τὸ Γ τὸ Α μετρεῖ τοσαῦται μονάδες ἔστωσαν ἐν τῷ Δ, ὁσάκις δὲ τὸ Γ τὸ Β μετρεῖ, τοσαῦται μονάδες ἔστωσαν ἐν τῷ Ε.
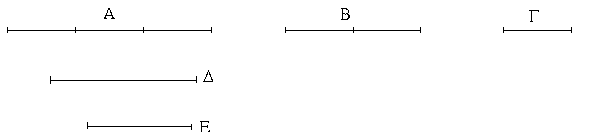
Ἐπεὶ οὖν τὸ Γ τὸ Α μετρεῖ κατὰ τὰς ἐν τῷ Δ μονάδας, μετρεῖ δὲ καὶ ἡ μονὰς τὸν Δ κατὰ τὰς ἐν αὐτῷ μονάδας, ἰσάκις ἄρα ἡ μονὰς τὸν Δ μετρεῖ ἀριθμὸν καὶ τὸ Γ μέγεθος τὸ Α· ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Α, οὕτως ἡ μονὰς πρὸς τὸν Δ· ἀνάπαλιν ἄρα, ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Δ πρὸς τὴν μονάδα. πάλιν ἐπεὶ τὸ Γ τὸ Β μετρεῖ κατὰ τὰς ἐν τῷ Ε μονάδας, μετρεῖ δὲ καὶ ἡ μονὰς τὸν Ε κατὰ τὰς ἐν αὐτῷ μονάδας, ἰσάκις ἄρα ἡ μονὰς τὸν Ε μετρεῖ καὶ τὸ Γ τὸ Β· ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Β, οὕτως ἡ μονὰς πρὸς τὸν Ε. ἐδείχθη δὲ καὶ ὡς τὸ Α πρὸς τὸ Γ, ὁ Δ πρὸς τὴν μονάδα· δι' ἴσου ἄρα ἐστὶν ὡς τὸ Α πρὸς τὸ Β, οὕτως ὁ Δ ἀριθμὸς πρὸς τὸν Ε.
Τὰ ἄρα σύμμετρα μεγέθη τὰ Α, Β πρὸς ἄλληλα λόγον ἔχει, ὃν ἀριθμὸς ὁ Δ πρὸς ἀριθμὸν τὸν Ε· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον X
Ἐὰν δύο μεγέθη πρὸς ἄλληλα λόγον ἔχῃ, ὃν ἀριθμὸς πρὸς ἀριθμόν, σύμμετρα ἔσται τὰ μεγέθη.
Δύο γὰρ μεγέθη τὰ Α, Β πρὸς ἄλληλα λόγον ἐχέτω, ὃν ἀριθμὸς ὁ Δ πρὸς ἀριθμὸν τὸν Ε· λέγω, ὅτι σύμμετρά ἐστι τὰ Α, Β μεγέθη.
Ὅσαι γάρ εἰσιν ἐν τῷ Δ μονάδες, εἰς τοσαῦτα ἴσα διῃρήσθω τὸ Α, καὶ ἑνὶ αὐτῶν ἴσον ἔστω τὸ Γ· ὅσαι δέ εἰσιν ἐν τῷ Ε μονάδες, ἐκ τοσούτων μεγεθῶν ἴσων τῷ Γ συγκείσθω τὸ Ζ.
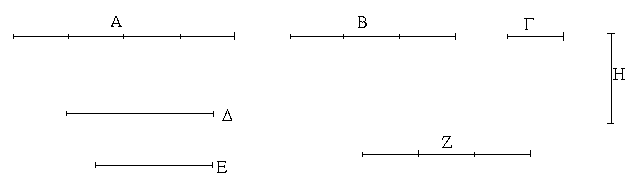
Ἐπεὶ οὖν, ὅσαι εἰσὶν ἐν τῷ Δ μονάδες, τοσαῦτά εἰσι καὶ ἐν τῷ Α μεγέθη ἴσα τῷ Γ, ὃ ἄρα μέρος ἐστὶν ἡ μονὰς τοῦ Δ, τὸ αὐτὸ μέρος ἐστὶ καὶ τὸ Γ τοῦ Α· ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Α, οὕτως ἡ μονὰς πρὸς τὸν Δ. μετρεῖ δὲ ἡ μονὰς τὸν Δ ἀριθμόν· μετρεῖ ἄρα καὶ τὸ Γ τὸ Α. καὶ ἐπεί ἐστιν ὡς τὸ Γ πρὸς τὸ Α, οὕτως ἡ μονὰς πρὸς τὸν Δ [ἀριθμόν], ἀνάπαλιν ἄρα ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Δ ἀριθμὸς πρὸς τὴν μονάδα. πάλιν ἐπεί, ὅσαι εἰσὶν ἐν τῷ Ε μονάδες, τοσαῦτά εἰσι καὶ ἐν τῷ Ζ ἴσα τῷ Γ, ἔστιν ἄρα ὡς τὸ Γ πρὸς τὸ Ζ, οὕτως ἡ μονὰς πρὸς τὸν Ε [ἀριθμόν]. ἐδείχθη δὲ καὶ ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Δ πρὸς τὴν μονάδα· δι' ἴσου ἄρα ἐστὶν ὡς τὸ Α πρὸς τὸ Ζ, οὕτως ὁ Δ πρὸς τὸν Ε. ἀλλ' ὡς ὁ Δ πρὸς τὸν Ε, οὕτως ἐστὶ τὸ Α πρὸς τὸ Β· καὶ ὡς ἄρα τὸ Α πρὸς τὸ Β, οὕτως καὶ πρὸς τὸ Ζ. τὸ Α ἄρα πρὸς ἑκάτερον τῶν Β, Ζ τὸν αὐτὸν ἔχει λόγον· ἴσον ἄρα ἐστὶ τὸ Β τῷ Ζ. μετρεῖ δὲ τὸ Γ τὸ Ζ· μετρεῖ ἄρα καὶ τὸ Β. ἀλλὰ μὴν καὶ τὸ Α· τὸ Γ ἄρα τὰ Α, Β μετρεῖ. σύμμετρον ἄρα ἐστὶ τὸ Α τῷ Β.
Ἐὰν ἄρα δύο μεγέθη πρὸς ἄλληλα, καὶ τὰ ἑξῆς.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι, ἐὰν ὦσι δύο ἀριθμοί, ὡς οἱ Δ, Ε, καὶ εὐθεῖα, ὡς ἡ Α, δύνατόν ἐστι ποιῆσαι ὡς ὁ Δ ἀριθμὸς πρὸς τὸν Ε ἀριθμόν, οὕτως τὴν εὐθεῖαν πρὸς εὐθεῖαν. ἐὰν δὲ καὶ τῶν Α, Ζ μέση ἀνάλογον ληφθῇ, ὡς ἡ Β, ἔσται ὡς ἡ Α πρὸς τὴν Ζ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β, τουτέστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον. ἀλλ' ὡς ἡ Α πρὸς τὴν Ζ, οὕτως ἐστὶν ὁ Δ ἀριθμὸς πρὸς τὸν Ε ἀριθμόν· γέγονεν ἄρα καὶ ὡς ὁ Δ ἀριθμὸς πρὸς τὸν Ε ἀριθμόν, οὕτως τὸ ἀπὸ τῆς Α εὐθείας πρὸς τὸ ἀπὸ τῆς Β εὐθείας· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον X
Τὰ ἀσύμμετρα μεγέθη πρὸς ἄλληλα λόγον οὐκ ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν.
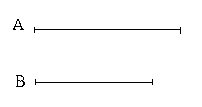
Ἔστω ἀσύμμετρα μεγέθη τὰ Α, Β· λέγω, ὅτι τὸ Α πρὸς τὸ Β λόγον οὐκ ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. εἰ γὰρ ἔχει τὸ Α πρὸς τὸ Β λόγον, ὃν ἀριθμὸς πρὸς ἀριθμόν, σύμμετρον ἔσται τὸ Α τῷ Β. οὐκ ἔστι δέ· οὐκ ἄρα τὸ Α πρὸς τὸ Β λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν.
Τὰ ἄρα ἀσύμμετρα μεγέθη πρὸς ἄλληλα λόγον οὐκ ἔχει, καὶ τὰ ἑξῆς.
Πρότασις η΄ 8 Βιβλίον X
Ἐὰν δύο μεγέθη πρὸς ἄλληλα λόγον μὴ ἔχῃ, ὃν ἀριθμὸς πρὸς ἀριθμόν, ἀσύμμετρα ἔσται τὰ μεγέθη.
Δύο γὰρ μεγέθη τὰ Α, Β πρὸς ἄλληλα λόγον μὴ ἐχέτω, ὃν ἀριθμὸς πρὸς ἀριθμόν· λέγω, ὅτι ἀσύμμετρά ἐστι τὰ Α, Β μεγέθη.
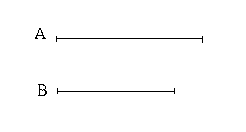
Εἰ γὰρ ἔσται σύμμετρα, τὸ Α πρὸς τὸ Β λόγον ἕξει, ὃν ἀριθμὸς πρὸς ἀριθμόν. οὐκ ἔχει δέ. ἀσύμμετρα ἄρα ἐστὶ τὰ Α, Β μεγέθη.
Ἐὰν ἄρα δύο μεγέθη πρὸς ἄλληλα, καὶ τὰ ἑξῆς.
Πρότασις θ΄ 9 Βιβλίον X
Τὰ ἀπὸ τῶν μήκει συμμέτρων εὐθειῶν τετράγωνα πρὸς ἄλληλα λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὰ τετράγωνα τὰ πρὸς ἄλληλα λόγον ἔχοντα, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ τὰς πλευρὰς ἕξει μήκει συμμέτρους. τὰ δὲ ἀπὸ τῶν μήκει ἀσυμμέτρων εὐθειῶν τετράγωνα πρὸς ἄλληλα λόγον οὐκ ἔχει, ὅνπερ τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὰ τετράγωνα τὰ πρὸς ἄλληλα λόγον μὴ ἔχοντα, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὰς πλευρὰς ἕξει μήκει συμμέτρους.
Ἔστωσαν γὰρ αἱ Α, Β μήκει σύμμετροι· λέγω, ὅτι τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β τετράγωνον λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
Ἐπεὶ γὰρ σύμμετρός ἐστιν ἡ Α τῇ Β μήκει, ἡ Α ἄρα πρὸς τὴν Β λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. ἐχέτω, ὃν ὁ Γ πρὸς τὸν Δ. ἐπεὶ οὖν ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ Γ πρὸς τὸν Δ, ἀλλὰ τοῦ μὲν τῆς Α πρὸς τὴν Β λόγου διπλασίων ἐστὶν ὁ τοῦ ἀπὸ τῆς Α τετραγώνου πρὸς τὸ ἀπὸ τῆς Β τετράγωνον· τὰ γὰρ ὅμοια σχήματα ἐν διπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· τοῦ δὲ τοῦ Γ [ἀριθμοῦ] πρὸς τὸν Δ [ἀριθμὸν] λόγου διπλασίων ἐστὶν ὁ τοῦ ἀπὸ τοῦ Γ τετραγώνου πρὸς τὸν ἀπὸ τοῦ Δ τετράγωνον· δύο γὰρ τετραγώνων ἀριθμῶν εἷς μέσος ἀνάλογόν ἐστιν ἀριθμός, καὶ ὁ τετράγωνος πρὸς τὸν τετράγωνον [ἀριθμὸν] διπλασίονα λόγον ἔχει, ἤπερ ἡ πλευρὰ πρὸς τὴν πλευράν· ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β τετράγωνον, οὕτως ὁ ἀπὸ τοῦ Γ τετράγωνος [ἀριθμὸς] πρὸς τὸν ἀπὸ τοῦ Δ [ἀριθμοῦ] τετράγωνον [ἀριθμόν].
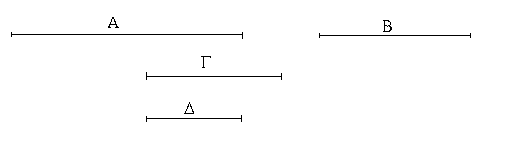
Ἀλλὰ δὴ ἔστω ὡς τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β, οὕτως ὁ ἀπὸ τοῦ Γ τετράγωνος πρὸς τὸν ἀπὸ τοῦ Δ [τετράγωνον]· λέγω, ὅτι σύμμετρός ἐστιν ἡ Α τῇ Β μήκει.
Ἐπεὶ γάρ ἐστιν ὡς τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον], οὕτως ὁ ἀπὸ τοῦ Γ τετράγωνος πρὸς τὸν ἀπὸ τοῦ Δ [τετράγωνον], ἀλλ' ὁ μὲν τοῦ ἀπὸ τῆς Α τετραγώνου πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον] λόγος διπλασίων ἐστὶ τοῦ τῆς Α πρὸς τὴν Β λόγου, ὁ δὲ τοῦ ἀπὸ τοῦ Γ [ἀριθμοῦ] τετραγώνου [ἀριθμοῦ] πρὸς τὸν ἀπὸ τοῦ Δ [ἀριθμοῦ] τετράγωνον [ἀριθμὸν] λόγος διπλασίων ἐστὶ τοῦ τοῦ Γ [ἀριθμοῦ] πρὸς τὸν Δ [ἀριθμὸν] λόγου, ἔστιν ἄρα καὶ ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ Γ [ἀριθμὸς] πρὸς τὸν Δ [ἀριθμόν]. ἡ Α ἄρα πρὸς τὴν Β, λόγον ἔχει, ὃν ἀριθμὸς ὁ Γ πρὸς ἀριθμὸν τὸν Δ· σύμμετρος ἄρα ἐστὶν ἡ Α τῇ Β μήκει.
Ἀλλὰ δὴ ἀσύμμετρος ἔστω ἡ Α τῇ Β μήκει· λέγω, ὅτι τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον] λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
Εἰ γὰρ ἔχει τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον] λόγον, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, σύμμετρος ἔσται ἡ Α τῇ Β. οὐκ ἔστι δέ· οὐκ ἄρα τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον] λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
Πάλιν δὴ τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Β [τετράγωνον] λόγον μὴ ἐχέτω, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· λέγω, ὅτι ἀσύμμετρός ἐστιν ἡ Α τῇ Β μήκει.
Εἰ γάρ ἐστι σύμμετρος ἡ Α τῇ Β, ἕξει τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β λόγον, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. οὐκ ἔχει δέ· οὐκ ἄρα σύμμετρός ἐστιν ἡ Α τῇ Β μήκει.
Τὰ ἄρα ἀπὸ τῶν μήκει συμμέτρων, καὶ τὰ ἑξῆς.
Πόρισμα
Καὶ φανερὸν ἐκ τῶν δεδειγμένων ἔσται, ὅτι αἱ μήκει σύμμετροι πάντως καὶ δυνάμει, αἱ δὲ δυνάμει οὐ πάντως καὶ μήκει [εἴπερ τὰ ἀπὸ τῶν μήκει συμμέτρων εὐθειῶν τετράγωνα λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, τὰ δὲ λόγον ἔχοντα, ὃν ἀριθμὸς πρὸς ἀριθμόν, σύμμετρά ἐστιν. ὥστε αἱ μήκει σύμμετροι εὐθεῖαι οὐ μόνον [εἰσὶ] μήκει σύμμετροι, ἀλλὰ καὶ δυνάμει. πάλιν ἐπεί, ὅσα τετράγωνα πρὸς ἄλληλα λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, μήκει ἐδείχθη σύμμετρα καὶ δυνάμει ὄντα σύμμετρα τῷ τὰ τετράγωνα λόγον ἔχειν, ὃν ἀριθμὸς πρὸς ἀριθμόν, ὅσα ἄρα τετράγωνα λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ἀλλὰ ἁπλῶς, ὃν ἀριθμὸς πρὸς ἀριθμόν, σύμμετρα μὲν ἔσται αὐτὰ τὰ τετράγωνα δυνάμει, οὐκέτι δὲ καὶ μήκει· ὥστε τὰ μὲν μήκει σύμμετρα πάντως καὶ δυνάμει, τὰ δὲ δυνάμει οὐ πάντως καὶ μήκει, εἰ μὴ καὶ λόγον ἔχοιεν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. λέγω δή, ὅτι [καὶ] αἱ μήκει ἀσύμμετροι οὐ πάντως καὶ δυνάμει, ἐπειδήπερ αἱ δυνάμει σύμμετροι δύνανται λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ διὰ τοῦτο δυνάμει οὖσαι σύμμετροι μήκει εἰσὶν ἀσύμμετροι. ὥστε οὐχ αἱ τῷ μήκει ἀσύμμετροι πάντως καὶ δυνάμει, ἀλλὰ δύνανται μήκει οὖσαι ἀσύμμετροι δυνάμει εἶναι καὶ ἀσύμμετροι καὶ σύμμετροι. αἱ δὲ δυνάμει ἀσύμμετροι πάντως καὶ μήκει ἀσύμμετροι· εἰ γὰρ [εἰσι] μήκει σύμμετροι, ἔσονται καὶ δυνάμει σύμμετροι. ὑπόκεινται δὲ καὶ ἀσύμμετροι· ὅπερ ἄτοπον. αἱ ἄρα δυνάμει ἀσύμμετροι πάντως καὶ μήκει].
Λῆμμα
Δέδεικται ἐν τοῖς ἀριθμητικοῖς, ὅτι οἱ ὅμοιοι ἐπίπεδοι ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ ὅτι, ἐὰν δύο ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχωσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ὅμοιοί εἰσιν ἐπίπεδοι. καὶ δῆλον ἐκ τούτων, ὅτι οἱ μὴ ὅμοιοι ἐπίπεδοι ἀριθμοί, τουτέστιν οἱ μὴ ἀνάλογον ἔχοντες τὰς πλευράς, πρὸς ἀλλήλους λόγον οὐκ ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. εἰ γὰρ ἕξουσιν, ὅμοιοι ἐπίπεδοι ἔσονται· ὅπερ οὐχ ὑπόκειται. οἱ ἄρα μὴ ὅμοιοι ἐπίπεδοι πρὸς ἀλλήλους λόγον οὐκ ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν.
Πρότασις ι΄ 10 Βιβλίον X
Τῇ προτεθείσῃ εὐθείᾳ προσευρεῖν δύο εὐθείας ἀσυμμέτρους, τὴν μὲν μήκει μόνον, τὴν δὲ καὶ δυνάμει.
Ἔστω ἡ προτεθεῖσα εὐθεῖα ἡ Α· δεῖ δὴ τῇ Α προσευρεῖν δύο εὐθείας ἀσυμμέτρους, τὴν μὲν μήκει μόνον, τὴν δὲ καὶ δυνάμει.
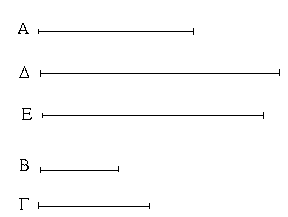
Ἐκκείσθωσαν γὰρ δύο ἀριθμοὶ οἱ Β, Γ πρὸς ἀλλήλους λόγον μὴ ἔχοντες, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, τουτέστι μὴ ὅμοιοι ἐπίπεδοι, καὶ γεγονέτω ὡς ὁ Β πρὸς τὸν Γ, οὕτως τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Δ τετράγωνον· ἐμάθομεν γάρ· σύμμετρον ἄρα τὸ ἀπὸ τῆς Α τῷ ἀπὸ τῆς Δ. καὶ ἐπεὶ ὁ Β πρὸς τὸν Γ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Δ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Α τῇ Δ μήκει. εἰλήφθω τῶν Α, Δ μέση ἀνάλογον ἡ Ε· ἔστιν ἄρα ὡς ἡ Α πρὸς τὴν Δ, οὕτως τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς Ε. ἀσύμμετρος δέ ἐστιν ἡ Α τῇ Δ μήκει· ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς Α τετράγωνον τῷ ἀπὸ τῆς Ε τετραγώνῳ· ἀσύμμετρος ἄρα ἐστὶν ἡ Α τῇ Ε δυνάμει. Τῇ ἄρα προτεθείσῃ εὐθείᾳ τῇ Α προσεύρηνται δύο εὐθεῖαι ἀσύμμετροι αἱ Δ, Ε, μήκει μὲν μόνον ἡ Δ, δυνάμει δὲ καὶ μήκει δηλαδὴ ἡ Ε [ὅπερ ἔδει δεῖξαι].
Πρότασις ια΄ 11 Βιβλίον X
Ἐὰν τέσσαρα μεγέθη ἀνάλογον ᾖ, τὸ δὲ πρῶτον τῷ δευτέρῳ σύμμετρον ᾖ, καὶ τὸ τρίτον τῷ τετάρτῳ σύμμετρον ἔσται· κἂν τὸ πρῶτον τῷ δευτέρῳ ἀσύμμετρον ᾖ, καὶ τὸ τρίτον τῷ τετάρτῳ ἀσύμμετρον ἔσται.
Ἔστωσαν τέσσαρα μεγέθη ἀνάλογον τὰ Α, Β, Γ, Δ, ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ, τὸ Α δὲ τῷ Β σύμμετρον ἔστω· λέγω, ὅτι καὶ τὸ Γ τῷ Δ σύμμετρον ἔσται.
Ἐπεὶ γὰρ σύμμετρόν ἐστι τὸ Α τῷ Β, τὸ Α ἄρα πρὸς τὸ Β λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. καί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ· καὶ τὸ Γ ἄρα πρὸς τὸ Δ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν· σύμμετρον ἄρα ἐστὶ τὸ Γ τῷ Δ.
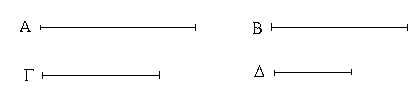
Ἀλλὰ δὴ τὸ Α τῷ Β ἀσύμμετρον ἔστω· λέγω, ὅτι καὶ τὸ Γ τῷ Δ ἀσύμμετρον ἔσται. ἐπεὶ γὰρ ἀσύμμετρόν ἐστι τὸ Α τῷ Β, τὸ Α ἄρα πρὸς τὸ Β λόγον οὐκ ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. καί ἐστιν ὡς τὸ Α πρὸς τὸ Β, οὕτως τὸ Γ πρὸς τὸ Δ· οὐδὲ τὸ Γ ἄρα πρὸς τὸ Δ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν· ἀσύμμετρον ἄρα ἐστὶ τὸ Γ τῷ Δ.
Ἐὰν ἄρα τέσσαρα μεγέθη, καὶ τὰ ἑξῆς.
Πρότασις ιβ΄ 12 Βιβλίον X
Τὰ τῷ αὐτῷ μεγέθει σύμμετρα καὶ ἀλλήλοις ἐστὶ σύμμετρα.
Ἑκάτερον γὰρ τῶν Α, Β τῷ Γ ἔστω σύμμετρον. λέγω, ὅτι καὶ τὸ Α τῷ Β ἐστι σύμμετρον.
Ἐπεὶ γὰρ σύμμετρόν ἐστι τὸ Α τῷ Γ, τὸ Α ἄρα πρὸς τὸ Γ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. ἐχέτω, ὃν ὁ Δ πρὸς τὸν Ε. πάλιν, ἐπεὶ σύμμετρόν ἐστι τὸ Γ τῷ Β, τὸ Γ ἄρα πρὸς τὸ Β λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. ἐχέτω, ὃν ὁ Ζ πρὸς τὸν Η. καὶ λόγων δοθέντων ὁποσωνοῦν τοῦ τε, ὃν ἔχει ὁ Δ πρὸς τὸν Ε, καὶ ὁ Ζ πρὸς τὸν Η εἰλήφθωσαν ἀριθμοὶ ἑξῆς ἐν τοῖς δοθεῖσι λόγοις οἱ Θ, Κ, Λ· ὥστε εἶναι ὡς μὲν τὸν Δ πρὸς τὸν Ε, οὕτως τὸν Θ πρὸς τὸν Κ, ὡς δὲ τὸν Ζ πρὸς τὸν Η, οὕτως τὸν Κ πρὸς τὸν Λ.
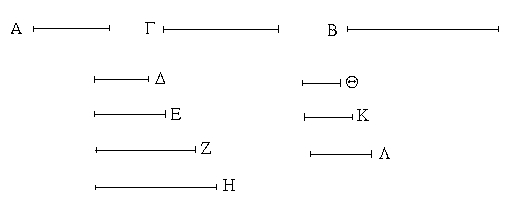
Ἐπεὶ οὖν ἐστιν ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Δ πρὸς τὸν Ε, ἀλλ' ὡς ὁ Δ πρὸς τὸν Ε, οὕτως ὁ Θ πρὸς τὸν Κ, ἔστιν ἄρα καὶ ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Θ πρὸς τὸν Κ. πάλιν, ἐπεί ἐστιν ὡς τὸ Γ πρὸς τὸ Β, οὕτως ὁ Ζ πρὸς τὸν Η, ἀλλ' ὡς ὁ Ζ πρὸς τὸν Η, [οὕτως] ὁ Κ πρὸς τὸν Λ, καὶ ὡς ἄρα τὸ Γ πρὸς τὸ Β, οὕτως ὁ Κ πρὸς τὸν Λ. ἔστι δὲ καὶ ὡς τὸ Α πρὸς τὸ Γ, οὕτως ὁ Θ πρὸς τὸν Κ· δι' ἴσου ἄρα ἐστὶν ὡς τὸ Α πρὸς τὸ Β, οὕτως ὁ Θ πρὸς τὸν Λ. τὸ Α ἄρα πρὸς τὸ Β λόγον ἔχει, ὃν ἀριθμὸς ὁ Θ πρὸς ἀριθμὸν τὸν Λ· σύμμετρον ἄρα ἐστὶ τὸ Α τῷ Β.
Τὰ ἄρα τῷ αὐτῷ μεγέθει σύμμετρα καὶ ἀλλήλοις ἐστὶ σύμμετρα· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον X
Ἐὰν ᾖ δύο μεγέθη σύμμετρα, τὸ δὲ ἕτερον αὐτῶν μεγέθει τινὶ ἀσύμμετρον ᾖ, καὶ τὸ λοιπὸν τῷ αὐτῷ ἀσύμμετρον ἔσται.
Ἔστω δύο μεγέθη σύμμετρα τὰ Α, Β, τὸ δὲ ἕτερον αὐτῶν τὸ Α ἄλλῳ τινὶ τῷ Γ ἀσύμμετρον ἔστω· λέγω, ὅτι καὶ τὸ λοιπὸν τὸ Β τῷ Γ ἀσύμμετρόν ἐστιν.
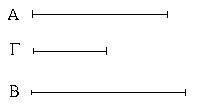
Εἰ γάρ ἐστι σύμμετρον τὸ Β τῷ Γ, ἀλλὰ καὶ τὸ Α τῷ Β σύμμετρόν ἐστιν, καὶ τὸ Α ἄρα τῷ Γ σύμμετρόν ἐστιν. ἀλλὰ καὶ ἀσύμμετρον· ὅπερ ἀδύνατον. οὐκ ἄρα σύμμετρόν ἐστι τὸ Β τῷ Γ· ἀσύμμετρον ἄρα.
Ἐὰν ἄρα ᾖ δύο μεγέθη σύμμετρα, καὶ τὰ ἑξῆς.
Λῆμμα
Δύο δοθεισῶν εὐθειῶν ἀνίσων εὑρεῖν, τίνι μεῖζον δύναται ἡ μείζων τῆς ἐλάσσονος.
Ἔστωσαν αἱ δοθεῖσαι δύο ἄνισοι εὐθεῖαι αἱ ΑΒ, Γ, ὧν μείζων ἔστω ἡ ΑΒ· δεῖ δὴ εὑρεῖν, τίνι μεῖζον δύναται ἡ ΑΒ τῆς Γ.
Γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ εἰς αὐτὸ ἐνηρμόσθω τῇ Γ ἴση ἡ ΑΔ, καὶ ἐπεζεύχθω ἡ ΔΒ. φανερὸν δή, ὅτι ὀρθή ἐστιν ἡ ὑπὸ ΑΔΒ γωνία, καὶ ὅτι ἡ ΑΒ τῆς ΑΔ, τουτέστι τῆς Γ, μεῖζον δύναται τῇ ΔΒ.
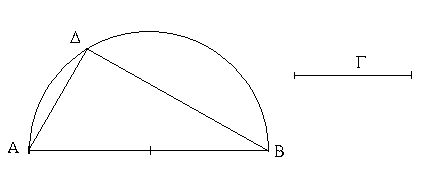
Ὁμοίως δὲ καὶ δύο δοθεισῶν εὐθειῶν ἡ δυναμένη αὐτὰς εὑρίσκεται οὕτως.
Ἔστωσαν αἱ δοθεῖσαι δύο εὐθεῖαι αἱ ΑΔ, ΔΒ, καὶ δέον ἔστω εὑρεῖν τὴν δυναμένην αὐτάς. κείσθωσαν γάρ, ὥστε ὀρθὴν γωνίαν περιέχειν τὴν ὑπὸ ΑΔ, ΔΒ, καὶ ἐπεζεύχθω ἡ ΑΒ· φανερὸν πάλιν, ὅτι ἡ τὰς ΑΔ, ΔΒ δυναμένη ἐστὶν ἡ ΑΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον X
Ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, δύνηται δὲ ἡ πρώτη τῆς δευτέρας μεῖζον τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει], καὶ ἡ τρίτη τῆς τετάρτης μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει]. καὶ ἐὰν ἡ πρώτη τῆς δευτέρας μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει], καὶ ἡ τρίτη τῆς τετάρτης μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει].
Ἔστωσαν τέσσαρες εὐθεῖαι ἀνάλογον αἱ Α, Β, Γ, Δ, ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ, καὶ ἡ Α μὲν τῆς Β μεῖζον δυνάσθω τῷ ἀπὸ τῆς Ε, ἡ δὲ Γ τῆς Δ μεῖζον δυνάσθω τῷ ἀπὸ τῆς Ζ· λέγω, ὅτι, εἴτε σύμμετρός ἐστιν ἡ Α τῇ Ε, σύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ, εἴτε ἀσύμμετρός ἐστιν ἡ Α τῇ Ε, ἀσύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ.
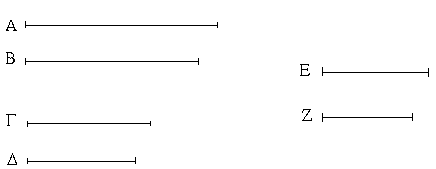
Ἐπεὶ γάρ ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ, ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὸ ἀπὸ τῆς Γ πρὸς τὸ ἀπὸ τῆς Δ. ἀλλὰ τῷ μὲν ἀπὸ τῆς Α ἴσα ἐστὶ τὰ ἀπὸ τῶν Ε, Β, τῷ δὲ ἀπὸ τῆς Γ ἴσα ἐστὶ τὰ ἀπὸ τῶν Δ, Ζ. ἔστιν ἄρα ὡς τὰ ἀπὸ τῶν Ε, Β πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὰ ἀπὸ τῶν Δ, Ζ πρὸς τὸ ἀπὸ τῆς Δ· διελόντι ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὸ ἀπὸ τῆς Ζ πρὸς τὸ ἀπὸ τῆς Δ· ἔστιν ἄρα καὶ ὡς ἡ Ε πρὸς τὴν Β, οὕτως ἡ Ζ πρὸς τὴν Δ· ἀνάπαλιν ἄρα ἐστὶν ὡς ἡ Β πρὸς τὴν Ε, οὕτως ἡ Δ πρὸς τὴν Ζ. ἔστι δὲ καὶ ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ· δι' ἴσου ἄρα ἐστὶν ὡς ἡ Α πρὸς τὴν Ε, οὕτως ἡ Γ πρὸς τὴν Ζ. εἴτε οὖν σύμμετρός ἐστιν ἡ Α τῇ Ε, σύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ, εἴτε ἀσύμμετρός ἐστιν ἡ Α τῇ Ε, ἀσύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ.
Ἐὰν ἄρα, καὶ τὰ ἑξῆς.
Πρότασις ιε΄ 15 Βιβλίον X
Ἐὰν δύο μεγέθη σύμμετρα συντεθῇ, καὶ τὸ ὅλον ἑκατέρῳ αὐτῶν σύμμετρον ἔσται· κἂν τὸ ὅλον ἑνὶ αὐτῶν σύμμετρον ᾖ, καὶ τὰ ἐξ ἀρχῆς μεγέθη σύμμετρα ἔσται.
Συγκείσθω γὰρ δύο μεγέθη σύμμετρα τὰ ΑΒ, ΒΓ· λέγω, ὅτι καὶ ὅλον τὸ ΑΓ ἑκατέρῳ τῶν ΑΒ, ΒΓ ἐστι σύμμετρον.
Ἐπεὶ γὰρ σύμμετρά ἐστι τὰ ΑΒ, ΒΓ, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΑΒ, ΒΓ μετρεῖ, καὶ ὅλον τὸ ΑΓ μετρήσει. μετρεῖ δὲ καὶ τὰ ΑΒ, ΒΓ. τὸ Δ ἄρα τὰ ΑΒ, ΒΓ, ΑΓ μετρεῖ· σύμμετρον ἄρα ἐστὶ τὸ ΑΓ ἑκατέρῳ τῶν ΑΒ, ΒΓ.
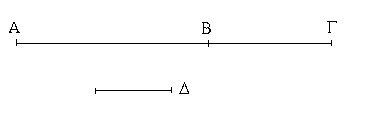
Ἀλλὰ δὴ τὸ ΑΓ ἔστω σύμμετρον τῷ ΑΒ· λέγω δή, ὅτι καὶ τὰ ΑΒ, ΒΓ σύμμετρά ἐστιν.
Ἐπεὶ γὰρ σύμμετρά ἐστι τὰ ΑΓ, ΑΒ, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΓΑ, ΑΒ μετρεῖ, καὶ λοιπὸν ἄρα τὸ ΒΓ μετρήσει. μετρεῖ δὲ καὶ τὸ ΑΒ· τὸ Δ ἄρα τὰ ΑΒ, ΒΓ μετρήσει· σύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΒΓ.
Ἐὰν ἄρα δύο μεγέθη, καὶ τὰ ἑξῆς.
Πρότασις ις΄ 16 Βιβλίον X
Ἐὰν δύο μεγέθη ἀσύμμετρα συντεθῇ, καὶ τὸ ὅλον ἑκατέρῳ αὐτῶν ἀσύμμετρον ἔσται· κἂν τὸ ὅλον ἑνὶ αὐτῶν ἀσύμμετρον ᾖ, καὶ τὰ ἐξ ἀρχῆς μεγέθη ἀσύμμετρα ἔσται.
Συγκείσθω γὰρ δύο μεγέθη ἀσύμμετρα τὰ ΑΒ, ΒΓ· λέγω, ὅτι καὶ ὅλον τὸ ΑΓ ἑκατέρῳ τῶν ΑΒ, ΒΓ ἀσύμμετρόν ἐστιν.
Εἰ γὰρ μή ἐστιν ἀσύμμετρα τὰ ΓΑ, ΑΒ, μετρήσει τι [αὐτὰ] μέγεθος. μετρείτω, εἰ δυνατόν, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΓΑ, ΑΒ μετρεῖ, καὶ λοιπὸν ἄρα τὸ ΒΓ μετρήσει. μετρεῖ δὲ καὶ τὸ ΑΒ· τὸ Δ ἄρα τὰ ΑΒ, ΒΓ μετρεῖ. σύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΒΓ· ὑπέκειντο δὲ καὶ ἀσύμμετρα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΓΑ, ΑΒ μετρήσει τι μέγεθος· ἀσύμμετρα ἄρα ἐστὶ τὰ ΓΑ, ΑΒ. ὁμοίως δὴ δείξομεν, ὅτι καὶ τὰ ΑΓ, ΓΒ ἀσύμμετρά ἐστιν. τὸ ΑΓ ἄρα ἑκατέρῳ τῶν ΑΒ, ΒΓ ἀσύμμετρόν ἐστιν.
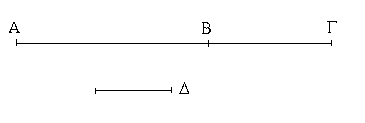
Ἀλλὰ δὴ τὸ ΑΓ ἑνὶ τῶν ΑΒ, ΒΓ ἀσύμμετρον ἔστω. ἔστω δὴ πρότερον τῷ ΑΒ· λέγω, ὅτι καὶ τὰ ΑΒ, ΒΓ ἀσύμμετρά ἐστιν. εἰ γὰρ ἔσται σύμμετρα, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΑΒ, ΒΓ μετρεῖ, καὶ ὅλον ἄρα τὸ ΑΓ μετρήσει. μετρεῖ δὲ καὶ τὸ ΑΒ· τὸ Δ ἄρα τὰ ΓΑ, ΑΒ μετρεῖ. σύμμετρα ἄρα ἐστὶ τὰ ΓΑ, ΑΒ· ὑπέκειτο δὲ καὶ ἀσύμμετρα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΑΒ, ΒΓ μετρήσει τι μέγεθος· ἀσύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΒΓ.
Ἐὰν ἄρα δύο μεγέθη, καὶ τὰ ἑξῆς.
Λῆμμα
Ἐὰν παρά τινα εὐθεῖαν παραβληθῇ παραλληλόγραμμον ἐλλεῖπον εἴδει τετραγώνῳ, τὸ παραβληθὲν ἴσον ἐστὶ τῷ ὑπὸ τῶν ἐκ τῆς παραβολῆς γενομένων τμημάτων τῆς εὐθείας.
Παρὰ γὰρ εὐθεῖαν τὴν ΑΒ παραβεβλήσθω παραλληλόγραμμον τὸ ΑΔ ἐλλεῖπον εἴδει τετραγώνῳ τῷ ΔΒ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΔ τῷ ὑπὸ τῶν ΑΓ, ΓΒ.
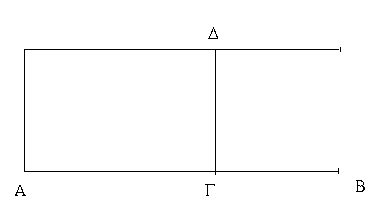
Καί ἐστιν αὐτόθεν φανερόν· ἐπεὶ γὰρ τετράγωνόν ἐστι τὸ ΔΒ, ἴση ἐστὶν ἡ ΔΓ τῇ ΓΒ, καί ἐστι τὸ ΑΔ τὸ ὑπὸ τῶν ΑΓ, ΓΔ, τουτέστι τὸ ὑπὸ τῶν ΑΓ, ΓΒ.
Ἐὰν ἄρα παρά τινα εὐθεῖαν, καὶ τὰ ἑξῆς.
Πρότασις ιζ΄ 17 Βιβλίον X
Ἐὰν ὦσι δύο εὐθεῖαι ἄνισοι, τῷ δὲ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς σύμμετρα αὐτὴν διαιρῇ μήκει, ἡ μείζων τῆς ἐλάσσονος μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει]. καὶ ἐὰν ἡ μείζων τῆς ἐλάσσονος μεῖζον δύνηται τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει], τῷ δὲ τετάρτῳ τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διαιρεῖ μήκει.
Ἔστωσαν δύο εὐθεῖαι ἄνισοι αἱ Α, ΒΓ, ὧν μείζων ἡ ΒΓ, τῷ δὲ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος τῆς Α, τουτέστι τῷ ἀπὸ τῆς ἡμισείας τῆς Α, ἴσον παρὰ τὴν ΒΓ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΒΔ, ΔΓ, σύμμετρος δὲ ἔστω ἡ ΒΔ τῇ ΔΓ μήκει· λέγω, ὅτι ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ.
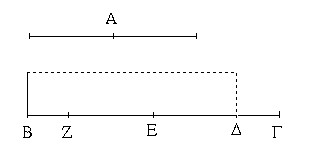
Τετμήσθω γὰρ ἡ ΒΓ δίχα κατὰ τὸ Ε σημεῖον, καὶ κείσθω τῇ ΔΕ ἴση ἡ ΕΖ. λοιπὴ ἄρα ἡ ΔΓ ἴση ἐστὶ τῇ ΒΖ. καὶ ἐπεὶ εὐθεῖα ἡ ΒΓ τέτμηται εἰς μὲν ἴσα κατὰ τὸ Ε, εἰς δὲ ἄνισα κατὰ τὸ Δ, τὸ ἄρα ὑπὸ ΒΔ, ΔΓ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΕΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΓ τετραγώνῳ· καὶ τὰ τετραπλάσια· τὸ ἄρα τετράκις ὑπὸ τῶν ΒΔ, ΔΓ μετὰ τοῦ τετραπλασίου τοῦ ἀπὸ τῆς ΔΕ ἴσον ἐστὶ τῷ τετράκις ἀπὸ τῆς ΕΓ τετραγώνῳ. ἀλλὰ τῷ μέν τετραπλασίῳ τοῦ ὑπὸ τῶν ΒΔ, ΔΓ ἴσον ἐστὶ τὸ ἀπὸ τῆς Α τετράγωνον, τῷ δὲ τετραπλασίῳ τοῦ ἀπὸ τῆς ΔΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΔΖ τετράγωνον· διπλασίων γάρ ἐστιν ἡ ΔΖ τῆς ΔΕ. τῷ δὲ τετραπλασίῳ τοῦ ἀπὸ τῆς ΕΓ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΒΓ τετράγωνον· διπλασίων γάρ ἐστι πάλιν ἡ ΒΓ τῆς ΓΕ. τὰ ἄρα ἀπὸ τῶν Α, ΔΖ τετράγωνα ἴσα ἐστὶ τῷ ἀπὸ τῆς ΒΓ τετραγώνῳ· ὥστε τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς Α μεῖζόν ἐστι τῷ ἀπὸ τῆς ΔΖ· ἡ ΒΓ ἄρα τῆς Α μεῖζον δύναται τῇ ΔΖ. δεικτέον, ὅτι καὶ σύμμετρός ἐστιν ἡ ΒΓ τῇ ΔΖ. ἐπεὶ γὰρ σύμμετρός ἐστιν ἡ ΒΔ τῇ ΔΓ μήκει, σύμμετρος ἄρα ἐστὶ καὶ ἡ ΒΓ τῇ ΓΔ μήκει. ἀλλὰ ἡ ΓΔ ταῖς ΓΔ, ΒΖ ἐστι σύμμετρος μήκει· ἴση γάρ ἐστιν ἡ ΓΔ τῇ ΒΖ. καὶ ἡ ΒΓ ἄρα σύμμετρός ἐστι ταῖς ΒΖ, ΓΔ μήκει· ὥστε καὶ λοιπῇ τῇ ΖΔ σύμμετρός ἐστιν ἡ ΒΓ μήκει· ἡ ΒΓ ἄρα τῆς Α μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ.
Ἀλλὰ δὴ ἡ ΒΓ τῆς Α μεῖζον δυνάσθω τῷ ἀπὸ συμμέτρου ἑαυτῇ, τῷ δὲ τετάρτῳ τοῦ ἀπὸ τῆς Α ἴσον παρὰ τὴν ΒΓ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΒΔ, ΔΓ. δεικτέον, ὅτι σύμμετρός ἐστιν ἡ ΒΔ τῇ ΔΓ μήκει.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ τῆς ΖΔ. δύναται δὲ ἡ ΒΓ τῆς Α μεῖζον τῷ ἀπὸ συμμέτρου ἑαυτῇ. σύμμετρος ἄρα ἐστὶν ἡ ΒΓ τῇ ΖΔ μήκει· ὥστε καὶ λοιπῇ συναμφοτέρῳ τῇ ΒΖ, ΔΓ σύμμετρός ἐστιν ἡ ΒΓ μήκει. ἀλλὰ συναμφότερος ἡ ΒΖ, ΔΓ σύμμετρός ἐστι τῇ ΔΓ [μήκει]. ὥστε καὶ ἡ ΒΓ τῇ ΓΔ σύμμετρός ἐστι μήκει· καὶ διελόντι ἄρα ἡ ΒΔ τῇ ΔΓ ἐστι σύμμετρος μήκει.
Ἐὰν ἄρα ὦσι δύο εὐθεῖαι ἄνισοι, καὶ τὰ ἑξῆς.
Πρότασις ιη΄ 18 Βιβλίον X
Ἐὰν ὦσι δύο εὐθεῖαι ἄνισοι, τῷ δὲ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, καὶ εἰς ἀσύμμετρα αὐτὴν διαιρῇ [μήκει], ἡ μείζων τῆς ἐλάσσονος μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ ἐὰν ἡ μείζων τῆς ἐλάσσονος μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, τῷ δὲ τετάρτῳ τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς ἀσύμμετρα αὐτὴν διαιρεῖ [μήκει].
Ἔστωσαν δύο εὐθεῖαι ἄνισοι αἱ Α, ΒΓ, ὧν μείζων ἡ ΒΓ, τῷ δὲ τετάρτῳ [μέρει] τοῦ ἀπὸ τῆς ἐλάσσονος τῆς Α ἴσον παρὰ τὴν ΒΓ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΒΔΓ, ἀσύμμετρος δὲ ἔστω ἡ ΒΔ τῇ ΔΓ μήκει· λέγω, ὅτι ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων τῷ πρότερον ὁμοίως δείξομεν, ὅτι ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ τῆς ΖΔ. δεικτέον [οὖν], ὅτι ἀσύμμετρός ἐστιν ἡ ΒΓ τῇ ΔΖ μήκει. ἐπεὶ γὰρ ἀσύμμετρός ἐστιν ἡ ΒΔ τῇ ΔΓ μήκει, ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΒΓ τῇ ΓΔ μήκει. ἀλλὰ ἡ ΔΓ σύμμετρός ἐστι συναμφοτέραις ταῖς ΒΖ, ΔΓ· καὶ ἡ ΒΓ ἄρα ἀσύμμετρός ἐστι συναμφοτέραις ταῖς ΒΖ, ΔΓ. ὥστε καὶ λοιπῇ τῇ ΖΔ ἀσύμμετρός ἐστιν ἡ ΒΓ μήκει. καὶ ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ τῆς ΖΔ· ἡ ΒΓ ἄρα τῆς Α μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ.
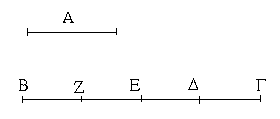
Δυνάσθω δὴ πάλιν ἡ ΒΓ τῆς Α μεῖζον τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, τῷ δὲ τετάρτῳ τοῦ ἀπὸ τῆς Α ἴσον παρὰ τὴν ΒΓ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΒΔ, ΔΓ. δεικτέον, ὅτι ἀσύμμετρός ἐστιν ἡ ΒΔ τῇ ΔΓ μήκει.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ὁμοίως δείξομεν, ὅτι ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ τῆς ΖΔ. ἀλλὰ ἡ ΒΓ τῆς Α μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΓ τῇ ΖΔ μήκει· ὥστε καὶ λοιπῇ συναμφοτέρῳ τῇ ΒΖ, ΔΓ ἀσύμμετρός ἐστιν ἡ ΒΓ. ἀλλὰ συναμφότερος ἡ ΒΖ, ΔΓ τῇ ΔΓ σύμμετρός ἐστι μήκει· καὶ ἡ ΒΓ ἄρα τῇ ΔΓ ἀσύμμετρός ἐστι μήκει· ὥστε καὶ διελόντι ἡ ΒΔ τῇ ΔΓ ἀσύμμετρός ἐστι μήκει.
Ἐὰν ἄρα ὦσι δύο εὐθεῖαι, καὶ τὰ ἑξῆς.
Λῆμμα
Ἐπεὶ δέδεικται, ὅτι αἱ μήκει σύμμετροι πάντως καὶ δυνάμει [εἰσὶ σύμμετροι], αἱ δὲ δυνάμει οὐ πάντως καὶ μήκει, ἀλλὰ δὴ δύνανται μήκει καὶ σύμμετροι εἶναι καὶ ἀσύμμετροι, φανερόν, ὅτι, ἐὰν τῇ ἐκκειμένῃ ῥητῇ σύμμετρός τις ᾖ μήκει, λέγεται ῥητὴ καὶ σύμμετρος αὐτῇ οὐ μόνον μήκει, ἀλλὰ καὶ δυνάμει, ἐπεὶ αἱ μήκει σύμμετροι πάντως καὶ δυνάμει. ἐὰν δὲ τῇ ἐκκειμένῃ ῥητῇ σύμμετρός τις ᾖ δυνάμει, εἰ μὲν καὶ μήκει, λέγεται καὶ οὕτως ῥητὴ καὶ σύμμετρος αὐτῇ μήκει καὶ δυνάμει· εἰ δὲ τῇ ἐκκειμένῃ πάλιν ῥητῇ σύμμετρός τις οὖσα δυνάμει μήκει αὐτῇ ᾖ ἀσύμμετρος, λέγεται καὶ οὕτως ῥητὴ δυνάμει μόνον σύμμετρος.
Πρότασις ιθ΄ 19 Βιβλίον X
Τὸ ὑπὸ ῥητῶν μήκει συμμέτρων κατά τινα τῶν προειρημένων τρόπων εὐθειῶν περιεχόμενον ὀρθογώνιον ῥητόν ἐστιν.
Ὑπὸ γὰρ ῥητῶν μήκει συμμέτρων εὐθειῶν τῶν ΑΒ, ΒΓ ὀρθογώνιον περιεχέσθω τὸ ΑΓ· λέγω, ὅτι ῥητόν ἐστι τὸ ΑΓ.
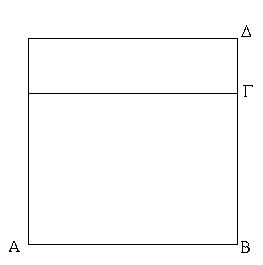
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔ· ῥητὸν ἄρα ἐστὶ τὸ ΑΔ. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, ἴση δέ ἐστιν ἡ ΑΒ τῇ ΒΔ, σύμμετρος ἄρα ἐστὶν ἡ ΒΔ τῇ ΒΓ μήκει. καί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΒΓ, οὕτως τὸ ΔΑ πρὸς τὸ ΑΓ. σύμμετρον ἄρα ἐστὶ τὸ ΔΑ τῷ ΑΓ. ῥητὸν δὲ τὸ ΔΑ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ΑΓ.
Τὸ ἄρα ὑπὸ ῥητῶν μήκει συμμέτρων, καὶ τὰ ἑξῆς.
Πρότασις κ΄ 20 Βιβλίον X
Ἐὰν ῥητὸν παρὰ ῥητὴν παραβληθῇ, πλάτος ποιεῖ ῥητὴν καὶ σύμμετρον τῇ, παρ' ἣν παράκειται, μήκει.
Ῥητὸν γὰρ τὸ ΑΓ παρὰ ῥητὴν κατά τινα πάλιν τῶν προειρημένων τρόπων τὴν ΑΒ παραβεβλήσθω πλάτος ποιοῦν τὴν ΒΓ· λέγω, ὅτι ῥητή ἐστιν ἡ ΒΓ καὶ σύμμετρος τῇ ΒΑ μήκει.
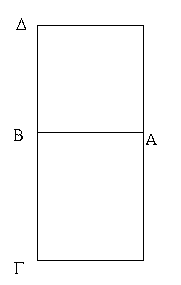
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔ· ῥητὸν ἄρα ἐστὶ τὸ ΑΔ. ῥητὸν δὲ καὶ τὸ ΑΓ· σύμμετρον ἄρα ἐστὶ τὸ ΔΑ τῷ ΑΓ. καί ἐστιν ὡς τὸ ΔΑ πρὸς τὸ ΑΓ, οὕτως ἡ ΔΒ πρὸς τὴν ΒΓ. σύμμετρος ἄρα ἐστὶ καὶ ἡ ΔΒ τῇ ΒΓ· ἴση δὲ ἡ ΔΒ τῇ ΒΑ· σύμμετρος ἄρα καὶ ἡ ΑΒ τῇ ΒΓ. ῥητὴ δέ ἐστιν ἡ ΑΒ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΒΓ καὶ σύμμετρος τῇ ΑΒ μήκει.
Ἐὰν ἄρα ῥητὸν παρὰ ῥητὴν παραβληθῇ, καὶ τὰ ἑξῆς.
Πρότασις κα΄ 21 Βιβλίον X
Τὸ ὑπὸ ῥητῶν δυνάμει μόνον συμμέτρων εὐθειῶν περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλείσθω δὲ μέση.
Ὑπὸ γὰρ ῥητῶν δυνάμει μόνον συμμέτρων εὐθειῶν τῶν ΑΒ, ΒΓ ὀρθογώνιον περιεχέσθω τὸ ΑΓ· λέγω, ὅτι ἄλογόν ἐστι τὸ ΑΓ, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλείσθω δὲ μέση.
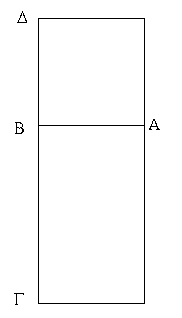
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔ· ῥητὸν ἄρα ἐστὶ τὸ ΑΔ. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει· δυνάμει γὰρ μόνον ὑπόκεινται σύμμετροι· ἴση δὲ ἡ ΑΒ τῇ ΒΔ, ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΔΒ τῇ ΒΓ μήκει. καί ἐστιν ὡς ἡ ΔΒ πρὸς τὴν ΒΓ, οὕτως τὸ ΑΔ πρὸς τὸ ΑΓ· ἀσύμμετρον ἄρα [ἐστὶ] τὸ ΔΑ τῷ ΑΓ. ῥητὸν δὲ τὸ ΔΑ· ἄλογον ἄρα ἐστὶ τὸ ΑΓ· ὥστε καὶ ἡ δυναμένη τὸ ΑΓ [τουτέστιν ἡ ἴσον αὐτῷ τετράγωνον δυναμένη] ἄλογός ἐστιν, καλείσθω δὲ μέση· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ἐὰν ὦσι δύο εὐθεῖαι, ἔστιν ὡς ἡ πρώτη πρὸς τὴν δευτέραν, οὕτως τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ὑπὸ τῶν δύο εὐθειῶν.
Ἔστωσαν δύο εὐθεῖαι αἱ ΖΕ, ΕΗ. λέγω, ὅτι ἐστὶν ὡς ἡ ΖΕ πρὸς τὴν ΕΗ, οὕτως τὸ ἀπὸ τῆς ΖΕ πρὸς τὸ ὑπὸ τῶν ΖΕ, ΕΗ.
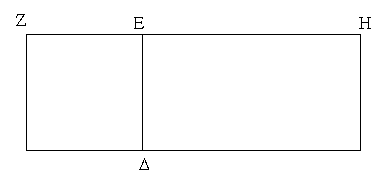
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΖΕ τετράγωνον τὸ ΔΖ, καὶ συμπεπληρώσθω τὸ ΗΔ. ἐπεὶ οὖν ἐστιν ὡς ἡ ΖΕ πρὸς τὴν ΕΗ, οὕτως τὸ ΖΔ πρὸς τὸ ΔΗ, καί ἐστι τὸ μὲν ΖΔ τὸ ἀπὸ τῆς ΖΕ, τὸ δὲ ΔΗ τὸ ὑπὸ τῶν ΔΕ, ΕΗ, τουτέστι τὸ ὑπὸ τῶν ΖΕ, ΕΗ, ἔστιν ἄρα ὡς ἡ ΖΕ τὴν ΕΗ, οὕτως τὸ ἀπὸ τῆς ΖΕ πρὸς τὸ ὑπὸ τῶν ΖΕ, ΕΗ. ὁμοίως δὲ καὶ ὡς τὸ ὑπὸ τῶν ΗΕ, ΕΖ πρὸς τὸ ἀπὸ τῆς ΕΖ, τουτέστιν ὡς τὸ ΗΔ πρὸς τὸ ΖΔ, οὕτως ἡ ΗΕ πρὸς τὴν ΕΖ· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον X
Τὸ ἀπὸ μέσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ῥητὴν καὶ ἀσύμμετρον τῇ, παρ' ἣν παράκειται, μήκει.
Ἔστω μέση μὲν ἡ Α, ῥητὴ δὲ ἡ ΓΒ, καὶ τῷ ἀπὸ τῆς Α ἴσον παρὰ τὴν ΒΓ παραβεβλήσθω χωρίον ὀρθογώνιον τὸ ΒΔ πλάτος ποιοῦν τὴν ΓΔ· λέγω, ὅτι ῥητή ἐστιν ἡ ΓΔ καὶ ἀσύμμετρος τῇ ΓΒ μήκει.
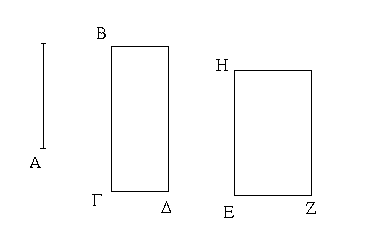
Ἐπεὶ γὰρ μέση ἐστὶν ἡ Α, δύναται χωρίον περιεχόμενον ὑπὸ ῥητῶν δυνάμει μόνον συμμέτρων. δυνάσθω τὸ ΗΖ. δύναται δὲ καὶ τὸ ΒΔ· ἴσον ἄρα ἐστὶ τὸ ΒΔ τῷ ΗΖ. ἔστι δὲ αὐτῷ καὶ ἰσογώνιον· τῶν δὲ ἴσων τε καὶ ἰσογωνίων παραλληλογράμμων ἀντιπεπόνθασιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΓ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΖ πρὸς τὴν ΓΔ. ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς ΒΓ πρὸς τὸ ἀπὸ τῆς ΕΗ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΓΔ. σύμμετρον δέ ἐστι τὸ ἀπὸ τῆς ΓΒ τῷ ἀπὸ τῆς ΕΗ· ῥητὴ γάρ ἐστιν ἑκατέρα αὐτῶν· σύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΕΖ τῷ ἀπὸ τῆς ΓΔ. ῥητὸν δέ ἐστι τὸ ἀπὸ τῆς ΕΖ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΓΔ· ῥητὴ ἄρα ἐστὶν ἡ ΓΔ. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΕΖ τῇ ΕΗ μήκει· δυνάμει γὰρ μόνον εἰσὶ σύμμετροι· ὡς δὲ ἡ ΕΖ πρὸς τὴν ΕΗ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ὑπὸ τῶν ΖΕ, ΕΗ, ἀσύμμετρον ἄρα [ἐστὶ] τὸ ἀπὸ τῆς ΕΖ τῷ ὑπὸ τῶν ΖΕ, ΕΗ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΕΖ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΓΔ· ῥηταὶ γάρ εἰσι δυνάμει· τῷ δὲ ὑπὸ τῶν ΖΕ, ΕΗ σύμμετρόν ἐστι τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴσα γάρ ἐστι τῷ ἀπὸ τῆς Α· ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΓΔ τῷ ὑπὸ τῶν ΔΓ, ΓΒ. ὡς δὲ τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ὑπὸ τῶν ΔΓ, ΓΒ, οὕτως ἐστὶν ἡ ΔΓ πρὸς τὴν ΓΒ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΔΓ τῇ ΓΒ μήκει. ῥητὴ ἄρα ἐστὶν ἡ ΓΔ καὶ ἀσύμμετρος τῇ ΓΒ μήκει· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον X
Ἡ τῇ μέσῃ σύμμετρος μέση ἐστίν.
Ἔστω μέση ἡ Α, καὶ τῇ Α σύμμετρος ἔστω ἡ Β· λέγω, ὅτι καὶ ἡ Β μέση ἐστίν.
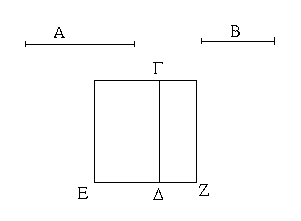
Ἐκκείσθω γὰρ ῥητὴ ἡ ΓΔ, καὶ τῷ μὲν ἀπὸ τῆς Α ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω χωρίον ὀρθογώνιον τὸ ΓΕ πλάτος ποιοῦν τὴν ΕΔ· ῥητὴ ἄρα ἐστὶν ἡ ΕΔ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. τῷ δὲ ἀπὸ τῆς Β ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω χωρίον ὀρθογώνιον τὸ ΓΖ πλάτος ποιοῦν τὴν ΔΖ. ἐπεὶ οὖν σύμμετρός ἐστιν ἡ Α τῇ Β, σύμμετρόν ἐστι καὶ τὸ ἀπὸ τῆς Α τῷ ἀπὸ τῆς Β. ἀλλὰ τῷ μὲν ἀπὸ τῆς Α ἴσον ἐστὶ τὸ ΕΓ, τῷ δὲ ἀπὸ τῆς Β ἴσον ἐστὶ τὸ ΓΖ· σύμμετρον ἄρα ἐστὶ τὸ ΕΓ τῷ ΓΖ. καί ἐστιν ὡς τὸ ΕΓ πρὸς τὸ ΓΖ, οὕτως ἡ ΕΔ πρὸς τὴν ΔΖ· σύμμετρος ἄρα ἐστὶν ἡ ΕΔ τῇ ΔΖ μήκει. ῥητὴ δέ ἐστιν ἡ ΕΔ καὶ ἀσύμμετρος τῇ ΔΓ μήκει· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΔΖ καὶ ἀσύμμετρος τῇ ΔΓ μήκει· αἱ ΓΔ, ΔΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ἡ δὲ τὸ ὑπὸ ῥητῶν δυνάμει μόνον συμμέτρων δυναμένη μέση ἐστίν. ἡ ἄρα τὸ ὑπὸ τῶν ΓΔ, ΔΖ δυναμένη μέση ἐστίν· καὶ δύναται τὸ ὑπὸ τῶν ΓΔ, ΔΖ ἡ Β· μέση ἄρα ἐστὶν ἡ Β.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι τὸ τῷ μέσῳ χωρίῳ σύμμετρον μέσον ἐστίν. [δύνανται γὰρ αὐτὰ εὐθεῖαι, αἵ εἰσι δυνάμει σύμμετροι, ὧν ἡ ἑτέρα μέση· ὥστε καὶ ἡ λοιπὴ μέση ἐστίν.]
Ὡσαύτως δὲ τοῖς ἐπὶ τῶν ῥητῶν εἰρημένοις καὶ ἐπὶ τῶν μέσων ἐξακολουθεῖ, τὴν τῇ μέσῃ μήκει σύμμετρον λέγεσθαι μέσην καὶ σύμμετρον αὐτῇ μὴ μόνον μήκει, ἀλλὰ καὶ δυνάμει, ἐπειδήπερ καθόλου αἱ μήκει σύμμετροι πάντως καὶ δυνάμει. ἐὰν δὲ τῇ μέσῃ σύμμετρός τις ᾖ δυνάμει, εἰ μὲν καὶ μήκει, λέγονται καὶ οὕτως μέσαι καὶ σύμμετροι μήκει καὶ δυνάμει, εἰ δὲ δυνάμει μόνον, λέγονται μέσαι δυνάμει μόνον σύμμετροι.
Πρότασις κδ΄ 24 Βιβλίον X
Τὸ ὑπὸ μέσων μήκει συμμέτρων εὐθειῶν κατά τινα τῶν εἰρημένων τρόπων περιεχόμενον ὀρθογώνιον μέσον ἐστίν.
Ὑπὸ γὰρ μέσων μήκει συμμέτρων εὐθειῶν τῶν ΑΒ, ΒΓ περιεχέσθω ὀρθογώνιον τὸ ΑΓ· λέγω, ὅτι τὸ ΑΓ μέσον ἐστίν.
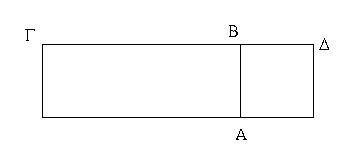
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔ· μέσον ἄρα ἐστὶ τὸ ΑΔ. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, ἴση δὲ ἡ ΑΒ τῇ ΒΔ, σύμμετρος ἄρα ἐστὶ καὶ ἡ ΔΒ τῇ ΒΓ μήκει· ὥστε καὶ τὸ ΔΑ τῷ ΑΓ σύμμετρόν ἐστιν. μέσον δὲ τὸ ΔΑ· μέσον ἄρα καὶ τὸ ΑΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον X
Τὸ ὑπὸ μέσων δυνάμει μόνον συμμέτρων εὐθειῶν περιεχόμενον ὀρθογώνιον ἤτοι ῥητὸν ἢ μέσον ἐστίν.
Ὑπὸ γὰρ μέσων δυνάμει μόνον συμμέτρων εὐθειῶν τῶν ΑΒ, ΒΓ ὀρθογώνιον περιεχέσθω τὸ ΑΓ· λέγω, ὅτι τὸ ΑΓ ἤτοι ῥητὸν ἢ μέσον ἐστίν.
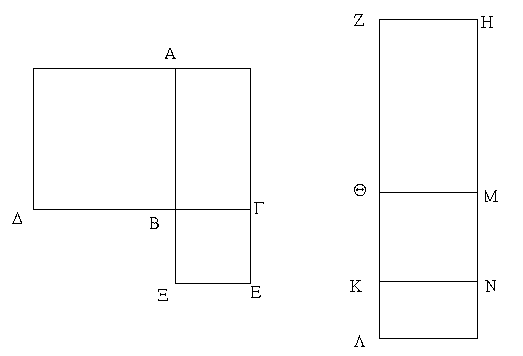
Ἀναγεγράφθω γὰρ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα τὰ ΑΔ, ΒΕ· μέσον ἄρα ἐστὶν ἑκάτερον τῶν ΑΔ, ΒΕ. καὶ ἐκκείσθω ῥητὴ ἡ ΖΗ, καὶ τῷ μὲν ΑΔ ἴσον παρὰ τὴν ΖΗ παραβεβλήσθω ὀρθογώνιον παραλληλόγραμμον τὸ ΗΘ πλάτος ποιοῦν τὴν ΖΘ, τῷ δὲ ΑΓ ἴσον παρὰ τὴν ΘΜ παραβεβλήσθω ὀρθογώνιον παραλληλόγραμμον τὸ ΜΚ πλάτος ποιοῦν τὴν ΘΚ, καὶ ἔτι τῷ ΒΕ ἴσον ὁμοίως παρὰ τὴν ΚΝ παραβεβλήσθω τὸ ΝΛ πλάτος ποιοῦν τὴν ΚΛ· ἐπ᾿ εὐθείας ἄρα εἰσὶν αἱ ΖΘ, ΘΚ, ΚΛ. ἐπεὶ οὖν μέσον ἐστὶν ἑκάτερον τῶν ΑΔ, ΒΕ, καί ἐστιν ἴσον τὸ μὲν ΑΔ τῷ ΗΘ, τὸ δὲ ΒΕ τῷ ΝΛ, μέσον ἄρα καὶ ἑκάτερον τῶν ΗΘ, ΝΛ. καὶ παρὰ ῥητὴν τὴν ΖΗ παράκειται· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΖΘ, ΚΛ καὶ ἀσύμμετρος τῇ ΖΗ μήκει. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ΑΔ τῷ ΒΕ, σύμμετρον ἄρα ἐστὶ καὶ τὸ ΗΘ τῷ ΝΛ. καί ἐστιν ὡς τὸ ΗΘ πρὸς τὸ ΝΛ, οὕτως ἡ ΖΘ πρὸς τὴν ΚΛ· σύμμετρος ἄρα ἐστὶν ἡ ΖΘ τῇ ΚΛ μήκει. αἱ ΖΘ, ΚΛ ἄρα ῥηταί εἰσι μήκει σύμμετροι· ῥητὸν ἄρα ἐστὶ τὸ ὑπὸ τῶν ΖΘ, ΚΛ. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΔΒ τῇ ΒΑ, ἡ δὲ ΞΒ τῇ ΒΓ, ἔστιν ἄρα ὡς ἡ ΔΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΑΒ πρὸς τὴν ΒΞ. ἀλλ' ὡς μὲν ἡ ΔΒ πρὸς τὴν ΒΓ, οὕτως τὸ ΔΑ πρὸς τὸ ΑΓ· ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΞ, οὕτως τὸ ΑΓ πρὸς τὸ ΓΞ· ἔστιν ἄρα ὡς τὸ ΔΑ πρὸς τὸ ΑΓ, οὕτως τὸ ΑΓ πρὸς τὸ ΓΞ. ἴσον δέ ἐστι τὸ μὲν ΑΔ τῷ ΗΘ, τὸ δὲ ΑΓ τῷ ΜΚ, τὸ δὲ ΓΞ τῷ ΝΛ· ἔστιν ἄρα ὡς τὸ ΗΘ πρὸς τὸ ΜΚ, οὕτως τὸ ΜΚ πρὸς τὸ ΝΛ· ἔστιν ἄρα καὶ ὡς ἡ ΖΘ πρὸς τὴν ΘΚ, οὕτως ἡ ΘΚ πρὸς τὴν ΚΛ· τὸ ἄρα ὑπὸ τῶν ΖΘ, ΚΛ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΘΚ. ῥητὸν δὲ τὸ ὑπὸ τῶν ΖΘ, ΚΛ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΘΚ· ῥητὴ ἄρα ἐστὶν ἡ ΘΚ. καὶ εἰ μὲν σύμμετρός ἐστι τῇ ΖΗ μήκει, ῥητόν ἐστι τὸ ΘΝ· εἰ δὲ ἀσύμμετρός ἐστι τῇ ΖΗ μήκει, αἱ ΚΘ, ΘΜ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· μέσον ἄρα τὸ ΘΝ. τὸ ΘΝ ἄρα ἤτοι ῥητὸν ἢ μέσον ἐστίν. ἴσον δὲ τὸ ΘΝ τῷ ΑΓ· τὸ ΑΓ ἄρα ἤτοι ῥητὸν ἢ μέσον ἐστίν.
Τὸ ἄρα ὑπὸ μέσων δυνάμει μόνον συμμέτρων, καὶ τὰ ἑξῆς.
Πρότασις κς΄ 26 Βιβλίον X
Μέσον μέσου οὐχ ὑπερέχει ῥητῷ.
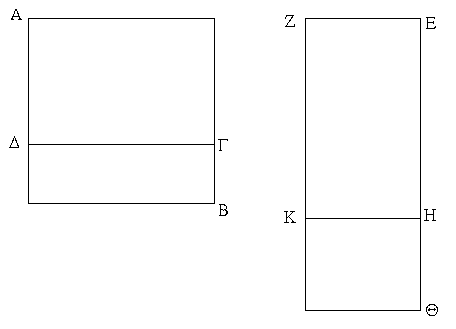
Εἰ γὰρ δυνατόν, μέσον τὸ ΑΒ μέσου τοῦ ΑΓ ὑπερεχέτω ῥητῷ τῷ ΔΒ, καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τῷ ΑΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω παραλληλόγραμμον ὀρθογώνιον τὸ ΖΘ πλάτος ποιοῦν τὴν ΕΘ, τῷ δὲ ΑΓ ἴσον ἀφῃρήσθω τὸ ΖΗ· λοιπὸν ἄρα τὸ ΒΔ λοιπῷ τῷ ΚΘ ἐστιν ἴσον. ῥητὸν δέ ἐστι τὸ ΔΒ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ΚΘ. ἐπεὶ οὖν μέσον ἐστὶν ἑκάτερον τῶν ΑΒ, ΑΓ, καί ἐστι τὸ μὲν ΑΒ τῷ ΖΘ ἴσον, τὸ δὲ ΑΓ τῷ ΖΗ, μέσον ἄρα καὶ ἑκάτερον τῶν ΖΘ, ΖΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΘΕ, ΕΗ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ῥητόν ἐστι τὸ ΔΒ καί ἐστιν ἴσον τῷ ΚΘ, ῥητὸν ἄρα ἐστὶ καὶ τὸ ΚΘ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΗΘ καὶ σύμμετρος τῇ ΕΖ μήκει. ἀλλὰ καὶ ἡ ΕΗ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΗ τῇ ΗΘ μήκει. καί ἐστιν ὡς ἡ ΕΗ πρὸς τὴν ΗΘ, οὕτως τὸ ἀπὸ τῆς ΕΗ πρὸς τὸ ὑπὸ τῶν ΕΗ, ΗΘ· ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΕΗ τῷ ὑπὸ τῶν ΕΗ, ΗΘ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΕΗ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΕΗ, ΗΘ τετράγωνα· ῥητὰ γὰρ ἀμφότερα· τῷ δὲ ὑπὸ τῶν ΕΗ, ΗΘ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΕΗ, ΗΘ· διπλάσιον γάρ ἐστιν αὐτοῦ· ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΕΗ, ΗΘ τῷ δὶς ὑπὸ τῶν ΕΗ, ΗΘ· καὶ συναμφότερα ἄρα τά τε ἀπὸ τῶν ΕΗ, ΗΘ καὶ τὸ δὶς ὑπὸ τῶν ΕΗ, ΗΘ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΕΘ, ἀσύμμετρόν ἐστι τοῖς ἀπὸ τῶν ΕΗ, ΗΘ. ῥητὰ δὲ τὰ ἀπὸ τῶν ΕΗ, ΗΘ· ἄλογον ἄρα τὸ ἀπὸ τῆς ΕΘ. ἄλογος ἄρα ἐστὶν ἡ ΕΘ. ἀλλὰ καὶ ῥητή· ὅπερ ἐστὶν ἀδύνατον.
Μέσον ἄρα μέσου οὐχ ὑπερέχει ῥητῷ· ὅπερ ἔδει δεῖξαι.
Πρότασις κζ΄ 27 Βιβλίον X
Μέσας εὑρεῖν δυνάμει μόνον συμμέτρους ῥητὸν περιεχούσας.
Ἐκκείσθωσαν δύο ῥηταὶ δυνάμει μόνον σύμμετροι αἱ Α, Β, καὶ εἰλήφθω τῶν Α, Β μέση ἀνάλογον ἡ Γ, καὶ γεγονέτω ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ.
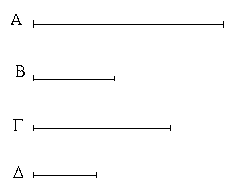
Καὶ ἐπεὶ αἱ Α, Β ῥηταί εἰσι δυνάμει μόνον σύμμετροι, τὸ ἄρα ὑπὸ τῶν Α, Β, τουτέστι τὸ ἀπὸ τῆς Γ, μέσον ἐστίν. μέση ἄρα ἡ Γ. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, [οὕτως] ἡ Γ πρὸς τὴν Δ, αἱ δὲ Α, Β δυνάμει μόνον [εἰσὶ] σύμμετροι, καὶ αἱ Γ, Δ ἄρα δυνάμει μόνον εἰσὶ σύμμετροι. καί ἐστι μέση ἡ Γ· μέση ἄρα καὶ ἡ Δ. αἱ Γ, Δ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. λέγω, ὅτι καὶ ῥητὸν περιέχουσιν. ἐπεὶ γάρ ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ, ἐναλλὰξ ἄρα ἐστὶν ὡς ἡ Α πρὸς τὴν Γ, ἡ Β πρὸς τὴν Δ. ἀλλ' ὡς ἡ Α πρὸς τὴν Γ, ἡ Γ πρὸς τὴν Β· καὶ ὡς ἄρα ἡ Γ πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Δ· τὸ ἄρα ὑπὸ τῶν Γ, Δ ἴσον ἐστὶ τῷ ἀπὸ τῆς Β. ῥητὸν δὲ τὸ ἀπὸ τῆς Β· ῥητὸν ἄρα [ἐστὶ] καὶ τὸ ὑπὸ τῶν Γ, Δ.
Εὕρηνται ἄρα μέσαι δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κη΄ 28 Βιβλίον X
Μέσας εὑρεῖν δυνάμει μόνον συμμέτρους μέσον περιεχούσας.
Ἐκκείσθωσαν [τρεῖς] ῥηταὶ δυνάμει μόνον σύμμετροι αἱ Α, Β, Γ, καὶ εἰλήφθω τῶν Α, Β μέση ἀνάλογον ἡ Δ, καὶ γεγονέτω ὡς ἡ Β πρὸς τὴν Γ, ἡ Δ πρὸς τὴν Ε.
Ἐπεὶ αἱ Α, Β ῥηταί εἰσι δυνάμει μόνον σύμμετροι, τὸ ἄρα ὑπὸ τῶν Α, Β, τουτέστι τὸ ἀπὸ τῆς Δ, μέσον ἐστίν. μέση ἄρα ἡ Δ. καὶ ἐπεὶ αἱ Β, Γ δυνάμει μόνον εἰσὶ σύμμετροι, καί ἐστιν ὡς ἡ Β πρὸς τὴν Γ, ἡ Δ πρὸς τὴν Ε, καὶ αἱ Δ, Ε ἄρα δυνάμει μόνον εἰσὶ σύμμετροι. μέση δὲ ἡ Δ· μέση ἄρα καὶ ἡ Ε· αἱ Δ, Ε ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. λέγω δή, ὅτι καὶ μέσον περιέχουσιν. ἐπεὶ γάρ ἐστιν ὡς ἡ Β πρὸς τὴν Γ, ἡ Δ πρὸς τὴν Ε, ἐναλλὰξ ἄρα ὡς ἡ Β πρὸς τὴν Δ, ἡ Γ πρὸς τὴν Ε. ὡς δὲ ἡ Β πρὸς τὴν Δ, ἡ Δ πρὸς τὴν Α· καὶ ὡς ἄρα ἡ Δ πρὸς τὴν Α, ἡ Γ πρὸς τὴν Ε· τὸ ἄρα ὑπὸ τῶν Α, Γ ἴσον ἐστὶ τῷ ὑπὸ τῶν Δ, Ε. μέσον δὲ τὸ ὑπὸ τῶν Α, Γ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν Δ, Ε.
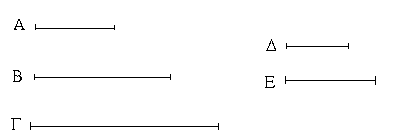
Εὕρηνται ἄρα μέσαι δυνάμει μόνον σύμμετροι μέσον περιέχουσαι· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Εὑρεῖν δύο τετραγώνους ἀριθμούς, ὥστε καὶ τὸν συγκείμενον ἐξ αὐτῶν εἶναι τετράγωνον.
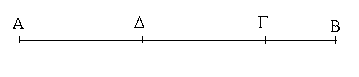
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΒ, ΒΓ, ἔστωσαν δὲ ἤτοι ἄρτιοι ἢ περιττοί. καὶ ἐπεί, ἐάν τε ἀπὸ ἀρτίου ἄρτιος ἀφαιρεθῇ, ἐάν τε ἀπὸ περισσοῦ περισσός, ὁ λοιπὸς ἄρτιός ἐστιν, ὁ λοιπὸς ἄρα ὁ ΑΓ ἄρτιός ἐστιν. τετμήσθω ὁ ΑΓ δίχα κατὰ τὸ Δ. ἔστωσαν δὲ καὶ οἱ ΑΒ, ΒΓ ἤτοι ὅμοιοι ἐπίπεδοι ἢ τετράγωνοι, οἳ καὶ αὐτοὶ ὅμοιοί εἰσιν ἐπίπεδοι· ὁ ἄρα ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ [τοῦ] ΓΔ τετραγώνου ἴσος ἐστὶ τῷ ἀπὸ τοῦ ΒΔ τετραγώνῳ. καί ἐστι τετράγωνος ὁ ἐκ τῶν ΑΒ, ΒΓ, ἐπειδήπερ ἐδείχθη, ὅτι, ἐὰν δύο ὅμοιοι ἐπίπεδοι πολλαπλασιάσαντες ἀλλήλους ποιῶσί τινα, ὁ γενόμενος τετράγωνός ἐστιν. εὕρηνται ἄρα δύο τετράγωνοι ἀριθμοὶ ὅ τε ἐκ τῶν ΑΒ, ΒΓ καὶ ὁ ἀπὸ τοῦ ΓΔ, οἳ συντεθέντες ποιοῦσι τὸν ἀπὸ τοῦ ΒΔ τετράγωνον.
Καὶ φανερόν, ὅτι εὕρηνται πάλιν δύο τετράγωνοι ὅ τε ἀπὸ τοῦ ΒΔ καὶ ὁ ἀπὸ τοῦ ΓΔ, ὥστε τὴν ὑπεροχὴν αὐτῶν τὸν ὑπὸ ΑΒ, ΒΓ εἶναι τετράγωνον, ὅταν οἱ ΑΒ, ΒΓ ὅμοιοι ὦσιν ἐπίπεδοι. ὅταν δὲ μὴ ὦσιν ὅμοιοι ἐπίπεδοι, εὕρηνται δύο τετράγωνοι ὅ τε ἀπὸ τοῦ ΒΔ καὶ ὁ ἀπὸ τοῦ ΔΓ, ὧν ἡ ὑπεροχὴ ὁ ὑπὸ τῶν ΑΒ, ΒΓ οὐκ ἔστι τετράγωνος· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Εὑρεῖν δύο τετραγώνους ἀριθμούς, ὥστε τὸν ἐξ αὐτῶν συγκείμενον μὴ εἶναι τετράγωνον.
Ἔστω γὰρ ὁ ἐκ τῶν ΑΒ, ΒΓ, ὡς ἔφαμεν, τετράγωνος, καὶ ἄρτιος ὁ ΓΑ, καὶ τετμήσθω ὁ ΓΑ δίχα τῷ Δ. φανερὸν δή, ὅτι ὁ ἐκ τῶν ΑΒ, ΒΓ τετράγωνος μετὰ τοῦ ἀπὸ [τοῦ] ΓΔ τετραγώνου ἴσος ἐστὶ τῷ ἀπὸ [τοῦ] ΒΔ τετραγώνῳ. ἀφῃρήσθω μονὰς ἡ ΔΕ· ὁ ἄρα ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ [τοῦ] ΓΕ ἐλάσσων ἐστὶ τοῦ ἀπὸ [τοῦ] ΒΔ τετραγώνου. λέγω οὖν, ὅτι ὁ ἐκ τῶν ΑΒ, ΒΓ τετράγωνος μετὰ τοῦ ἀπὸ [τοῦ] ΓΕ οὐκ ἔσται τετράγωνος.
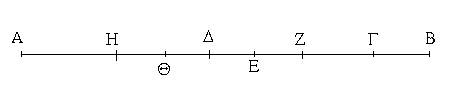
Εἰ γὰρ ἔσται τετράγωνος, ἤτοι ἴσος ἐστὶ τῷ ἀπὸ [τοῦ] ΒΕ ἢ ἐλάσσων τοῦ ἀπὸ [τοῦ] ΒΕ, οὐκέτι δὲ καὶ μείζων, ἵνα μὴ τμηθῇ ἡ μονάς. ἔστω, εἰ δυνατόν, πρότερον ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος τῷ ἀπὸ ΒΕ, καὶ ἔστω τῆς ΔΕ μονάδος διπλασίων ὁ ΗΑ. ἐπεὶ οὖν ὅλος ὁ ΑΓ ὅλου τοῦ ΓΔ ἐστι διπλασίων, ὧν ὁ ΑΗ τοῦ ΔΕ ἐστι διπλασίων, καὶ λοιπὸς ἄρα ὁ ΗΓ λοιποῦ τοῦ ΕΓ ἐστι διπλασίων· δίχα ἄρα τέτμηται ὁ ΗΓ τῷ Ε. ὁ ἄρα ἐκ τῶν ΗΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος ἐστὶ τῷ ἀπὸ ΒΕ τετραγώνῳ. ἀλλὰ καὶ ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος ὑπόκειται τῷ ἀπὸ [τοῦ] ΒΕ τετραγώνῳ· ὁ ἄρα ἐκ τῶν ΗΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος ἐστὶ τῷ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ. καὶ κοινοῦ ἀφαιρεθέντος τοῦ ἀπὸ ΓΕ συνάγεται ὁ ΑΒ ἴσος τῷ ΗΒ· ὅπερ ἄτοπον. οὐκ ἄρα ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ [τοῦ] ΓΕ ἴσος ἐστὶ τῷ ἀπὸ ΒΕ. λέγω δή, ὅτι οὐδὲ ἐλάσσων τοῦ ἀπὸ ΒΕ. εἰ γὰρ δυνατόν, ἔστω τῷ ἀπὸ ΒΖ ἴσος, καὶ τοῦ ΔΖ διπλασίων ὁ ΘΑ. καὶ συναχθήσεται πάλιν διπλασίων ὁ ΘΓ τοῦ ΓΖ· ὥστε καὶ τὸν ΓΘ δίχα τετμῆσθαι κατὰ τὸ Ζ, καὶ διὰ τοῦτο τὸν ἐκ τῶν ΘΒ, ΒΓ μετὰ τοῦ ἀπὸ ΖΓ ἴσον γίνεσθαι τῷ ἀπὸ ΒΖ. ὑπόκειται δὲ καὶ ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος τῷ ἀπὸ ΒΖ. ὥστε καὶ ὁ ἐκ τῶν ΘΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΖ ἴσος ἔσται τῷ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ· ὅπερ ἄτοπον. οὐκ ἄρα ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ ἴσος ἐστὶ [τῷ] ἐλάσσονι τοῦ ἀπὸ ΒΕ. ἐδείχθη δέ, ὅτι οὐδὲ [αὐτῷ] τῷ ἀπὸ ΒΕ. οὐκ ἄρα ὁ ἐκ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΕ τετράγωνός ἐστιν. [δυνατοῦ δὲ ὄντος καὶ κατὰ πλείονας τρόπους τοὺς εἰρημένους ἀριθμοὺς ἐπιδεικνύειν, ἀρκείσθωσαν ἡμῖν οἱ εἰρημένοι, ἵνα μὴ μακροτέρας οὔσης τῆς πραγματείας ἐπὶ πλέον αὐτὴν μηκύνωμεν.] ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον X
Εὑρεῖν δύο ῥητὰς δυνάμει μόνον συμμέτρους, ὥστε τὴν μείζονα τῆς ἐλάσσονος μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει.
Ἐκκείσθω γάρ τις ῥητὴ ἡ ΑΒ καὶ δύο τετράγωνοι ἀριθμοὶ οἱ ΓΔ, ΔΕ, ὥστε τὴν ὑπεροχὴν αὐτῶν τὸν ΓΕ μὴ εἶναι τετράγωνον, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΖΒ, καὶ πεποιήσθω ὡς ὁ ΔΓ πρὸς τὸν ΓΕ, οὕτως τὸ ἀπὸ τῆς ΒΑ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΑΖ τετράγωνον καὶ ἐπεζεύχθω ἡ ΖΒ.
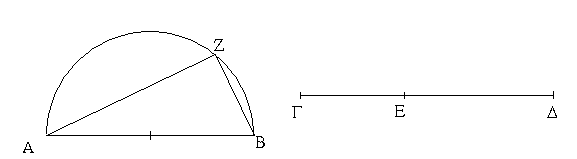
Ἐπεὶ [οὖν] ἐστιν ὡς τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΖ, οὕτως ὁ ΔΓ πρὸς τὸν ΓΕ, τὸ ἀπὸ τῆς ΒΑ ἄρα πρὸς τὸ ἀπὸ τῆς ΑΖ λόγον ἔχει, ὃν ἀριθμὸς ὁ ΔΓ πρὸς ἀριθμὸν τὸν ΓΕ· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΒΑ τῷ ἀπὸ τῆς ΑΖ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΑΒ· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΑΖ· ῥητὴ ἄρα καὶ ἡ ΑΖ. καὶ ἐπεὶ ὁ ΔΓ πρὸς τὸν ΓΕ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΒΑ ἄρα πρὸς τὸ ἀπὸ τῆς ΑΖ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΒ τῇ ΑΖ μήκει· αἱ ΒΑ, ΑΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ ἐπεί [ἐστιν] ὡς ὁ ΔΓ πρὸς τὸν ΓΕ, οὕτως τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΖ, ἀναστρέψαντι ἄρα ὡς ὁ ΓΔ πρὸς τὸν ΔΕ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΖ. ὁ δὲ ΓΔ πρὸς τὸν ΔΕ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΑΒ ἄρα πρὸς τὸ ἀπὸ τῆς ΒΖ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· σύμμετρος ἄρα ἐστὶν ἡ ΑΒ τῇ ΒΖ μήκει. καί ἐστι τὸ ἀπὸ τῆς ΑΒ ἴσον τοῖς ἀπὸ τῶν ΑΖ, ΖΒ· ἡ ΑΒ ἄρα τῆς ΑΖ μεῖζον δύναται τῇ ΒΖ συμμέτρῳ ἑαυτῇ.
Εὕρηνται ἄρα δύο ῥηταὶ δυνάμει μόνον σύμμετροι αἱ ΒΑ, ΑΖ, ὥστε τὴν μείζονα τὴν ΑΒ τῆς ἐλάσσονος τῆς ΑΖ μεῖζον δύνασθαι τῷ ἀπὸ τῆς ΒΖ συμμέτρου ἑαυτῇ μήκει· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον X
Εὑρεῖν δύο ῥητὰς δυνάμει μόνον συμμέτρους, ὥστε τὴν μείζονα τῆς ἐλάσσονος μεῖζον δύνασθαι τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει.
Ἐκκείσθω ῥητὴ ἡ ΑΒ καὶ δύο τετράγωνοι ἀριθμοὶ οἱ ΓΕ, ΕΔ, ὥστε τὸν συγκείμενον ἐξ αὐτῶν τὸν ΓΔ μὴ εἶναι τετράγωνον, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΖΒ, καὶ πεποιήσθω ὡς ὁ ΔΓ πρὸς τὸν ΓΕ, οὕτως τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΖ, καὶ ἐπεζεύχθω ἡ ΖΒ.
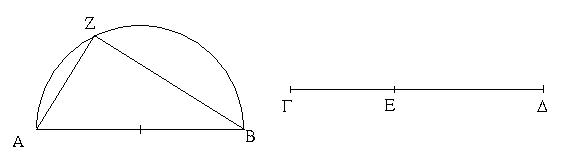
Ὁμοίως δὴ δείξομεν τῷ πρὸ τούτου, ὅτι αἱ ΒΑ, ΑΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ ἐπεί ἐστιν ὡς ὁ ΔΓ πρὸς τὸν ΓΕ, οὕτως τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΖ, ἀναστρέψαντι ἄρα ὡς ὁ ΓΔ πρὸς τὸν ΔΕ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΖ. ὁ δὲ ΓΔ πρὸς τὸν ΔΕ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΖ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΒ τῇ ΒΖ μήκει. καὶ δύναται ἡ ΑΒ τῆς ΑΖ μεῖζον τῷ ἀπὸ τῆς ΖΒ ἀσυμμέτρου ἑαυτῇ.
Αἱ ΑΒ, ΑΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΒ τῆς ΑΖ μεῖζον δύναται τῷ ἀπὸ τῆς ΖΒ συμμέτρου ἑαυτῇ μήκει· ὅπερ ἔδει δεῖξαι.
Πρότασις λα΄ 31 Βιβλίον X
Εὑρεῖν δύο μέσας δυνάμει μόνον συμμέτρους ῥητὸν περιεχούσας, ὥστε τὴν μείζονα τῆς ἐλάσσονος μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει.
Ἐκκείσθωσαν δύο ῥηταὶ δυνάμει μόνον σύμμετροι αἱ Α, Β, ὥστε τὴν Α μείζονα οὖσαν τῆς ἐλάσσονος τῆς Β μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. καὶ τῷ ὑπὸ τῶν Α, Β ἴσον ἔστω τὸ ἀπὸ τῆς Γ. μέσον δὲ τὸ ὑπὸ τῶν Α, Β· μέσον ἄρα καὶ τὸ ἀπὸ τῆς Γ· μέση ἄρα καὶ ἡ Γ. τῷ δὲ ἀπὸ τῆς Β ἴσον ἔστω τὸ ὑπὸ τῶν Γ, Δ. ῥητὸν δὲ τὸ ἀπὸ τῆς Β· ῥητὸν ἄρα καὶ τὸ ὑπὸ τῶν Γ, Δ. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως τὸ ὑπὸ τῶν Α, Β πρὸς τὸ ἀπὸ τῆς Β, ἀλλὰ τῷ μὲν ὑπὸ τῶν Α, Β ἴσον ἐστὶ τὸ ἀπὸ τῆς Γ, τῷ δὲ ἀπὸ τῆς Β ἴσον τὸ ὑπὸ τῶν Γ, Δ, ὡς ἄρα ἡ Α πρὸς τὴν Β, οὕτως τὸ ἀπὸ τῆς Γ πρὸς τὸ ὑπὸ τῶν Γ, Δ.
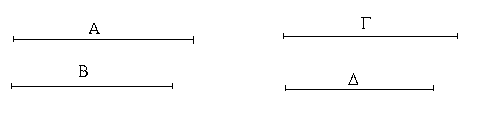
ὡς δὲ τὸ ἀπὸ τῆς Γ πρὸς τὸ ὑπὸ τῶν Γ, Δ, οὕτως ἡ Γ πρὸς τὴν Δ· καὶ ὡς ἄρα ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ. σύμμετρος δὲ ἡ Α τῇ Β δυνάμει μόνον· σύμμετρος ἄρα καὶ ἡ Γ τῇ Δ δυνάμει μόνον. καί ἐστι μέση ἡ Γ· μέση ἄρα καὶ ἡ Δ. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, ἡ Γ πρὸς τὴν Δ, ἡ δὲ Α τῆς Β μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ Γ ἄρα τῆς Δ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ.
Εὕρηνται ἄρα δύο μέσαι δυνάμει μόνον σύμμετροι αἱ Γ, Δ ῥητὸν περιέχουσαι, καὶ ἡ Γ τῆς Δ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει.
Ὁμοίως δὴ δειχθήσεται καὶ τῷ ἀπὸ ἀσυμμέτρου, ὅταν ἡ Α τῆς Β μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ.
Πρότασις λβ΄ 32 Βιβλίον X
Εὑρεῖν δύο μέσας δυνάμει μόνον συμμέτρους μέσον περιεχούσας, ὥστε τὴν μείζονα τῆς ἐλάσσονος μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ.
Ἐκκείσθωσαν τρεῖς ῥηταὶ δυνάμει μόνον σύμμετροι αἱ Α, Β, Γ, ὥστε τὴν Α τῆς Γ μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ τῷ μὲν ὑπὸ τῶν Α, Β ἴσον ἔστω τὸ ἀπὸ τῆς Δ. μέσον ἄρα τὸ ἀπὸ τῆς Δ· καὶ ἡ Δ ἄρα μέση ἐστίν. τῷ δὲ ὑπὸ τῶν Β, Γ ἴσον ἔστω τὸ ὑπὸ τῶν Δ, Ε. καὶ ἐπεί ἐστιν ὡς τὸ ὑπὸ τῶν Α, Β πρὸς τὸ ὑπὸ τῶν Β, Γ, οὕτως ἡ Α πρὸς τὴν Γ, ἀλλὰ τῷ μὲν ὑπὸ τῶν Α, Β ἴσον ἐστὶ τὸ ἀπὸ τῆς Δ, τῷ δὲ ὑπὸ τῶν Β, Γ ἴσον τὸ ὑπὸ τῶν Δ, Ε, ἔστιν ἄρα ὡς ἡ Α πρὸς τὴν Γ, οὕτως τὸ ἀπὸ τῆς Δ πρὸς τὸ ὑπὸ τῶν Δ, Ε.
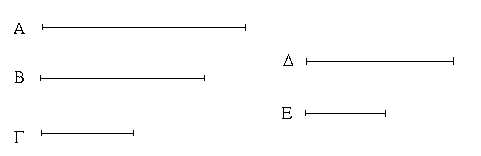
ὡς δὲ τὸ ἀπὸ τῆς Δ πρὸς τὸ ὑπὸ τῶν Δ, Ε, οὕτως ἡ Δ πρὸς τὴν Ε· καὶ ὡς ἄρα ἡ Α πρὸς τὴν Γ, οὕτως ἡ Δ πρὸς τὴν Ε· σύμμετρος δὲ ἡ Α τῇ Γ δυνάμει [μόνον]. σύμμετρος ἄρα καὶ ἡ Δ τῇ Ε δυνάμει μόνον. μέση δὲ ἡ Δ· μέση ἄρα καὶ ἡ Ε. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Γ, ἡ Δ πρὸς τὴν Ε, ἡ δὲ Α τῆς Γ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ Δ ἄρα τῆς Ε μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ. λέγω δή, ὅτι καὶ μέσον ἐστὶ τὸ ὑπὸ τῶν Δ, Ε. ἐπεὶ γὰρ ἴσον ἐστὶ τὸ ὑπὸ τῶν Β, Γ τῷ ὑπὸ τῶν Δ, Ε, μέσον δὲ τὸ ὑπὸ τῶν Β, Γ [αἱ γὰρ Β, Γ ῥηταί εἰσι δυνάμει μόνον σύμμετροι], μέσον ἄρα καὶ τὸ ὑπὸ τῶν Δ, Ε.
Εὕρηνται ἄρα δύο μέσαι δυνάμει μόνον σύμμετροι αἱ Δ, Ε μέσον περιέχουσαι, ὥστε τὴν μείζονα τῆς ἐλάσσονος μεῖζον δύνασθαι τῷ ἀπὸ συμμέτρου ἑαυτῇ.
Ὁμοίως δὴ πάλιν δειχθήσεται καὶ τῷ ἀπὸ ἀσυμμέτρου, ὅταν ἡ Α τῆς Γ μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ.
Λῆμμα
Ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν Α, καὶ ἤχθω κάθετος ἡ ΑΔ· λέγω, ὅτι τὸ μὲν ὑπὸ τῶν ΓΒΔ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΒΑ, τὸ δὲ ὑπὸ τῶν ΒΓΔ ἴσον τῷ ἀπὸ τῆς ΓΑ, καὶ τὸ ὑπὸ τῶν ΒΔ, ΔΓ ἴσον τῷ ἀπὸ τῆς ΑΔ, καὶ ἔτι τὸ ὑπὸ τῶν ΒΓ, ΑΔ ἴσον [ἐστὶ] τῷ ὑπὸ τῶν ΒΑ, ΑΓ.
Καὶ πρῶτον, ὅτι τὸ ὑπὸ τῶν ΓΒΔ ἴσον [ἐστὶ] τῷ ἀπὸ τῆς ΒΑ.
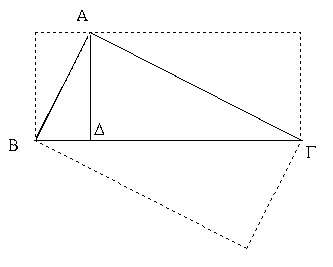
Ἐπεὶ γὰρ ἐν ὀρθογωνίῳ τριγώνῳ ἀπὸ τῆς ὀρθῆς γωνίας ἐπὶ τὴν βάσιν κάθετος ἦκται ἡ ΑΔ, τὰ ΑΒΔ, ΑΔΓ ἄρα τρίγωνα ὅμοιά ἐστι τῷ τε ὅλῳ τῷ ΑΒΓ καὶ ἀλλήλοις. καὶ ἐπεὶ ὅμοιόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΑΒΔ τριγώνῳ, ἔστιν ἄρα ὡς ἡ ΓΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΒΑ πρὸς τὴν ΒΔ· τὸ ἄρα ὑπὸ τῶν ΓΒΔ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ.
Διὰ τὰ αὐτὰ δὴ καὶ τὸ ὑπὸ τῶν ΒΓΔ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ.
Καὶ ἐπεί, ἐὰν ἐν ὀρθογωνίῳ τριγώνῳ ἀπὸ τῆς ὀρθῆς γωνίας ἐπὶ τὴν βάσιν κάθετος ἀχθῇ, ἡ ἀχθεῖσα τῶν τῆς βάσεως τμημάτων μέση ἀνάλογόν ἐστιν, ἔστιν ἄρα ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΑΔ πρὸς τὴν ΔΓ· τὸ ἄρα ὑπὸ τῶν ΒΔ, ΔΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΑ.
Λέγω, ὅτι καὶ τὸ ὑπὸ τῶν ΒΓ, ΑΔ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΒΑ, ΑΓ. ἐπεὶ γάρ, ὡς ἔφαμεν, ὅμοιόν ἐστι τὸ ΑΒΓ τῷ ΑΒΔ, ἔστιν ἄρα ὡς ἡ ΒΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΔ. [ἐὰν δὲ τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, τὸ ὑπὸ τῶν ἄκρων ἴσον ἐστὶ τῷ ὑπὸ τῶν μέσων.] τὸ ἄρα ὑπὸ τῶν ΒΓ, ΑΔ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΒΑ, ΑΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον X
Εὑρεῖν δύο εὐθείας δυνάμει ἀσυμμέτρους ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον.
Ἐκκείσθωσαν δύο ῥηταὶ δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ, ὥστε τὴν μείζονα τὴν ΑΒ τῆς ἐλάσσονος τῆς ΒΓ μεῖζον δύνασθαι τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ τετμήσθω ἡ ΒΓ δίχα κατὰ τὸ Δ, καὶ τῷ ἀφ' ὁποτέρας τῶν ΒΔ, ΔΓ ἴσον παρὰ τὴν ΑΒ παραβεβλήσθω παραλληλόγραμμον ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΕΒ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΖΒ, καὶ ἤχθω τῇ ΑΒ πρὸς ὀρθὰς ἡ ΕΖ, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΖΒ.
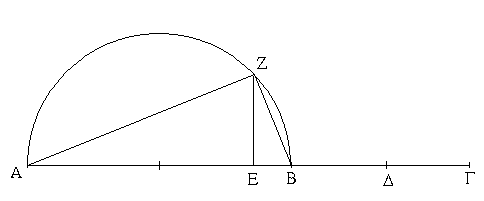
Καὶ ἐπεὶ [δύο] εὐθεῖαι ἄνισοί εἰσιν αἱ ΑΒ, ΒΓ, καὶ ἡ ΑΒ τῆς ΒΓ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, τῷ δὲ τετάρτῳ τοῦ ἀπὸ τῆς ΒΓ, τουτέστι τῷ ἀπὸ τῆς ἡμισείας αὐτῆς, ἴσον παρὰ τὴν ΑΒ παραβέβληται παραλληλόγραμμον ἐλλεῖπον εἴδει τετραγώνῳ καὶ ποιεῖ τὸ ὑπὸ τῶν ΑΕΒ, ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΕ τῇ ΕΒ. καί ἐστιν ὡς ἡ ΑΕ πρὸς ΕΒ, οὕτως τὸ ὑπὸ τῶν ΒΑ, ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΒ, ΒΕ, ἴσον δὲ τὸ μὲν ὑπὸ τῶν ΒΑ, ΑΕ τῷ ἀπὸ τῆς ΑΖ, τὸ δὲ ὑπὸ τῶν ΑΒ, ΒΕ τῷ ἀπὸ τῆς ΒΖ· ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΖ τῷ ἀπὸ τῆς ΖΒ· αἱ ΑΖ, ΖΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι. καὶ ἐπεὶ ἡ ΑΒ ῥητή ἐστιν, ῥητὸν ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΒ· ὥστε καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΖ, ΖΒ ῥητόν ἐστιν. καὶ ἐπεὶ πάλιν τὸ ὑπὸ τῶν ΑΕ, ΕΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΖ, ὑπόκειται δὲ τὸ ὑπὸ τῶν ΑΕ, ΕΒ καὶ τῷ ἀπὸ τῆς ΒΔ ἴσον, ἴση ἄρα ἐστὶν ἡ ΖΕ τῇ ΒΔ· διπλῆ ἄρα ἡ ΒΓ τῆς ΖΕ· ὥστε καὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ σύμμετρόν ἐστι τῷ ὑπὸ τῶν ΑΒ, ΕΖ. μέσον δὲ τὸ ὑπὸ τῶν ΑΒ, ΒΓ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν ΑΒ, ΕΖ. ἴσον δὲ τὸ ὑπὸ τῶν ΑΒ, ΕΖ τῷ ὑπὸ τῶν ΑΖ, ΖΒ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν ΑΖ, ΖΒ. ἐδείχθη δὲ καὶ ῥητὸν τὸ συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων.
Εὕρηνται ἄρα δύο εὐθεῖαι δυνάμει ἀσύμμετροι αἱ ΑΖ, ΖΒ ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δὲ ὑπ' αὐτῶν μέσον· ὅπερ ἔδει δεῖξαι.
Πρότασις λδ΄ 34 Βιβλίον X
Εὑρεῖν δύο εὐθείας δυνάμει ἀσυμμέτρους ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν.
Ἐκκείσθωσαν δύο μέσαι δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ ῥητὸν περιέχουσαι τὸ ὑπ' αὐτῶν, ὥστε τὴν ΑΒ τῆς ΒΓ μεῖζον δύνασθαι τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ τὸ ΑΔΒ ἡμικύκλιον, καὶ τετμήσθω ἡ ΒΓ δίχα κατὰ τὸ Ε, καὶ παραβεβλήσθω παρὰ τὴν ΑΒ τῷ ἀπὸ τῆς ΒΕ ἴσον παραλληλόγραμμον ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΑΖΒ· ἀσύμμετρος ἄρα [ἐστὶν] ἡ ΑΖ τῇ ΖΒ μήκει. καὶ ἤχθω ἀπὸ τοῦ Ζ τῇ ΑΒ πρὸς ὀρθὰς ἡ ΖΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΒ.
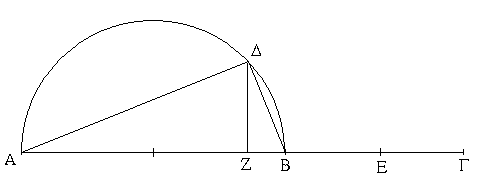
Ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΖ τῇ ΖΒ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΒΑ, ΑΖ τῷ ὑπὸ τῶν ΑΒ, ΒΖ. ἴσον δὲ τὸ μὲν ὑπὸ τῶν ΒΑ, ΑΖ τῷ ἀπὸ τῆς ΑΔ, τὸ δὲ ὑπὸ τῶν ΑΒ, ΒΖ τῷ ἀπὸ τῆς ΔΒ· ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΔ τῷ ἀπὸ τῆς ΔΒ. καὶ ἐπεὶ μέσον ἐστὶ τὸ ἀπὸ τῆς ΑΒ, μέσον ἄρα καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΒΓ τῆς ΔΖ, διπλάσιον ἄρα καὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ τοῦ ὑπὸ τῶν ΑΒ, ΖΔ. ῥητὸν δὲ τὸ ὑπὸ τῶν ΑΒ, ΒΓ· ῥητὸν ἄρα καὶ τὸ ὑπὸ τῶν ΑΒ, ΖΔ. τὸ δὲ ὑπὸ τῶν ΑΒ, ΖΔ ἴσον τῷ ὑπὸ τῶν ΑΔ, ΔΒ· ὥστε καὶ τὸ ὑπὸ τῶν ΑΔ, ΔΒ ῥητόν ἐστιν.
Εὕρηνται ἄρα δύο εὐθεῖαι δυνάμει ἀσύμμετροι αἱ ΑΔ, ΔΒ ποιοῦσαι τὸ [μὲν] συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν· ὅπερ ἔδει δεῖξαι.
Πρότασις λε΄ 35 Βιβλίον X
Εὑρεῖν δύο εὐθείας δυνάμει ἀσυμμέτρους ποιούσας τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τῷ συγκειμένῳ ἐκ τῶν ἀπ' αὐτῶν τετραγώνῳ.
Ἐκκείσθωσαν δύο μέσαι δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ μέσον περιέχουσαι, ὥστε τὴν ΑΒ τῆς ΒΓ μεῖζον δύνασθαι τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ τὰ λοιπὰ γεγονέτω τοῖς ἐπάνω ὁμοίως.
Καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΖ τῇ ΖΒ μήκει, ἀσύμμετρός ἐστι καὶ ἡ ΑΔ τῇ ΔΒ δυνάμει.
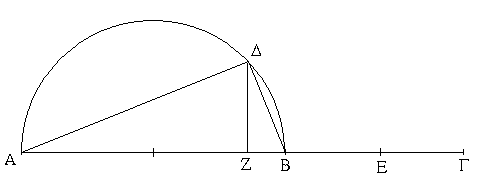
καὶ ἐπεὶ μέσον ἐστὶ τὸ ἀπὸ τῆς ΑΒ, μέσον ἄρα καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΖ, ΖΒ ἴσον ἐστὶ τῷ ἀφ' ἑκατέρας τῶν ΒΕ, ΔΖ, ἴση ἄρα ἐστὶν ἡ ΒΕ τῇ ΔΖ· διπλῆ ἄρα ἡ ΒΓ τῆς ΖΔ· ὥστε καὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ διπλάσιόν ἐστι τοῦ ὑπὸ τῶν ΑΒ, ΖΔ. μέσον δὲ τὸ ὑπὸ τῶν ΑΒ, ΒΓ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν ΑΒ, ΖΔ. καί ἐστιν ἴσον τῷ ὑπὸ τῶν ΑΔ, ΔΒ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, σύμμετρος δὲ ἡ ΓΒ τῇ ΒΕ, ἀσύμμετρος ἄρα καὶ ἡ ΑΒ τῇ ΒΕ μήκει· ὥστε καὶ τὸ ἀπὸ τῆς ΑΒ τῷ ὑπὸ τῶν ΑΒ, ΒΕ ἀσύμμετρόν ἐστιν. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΒ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ, τῷ δὲ ὑπὸ τῶν ΑΒ, ΒΕ ἴσον ἐστὶ τὸ ὑπὸ τῶν ΑΒ, ΖΔ, τουτέστι τὸ ὑπὸ τῶν ΑΔ, ΔΒ· ἀσύμμετρον ἄρα ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ τῷ ὑπὸ τῶν ΑΔ, ΔΒ.
Εὕρηνται ἄρα δύο εὐθεῖαι αἱ ΑΔ, ΔΒ δυνάμει ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τῷ συγκειμένῳ ἐκ τῶν ἀπ' αὐτῶν τετραγώνων· ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον X
Ἐὰν δύο ῥηταὶ δυνάμει μόνον σύμμετροι συντεθῶσιν, ἡ ὅλη ἄλογός ἐστιν, καλείσθω δὲ ἐκ δύο ὀνομάτων.
Συγκείσθωσαν γὰρ δύο ῥηταὶ δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ· λέγω, ὅτι ὅλη ἡ ΑΓ ἄλογός ἐστιν.
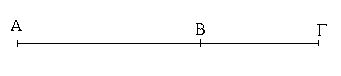
Ἐπεὶ γὰρ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει· δυνάμει γὰρ μόνον εἰσὶ σύμμετροι· ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ὑπὸ τῶν ΑΒΓ πρὸς τὸ ἀπὸ τῆς ΒΓ, ἀσύμμετρον ἄρα ἐστὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ τῷ ἀπὸ τῆς ΒΓ. ἀλλὰ τῷ μὲν ὑπὸ τῶν ΑΒ, ΒΓ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, τῷ δὲ ἀπὸ τῆς ΒΓ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ· αἱ γὰρ ΑΒ, ΒΓ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀσύμμετρον ἄρα ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ τοῖς ἀπὸ τῶν ΑΒ, ΒΓ. καὶ συνθέντι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ μετὰ τῶν ἀπὸ τῶν ΑΒ, ΒΓ, τουτέστι τὸ ἀπὸ τῆς ΑΓ, ἀσύμμετρόν ἐστι τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ. ῥητὸν δὲ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ· ἄλογον ἄρα [ἐστὶ] τὸ ἀπὸ τῆς ΑΓ· ὥστε καὶ ἡ ΑΓ ἄλογός ἐστιν, καλείσθω δὲ ἐκ δύο ὀνομάτων· ὅπερ ἔδει δεῖξαι.
Πρότασις λζ΄ 37 Βιβλίον X
Ἐὰν δύο μέσαι δυνάμει μόνον σύμμετροι συντεθῶσι ῥητὸν περιέχουσαι, ἡ ὅλη ἄλογός ἐστιν, καλείσθω δὲ ἐκ δύο μέσων πρώτη.
Συγκείσθωσαν γὰρ δύο μέσαι δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ ῥητὸν περιέχουσαι· λέγω, ὅτι ὅλη ἡ ΑΓ ἄλογός ἐστιν.
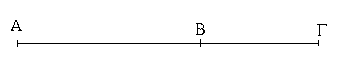
Ἐπεὶ γὰρ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, καὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ ἄρα ἀσύμμετρά ἐστι τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· καὶ συνθέντι τὰ ἀπὸ τῶν ΑΒ, ΒΓ μετὰ τοῦ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΑΓ, ἀσύμμετρόν ἐστι τῷ ὑπὸ τῶν ΑΒ, ΒΓ. ῥητὸν δὲ τὸ ὑπὸ τῶν ΑΒ, ΒΓ· ὑπόκεινται γὰρ αἱ ΑΒ, ΒΓ ῥητὸν περιέχουσαι· ἄλογον ἄρα τὸ ἀπὸ τῆς ΑΓ· ἄλογος ἄρα ἡ ΑΓ, καλείσθω δὲ ἐκ δύο μέσων πρώτη· ὅπερ ἔδει δεῖξαι.
Πρότασις λη΄ 38 Βιβλίον X
Ἐὰν δύο μέσαι δυνάμει μόνον σύμμετροι συντεθῶσι μέσον περιέχουσαι, ἡ ὅλη ἄλογός ἐστιν, καλείσθω δὲ ἐκ δύο μέσων δευτέρα.
Συγκείσθωσαν γὰρ δύο μέσαι δυνάμει μόνον σύμμετροι αἱ ΑΒ, ΒΓ μέσον περιέχουσαι· λέγω, ὅτι ἄλογός ἐστιν ἡ ΑΓ.
Ἐκκείσθω γὰρ ῥητὴ ἡ ΔΕ, καὶ τῷ ἀπὸ τῆς ΑΓ ἴσον παρὰ τὴν ΔΕ παραβεβλήσθω τὸ ΔΖ πλάτος ποιοῦν τὴν ΔΗ. καὶ ἐπεὶ τὸ ἀπὸ τῆς ΑΓ ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΒ, ΒΓ καὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, παραβεβλήσθω δὴ τοῖς ἀπὸ τῶν ΑΒ, ΒΓ παρὰ τὴν ΔΕ ἴσον τὸ ΕΘ· λοιπὸν ἄρα τὸ ΘΖ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. καὶ ἐπεὶ μέση ἐστὶν ἑκατέρα τῶν ΑΒ, ΒΓ, μέσα ἄρα ἐστὶ καὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ.
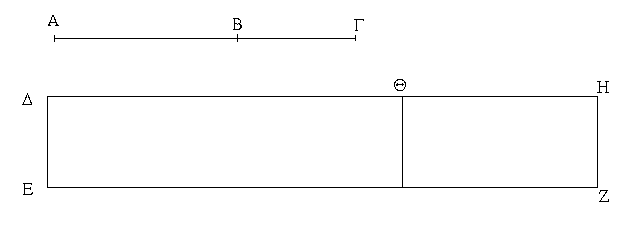
μέσον δὲ ὑπόκειται καὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. καί ἐστι τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ ἴσον τὸ ΕΘ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ἴσον τὸ ΖΘ· μέσον ἄρα ἑκάτερον τῶν ΕΘ, ΘΖ. καὶ παρὰ ῥητὴν τὴν ΔΕ παράκειται· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΔΘ, ΘΗ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. ἐπεὶ οὖν ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, καί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ὑπὸ τῶν ΑΒ, ΒΓ, ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τῷ ὑπὸ τῶν ΑΒ, ΒΓ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΒ σύμμετρόν ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τετραγώνων, τῷ δὲ ὑπὸ τῶν ΑΒ, ΒΓ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. ἀσύμμετρον ἄρα ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ ἴσον ἐστὶ τὸ ΕΘ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ἴσον ἐστὶ τὸ ΘΖ. ἀσύμμετρον ἄρα ἐστὶ τὸ ΕΘ τῷ ΘΖ· ὥστε καὶ ἡ ΔΘ τῇ ΘΗ ἐστιν ἀσύμμετρος μήκει. αἱ ΔΘ, ΘΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ὥστε ἡ ΔΗ ἄλογός ἐστιν. ῥητὴ δὲ ἡ ΔΕ· τὸ δὲ ὑπὸ ἀλόγου καὶ ῥητῆς περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν· ἄλογον ἄρα ἐστὶ τὸ ΔΖ χωρίον, καὶ ἡ δυναμένη [αὐτὸ] ἄλογός ἐστιν. δύναται δὲ τὸ ΔΖ ἡ ΑΓ· ἄλογος ἄρα ἐστὶν ἡ ΑΓ, καλείσθω δὲ ἐκ δύο μέσων δευτέρα. ὅπερ ἔδει δεῖξαι.
Πρότασις λθ΄ 39 Βιβλίον X
Ἐὰν δύο εὐθεῖαι δυνάμει ἀσύμμετροι συντεθῶσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον, ἡ ὅλη εὐθεῖα ἄλογός ἐστιν, καλείσθω δὲ μείζων.
Συγκείσθωσαν γὰρ δύο εὐθεῖαι δυνάμει ἀσύμμετροι αἱ ΑΒ, ΒΓ ποιοῦσαι τὰ προκείμενα· λέγω, ὅτι ἄλογός ἐστιν ἡ ΑΓ.
Ἐπεὶ γὰρ τὸ ὑπὸ τῶν ΑΒ, ΒΓ μέσον ἐστίν, καὶ τὸ δὶς [ἄρα] ὑπὸ τῶν ΑΒ, ΒΓ μέσον ἐστίν. τὸ δὲ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ ῥητόν· ἀσύμμετρον ἄρα ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ· ὥστε καὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ μετὰ τοῦ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΑΓ, ἀσύμμετρόν ἐστι τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ [ῥητὸν δὲ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ]· ἄλογον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΓ. ὥστε καὶ ἡ ΑΓ ἄλογός ἐστιν, καλείσθω δὲ μείζων. ὅπερ ἔδει δεῖξαι.
Πρότασις μ΄ 40 Βιβλίον X
Ἐὰν δύο εὐθεῖαι δυνάμει ἀσύμμετροι συντεθῶσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν, ἡ ὅλη εὐθεῖα ἄλογός ἐστιν, καλείσθω δὲ ῥητὸν καὶ μέσον δυναμένη.
Συγκείσθωσαν γὰρ δύο εὐθεῖαι δυνάμει ἀσύμμετροι αἱ ΑΒ, ΒΓ ποιοῦσαι τὰ προκείμενα· λέγω, ὅτι ἄλογός ἐστιν ἡ ΑΓ.
Ἐπεὶ γὰρ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ μέσον ἐστίν, τὸ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ῥητόν, ἀσύμμετρον ἄρα ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ὥστε καὶ τὸ ἀπὸ τῆς ΑΓ ἀσύμμετρόν ἐστι τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. ῥητὸν δὲ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἄλογον ἄρα τὸ ἀπὸ τῆς ΑΓ. ἄλογος ἄρα ἡ ΑΓ, καλείσθω δὲ ῥητὸν καὶ μέσον δυναμένη. ὅπερ ἔδει δεῖξαι.
Πρότασις μα΄ 41 Βιβλίον X
Ἐὰν δύο εὐθεῖαι δυνάμει ἀσύμμετροι συντεθῶσι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τῷ συγκειμένῳ ἐκ τῶν ἀπ' αὐτῶν τετραγώνων, ἡ ὅλη εὐθεῖα ἄλογός ἐστιν, καλείσθω δὲ δύο μέσα δυναμένη.
Συγκείσθωσαν γὰρ δύο εὐθεῖαι δυνάμει ἀσύμμετροι αἱ ΑΒ, ΒΓ ποιοῦσαι τὰ προκείμενα· λέγω, ὅτι ἡ ΑΓ ἄλογός ἐστιν.
Ἐκκείσθω ῥητὴ ἡ ΔΕ, καὶ παραβεβλήσθω παρὰ τὴν ΔΕ τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ ἴσον τὸ ΔΖ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ἴσον τὸ ΗΘ· ὅλον ἄρα τὸ ΔΘ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ τετραγώνῳ.
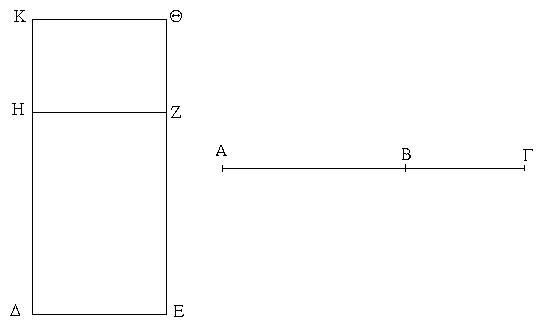
καὶ ἐπεὶ μέσον ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ, καί ἐστιν ἴσον τῷ ΔΖ, μέσον ἄρα ἐστὶ καὶ τὸ ΔΖ. καὶ παρὰ ῥητὴν τὴν ΔΕ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΔΗ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΗΚ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΗΖ, τουτέστι τῇ ΔΕ, μήκει. καὶ ἐπεὶ ἀσύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, ἀσύμμετρόν ἐστι τὸ ΔΖ τῷ ΗΘ· ὥστε καὶ ἡ ΔΗ τῇ ΗΚ ἀσύμμετρός ἐστιν. καί εἰσι ῥηταί· αἱ ΔΗ, ΗΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἄλογος ἄρα ἐστὶν ἡ ΔΚ ἡ καλουμένη ἐκ δύο ὀνομάτων. ῥητὴ δὲ ἡ ΔΕ· ἄλογον ἄρα ἐστὶ τὸ ΔΘ καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν. δύναται δὲ τὸ ΘΔ ἡ ΑΓ· ἄλογος ἄρα ἐστὶν ἡ ΑΓ, καλείσθω δὲ δύο μέσα δυναμένη. ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ὅτι δὲ αἱ εἰρημέναι ἄλογοι μοναχῶς διαιροῦνται εἰς τὰς εὐθείας, ἐξ ὧν σύγκεινται ποιουσῶν τὰ προκείμενα εἴδη, δείξομεν ἤδη προεκθέμενοι λημμάτιον τοιοῦτον·
Ἐκκείσθω εὐθεῖα ἡ ΑΒ καὶ τετμήσθω ἡ ὅλη εἰς ἄνισα καθ᾿ ἑκάτερον τῶν Γ, Δ, ὑποκείσθω δὲ μείζων ἡ ΑΓ τῆς ΔΒ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΓ, ΓΒ μείζονά ἐστι τῶν ἀπὸ τῶν ΑΔ, ΔΒ.
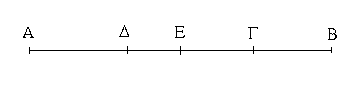
Τετμήσθω γὰρ ἡ ΑΒ δίχα κατὰ τὸ Ε. καὶ ἐπεὶ μείζων ἐστὶν ἡ ΑΓ τῆς ΔΒ, κοινὴ ἀφῃρήσθω ἡ ΔΓ· λοιπὴ ἄρα ἡ ΑΔ λοιπῆς τῆς ΓΒ μείζων ἐστίν. ἴση δὲ ἡ ΑΕ τῇ ΕΒ· ἐλάττων ἄρα ἡ ΔΕ τῆς ΕΓ· τὰ Γ, Δ ἄρα σημεῖα οὐκ ἴσον ἀπέχουσι τῆς διχοτομίας. καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΓ, ΓΒ μετὰ τοῦ ἀπὸ τῆς ΕΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΒ, ἀλλὰ μὴν καὶ τὸ ὑπὸ τῶν ΑΔ, ΔΒ μετὰ τοῦ ἀπὸ ΔΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΒ, τὸ ἄρα ὑπὸ τῶν ΑΓ, ΓΒ μετὰ τοῦ ἀπὸ τῆς ΕΓ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΔ, ΔΒ μετὰ τοῦ ἀπὸ τῆς ΔΕ· ὧν τὸ ἀπὸ τῆς ΔΕ ἔλασσόν ἐστι τοῦ ἀπὸ τῆς ΕΓ· καὶ λοιπὸν ἄρα τὸ ὑπὸ τῶν ΑΓ, ΓΒ ἔλασσόν ἐστι τοῦ ὑπὸ τῶν ΑΔ, ΔΒ. ὥστε καὶ τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἔλασσόν ἐστι τοῦ δὶς ὑπὸ ΑΔ, ΔΒ. καὶ λοιπὸν ἄρα τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ μεῖζόν ἐστι τοῦ συγκειμένου ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις μβ΄ 42 Βιβλίον X
Ἡ ἐκ δύο ὀνομάτων κατὰ ἓν μόνον σημεῖον διαιρεῖται εἰς τὰ ὀνόματα.
Ἔστω ἐκ δύο ὀνομάτων ἡ ΑΒ διῃρημένη εἰς τὰ ὀνόματα κατὰ τὸ Γ· αἱ ΑΓ, ΓΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται εἰς δύο ῥητὰς δυνάμει μόνον συμμέτρους.
Εἰ γὰρ δυνατόν, διῃρήσθω καὶ κατὰ τὸ Δ, ὥστε καὶ τὰς ΑΔ, ΔΒ ῥητὰς εἶναι δυνάμει μόνον συμμέτρους. φανερὸν δή, ὅτι ἡ ΑΓ τῇ ΔΒ οὐκ ἔστιν ἡ αὐτή. εἰ γὰρ δυνατόν, ἔστω. ἔσται δὴ καὶ ἡ ΑΔ τῇ ΓΒ ἡ αὐτή· καὶ ἔσται ὡς ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως ἡ ΒΔ πρὸς τὴν ΔΑ, καὶ ἔσται ἡ ΑΒ κατὰ τὸ αὐτὸ τῇ κατὰ τὸ Γ διαιρέσει διαιρεθεῖσα καὶ κατὰ τὸ Δ· ὅπερ οὐχ ὑπόκειται. οὐκ ἄρα ἡ ΑΓ τῇ ΔΒ ἐστιν ἡ αὐτή.
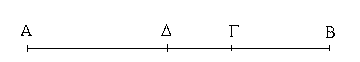
διὰ δὴ τοῦτο καὶ τὰ Γ, Δ σημεῖα οὐκ ἴσον ἀπέχουσι τῆς διχοτομίας. ᾧ ἄρα διαφέρει τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ, τούτῳ διαφέρει καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ διὰ τὸ καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ μετὰ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ μετὰ τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ἴσα εἶναι τῷ ἀπὸ τῆς ΑΒ. ἀλλὰ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ διαφέρει ῥητῷ· ῥητὰ γὰρ ἀμφότερα· καὶ τὸ δὶς ἄρα ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ διαφέρει ῥητῷ μέσα ὄντα· ὅπερ ἄτοπον· μέσον γὰρ μέσου οὐχ ὑπερέχει ῥητῷ.
Οὐκ ἄρα ἡ ἐκ δύο ὀνομάτων κατ' ἄλλο καὶ ἄλλο σημεῖον διαιρεῖται· καθ᾿ ἓν ἄρα μόνον· ὅπερ ἔδει δεῖξαι.
Πρότασις μγ΄ 43 Βιβλίον X
Ἡ ἐκ δύο μέσων πρώτη καθ᾿ ἓν μόνον σημεῖον διαιρεῖται.
Ἔστω ἐκ δύο μέσων πρώτη ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε τὰς ΑΓ, ΓΒ μέσας εἶναι δυνάμει μόνον συμμέτρους ῥητὸν περιεχούσας· λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται.
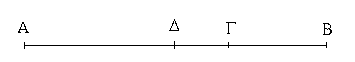
Εἰ γὰρ δυνατόν, διῃρήσθω καὶ κατὰ τὸ Δ, ὥστε καὶ τὰς ΑΔ, ΔΒ μέσας εἶναι δυνάμει μόνον συμμέτρους ῥητὸν περιεχούσας. ἐπεὶ οὖν, ᾧ διαφέρει τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, τούτῳ διαφέρει τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ, ῥητῷ δὲ διαφέρει τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ· ῥητὰ γὰρ ἀμφότερα· ῥητῷ ἄρα διαφέρει καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ μέσα ὄντα· ὅπερ ἄτοπον.
Οὐκ ἄρα ἡ ἐκ δύο μέσων πρώτη κατ' ἄλλο καὶ ἄλλο σημεῖον διαιρεῖται εἰς τὰ ὀνόματα· καθ᾿ ἓν ἄρα μόνον· ὅπερ ἔδει δεῖξαι
Πρότασις μδ΄ 44 Βιβλίον X
Ἡ ἐκ μέσων δευτέρα καθ᾿ ἓν μόνον σημεῖον διαιρεῖται.
Ἔστω ἐκ δύο μέσων δευτέρα ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε τὰς ΑΓ, ΓΒ μέσας εἶναι δυνάμει μόνον συμμέτρους μέσον περιεχούσας· φανερὸν δή, ὅτι τὸ Γ οὐκ ἔστι κατὰ τῆς διχοτομίας, ὅτι οὐκ εἰσὶ μήκει σύμμετροι. λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται.
Εἰ γὰρ δυνατόν, διῃρήσθω καὶ κατὰ τὸ Δ, ὥστε τὴν ΑΓ τῇ ΔΒ μὴ εἶναι τὴν αὐτήν, ἀλλὰ μείζονα καθ᾿ ὑπόθεσιν τὴν ΑΓ· δῆλον δή, ὅτι καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ, ὡς ἐπάνω ἐδείξαμεν, ἐλάσσονα τῶν ἀπὸ τῶν ΑΓ, ΓΒ· καὶ τὰς ΑΔ, ΔΒ μέσας εἶναι δυνάμει μόνον συμμέτρους μέσον περιεχούσας. καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τῷ μὲν ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΕΖ παραλληλόγραμμον ὀρθογώνιον παραβεβλήσθω τὸ ΕΚ, τοῖς δὲ ἀπὸ τῶν ΑΓ, ΓΒ ἴσον ἀφῃρήσθω τὸ ΕΗ· λοιπὸν ἄρα τὸ ΘΚ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. πάλιν δὴ τοῖς ἀπὸ τῶν ΑΔ, ΔΒ, ἅπερ ἐλάσσονα ἐδείχθη τῶν ἀπὸ τῶν ΑΓ, ΓΒ, ἴσον ἀφῃρήσθω τὸ ΕΛ· καὶ λοιπὸν ἄρα τὸ ΜΚ ἴσον τῷ δὶς ὑπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεὶ μέσα ἐστὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ, μέσον ἄρα [καὶ] τὸ ΕΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΕΘ καὶ ἀσύμμετρος τῇ ΕΖ μήκει.
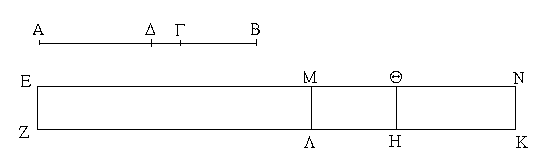
διὰ τὰ αὐτὰ δὴ καὶ ἡ ΘΝ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ αἱ ΑΓ, ΓΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι, ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΓ τῇ ΓΒ μήκει. ὡς δὲ ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως τὸ ἀπὸ τῆς ΑΓ πρὸς τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΓ τῷ ὑπὸ τῶν ΑΓ, ΓΒ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΓ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΓ, ΓΒ· δυνάμει γάρ εἰσι σύμμετροι αἱ ΑΓ, ΓΒ. τῷ δὲ ὑπὸ τῶν ΑΓ, ΓΒ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ ἄρα ἀσύμμετρά ἐστι τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΑΓ, ΓΒ ἴσον ἐστὶ τὸ ΕΗ, τῷ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον τὸ ΘΚ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΕΗ τῷ ΘΚ· ὥστε καὶ ἡ ΕΘ τῇ ΘΝ ἀσύμμετρός ἐστι μήκει. καί εἰσι ῥηταί· αἱ ΕΘ, ΘΝ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ἐὰν δὲ δύο ῥηταὶ δυνάμει μόνον σύμμετροι συντεθῶσιν, ἡ ὅλη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο ὀνομάτων· ἡ ΕΝ ἄρα ἐκ δύο ὀνομάτων ἐστὶ διῃρημένη κατὰ τὸ Θ. κατὰ τὰ αὐτὰ δὴ δειχθήσονται καὶ αἱ ΕΜ, ΜΝ ῥηταὶ δυνάμει μόνον σύμμετροι· καὶ ἔσται ἡ ΕΝ ἐκ δύο ὀνομάτων κατ' ἄλλο καὶ ἄλλο διῃρημένη τό τε Θ καὶ τὸ Μ, καὶ οὐκ ἔστιν ἡ ΕΘ τῇ ΜΝ ἡ αὐτή, ὅτι τὰ ἀπὸ τῶν ΑΓ, ΓΒ μείζονά ἐστι τῶν ἀπὸ τῶν ΑΔ, ΔΒ. ἀλλὰ τὰ ἀπὸ τῶν ΑΔ, ΔΒ μείζονά ἐστι τοῦ δὶς ὑπὸ ΑΔ, ΔΒ· πολλῷ ἄρα καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ, τουτέστι τὸ ΕΗ, μεῖζόν ἐστι τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ, τουτέστι τοῦ ΜΚ· ὥστε καὶ ἡ ΕΘ τῆς ΜΝ μείζων ἐστίν. ἡ ἄρα ΕΘ τῇ ΜΝ οὐκ ἔστιν ἡ αὐτή· ὅπερ ἔδει δεῖξαι.
Πρότασις με΄ 45 Βιβλίον X
Ἡ μείζων κατὰ τὸ αὐτὸ μόνον σημεῖον διαιρεῖται.
Ἔστω μείζων ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε τὰς ΑΓ, ΓΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνων ῥητόν, τὸ δ' ὑπὸ τῶν ΑΓ, ΓΒ μέσον· λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται.
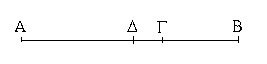
Εἰ γὰρ δυνατόν, διῃρήσθω καὶ κατὰ τὸ Δ, ὥστε καὶ τὰς ΑΔ, ΔΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον. καὶ ἐπεί, ᾧ διαφέρει τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ, τούτῳ διαφέρει καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, ἀλλὰ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῶν ἀπὸ τῶν ΑΔ, ΔΒ ὑπερέχει ῥητῷ· ῥητὰ γὰρ ἀμφότερα· καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ἄρα τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ μέσα ὄντα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ μείζων κατ' ἄλλο καὶ ἄλλο σημεῖον διαιρεῖται· κατὰ τὸ αὐτὸ ἄρα μόνον διαιρεῖται· ὅπερ ἔδει δεῖξαι.
Πρότασις μς΄ 46 Βιβλίον X
Ἡ ῥητὸν καὶ μέσον δυναμένη καθ᾿ ἓν μόνον σημεῖον διαιρεῖται.
Ἔστω ῥητὸν καὶ μέσον δυναμένη ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε τὰς ΑΓ, ΓΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ μέσον, τὸ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ῥητόν· λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται.
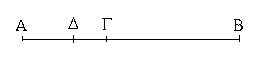
Εἰ γὰρ δυνατόν, διῃρήσθω καὶ κατὰ τὸ Δ, ὥστε καὶ τὰς ΑΔ, ΔΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΔ, ΔΒ μέσον, τὸ δὲ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ῥητόν. ἐπεὶ οὖν, ᾧ διαφέρει τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ, τούτῳ διαφέρει καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, τὸ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ὑπερέχει ῥητῷ, καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ ἄρα τῶν ἀπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ μέσα ὄντα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ῥητὸν καὶ μέσον δυναμένη κατ' ἄλλο καὶ ἄλλο σημεῖον διαιρεῖται. κατὰ ἓν ἄρα σημεῖον διαιρεῖται· ὅπερ ἔδει δεῖξαι.
Πρότασις μζ΄ 47 Βιβλίον X
Ἡ δύο μέσα δυναμένη καθ᾿ ἓν μόνον σημεῖον διαιρεῖται.
Ἔστω [δύο μέσα δυναμένη] ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε τὰς ΑΓ, ΓΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τό τε συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ μέσον καὶ τὸ ὑπὸ τῶν ΑΓ, ΓΒ μέσον καὶ ἔτι ἀσύμμετρον τῷ συγκειμένῳ ἐκ τῶν ἀπ' αὐτῶν. λέγω, ὅτι ἡ ΑΒ κατ' ἄλλο σημεῖον οὐ διαιρεῖται ποιοῦσα τὰ προκείμενα.
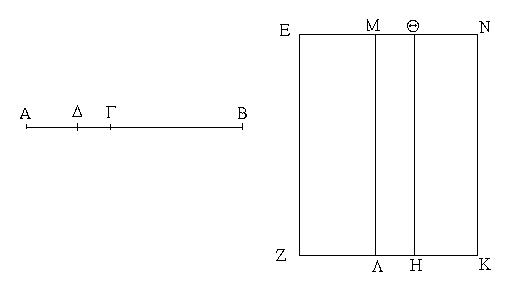
Εἰ γὰρ δυνατόν, διῃρήσθω κατὰ τὸ Δ, ὥστε πάλιν δηλονότι τὴν ΑΓ τῇ ΔΒ μὴ εἶναι τὴν αὐτήν, ἀλλὰ μείζονα καθ᾿ ὑπόθεσιν τὴν ΑΓ, καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ παραβεβλήσθω παρὰ τὴν ΕΖ τοῖς μὲν ἀπὸ τῶν ΑΓ, ΓΒ ἴσον τὸ ΕΗ, τῷ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον τὸ ΘΚ· ὅλον ἄρα τὸ ΕΚ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ. πάλιν δὴ παραβεβλήσθω παρὰ τὴν ΕΖ τοῖς ἀπὸ τῶν ΑΔ, ΔΒ ἴσον τὸ ΕΛ· λοιπὸν ἄρα τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ λοιπῷ τῷ ΜΚ ἴσον ἐστίν. καὶ ἐπεὶ μέσον ὑπόκειται τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, μέσον ἄρα ἐστὶ καὶ τὸ ΕΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΘΕ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΘΝ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, καὶ τὸ ΕΗ ἄρα τῷ ΗΝ ἀσύμμετρόν ἐστιν· ὥστε καὶ ἡ ΕΘ τῇ ΘΝ ἀσύμμετρός ἐστιν. καί εἰσι ῥηταί· αἱ ΕΘ, ΘΝ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΕΝ ἄρα ἐκ δύο ὀνομάτων ἐστὶ διῃρημένη κατὰ τὸ Θ. ὁμοίως δὴ δείξομεν, ὅτι καὶ κατὰ τὸ Μ διῄρηται. καὶ οὐκ ἔστιν ἡ ΕΘ τῇ ΜΝ ἡ αὐτή· ἡ ἄρα ἐκ δύο ὀνομάτων κατ' ἄλλο καὶ ἄλλο σημεῖον διῄρηται· ὅπερ ἐστὶν ἄτοπον. οὐκ ἄρα ἡ δύο μέσα δυναμένη κατ' ἄλλο καὶ ἄλλο σημεῖον διαιρεῖται· καθ᾿ ἓν ἄρα μόνον [σημεῖον] διαιρεῖται.
ἡ συνέχεια προτάσεων μη΄ 48 ἔως πδ΄ 84 μετά τοὺς ὃρους δεύτερους.
Ὅροι δεύτεροι ς΄ 6.
α΄ 1. Ὑποκειμένης ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων διῃρημένης εἰς τὰ ὀνόματα, ἧς τὸ μεῖζον ὄνομα τοῦ ἐλάσσονος μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει, ἐὰν μὲν τὸ μεῖζον ὄνομα σύμμετρον ᾖ μήκει τῇ ἐκκειμένῃ ῥητῇ, καλείσθω [ἡ ὅλη] ἐκ δύο ὀνομάτων πρώτη.
β΄ 2. Ἐὰν δὲ τὸ ἔλασσον ὄνομα σύμμετρον ᾖ μήκει τῇ ἐκκειμένῃ ῥητῇ, καλείσθω ἐκ δύο ὀνομάτων δευτέρα.
γ΄ 3. Ἐὰν δὲ μηδέτερον τῶν ὀνομάτων σύμμετρον ᾖ μήκει τῇ ἐκκειμένῃ ῥητῇ, καλείσθω ἐκ δύο ὀνομάτων τρίτη.
δ΄ 4. Πάλιν δὴ ἐὰν τὸ μεῖζον ὄνομα [τοῦ ἐλάσσονος] μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει, ἐὰν μὲν τὸ μεῖζον ὄνομα σύμμετρον ᾖ μήκει τῇ ἐκκειμένῃ ῥητῇ, καλείσθω ἐκ δύο ὀνομάτων τετάρτη.
ε΄ 5. Ἐὰν δὲ τὸ ἔλασσον, πέμπτη.
ς΄ 6. Ἐὰν δὲ μηδέτερον, ἕκτη.
Πρότασις μη΄ 48 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων πρώτην.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν συγκείμενον ἐξ αὐτῶν τὸν ΑΒ πρὸς μὲν τὸν ΒΓ λόγον ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, πρὸς δὲ τὸν ΓΑ λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ ἐκκείσθω τις ῥητὴ ἡ Δ, καὶ τῇ Δ σύμμετρος ἔστω μήκει ἡ ΕΖ. ῥητὴ ἄρα ἐστὶ καὶ ἡ ΕΖ. καὶ γεγονέτω ὡς ὁ ΒΑ ἀριθμὸς πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ. ὁ δὲ ΑΒ πρὸς τὸν ΑΓ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΕΖ ἄρα πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν· ὥστε σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΕΖ τῷ ἀπὸ τῆς ΖΗ. καί ἐστι ῥητὴ ἡ ΕΖ· ῥητὴ ἄρα καὶ ἡ ΖΗ. καὶ ἐπεὶ ὁ ΒΑ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΕΖ ἄρα πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ ΖΗ μήκει. αἱ ΕΖ, ΖΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΗ.
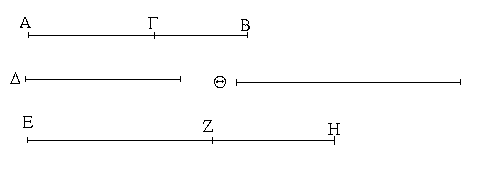
Λέγω, ὅτι καὶ πρώτη.
Ἐπεὶ γάρ ἐστιν ὡς ὁ ΒΑ ἀριθμὸς πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ, μείζων δὲ ὁ ΒΑ τοῦ ΑΓ, μεῖζον ἄρα καὶ τὸ ἀπὸ τῆς ΕΖ τοῦ ἀπὸ τῆς ΖΗ. ἔστω οὖν τῷ ἀπὸ τῆς ΕΖ ἴσα τὰ ἀπὸ τῶν ΖΗ, Θ. καὶ ἐπεί ἐστιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ, ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΑΒ πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΑΒ πρὸς τὸν ΒΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΕΖ ἄρα πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. σύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ Θ μήκει· ἡ ΕΖ ἄρα τῆς ΖΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί εἰσι ῥηταὶ αἱ ΕΖ, ΖΗ, καὶ σύμμετρος ἡ ΕΖ τῇ Δ μήκει.
Ἡ ΕΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ πρώτη· ὅπερ ἔδει δεῖξαι.
Πρότασις μθ΄ 49 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων δευτέραν.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν συγκείμενον ἐξ αὐτῶν τὸν ΑΒ πρὸς μὲν τὸν ΒΓ λόγον ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, πρὸς δὲ τὸν ΑΓ λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ ἐκκείσθω ῥητὴ ἡ Δ, καὶ τῇ Δ σύμμετρος ἔστω ἡ ΕΖ μήκει· ῥητὴ ἄρα ἐστὶν ἡ ΕΖ. γεγονέτω δὴ καὶ ὡς ὁ ΓΑ ἀριθμὸς πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΕΖ τῷ ἀπὸ τῆς ΖΗ. ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΗ. καὶ ἐπεὶ ὁ ΓΑ ἀριθμὸς πρὸς τὸν ΑΒ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ ΖΗ μήκει· αἱ ΕΖ, ΖΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΗ.
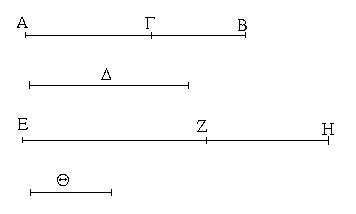
Δεικτέον δή, ὅτι καὶ δευτέρα.
Ἐπεὶ γὰρ ἀνάπαλίν ἐστιν ὡς ὁ ΒΑ ἀριθμὸς πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΗΖ πρὸς τὸ ἀπὸ τῆς ΖΕ, μείζων δὲ ὁ ΒΑ τοῦ ΑΓ, μεῖζον ἄρα [καὶ] τὸ ἀπὸ τῆς ΗΖ τοῦ ἀπὸ τῆς ΖΕ. ἔστω τῷ ἀπὸ τῆς ΗΖ ἴσα τὰ ἀπὸ τῶν ΕΖ, Θ· ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΑΒ πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς Θ. ἀλλ' ὁ ΑΒ πρὸς τὸν ΒΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΖΗ ἄρα πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. σύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ Θ μήκει· ὥστε ἡ ΖΗ τῆς ΖΕ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί εἰσι ῥηταὶ αἱ ΖΗ, ΖΕ δυνάμει μόνον σύμμετροι, καὶ τὸ ΕΖ ἔλασσον ὄνομα τῇ ἐκκειμένῃ ῥητῇ σύμμετρόν ἐστι τῇ Δ μήκει.
Ἡ ΕΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ δευτέρα· ὅπερ ἔδει δεῖξαι.
Πρότασις ν΄ 50 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων τρίτην.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν συγκείμενον ἐξ αὐτῶν τὸν ΑΒ πρὸς μὲν τὸν ΒΓ λόγον ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, πρὸς δὲ τὸν ΑΓ λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. ἐκκείσθω δέ τις καὶ ἄλλος μὴ τετράγωνος ἀριθμὸς ὁ Δ, καὶ πρὸς ἑκάτερον τῶν ΒΑ, ΑΓ λόγον μὴ ἐχέτω, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ ἐκκείσθω τις ῥητὴ εὐθεῖα ἡ Ε, καὶ γεγονέτω ὡς ὁ Δ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΖΗ· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς Ε τῷ ἀπὸ τῆς ΖΗ. καί ἐστι ῥητὴ ἡ Ε· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΗ. καὶ ἐπεὶ ὁ Δ πρὸς τὸν ΑΒ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Ε τῇ ΖΗ μήκει. γεγονέτω δὴ πάλιν ὡς ὁ ΒΑ ἀριθμὸς πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΖΗ τῷ ἀπὸ τῆς ΗΘ. ῥητὴ δὲ ἡ ΖΗ· ῥητὴ ἄρα καὶ ἡ ΗΘ. καὶ ἐπεὶ ὁ ΒΑ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὅν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΘΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ ΗΘ μήκει. αἱ ΖΗ, ΗΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΖΘ ἄρα ἐκ δύο ὀνομάτων ἐστίν.
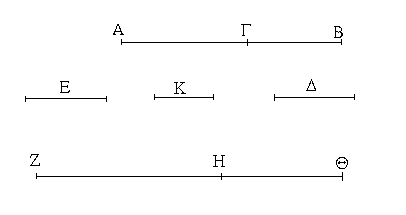
Λέγω δή, ὅτι καὶ τρίτη.
Ἐπεὶ γάρ ἐστιν ὡς ὁ Δ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΖΗ, ὡς δὲ ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Δ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΗΘ. ὁ δὲ Δ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδὲ τὸ ἀπὸ τῆς Ε ἄρα πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Ε τῇ ΗΘ μήκει. καὶ ἐπεί ἐστιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, μεῖζον ἄρα τὸ ἀπὸ τῆς ΖΗ τοῦ ἀπὸ τῆς ΗΘ. ἔστω οὖν τῷ ἀπὸ τῆς ΖΗ ἴσα τὰ ἀπὸ τῶν ΗΘ, Κ· ἀναστρέψαντι ἄρα [ἐστὶν] ὡς ὁ ΑΒ πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς Κ. ὁ δὲ ΑΒ πρὸς τὸν ΒΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΖΗ ἄρα πρὸς τὸ ἀπὸ τῆς Κ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· σύμμετρος ἄρα [ἐστὶν] ἡ ΖΗ τῇ Κ μήκει. ἡ ΖΗ ἄρα τῆς ΗΘ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΖΗ, ΗΘ ῥηταὶ δυνάμει μόνον σύμμετροι, καὶ οὐδετέρα αὐτῶν σύμμετρός ἐστι τῇ Ε μήκει.
Ἡ ΖΘ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τρίτη· ὅπερ ἔδει δεῖξαι.
Πρότασις να΄ 51 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων τετάρτην.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν ΑΒ πρὸς τὸν ΒΓ λόγον μὴ ἔχειν μήτε μὴν πρὸς τὸν ΑΓ, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. καὶ ἐκκείσθω ῥητὴ ἡ Δ, καὶ τῇ Δ σύμμετρος ἔστω μήκει ἡ ΕΖ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΕΖ. καὶ γεγονέτω ὡς ὁ ΒΑ ἀριθμὸς πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΕΖ τῷ ἀπὸ τῆς ΖΗ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΗ. καὶ ἐπεὶ ὁ ΒΑ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ ΖΗ μήκει. αἱ ΕΖ, ΖΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ὥστε ἡ ΕΗ ἐκ δύο ὀνομάτων ἐστίν.
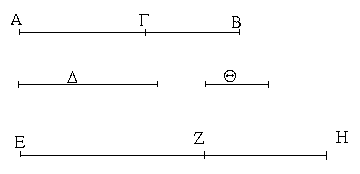
Λέγω δή, ὅτι καὶ τετάρτη.
Ἐπεὶ γάρ ἐστιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ [μείζων δὲ ὁ ΒΑ τοῦ ΑΓ], μεῖζον ἄρα τὸ ἀπὸ τῆς ΕΖ τοῦ ἀπὸ τῆς ΖΗ. ἔστω οὖν τῷ ἀπὸ τῆς ΕΖ ἴσα τὰ ἀπὸ τῶν ΖΗ, Θ· ἀναστρέψαντι ἄρα ὡς ὁ ΑΒ ἀριθμὸς πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΑΒ πρὸς τὸν ΒΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ Θ μήκει· ἡ ΕΖ ἄρα τῆς ΗΖ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΕΖ, ΖΗ ῥηταὶ δυνάμει μόνον σύμμετροι, καὶ ἡ ΕΖ τῇ Δ σύμμετρός ἐστι μήκει.
Ἡ ΕΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τετάρτη· ὅπερ ἔδει δεῖξαι.
Πρότασις νβ΄ 52 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων πέμπτην.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν ΑΒ πρὸς ἑκάτερον αὐτῶν λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ ἐκκείσθω ῥητή τις εὐθεῖα ἡ Δ, καὶ τῇ Δ σύμμετρος ἔστω [μήκει] ἡ ΕΖ· ῥητὴ ἄρα ἡ ΕΖ. καὶ γεγονέτω ὡς ὁ ΓΑ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ. ὁ δὲ ΓΑ πρὸς τὸν ΑΒ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδὲ τὸ ἀπὸ τῆς ΕΖ ἄρα πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. αἱ ΕΖ, ΖΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΗ.
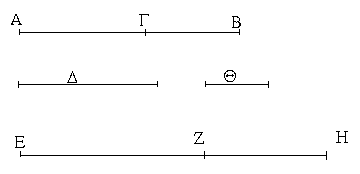
Λέγω δή, ὅτι καὶ πέμπτη.
Ἐπεὶ γάρ ἐστιν ὡς ὁ ΓΑ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς ΕΖ πρὸς τὸ ἀπὸ τῆς ΖΗ, ἀνάπαλιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΖΕ· μεῖζον ἄρα τὸ ἀπὸ τῆς ΗΖ τοῦ ἀπὸ τῆς ΖΕ. ἔστω οὖν τῷ ἀπὸ τῆς ΗΖ ἴσα τὰ ἀπὸ τῶν ΕΖ, Θ· ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΑΒ ἀριθμὸς πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΗΖ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΑΒ πρὸς τὸν ΒΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ Θ μήκει· ὥστε ἡ ΖΗ τῆς ΖΕ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΗΖ, ΖΕ ῥηταὶ δυνάμει μόνον σύμμετροι καὶ τὸ ΕΖ ἔλαττον ὄνομα σύμμετρόν ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ Δ μήκει.
Ἡ ΕΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ πέμπτη· ὅπερ ἔδει δεῖξαι.
Πρότασις νγ΄ 53 Βιβλίον X
Εὑρεῖν τὴν ἐκ δύο ὀνομάτων ἕκτην.
Ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΑΓ, ΓΒ, ὥστε τὸν ΑΒ πρὸς ἑκάτερον αὐτῶν λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἔστω δὲ καὶ ἕτερος ἀριθμὸς ὁ Δ μὴ τετράγωνος ὢν μηδὲ πρὸς ἑκάτερον τῶν ΒΑ, ΑΓ λόγον ἔχων, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ ἐκκείσθω τις ῥητὴ εὐθεῖα ἡ Ε, καὶ γεγονέτω ὡς ὁ Δ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΖΗ· σύμμετρον ἄρα τὸ ἀπὸ τῆς Ε τῷ ἀπὸ τῆς ΖΗ. καί ἐστι ῥητὴ ἡ Ε· ῥητὴ ἄρα καὶ ἡ ΖΗ. καὶ ἐπεὶ οὐκ ἔχει ὁ Δ πρὸς τὸν ΑΒ λόγον, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς Ε ἄρα πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἡ Ε τῇ ΖΗ μήκει. γεγονέτω δὴ πάλιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ. σύμμετρον ἄρα τὸ ἀπὸ τῆς ΖΗ τῷ ἀπὸ τῆς ΘΗ. ῥητὸν ἄρα τὸ ἀπὸ τῆς ΘΗ· ῥητὴ ἄρα ἡ ΘΗ. καὶ ἐπεὶ ὁ ΒΑ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδὲ τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ ΗΘ μήκει. αἱ ΖΗ, ΗΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΖΘ.
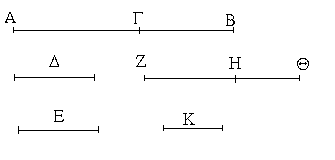
Δεικτέον δή, ὅτι καὶ ἕκτη.
Ἐπεὶ γάρ ἐστιν ὡς ὁ Δ πρὸς τὸν ΑΒ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΖΗ, ἔστι δὲ καὶ ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Δ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς ΗΘ. ὁ δὲ Δ πρὸς τὸν ΑΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδὲ τὸ ἀπὸ τῆς Ε ἄρα πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Ε τῇ ΗΘ μήκει. ἐδείχθη δὲ καὶ τῇ ΖΗ ἀσύμμετρος· ἑκατέρα ἄρα τῶν ΖΗ, ΗΘ ἀσύμμετρός ἐστι τῇ Ε μήκει. καὶ ἐπεί ἐστιν ὡς ὁ ΒΑ πρὸς τὸν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, μεῖζον ἄρα τὸ ἀπὸ τῆς ΖΗ τοῦ ἀπὸ τῆς ΗΘ. ἔστω οὖν τῷ ἀπὸ [τῆς] ΖΗ ἴσα τὰ ἀπὸ τῶν ΗΘ, Κ· ἀναστρέψαντι ἄρα ὡς ὁ ΑΒ πρὸς ΒΓ, οὕτως τὸ ἀπὸ ΖΗ πρὸς τὸ ἀπὸ τῆς Κ. ὁ δὲ ΑΒ πρὸς τὸν ΒΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ὥστε οὐδὲ τὸ ἀπὸ ΖΗ πρὸς τὸ ἀπὸ τῆς Κ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ Κ μήκει· ἡ ΖΗ ἄρα τῆς ΗΘ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΖΗ, ΗΘ ῥηταὶ δυνάμει μόνον σύμμετροι, καὶ οὐδετέρα αὐτῶν σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ Ε.
Ἡ ΖΘ ἄρα ἐκ δύο ὀνομάτων ἐστὶν ἕκτη· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ἔστω δύο τετράγωνα τὰ ΑΒ, ΒΓ καὶ κείσθωσαν ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΔΒ τῇ ΒΕ· ἐπ᾿ εὐθείας ἄρα ἐστὶ καὶ ἡ ΖΒ τῇ ΒΗ. καὶ συμπεπληρώσθω τὸ ΑΓ παραλληλόγραμμον· λέγω, ὅτι τετράγωνόν ἐστι τὸ ΑΓ, καὶ ὅτι τῶν ΑΒ, ΒΓ μέσον ἀνάλογόν ἐστι τὸ ΔΗ, καὶ ἔτι τῶν ΑΓ, ΓΒ μέσον ἀνάλογόν ἐστι τὸ ΔΓ.
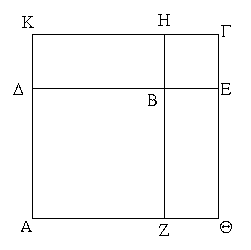
Ἐπεὶ γὰρ ἴση ἐστὶν ἡ μὲν ΔΒ τῇ ΒΖ, ἡ δὲ ΒΕ τῇ ΒΗ, ὅλη ἄρα ἡ ΔΕ ὅλῃ τῇ ΖΗ ἐστιν ἴση. ἀλλ' ἡ μὲν ΔΕ ἑκατέρᾳ τῶν ΑΘ, ΚΓ ἐστιν ἴση, ἡ δὲ ΖΗ ἑκατέρᾳ τῶν ΑΚ, ΘΓ ἐστιν ἴση· καὶ ἑκατέρα ἄρα τῶν ΑΘ, ΚΓ ἑκατέρᾳ τῶν ΑΚ, ΘΓ ἐστιν ἴση. ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΓ παραλληλόγραμμον· ἔστι δὲ καὶ ὀρθογώνιον· τετράγωνον ἄρα ἐστὶ τὸ ΑΓ.
Καὶ ἐπεί ἐστιν ὡς ἡ ΖΒ πρὸς τὴν ΒΗ, οὕτως ἡ ΔΒ πρὸς τὴν ΒΕ, ἀλλ' ὡς μὲν ἡ ΖΒ πρὸς τὴν ΒΗ, οὕτως τὸ ΑΒ πρὸς τὸ ΔΗ, ὡς δὲ ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως τὸ ΔΗ πρὸς τὸ ΒΓ, καὶ ὡς ἄρα τὸ ΑΒ πρὸς τὸ ΔΗ, οὕτως τὸ ΔΗ πρὸς τὸ ΒΓ. τῶν ΑΒ, ΒΓ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΔΗ.
Λέγω δή, ὅτι καὶ τῶν ΑΓ, ΓΒ μέσον ἀνάλογόν [ἐστι] τὸ ΔΓ.
Ἐπεὶ γάρ ἐστιν ὡς ἡ ΑΔ πρὸς τὴν ΔΚ, οὕτως ἡ ΚΗ πρὸς τὴν ΗΓ· ἴση γάρ [ἐστιν] ἑκατέρα ἑκατέρᾳ· καὶ συνθέντι ὡς ἡ ΑΚ πρὸς ΚΔ, οὕτως ἡ ΚΓ πρὸς ΓΗ, ἀλλ' ὡς μὲν ἡ ΑΚ πρὸς ΚΔ, οὕτως τὸ ΑΓ πρὸς τὸ ΓΔ, ὡς δὲ ἡ ΚΓ πρὸς ΓΗ, οὕτως τὸ ΔΓ πρὸς ΓΒ, καὶ ὡς ἄρα τὸ ΑΓ πρὸς ΔΓ, οὕτως τὸ ΔΓ πρὸς τὸ ΒΓ. τῶν ΑΓ, ΓΒ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΔΓ· ἃ προέκειτο δεῖξαι.
Πρότασις νδ΄ 54 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων πρώτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο ὀνομάτων.
Χωρίον γὰρ τὸ ΑΓ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων πρώτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο ὀνομάτων.
Ἐπεὶ γὰρ ἐκ δύο ὀνομάτων ἐστὶ πρώτη ἡ ΑΔ, διῃρήσθω εἰς τὰ ὀνόματα κατὰ τὸ Ε, καὶ ἔστω τὸ μεῖζον ὄνομα τὸ ΑΕ. φανερὸν δή, ὅτι αἱ ΑΕ, ΕΔ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ ΑΕ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΒ μήκει. τετμήσθω δὴ ἡ ΕΔ δίχα κατὰ τὸ Ζ σημεῖον. καὶ ἐπεὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος, τουτέστι τῷ ἀπὸ τῆς ΕΖ, ἴσον παρὰ τὴν μείζονα τὴν ΑΕ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διαιρεῖ. παραβεβλήσθω οὖν παρὰ τὴν ΑΕ τῷ ἀπὸ τῆς ΕΖ ἴσον τὸ ὑπὸ ΑΗ, ΗΕ· σύμμετρος ἄρα ἐστὶν ἡ ΑΗ τῇ ΕΗ μήκει. καὶ ἤχθωσαν ἀπὸ τῶν Η, Ε, Ζ ὁποτέρᾳ τῶν ΑΒ, ΓΔ παράλληλοι αἱ ΗΘ, ΕΚ, ΖΛ· καὶ τῷ μὲν ΑΘ παραλληλογράμμῳ ἴσον τετράγωνον συνεστάτω τὸ ΣΝ, τῷ δὲ ΗΚ ἴσον τὸ ΝΠ, καὶ κείσθω ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΜΝ τῇ ΝΞ· ἐπ᾿ εὐθείας ἄρα ἐστὶ καὶ ἡ ΡΝ τῇ ΝΟ. καὶ συμπεπληρώσθω τὸ ΣΠ παραλληλόγραμμον· τετράγωνον ἄρα ἐστὶ τὸ ΣΠ. καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΗ, ΗΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΖ, ἔστιν ἄρα ὡς ἡ ΑΗ πρὸς ΕΖ, οὕτως ἡ ΖΕ πρὸς ΕΗ· καὶ ὡς ἄρα τὸ ΑΘ πρὸς ΕΛ, τὸ ΕΛ πρὸς ΚΗ· τῶν ΑΘ, ΗΚ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΕΛ. ἀλλὰ τὸ μὲν ΑΘ ἴσον ἐστὶ τῷ ΣΝ, τὸ δὲ ΗΚ ἴσον τῷ ΝΠ· τῶν ΣΝ, ΝΠ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΕΛ. ἔστι δὲ τῶν αὐτῶν τῶν ΣΝ, ΝΠ μέσον ἀνάλογον καὶ τὸ ΜΡ· ἴσον ἄρα ἐστὶ τὸ ΕΛ τῷ ΜΡ· ὥστε καὶ τῷ ΟΞ ἴσον ἐστίν. ἔστι δὲ καὶ τὰ ΑΘ, ΗΚ τοῖς ΣΝ, ΝΠ ἴσα· ὅλον ἄρα τὸ ΑΓ ἴσον ἐστὶν ὅλῳ τῷ ΣΠ, τουτέστι τῷ ἀπὸ τῆς ΜΞ τετραγώνῳ· τὸ ΑΓ ἄρα δύναται ἡ ΜΞ.
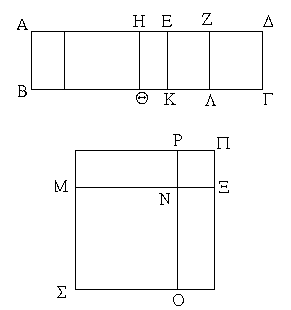
Λέγω, ὅτι ἡ ΜΞ ἐκ δύο ὀνομάτων ἐστίν.
Ἐπεὶ γὰρ σύμμετρός ἐστιν ἡ ΑΗ τῇ ΗΕ, σύμμετρός ἐστι καὶ ἡ ΑΕ ἑκατέρᾳ τῶν ΑΗ, ΗΕ. ὑπόκειται δὲ καὶ ἡ ΑΕ τῇ ΑΒ σύμμετρος· καὶ αἱ ΑΗ, ΗΕ ἄρα τῇ ΑΒ σύμμετροί εἰσιν. καί ἐστι ῥητὴ ἡ ΑΒ· ῥητὴ ἄρα ἐστὶ καὶ ἑκατέρα τῶν ΑΗ, ΗΕ· ῥητὸν ἄρα ἐστὶν ἑκάτερον τῶν ΑΘ, ΗΚ, καί ἐστι σύμμετρον τὸ ΑΘ τῷ ΗΚ. ἀλλὰ τὸ μὲν ΑΘ τῷ ΣΝ ἴσον ἐστίν, τὸ δὲ ΗΚ τῷ ΝΠ· καὶ τὰ ΣΝ, ΝΠ ἄρα, τουτέστι τὰ ἀπὸ τῶν ΜΝ, ΝΞ, ῥητά ἐστι καὶ σύμμετρα. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΕ τῇ ΕΔ μήκει, ἀλλ' ἡ μὲν ΑΕ τῇ ΑΗ ἐστι σύμμετρος, ἡ δὲ ΔΕ τῇ ΕΖ σύμμετρος, ἀσύμμετρος ἄρα καὶ ἡ ΑΗ τῇ ΕΖ· ὥστε καὶ τὸ ΑΘ τῷ ΕΛ ἀσύμμετρόν ἐστιν. ἀλλὰ τὸ μὲν ΑΘ τῷ ΣΝ ἐστιν ἴσον, τὸ δὲ ΕΛ τῷ ΜΡ· καὶ τὸ ΣΝ ἄρα τῷ ΜΡ ἀσύμμετρόν ἐστιν. ἀλλ' ὡς τὸ ΣΝ πρὸς ΜΡ, ἡ ΟΝ πρὸς τὴν ΝΡ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΟΝ τῇ ΝΡ. ἴση δὲ ἡ μὲν ΟΝ τῇ ΜΝ, ἡ δὲ ΝΡ τῇ ΝΞ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΜΝ τῇ ΝΞ. καί ἐστι τὸ ἀπὸ τῆς ΜΝ σύμμετρον τῷ ἀπὸ τῆς ΝΞ, καὶ ῥητὸν ἑκάτερον· αἱ ΜΝ, ΝΞ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι.
Ἡ ΜΞ ἄρα ἐκ δύο ὀνομάτων ἐστὶ καὶ δύναται τὸ ΑΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις νε΄ 55 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων δευτέρας, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο μέσων πρώτη.
Περιεχέσθω γὰρ χωρίον τὸ ΑΒΓΔ ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων δευτέρας τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἐκ δύο μέσων πρώτη ἐστίν.
Ἐπεὶ γὰρ ἐκ δύο ὀνομάτων δευτέρα ἐστὶν ἡ ΑΔ, διῃρήσθω εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὥστε τὸ μεῖζον ὄνομα εἶναι τὸ ΑΕ· αἱ ΑΕ, ΕΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ τὸ ἔλαττον ὄνομα ἡ ΕΔ σύμμετρόν ἐστι τῇ ΑΒ μήκει. τετμήσθω ἡ ΕΔ δίχα κατὰ τὸ Ζ, καὶ τῷ ἀπὸ τῆς ΕΖ ἴσον παρὰ τὴν ΑΕ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΑΗΕ· σύμμετρος ἄρα ἡ ΑΗ τῇ ΗΕ μήκει.
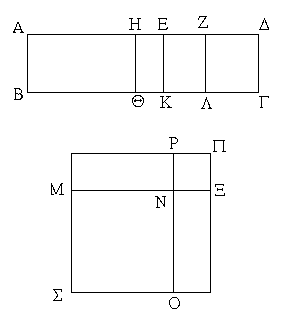
καὶ διὰ τῶν Η, Ε, Ζ παράλληλοι ἤχθωσαν ταῖς ΑΒ, ΓΔ αἱ ΗΘ, ΕΚ, ΖΛ, καὶ τῷ μὲν ΑΘ παραλληλογράμμῳ ἴσον τετράγωνον συνεστάτω τὸ ΣΝ, τῷ δὲ ΗΚ ἴσον τετράγωνον τὸ ΝΠ, καὶ κείσθω ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΜΝ τῇ ΝΞ· ἐπ᾿ εὐθείας ἄρα [ἐστὶ] καὶ ἡ ΡΝ τῇ ΝΟ. καὶ συμπεπληρώσθω τὸ ΣΠ τετράγωνον· φανερὸν δὴ ἐκ τοῦ προδεδειγμένου, ὅτι τὸ ΜΡ μέσον ἀνάλογόν ἐστι τῶν ΣΝ, ΝΠ, καὶ ἴσον τῷ ΕΛ, καὶ ὅτι τὸ ΑΓ χωρίον δύναται ἡ ΜΞ. δεικτέον δή, ὅτι ἡ ΜΞ ἐκ δύο μέσων ἐστὶ πρώτη. ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΕ τῇ ΕΔ μήκει, σύμμετρος δὲ ἡ ΕΔ τῇ ΑΒ, ἀσύμμετρος ἄρα ἡ ΑΕ τῇ ΑΒ. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΗ τῇ ΕΗ, σύμμετρός ἐστι καὶ ἡ ΑΕ ἑκατέρᾳ τῶν ΑΗ, ΗΕ. ἀλλὰ ἡ ΑΕ ἀσύμμετρος τῇ ΑΒ μήκει· καὶ αἱ ΑΗ, ΗΕ ἄρα ἀσύμμετροί εἰσι τῇ ΑΒ. αἱ ΒΑ, ΑΗ, ΗΕ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ὥστε μέσον ἐστὶν ἑκάτερον τῶν ΑΘ, ΗΚ. ὥστε καὶ ἑκάτερον τῶν ΣΝ, ΝΠ μέσον ἐστίν. καὶ αἱ ΜΝ, ΝΞ ἄρα μέσαι εἰσίν. καὶ ἐπεὶ σύμμετρος ἡ ΑΗ τῇ ΗΕ μήκει, σύμμετρόν ἐστι καὶ τὸ ΑΘ τῷ ΗΚ, τουτέστι τὸ ΣΝ τῷ ΝΠ, τουτέστι τὸ ἀπὸ τῆς ΜΝ τῷ ἀπὸ τῆς ΝΞ [ὥστε δυνάμει εἰσὶ σύμμετροι αἱ ΜΝ, ΝΞ]. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΕ τῇ ΕΔ μήκει, ἀλλ' ἡ μὲν ΑΕ σύμμετρός ἐστι τῇ ΑΗ, ἡ δὲ ΕΔ τῇ ΕΖ σύμμετρος, ἀσύμμετρος ἄρα ἡ ΑΗ τῇ ΕΖ· ὥστε καὶ τὸ ΑΘ τῷ ΕΛ ἀσύμμετρόν ἐστιν, τουτέστι τὸ ΣΝ τῷ ΜΡ, τουτέστιν ἡ ΟΝ τῇ ΝΡ, τουτέστιν ἡ ΜΝ τῇ ΝΞ ἀσύμμετρός ἐστι μήκει. ἐδείχθησαν δὲ αἱ ΜΝ, ΝΞ καὶ μέσαι οὖσαι καὶ δυνάμει σύμμετροι· αἱ ΜΝ, ΝΞ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. λέγω δή, ὅτι καὶ ῥητὸν περιέχουσιν. ἐπεὶ γὰρ ἡ ΔΕ ὑπόκειται ἑκατέρᾳ τῶν ΑΒ, ΕΖ σύμμετρος, σύμμετρος ἄρα καὶ ἡ ΕΖ τῇ ΕΚ. καὶ ῥητὴ ἑκατέρα αὐτῶν· ῥητὸν ἄρα τὸ ΕΛ, τουτέστι τὸ ΜΡ· τὸ δὲ ΜΡ ἐστι τὸ ὑπὸ τῶν ΜΝΞ. ἐὰν δὲ δύο μέσαι δυνάμει μόνον σύμμετροι συντεθῶσι ῥητὸν περιέχουσαι, ἡ ὅλη ἄλογός ἐστιν, καλεῖται δὲ ἐκ δύο μέσων πρώτη.
Ἡ ἄρα ΜΞ ἐκ δύο μέσων ἐστὶ πρώτη· ὅπερ ἔδει δεῖξαι.
Πρότασις νς΄ 56 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων τρίτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο μέσων δευτέρα.
Χωρίον γὰρ τὸ ΑΒΓΔ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων τρίτης τῆς ΑΔ διῃρημένης εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὧν μεῖζόν ἐστι τὸ ΑΕ· λέγω, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο μέσων δευτέρα.
Κατεσκευάσθω γὰρ τὰ αὐτὰ τοῖς πρότερον. καὶ ἐπεὶ ἐκ δύο ὀνομάτων ἐστὶ τρίτη ἡ ΑΔ, αἱ ΑΕ, ΕΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ οὐδετέρα τῶν ΑΕ, ΕΔ σύμμετρός [ἐστι] τῇ ΑΒ μήκει. ὁμοίως δὴ τοῖς προδεδειγμένοις δείξομεν, ὅτι ἡ ΜΞ ἐστιν ἡ τὸ ΑΓ χωρίον δυναμένη, καὶ αἱ ΜΝ, ΝΞ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι· ὥστε ἡ ΜΞ ἐκ δύο μέσων ἐστίν.
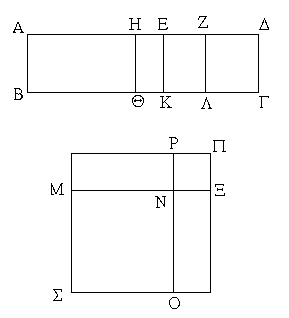
Δεικτέον δή, ὅτι καὶ δευτέρα.
[Καὶ] ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΔΕ τῇ ΑΒ μήκει, τουτέστι τῇ ΕΚ, σύμμετρος δὲ ἡ ΔΕ τῇ ΕΖ, ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΖ τῇ ΕΚ μήκει. καί εἰσι ῥηταί· αἱ ΖΕ, ΕΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. μέσον ἄρα [ἐστὶ] τὸ ΕΛ, τουτέστι τὸ ΜΡ· καὶ περιέχεται ὑπὸ τῶν ΜΝΞ· μέσον ἄρα ἐστὶ τὸ ὑπὸ τῶν ΜΝΞ.
Ἡ ΜΞ ἄρα ἐκ δύο μέσων ἐστὶ δευτέρα· ὅπερ ἔδει δεῖξαι.
Πρότασις νζ΄ 57 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων τετάρτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη μείζων.
Χωρίον γὰρ τὸ ΑΓ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων τετάρτης τῆς ΑΔ διῃρημένης εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὧν μεῖζον ἔστω τὸ ΑΕ· λέγω, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη μείζων.
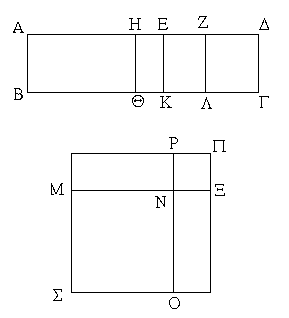
Ἐπεὶ γὰρ ἡ ΑΔ ἐκ δύο ὀνομάτων ἐστὶ τετάρτη, αἱ ΑΕ, ΕΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ἡ ΑΕ τῇ ΑΒ σύμμετρός [ἐστι] μήκει. τετμήσθω ἡ ΔΕ δίχα κατὰ τὸ Ζ, καὶ τῷ ἀπὸ τῆς ΕΖ ἴσον παρὰ τὴν ΑΕ παραβεβλήσθω παραλληλόγραμμον τὸ ὑπὸ ΑΗ, ΗΕ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΗ τῇ ΗΕ μήκει. ἤχθωσαν παράλληλοι τῇ ΑΒ αἱ ΗΘ, ΕΚ, ΖΛ, καὶ τὰ λοιπὰ τὰ αὐτὰ τοῖς πρὸ τούτου γεγονέτω· φανερὸν δή, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἐστὶν ἡ ΜΞ. δεικτέον δή, ὅτι ἡ ΜΞ ἄλογός ἐστιν ἡ καλουμένη μείζων. ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΗ τῇ ΕΗ μήκει, ἀσύμμετρόν ἐστι καὶ τὸ ΑΘ τῷ ΗΚ, τουτέστι τὸ ΣΝ τῷ ΝΠ· αἱ ΜΝ, ΝΞ ἄρα δυνάμει εἰσὶν ἀσύμμετροι. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΕ τῇ ΑΒ μήκει, ῥητόν ἐστι τὸ ΑΚ· καί ἐστιν ἴσον τοῖς ἀπὸ τῶν ΜΝ, ΝΞ· ῥητὸν ἄρα [ἐστὶ] καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΜΝ, ΝΞ. καὶ ἐπεὶ ἀσύμμετρός [ἐστιν] ἡ ΔΕ τῇ ΑΒ μήκει, τουτέστι τῇ ΕΚ, ἀλλὰ ἡ ΔΕ σύμμετρός ἐστι τῇ ΕΖ, ἀσύμμετρος ἄρα ἡ ΕΖ τῇ ΕΚ μήκει. αἱ ΕΚ, ΕΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· μέσον ἄρα τὸ ΛΕ, τουτέστι τὸ ΜΡ. καὶ περιέχεται ὑπὸ τῶν ΜΝ, ΝΞ· μέσον ἄρα ἐστὶ τὸ ὑπὸ τῶν ΜΝ, ΝΞ. καὶ ῥητὸν τὸ [συγκείμενον] ἐκ τῶν ἀπὸ τῶν ΜΝ, ΝΞ, καί εἰσιν ἀσύμμετροι αἱ ΜΝ, ΝΞ δυνάμει. ἐὰν δὲ δύο εὐθεῖαι δυνάμει ἀσύμμετροι συντεθῶσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον, ἡ ὅλη ἄλογός ἐστιν, καλεῖται δὲ μείζων.
Ἡ ΜΞ ἄρα ἄλογός ἐστιν ἡ καλουμένη μείζων, καὶ δύναται τὸ ΑΓ χωρίον· ὅπερ ἔδει δεῖξαι.
Πρότασις νη΄ 58 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων πέμπτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ῥητὸν καὶ μέσον δυναμένη.
Χωρίον γὰρ τὸ ΑΓ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων πέμπτης τῆς ΑΔ διῃρημένης εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὥστε τὸ μεῖζον ὄνομα εἶναι τὸ ΑΕ· λέγω [δή], ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ῥητὸν καὶ μέσον δυναμένη.
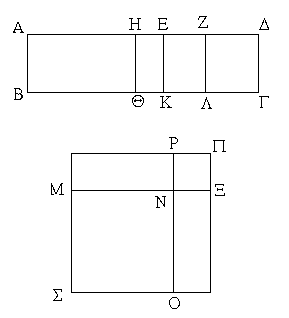
Κατεσκευάσθω γὰρ τὰ αὐτὰ τοῖς πρότερον δεδειγμένοις· φανερὸν δή, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἐστὶν ἡ ΜΞ. δεικτέον δή, ὅτι ἡ ΜΞ ἐστιν ἡ ῥητὸν καὶ μέσον δυναμένη. ἐπεὶ γὰρ ἀσύμμετρός ἐστιν ἡ ΑΗ τῇ ΗΕ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΑΘ τῷ ΘΕ, τουτέστι τὸ ἀπὸ τῆς ΜΝ τῷ ἀπὸ τῆς ΝΞ· αἱ ΜΝ, ΝΞ ἄρα δυνάμει εἰσὶν ἀσύμμετροι. καὶ ἐπεὶ ἡ ΑΔ ἐκ δύο ὀνομάτων ἐστὶ πέμπτη, καί [ἐστιν] ἔλασσον αὐτῆς τμῆμα τὸ ΕΔ, σύμμετρος ἄρα ἡ ΕΔ τῇ ΑΒ μήκει. ἀλλὰ ἡ ΑΕ τῇ ΕΔ ἐστιν ἀσύμμετρος· καὶ ἡ ΑΒ ἄρα τῇ ΑΕ ἐστιν ἀσύμμετρος μήκει. [αἱ ΒΑ, ΑΕ ῥηταί εἰσι δυνάμει μόνον σύμμετροι.] μέσον ἄρα ἐστὶ τὸ ΑΚ, τουτέστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΜΝ, ΝΞ. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΔΕ τῇ ΑΒ μήκει, τουτέστι τῇ ΕΚ, ἀλλὰ ἡ ΔΕ τῇ ΕΖ σύμμετρός ἐστιν, καὶ ἡ ΕΖ ἄρα τῇ ΕΚ σύμμετρός ἐστιν. καὶ ῥητὴ ἡ ΕΚ· ῥητὸν ἄρα καὶ τὸ ΕΛ, τουτέστι τὸ ΜΡ, τουτέστι τὸ ὑπὸ ΜΝΞ· αἱ ΜΝ, ΝΞ ἄρα δυνάμει ἀσύμμετροί εἰσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν.
Ἡ ΜΞ ἄρα ῥητὸν καὶ μέσον δυναμένη ἐστὶ καὶ δύναται τὸ ΑΓ χωρίον· ὅπερ ἔδει δεῖξαι.
Πρότασις νθ΄ 59 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων ἕκτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη δύο μέσα δυναμένη.
Χωρίον γὰρ τὸ ΑΒΓΔ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων ἕκτης τῆς ΑΔ διῃρημένης εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὥστε τὸ μεῖζον ὄνομα εἶναι τὸ ΑΕ· λέγω, ὅτι ἡ τὸ ΑΓ δυναμένη ἡ δύο μέσα δυναμένη ἐστίν.
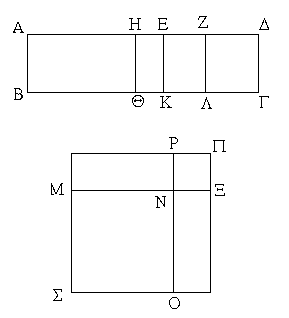
Κατεσκευάσθω [γὰρ] τὰ αὐτὰ τοῖς προδεδειγμένοις. φανερὸν δή, ὅτι [ἡ] τὸ ΑΓ δυναμένη ἐστὶν ἡ ΜΞ, καὶ ὅτι ἀσύμμετρός ἐστι ἡ ΜΝ τῇ ΝΞ δυνάμει. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΕΑ τῇ ΑΒ μήκει, αἱ ΕΑ, ΑΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· μέσον ἄρα ἐστὶ τὸ ΑΚ, τουτέστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΜΝ, ΝΞ. πάλιν, ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΕΔ τῇ ΑΒ μήκει, ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΖΕ τῇ ΕΚ· αἱ ΖΕ, ΕΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· μέσον ἄρα ἐστὶ τὸ ΕΛ, τουτέστι τὸ ΜΡ, τουτέστι τὸ ὑπὸ τῶν ΜΝΞ. καὶ ἐπεὶ ἀσύμμετρος ἡ ΑΕ τῇ ΕΖ, καὶ τὸ ΑΚ τῷ ΕΛ ἀσύμμετρόν ἐστιν. ἀλλὰ τὸ μὲν ΑΚ ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΜΝ, ΝΞ, τὸ δὲ ΕΛ ἐστι τὸ ὑπὸ τῶν ΜΝΞ· ἀσύμμετρον ἄρα ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΜΝΞ τῷ ὑπὸ τῶν ΜΝΞ. καί ἐστι μέσον ἑκάτερον αὐτῶν, καὶ αἱ ΜΝ, ΝΞ δυνάμει εἰσὶν ἀσύμμετροι.
Ἡ ΜΞ ἄρα δύο μέσα δυναμένη ἐστὶ καὶ δύναται τὸ ΑΓ· ὅπερ ἔδει δεῖξαι.
[Λῆμμα
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἄνισα, τὰ ἀπὸ τῶν ἀνίσων τετράγωνα μείζονά ἐστι τοῦ δὶς ὑπὸ τῶν ἀνίσων περιεχομένου ὀρθογωνίου.
Ἔστω εὐθεῖα ἡ ΑΒ καὶ τετμήσθω εἰς ἄνισα κατὰ τὸ Γ, καὶ ἔστω μείζων ἡ ΑΓ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΓ, ΓΒ μείζονά ἐστι τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ.
Τετμήσθω γὰρ ἡ ΑΒ δίχα κατὰ τὸ Δ. ἐπεὶ οὖν εὐθεῖα γραμμὴ τέτμηται εἰς μὲν ἴσα κατὰ τὸ Δ, εἰς δὲ ἄνισα κατὰ τὸ Γ, τὸ ἄρα ὑπὸ τῶν ΑΓ, ΓΒ μετὰ τοῦ ἀπὸ ΓΔ ἴσον ἐστὶ τῷ ἀπὸ ΑΔ· ὥστε τὸ ὑπὸ τῶν ΑΓ, ΓΒ ἔλαττόν ἐστι τοῦ ἀπὸ ΑΔ· τὸ ἄρα δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἔλαττον ἢ διπλάσιόν ἐστι τοῦ ἀπὸ ΑΔ. ἀλλὰ τὰ ἀπὸ τῶν ΑΓ, ΓΒ διπλάσιά [ἐστι] τῶν ἀπὸ τῶν ΑΔ, ΔΓ· τὰ ἄρα ἀπὸ τῶν ΑΓ, ΓΒ μείζονά ἐστι τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ· ὅπερ ἔδει δεῖξαι.]
Πρότασις ξ΄ 60 Βιβλίον X
Τὸ ἀπὸ τῆς ἐκ δύο ὀνομάτων παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πρώτην.
Ἔστω ἐκ δύο ὀνομάτων ἡ ΑΒ διῃρημένη εἰς τὰ ὀνόματα κατὰ τὸ Γ, ὥστε τὸ μεῖζον ὄνομα εἶναι τὸ ΑΓ, καὶ ἐκκείσθω ῥητὴ ἡ ΔΕ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΔΕ παραβεβλήσθω τὸ ΔΕΖΗ πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶ πρώτη.
Παραβεβλήσθω γὰρ παρὰ τὴν ΔΕ τῷ μὲν ἀπὸ τῆς ΑΓ ἴσον τὸ ΔΘ, τῷ δὲ ἀπὸ τῆς ΒΓ ἴσον τὸ ΚΛ· λοιπὸν ἄρα τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον ἐστὶ τῷ ΜΖ. τετμήσθω ἡ ΜΗ δίχα κατὰ τὸ Ν, καὶ παράλληλος ἤχθω ἡ ΝΞ [ἑκατέρᾳ τῶν ΜΛ, ΗΖ]. ἑκάτερον ἄρα τῶν ΜΞ, ΝΖ ἴσον ἐστὶ τῷ ἅπαξ ὑπὸ τῶν ΑΓΒ. καὶ ἐπεὶ ἐκ δύο ὀνομάτων ἐστὶν ἡ ΑΒ διῃρημένη εἰς τὰ ὀνόματα κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· τὰ ἄρα ἀπὸ τῶν ΑΓ, ΓΒ ῥητά ἐστι καὶ σύμμετρα ἀλλήλοις· ὥστε καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ [σύμμετρόν ἐστι τοῖς ἀπὸ τῶν ΑΓ, ΓΒ· ῥητὸν ἄρα ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ]. καί ἐστιν ἴσον τῷ ΔΛ· ῥητὸν ἄρα ἐστὶ τὸ ΔΛ. καὶ παρὰ ῥητὴν τὴν ΔΕ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΔΜ καὶ σύμμετρος τῇ ΔΕ μήκει. πάλιν, ἐπεὶ αἱ ΑΓ, ΓΒ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, μέσον ἄρα ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, τουτέστι τὸ ΜΖ. καὶ παρὰ ῥητὴν τὴν ΜΛ παράκειται· ῥητὴ ἄρα καὶ ἡ ΜΗ ἐστι καὶ ἀσύμμετρος τῇ ΜΛ, τουτέστι τῇ ΔΕ, μήκει. ἔστι δὲ καὶ ἡ ΜΔ ῥητὴ καὶ τῇ ΔΕ μήκει σύμμετρος· ἀσύμμετρος ἄρα ἐστὶν ἡ ΔΜ τῇ ΜΗ μήκει. καί εἰσι ῥηταί· αἱ ΔΜ, ΜΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
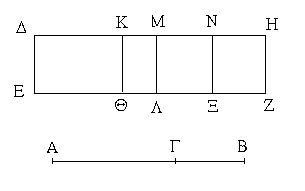
Δεικτέον δή, ὅτι καὶ πρώτη.
Ἐπεὶ τῶν ἀπὸ τῶν ΑΓ, ΓΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΓΒ, καὶ τῶν ΔΘ, ΚΛ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΜΞ. ἔστιν ἄρα ὡς τὸ ΔΘ πρὸς τὸ ΜΞ, οὕτως τὸ ΜΞ πρὸς τὸ ΚΛ, τουτέστιν ὡς ἡ ΔΚ πρὸς τὴν ΜΝ, ἡ ΜΝ πρὸς τὴν ΜΚ· τὸ ἄρα ὑπὸ τῶν ΔΚ, ΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΜΝ. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΓ τῷ ἀπὸ τῆς ΓΒ, σύμμετρόν ἐστι καὶ τὸ ΔΘ τῷ ΚΛ· ὥστε καὶ ἡ ΔΚ τῇ ΚΜ σύμμετρός ἐστιν. καὶ ἐπεὶ μείζονά ἐστι τὰ ἀπὸ τῶν ΑΓ, ΓΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, μεῖζον ἄρα καὶ τὸ ΔΛ τοῦ ΜΖ· ὥστε καὶ ἡ ΔΜ τῆς ΜΗ μείζων ἐστίν. καί ἐστιν ἴσον τὸ ὑπὸ τῶν ΔΚ, ΚΜ τῷ ἀπὸ τῆς ΜΝ, τουτέστι τῷ τετάρτῳ τοῦ ἀπὸ τῆς ΜΗ, καὶ σύμμετρος ἡ ΔΚ τῇ ΚΜ. ἐὰν δὲ ὦσι δύο εὐθεῖαι ἄνισοι, τῷ δὲ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς σύμμετρα αὐτὴν διαιρῇ, ἡ μείζων τῆς ἐλάσσονος μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ· ἡ ΔΜ ἄρα τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί εἰσι ῥηταὶ αἱ ΔΜ, ΜΗ, καὶ ἡ ΔΜ μεῖζον ὄνομα σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΔΕ μήκει.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ πρώτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ξα΄ 61 Βιβλίον X
Τὸ ἀπὸ τῆς ἐκ δύο μέσων πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων δευτέραν.
Ἔστω ἐκ δύο μέσων πρώτη ἡ ΑΒ διῃρημένη εἰς τὰς μέσας κατὰ τὸ Γ, ὧν μείζων ἡ ΑΓ, καὶ ἐκκείσθω ῥητὴ ἡ ΔΕ, καὶ παραβεβλήσθω παρὰ τὴν ΔΕ τῷ ἀπὸ τῆς ΑΒ ἴσον παραλληλόγραμμον τὸ ΔΖ πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶ δευτέρα.
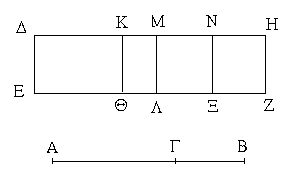
Κατεσκευάσθω γὰρ τὰ αὐτὰ τοῖς πρὸ τούτου. καὶ ἐπεὶ ἡ ΑΒ ἐκ δύο μέσων ἐστὶ πρώτη διῃρημένη κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι· ὥστε καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ μέσα ἐστίν. μέσον ἄρα ἐστὶ τὸ ΔΛ. καὶ παρὰ ῥητὴν τὴν ΔΕ παραβέβληται· ῥητὴ ἄρα ἐστίν ἡ ΜΔ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. πάλιν, ἐπεὶ ῥητόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, ῥητόν ἐστι καὶ τὸ ΜΖ. καὶ παρὰ ῥητὴν τὴν ΜΛ παράκειται· ῥητὴ ἄρα [ἐστὶ] καὶ ἡ ΜΗ καὶ μήκει σύμμετρος τῇ ΜΛ, τουτέστι τῇ ΔΕ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΔΜ τῇ ΜΗ μήκει. καί εἰσι ῥηταί· αἱ ΔΜ, ΜΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
Δεικτέον δή, ὅτι καὶ δευτέρα.
Ἐπεὶ γὰρ τὰ ἀπὸ τῶν ΑΓ, ΓΒ μείζονά ἐστι τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, μεῖζον ἄρα καὶ τὸ ΔΛ τοῦ ΜΖ· ὥστε καὶ ἡ ΔΜ τῆς ΜΗ. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΓ τῷ ἀπὸ τῆς ΓΒ, σύμμετρόν ἐστι καὶ τὸ ΔΘ τῷ ΚΛ· ὥστε καὶ ἡ ΔΚ τῇ ΚΜ σύμμετρός ἐστιν. καί ἐστι τὸ ὑπὸ τῶν ΔΚΜ ἴσον τῷ ἀπὸ τῆς ΜΝ· ἡ ΔΜ ἄρα τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί ἐστιν ἡ ΜΗ σύμμετρος τῇ ΔΕ μήκει.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ δευτέρα.
Πρότασις ξβ΄ 62 Βιβλίον X
Τὸ ἀπὸ τῆς ἐκ δύο μέσων δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τρίτην.
Ἔστω ἐκ δύο μέσων δευτέρα ἡ ΑΒ διῃρημένη εἰς τὰς μέσας κατὰ τὸ Γ, ὥστε τὸ μεῖζον τμῆμα εἶναι τὸ ΑΓ, ῥητὴ δέ τις ἔστω ἡ ΔΕ, καὶ παρὰ τὴν ΔΕ τῷ ἀπὸ τῆς ΑΒ ἴσον παραλληλόγραμμον παραβεβλήσθω τὸ ΔΖ πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶ τρίτη.
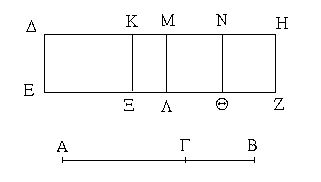
Κατεσκευάσθω τὰ αὐτὰ τοῖς προδεδειγμένοις. καὶ ἐπεὶ ἐκ δύο μέσων δευτέρα ἐστὶν ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι· ὥστε καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ μέσον ἐστίν. καί ἐστιν ἴσον τῷ ΔΛ· μέσον ἄρα καὶ τὸ ΔΛ. καὶ παράκειται παρὰ ῥητὴν τὴν ΔΕ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΜΔ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΜΗ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΜΛ, τουτέστι τῇ ΔΕ, μήκει· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΔΜ, ΜΗ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΓ τῇ ΓΒ μήκει, ὡς δὲ ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως τὸ ἀπὸ τῆς ΑΓ πρὸς τὸ ὑπὸ τῶν ΑΓΒ, ἀσύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΑΓ τῷ ὑπὸ τῶν ΑΓΒ. ὥστε καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ τῷ δὶς ὑπὸ τῶν ΑΓΒ ἀσύμμετρόν ἐστιν, τουτέστι τὸ ΔΛ τῷ ΜΖ· ὥστε καὶ ἡ ΔΜ τῇ ΜΗ ἀσύμμετρός ἐστιν. καί εἰσι ῥηταί· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
Δεικτέον [δή], ὅτι καὶ τρίτη.
Ὁμοίως δὴ τοῖς προτέροις ἐπιλογιούμεθα, ὅτι μείζων ἐστὶν ἡ ΔΜ τῆς ΜΗ, καὶ σύμμετρος ἡ ΔΚ τῇ ΚΜ. καί ἐστι τὸ ὑπὸ τῶν ΔΚΜ ἴσον τῷ ἀπὸ τῆς ΜΝ· ἡ ΔΜ ἄρα τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ οὐδετέρα τῶν ΔΜ, ΜΗ σύμμετρός ἐστι τῇ ΔΕ μήκει.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τρίτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ξγ΄ 63 Βιβλίον X
Τὸ ἀπὸ τῆς μείζονος παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τετάρτην.
Ἔστω μείζων ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ὥστε μείζονα εἶναι τὴν ΑΓ τῆς ΓΒ, ῥητὴ δὲ ἡ ΔΕ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΔΕ παραβεβλήσθω τὸ ΔΖ παραλληλόγραμμον πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶ τετάρτη.
Κατεσκευάσθω τὰ αὐτὰ τοῖς προδεδειγμένοις. καὶ ἐπεὶ μείζων ἐστὶν ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δὲ ὑπ' αὐτῶν μέσον. ἐπεὶ οὖν ῥητόν ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, ῥητὸν ἄρα ἐστὶ τὸ ΔΛ· ῥητὴ ἄρα καὶ ἡ ΔΜ καὶ σύμμετρος τῇ ΔΕ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, τουτέστι τὸ ΜΖ, καὶ παρὰ ῥητήν ἐστι τὴν ΜΛ, ῥητὴ ἄρα ἐστὶ καὶ ἡ ΜΗ καὶ ἀσύμμετρος τῇ ΔΕ μήκει· ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΔΜ τῇ ΜΗ μήκει. αἱ ΔΜ, ΜΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
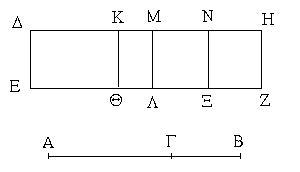
Δεικτέον [δή], ὅτι καὶ τετάρτη.
Ὁμοίως δὴ δείξομεν τοῖς πρότερον, ὅτι μείζων ἐστὶν ἡ ΔΜ τῆς ΜΗ, καὶ ὅτι τὸ ὑπὸ ΔΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΜΝ. ἐπεὶ οὖν ἀσύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΓ τῷ ἀπὸ τῆς ΓΒ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΔΘ τῷ ΚΛ· ὥστε ἀσύμμετρος καὶ ἡ ΔΚ τῇ ΚΜ ἐστιν. ἐὰν δὲ ὦσι δύο εὐθεῖαι ἄνισοι, τῷ δὲ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ἐλάσσονος ἴσον παραλληλόγραμμον παρὰ τὴν μείζονα παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς ἀσύμμετρα αὐτὴν διαιρῇ, ἡ μείζων τῆς ἐλάσσονος μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει· ἡ ΔΜ ἄρα τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΔΜ, ΜΗ ῥηταὶ δυνάμει μόνον σύμμετροι, καὶ ἡ ΔΜ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΔΕ.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τετάρτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ξδ΄ 64 Βιβλίον X
Τὸ ἀπὸ τῆς ῥητὸν καὶ μέσον δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πέμπτην.
Ἔστω ῥητὸν καὶ μέσον δυναμένη ἡ ΑΒ διῃρημένη εἰς τὰς εὐθείας κατὰ τὸ Γ, ὥστε μείζονα εἶναι τὴν ΑΓ, καὶ ἐκκείσθω ῥητὴ ἡ ΔΕ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΔΕ παραβεβλήσθω τὸ ΔΖ πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶ πέμπτη.
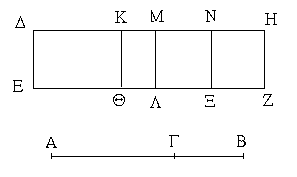
Κατεσκευάσθω τὰ αὐτὰ τοῖς πρὸ τούτου. ἐπεὶ οὖν ῥητὸν καὶ μέσον δυναμένη ἐστὶν ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν. ἐπεὶ οὖν μέσον ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, μέσον ἄρα ἐστὶ τὸ ΔΛ· ὥστε ῥητή ἐστιν ἡ ΔΜ καὶ μήκει ἀσύμμετρος τῇ ΔΕ. πάλιν, ἐπεὶ ῥητόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΓΒ, τουτέστι τὸ ΜΖ, ῥητὴ ἄρα ἡ ΜΗ καὶ σύμμετρος τῇ ΔΕ. ἀσύμμετρος ἄρα ἡ ΔΜ τῇ ΜΗ· αἱ ΔΜ, ΜΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
Λέγω δή, ὅτι καὶ πέμπτη.
Ὁμοίως γὰρ δειχθήσεται, ὅτι τὸ ὑπὸ τῶν ΔΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΜΝ, καὶ ἀσύμμετρος ἡ ΔΚ τῇ ΚΜ μήκει· ἡ ΔΜ ἄρα τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί εἰσιν αἱ ΔΜ, ΜΗ [ῥηταὶ] δυνάμει μόνον σύμμετροι, καὶ ἡ ἐλάσσων ἡ ΜΗ σύμμετρος τῇ ΔΕ μήκει.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶ πέμπτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ξε΄ 65 Βιβλίον X
Τὸ ἀπὸ τῆς δύο μέσα δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων ἕκτην.
Ἔστω δύο μέσα δυναμένη ἡ ΑΒ διῃρημένη κατὰ τὸ Γ, ῥητὴ δὲ ἔστω ἡ ΔΕ. καὶ παρὰ τὴν ΔΕ τῷ ἀπὸ τῆς ΑΒ ἴσον παραβεβλήσθω τὸ ΔΖ πλάτος ποιοῦν τὴν ΔΗ· λέγω, ὅτι ἡ ΔΗ ἐκ δύο ὀνομάτων ἐστὶν ἕκτη.
Κατεσκευάσθω γὰρ τὰ αὐτὰ τοῖς πρότερον. καὶ ἐπεὶ ἡ ΑΒ δύο μέσα δυναμένη ἐστὶ διῃρημένη κατὰ τὸ Γ, αἱ ΑΓ, ΓΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τὸ ἐκ τῶν ἀπ' αὐτῶν τετραγώνων συγκείμενον τῷ ὑπ' αὐτῶν· ὥστε κατὰ τὰ προδεδειγμένα μέσον ἐστὶν ἑκάτερον τῶν ΔΛ, ΜΖ. καὶ παρὰ ῥητὴν τὴν ΔΕ παράκειται· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΔΜ, ΜΗ καὶ ἀσύμμετρος τῇ ΔΕ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, ἀσύμμετρον ἄρα ἐστὶ τὸ ΔΛ τῷ ΜΖ. ἀσύμμετρος ἄρα καὶ ἡ ΔΜ τῇ ΜΗ· αἱ ΔΜ, ΜΗ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΔΗ.
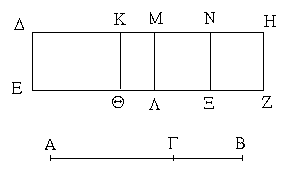
Λέγω δή, ὅτι καὶ ἕκτη.
Ὁμοίως δὴ πάλιν δείξομεν, ὅτι τὸ ὑπὸ τῶν ΔΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΜΝ, καὶ ὅτι ἡ ΔΚ τῇ ΚΜ μήκει ἐστὶν ἀσύμμετρος· καὶ διὰ τὰ αὐτὰ δὴ ἡ ΔΜ τῆς ΜΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει. καὶ οὐδετέρα τῶν ΔΜ, ΜΗ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΔΕ μήκει.
Ἡ ΔΗ ἄρα ἐκ δύο ὀνομάτων ἐστὶν ἕκτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ξε΄ 66 Βιβλίον X
Ἡ τῇ ἐκ δύο ὀνομάτων μήκει σύμμετρος καὶ αὐτὴ ἐκ δύο ὀνομάτων ἐστὶ καὶ τῇ τάξει ἡ αὐτή.
Ἔστω ἐκ δύο ὀνομάτων ἡ ΑΒ, καὶ τῇ ΑΒ μήκει σύμμετρος ἔστω ἡ ΓΔ· λέγω, ὅτι ἡ ΓΔ ἐκ δύο ὀνομάτων ἐστὶ καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ γὰρ ἐκ δύο ὀνομάτων ἐστὶν ἡ ΑΒ, διῃρήσθω εἰς τὰ ὀνόματα κατὰ τὸ Ε, καὶ ἔστω μεῖζον ὄνομα τὸ ΑΕ· αἱ ΑΕ, ΕΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. γεγονέτω ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΑΕ πρὸς τὴν ΓΖ· καὶ λοιπὴ ἄρα ἡ ΕΒ πρὸς λοιπὴν τὴν ΖΔ ἐστιν, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ μήκει. σύμμετρος ἄρα ἐστὶ καὶ ἡ μὲν ΑΕ τῇ ΓΖ, ἡ δὲ ΕΒ τῇ ΖΔ. καί εἰσι ῥηταὶ αἱ ΑΕ, ΕΒ· ῥηταὶ ἄρα εἰσὶ καὶ αἱ ΓΖ, ΖΔ. καὶ [ἐπεί] ἐστιν ὡς ἡ ΑΕ πρὸς ΓΖ, ἡ ΕΒ πρὸς ΖΔ. ἐναλλὰξ ἄρα ἐστὶν ὡς ἡ ΑΕ πρὸς ΕΒ, ἡ ΓΖ πρὸς ΖΔ. αἱ δὲ ΑΕ, ΕΒ δυνάμει μόνον [εἰσὶ] σύμμετροι· καὶ αἱ ΓΖ, ΖΔ ἄρα δυνάμει μόνον εἰσὶ σύμμετροι. καί εἰσι ῥηταί· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΓΔ.
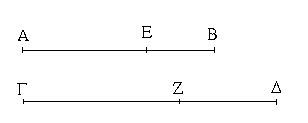
Λέγω δή, ὅτι τῇ τάξει ἐστὶν ἡ αὐτὴ τῇ ΑΒ.
Ἡ γὰρ ΑΕ τῆς ΕΒ μεῖζον δύναται ἤτοι τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου. εἰ μὲν οὖν ἡ ΑΕ τῆς ΕΒ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ ΓΖ τῆς ΖΔ μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΑΕ τῇ ἐκκειμένῃ ῥητῇ, καὶ ἡ ΓΖ σύμμετρος αὐτῇ ἔσται, καὶ διὰ τοῦτο ἑκατέρα τῶν ΑΒ, ΓΔ ἐκ δύο ὀνομάτων ἐστὶ πρώτη, τουτέστι τῇ τάξει ἡ αὐτή. εἰ δὲ ἡ ΕΒ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ, καὶ ἡ ΖΔ σύμμετρός ἐστιν αὐτῇ, καὶ διὰ τοῦτο πάλιν τῇ τάξει ἡ αὐτὴ ἔσται τῇ ΑΒ· ἑκατέρα γὰρ αὐτῶν ἔσται ἐκ δύο ὀνομάτων δευτέρα. εἰ δὲ οὐδετέρα τῶν ΑΕ, ΕΒ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ, οὐδετέρα τῶν ΓΖ, ΖΔ σύμμετρος αὐτῇ ἔσται, καί ἐστιν ἑκατέρα τρίτη. εἰ δὲ ἡ ΑΕ τῆς ΕΒ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ἡ ΓΖ τῆς ΖΔ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ εἰ μὲν ἡ ΑΕ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ, καὶ ἡ ΓΖ σύμμετρός ἐστιν αὐτῇ, καί ἐστιν ἑκατέρα τετάρτη. εἰ δὲ ἡ ΕΒ, καὶ ἡ ΖΔ, καὶ ἔσται ἑκατέρα πέμπτη. εἰ δὲ οὐδετέρα τῶν ΑΕ, ΕΒ, καὶ τῶν ΓΖ, ΖΔ οὐδετέρα σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ, καὶ ἔσται ἑκατέρα ἕκτη.
Ὥστε ἡ τῇ ἐκ δύο ὀνομάτων μήκει σύμμετρος ἐκ δύο ὀνομάτων ἐστὶ καὶ τῇ τάξει ἡ αὐτή· ὅπερ ἔδει δεῖξαι.
Πρότασις ξζ΄ 67 Βιβλίον X
Ἡ τῇ ἐκ δύο μέσων μήκει σύμμετρος καὶ αὐτὴ ἐκ δύο μέσων ἐστὶ καὶ τῇ τάξει ἡ αὐτή.
Ἔστω ἐκ δύο μέσων ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἔστω μήκει ἡ ΓΔ· λέγω, ὅτι ἡ ΓΔ ἐκ δύο μέσων ἐστὶ καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ γὰρ ἐκ δύο μέσων ἐστὶν ἡ ΑΒ, διῃρήσθω εἰς τὰς μέσας κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. καὶ γεγονέτω ὡς ἡ ΑΒ πρὸς ΓΔ, ἡ ΑΕ πρὸς ΓΖ· καὶ λοιπὴ ἄρα ἡ ΕΒ πρὸς λοιπὴν τὴν ΖΔ ἐστιν, ὡς ἡ ΑΒ πρὸς ΓΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ μήκει· σύμμετρος ἄρα καὶ ἑκατέρα τῶν ΑΕ, ΕΒ ἑκατέρᾳ τῶν ΓΖ, ΖΔ. μέσαι δὲ αἱ ΑΕ, ΕΒ· μέσαι ἄρα καὶ αἱ ΓΖ, ΖΔ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΕ πρὸς ΕΒ, ἡ ΓΖ πρὸς ΖΔ, αἱ δὲ ΑΕ, ΕΒ δυνάμει μόνον σύμμετροί εἰσιν, καὶ αἱ ΓΖ, ΖΔ [ἄρα] δυνάμει μόνον σύμμετροί εἰσιν. ἐδείχθησαν δὲ καὶ μέσαι· ἡ ΓΔ ἄρα ἐκ δύο μέσων ἐστίν.
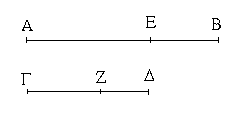
Λέγω δή, ὅτι καὶ τῇ τάξει ἡ αὐτή ἐστι τῇ ΑΒ.
Ἐπεὶ γάρ ἐστιν ὡς ἡ ΑΕ πρὸς ΕΒ, ἡ ΓΖ πρὸς ΖΔ, καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ὑπὸ τῶν ΓΖΔ· ἐναλλὰξ ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΓΖ, οὕτως τὸ ὑπὸ τῶν ΑΕΒ πρὸς τὸ ὑπὸ τῶν ΓΖΔ. σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΕ τῷ ἀπὸ τῆς ΓΖ· σύμμετρον ἄρα καὶ τὸ ὑπὸ τῶν ΑΕΒ τῷ ὑπὸ τῶν ΓΖΔ. εἴτε οὖν ῥητόν ἐστι τὸ ὑπὸ τῶν ΑΕΒ, καὶ τὸ ὑπὸ τῶν ΓΖΔ ῥητόν ἐστιν [καὶ διὰ τοῦτό ἐστιν ἐκ δύο μέσων πρώτη]. εἴτε μέσον, μέσον, καί ἐστιν ἑκατέρα δευτέρα
.Καὶ διὰ τοῦτο ἔσται ἡ ΓΔ τῇ ΑΒ τῇ τάξει ἡ αὐτή· ὅπερ ἔδει δεῖξαι.
Πρότασις ξη΄ 68 Βιβλίον X
Ἡ τῇ μείζονι σύμμετρος καὶ αὐτὴ μείζων ἐστίν.
Ἔστω μείζων ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἔστω ἡ ΓΔ· λέγω, ὅτι ἡ ΓΔ μείζων ἐστίν.
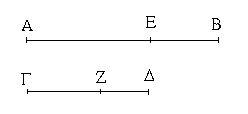
Διῃρήσθω ἡ ΑΒ κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον· καὶ γεγονέτω τὰ αὐτὰ τοῖς πρότερον. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἥ τε ΑΕ πρὸς τὴν ΓΖ καὶ ἡ ΕΒ πρὸς τὴν ΖΔ, καὶ ὡς ἄρα ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΒ πρὸς τὴν ΖΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ. σύμμετρος ἄρα καὶ ἑκατέρα τῶν ΑΕ, ΕΒ ἑκατέρᾳ τῶν ΓΖ, ΖΔ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΒ πρὸς τὴν ΖΔ, καὶ ἐναλλὰξ ὡς ἡ ΑΕ πρὸς ΕΒ, οὕτως ἡ ΓΖ πρὸς ΖΔ, καὶ συνθέντι ἄρα ἐστὶν ὡς ἡ ΑΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΓΔ πρὸς τὴν ΔΖ· καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΕ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΔΖ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ὡς τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΑΕ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΓΖ. καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΒ πρὸς τὰ ἀπὸ τῶν ΑΕ, ΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὰ ἀπὸ τῶν ΓΖ, ΖΔ· καὶ ἐναλλὰξ ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΓΔ, οὕτως τὰ ἀπὸ τῶν ΑΕ, ΕΒ πρὸς τὰ ἀπὸ τῶν ΓΖ, ΖΔ. σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΓΔ· σύμμετρα ἄρα καὶ τὰ ἀπὸ τῶν ΑΕ, ΕΒ τοῖς ἀπὸ τῶν ΓΖ, ΖΔ. καί ἐστι τὰ ἀπὸ τῶν ΑΕ, ΕΒ ἅμα ῥητόν, καὶ τὰ ἀπὸ τῶν ΓΖ, ΖΔ ἅμα ῥητόν ἐστιν. ὁμοίως δὲ καὶ τὸ δὶς ὑπὸ τῶν ΑΕ, ΕΒ σύμμετρόν ἐστι τῷ δὶς ὑπὸ τῶν ΓΖ, ΖΔ. καί ἐστι μέσον τὸ δὶς ὑπὸ τῶν ΑΕ, ΕΒ· μέσον ἄρα καὶ τὸ δὶς ὑπὸ τῶν ΓΖ, ΖΔ. αἱ ΓΖ, ΖΔ ἄρα δυνάμει ἀσύμμετροί εἰσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ἅμα ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον· ὅλη ἄρα ἡ ΓΔ ἄλογός ἐστιν ἡ καλουμένη μείζων.
Ἡ ἄρα τῇ μείζονι σύμμετρος μείζων ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ξθ΄ 69 Βιβλίον X
Ἡ τῇ ῥητὸν καὶ μέσον δυναμένῃ σύμμετρος [καὶ αὐτὴ] ῥητὸν καὶ μέσον δυναμένη ἐστίν.
Ἔστω ῥητὸν καὶ μέσον δυναμένη ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἔστω ἡ ΓΔ· δεικτέον, ὅτι καὶ ἡ ΓΔ ῥητὸν καὶ μέσον δυναμένη ἐστίν.
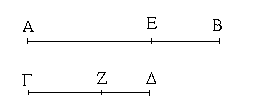
Διῃρήσθω ἡ ΑΒ εἰς τὰς εὐθείας κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν· καὶ τὰ αὐτὰ κατεσκευάσθω τοῖς πρότερον. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ΓΖ, ΖΔ δυνάμει εἰσὶν ἀσύμμετροι, καὶ σύμμετρον τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ, τὸ δὲ ὑπὸ ΑΕ, ΕΒ τῷ ὑπὸ ΓΖ, ΖΔ· ὥστε καὶ τὸ [μὲν] συγκείμενον ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων ἐστὶ μέσον, τὸ δ' ὑπὸ τῶν ΓΖ, ΖΔ ῥητόν.
Ῥητὸν ἄρα καὶ μέσον δυναμένη ἐστὶν ἡ ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις ο΄ 70 Βιβλίον X
Ἡ τῇ δύο μέσα δυναμένῃ σύμμετρος δύο μέσα δυναμένη ἐστίν.
Ἔστω δύο μέσα δυναμένη ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἡ ΓΔ· δεικτέον, ὅτι καὶ ἡ ΓΔ δύο μέσα δυναμένη ἐστίν.
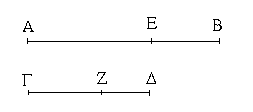
Ἔπεὶ γὰρ δύο μέσα δυναμένη ἐστὶν ἡ ΑΒ, διῃρήσθω εἰς τὰς εὐθείας κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν [τετραγώνων] μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων τῷ ὑπὸ τῶν ΑΕ, ΕΒ· καὶ κατεσκευάσθω τὰ αὐτὰ τοῖς πρότερον. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ΓΖ, ΖΔ δυνάμει εἰσὶν ἀσύμμετροι καὶ σύμμετρον τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ, τὸ δὲ ὑπὸ τῶν ΑΕ, ΕΒ τῷ ὑπὸ τῶν ΓΖ, ΖΔ· ὥστε καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων μέσον ἐστὶ καὶ τὸ ὑπὸ τῶν ΓΖ, ΖΔ μέσον καὶ ἔτι ἀσύμμετρον τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων τῷ ὑπὸ τῶν ΓΖ, ΖΔ.
Ἡ ἄρα ΓΔ δύο μέσα δυναμένη ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις οα΄ 71 Βιβλίον X
Ῥητοῦ καὶ μέσου συντιθεμένου τέσσαρες ἄλογοι γίγνονται ἤτοι ἐκ δύο ὀνομάτων ἢ ἐκ δύο μέσων πρώτη ἢ μείζων ἢ ῥητὸν καὶ μέσον δυναμένη.
Ἔστω ῥητὸν μὲν τὸ ΑΒ, μέσον δὲ τὸ ΓΔ· λέγω, ὅτι ἡ τὸ ΑΔ χωρίον δυναμένη ἤτοι ἐκ δύο ὀνομάτων ἐστὶν ἢ ἐκ δύο μέσων πρώτη ἢ μείζων ἢ ῥητὸν καὶ μέσον δυναμένη.
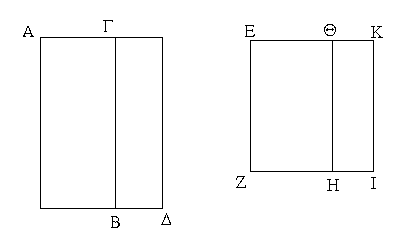
Τὸ γὰρ ΑΒ τοῦ ΓΔ ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. ἔστω πρότερον μεῖζον· καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ παραβεβλήσθω παρὰ τὴν ΕΖ τῷ ΑΒ ἴσον τὸ ΕΗ πλάτος ποιοῦν τὴν ΕΘ· τῷ δὲ ΔΓ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΘΙ πλάτος ποιοῦν τὴν ΘΚ. καὶ ἐπεὶ ῥητόν ἐστι τὸ ΑΒ καί ἐστιν ῥητόν ἐστι τὸ ΑΒ καί ἐστιν ἴσον τῷ ΕΗ, ῥητὸν ἄρα καὶ τὸ ΕΗ. καὶ παρὰ [ῥητὴν] τὴν ΕΖ παραβέβληται πλάτος ποιοῦν τὴν ΕΘ· ἡ ΕΘ ἄρα ῥητή ἐστι καὶ σύμμετρος τῇ ΕΖ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ ΓΔ καί ἐστιν ἴσον τῷ ΘΙ, μέσον ἄρα ἐστὶ καὶ τὸ ΘΙ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΘΚ· ῥητὴ ἄρα ἐστὶν ἡ ΘΚ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ μέσον ἐστὶ τὸ ΓΔ, ῥητὸν δὲ τὸ ΑΒ, ἀσύμμετρον ἄρα ἐστὶ τὸ ΑΒ τῷ ΓΔ· ὥστε καὶ τὸ ΕΗ ἀσύμμετρόν ἐστι τῷ ΘΙ. ὡς δὲ τὸ ΕΗ πρὸς τὸ ΘΙ, οὕτως ἐστὶν ἡ ΕΘ πρὸς τὴν ΘΚ· ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΕΘ τῇ ΘΚ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΕΘ, ΘΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΚ διῃρημένη κατὰ τὸ Θ. καὶ ἐπεὶ μεῖζόν ἐστι τὸ ΑΒ τοῦ ΓΔ, ἴσον δὲ τὸ μὲν ΑΒ τῷ ΕΗ, τὸ δὲ ΓΔ τῷ ΘΙ, μεῖζον ἄρα καὶ τὸ ΕΗ τοῦ ΘΙ· καὶ ἡ ΕΘ ἄρα μείζων ἐστὶ τῆς ΘΚ. ἤτοι οὖν ἡ ΕΘ τῆς ΘΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει ἢ τῷ ἀπὸ ἀσυμμέτρου. δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου ἑαυτῇ. καί ἐστιν ἡ μείζων ἡ ΘΕ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶ πρώτη. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων πρώτης, ἡ τὸ χωρίον δυναμένη ἐκ δύο ὀνομάτων ἐστίν. ἡ ἄρα τὸ ΕΙ δυναμένη ἐκ δύο ὀνομάτων ἐστίν· ὥστε καὶ ἡ τὸ ΑΔ δυναμένη ἐκ δύο ὀνομάτων ἐστίν. ἀλλὰ δὴ δυνάσθω ἡ ΕΘ τῆς ΘΚ μεῖζον τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ· καί ἐστιν ἡ μείζων ἡ ΕΘ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ μήκει· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶ τετάρτη. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων τετάρτης, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη μείζων. ἡ ἄρα τὸ ΕΙ χωρίον δυναμένη μείζων ἐστίν· ὥστε καὶ ἡ τὸ ΑΔ δυναμένη μείζων ἐστίν.
Ἀλλὰ δὴ ἔστω ἔλασσον τὸ ΑΒ τοῦ ΓΔ· καὶ τὸ ΕΗ ἄρα ἔλασσόν ἐστι τοῦ ΘΙ· ὥστε καὶ ἡ ΕΘ ἐλάσσων ἐστὶ τῆς ΘΚ. ἤτοι δὲ ἡ ΘΚ τῆς ΕΘ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου. δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει· καί ἐστιν ἡ ἐλάσσων ἡ ΕΘ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ μήκει· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶ δευτέρα. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων δευτέρας, ἡ τὸ χωρίον δυναμένη ἐκ δύο μέσων ἐστὶ πρώτη. ἡ ἄρα τὸ ΕΙ χωρίον δυναμένη ἐκ δύο μέσων ἐστὶ πρώτη· ὥστε καὶ ἡ τὸ ΑΔ δυναμένη ἐκ δύο μέσων ἐστὶ πρώτη. ἀλλὰ δὴ ἡ ΘΚ τῆς ΘΕ μεῖζον δυνάσθω τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί ἐστιν ἡ ἐλάσσων ἡ ΕΘ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶ πέμπτη. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων πέμπτης, ἡ τὸ χωρίον δυναμένη ῥητὸν καὶ μέσον δυναμένη ἐστίν. ἡ ἄρα τὸ ΕΙ χωρίον δυναμένη ῥητὸν καὶ μέσον δυναμένη ἐστίν· ὥστε καὶ ἡ τὸ ΑΔ χωρίον δυναμένη ῥητὸν καὶ μέσον δυναμένη ἐστίν.
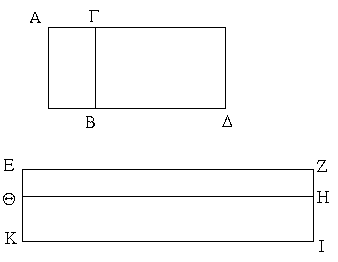
Ῥητοῦ ἄρα καὶ μέσου συντιθεμένου τέσσαρες ἄλογοι γίγνονται ἤτοι ἐκ δύο ὀνομάτων ἢ ἐκ δύο μέσων πρώτη ἢ μείζων ἢ ῥητὸν καὶ μέσον δυναμένη· ὅπερ ἔδει δεῖξαι.
Πρότασις οβ΄ 72 Βιβλίον X
Δύο μέσων ἀσυμμέτρων ἀλλήλοις συντιθεμένων αἱ λοιπαὶ δύο ἄλογοι γίγνονται ἤτοι ἐκ δύο μέσων δευτέρα ἢ [ἡ] δύο μέσα δυναμένη.
Συγκείσθω γὰρ δύο μέσα ἀσύμμετρα ἀλλήλοις τὰ ΑΒ, ΓΔ· λέγω, ὅτι ἡ τὸ ΑΔ χωρίον δυναμένη ἤτοι ἐκ δύο μέσων ἐστὶ δευτέρα ἢ δύο μέσα δυναμένη.
Τὸ γὰρ ΑΒ τοῦ ΓΔ ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. ἔστω, εἰ τύχοι, πρότερον μεῖζον τὸ ΑΒ τοῦ ΓΔ· καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τῷ μὲν ΑΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΗ πλάτος ποιοῦν τὴν ΕΘ, τῷ δὲ ΓΔ ἴσον τὸ ΘΙ πλάτος ποιοῦν τὴν ΘΚ. καὶ ἐπεὶ μέσον ἐστὶν ἑκάτερον τῶν ΑΒ, ΓΔ, μέσον ἄρα καὶ ἑκάτερον τῶν ΕΗ, ΘΙ. καὶ παρὰ ῥητὴν τὴν ΖΕ παράκειται πλάτος ποιοῦν τὰς ΕΘ, ΘΚ· ἑκατέρα ἄρα τῶν ΕΘ, ΘΚ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΑΒ τῷ ΓΔ, καί ἐστιν ἴσον τὸ μὲν ΑΒ τῷ ΕΗ, τὸ δὲ ΓΔ τῷ ΘΙ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΕΗ τῷ ΘΙ. ὡς δὲ τὸ ΕΗ πρὸς τὸ ΘΙ, οὕτως ἐστὶν ἡ ΕΘ πρὸς ΘΚ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΘ τῇ ΘΚ μήκει. αἱ ΕΘ, ΘΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΚ. ἤτοι δὲ ἡ ΕΘ τῆς ΘΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου. δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει· καὶ οὐδετέρα τῶν ΕΘ, ΘΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ μήκει· ἡ ΕΚ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τρίτη. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων τρίτης, ἡ τὸ χωρίον δυναμένη ἐκ δύο μέσων ἐστὶ δευτέρα· ἡ ἄρα τὸ ΕΙ, τουτέστι τὸ ΑΔ, δυναμένη ἐκ δύο μέσων ἐστὶ δευτέρα. ἀλλὰ δὴ ἡ ΕΘ τῆς ΘΚ μεῖζον δυνάσθω τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει· καὶ ἀσύμμετρός ἐστιν ἑκατέρα τῶν ΕΘ, ΘΚ τῇ ΕΖ μήκει· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶν ἕκτη. ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων ἕκτης, ἡ τὸ χωρίον δυναμένη ἡ δύο μέσα δυναμένη ἐστίν· ὥστε καὶ ἡ τὸ ΑΔ χωρίον δυναμένη ἡ δύο μέσα δυναμένη ἐστίν.
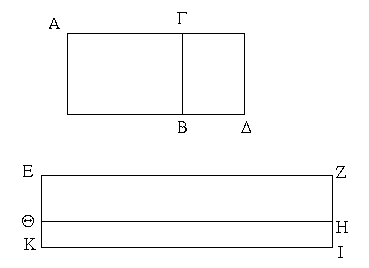
[Ὁμοίως δὴ δείξομεν, ὅτι κἂν ἔλαττον ᾖ τὸ ΑΒ τοῦ ΓΔ, ἡ τὸ ΑΔ χωρίον δυναμένη ἢ ἐκ δύο μέσων δευτέρα ἐστὶν ἤτοι δύο μέσα δυναμένη].
Δύο ἄρα μέσων ἀσυμμέτρων ἀλλήλοις συντιθεμένων αἱ λοιπαὶ δύο ἄλογοι γίγνονται ἤτοι ἐκ δύο μέσων δευτέρα ἢ δύο μέσα δυναμένη.
Ἡ ἐκ δύο ὀνομάτων καὶ αἱ μετ' αὐτὴν ἄλογοι οὔτε τῇ μέσῃ οὔτε ἀλλήλαις εἰσὶν αἱ αὐταί. τὸ μὲν γὰρ ἀπὸ μέσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ῥητὴν καὶ ἀσύμμετρον τῇ παρ' ἣν παράκειται μήκει. τὸ δὲ ἀπὸ τῆς ἐκ δύο ὀνομάτων παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πρώτην. τὸ δὲ ἀπὸ τῆς ἐκ δύο μέσων πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων δευτέραν. τὸ δὲ ἀπὸ τῆς ἐκ δύο μέσων δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τρίτην. τὸ δὲ ἀπὸ τῆς μείζονος παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τετάρτην. τὸ δὲ ἀπὸ τῆς ῥητὸν καὶ μέσον δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πέμπτην. τὸ δὲ ἀπὸ τῆς δύο μέσα δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων ἕκτην. τὰ δ' εἰρημένα πλάτη διαφέρει τοῦ τε πρώτου καὶ ἀλλήλων, τοῦ μὲν πρώτου, ὅτι ῥητή ἐστιν, ἀλλήλων δέ, ὅτι τῇ τάξει οὐκ εἰσὶν αἱ αὐταί· ὥστε καὶ αὐταὶ αἱ ἄλογοι διαφέρουσιν ἀλλήλων.
Πρότασις ογ΄ 73 Βιβλίον X
Ἐὰν ἀπὸ ῥητῆς ῥητὴ ἀφαιρεθῇ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ ἀποτομή.
Ἀπὸ γὰρ ῥητῆς τῆς ΑΒ ῥητὴ ἀφῃρήσθω ἡ ΒΓ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ· λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.

Ἐπεὶ γὰρ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει, καί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ὑπὸ τῶν ΑΒ, ΒΓ, ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τῷ ὑπὸ τῶν ΑΒ, ΒΓ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΒ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα, τῷ δὲ ὑπὸ τῶν ΑΒ, ΒΓ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. καὶ ἐπειδήπερ τὰ ἀπὸ τῶν ΑΒ, ΒΓ ἴσα ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ μετὰ τοῦ ἀπὸ ΓΑ, καὶ λοιπῷ ἄρα τῷ ἀπὸ τῆς ΑΓ ἀσύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ. ῥητὰ δὲ τὰ ἀπὸ τῶν ΑΒ, ΒΓ· ἄλογος ἄρα ἐστὶν ἡ ΑΓ· καλείσθω δὲ ἀποτομή. ὅπερ ἔδει δεῖξαι.
Πρότασις οδ΄ 74 Βιβλίον X
Ἐὰν ἀπὸ μέσης μέση ἀφαιρεθῇ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ῥητὸν περιέχουσα, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ μέσης ἀποτομὴ πρώτη.
Ἀπὸ γὰρ μέσης τῆς ΑΒ μέση ἀφῃρήσθω ἡ ΒΓ δυνάμει μόνον σύμμετρος οὖσα τῇ ΑΒ, μετὰ δὲ τῆς ΑΒ ῥητὸν ποιοῦσα τὸ ὑπὸ τῶν ΑΒ, ΒΓ· λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν· καλείσθω δὲ μέσης ἀποτομὴ πρώτη.

Ἐπεὶ γὰρ αἱ ΑΒ, ΒΓ μέσαι εἰσίν, μέσα ἐστὶ καὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ. ῥητὸν δὲ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἀσύμμετρα ἄρα τὰ ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· καὶ λοιπῷ ἄρα τῷ ἀπὸ τῆς ΑΓ ἀσύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, ἐπεὶ κἂν τὸ ὅλον ἑνὶ αὐτῶν ἀσύμμετρον ᾖ, καὶ τὰ ἐξ ἀρχῆς μεγέθη ἀσύμμετρα ἔσται. ῥητὸν δὲ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἄλογον ἄρα τὸ ἀπὸ τῆς ΑΓ· ἄλογος ἄρα ἐστὶν ἡ ΑΓ· καλείσθω δὲ μέσης ἀποτομὴ πρώτη.
Πρότασις οε΄ 75 Βιβλίον X
Ἐὰν ἀπὸ μέσης μέση ἀφαιρεθῇ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλη, μετὰ δὲ τῆς ὅλης μέσον περιέχουσα, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ μέσης ἀποτομὴ δευτέρα.
Ἀπὸ γὰρ μέσης τῆς ΑΒ μέση ἀφῃρήσθω ἡ ΓΒ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ τῇ ΑΒ, μετὰ δὲ τῆς ὅλης τῆς ΑΒ μέσον περιέχουσα τὸ ὑπὸ τῶν ΑΒ, ΒΓ· λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν· καλείσθω δὲ μέσης ἀποτομὴ δευτέρα.
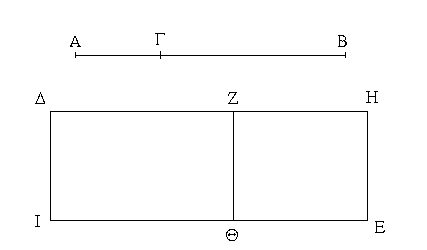
Ἐκκείσθω γὰρ ῥητὴ ἡ ΔΙ, καὶ τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ ἴσον παρὰ τὴν ΔΙ παραβεβλήσθω τὸ ΔΕ πλάτος ποιοῦν τὴν ΔΗ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ἴσον παρὰ τὴν ΔΙ παραβεβλήσθω τὸ ΔΘ πλάτος ποιοῦν τὴν ΔΖ· λοιπὸν ἄρα τὸ ΖΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ. καὶ ἐπεὶ μέσα καὶ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ, μέσον ἄρα καὶ τὸ ΔΕ. καὶ παρὰ ῥητὴν τὴν ΔΙ παράκειται πλάτος ποιοῦν τὴν ΔΗ· ῥητὴ ἄρα ἐστὶν ἡ ΔΗ καὶ ἀσύμμετρος τῇ ΔΙ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ ὑπὸ τῶν ΑΒ, ΒΓ, καὶ τὸ δὶς ἄρα ὑπὸ τῶν ΑΒ, ΒΓ μέσον ἐστίν. καί ἐστιν ἴσον τῷ ΔΘ· καὶ τὸ ΔΘ ἄρα μέσον ἐστίν. καὶ παρὰ ῥητὴν τὴν ΔΙ παραβέβληται πλάτος ποιοῦν τὴν ΔΖ· ῥητὴ ἄρα ἐστὶν ἡ ΔΖ καὶ ἀσύμμετρος τῇ ΔΙ μήκει. καὶ ἐπεὶ αἱ ΑΒ, ΒΓ δυνάμει μόνον σύμμετροί εἰσιν, ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΒ τῇ ΒΓ μήκει· ἀσύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΑΒ τετράγωνον τῷ ὑπὸ τῶν ΑΒ, ΒΓ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΒ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ, τῷ δὲ ὑπὸ τῶν ΑΒ, ΒΓ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἀσύμμετρον ἄρα ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ τοῖς ἀπὸ τῶν ΑΒ, ΒΓ. ἴσον δὲ τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ τὸ ΔΕ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ τὸ ΔΘ· ἀσύμμετρον ἄρα [ἐστὶ] τὸ ΔΕ τῷ ΔΘ. ὡς δὲ τὸ ΔΕ πρὸς τὸ ΔΘ, οὕτως ἡ ΗΔ πρὸς τὴν ΔΖ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΗΔ τῇ ΔΖ. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΗΔ, ΔΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΖΗ ἄρα ἀποτομή ἐστιν. ῥητὴ δὲ ἡ ΔΙ· τὸ δὲ ὑπὸ ῥητῆς καὶ ἀλόγου περιεχόμενον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν. καὶ δύναται τὸ ΖΕ ἡ ΑΓ· ἡ ΑΓ ἄρα ἄλογός ἐστιν· καλείσθω δὲ μέσης ἀποτομὴ δευτέρα. ὅπερ ἔδει δεῖξαι.
Πρότασις ος΄ 76 Βιβλίον X
Ἐὰν ἀπὸ εὐθείας εὐθεῖα ἀφαιρεθῇ δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τὰ μὲν ἀπ' αὐτῶν ἅμα ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ ἐλάσσων.
Ἀπὸ γὰρ εὐθείας τῆς ΑΒ εὐθεῖα ἀφῃρήσθω ἡ ΒΓ δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ ποιοῦσα τὰ προκείμενα. λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
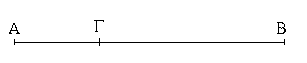
Ἐπεὶ γὰρ τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τετραγώνων ῥητόν ἐστιν, τὸ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ μέσον, ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· καὶ ἀναστρέψαντι λοιπῷ τῷ ἀπὸ τῆς ΑΓ ἀσύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ. ῥητὰ δὲ τὰ ἀπὸ τῶν ΑΒ, ΒΓ. ἄλογον ἄρα τὸ ἀπὸ τῆς ΑΓ· ἄλογος ἄρα ἡ ΑΓ· καλείσθω δὲ ἐλάσσων. ὅπερ ἔδει δεῖξαι.
Πρότασις οζ΄ 77 Βιβλίον X
Ἐὰν ἀπὸ εὐθείας εὐθεῖα ἀφαιρεθῇ δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δὲ δὶς ὑπ' αὐτῶν ῥητόν, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ ἡ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα.
Ἀπὸ γὰρ εὐθείας τῆς ΑΒ εὐθεῖα ἀφῃρήσθω ἡ ΒΓ δυνάμει ἀσύμμετρος οὖσα τῇ ΑΒ ποιοῦσα τὰ προκείμενα· λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν ἡ προειρημένη
.
Ἐπεὶ γὰρ τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τετραγώνων μέσον ἐστίν, τὸ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ῥητόν, ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· καὶ λοιπὸν ἄρα τὸ ἀπὸ τῆς ΑΓ ἀσύμμετρόν ἐστι τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. καί ἐστι τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ῥητόν· τὸ ἄρα ἀπὸ τῆς ΑΓ ἄλογόν ἐστιν· ἄλογος ἄρα ἐστὶν ἡ ΑΓ· καλείσθω δὲ ἡ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα. ὅπερ ἔδει δεῖξαι.
Πρότασις οη΄ 78 Βιβλίον X
Ἐὰν ἀπὸ εὐθείας εὐθεῖα ἀφαιρεθῇ δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον τό τε δὶς ὑπ' αὐτῶν μέσον καὶ ἔτι τὰ ἀπ' αὐτῶν τετράγωνα ἀσύμμετρα τῷ δὶς ὑπ' αὐτῶν, ἡ λοιπὴ ἄλογός ἐστιν· καλείσθω δὲ ἡ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα.
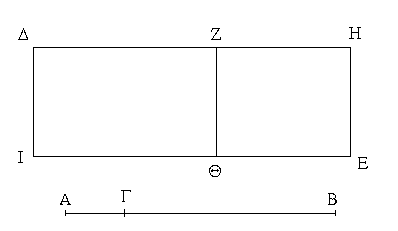
Ἀπὸ γὰρ εὐθείας τῆς ΑΒ εὐθεῖα ἀφῃρήσθω ἡ ΒΓ δυνάμει ἀσύμμετρος οὖσα τῇ ΑΒ ποιοῦσα τὰ προκείμενα· λέγω, ὅτι ἡ λοιπὴ ἡ ΑΓ ἄλογός ἐστιν ἡ καλουμένη ἡ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα. Ἐκκείσθω γὰρ ῥητὴ ἡ ΔΙ, καὶ τοῖς μὲν ἀπὸ τῶν ΑΒ, ΒΓ ἴσον παρὰ τὴν ΔΙ παραβεβλήσθω τὸ ΔΕ πλάτος ποιοῦν τὴν ΔΗ, τῷ δὲ δὶς ὑπὸ τῶν ΑΒ, ΒΓ ἴσον ἀφῃρήσθω τὸ ΔΘ [πλάτος ποιοῦν τὴν ΔΖ]. λοιπὸν ἄρα τὸ ΖΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ· ὥστε ἡ ΑΓ δύναται τὸ ΖΕ. καὶ ἐπεὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΒ, ΒΓ τετραγώνων μέσον ἐστὶ καί ἐστιν ἴσον τῷ ΔΕ, μέσον ἄρα [ἐστὶ] τὸ ΔΕ. καὶ παρὰ ῥητὴν τὴν ΔΙ παράκειται πλάτος ποιοῦν τὴν ΔΗ· ῥητὴ ἄρα ἐστὶν ἡ ΔΗ καὶ ἀσύμμετρος τῇ ΔΙ μήκει. πάλιν, ἐπεὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ μέσον ἐστὶ καί ἐστιν ἴσον τῷ ΔΘ, τὸ ἄρα ΔΘ μέσον ἐστίν. καὶ παρὰ ῥητὴν τὴν ΔΙ παράκειται πλάτος ποιοῦν τὴν ΔΖ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΔΖ καὶ ἀσύμμετρος τῇ ΔΙ μήκει. καὶ ἐπεὶ ἀσύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ, ἀσύμμετρον ἄρα καὶ τὸ ΔΕ τῷ ΔΘ. ὡς δὲ τὸ ΔΕ πρὸς τὸ ΔΘ, οὕτως ἐστὶ καὶ ἡ ΔΗ πρὸς τὴν ΔΖ· ἀσύμμετρος ἄρα ἡ ΔΗ τῇ ΔΖ. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΗΔ, ΔΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ἀποτομὴ ἄρα ἐστὶν ἡ ΖΗ· ῥητὴ δὲ ἡ ΖΘ. τὸ δὲ ὑπὸ ῥητῆς καὶ ἀποτομῆς περιεχόμενον [ὀρθογώνιον] ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν. καὶ δύναται τὸ ΖΕ ἡ ΑΓ· ἡ ΑΓ ἄρα ἄλογός ἐστιν· καλείσθω δὲ ἡ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα. ὅπερ ἔδει δεῖξαι.
Πρότασις οθ΄ 79 Βιβλίον X
Τῇ ἀποτομῇ μία [μόνον] προσαρμόζει εὐθεῖα ῥητὴ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ.
Ἔστω ἀποτομὴ ἡ ΑΒ, προσαρμόζουσα δὲ αὐτῇ ἡ ΒΓ· αἱ ΑΓ, ΓΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· λέγω, ὅτι τῇ ΑΒ ἑτέρα οὐ προσαρμόζει ῥητὴ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ.

Εἰ γὰρ δυνατόν, προσαρμοζέτω ἡ ΒΔ· καὶ αἱ ΑΔ, ΔΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ ἐπεί, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ, τούτῳ ὑπερέχει καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ· τῷ γὰρ αὐτῷ τῷ ἀπὸ τῆς ΑΒ ἀμφότερα ὑπερέχει· ἐναλλὰξ ἄρα, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, τούτῳ ὑπερέχει [καὶ] τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. τὰ δὲ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ῥητὰ γὰρ ἀμφότερα. καὶ τὸ δὶς ἄρα ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ὅπερ ἐστὶν ἀδύνατον· μέσα γὰρ ἀμφότερα, μέσον δὲ μέσου οὐχ ὑπερέχει ῥητῷ. τῇ ἄρα ΑΒ ἑτέρα οὐ προσαρμόζει ῥητὴ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ.
Μία ἄρα μόνη τῇ ἀποτομῇ προσαρμόζει ῥητὴ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ· ὅπερ ἔδει δεῖξαι.
Πρότασις π΄ 80 Βιβλίον X
Τῇ μέσης ἀποτομῇ πρώτῃ μία μόνον προσαρμόζει εὐθεῖα μέση δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ῥητὸν περιέχουσα.
Ἔστω γὰρ μέσης ἀποτομὴ πρώτη ἡ ΑΒ, καὶ τῇ ΑΒ προσαρμοζέτω ἡ ΒΓ· αἱ ΑΓ, ΓΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι τὸ ὑπὸ τῶν ΑΓ, ΓΒ· λέγω, ὅτι τῇ ΑΒ ἑτέρα οὐ προσαρμόζει μέση δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ῥητὸν περιέχουσα.

Εἰ γὰρ δυνατόν, προσαρμοζέτω καὶ ἡ ΔΒ. αἱ ἄρα ΑΔ, ΔΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι τὸ ὑπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεί, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΔ, ΔΒ, τούτῳ ὑπερέχει καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ· τῷ γὰρ αὐτῷ [πάλιν] ὑπερέχουσι τῷ ἀπὸ τῆς ΑΒ· ἐναλλὰξ ἄρα, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, τούτῳ ὑπερέχει καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. τὸ δὲ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ῥητὰ γὰρ ἀμφότερα. καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ ἄρα τῶν ἀπὸ τῶν ΑΓ, ΓΒ [τετραγώνων] ὑπερέχει ῥητῷ· ὅπερ ἐστὶν ἀδύνατον· μέσα γάρ ἐστιν ἀμφότερα, μέσον δὲ μέσου οὐχ ὑπερέχει ῥητῷ.
Τῇ ἄρα μέσης ἀποτομῇ πρώτῃ μία μόνον προσαρμόζει εὐθεῖα μέση δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ῥητὸν περιέχουσα· ὅπερ ἔδει δεῖξαι.
Πρότασις πα΄ 81 Βιβλίον X
Τῇ μέσης ἀποτομῇ δευτέρᾳ μία μόνον προσαρμόζει εὐθεῖα μέση δυνάμει μόνον σύμμετρος τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης μέσον περιέχουσα.
Ἔστω μέσης ἀποτομὴ δευτέρα ἡ ΑΒ καὶ τῇ ΑΒ προσαρμόζουσα ἡ ΒΓ· αἱ ἄρα ΑΓ, ΓΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι τὸ ὑπὸ τῶν ΑΓ, ΓΒ· λέγω, ὅτι τῇ ΑΒ ἑτέρα οὐ προσαρμόσει εὐθεῖα μέση δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης μέσον περιέχουσα.
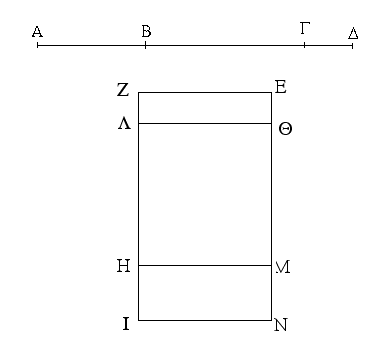
Εἰ γὰρ δυνατόν, προσαρμοζέτω ἡ ΒΔ· καὶ αἱ ΑΔ, ΔΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι τὸ ὑπὸ τῶν ΑΔ, ΔΒ. καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τοῖς μὲν ἀπὸ τῶν ΑΓ, ΓΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΗ πλάτος ποιοῦν τὴν ΕΜ· τῷ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον ἀφῃρήσθω τὸ ΘΗ πλάτος ποιοῦν τὴν ΘΜ· λοιπὸν ἄρα τὸ ΕΛ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ· ὥστε ἡ ΑΒ δύναται τὸ ΕΛ. πάλιν δὴ τοῖς ἀπὸ τῶν ΑΔ, ΔΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΙ πλάτος ποιοῦν τὴν ΕΝ· ἔστι δὲ καὶ τὸ ΕΛ ἴσον τῷ ἀπὸ τῆς ΑΒ τετραγώνῳ· λοιπὸν ἄρα τὸ ΘΙ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΔ, ΔΒ. καὶ ἐπεὶ μέσαι εἰσὶν αἱ ΑΓ, ΓΒ, μέσα ἄρα ἐστὶ καὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ. καί ἐστιν ἴσα τῷ ΕΗ· μέσον ἄρα καὶ τὸ ΕΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΕΜ· ῥητὴ ἄρα ἐστὶν ἡ ΕΜ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ ὑπὸ τῶν ΑΓ, ΓΒ, καὶ τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ μέσον ἐστίν. καί ἐστιν ἴσον τῷ ΘΗ· καὶ τὸ ΘΗ ἄρα μέσον ἐστίν. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΘΜ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΘΜ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ αἱ ΑΓ, ΓΒ δυνάμει μόνον σύμμετροί εἰσιν, ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΓ τῇ ΓΒ μήκει. ὡς δὲ ἡ ΑΓ πρὸς τὴν ΓΒ, οὕτως ἐστὶ τὸ ἀπὸ τῆς ΑΓ πρὸς τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΓ τῷ ὑπὸ τῶν ΑΓ, ΓΒ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΓ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΓ, ΓΒ, τῷ δὲ ὑπὸ τῶν ΑΓ, ΓΒ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ· ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. καί ἐστι τοῖς μὲν ἀπὸ τῶν ΑΓ, ΓΒ ἴσον τὸ ΕΗ, τῷ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον τὸ ΗΘ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΕΗ τῷ ΘΗ. ὡς δὲ τὸ ΕΗ πρὸς τὸ ΘΗ, οὕτως ἐστὶν ἡ ΕΜ πρὸς τὴν ΘΜ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΜ τῇ ΜΘ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΕΜ, ΜΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΕΘ, προσαρμόζουσα δὲ αὐτῇ ἡ ΘΜ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΘΝ αὐτῇ προσαρμόζει· τῇ ἄρα ἀποτομῇ ἄλλη καὶ ἄλλη προσαρμόζει εὐθεῖα δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ· ὅπερ ἐστὶν ἀδύνατον.
Τῇ ἄρα μέσης ἀποτομῇ δευτέρᾳ μία μόνον προσαρμόζει εὐθεῖα μέση δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης μέσον περιέχουσα· ὅπερ ἔδει δεῖξαι.
Πρότασις πβ΄ 82 Βιβλίον X
Τῇ ἐλάσσονι μία μόνον προσαρμόζει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ ποιοῦσα μετὰ τῆς ὅλης τὸ μὲν ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον.
Ἔστω ἡ ἐλάσσων ἡ ΑΒ, καὶ τῇ ΑΒ προσαρμόζουσα ἔστω ἡ ΒΓ· αἱ ἄρα ΑΓ, ΓΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον· λέγω, ὅτι τῇ ΑΒ ἑτέρα εὐθεῖα οὐ προσαρμόσει τὰ αὐτὰ ποιοῦσα.
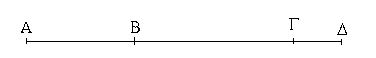
Εἰ γὰρ δυνατόν, προσαρμοζέτω ἡ ΒΔ· καὶ αἱ ΑΔ, ΔΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὰ προειρημένα. καὶ ἐπεί, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, τούτῳ ὑπερέχει καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, τὰ δὲ ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα τῶν ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνων ὑπερέχει ῥητῷ· ῥητὰ γάρ ἐστιν ἀμφότερα· καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ἄρα τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ὅπερ ἐστὶν ἀδύνατον· μέσα γάρ ἐστιν ἀμφότερα.
Τῇ ἄρα ἐλάσσονι μία μόνον προσαρμόζει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ καὶ ποιοῦσα τὰ μὲν ἀπ' αὐτῶν τετράγωνα ἅμα ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον· ὅπερ ἔδει δεῖξαι.
Πρότασις πγ΄ 83 Βιβλίον X
Τῇ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιούσῃ μία μόνον προσαρμόζει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δὲ δὶς ὑπ' αὐτῶν ῥητόν.
Ἔστω ἡ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ, καὶ τῇ ΑΒ προσαρμοζέτω ἡ ΒΓ· αἱ ἄρα ΑΓ, ΓΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὰ προκείμενα· λέγω, ὅτι τῇ ΑΒ ἑτέρα οὐ προσαρμόσει τὰ αὐτὰ ποιοῦσα.
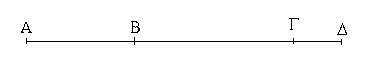
Εἰ γὰρ δυνατόν, προσαρμοζέτω ἡ ΒΔ· καὶ αἱ ΑΔ, ΔΒ ἄρα εὐθεῖαι δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὰ προκείμενα. ἐπεὶ οὖν, ᾧ ὑπερέχει τὰ ἀπὸ τῶν ΑΔ, ΔΒ τῶν ἀπὸ τῶν ΑΓ, ΓΒ, τούτῳ ὑπερέχει καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἀκολούθως τοῖς πρὸ αὐτοῦ, τὸ δὲ δὶς ὑπὸ τῶν ΑΔ, ΔΒ τοῦ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ῥητὰ γάρ ἐστιν ἀμφότερα· καὶ τὰ ἀπὸ τῶν ΑΔ, ΔΒ ἄρα τῶν ἀπὸ τῶν ΑΓ, ΓΒ ὑπερέχει ῥητῷ· ὅπερ ἐστὶν ἀδύνατον· μέσα γάρ ἐστιν ἀμφότερα. οὐκ ἄρα τῇ ΑΒ ἑτέρα προσαρμόσει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τὰ προειρημένα· μία ἄρα μόνον προσαρμόσει· ὅπερ ἔδει δεῖξαι.
Πρότασις πδ΄ 84 Βιβλίον X
Τῇ μετὰ μέσου μέσον τὸ ὅλον ποιούσῃ μία μόνη προσαρμόζει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον τό τε δὶς ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τῷ συγκειμένῳ ἐκ τῶν ἀπ' αὐτῶν.
Ἔστω ἡ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ, προσαρμόζουσα δὲ αὐτῇ ἡ ΒΓ· αἱ ἄρα ΑΓ, ΓΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὰ προειρημένα. λέγω, ὅτι τῇ ΑΒ ἑτέρα οὐ προσαρμόσει ποιοῦσα τὰ προειρημένα.
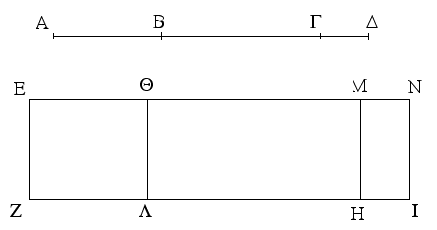
Εἰ γὰρ δυνατόν, προσαρμοζέτω ἡ ΒΔ, ὥστε καὶ τὰς ΑΔ, ΔΒ δυνάμει ἀσυμμέτρους εἶναι ποιούσας τά τε ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα ἅμα μέσον καὶ τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ μέσον καὶ ἔτι τὰ ἀπὸ τῶν ΑΔ, ΔΒ ἀσύμμετρα τῷ δὶς ὑπὸ τῶν ΑΔ, ΔΒ· καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τοῖς μὲν ἀπὸ τῶν ΑΓ, ΓΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΗ πλάτος ποιοῦν τὴν ΕΜ, τῷ δὲ δὶς ὑπὸ τῶν ΑΓ, ΓΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΘΗ πλάτος ποιοῦν τὴν ΘΜ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τῷ ΕΛ· ἡ ἄρα ΑΒ δύναται τὸ ΕΛ. πάλιν τοῖς ἀπὸ τῶν ΑΔ, ΔΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΙ πλάτος ποιοῦν τὴν ΕΝ. ἔστι δὲ καὶ τὸ ἀπὸ τῆς ΑΒ ἴσον τῷ ΕΛ· λοιπὸν ἄρα τὸ δὶς ὑπὸ τῶν ΑΔ, ΔΒ ἴσον [ἐστὶ] τῷ ΘΙ. καὶ ἐπεὶ μέσον ἐστὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΓ, ΓΒ καί ἐστιν ἴσον τῷ ΕΗ, μέσον ἄρα ἐστὶ καὶ τὸ ΕΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΕΜ· ῥητὴ ἄρα ἐστὶν ἡ ΕΜ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ καί ἐστιν ἴσον τῷ ΘΗ, μέσον ἄρα καὶ τὸ ΘΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΘΜ· ῥητὴ ἄρα ἐστὶν ἡ ΘΜ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ἀσύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΓ, ΓΒ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ, ἀσύμμετρόν ἐστι καὶ τὸ ΕΗ τῷ ΘΗ· ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΕΜ τῇ ΜΘ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΕΜ, ΜΘ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΕΘ, προσαρμόζουσα δὲ αὐτῇ ἡ ΘΜ. ὁμοίως δὴ δείξομεν, ὅτι ἡ ΕΘ πάλιν ἀποτομή ἐστιν, προσαρμόζουσα δὲ αὐτῇ ἡ ΘΝ. τῇ ἄρα ἀποτομῇ ἄλλη καὶ ἄλλη προσαρμόζει ῥητὴ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ· ὅπερ ἐδείχθη ἀδύνατον. οὐκ ἄρα τῇ ΑΒ ἑτέρα προσαρμόσει εὐθεῖα.
Τῇ ἄρα ΑΒ μία μόνον προσαρμόζει εὐθεῖα δυνάμει ἀσύμμετρος οὖσα τῇ ὅλῃ, μετὰ δὲ τῆς ὅλης ποιοῦσα τά τε ἀπ' αὐτῶν τετράγωνα ἅμα μέσον καὶ τὸ δὶς ὑπ' αὐτῶν μέσον καὶ ἔτι τὰ ἀπ' αὐτῶν τετράγωνα ἀσύμμετρα τῷ δὶς ὑπ' αὐτῶν· ὅπερ ἔδει δεῖξαι.
ἡ συνέχεια προτάσεων πε΄ 85 ἔως ριε΄ 115 μετά τοὺς ὃρους τρίτους
Ὅροι τρίτοι ς΄ 6.
α΄ 1. Ὑποκειμένης ῥητῆς καὶ ἀποτομῆς, ἐὰν μὲν ἡ ὅλη τῆς προσαρμοζούσης μεῖζον δύνηται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει, καὶ ἡ ὅλη σύμμετρος ᾖ τῇ ἐκκειμένῃ ῥητῇ μήκει, καλείσθω ἀποτομὴ πρώτη.
β΄ 2. Ἐὰν δὲ ἡ προσαρμόζουσα σύμμετρος ᾖ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ὅλη τῆς προσαρμοζούσης μεῖζον δύνηται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καλείσθω ἀποτομὴ δευτέρα.
γ΄ 3. Ἐὰν δὲ μηδετέρα σύμμετρος ᾖ τῇ ἐκκειμένῃ ῥητῇ μήκει, ἡ δὲ ὅλη τῆς προσαρμοζούσης μεῖζον δύνηται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καλείσθω ἀποτομὴ τρίτη.
δ΄ 4. Πάλιν, ἐὰν ἡ ὅλη τῆς προσαρμοζούσης μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει], ἐὰν μὲν ἡ ὅλη σύμμετρος ᾖ τῇ ἐκκειμένῃ ῥητῇ μήκει, καλείσθω ἀποτομὴ τετάρτη.
ε΄ 5. Ἐὰν δὲ ἡ προσαρμόζουσα, πέμπτη.
ς΄ 6. Ἐὰν δὲ μηδετέρα, ἕκτη.
Πρότασις πε΄ 85 Βιβλίον X
Εὑρεῖν τὴν πρώτην ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α, καὶ τῇ Α μήκει σύμμετρος ἔστω ἡ ΒΗ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΒΗ. καὶ ἐκκείσθωσαν δύο τετράγωνοι ἀριθμοὶ οἱ ΔΕ, ΕΖ, ὧν ἡ ὑπεροχὴ ὁ ΖΔ μὴ ἔστω τετράγωνος· οὐδ' ἄρα ὁ ΕΔ πρὸς τὸν ΔΖ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. καὶ πεποιήσθω ὡς ὁ ΕΔ πρὸς τὸν ΔΖ, οὕτως τὸ ἀπὸ τῆς ΒΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΓ τετράγωνον· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΒΗ τῷ ἀπὸ τῆς ΗΓ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΒΗ· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΗΓ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΗΓ. καὶ ἐπεὶ ὁ ΕΔ πρὸς τὸν ΔΖ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ ΗΓ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΒΗ, ΗΓ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ἄρα ΒΓ ἀποτομή ἐστιν.
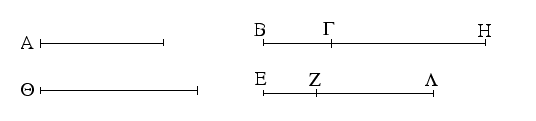
Λέγω δή, ὅτι καὶ πρώτη.
Ὧι γὰρ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΗ τοῦ ἀπὸ τῆς ΗΓ, ἔστω τὸ ἀπὸ τῆς Θ. καὶ ἐπεί ἐστιν ὡς ὁ ΕΔ πρὸς τὸν ΖΔ, οὕτως τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ, καὶ ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΔΕ πρὸς τὸν ΕΖ, οὕτως τὸ ἀπὸ τῆς ΗΒ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΔΕ πρὸς τὸν ΕΖ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἑκάτερος γὰρ τετράγωνός ἐστιν· καὶ τὸ ἀπὸ τῆς ΗΒ ἄρα πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· σύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ Θ μήκει. καὶ δύναται ἡ ΒΗ τῆς ΗΓ μεῖζον τῷ ἀπὸ τῆς Θ· ἡ ΒΗ ἄρα τῆς ΗΓ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. καί ἐστιν ἡ ὅλη ἡ ΒΗ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ Α. ἡ ΒΓ ἄρα ἀποτομή ἐστι πρώτη.
Εὕρηται ἄρα ἡ πρώτη ἀποτομὴ ἡ ΒΓ· ὅπερ ἔδει εὑρεῖν.
Πρότασις πς΄ 86 Βιβλίον X
Εὑρεῖν τὴν δευτέραν ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α καὶ τῇ Α σύμμετρος μήκει ἡ ΗΓ. ῥητὴ ἄρα ἐστὶν ἡ ΗΓ. καὶ ἐκκείσθωσαν δύο τετράγωνοι ἀριθμοὶ οἱ ΔΕ, ΕΖ, ὧν ἡ ὑπεροχὴ ὁ ΔΖ μὴ ἔστω τετράγωνος. καὶ πεποιήσθω ὡς ὁ ΖΔ πρὸς τὸν ΔΕ, οὕτως τὸ ἀπὸ τῆς ΓΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΒ τετράγωνον. σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΓΗ τετράγωνον τῷ ἀπὸ τῆς ΗΒ τετραγώνῳ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΗΓ. ῥητὸν ἄρα [ἐστὶ] καὶ τὸ ἀπὸ τῆς ΗΒ· ῥητὴ ἄρα ἐστὶν ἡ ΒΗ. καὶ ἐπεὶ τὸ ἀπὸ τῆς ΗΓ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΒ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ἀσύμμετρός ἐστιν ἡ ΓΗ τῇ ΗΒ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΓΗ, ΗΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΒΓ ἄρα ἀποτομή ἐστιν.
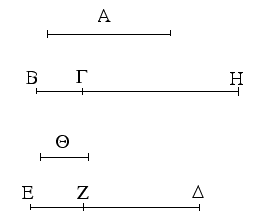
Λέγω δή, ὅτι καὶ δευτέρα.
Ὧι γὰρ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΗ τοῦ ἀπὸ τῆς ΗΓ, ἔστω τὸ ἀπὸ τῆς Θ. ἐπεὶ οὖν ἐστιν ὡς τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ, οὕτως ὁ ΕΔ ἀριθμὸς πρὸς τὸν ΔΖ ἀριθμόν, ἀναστρέψαντι ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς Θ, οὕτως ὁ ΔΕ πρὸς τὸν ΕΖ. καί ἐστιν ἑκάτερος τῶν ΔΕ, ΕΖ τετράγωνος· τὸ ἄρα ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· σύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ Θ μήκει. καὶ δύναται ἡ ΒΗ τῆς ΗΓ μεῖζον τῷ ἀπὸ τῆς Θ· ἡ ΒΗ ἄρα τῆς ΗΓ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. καί ἐστιν ἡ προσαρμόζουσα ἡ ΓΗ τῇ ἐκκειμένῃ ῥητῇ σύμμετρος τῇ Α. ἡ ΒΓ ἄρα ἀποτομή ἐστι δευτέρα.
Εὕρηται ἄρα δευτέρα ἀποτομὴ ἡ ΒΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις πζ΄ 87 Βιβλίον X
Εὑρεῖν τὴν τρίτην ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α, καὶ ἐκκείσθωσαν τρεῖς ἀριθμοὶ οἱ Ε, ΒΓ, ΓΔ λόγον μὴ ἔχοντες πρὸς ἀλλήλους, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ὁ δὲ ΓΒ πρὸς τὸν ΒΔ λόγον ἐχέτω, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, καὶ πεποιήσθω ὡς μὲν ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΗ τετράγωνον, ὡς δὲ ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΘ. ἐπεὶ οὖν ἐστιν ὡς ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΗ τετράγωνον, σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς Α τετράγωνον τῷ ἀπὸ τῆς ΖΗ τετραγώνῳ. ῥητὸν δὲ τὸ ἀπὸ τῆς Α τετράγωνον. ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΖΗ· ῥητὴ ἄρα ἐστὶν ἡ ΖΗ. καὶ ἐπεὶ ὁ Ε πρὸς τὸν ΒΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΗ [τετράγωνον] λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Α τῇ ΖΗ μήκει. πάλιν, ἐπεί ἐστιν ὡς ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΘ, σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΖΗ τῷ ἀπὸ τῆς ΗΘ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΖΗ· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΗΘ· ῥητὴ ἄρα ἐστὶν ἡ ΗΘ. καὶ ἐπεὶ ὁ ΒΓ πρὸς τὸν ΓΔ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ ΗΘ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΖΗ, ΗΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΖΘ.
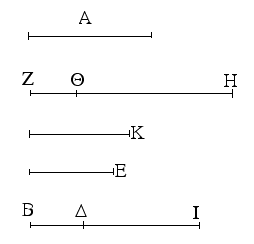
Λέγω δή, ὅτι καὶ τρίτη.
Ἐπεὶ γάρ ἐστιν ὡς μὲν ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΗ, ὡς δὲ ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΘΗ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Ε πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΘΗ. ὁ δὲ Ε πρὸς τὸν ΓΔ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἡ Α τῇ ΗΘ μήκει. οὐδετέρα ἄρα τῶν ΖΗ, ΗΘ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ Α μήκει. ᾧ οὖν μεῖζόν ἐστι τὸ ἀπὸ τῆς ΖΗ τοῦ ἀπὸ τῆς ΗΘ, ἔστω τὸ ἀπὸ τῆς Κ. ἐπεὶ οὖν ἐστιν ὡς ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΒΓ πρὸς τὸν ΒΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς Κ. ὁ δὲ ΒΓ πρὸς τὸν ΒΔ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ τὸ ἀπὸ τῆς ΖΗ ἄρα πρὸς τὸ ἀπὸ τῆς Κ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. σύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ Κ μήκει, καὶ δύναται ἡ ΖΗ τῆς ΗΘ μεῖζον τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ οὐδετέρα τῶν ΖΗ, ΗΘ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ Α μήκει· ἡ ΖΘ ἄρα ἀποτομή ἐστι τρίτη.
Εὕρηται ἄρα ἡ τρίτη ἀποτομὴ ἡ ΖΘ· ὅπερ ἔδει δεῖξαι.
Πρότασις πη΄ 88 Βιβλίον X
Εὑρεῖν τὴν τετάρτην ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α καὶ τῇ Α μήκει σύμμετρος ἡ ΒΗ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΒΗ. καὶ ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΔΖ, ΖΕ, ὥστε τὸν ΔΕ ὅλον πρὸς ἑκάτερον τῶν ΔΖ, ΕΖ λόγον μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. καὶ πεποιήσθω ὡς ὁ ΔΕ πρὸς τὸν ΕΖ, οὕτως τὸ ἀπὸ τῆς ΒΗ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΓ. σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΒΗ τῷ ἀπὸ τῆς ΗΓ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΒΗ· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΗΓ· ῥητὴ ἄρα ἐστὶν ἡ ΗΓ. καὶ ἐπεὶ ὁ ΔΕ πρὸς τὸν ΕΖ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ ΗΓ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΒΗ, ΗΓ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΒΓ.
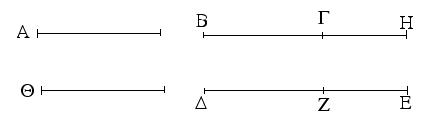
[Λέγω δή, ὅτι καὶ τετάρτη].
Ὧι οὖν μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΗ τοῦ ἀπὸ τῆς ΗΓ, ἔστω τὸ ἀπὸ τῆς Θ. ἐπεὶ οὖν ἐστιν ὡς ὁ ΔΕ πρὸς τὸν ΕΖ, οὕτως τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ, καὶ ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΕΔ πρὸς τὸν ΔΖ, οὕτως τὸ ἀπὸ τῆς ΗΒ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΕΔ πρὸς τὸν ΔΖ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΗΒ πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ Θ μήκει. καὶ δύναται ἡ ΒΗ τῆς ΗΓ μεῖζον τῷ ἀπὸ τῆς Θ· ἡ ἄρα ΒΗ τῆς ΗΓ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί ἐστιν ὅλη ἡ ΒΗ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ Α. ἡ ἄρα ΒΓ ἀποτομή ἐστι τετάρτη.
Εὕρηται ἄρα ἡ τετάρτη ἀποτομή· ὅπερ ἔδει δεῖξαι.
Πρότασις πθ΄ 89 Βιβλίον X
Εὑρεῖν τὴν πέμπτην ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α, καὶ τῇ Α μήκει σύμμετρος ἔστω ἡ ΓΗ· ῥητὴ ἄρα [ἐστὶν] ἡ ΓΗ. καὶ ἐκκείσθωσαν δύο ἀριθμοὶ οἱ ΔΖ, ΖΕ, ὥστε τὸν ΔΕ πρὸς ἑκάτερον τῶν ΔΖ, ΖΕ λόγον πάλιν μὴ ἔχειν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ πεποιήσθω ὡς ὁ ΖΕ πρὸς τὸν ΕΔ, οὕτως τὸ ἀπὸ τῆς ΓΗ πρὸς τὸ ἀπὸ τῆς ΗΒ. ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΗΒ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΒΗ. καὶ ἐπεί ἐστιν ὡς ὁ ΔΕ πρὸς τὸν ΕΖ, οὕτως τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ, ὁ δὲ ΔΕ πρὸς τὸν ΕΖ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ ΗΓ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΒΗ, ΗΓ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΒΓ ἄρα ἀποτομή ἐστιν.
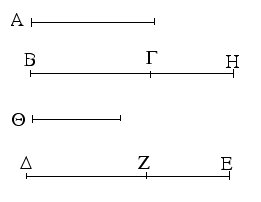
Λέγω δή, ὅτι καὶ πέμπτη.
Ὧι γὰρ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΗ τοῦ ἀπὸ τῆς ΗΓ, ἔστω τὸ ἀπὸ τῆς Θ. ἐπεὶ οὖν ἐστιν ὡς τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς ΗΓ, οὕτως ὁ ΔΕ πρὸς τὸν ΕΖ, ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΕΔ πρὸς τὸν ΔΖ, οὕτως τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς Θ. ὁ δὲ ΕΔ πρὸς τὸν ΔΖ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΒΗ πρὸς τὸ ἀπὸ τῆς Θ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΗ τῇ Θ μήκει. καὶ δύναται ἡ ΒΗ τῆς ΗΓ μεῖζον τῷ ἀπὸ τῆς Θ· ἡ ΗΒ ἄρα τῆς ΗΓ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει. καί ἐστιν ἡ προσαρμόζουσα ἡ ΓΗ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ Α μήκει· ἡ ἄρα ΒΓ ἀποτομή ἐστι πέμπτη.
Εὕρηται ἄρα ἡ πέμπτη ἀποτομὴ ἡ ΒΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟ΄ 90 Βιβλίον X
Εὑρεῖν τὴν ἕκτην ἀποτομήν.
Ἐκκείσθω ῥητὴ ἡ Α καὶ τρεῖς ἀριθμοὶ οἱ Ε, ΒΓ, ΓΔ λόγον μὴ ἔχοντες πρὸς ἀλλήλους, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἔτι δὲ καὶ ὁ ΓΒ πρὸς τὸν ΒΔ λόγον μὴ ἐχέτω, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· καὶ πεποιήσθω ὡς μὲν ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΖΗ, ὡς δὲ ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ.
Ἐπεὶ οὖν ἐστιν ὡς ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΖΗ, σύμμετρον ἄρα τὸ ἀπὸ τῆς Α τῷ ἀπὸ τῆς ΖΗ. ῥητὸν δὲ τὸ ἀπὸ τῆς Α· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΖΗ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΗ. καὶ ἐπεὶ ὁ Ε πρὸς τὸν ΒΓ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΖΗ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Α τῇ ΖΗ μήκει. πάλιν, ἐπεί ἐστιν ὡς ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, σύμμετρον ἄρα τὸ ἀπὸ τῆς ΖΗ τῷ ἀπὸ τῆς ΗΘ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΖΗ· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΗΘ· ῥητὴ ἄρα καὶ ἡ ΗΘ. καὶ ἐπεὶ ὁ ΒΓ πρὸς τὸν ΓΔ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, οὐδ' ἄρα τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ ΗΘ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΖΗ, ΗΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ἄρα ΖΘ ἀποτομή ἐστιν.
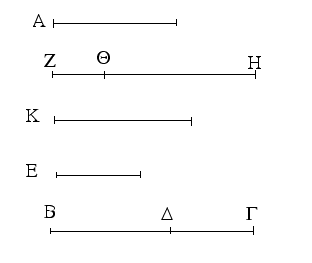
Λέγω δή, ὅτι καὶ ἕκτη.
Ἐπεὶ γάρ ἐστιν ὡς μὲν ὁ Ε πρὸς τὸν ΒΓ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΖΗ, ὡς δὲ ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, δι' ἴσου ἄρα ἐστὶν ὡς ὁ Ε πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΗΘ. ὁ δὲ Ε πρὸς τὸν ΓΔ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς ΗΘ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ Α τῇ ΗΘ μήκει· οὐδετέρα ἄρα τῶν ΖΗ, ΗΘ σύμμετρός ἐστι τῇ Α ῥητῇ μήκει. ᾧ οὖν μεῖζόν ἐστι τὸ ἀπὸ τῆς ΖΗ τοῦ ἀπὸ τῆς ΗΘ, ἔστω τὸ ἀπὸ τῆς Κ. ἐπεὶ οὖν ἐστιν ὡς ὁ ΒΓ πρὸς τὸν ΓΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς ΗΘ, ἀναστρέψαντι ἄρα ἐστὶν ὡς ὁ ΓΒ πρὸς τὸν ΒΔ, οὕτως τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς Κ. ὁ δὲ ΓΒ πρὸς τὸν ΒΔ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· οὐδ' ἄρα τὸ ἀπὸ τῆς ΖΗ πρὸς τὸ ἀπὸ τῆς Κ λόγον ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΗ τῇ Κ μήκει. καὶ δύναται ἡ ΖΗ τῆς ΗΘ μεῖζον τῷ ἀπὸ τῆς Κ· ἡ ΖΗ ἄρα τῆς ΗΘ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει. καὶ οὐδετέρα τῶν ΖΗ, ΗΘ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ Α. ἡ ἄρα ΖΘ ἀποτομή ἐστιν ἕκτη.
Εὕρηται ἄρα ἡ ἕκτη ἀποτομὴ ἡ ΖΘ· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟα΄ 91 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς πρώτης, ἡ τὸ χωρίον δυναμένη ἀποτομή ἐστιν.
Περιεχέσθω γὰρ χωρίον τὸ ΑΒ ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς πρώτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη ἀποτομή ἐστιν.
Ἐπεὶ γὰρ ἀποτομή ἐστι πρώτη ἡ ΑΔ, ἔστω αὐτῇ προσαρμόζουσα ἡ ΔΗ· αἱ ΑΗ, ΗΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ ὅλη ἡ ΑΗ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ, καὶ ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει· ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διαιρεῖ. τετμήσθω ἡ ΔΗ δίχα κατὰ τὸ Ε, καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ· σύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΖΗ. καὶ διὰ τῶν Ε, Ζ, Η σημείων τῇ ΑΓ παράλληλοι ἤχθωσαν αἱ ΕΘ, ΖΙ, ΗΚ.
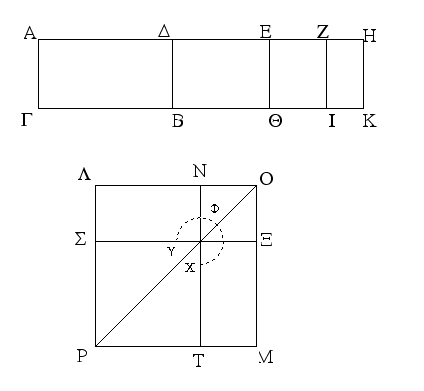
Καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΖ τῇ ΖΗ μήκει, καὶ ἡ ΑΗ ἄρα ἑκατέρᾳ τῶν ΑΖ, ΖΗ σύμμετρός ἐστι μήκει. ἀλλὰ ἡ ΑΗ σύμμετρός ἐστι τῇ ΑΓ· καὶ ἑκατέρα ἄρα τῶν ΑΖ, ΖΗ σύμμετρός ἐστι τῇ ΑΓ μήκει. καί ἐστι ῥητὴ ἡ ΑΓ· ῥητὴ ἄρα καὶ ἑκατέρα τῶν ΑΖ, ΖΗ· ὥστε καὶ ἑκάτερον τῶν ΑΙ, ΖΚ ῥητόν ἐστιν. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΔΕ τῇ ΕΗ μήκει, καὶ ἡ ΔΗ ἄρα ἑκατέρᾳ τῶν ΔΕ, ΕΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΔΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ῥητὴ ἄρα καὶ ἑκατέρα τῶν ΔΕ, ΕΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ἑκάτερον ἄρα τῶν ΔΘ, ΕΚ μέσον ἐστίν.
Κείσθω δὴ τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον τετράγωνον ἀφῃρήσθω κοινὴν γωνίαν ἔχον αὐτῷ τὴν ὑπὸ ΛΟΜ τὸ ΝΞ· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ τετράγωνα. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν ἴσον ἐστὶ τὸ ὑπὸ τῶν ΑΖ, ΖΗ περιεχόμενον ὀρθογώνιον τῷ ἀπὸ τῆς ΕΗ τετραγώνῳ, ἔστιν ἄρα ὡς ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΗ. ἀλλ' ὡς μὲν ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως τὸ ΑΙ πρὸς τὸ ΕΚ, ὡς δὲ ἡ ΕΗ πρὸς τὴν ΖΗ, οὕτως ἐστὶ τὸ ΕΚ πρὸς τὸ ΚΖ· τῶν ἄρα ΑΙ, ΚΖ μέσον ἀνάλογόν ἐστι τὸ ΕΚ. ἔστι δὲ καὶ τῶν ΛΜ, ΝΞ μέσον ἀνάλογον τὸ ΜΝ, ὡς ἐν τοῖς ἔμπροσθεν ἐδείχθη, καί ἐστι τὸ [μὲν] ΑΙ τῷ ΛΜ τετραγώνῳ ἴσον, τὸ δὲ ΚΖ τῷ ΝΞ· καὶ τὸ ΜΝ ἄρα τῷ ΕΚ ἴσον ἐστίν. ἀλλὰ τὸ μὲν ΕΚ τῷ ΔΘ ἐστιν ἴσον, τὸ δὲ ΜΝ τῷ ΛΞ· τὸ ἄρα ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ. ἔστι δὲ καὶ τὸ ΑΚ ἴσον τοῖς ΛΜ, ΝΞ τετραγώνοις· λοιπὸν ἄρα τὸ ΑΒ ἴσον ἐστὶ τῷ ΣΤ. τὸ δὲ ΣΤ τὸ ἀπὸ τῆς ΛΝ ἐστι τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΛΝ τετράγωνον ἴσον ἐστὶ τῷ ΑΒ· ἡ ΛΝ ἄρα δύναται τὸ ΑΒ.
Λέγω δή, ὅτι ἡ ΛΝ ἀποτομή ἐστιν.
Ἐπεὶ γὰρ ῥητόν ἐστιν ἑκάτερον τῶν ΑΙ, ΖΚ, καί ἐστιν ἴσον τοῖς ΛΜ, ΝΞ, καὶ ἑκάτερον ἄρα τῶν ΛΜ, ΝΞ ῥητόν ἐστιν, τουτέστι τὸ ἀπὸ ἑκατέρας τῶν ΛΟ, ΟΝ· καὶ ἑκατέρα ἄρα τῶν ΛΟ, ΟΝ ῥητή ἐστιν. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ ΔΘ καί ἐστιν ἴσον τῷ ΛΞ, μέσον ἄρα ἐστὶ καὶ τὸ ΛΞ. ἐπεὶ οὖν τὸ μὲν ΛΞ μέσον ἐστίν, τὸ δὲ ΝΞ ῥητόν, ἀσύμμετρον ἄρα ἐστὶ τὸ ΛΞ τῷ ΝΞ· ὡς δὲ τὸ ΛΞ πρὸς τὸ ΝΞ, οὕτως ἐστὶν ἡ ΛΟ πρὸς τὴν ΟΝ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΛΟ τῇ ΟΝ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ΛΟ, ΟΝ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΛΝ. καὶ δύναται τὸ ΑΒ χωρίον· ἡ ἄρα τὸ ΑΒ χωρίον δυναμένη ἀποτομή ἐστιν.
Ἐὰν ἄρα χωρίον περιέχηται ὑπὸ ῥητῆς, καὶ τὰ ἑξῆς.
Πρότασις Ϟβ΄ 92 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς δευτέρας, ἡ τὸ χωρίον δυναμένη μέσης ἀποτομή ἐστι πρώτη.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς δευτέρας τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι πρώτη.
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ἄρα ΑΗ, ΗΔ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ προσαρμόζουσα ἡ ΔΗ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. ἐπεὶ οὖν ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΗΔ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διαιρεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε· καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ· σύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΖΗ μήκει. καὶ ἡ ΑΗ ἄρα ἑκατέρᾳ τῶν ΑΖ, ΖΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΑΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· καὶ ἑκατέρα ἄρα τῶν ΑΖ, ΖΗ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ἑκάτερον ἄρα τῶν ΑΙ, ΖΚ μέσον ἐστίν. πάλιν, ἐπεὶ σύμμετρός ἐστιν ἡ ΔΕ τῇ ΕΗ, καὶ ἡ ΔΗ ἄρα ἑκατέρᾳ τῶν ΔΕ, ΕΗ σύμμετρός ἐστιν. ἀλλ' ἡ ΔΗ σύμμετρός ἐστι τῇ ΑΓ μήκει. [ῥητὴ ἄρα καὶ ἑκατέρα τῶν ΔΕ, ΕΗ καὶ σύμμετρος τῇ ΑΓ μήκει.] ἑκάτερον ἄρα τῶν ΔΘ, ΕΚ ῥητόν ἐστιν.
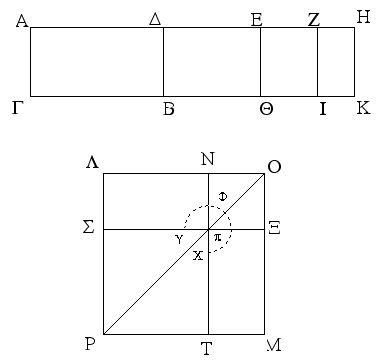
Συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον ἀφῃρήσθω τὸ ΝΞ περὶ τὴν αὐτὴν γωνίαν ὂν τῷ ΛΜ τὴν ὑπὸ τῶν ΛΟΜ· περὶ τὴν αὐτὴν ἄρα ἐστὶ διάμετρον τὰ ΛΜ, ΝΞ τετράγωνα. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν τὰ ΑΙ, ΖΚ μέσα ἐστὶ καί ἐστιν ἴσα τοῖς ἀπὸ τῶν ΛΟ, ΟΝ, καὶ τὰ ἀπὸ τῶν ΛΟ, ΟΝ [ἄρα] μέσα ἐστίν· καὶ αἱ ΛΟ, ΟΝ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΖ, ΖΗ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΗ, ἔστιν ἄρα ὡς ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΗ· ἀλλ' ὡς μὲν ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως τὸ ΑΙ πρὸς τὸ ΕΚ· ὡς δὲ ἡ ΕΗ πρὸς τὴν ΖΗ, οὕτως [ἐστὶ] τὸ ΕΚ πρὸς τὸ ΖΚ· τῶν ἄρα ΑΙ, ΖΚ μέσον ἀνάλογόν ἐστι τὸ ΕΚ. ἔστι δὲ καὶ τῶν ΛΜ, ΝΞ τετραγώνων μέσον ἀνάλογον τὸ ΜΝ· καί ἐστιν ἴσον τὸ μὲν ΑΙ τῷ ΛΜ, τὸ δὲ ΖΚ τῷ ΝΞ· καὶ τὸ ΜΝ ἄρα ἴσον ἐστὶ τῷ ΕΚ. ἀλλὰ τῷ μὲν ΕΚ ἴσον [ἐστὶ] τὸ ΔΘ, τῷ δὲ ΜΝ ἴσον τὸ ΛΞ· ὅλον ἄρα τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ. ἐπεὶ οὖν ὅλον τὸ ΑΚ ἴσον ἐστὶ τοῖς ΛΜ, ΝΞ, ὧν τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ, λοιπὸν ἄρα τὸ ΑΒ ἴσον ἐστὶ τῷ ΤΣ. τὸ δὲ ΤΣ ἐστι τὸ ἀπὸ τῆς ΛΝ· τὸ ἀπὸ τῆς ΛΝ ἄρα ἴσον ἐστὶ τῷ ΑΒ χωρίῳ· ἡ ΛΝ ἄρα δύναται τὸ ΑΒ χωρίον.
Λέγω [δή], ὅτι ἡ ΛΝ μέσης ἀποτομή ἐστι πρώτη.
Ἐπεὶ γὰρ ῥητόν ἐστι τὸ ΕΚ καί ἐστιν ἴσον τῷ ΛΞ, ῥητὸν ἄρα ἐστὶ τὸ ΛΞ, τουτέστι τὸ ὑπὸ τῶν ΛΟ, ΟΝ. μέσον δὲ ἐδείχθη τὸ ΝΞ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΛΞ τῷ ΝΞ· ὡς δὲ τὸ ΛΞ πρὸς τὸ ΝΞ, οὕτως ἐστὶν ἡ ΛΟ πρὸς ΟΝ· αἱ ΛΟ, ΟΝ ἄρα ἀσύμμετροί εἰσι μήκει. αἱ ἄρα ΛΟ, ΟΝ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι· ἡ ΛΝ ἄρα μέσης ἀποτομή ἐστι πρώτη· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ ἄρα τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι πρώτη· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟγ΄ 93 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς τρίτης, ἡ τὸ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς τρίτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ΑΗ, ΗΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ οὐδετέρα τῶν ΑΗ, ΗΔ σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΔΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. ἐπεὶ οὖν ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διελεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε, καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ. καὶ ἤχθωσαν διὰ τῶν Ε, Ζ, Η σημείων τῇ ΑΓ παράλληλοι αἱ ΕΘ, ΖΙ, ΗΚ· σύμμετροι ἄρα εἰσὶν αἱ ΑΖ, ΖΗ· σύμμετρον ἄρα καὶ τὸ ΑΙ τῷ ΖΚ. καὶ ἐπεὶ αἱ ΑΖ, ΖΗ σύμμετροί εἰσι μήκει, καὶ ἡ ΑΗ ἄρα ἑκατέρᾳ τῶν ΑΖ, ΖΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΑΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ὥστε καὶ αἱ ΑΖ, ΖΗ. ἑκάτερον ἄρα τῶν ΑΙ, ΖΚ μέσον ἐστίν. πάλιν, ἐπεὶ σύμμετρός ἐστιν ἡ ΔΕ τῇ ΕΗ μήκει, καὶ ἡ ΔΗ ἄρα ἑκατέρᾳ τῶν ΔΕ, ΕΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΗΔ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ῥητὴ ἄρα καὶ ἑκατέρα τῶν ΔΕ, ΕΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ἑκάτερον ἄρα τῶν ΔΘ, ΕΚ μέσον ἐστίν. καὶ ἐπεὶ αἱ ΑΗ, ΗΔ δυνάμει μόνον σύμμετροί εἰσιν, ἀσύμμετρος ἄρα ἐστὶ μήκει ἡ ΑΗ τῇ ΗΔ. ἀλλ' ἡ μὲν ΑΗ τῇ ΑΖ σύμμετρός ἐστι μήκει, ἡ δὲ ΔΗ τῇ ΕΗ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΕΗ μήκει. ὡς δὲ ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΕΚ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΑΙ τῷ ΕΚ.
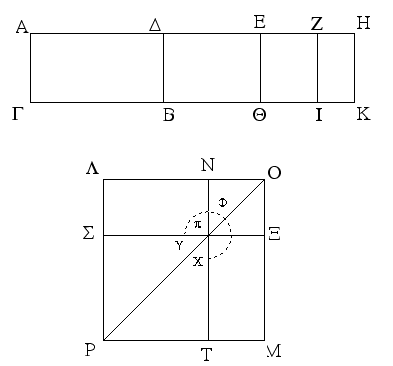
Συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον ἀφῃρήσθω τὸ ΝΞ περὶ τὴν αὐτὴν γωνίαν ὂν τῷ ΛΜ· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν τὸ ὑπὸ τῶν ΑΖ, ΖΗ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΗ, ἔστιν ἄρα ὡς ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΗ. ἀλλ' ὡς μὲν ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΕΚ· ὡς δὲ ἡ ΕΗ πρὸς τὴν ΖΗ, οὕτως ἐστὶ τὸ ΕΚ πρὸς τὸ ΖΚ· καὶ ὡς ἄρα τὸ ΑΙ πρὸς τὸ ΕΚ, οὕτως τὸ ΕΚ πρὸς τὸ ΖΚ· τῶν ἄρα ΑΙ, ΖΚ μέσον ἀνάλογόν ἐστι τὸ ΕΚ. ἔστι δὲ καὶ τῶν ΛΜ, ΝΞ τετραγώνων μέσον ἀνάλογον τὸ ΜΝ· καί ἐστιν ἴσον τὸ μὲν ΑΙ τῷ ΛΜ, τὸ δὲ ΖΚ τῷ ΝΞ· καὶ τὸ ΕΚ ἄρα ἴσον ἐστὶ τῷ ΜΝ. ἀλλὰ τὸ μὲν ΜΝ ἴσον ἐστὶ τῷ ΛΞ, τὸ δὲ ΕΚ ἴσον [ἐστὶ] τῷ ΔΘ· καὶ ὅλον ἄρα τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ. ἔστι δὲ καὶ τὸ ΑΚ ἴσον τοῖς ΛΜ, ΝΞ· λοιπὸν ἄρα τὸ ΑΒ ἴσον ἐστὶ τῷ ΣΤ, τουτέστι τῷ ἀπὸ τῆς ΛΝ τετραγώνῳ· ἡ ΛΝ ἄρα δύναται τὸ ΑΒ χωρίον.
Λέγω, ὅτι ἡ ΛΝ μέσης ἀποτομή ἐστι δευτέρα.
Ἐπεὶ γὰρ μέσα ἐδείχθη τὰ ΑΙ, ΖΚ καί ἐστιν ἴσα τοῖς ἀπὸ τῶν ΛΟ, ΟΝ, μέσον ἄρα καὶ ἑκάτερον τῶν ἀπὸ τῶν ΛΟ, ΟΝ· μέση ἄρα ἑκατέρα τῶν ΛΟ, ΟΝ. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ΑΙ τῷ ΖΚ, σύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΛΟ τῷ ἀπὸ τῆς ΟΝ. πάλιν, ἐπεὶ ἀσύμμετρον ἐδείχθη τὸ ΑΙ τῷ ΕΚ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΛΜ τῷ ΜΝ, τουτέστι τὸ ἀπὸ τῆς ΛΟ τῷ ὑπὸ τῶν ΛΟ, ΟΝ· ὥστε καὶ ἡ ΛΟ ἀσύμμετρός ἐστι τῇ ΟΝ· αἱ ΛΟ, ΟΝ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι.
Λέγω δή, ὅτι καὶ μέσον περιέχουσιν.
Ἐπεὶ γὰρ μέσον ἐδείχθη τὸ ΕΚ καί ἐστιν ἴσον τῷ ὑπὸ τῶν ΛΟ, ΟΝ, μέσον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΛΟ, ΟΝ· ὥστε αἱ ΛΟ, ΟΝ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι. ἡ ΛΝ ἄρα μέσης ἀποτομή ἐστι δευτέρα· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ ἄρα τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟδ΄ 94 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς τετάρτης, ἡ τὸ χωρίον δυναμένη ἐλάσσων ἐστίν.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς τετάρτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη ἐλάσσων ἐστίν.
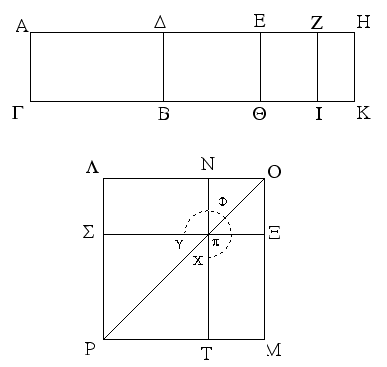
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ἄρα ΑΗ, ΗΔ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΗ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ μήκει, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΔΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει. ἐπεὶ οὖν ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς ἀσύμμετρα αὐτὴν διελεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε, καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ· ἀσύμμετρος ἄρα ἐστὶ μήκει ἡ ΑΖ τῇ ΖΗ. ἤχθωσαν οὖν διὰ τῶν Ε, Ζ, Η παράλληλοι ταῖς ΑΓ, ΒΔ αἱ ΕΘ, ΖΙ, ΗΚ. ἐπεὶ οὖν ῥητή ἐστιν ἡ ΑΗ καὶ σύμμετρος τῇ ΑΓ μήκει, ῥητὸν ἄρα ἐστὶν ὅλον τὸ ΑΚ. πάλιν, ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΔΗ τῇ ΑΓ μήκει, καί εἰσιν ἀμφότεραι ῥηταί, μέσον ἄρα ἐστὶ τὸ ΔΚ. πάλιν, ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΖ τῇ ΖΗ μήκει, ἀσύμμετρον ἄρα καὶ τὸ ΑΙ τῷ ΖΚ. συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον ἀφῃρήσθω περὶ τὴν αὐτὴν γωνίαν τὴν ὑπὸ τῶν ΛΟΜ τὸ ΝΞ. περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ τετράγωνα. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν τὸ ὑπὸ τῶν ΑΖ, ΖΗ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΗ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΗ. ἀλλ' ὡς μὲν ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΕΚ, ὡς δὲ ἡ ΕΗ πρὸς τὴν ΖΗ, οὕτως ἐστὶ τὸ ΕΚ πρὸς τὸ ΖΚ· τῶν ἄρα ΑΙ, ΖΚ μέσον ἀνάλογόν ἐστι τὸ ΕΚ. ἔστι δὲ καὶ τῶν ΛΜ, ΝΞ τετραγώνων μέσον ἀνάλογον τὸ ΜΝ, καί ἐστιν ἴσον τὸ μὲν ΑΙ τῷ ΛΜ, τὸ δὲ ΖΚ τῷ ΝΞ· καὶ τὸ ΕΚ ἄρα ἴσον ἐστὶ τῷ ΜΝ. ἀλλὰ τῷ μὲν ΕΚ ἴσον ἐστὶ τὸ ΔΘ, τῷ δὲ ΜΝ ἴσον ἐστὶ τὸ ΛΞ· ὅλον ἄρα τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ. ἐπεὶ οὖν ὅλον τὸ ΑΚ ἴσον ἐστὶ τοῖς ΛΜ, ΝΞ τετραγώνοις, ὧν τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ τετραγώνῳ, λοιπὸν ἄρα τὸ ΑΒ ἴσον ἐστὶ τῷ ΣΤ, τουτέστι τῷ ἀπὸ τῆς ΛΝ τετραγώνῳ· ἡ ΛΝ ἄρα δύναται τὸ ΑΒ χωρίον.
Λέγω, ὅτι ἡ ΛΝ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Ἐπεὶ γὰρ ῥητόν ἐστι τὸ ΑΚ καί ἐστιν ἴσον τοῖς ἀπὸ τῶν ΛΟ, ΟΝ τετραγώνοις, τὸ ἄρα συγκείμενον ἐκ τῶν ἀπὸ τῶν ΛΟ, ΟΝ ῥητόν ἐστιν. πάλιν, ἐπεὶ τὸ ΔΚ μέσον ἐστίν, καί ἐστιν ἴσον τὸ ΔΚ τῷ δὶς ὑπὸ τῶν ΛΟ, ΟΝ, τὸ ἄρα δὶς ὑπὸ τῶν ΛΟ, ΟΝ μέσον ἐστίν. καὶ ἐπεὶ ἀσύμμετρον ἐδείχθη τὸ ΑΙ τῷ ΖΚ, ἀσύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΛΟ τετράγωνον τῷ ἀπὸ τῆς ΟΝ τετραγώνῳ. αἱ ΛΟ, ΟΝ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον. ἡ ΛΝ ἄρα ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ ἄρα τὸ ΑΒ χωρίον δυναμένη ἐλάσσων ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟε΄ 95 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς πέμπτης, ἡ τὸ χωρίον δυναμένη [ἡ] μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς πέμπτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη [ἡ] μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ἄρα ΑΗ, ΗΔ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ προσαρμόζουσα ἡ ΗΔ σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΔΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς ἀσύμμετρα αὐτὴν διελεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε σημεῖον, καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΖΗ μήκει. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΗ τῇ ΓΑ μήκει, καί εἰσιν ἀμφότεραι ῥηταί, μέσον ἄρα ἐστὶ τὸ ΑΚ. πάλιν, ἐπεὶ ῥητή ἐστιν ἡ ΔΗ καὶ σύμμετρος τῇ ΑΓ μήκει, ῥητόν ἐστι τὸ ΔΚ. συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον τετράγωνον ἀφῃρήσθω τὸ ΝΞ περὶ τὴν αὐτὴν γωνίαν τὴν ὑπὸ ΛΟΜ· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ τετράγωνα. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ὁμοίως δὴ δείξομεν, ὅτι ἡ ΛΝ δύναται τὸ ΑΒ χωρίον.
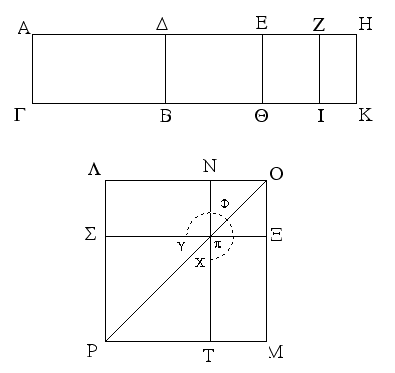
Λέγω, ὅτι ἡ ΛΝ ἡ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἐπεὶ γὰρ μέσον ἐδείχθη τὸ ΑΚ καί ἐστιν ἴσον τοῖς ἀπὸ τῶν ΛΟ, ΟΝ, τὸ ἄρα συγκείμενον ἐκ τῶν ἀπὸ τῶν ΛΟ, ΟΝ μέσον ἐστίν. πάλιν, ἐπεὶ ῥητόν ἐστι τὸ ΔΚ καί ἐστιν ἴσον τῷ δὶς ὑπὸ τῶν ΛΟ, ΟΝ, καὶ αὐτὸ ῥητόν ἐστιν. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΑΙ τῷ ΖΚ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΛΟ τῷ ἀπὸ τῆς ΟΝ· αἱ ΛΟ, ΟΝ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δὲ δὶς ὑπ' αὐτῶν ῥητόν. ἡ λοιπὴ ἄρα ἡ ΛΝ ἄλογός ἐστιν ἡ καλουμένη μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ τὸ ΑΒ ἄρα χωρίον δυναμένη μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟς΄ 96 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς ἕκτης, ἡ τὸ χωρίον δυναμένη μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς ἕκτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη [ἡ] μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ἄρα ΑΗ, ΗΔ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ οὐδετέρα αὐτῶν σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ μήκει, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΔΗ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει. ἐπεὶ οὖν ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς ἀσύμμετρα αὐτὴν διελεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε [σημεῖον], καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΖΗ μήκει. ὡς δὲ ἡ ΑΖ πρὸς τὴν ΖΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΖΚ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΑΙ τῷ ΖΚ. καὶ ἐπεὶ αἱ ΑΗ, ΑΓ ῥηταί εἰσι δυνάμει μόνον σύμμετροι, μέσον ἐστὶ τὸ ΑΚ. πάλιν, ἐπεὶ αἱ ΑΓ, ΔΗ ῥηταί εἰσι καὶ ἀσύμμετροι μήκει, μέσον ἐστὶ καὶ τὸ ΔΚ. ἐπεὶ οὖν αἱ ΑΗ, ΗΔ δυνάμει μόνον σύμμετροί εἰσιν, ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΗ τῇ ΗΔ μήκει. ὡς δὲ ἡ ΑΗ πρὸς τὴν ΗΔ, οὕτως ἐστὶ τὸ ΑΚ πρὸς τὸ ΚΔ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΑΚ τῷ ΚΔ. συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον ἀφῃρήσθω περὶ τὴν αὐτὴν γωνίαν τὸ ΝΞ· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ τετράγωνα. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ὁμοίως δὴ τοῖς ἐπάνω δείξομεν, ὅτι ἡ ΛΝ δύναται τὸ ΑΒ χωρίον.
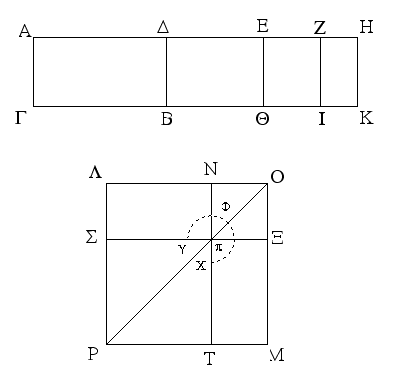
Λέγω, ὅτι ἡ ΛΝ [ἡ] μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἐπεὶ γὰρ μέσον ἐδείχθη τὸ ΑΚ καί ἐστιν ἴσον τοῖς ἀπὸ τῶν ΛΟ, ΟΝ, τὸ ἄρα συγκείμενον ἐκ τῶν ἀπὸ τῶν ΛΟ, ΟΝ μέσον ἐστίν. πάλιν, ἐπεὶ μέσον ἐδείχθη τὸ ΔΚ καί ἐστιν ἴσον τῷ δὶς ὑπὸ τῶν ΛΟ, ΟΝ, καὶ τὸ δὶς ὑπὸ τῶν ΛΟ, ΟΝ μέσον ἐστίν. καὶ ἐπεὶ ἀσύμμετρον ἐδείχθη τὸ ΑΚ τῷ ΔΚ, ἀσύμμετρα [ἄρα] ἐστὶ καὶ τὰ ἀπὸ τῶν ΛΟ, ΟΝ τετράγωνα τῷ δὶς ὑπὸ τῶν ΛΟ, ΟΝ. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΑΙ τῷ ΖΚ, ἀσύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΛΟ τῷ ἀπὸ τῆς ΟΝ· αἱ ΛΟ, ΟΝ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ δὶς ὑπ' αὐτῶν μέσον ἔτι τε τὰ ἀπ' αὐτῶν τετράγωνα ἀσύμμετρα τῷ δὶς ὑπ' αὐτῶν. ἡ ἄρα ΛΝ ἄλογός ἐστιν ἡ καλουμένη μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ ἄρα τὸ χωρίον δυναμένη μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟζ΄ 97 Βιβλίον X
Τὸ ἀπὸ ἀποτομῆς παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πρώτην.
Ἔστω ἀποτομὴ ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι πρώτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΒΗ τὸ ΚΛ. ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ· ὧν τὸ ΓΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ· λοιπὸν ἄρα τὸ ΖΛ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. τετμήσθω ἡ ΖΜ δίχα κατὰ τὸ Ν σημεῖον, καὶ ἤχθω διὰ τοῦ Ν τῇ ΓΔ παράλληλος ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΛΝ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. καὶ ἐπεὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ ῥητά ἐστιν, καί ἐστι τοῖς ἀπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΔΜ, ῥητὸν ἄρα ἐστὶ τὸ ΔΜ. καὶ παρὰ ῥητὴν τὴν ΓΔ παραβέβληται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ σύμμετρος τῇ ΓΔ μήκει. πάλιν, ἐπεὶ μέσον ἐστὶ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ, καὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΖΛ, μέσον ἄρα τὸ ΖΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα ἐστὶν ἡ ΖΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ τὰ μὲν ἀπὸ τῶν ΑΗ, ΗΒ ῥητά ἐστιν, τὸ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον, ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. καὶ τοῖς μὲν ἀπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τὸ ΓΛ, τῷ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ τὸ ΖΛ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΔΜ τῷ ΖΛ. ὡς δὲ τὸ ΔΜ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΖΜ. ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΖΜ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΓΖ ἄρα ἀποτομή ἐστιν.
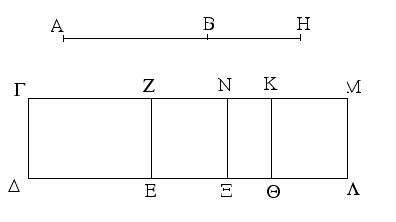
Λέγω δή, ὅτι καὶ πρώτη.
Ἐπεὶ γὰρ τῶν ἀπὸ τῶν ΑΗ, ΗΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΒΗ ἴσον τὸ ΚΛ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ τὸ ΝΛ, καὶ τῶν ΓΘ, ΚΛ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. ἀλλ' ὡς μὲν τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΝΜ· ὡς δὲ τὸ ΝΛ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΚΜ· τὸ ἄρα ὑπὸ τῶν ΓΚ, ΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΝΜ, τουτέστι τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ, σύμμετρόν [ἐστι] καὶ τὸ ΓΘ τῷ ΚΛ. ὡς δὲ τὸ ΓΘ πρὸς τὸ ΚΛ, οὕτως ἡ ΓΚ πρὸς τὴν ΚΜ· σύμμετρος ἄρα ἐστὶν ἡ ΓΚ τῇ ΚΜ. ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ ἴσον παρὰ τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΓΚ, ΚΜ, καί ἐστι σύμμετρος ἡ ΓΚ τῇ ΚΜ, ἡ ἄρα ΓΜ τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. καί ἐστιν ἡ ΓΜ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ μήκει· ἡ ἄρα ΓΖ ἀποτομή ἐστι πρώτη.
Τὸ ἄρα ἀπὸ ἀποτομῆς παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πρώτην· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟη΄ 98 Βιβλίον X
Τὸ ἀπὸ μέσης ἀποτομῆς πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν δευτέραν.
Ἔστω μέσης ἀποτομὴ πρώτη ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι δευτέρα.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι ῥητὸν περιέχουσαι. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ πλάτος ποιοῦν τὴν ΓΚ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ πλάτος ποιοῦν τὴν ΚΜ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ· μέσον ἄρα καὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παράκειται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τῷ ΓΕ, λοιπὸν ἄρα τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τῷ ΖΛ. ῥητὸν δὲ [ἐστι] τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ· ῥητὸν ἄρα τὸ ΖΛ. καὶ παρὰ ῥητὴν τὴν ΖΕ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΜ καὶ σύμμετρος τῇ ΓΔ μήκει. ἐπεὶ οὖν τὰ μὲν ἀπὸ τῶν ΑΗ, ΗΒ, τουτέστι τὸ ΓΛ, μέσον ἐστίν, τὸ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ, τουτέστι τὸ ΖΛ, ῥητόν, ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΖΜ· ἀσύμμετρος ἄρα ἡ ΓΜ τῇ ΖΜ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἡ ΓΖ ἄρα ἀποτομή ἐστιν.
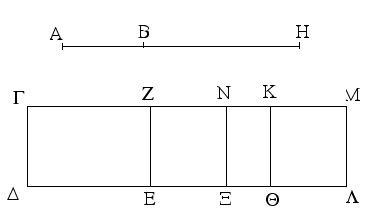
Λέγω δή, ὅτι καὶ δευτέρα.
Τετμήσθω γὰρ ἡ ΖΜ δίχα κατὰ τὸ Ν, καὶ ἤχθω διὰ τοῦ Ν τῇ ΓΔ παράλληλος ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. καὶ ἐπεὶ τῶν ἀπὸ τῶν ΑΗ, ΗΒ τετραγώνων μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστιν ἴσον τὸ μὲν ἀπὸ τῆς ΑΗ τῷ ΓΘ, τὸ δὲ ὑπὸ τῶν ΑΗ, ΗΒ τῷ ΝΛ, τὸ δὲ ἀπὸ τῆς ΒΗ τῷ ΚΛ, καὶ τῶν ΓΘ, ΚΛ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. ἀλλ' ὡς μὲν τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΝΜ, ὡς δὲ τὸ ΝΛ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΜΚ· ὡς ἄρα ἡ ΓΚ πρὸς τὴν ΝΜ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΚΜ· τὸ ἄρα ὑπὸ τῶν ΓΚ, ΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΝΜ, τουτέστι τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. [καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΒΗ, σύμμετρόν ἐστι καὶ τὸ ΓΘ τῷ ΚΛ, τουτέστιν ἡ ΓΚ τῇ ΚΜ.] ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΜΖ ἴσον παρὰ τὴν μείζονα τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΓΚ, ΚΜ καὶ εἰς σύμμετρα αὐτὴν διαιρεῖ, ἡ ἄρα ΓΜ τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει. καί ἐστιν ἡ προσαρμόζουσα ἡ ΖΜ σύμμετρος μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ἄρα ΓΖ ἀποτομή ἐστι δευτέρα.
Τὸ ἄρα ἀπὸ μέσης ἀποτομῆς πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν δευτέραν· ὅπερ ἔδει δεῖξαι.
Πρότασις Ϟθ΄ 99 Βιβλίον X
Τὸ ἀπὸ μέσης ἀποτομῆς δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τρίτην.
Ἔστω μέσης ἀποτομὴ δευτέρα ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι τρίτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ πλάτος ποιοῦν τὴν ΓΚ, τῷ δὲ ἀπὸ τῆς ΒΗ ἴσον παρὰ τὴν ΚΘ παραβεβλήσθω τὸ ΚΛ πλάτος ποιοῦν τὴν ΚΜ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ [καί ἐστι μέσα τὰ ἀπὸ τῶν ΑΗ, ΗΒ]· μέσον ἄρα καὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παραβέβληται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ ὅλον τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ΓΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ, λοιπὸν ἄρα τὸ ΛΖ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. τετμήσθω οὖν ἡ ΖΜ δίχα κατὰ τὸ Ν σημεῖον, καὶ τῇ ΓΔ παράλληλος ἤχθω ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. μέσον δὲ τὸ ὑπὸ τῶν ΑΗ, ΗΒ· μέσον ἄρα ἐστὶ καὶ τὸ ΖΛ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα καὶ ἡ ΖΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ αἱ ΑΗ, ΗΒ δυνάμει μόνον εἰσὶ σύμμετροι, ἀσύμμετρος ἄρα [ἐστὶ] μήκει ἡ ΑΗ τῇ ΗΒ· ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΗ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΗ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΗ, ΗΒ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ· ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τὸ ΓΛ, τῷ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τὸ ΖΛ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΖΜ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΖΜ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΓΖ.
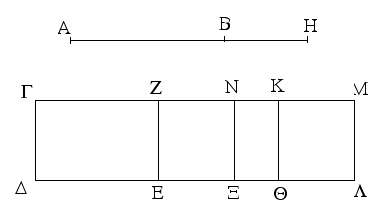
Λέγω δή, ὅτι καὶ τρίτη.
Ἐπεὶ γὰρ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ, σύμμετρον ἄρα καὶ τὸ ΓΘ τῷ ΚΛ· ὥστε καὶ ἡ ΓΚ τῇ ΚΜ. καὶ ἐπεὶ τῶν ἀπὸ τῶν ΑΗ, ΗΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΝΛ, καὶ τῶν ΓΘ, ΚΛ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. ἀλλ' ὡς μὲν τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΝΜ, ὡς δὲ τὸ ΝΛ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΚΜ· ὡς ἄρα ἡ ΓΚ πρὸς τὴν ΜΝ, οὕτως ἐστὶν ἡ ΜΝ πρὸς τὴν ΚΜ· τὸ ἄρα ὑπὸ τῶν ΓΚ, ΚΜ ἴσον ἐστὶ τῷ [ἀπὸ τῆς ΜΝ, τουτέστι τῷ] τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ ἴσον παρὰ τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς σύμμετρα αὐτὴν διαιρεῖ, ἡ ΓΜ ἄρα τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ οὐδετέρα τῶν ΓΜ, ΜΖ σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ἄρα ΓΖ ἀποτομή ἐστι τρίτη.
Τὸ ἄρα ἀπὸ μέσης ἀποτομῆς δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τρίτην· ὅπερ ἔδει δεῖξαι.
Πρότασις ρ΄ 100 Βιβλίον X
Τὸ ἀπὸ ἐλάσσονος παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τετάρτην.
Ἔστω ἐλάσσων ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ ῥητὴν τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι τετάρτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΗ, ΗΒ τετραγώνων ῥητόν, τὸ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ πλάτος ποιοῦν τὴν ΓΚ, τῷ δὲ ἀπὸ τῆς ΒΗ ἴσον τὸ ΚΛ πλάτος ποιοῦν τὴν ΚΜ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ. καί ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΗ, ΗΒ ῥητόν· ῥητὸν ἄρα ἐστὶ καὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παράκειται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα καὶ ἡ ΓΜ καὶ σύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ ὅλον τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ΓΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ, λοιπὸν ἄρα τὸ ΖΛ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. τετμήσθω οὖν ἡ ΖΜ δίχα κατὰ τὸ Ν σημεῖον, καὶ ἤχθω διὰ τοῦ Ν ὁποτέρᾳ τῶν ΓΔ, ΜΛ παράλληλος ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. καὶ ἐπεὶ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον ἐστὶ καί ἐστιν ἴσον τῷ ΖΛ, καὶ τὸ ΖΛ ἄρα μέσον ἐστίν. καὶ παρὰ ῥητὴν τὴν ΖΕ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα ἐστὶν ἡ ΖΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΗ, ΗΒ ῥητόν ἐστιν, τὸ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον, ἀσύμμετρα [ἄρα] ἐστὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. ἴσον δέ [ἐστι] τὸ ΓΛ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, τῷ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΖΛ· ἀσύμμετρον ἄρα [ἐστὶ] τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΜΖ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΜΖ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΓΖ.
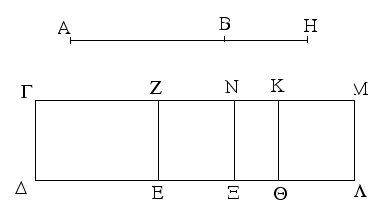
Λέγω [δή], ὅτι καὶ τετάρτη.
Ἐπεὶ γὰρ αἱ ΑΗ, ΗΒ δυνάμει εἰσὶν ἀσύμμετροι, ἀσύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ. καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΘ τῷ ΚΛ. ὡς δὲ τὸ ΓΘ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΚΜ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΚ τῇ ΚΜ μήκει. καὶ ἐπεὶ τῶν ἀπὸ τῶν ΑΗ, ΗΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστιν ἴσον τὸ μὲν ἀπὸ τῆς ΑΗ τῷ ΓΘ, τὸ δὲ ἀπὸ τῆς ΗΒ τῷ ΚΛ, τὸ δὲ ὑπὸ τῶν ΑΗ, ΗΒ τῷ ΝΛ, τῶν ἄρα ΓΘ, ΚΛ μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. ἀλλ' ὡς μὲν τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΝΜ, ὡς δὲ τὸ ΝΛ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΚΜ· ὡς ἄρα ἡ ΓΚ πρὸς τὴν ΜΝ, οὕτως ἐστὶν ἡ ΜΝ πρὸς τὴν ΚΜ· τὸ ἄρα ὑπὸ τῶν ΓΚ, ΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΜΝ, τουτέστι τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΜΖ ἴσον παρὰ τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΓΚ, ΚΜ καὶ εἰς ἀσύμμετρα αὐτὴν διαιρεῖ, ἡ ἄρα ΓΜ τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί ἐστιν ὅλη ἡ ΓΜ σύμμετρος μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ἄρα ΓΖ ἀποτομή ἐστι τετάρτη.
Τὸ ἄρα ἀπὸ ἐλάσσονος καὶ τὰ ἑξῆς.
Πρότασις ρα΄ 101 Βιβλίον X
Τὸ ἀπὸ τῆς μετὰ ῥητοῦ μέσον τὸ ὅλον ποιούσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πέμπτην.
Ἔστω ἡ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι πέμπτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ εὐθεῖαι δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον, τὸ δὲ δὶς ὑπ' αὐτῶν ῥητόν. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ. τὸ δὲ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΗ, ΗΒ ἅμα μέσον ἐστίν· μέσον ἄρα ἐστὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παράκειται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ ἀσύμμετρος τῇ ΓΔ. καὶ ἐπεὶ ὅλον τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ΓΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ, λοιπὸν ἄρα τὸ ΖΛ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. τετμήσθω οὖν ἡ ΖΜ δίχα κατὰ τὸ Ν, καὶ ἤχθω διὰ τοῦ Ν ὁποτέρᾳ τῶν ΓΔ, ΜΛ παράλληλος ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. καὶ ἐπεὶ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ῥητόν ἐστι καί [ἐστιν] ἴσον τῷ ΖΛ, ῥητὸν ἄρα ἐστὶ τὸ ΖΛ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα ἐστὶν ἡ ΖΜ καὶ σύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ τὸ μὲν ΓΛ μέσον ἐστίν, τὸ δὲ ΖΛ ῥητόν, ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἡ ΓΜ πρὸς τὴν ΜΖ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΜΖ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΓΖ.
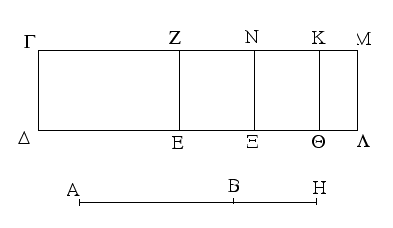
Λέγω δή, ὅτι καὶ πέμπτη.
Ὁμοίως γὰρ δείξομεν, ὅτι τὸ ὑπὸ τῶν ΓΚΜ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΝΜ, τουτέστι τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ, ἴσον δὲ τὸ μὲν ἀπὸ τῆς ΑΗ τῷ ΓΘ, τὸ δὲ ἀπὸ τῆς ΗΒ τῷ ΚΛ, ἀσύμμετρον ἄρα τὸ ΓΘ τῷ ΚΛ. ὡς δὲ τὸ ΓΘ πρὸς τὸ ΚΛ, οὕτως ἡ ΓΚ πρὸς τὴν ΚΜ· ἀσύμμετρος ἄρα ἡ ΓΚ τῇ ΚΜ μήκει. ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ ἴσον παρὰ τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς ἀσύμμετρα αὐτὴν διαιρεῖ, ἡ ἄρα ΓΜ τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καί ἐστιν ἡ προσαρμόζουσα ἡ ΖΜ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ἄρα ΓΖ ἀποτομή ἐστι πέμπτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ρβ΄ 102 Βιβλίον X
Τὸ ἀπὸ τῆς μετὰ μέσου μέσον τὸ ὅλον ποιούσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν ἕκτην.
Ἔστω ἡ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστιν ἕκτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον καὶ ἀσύμμετρον τὰ ἀπὸ τῶν ΑΗ, ΗΒ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. παραβεβλήσθω οὖν παρὰ τὴν ΓΔ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ πλάτος ποιοῦν τὴν ΓΚ, τῷ δὲ ἀπὸ τῆς ΒΗ τὸ ΚΛ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ· μέσον ἄρα [ἐστὶ] καὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παράκειται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. ἐπεὶ οὖν τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ΓΕ ἴσον τῷ ἀπὸ τῆς ΑΒ, λοιπὸν ἄρα τὸ ΖΛ ἴσον ἐστὶ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. καί ἐστι τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ μέσον· καὶ τὸ ΖΛ ἄρα μέσον ἐστίν. καὶ παρὰ ῥητὴν τὴν ΖΕ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα ἐστὶν ἡ ΖΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ ἀσύμμετρά ἐστι τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστι τοῖς μὲν ἀπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΓΛ, τῷ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΖΛ, ἀσύμμετρον ἄρα [ἐστὶ] τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΜΖ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΜΖ μήκει. καί εἰσιν ἀμφότεραι ῥηταί. αἱ ΓΜ, ΜΖ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΓΖ.
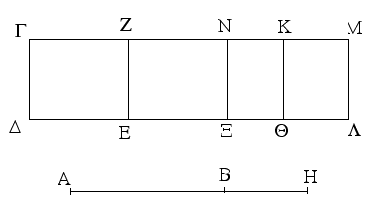
Λέγω δή, ὅτι καὶ ἕκτη.
Ἐπεὶ γὰρ τὸ ΖΛ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ, τετμήσθω δίχα ἡ ΖΜ κατὰ τὸ Ν, καὶ ἤχθω διὰ τοῦ Ν τῇ ΓΔ παράλληλος ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. καὶ ἐπεὶ αἱ ΑΗ, ΗΒ δυνάμει εἰσὶν ἀσύμμετροι, ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον ἐστὶ τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον ἐστὶ τὸ ΚΛ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΘ τῷ ΚΛ. ὡς δὲ τὸ ΓΘ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΚΜ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΚ τῇ ΚΜ. καὶ ἐπεὶ τῶν ἀπὸ τῶν ΑΗ, ΗΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΝΛ, καὶ τῶν ἄρα ΓΘ, ΚΛ μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. καὶ διὰ τὰ αὐτὰ ἡ ΓΜ τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ οὐδετέρα αὐτῶν σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ΓΖ ἄρα ἀποτομή ἐστιν ἕκτη· ὅπερ ἔδει δεῖξαι.
Πρότασις ργ΄ 103 Βιβλίον X
Ἡ τῇ ἀποτομῇ μήκει σύμμετρος ἀποτομή ἐστι καὶ τῇ τάξει ἡ αὐτή.
Ἔστω ἀποτομὴ ἡ ΑΒ, καὶ τῇ ΑΒ μήκει σύμμετρος ἔστω ἡ ΓΔ· λέγω, ὅτι καὶ ἡ ΓΔ ἀποτομή ἐστι καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ γὰρ ἀποτομή ἐστιν ἡ ΑΒ, ἔστω αὐτῇ προσαρμόζουσα ἡ ΒΕ· αἱ ΑΕ, ΕΒ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ τῷ τῆς ΑΒ πρὸς τὴν ΓΔ λόγῳ ὁ αὐτὸς γεγονέτω ὁ τῆς ΒΕ πρὸς τὴν ΔΖ· καὶ ὡς ἓν ἄρα πρὸς ἕν, πάντα [ἐστὶ] πρὸς πάντα· ἔστιν ἄρα καὶ ὡς ὅλη ἡ ΑΕ πρὸς ὅλην τὴν ΓΖ, οὕτως ἡ ΑΒ πρὸς τὴν ΓΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ μήκει. σύμμετρος ἄρα καὶ ἡ ΑΕ μὲν τῇ ΓΖ, ἡ δὲ ΒΕ τῇ ΔΖ. καὶ αἱ ΑΕ, ΕΒ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· καὶ αἱ ΓΖ, ΖΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. [ἀποτομὴ ἄρα ἐστὶν ἡ ΓΔ.
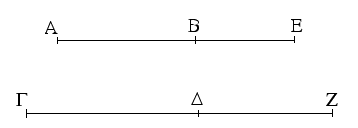
Λέγω δή, ὅτι καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.]
Ἐπεὶ οὖν ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΒΕ πρὸς τὴν ΔΖ, ἐναλλὰξ ἄρα ἐστὶν ὡς ἡ ΑΕ πρὸς τὴν ΕΒ, οὕτως ἡ ΓΖ πρὸς τὴν ΖΔ. ἤτοι δὴ ἡ ΑΕ τῆς ΕΒ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου. εἰ μὲν οὖν ἡ ΑΕ τῆς ΕΒ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ ΓΖ τῆς ΖΔ μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΑΕ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΓΖ, εἰ δὲ ἡ ΒΕ, καὶ ἡ ΔΖ, εἰ δὲ οὐδετέρα τῶν ΑΕ, ΕΒ, καὶ οὐδετέρα τῶν ΓΖ, ΖΔ. εἰ δὲ ἡ ΑΕ [τῆς ΕΒ] μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ἡ ΓΖ τῆς ΖΔ μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΑΕ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΓΖ, εἰ δὲ ἡ ΒΕ, καὶ ἡ ΔΖ, εἰ δὲ οὐδετέρα τῶν ΑΕ, ΕΒ, οὐδετέρα τῶν ΓΖ, ΖΔ.
Ἀποτομὴ ἄρα ἐστὶν ἡ ΓΔ καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις ρδ΄ 104 Βιβλίον X
Ἡ τῇ μέσης ἀποτομῇ σύμμετρος μέσης ἀποτομή ἐστι καὶ τῇ τάξει ἡ αὐτή.
Ἔστω μέσης ἀποτομὴ ἡ ΑΒ, καὶ τῇ ΑΒ μήκει σύμμετρος ἔστω ἡ ΓΔ· λέγω, ὅτι καὶ ἡ ΓΔ μέσης ἀποτομή ἐστι καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ γὰρ μέσης ἀποτομή ἐστιν ἡ ΑΒ, ἔστω αὐτῇ προσαρμόζουσα ἡ ΕΒ. αἱ ΑΕ, ΕΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. καὶ γεγονέτω ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΒΕ πρὸς τὴν ΔΖ· σύμμετρος ἄρα [ἐστὶ] καὶ ἡ ΑΕ τῇ ΓΖ, ἡ δὲ ΒΕ τῇ ΔΖ. αἱ δὲ ΑΕ, ΕΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι· καὶ αἱ ΓΖ, ΖΔ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι· μέσης ἄρα ἀποτομή ἐστιν ἡ ΓΔ.
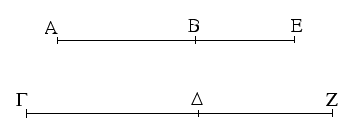
Λέγω δή, ὅτι καὶ τῇ τάξει ἐστὶν ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ [γάρ] ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΕΒ, οὕτως ἡ ΓΖ πρὸς τὴν ΖΔ [ἀλλ' ὡς μὲν ἡ ΑΕ πρὸς τὴν ΕΒ, οὕτως τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΕ, ΕΒ, ὡς δὲ ἡ ΓΖ πρὸς τὴν ΖΔ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ὑπὸ τῶν ΓΖ, ΖΔ], ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΕ, ΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ὑπὸ τῶν ΓΖ, ΖΔ [καὶ ἐναλλὰξ ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΓΖ, οὕτως τὸ ὑπὸ τῶν ΑΕ, ΕΒ πρὸς τὸ ὑπὸ τῶν ΓΖ, ΖΔ]. σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΕ τῷ ἀπὸ τῆς ΓΖ· σύμμετρον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΑΕ, ΕΒ τῷ ὑπὸ τῶν ΓΖ, ΖΔ. εἴτε οὖν ῥητόν ἐστι τὸ ὑπὸ τῶν ΑΕ, ΕΒ, ῥητὸν ἔσται καὶ τὸ ὑπὸ τῶν ΓΖ, ΖΔ, εἴτε μέσον [ἐστὶ] τὸ ὑπὸ τῶν ΑΕ, ΕΒ, μέσον [ἐστὶ] καὶ τὸ ὑπὸ τῶν ΓΖ, ΖΔ.
Μέσης ἄρα ἀποτομή ἐστιν ἡ ΓΔ καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις ρε΄ 105 Βιβλίον X
Ἡ τῇ ἐλάσσονι σύμμετρος ἐλάσσων ἐστίν.
Ἔστω γὰρ ἐλάσσων ἡ ΑΒ καὶ τῇ ΑΒ σύμμετρος ἡ ΓΔ· λέγω, ὅτι καὶ ἡ ΓΔ ἐλάσσων ἐστίν.
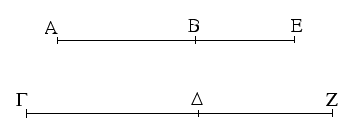
Γεγονέτω γὰρ τὰ αὐτά· καὶ ἐπεὶ αἱ ΑΕ, ΕΒ δυνάμει εἰσὶν ἀσύμμετροι, καὶ αἱ ΓΖ, ΖΔ ἄρα δυνάμει εἰσὶν ἀσύμμετροι. ἐπεὶ οὖν ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΕΒ, οὕτως ἡ ΓΖ πρὸς τὴν ΖΔ, ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ἀπὸ τῆς ΖΔ. συνθέντι ἄρα ἐστὶν ὡς τὰ ἀπὸ τῶν ΑΕ, ΕΒ πρὸς τὸ ἀπὸ τῆς ΕΒ, οὕτως τὰ ἀπὸ τῶν ΓΖ, ΖΔ πρὸς τὸ ἀπὸ τῆς ΖΔ [καὶ ἐναλλάξ]· σύμμετρον δέ ἐστι τὸ ἀπὸ τῆς ΒΕ τῷ ἀπὸ τῆς ΔΖ· σύμμετρον ἄρα καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων. ῥητὸν δέ ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων· ῥητὸν ἄρα ἐστὶ καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων. πάλιν, ἐπεί ἐστιν ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΕ, ΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ὑπὸ τῶν ΓΖ, ΖΔ, σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΕ τετράγωνον τῷ ἀπὸ τῆς ΓΖ τετραγώνῳ, σύμμετρον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΑΕ, ΕΒ τῷ ὑπὸ τῶν ΓΖ, ΖΔ. μέσον δὲ τὸ ὑπὸ τῶν ΑΕ, ΕΒ· μέσον ἄρα καὶ τὸ ὑπὸ τῶν ΓΖ, ΖΔ· αἱ ΓΖ, ΖΔ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον.
Ἐλάσσων ἄρα ἐστὶν ἡ ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις ρς΄ 106 Βιβλίον X
Ἡ τῇ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιούσῃ σύμμετρος μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἔστω μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ καὶ τῇ ΑΒ σύμμετρος ἡ ΓΔ· λέγω, ὅτι καὶ ἡ ΓΔ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν.
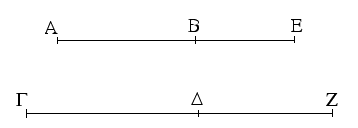
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΕ· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν. καὶ τὰ αὐτὰ κατεσκευάσθω. ὁμοίως δὴ δείξομεν τοῖς πρότερον, ὅτι αἱ ΓΖ, ΖΔ ἐν τῷ αὐτῷ λόγῳ εἰσὶ ταῖς ΑΕ, ΕΒ, καὶ σύμμετρόν ἐστι τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων, τὸ δὲ ὑπὸ τῶν ΑΕ, ΕΒ τῷ ὑπὸ τῶν ΓΖ, ΖΔ· ὥστε καὶ αἱ ΓΖ, ΖΔ δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ τετραγώνων μέσον, τὸ δ' ὑπ' αὐτῶν ῥητόν.
Ἡ ΓΔ ἄρα μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ρζ΄ 107 Βιβλίον X
Ἡ τῇ μετὰ μέσου μέσον τὸ ὅλον ποιούσῃ σύμμετρος καὶ αὐτὴ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν.
Ἔστω μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα ἡ ΑΒ, καὶ τῇ ΑΒ ἔστω σύμμετρος ἡ ΓΔ· λέγω, ὅτι καὶ ἡ ΓΔ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν.
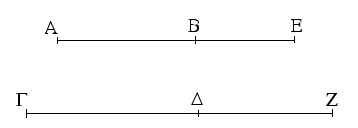
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΕ, καὶ τὰ αὐτὰ κατεσκευάσθω· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τὸ συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων τῷ ὑπ' αὐτῶν. καί εἰσιν, ὡς ἐδείχθη, αἱ ΑΕ, ΕΒ σύμμετροι ταῖς ΓΖ, ΖΔ, καὶ τὸ συγκείμενον ἐκ τῶν ἀπὸ τῶν ΑΕ, ΕΒ τετραγώνων τῷ συγκειμένῳ ἐκ τῶν ἀπὸ τῶν ΓΖ, ΖΔ, τὸ δὲ ὑπὸ τῶν ΑΕ, ΕΒ τῷ ὑπὸ τῶν ΓΖ, ΖΔ· καὶ αἱ ΓΖ, ΖΔ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τό τε συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων μέσον καὶ τὸ ὑπ' αὐτῶν μέσον καὶ ἔτι ἀσύμμετρον τὸ συγκείμενον ἐκ τῶν ἀπ' αὐτῶν [τετραγώνων] τῷ ὑπ' αὐτῶν.
Ἡ ΓΔ ἄρα μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ρη΄ 108 Βιβλίον X
Ἀπὸ ῥητοῦ μέσου ἀφαιρουμένου ἡ τὸ λοιπὸν χωρίον δυναμένη μία δύο ἀλόγων γίνεται ἤτοι ἀποτομὴ ἢ ἐλάσσων.
Ἀπὸ γὰρ ῥητοῦ τοῦ ΒΓ μέσον ἀφῃρήσθω τὸ ΒΔ· λέγω, ὅτι ἡ τὸ λοιπὸν δυναμένη τὸ ΕΓ μία δύο ἀλόγων γίνεται ἤτοι ἀποτομὴ ἢ ἐλάσσων.
Ἐκκείσθω γὰρ ῥητὴ ἡ ΖΗ, καὶ τῷ μὲν ΒΓ ἴσον παρὰ τὴν ΖΗ παραβεβλήσθω ὀρθογώνιον παραλληλόγραμμον τὸ ΗΘ, τῷ δὲ ΔΒ ἴσον ἀφῃρήσθω τὸ ΗΚ· λοιπὸν ἄρα τὸ ΕΓ ἴσον ἐστὶ τῷ ΛΘ. ἐπεὶ οὖν ῥητὸν μέν ἐστι τὸ ΒΓ, μέσον δὲ τὸ ΒΔ, ἴσον δὲ τὸ μὲν ΒΓ τῷ ΗΘ, τὸ δὲ ΒΔ τῷ ΗΚ, ῥητὸν μὲν ἄρα ἐστὶ τὸ ΗΘ, μέσον δὲ τὸ ΗΚ. καὶ παρὰ ῥητὴν τὴν ΖΗ παράκειται· ῥητὴ μὲν ἄρα ἡ ΖΘ καὶ σύμμετρος τῇ ΖΗ μήκει, ῥητὴ δὲ ἡ ΖΚ καὶ ἀσύμμετρος τῇ ΖΗ μήκει· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΘ τῇ ΖΚ μήκει. αἱ ΖΘ, ΖΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΘ, προσαρμόζουσα δὲ αὐτῇ ἡ ΚΖ. ἤτοι δὴ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἢ οὔ.
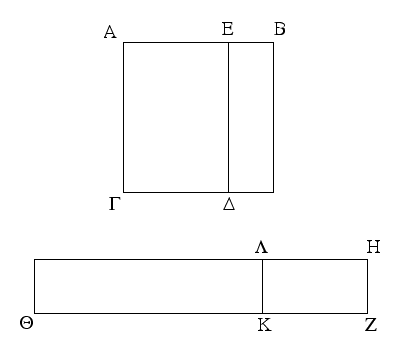
Δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου. καί ἐστιν ὅλη ἡ ΘΖ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ· ἀποτομὴ ἄρα πρώτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς πρώτης περιεχόμενον ἡ δυναμένη ἀποτομή ἐστιν. ἡ ἄρα τὸ ΛΘ, τουτέστι τὸ ΕΓ, δυναμένη ἀποτομή ἐστιν.
Εἰ δὲ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καί ἐστιν ὅλη ἡ ΖΘ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ τετάρτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς τετάρτης περιεχόμενον ἡ δυναμένη ἐλάσσων ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις ρθ΄ 109 Βιβλίον X
Ἀπὸ μέσου ῥητοῦ ἀφαιρουμένου ἄλλαι δύο ἄλογοι γίνονται ἤτοι μέσης ἀποτομὴ πρώτη ἢ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα.
Ἀπὸ γὰρ μέσου τοῦ ΒΓ ῥητὸν ἀφῃρήσθω τὸ ΒΔ. λέγω, ὅτι ἡ τὸ λοιπὸν τὸ ΕΓ δυναμένη μία δύο ἀλόγων γίνεται ἤτοι μέσης ἀποτομὴ πρώτη ἢ μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσα.
Ἐκκείσθω γὰρ ῥητὴ ἡ ΖΗ, καὶ παραβεβλήσθω ὁμοίως τὰ χωρία. ἔστι δὴ ἀκολούθως ῥητὴ μὲν ἡ ΖΘ καὶ ἀσύμμετρος τῇ ΖΗ μήκει, ῥητὴ δὲ ἡ ΚΖ καὶ σύμμετρος τῇ ΖΗ μήκει· αἱ ΖΘ, ΖΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΘ, προσαρμόζουσα δὲ ταύτῃ ἡ ΖΚ. ἤτοι δὴ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου.
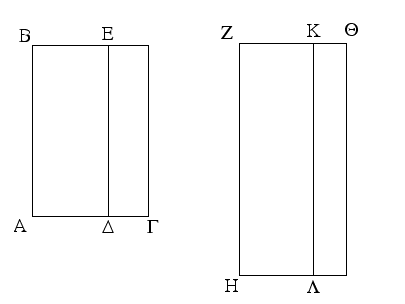
Εἰ μὲν οὖν ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καί ἐστιν ἡ προσαρμόζουσα ἡ ΖΚ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ δευτέρα ἐστὶν ἡ ΚΘ. ῥητὴ δὲ ἡ ΖΗ· ὥστε ἡ τὸ ΛΘ, τουτέστι τὸ ΕΓ, δυναμένη μέσης ἀποτομὴ πρώτη ἐστίν.
Εἰ δὲ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου, καί ἐστιν ἡ προσαρμόζουσα ἡ ΖΚ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ πέμπτη ἐστὶν ἡ ΚΘ· ὥστε ἡ τὸ ΕΓ δυναμένη μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ρι΄ 110 Βιβλίον X
Ἀπὸ μέσου μέσου ἀφαιρουμένου ἀσυμμέτρου τῷ ὅλῳ αἱ λοιπαὶ δύο ἄλογοι γίνονται ἤτοι μέσης ἀποτομὴ δευτέρα ἢ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα.
Ἀφῃρήσθω γὰρ ὡς ἐπὶ τῶν προκειμένων καταγραφῶν ἀπὸ μέσου τοῦ ΒΓ μέσον τὸ ΒΔ ἀσύμμετρον τῷ ὅλῳ· λέγω, ὅτι ἡ τὸ ΕΓ δυναμένη μία ἐστὶ δύο ἀλόγων ἤτοι μέσης ἀποτομὴ δευτέρα ἢ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα.
Ἐπεὶ γὰρ μέσον ἐστὶν ἑκάτερον τῶν ΒΓ, ΒΔ, καὶ ἀσύμμετρον τὸ ΒΓ τῷ ΒΔ, ἔσται ἀκολούθως ῥητὴ ἑκατέρα τῶν ΖΘ, ΖΚ καὶ ἀσύμμετρος τῇ ΖΗ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΒΓ τῷ ΒΔ, τουτέστι τὸ ΗΘ τῷ ΗΚ, ἀσύμμετρος καὶ ἡ ΘΖ τῇ ΖΚ· αἱ ΖΘ, ΖΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΘ [προσαρμόζουσα δὲ ἡ ΖΚ. ἤτοι δὴ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἢ τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ].
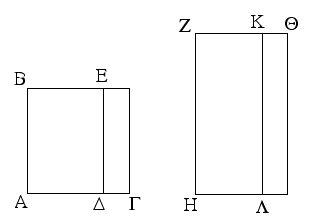
Εἰ μὲν δὴ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ οὐθετέρα τῶν ΖΘ, ΖΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ τρίτη ἐστὶν ἡ ΚΘ. ῥητὴ δὲ ἡ ΚΛ, τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς τρίτης περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλεῖται δὲ μέσης ἀποτομὴ δευτέρα· ὥστε ἡ τὸ ΛΘ, τουτέστι τὸ ΕΓ, δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Εἰ δὲ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει], καὶ οὐθετέρα τῶν ΘΖ, ΖΚ σύμμετρός ἐστι τῇ ΖΗ μήκει, ἀποτομὴ ἕκτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς ἕκτης ἡ δυναμένη ἐστὶ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα. ἡ τὸ ΛΘ ἄρα, τουτέστι τὸ ΕΓ, δυναμένη μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ρια΄ 111 Βιβλίον X
Ἡ ἀποτομὴ οὐκ ἔστιν ἡ αὐτὴ τῇ ἐκ δύο ὀνομάτων.
Ἔστω ἀποτομὴ ἡ ΑΒ· λέγω, ὅτι ἡ ΑΒ οὐκ ἔστιν ἡ αὐτὴ τῇ ἐκ δύο ὀνομάτων.
Εἰ γὰρ δυνατόν, ἔστω· καὶ ἐκκείσθω ῥητὴ ἡ ΔΓ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω ὀρθογώνιον τὸ ΓΕ πλάτος ποιοῦν τὴν ΔΕ. ἐπεὶ οὖν ἀποτομή ἐστιν ἡ ΑΒ, ἀποτομὴ πρώτη ἐστὶν ἡ ΔΕ. ἔστω αὐτῇ προσαρμόζουσα ἡ ΕΖ· αἱ ΔΖ, ΖΕ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΔΖ τῆς ΖΕ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ ΔΖ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΔΓ. πάλιν, ἐπεὶ ἐκ δύο ὀνομάτων ἐστὶν ἡ ΑΒ, ἐκ δύο ἄρα ὀνομάτων πρώτη ἐστὶν ἡ ΔΕ. διῃρήσθω εἰς τὰ ὀνόματα κατὰ τὸ Η, καὶ ἔστω μεῖζον ὄνομα τὸ ΔΗ· αἱ ΔΗ, ΗΕ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΔΗ τῆς ΗΕ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ τὸ μεῖζον ἡ ΔΗ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΔΓ. καὶ ἡ ΔΖ ἄρα τῇ ΔΗ σύμμετρός ἐστι μήκει· καὶ λοιπὴ ἄρα ἡ ΗΖ σύμμετρός ἐστι τῇ ΔΖ μήκει. [ἐπεὶ οὖν σύμμετρός ἐστιν ἡ ΔΖ τῇ ΗΖ, ῥητὴ δέ ἐστιν ἡ ΔΖ, ῥητὴ ἄρα ἐστὶ καὶ ἡ ΗΖ. ἐπεὶ οὖν σύμμετρός ἐστιν ἡ ΔΖ τῇ ΗΖ μήκει] ἀσύμμετρος δὲ ἡ ΔΖ τῇ ΕΖ μήκει· ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΖΗ τῇ ΕΖ μήκει. αἱ ΗΖ, ΖΕ ἄρα ῥηταί [εἰσι] δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΕΗ. ἀλλὰ καὶ ῥητή· ὅπερ ἐστὶν ἀδύνατον.
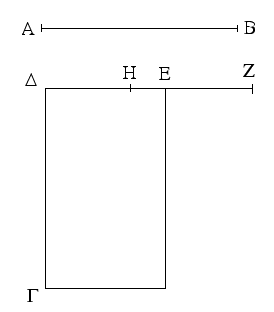
Ἡ ἄρα ἀποτομὴ οὐκ ἔστιν ἡ αὐτὴ τῇ ἐκ δύο ὀνομάτων· ὅπερ ἔδει δεῖξαι.
[Πόρισμα]
Ἡ ἀποτομὴ καὶ αἱ μετ' αὐτὴν ἄλογοι οὔτε τῇ μέσῃ οὔτε ἀλλήλαις εἰσὶν αἱ αὐταί.
Τὸ μὲν γὰρ ἀπὸ μέσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ῥητὴν καὶ ἀσύμμετρον τῇ, παρ' ἣν παράκειται, μήκει, τὸ δὲ ἀπὸ ἀποτομῆς παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πρώτην, τὸ δὲ ἀπὸ μέσης ἀποτομῆς πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν δευτέραν, τὸ δὲ ἀπὸ μέσης ἀποτομῆς δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τρίτην, τὸ δὲ ἀπὸ ἐλάσσονος παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τετάρτην, τὸ δὲ ἀπὸ τῆς μετὰ ῥητοῦ μέσον τὸ ὅλον ποιούσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πέμπτην, τὸ δὲ ἀπὸ τῆς μετὰ μέσου μέσον τὸ ὅλον ποιούσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν ἕκτην. ἐπεὶ οὖν τὰ εἰρημένα πλάτη διαφέρει τοῦ τε πρώτου καὶ ἀλλήλων, τοῦ μὲν πρώτου, ὅτι ῥητή ἐστιν, ἀλλήλων δέ, ἐπεὶ τῇ τάξει οὐκ εἰσὶν αἱ αὐταί, δῆλον, ὡς καὶ αὐταὶ αἱ ἄλογοι διαφέρουσιν ἀλλήλων. καὶ ἐπεὶ δέδεικται ἡ ἀποτομὴ οὐκ οὖσα ἡ αὐτὴ τῇ ἐκ δύο ὀνομάτων, ποιοῦσι δὲ πλάτη παρὰ ῥητὴν παραβαλλόμεναι αἱ μετὰ τὴν ἀποτομὴν ἀποτομὰς ἀκολούθως ἑκάστη τῇ τάξει τῇ καθ᾿ αὑτήν, αἱ δὲ μετὰ τὴν ἐκ δύο ὀνομάτων τὰς ἐκ δύο ὀνομάτων καὶ αὐταὶ τῇ τάξει ἀκολούθως, ἕτεραι ἄρα εἰσὶν αἱ μετὰ τὴν ἀποτομὴν καὶ ἕτεραι αἱ μετὰ τὴν ἐκ δύο ὀνομάτων, ὡς εἶναι τῇ τάξει πάσας ἀλόγους ,
Μέσην,
Ἐκ δύο ὀνομάτων,
Ἐκ δύο μέσων πρώτην,
Ἐκ δύο μέσων δευτέραν,
Μείζονα,
Ῥητὸν καὶ μέσον δυναμένην,
Δύο μέσα δυναμένην,
Ἀποτομήν,
Μέσης ἀποτομὴν πρώτην,
Μέσης ἀποτομὴν δευτέραν,
Ἐλάσσονα,
Μετὰ ῥητοῦ μέσον τὸ ὅλον ποιοῦσαν,
Μετὰ μέσου μέσον τὸ ὅλον ποιοῦσαν.
Πρότασις ριβ΄ 112 Βιβλίον X
Τὸ ἀπὸ ῥητῆς παρὰ τὴν ἐκ δύο ὀνομάτων παραβαλλόμενον πλάτος ποιεῖ ἀποτομήν, ἧς τὰ ὀνόματα σύμμετρά ἐστι τοῖς τῆς ἐκ δύο ὀνομάτων ὀνόμασι καὶ ἔτι ἐν τῷ αὐτῷ λόγῳ, καὶ ἔτι ἡ γινομένη ἀποτομὴ τὴν αὐτὴν ἕξει τάξιν τῇ ἐκ δύο ὀνομάτων.
Ἔστω ῥητὴ μὲν ἡ Α, ἐκ δύο ὀνομάτων δὲ ἡ ΒΓ, ἧς μεῖζον ὄνομα ἔστω ἡ ΔΓ, καὶ τῷ ἀπὸ τῆς Α ἴσον ἔστω τὸ ὑπὸ τῶν ΒΓ, ΕΖ· λέγω, ὅτι ἡ ΕΖ ἀποτομή ἐστιν, ἧς τὰ ὀνόματα σύμμετρά ἐστι τοῖς ΓΔ, ΔΒ, καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ ἔτι ἡ ΕΖ τὴν αὐτὴν ἕξει τάξιν τῇ ΒΓ.
Ἔστω γὰρ πάλιν τῷ ἀπὸ τῆς Α ἴσον τὸ ὑπὸ τῶν ΒΔ, Η. ἐπεὶ οὖν τὸ ὑπὸ τῶν ΒΓ, ΕΖ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΒΔ, Η, ἔστιν ἄρα ὡς ἡ ΓΒ πρὸς τὴν ΒΔ, οὕτως ἡ Η πρὸς τὴν ΕΖ. μείζων δὲ ἡ ΓΒ τῆς ΒΔ· μείζων ἄρα ἐστὶ καὶ ἡ Η τῆς ΕΖ. ἔστω τῇ Η ἴση ἡ ΕΘ· ἔστιν ἄρα ὡς ἡ ΓΒ πρὸς τὴν ΒΔ, οὕτως ἡ ΘΕ πρὸς τὴν ΕΖ· διελόντι ἄρα ἐστὶν ὡς ἡ ΓΔ πρὸς τὴν ΒΔ, οὕτως ἡ ΘΖ πρὸς τὴν ΖΕ. γεγονέτω ὡς ἡ ΘΖ πρὸς τὴν ΖΕ, οὕτως ἡ ΖΚ πρὸς τὴν ΚΕ· καὶ ὅλη ἄρα ἡ ΘΚ πρὸς ὅλην τὴν ΚΖ ἐστιν, ὡς ἡ ΖΚ πρὸς ΚΕ· ὡς γὰρ ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα. ὡς δὲ ἡ ΖΚ πρὸς ΚΕ, οὕτως ἐστὶν ἡ ΓΔ πρὸς τὴν ΔΒ· καὶ ὡς ἄρα ἡ ΘΚ πρὸς ΚΖ, οὕτως ἡ ΓΔ πρὸς τὴν ΔΒ. σύμμετρον δὲ τὸ ἀπὸ τῆς ΓΔ τῷ ἀπὸ τῆς ΔΒ· σύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΘΚ τῷ ἀπὸ τῆς ΚΖ. καί ἐστιν ὡς τὸ ἀπὸ τῆς ΘΚ πρὸς τὸ ἀπὸ τῆς ΚΖ, οὕτως ἡ ΘΚ πρὸς τὴν ΚΕ, ἐπεὶ αἱ τρεῖς αἱ ΘΚ, ΚΖ, ΚΕ ἀνάλογόν εἰσιν. σύμμετρος ἄρα ἡ ΘΚ τῇ ΚΕ μήκει· ὥστε καὶ ἡ ΘΕ τῇ ΕΚ σύμμετρός ἐστι μήκει. καὶ ἐπεὶ τὸ ἀπὸ τῆς Α ἴσον ἐστὶ τῷ ὑπὸ τῶν ΕΘ, ΒΔ, ῥητὸν δέ ἐστι τὸ ἀπὸ τῆς Α, ῥητὸν ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΕΘ, ΒΔ. καὶ παρὰ ῥητὴν τὴν ΒΔ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΕΘ καὶ σύμμετρος τῇ ΒΔ μήκει· ὥστε καὶ ἡ σύμμετρος αὐτῇ ἡ ΕΚ ῥητή ἐστι καὶ σύμμετρος τῇ ΒΔ μήκει. ἐπεὶ οὖν ἐστιν ὡς ἡ ΓΔ πρὸς ΔΒ, οὕτως ἡ ΖΚ πρὸς ΚΕ, αἱ δὲ ΓΔ, ΔΒ δυνάμει μόνον εἰσὶ σύμμετροι, καὶ αἱ ΖΚ, ΚΕ δυνάμει μόνον εἰσὶ σύμμετροι. ῥητὴ δέ ἐστιν ἡ ΚΕ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΖΚ. αἱ ΖΚ, ΚΕ ἄρα ῥηταὶ δυνάμει μόνον εἰσὶ σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΕΖ.
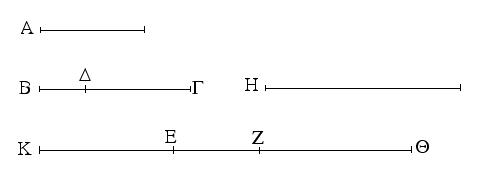
Ἤτοι δὲ ἡ ΓΔ τῆς ΔΒ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου.
Εἰ μὲν οὖν ἡ ΓΔ τῆς ΔΒ μεῖζον δύναται τῷ ἀπὸ συμμέτρου [ἑαυτῇ], καὶ ἡ ΖΚ τῆς ΚΕ μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΓΔ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΖΚ· εἰ δὲ ἡ ΒΔ, καὶ ἡ ΚΕ· εἰ δὲ οὐδετέρα τῶν ΓΔ, ΔΒ, καὶ οὐδετέρα τῶν ΖΚ, ΚΕ.
Εἰ δὲ ἡ ΓΔ τῆς ΔΒ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ἡ ΖΚ τῆς ΚΕ μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ εἰ μὲν ἡ ΓΔ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΖΚ· εἰ δὲ ἡ ΒΔ, καὶ ἡ ΚΕ· εἰ δὲ οὐδετέρα τῶν ΓΔ, ΔΒ, καὶ οὐδετέρα τῶν ΖΚ, ΚΕ· ὥστε ἀποτομή ἐστιν ἡ ΖΕ, ἧς τὰ ὀνόματα τὰ ΖΚ, ΚΕ σύμμετρά ἐστι τοῖς τῆς ἐκ δύο ὀνομάτων ὀνόμασι τοῖς ΓΔ, ΔΒ καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ τὴν αὐτὴν τάξιν ἔχει τῇ ΒΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις ριγ΄ 113 Βιβλίον X
Τὸ ἀπὸ ῥητῆς παρὰ ἀποτομὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων, ἧς τὰ ὀνόματα σύμμετρά ἐστι τοῖς τῆς ἀποτομῆς ὀνόμασι καὶ ἐν τῷ αὐτῷ λόγῳ, ἔτι δὲ ἡ γινομένη ἐκ δύο ὀνομάτων τὴν αὐτὴν τάξιν ἔχει τῇ ἀποτομῇ.
Ἔστω ῥητὴ μὲν ἡ Α, ἀποτομὴ δὲ ἡ ΒΔ, καὶ τῷ ἀπὸ τῆς Α ἴσον ἔστω τὸ ὑπὸ τῶν ΒΔ, ΚΘ, ὥστε τὸ ἀπὸ τῆς Α ῥητῆς παρὰ τὴν ΒΔ ἀποτομὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ΚΘ· λέγω, ὅτι ἐκ δύο ὀνομάτων ἐστὶν ἡ ΚΘ, ἧς τὰ ὀνόματα σύμμετρά ἐστι τοῖς τῆς ΒΔ ὀνόμασι καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ ἔτι ἡ ΚΘ τὴν αὐτὴν ἔχει τάξιν τῇ ΒΔ.
Ἔστω γὰρ τῇ ΒΔ προσαρμόζουσα ἡ ΔΓ· αἱ ΒΓ, ΓΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. καὶ τῷ ἀπὸ τῆς Α ἴσον ἔστω καὶ τὸ ὑπὸ τῶν ΒΓ, Η. ῥητὸν δὲ τὸ ἀπὸ τῆς Α· ῥητὸν ἄρα καὶ τὸ ὑπὸ τῶν ΒΓ, Η. καὶ παρὰ ῥητὴν τὴν ΒΓ παραβέβληται· ῥητὴ ἄρα ἐστὶν ἡ Η καὶ σύμμετρος τῇ ΒΓ μήκει. ἐπεὶ οὖν τὸ ὑπὸ τῶν ΒΓ, Η ἴσον ἐστὶ τῷ ὑπὸ τῶν ΒΔ, ΚΘ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΓΒ πρὸς ΒΔ, οὕτως ἡ ΚΘ πρὸς Η. μείζων δὲ ἡ ΒΓ τῆς ΒΔ· μείζων ἄρα καὶ ἡ ΚΘ τῆς Η. κείσθω τῇ Η ἴση ἡ ΚΕ· σύμμετρος ἄρα ἐστὶν ἡ ΚΕ τῇ ΒΓ μήκει. καὶ ἐπεί ἐστιν ὡς ἡ ΓΒ πρὸς ΒΔ, οὕτως ἡ ΘΚ πρὸς ΚΕ, ἀναστρέψαντι ἄρα ἐστὶν ὡς ἡ ΒΓ πρὸς τὴν ΓΔ, οὕτως ἡ ΚΘ πρὸς ΘΕ. γεγονέτω ὡς ἡ ΚΘ πρὸς ΘΕ, οὕτως ἡ ΘΖ πρὸς ΖΕ· καὶ λοιπὴ ἄρα ἡ ΚΖ πρὸς ΖΘ ἐστιν, ὡς ἡ ΚΘ πρὸς ΘΕ, τουτέστιν [ὡς] ἡ ΒΓ πρὸς ΓΔ. αἱ δὲ ΒΓ, ΓΔ δυνάμει μόνον [εἰσὶ] σύμμετροι· καὶ αἱ ΚΖ, ΖΘ ἄρα δυνάμει μόνον εἰσὶ σύμμετροι. καὶ ἐπεί ἐστιν ὡς ἡ ΚΘ πρὸς ΘΕ, ἡ ΚΖ πρὸς ΖΘ, ἀλλ' ὡς ἡ ΚΘ πρὸς ΘΕ, ἡ ΘΖ πρὸς ΖΕ, καὶ ὡς ἄρα ἡ ΚΖ πρὸς ΖΘ, ἡ ΘΖ πρὸς ΖΕ· ὥστε καὶ ὡς ἡ πρώτη πρὸς τὴν τρίτην, τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ἀπὸ τῆς δευτέρας· καὶ ὡς ἄρα ἡ ΚΖ πρὸς ΖΕ, οὕτως τὸ ἀπὸ τῆς ΚΖ πρὸς τὸ ἀπὸ τῆς ΖΘ. σύμμετρον δέ ἐστι τὸ ἀπὸ τῆς ΚΖ τῷ ἀπὸ τῆς ΖΘ· αἱ γὰρ ΚΖ, ΖΘ δυνάμει εἰσὶ σύμμετροι· σύμμετρος ἄρα ἐστὶ καὶ ἡ ΚΖ τῇ ΖΕ μήκει· ὥστε ἡ ΚΖ καὶ τῇ ΚΕ σύμμετρός [ἐστι] μήκει. ῥητὴ δέ ἐστιν ἡ ΚΕ καὶ σύμμετρος τῇ ΒΓ μήκει· ῥητὴ ἄρα καὶ ἡ ΚΖ καὶ σύμμετρος τῇ ΒΓ μήκει. καὶ ἐπεί ἐστιν ὡς ἡ ΒΓ πρὸς ΓΔ, οὕτως ἡ ΚΖ πρὸς ΖΘ, ἐναλλὰξ ὡς ἡ ΒΓ πρὸς ΚΖ, οὕτως ἡ ΔΓ πρὸς ΖΘ. σύμμετρος δὲ ἡ ΒΓ τῇ ΚΖ· σύμμετρος ἄρα καὶ ἡ ΖΘ τῇ ΓΔ μήκει. αἱ ΒΓ, ΓΔ δὲ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· καὶ αἱ ΚΖ, ΖΘ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ὀνομάτων ἐστὶν ἄρα ἡ ΚΘ.
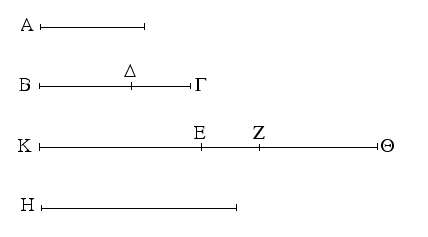
Εἰ μὲν οὖν ἡ ΒΓ τῆς ΓΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ ἡ ΚΖ τῆς ΖΘ μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΒΓ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΚΖ, εἰ δὲ ἡ ΓΔ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΖΘ, εἰ δὲ οὐδετέρα τῶν ΒΓ, ΓΔ, οὐδετέρα τῶν ΚΖ, ΖΘ.
Εἰ δὲ ἡ ΒΓ τῆς ΓΔ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ἡ ΚΖ τῆς ΖΘ μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. καὶ εἰ μὲν σύμμετρός ἐστιν ἡ ΒΓ τῇ ἐκκειμένῃ ῥητῇ μήκει, καὶ ἡ ΚΖ, εἰ δὲ ἡ ΓΔ, καὶ ἡ ΖΘ, εἰ δὲ οὐδετέρα τῶν ΒΓ, ΓΔ, οὐδετέρα τῶν ΚΖ, ΖΘ.
Ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΚΘ, ἧς τὰ ὀνόματα τὰ ΚΖ, ΖΘ σύμμετρά [ἐστι] τοῖς τῆς ἀποτομῆς ὀνόμασι τοῖς ΒΓ, ΓΔ καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ ἔτι ἡ ΚΘ τῇ ΒΓ τὴν αὐτὴν ἕξει τάξιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ριδ΄ 114 Βιβλίον X
Ἐὰν χωρίον περιέχηται ὑπὸ ἀποτομῆς καὶ τῆς ἐκ δύο ὀνομάτων, ἧς τὰ ὀνόματα σύμμετρά τέ ἐστι τοῖς τῆς ἀποτομῆς ὀνόμασι καὶ ἐν τῷ αὐτῷ λόγῳ, ἡ τὸ χωρίον δυναμένη ῥητή ἐστιν.
Περιεχέσθω γὰρ χωρίον τὸ ὑπὸ τῶν ΑΒ, ΓΔ ὑπὸ ἀποτομῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων τῆς ΓΔ, ἧς μεῖζον ὄνομα ἔστω τὸ ΓΕ, καὶ ἔστω τὰ ὀνόματα τῆς ἐκ δύο ὀνομάτων τὰ ΓΕ, ΕΔ σύμμετρά τε τοῖς τῆς ἀποτομῆς ὀνόμασι τοῖς ΑΖ, ΖΒ καὶ ἐν τῷ αὐτῷ λόγῳ, καὶ ἔστω ἡ τὸ ὑπὸ τῶν ΑΒ, ΓΔ δυναμένη ἡ Η· λέγω, ὅτι ῥητή ἐστιν ἡ Η.
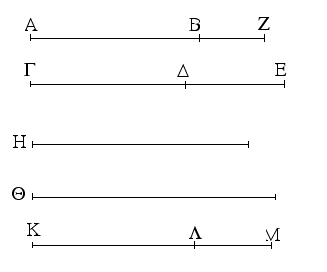
Ἐκκείσθω γὰρ ῥητὴ ἡ Θ, καὶ τῷ ἀπὸ τῆς Θ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω πλάτος ποιοῦν τὴν ΚΛ· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΛ, ἧς τὰ ὀνόματα ἔστω τὰ ΚΜ, ΜΛ σύμμετρα τοῖς τῆς ἐκ δύο ὀνομάτων ὀνόμασι τοῖς ΓΕ, ΕΔ καὶ ἐν τῷ αὐτῷ λόγῳ. ἀλλὰ καὶ αἱ ΓΕ, ΕΔ σύμμετροί τέ εἰσι ταῖς ΑΖ, ΖΒ καὶ ἐν τῷ αὐτῷ λόγῳ· ἔστιν ἄρα ὡς ἡ ΑΖ πρὸς τὴν ΖΒ, οὕτως ἡ ΚΜ πρὸς ΜΛ. ἐναλλὰξ ἄρα ἐστὶν ὡς ἡ ΑΖ πρὸς τὴν ΚΜ, οὕτως ἡ ΒΖ πρὸς τὴν ΛΜ· καὶ λοιπὴ ἄρα ἡ ΑΒ πρὸς λοιπὴν τὴν ΚΛ ἐστιν ὡς ἡ ΑΖ πρὸς ΚΜ. σύμμετρος δὲ ἡ ΑΖ τῇ ΚΜ· σύμμετρος ἄρα ἐστὶ καὶ ἡ ΑΒ τῇ ΚΛ. καί ἐστιν ὡς ἡ ΑΒ πρὸς ΚΛ, οὕτως τὸ ὑπὸ τῶν ΓΔ, ΑΒ πρὸς τὸ ὑπὸ τῶν ΓΔ, ΚΛ· σύμμετρον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΓΔ, ΑΒ τῷ ὑπὸ τῶν ΓΔ, ΚΛ. ἴσον δὲ τὸ ὑπὸ τῶν ΓΔ, ΚΛ τῷ ἀπὸ τῆς Θ· σύμμετρον ἄρα ἐστὶ τὸ ὑπὸ τῶν ΓΔ, ΑΒ τῷ ἀπὸ τῆς Θ. τῷ δὲ ὑπὸ τῶν ΓΔ, ΑΒ ἴσον ἐστὶ τὸ ἀπὸ τῆς Η· σύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς Η τῷ ἀπὸ τῆς Θ. ῥητὸν δὲ τὸ ἀπὸ τῆς Θ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς Η· ῥητὴ ἄρα ἐστὶν ἡ Η. καὶ δύναται τὸ ὑπὸ τῶν ΓΔ, ΑΒ.
Ἐὰν ἄρα χωρίον περιέχηται ὑπὸ ἀποτομῆς καὶ τῆς ἐκ δύο ὀνομάτων, ἧς τὰ ὀνόματα σύμμετρά ἐστι τοῖς τῆς ἀποτομῆς ὀνόμασι καὶ ἐν τῷ αὐτῷ λόγῳ, ἡ τὸ χωρίον δυναμένη ῥητή ἐστιν.
Πόρισμα
Καὶ γέγονεν ἡμῖν καὶ διὰ τούτου φανερόν, ὅτι δυνατόν ἐστι ῥητὸν χωρίον ὑπὸ ἀλόγων εὐθειῶν περιέχεσθαι. ὅπερ ἔδει δεῖξαι.
Πρότασις ριε΄ 115 Βιβλίον X
Ἀπὸ μέσης ἄπειροι ἄλογοι γίνονται, καὶ οὐδεμία οὐδεμιᾷ τῶν πρότερον ἡ αὐτή.
Ἔστω μέση ἡ Α· λέγω, ὅτι ἀπὸ τῆς Α ἄπειροι ἄλογοι γίνονται, καὶ οὐδεμία οὐδεμιᾷ τῶν πρότερον ἡ αὐτή.
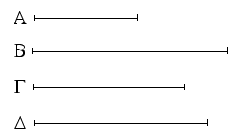
Ἐκκείσθω ῥητὴ ἡ Β, καὶ τῷ ὑπὸ τῶν Β, Α ἴσον ἔστω τὸ ἀπὸ τῆς Γ· ἄλογος ἄρα ἐστὶν ἡ Γ· τὸ γὰρ ὑπὸ ἀλόγου καὶ ῥητῆς ἄλογόν ἐστιν. καὶ οὐδεμιᾷ τῶν πρότερον ἡ αὐτή· τὸ γὰρ ἀπ' οὐδεμιᾶς τῶν πρότερον παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ μέσην. πάλιν δὴ τῷ ὑπὸ τῶν Β, Γ ἴσον ἔστω τὸ ἀπὸ τῆς Δ· ἄλογον ἄρα ἐστὶ τὸ ἀπὸ τῆς Δ. ἄλογος ἄρα ἐστὶν ἡ Δ· καὶ οὐδεμιᾷ τῶν πρότερον ἡ αὐτή· τὸ γὰρ ἀπ' οὐδεμιᾶς τῶν πρότερον παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν Γ. ὁμοίως δὴ τῆς τοιαύτης τάξεως ἐπ᾿ ἄπειρον προβαινούσης φανερόν, ὅτι ἀπὸ τῆς μέσης ἄπειροι ἄλογοι γίνονται, καὶ οὐδεμία οὐδεμιᾷ τῶν πρότερον ἡ αὐτή· ὅπερ ἔδει δεῖξαι].
Παράρτημα 27
Ἀσύμμετρος ἡ διάμετρος τῇ πλευρᾷ μήκει.
Προκείσθω ἡμῖν δεῖξαι, ὅτι ἐπὶ τῶν τετραγώνων σχημάτων ἀσύμμετρός ἐστιν ἡ διάμετρος τῇ πλευρᾷ μήκει.
Ἔστω τετράγωνον τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ· λέγω, ὅτι ἡ ΓΑ ἀσύμμετρός ἐστι τῇ ΑΒ μήκει.
Εἰ γὰρ δυνατόν, ἔστω σύμμετρος· λέγω, ὅτι συμβήσεται τὸν αὐτὸν ἀριθμὸν ἄρτιον εἶναι καὶ περισσόν. φανερὸν μὲν οὖν, ὅτι τὸ ἀπὸ τῆς ΑΓ διπλάσιον τοῦ ἀπὸ τῆς ΑΒ. καὶ ἐπὶ σύμμετρός ἐστιν ἡ ΓΑ τῇ ΑΒ, ἡ ΓΑ ἄρα πρὸς τὴν ΑΒ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. ἐχέτω, ὃν ὁ ΕΖ πρὸς Η, καὶ ἔστωσαν οἱ ΕΖ, Η ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς· οὐκ ἄρα μονὰς ἐστὶν ὁ ΕΖ. εἰ γὰρ ἔσται μονὰς ὁ ΕΖ, ἔχει δὲ λόγον πρὸς τὸν Η, ὃν ἔχει ἡ ΑΓ πρὸς τὴν ΑΒ, καὶ μείζων ἡ ΑΓ τῆς ΑΒ, μείζων ἄρα καὶ ἡ ΕΖ τοῦ Η ἀριθμοῦ· ὅπερ ἄτοπον· οὐκ ἄρα μονάς ἐστιν ὁ ΕΖ· ἀριθμὸς ἄρα. καὶ ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς τὴν ΑΒ, οὕτως ὁ ΕΖ πρὸς τὸν Η, καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΓΑ πρὸς τὸ ἀπὸ τῆς ΑΒ, οὕτως ὁ ἀπὸ τοῦ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η.
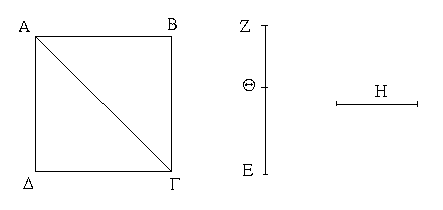
διπλάσιον δὲ τὸ ἀπὸ τῆς ΓΑ τοῦ ἀπὸ τῆς ΑΒ· διπλάσιον ἄρα καὶ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η· ἄρτιος ἄρα ἐστὶν ὁ ἀπὸ τοῦ ΕΖ· ὥστε καὶ αὐτὸς ἄρτιός ἐστιν. εἰ γὰρ ἦν περισσός, καὶ ὁ ἀπ᾿ αὐτοῦ τετράγωνος περισσὸς ἦν, ἐπειδήπερ, ἐὰν περισσοὶ ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, τὸ δὲ πλῆθος αὐτῶν περισσὸν ᾖ, ὁ ὅλος περισσὸς ἐστιν. ὁ ΕΖ ἄρα ἄρτιός ἐστιν. τετμήσθω δίχα κατὰ τὸ Θ. καὶ ἐπεὶ οἱ ΕΖ, Η ἐλάχιστοί είσι τῶν τὸν αὐτὸν λόγον ἐχόντων [αὐτοῖς], πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ὁ ΕΖ ἄρτιος· περισσὸς ἄρα ἐστὶν ὁ Η. εἰ γὰρ ἦν ἄρτιος, τοὺς ΕΖ, Η δυὰς ἐμέτρει· πᾶς γὰρ ἄρτιος ἔχει μέρος ἥμισυ· πρώτους ὄντας πρὸς ἀλλήλους. ὅπερ ἐστὶν ἀδὺνατον· οὐκ ἄρα ἄρτιός ἐστιν ὁ Η· περισσὸς ἄρα, καὶ ἐπὶ διπλάσιος ὁ ΕΖ τοῦ ΕΘ, τετραπλάσιος ἄρα ὁ ἀπὸ ΕΖ τοῦ ἀπὸ ΕΘ. διπλάσιος δὲ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η. διπλάσιος ἄρα ὁ ἀπὸ τοῦ Η τοῦ ἀπὸ ΕΘ· ἄρτιος ἄρα ἐστὶν ὁ ἀπὸ τοῦ Η. ἄρτιος ἄρα διὰ τὰ εἰρημένα ὁ Η· ἀλλὰ καὶ περισσός. ὅσπερ ἐστὶν ἀδύνατον. οὐκ ἄρα σύμμετρός ἐστιν ἡ ΓΑ τῇ ΑΒ μήκει· ὅπερ ἔδει δεῖξαι.
Ἄλλως
[Δεικτέον καὶ ἑτέρως, ὅτι ἀσύμμετρός ἐστιν ἡ τοῦ τετραγώνου διάμετρος τῇ πλευρᾷ].
Ἔστω ἀντὶ μὲν τῆς διαμέτρου ἡ Α, ἀντὶ δὲ τῆς πλευρᾶς ἡ Β. λέγω, ὅτι ἀσύμμετρός ἐστιν ἡ Α τῇ Β μήκει. εἰ γὰρ δυνατόν, ἔστω [σύμμετρος· καὶ γεγονέτω] πάλιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ ΕΖ ἀριθμὸς πρὸς τὸν Η, καὶ ἔστωσαν ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς οἱ ΕΖ, Η· οἱ ΕΖ, Η ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. λέγω πρῶτον, ὅτι ὁ Η οὐκ ἔστι μονάς. εἰ γὰρ δυνατόν, ἔστω μονάς. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ ΕΖ πρὸς τὸν Η, καὶ ὡς ἄρα τὸ ἀπὸ τῆς Α, πρὸς τὸ ἀπὸ τῆς Β, οὕτως ὁ ἀπὸ τοῦ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η. διπλάσιον δὲ τὸ ἀπὸ τῆς Α τοῦ ἀπὸ τῆς Β· διπλάσιος ἄρα καὶ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η. καὶ ἐστι μονὰς ὁ Η· δυὰς ἄρα ὁ ἀπὸ ΕΖ τετράγωνος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα μονάς ἐστιν ὁ Η· ἀριθμὸς ἄρα. καὶ ἐπεί ἐστιν ὡς τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β, οὕτως ὁ ἀπὸ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η, καὶ ἀνάπαλιν ὡς τὸ ἀπὸ τῆς Β πρὸς τὸ ἀπὸ τῆς Α, οὕτως ὁ ἀπὸ τοῦ Η πρὸς τὸν ἀπὸ τοῦ ΕΖ, μετρεῖ δὲ τὸ ἀπὸ τῆς Β τὸ ἀπὸ τῆς Α, μετρεῖ ἄρα καὶ ὁ ἀπὸ τοῦ Η τετράγωνος τὸν ἀπὸ τοῦ ΕΖ· ὥστε καὶ ἡ πλευρὰ αὐτὴ ὁ Η τὸν ΕΖ μετρεῖ. μετρεῖ δὲ καὶ ἑαυτὸν ὁ Η· ὁ Η ἄρα τοὺς ΕΖ, Η μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα σύμμετρός ἐστιν ἡ Α τῇ Β μήκει. ἀσύμμετρος ἄρα ἐστίν· ὅπερ ἔδει δεῖξαι.
Παράρτημα 28
Σχόλιον
Ἐπίπεδα, ἀσύμμετρα ἀλληλοις.
Εὑρημένων δὴ τῶν μήκει ἀσυμμέτρων εὐθειῶν, ὡς τῶν Α, Β, εὑρίσκεται καὶ ἄλλα πλεῖστα μεγέθη ἐκ δύο διαστάσεων, λέγω δὴ ἐπίπεδα, ἀσύμμετρα ἀλλήλοις. ἐὰν γὰρ τῶν Α, Β εὐθειῶν μέσην ἀνάλογον λάβωμεν τὴν Γ, ἔσται ὡς ἡ Α πρὸς τὴν Β, οὕτως τὸ ἀπὸ τῆς Α ἐπίπεδον πρὸς τὸ ἀπὸ τῆς Γ τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον, εἴτε τετράγωνα εἴη τὰ ἀναγραφόμενα εἴτε ἕτερα εὐθύγραμμα ὅμοια, εἴτε κύκλοι περὶ διαμέτρους τὰς Α, Γ, ἐπείπερ οἱ κύκλοι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα. εὕρηνται ἄρα καὶ ἐπίπεδα χωρία ἀσύμμετρα ἀλλήλοις· ὅπερ ἔδει δεῖξαι.
Δεδειγμένων δὴ καὶ τῶν ἐκ δύο διαστάσεων διαφόρων ἀσυμμέτρων χωρίων δείξομεν τοῖς ἀπὸ τῆς τῶν στερεῶν θεωρίας, ὡς ἔστι καὶ στερεὰ σύμμετρά τε καὶ ἀσύμμετρα ἀλλήλοις. ἐὰν γὰρ ἐπὶ τῶν Α, Β τετραγώνων ἢ τῶν ἴσων αὐτοῖς εὐθυγράμμων ἀναστήσωμεν ἰσοϋψῆ στερεὰ παραλληλεπίπεδα ἢ πυραμίδας, ἢ πρίσματα, ἔσται τὰ ἀνασταθέντα πρὸς ἄλληλα ὡς αἱ βάσεις. καὶ εἰ μὲν σύμμετροί εἰσιν αἱ βάσεις, σύμμετρα ἔσται καὶ τὰ στερεά, εἰ δὲ ἀσύμμετροι, ἀσύμμετρα. ὅπερ ἔδει δεῖξαι.
Ἀλλὰ μὴν καὶ δύο κύκλων ὄντων τῶν Α, Β, ἐὰν ἀπ᾿ αὐτῶν ἰσοϋψεῖς κώνους ἢ κυλίνδρους ἀναγράψωμεν, ἔσονται πρὸς ἀλλήλους ὡς αἱ βάσεις, τουτέστιν ὡς οἱ Α, Β κύκλοι. καὶ εἰ μὲν σύμμετροί εἰσιν οἱ κύκλοι, σύμμετροι ἔσονται καὶ οἱ τε κῶνοι πρὸς ἀλλήλους καὶ οἱ κύλινδροι, εἰ δὲ ἀσύμμετροί εἰσιν οἱ κύκλοι, ἀσύμμετροι ἔσονται καὶ οἱ κῶνοι καὶ οἱ κύλινδροι. καὶ φανερὸν ἡμῖν γέγονεν, ὅτι οὐ μόνον ἐπὶ γραμμῶν καὶ ἐπιφανειῶν ἐστι συμμετρία τε καὶ ἀσυμμετρία, ἀλλα καὶ ἐπὶ τῶν στερεῶν σχημάτων.
Στοιχεῖα Εὐκλείδου ια΄
Βιβλίον XI
Ὅροι κη΄ 28.
α΄ 1. Στερεόν ἐστι τὸ μῆκος καὶ πλάτος καὶ βάθος ἔχον.
β΄ 2. Στερεοῦ δὲ πέρας ἐπιφάνεια.
γ΄ 3. Εὐθεῖα πρὸς ἐπίπεδον ὀρθή ἐστιν, ὅταν πρὸς πάσας τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ [ὑποκειμένῳ] ἐπιπέδῳ ὀρθὰς ποιῇ γωνίας.
δ΄ 4. Ἐπίπεδον πρὸς ἐπίπεδον ὀρθόν ἐστιν, ὅταν αἱ τῇ κοινῇ τομῇ τῶν ἐπιπέδων πρὸς ὀρθὰς ἀγόμεναι εὐθεῖαι ἐν ἑνὶ τῶν ἐπιπέδων τῷ λοιπῷ ἐπιπέδῳ πρὸς ὀρθὰς ὦσιν.
ε΄ 5. Εὐθείας πρὸς ἐπίπεδον κλίσις ἐστίν, ὅταν ἀπὸ τοῦ μετεώρου πέρατος τῆς εὐθείας ἐπὶ τὸ ἐπίπεδον κάθετος ἀχθῇ, καὶ ἀπὸ τοῦ γενομένου σημείου ἐπὶ τὸ ἐν τῷ ἐπιπέδῳ πέρας τῆς εὐθείας εὐθεῖα ἐπιζευχθῇ, ἡ περιεχομένη γωνία ὑπὸ τῆς ἀχθείσης καὶ τῆς ἐφεστώσης.
ς΄ 6. Ἐπιπέδου πρὸς ἐπίπεδον κλίσις ἐστὶν ἡ περιεχομένη ὀξεῖα γωνία ὑπὸ τῶν πρὸς ὀρθὰς τῇ κοινῇ τομῇ ἀγομένων πρὸς τῷ αὐτῷ σημείῳ ἐν ἑκατέρῳ τῶν ἐπιπέδων.
ζ΄ 7. Ἐπίπεδον πρὸς ἐπίπεδον ὁμοίως κεκλίσθαι λέγεται καὶ ἕτερον πρὸς ἕτερον, ὅταν αἱ εἰρημέναι τῶν κλίσεων γωνίαι ἴσαι ἀλλήλαις ὦσιν.
η΄ 8. Παράλληλα ἐπίπεδά ἐστι τὰ ἀσύμπτωτα.
θ΄ 9. Ὅμοια στερεὰ σχήματά ἐστι τὰ ὑπὸ ὁμοίων ἐπιπέδων περιεχόμενα ἴσων τὸ πλῆθος.
ι΄ 10. Ἴσα δὲ καὶ ὅμοια στερεὰ σχήματά ἐστι τὰ ὑπὸ ὁμοίων ἐπιπέδων περιεχόμενα ἴσων τῷ πλήθει καὶ τῷ μεγέθει.
ια΄ 11. Στερεὰ γωνία ἐστὶν ἡ ὑπὸ πλειόνων ἢ δύο γραμμῶν ἁπτομένων ἀλλήλων καὶ μὴ ἐν τῇ αὐτῇ ἐπιφανείᾳ οὐσῶν πρὸς πάσαις ταῖς γραμμαῖς κλίσις. Ἄλλως· στερεὰ γωνία ἐστὶν ἡ ὑπὸ πλειόνων ἢ δύο γωνιῶν ἐπιπέδων περιεχομένη μὴ οὐσῶν ἐν τῷ αὐτῷ ἐπιπέδῳ πρὸς ἑνὶ σημείῳ συνισταμένων.
ιβ΄ 12. Πυραμίς ἐστι σχῆμα στερεὸν ἐπιπέδοις περιεχόμενον ἀπὸ ἑνὸς ἐπιπέδου πρὸς ἑνὶ σημείῳ συνεστώς.
ιγ΄ 13. Πρίσμα ἐστὶ σχῆμα στερεὸν ἐπιπέδοις περιεχόμενον, ὧν δύο τὰ ἀπεναντίον ἴσα τε καὶ ὅμοιά ἐστι καὶ παράλληλα, τὰ δὲ λοιπὰ παραλληλόγραμμα.
ιδ΄ 14. Σφαῖρά ἐστιν, ὅταν ἡμικυκλίου μενούσης τῆς διαμέτρου περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, τὸ περιληφθὲν σχῆμα.
ιε΄ 15. Ἄξων δὲ τῆς σφαίρας ἐστὶν ἡ μένουσα εὐθεῖα, περὶ ἣν τὸ ἡμικύκλιον στρέφεται.
ις΄ 16. Κέντρον δὲ τῆς σφαίρας ἐστὶ τὸ αὐτό, ὃ καὶ τοῦ ἡμικυκλίου.
ιζ΄ 17. Διάμετρος δὲ τῆς σφαίρας ἐστὶν εὐθεῖά τις διὰ τοῦ κέντρου ἠγμένη καὶ περατουμένη ἐφ' ἑκάτερα τὰ μέρη ὑπὸ τῆς ἐπιφανείας τῆς σφαίρας.
ιη΄ 18. Κῶνός ἐστιν, ὅταν ὀρθογωνίου τριγώνου μενούσης μιᾶς πλευρᾶς τῶν περὶ τὴν ὀρθὴν γωνίαν περιενεχθὲν τὸ τρίγωνον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, τὸ περιληφθὲν σχῆμα. κἂν μὲν ἡ μένουσα εὐθεῖα ἴση ᾖ τῇ λοιπῇ [τῇ] περὶ τὴν ὀρθὴν περιφερομένῃ, ὀρθογώνιος ἔσται ὁ κῶνος, ἐὰν δὲ ἐλάττων, ἀμβλυγώνιος, ἐὰν δὲ μείζων, ὀξυγώνιος.
ιθ΄ 19. Ἄξων δὲ τοῦ κώνου ἐστὶν ἡ μένουσα εὐθεῖα, περὶ ἣν τὸ τρίγωνον στρέφεται.
κ΄ 20. Βάσις δὲ ὁ κύκλος ὁ ὑπὸ τῆς περιφερομένης εὐθείας γραφόμενος.
κα΄ 21. Κύλινδρός ἐστιν, ὅταν ὀρθογωνίου παραλληλογράμμου μενούσης μιᾶς πλευρᾶς τῶν περὶ τὴν ὀρθὴν γωνίαν περιενεχθὲν τὸ παραλληλόγραμμον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, τὸ περιληφθὲν σχῆμα.
κβ΄ 22. Ἄξων δὲ τοῦ κυλίνδρου ἐστὶν ἡ μένουσα εὐθεῖα, περὶ ἣν τὸ παραλληλόγραμμον στρέφεται.
κγ΄ 23. Βάσεις δὲ οἱ κύκλοι οἱ ὑπὸ τῶν ἀπεναντίον περιαγομένων δύο πλευρῶν γραφόμενοι.
κδ΄ 24. Ὅμοιοι κῶνοι καὶ κύλινδροί εἰσιν, ὧν οἵ τε ἄξονες καὶ αἱ διάμετροι τῶν βάσεων ἀνάλογόν εἰσιν.
κε΄ 25. Κύβος ἐστὶ σχῆμα στερεὸν ὑπὸ ἓξ τετραγώνων ἴσων περιεχόμενον.
κς΄ 26. Ὀκτάεδρόν ἐστι σχῆμα στερεὸν ὑπὸ ὀκτὼ τριγώνων ἴσων καὶ ἰσοπλεύρων περιεχόμενον.
κζ΄ 27. Εἰκοσάεδρόν ἐστι σχῆμα στερεὸν ὑπὸ εἴκοσι τριγώνων ἴσων καὶ ἰσοπλεύρων περιεχόμενον.
κη΄ 28. Δωδεκάεδρόν ἐστι σχῆμα στερεὸν ὑπὸ δώδεκα πενταγώνων ἴσων καὶ ἰσοπλεύρων καὶ ἰσογωνίων περιεχόμενον.
Στοιχεῖα Εὐκλείδου ια΄
Βιβλίον XI
Προτάσεις λθ΄ 39
Πρότασις α΄ 1 Βιβλίον XI
Εὐθείας γραμμῆς μέρος μέν τι οὐκ ἔστιν ἐν τῷ ὑποκειμένῳ, ἐπιπέδῳ, μέρος δέ τι ἐν μετεωροτέρῳ.
Εἰ γὰρ δυνατόν, εὐθείας γραμμῆς τῆς ΑΒΓ μέρος μέν τι τὸ ΑΒ ἔστω ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, μέρος δέ τι τὸ ΒΓ ἐν μετεωροτέρῳ.
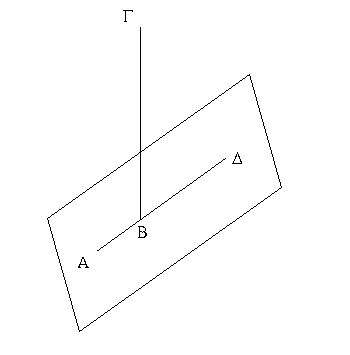
Ἔσται δή τις τῇ ΑΒ συνεχὴς εὐθεῖα ἐπ᾿ εὐθείας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ. ἔστω ἡ ΒΔ· δύο ἄρα εὐθειῶν τῶν ΑΒΓ, ΑΒΔ κοινὸν τμῆμά ἐστιν ἡ ΑΒ· ὅπερ ἐστὶν ἀδύνατον, ἐπειδήπερ ἐὰν κέντρῳ τῷ Β καὶ διαστήματι τῷ ΑΒ κύκλον γράψωμεν, αἱ διάμετροι ἀνίσους ἀπολήψονται τοῦ κύκλου περιφερείας.
Εὐθείας ἄρα γραμμῆς μέρος μέν τι οὐκ ἔστιν ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, τὸ δὲ ἐν μετεωροτέρῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον XI
Ἐὰν δύο εὐθεῖαι τέμνωσιν ἀλλήλας, ἐν ἑνί εἰσιν ἐπιπέδῳ, καὶ πᾶν τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΓΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε σημεῖον· λέγω, ὅτι αἱ ΑΒ, ΓΔ ἐν ἑνί εἰσιν ἐπιπέδῳ, καὶ πᾶν τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ.
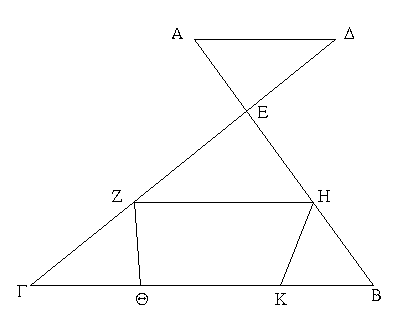
Εἰλήφθω γὰρ ἐπὶ τῶν ΕΓ, ΕΒ τυχόντα σημεῖα τὰ Ζ, Η, καὶ ἐπεζεύχθωσαν αἱ ΓΒ, ΖΗ, καὶ διήχθωσαν αἱ ΖΘ, ΗΚ· λέγω πρῶτον, ὅτι τὸ ΕΓΒ τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ. εἰ γάρ ἐστι τοῦ ΕΓΒ τριγώνου μέρος ἤτοι τὸ ΖΘΓ ἢ τὸ ΗΒΚ ἐν τῷ ὑποκειμένῳ [ἐπιπέδῳ], τὸ δὲ λοιπὸν ἐν ἄλλῳ, ἔσται καὶ μιᾶς τῶν ΕΓ, ΕΒ εὐθειῶν μέρος μέν τι ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, τὸ δὲ ἐν ἄλλῳ. εἰ δὲ τοῦ ΕΓΒ τριγώνου τὸ ΖΓΒΗ μέρος ᾖ ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, τὸ δὲ λοιπὸν ἐν ἄλλῳ, ἔσται καὶ ἀμφοτέρων τῶν ΕΓ, ΕΒ εὐθειῶν μέρος μέν τι ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, τὸ δὲ ἐν ἄλλῳ· ὅπερ ἄτοπον ἐδείχθη. τὸ ἄρα ΕΓΒ τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ. ἐν ᾧ δέ ἐστι τὸ ΕΓΒ τρίγωνον, ἐν τούτῳ καὶ ἑκατέρα τῶν ΕΓ, ΕΒ, ἐν ᾧ δὲ ἑκατέρα τῶν ΕΓ, ΕΒ, ἐν τούτῳ καὶ αἱ ΑΒ, ΓΔ. αἱ ΑΒ, ΓΔ ἄρα εὐθεῖαι ἐν ἑνί εἰσιν ἐπιπέδῳ, καὶ πᾶν τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον XI
Ἐὰν δύο ἐπίπεδα τέμνῃ ἄλληλα, ἡ κοινὴ αὐτῶν τομὴ εὐθεῖά ἐστιν.
Δύο γὰρ ἐπίπεδα τὰ ΑΒ, ΒΓ τεμνέτω ἄλληλα, κοινὴ δὲ αὐτῶν τομὴ ἔστω ἡ ΔΒ γραμμή· λέγω, ὅτι ἡ ΔΒ γραμμὴ εὐθεῖά ἐστιν.
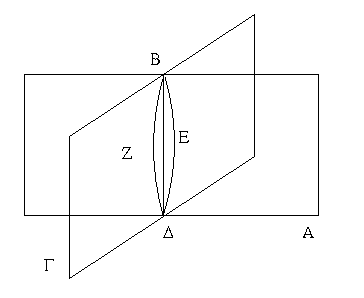
Εἰ γὰρ μή, ἐπεζεύχθω ἀπὸ τοῦ Δ ἐπὶ τὸ Β ἐν μὲν τῷ ΑΒ ἐπιπέδῳ εὐθεῖα ἡ ΔΕΒ, ἐν δὲ τῷ ΒΓ ἐπιπέδῳ εὐθεῖα ἡ ΔΖΒ. ἔσται δὴ δύο εὐθειῶν τῶν ΔΕΒ, ΔΖΒ τὰ αὐτὰ πέρατα, καὶ περιέξουσι δηλαδὴ χωρίον· ὅπερ ἄτοπον. οὐκ ἄρα αἱ ΔΕΒ, ΔΖΒ εὐθεῖαί εἰσιν. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἄλλη τις ἀπὸ τοῦ Δ ἐπὶ τὸ Β ἐπιζευγνυμένη εὐθεῖα ἔσται πλὴν τῆς ΔΒ κοινῆς τομῆς τῶν ΑΒ, ΒΓ ἐπιπέδων.
Ἐὰν ἄρα δύο ἐπίπεδα τέμνῃ ἄλληλα, ἡ κοινὴ αὐτῶν τομὴ εὐθεῖά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον XI
Ἐὰν εὐθεῖα δύο εὐθείαις τεμνούσαις ἀλλήλας πρὸς ὀρθὰς ἐπὶ τῆς κοινῆς τομῆς ἐπισταθῇ, καὶ τῷ δι' αὐτῶν ἐπιπέδῳ πρὸς ὀρθὰς ἔσται.
Εὐθεῖα γάρ τις ἡ ΕΖ δύο εὐθείαις ταῖς ΑΒ, ΓΔ τεμνούσαις ἀλλήλας κατὰ τὸ Ε σημεῖον ἀπὸ τοῦ Ε πρὸς ὀρθὰς ἐφεστάτω· λέγω, ὅτι ἡ ΕΖ καὶ τῷ διὰ τῶν ΑΒ, ΓΔ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
Ἀπειλήφθωσαν γὰρ αἱ ΑΕ, ΕΒ, ΓΕ, ΕΔ ἴσαι ἀλλήλαις, καὶ διήχθω τις διὰ τοῦ Ε, ὡς ἔτυχεν, ἡ ΗΕΘ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΓΒ, καὶ ἔτι ἀπὸ τυχόντος τοῦ Ζ ἐπεζεύχθωσαν αἱ ΖΑ, ΖΗ, ΖΔ, ΖΓ, ΖΘ, ΖΒ. καὶ ἐπεὶ δύο αἱ ΑΕ, ΕΔ δυσὶ ταῖς ΓΕ, ΕΒ ἴσαι εἰσὶ καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΑΔ βάσει τῇ ΓΒ ἴση ἐστίν, καὶ τὸ ΑΕΔ τρίγωνον τῷ ΓΕΒ τριγώνῳ ἴσον ἔσται· ὥστε καὶ γωνία ἡ ὑπὸ ΔΑΕ γωνίᾳ τῇ ὑπὸ ΕΒΓ ἴση [ἐστίν].
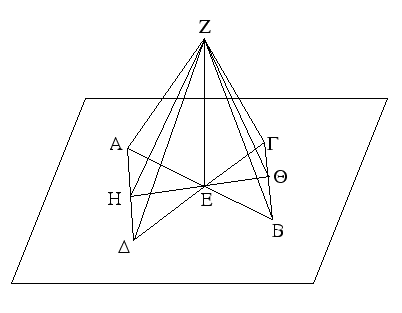
ἔστι δὲ καὶ ἡ ὑπὸ ΑΕΗ γωνία τῇ ὑπὸ ΒΕΘ ἴση. δύο δὴ τρίγωνά ἐστι τὰ ΑΗΕ, ΒΕΘ τὰς δύο γωνίας δυσὶ γωνίαις ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν πρὸς ταῖς ἴσαις γωνίαις τὴν ΑΕ τῇ ΕΒ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξουσιν. ἴση ἄρα ἡ μὲν ΗΕ τῇ ΕΘ, ἡ δὲ ΑΗ τῇ ΒΘ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΕ τῇ ΕΒ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΖΕ, βάσις ἄρα ἡ ΖΑ βάσει τῇ ΖΒ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΖΓ τῇ ΖΔ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΓΒ, ἔστι δὲ καὶ ἡ ΖΑ τῇ ΖΒ ἴση, δύο δὴ αἱ ΖΑ, ΑΔ δυσὶ ταῖς ΖΒ, ΒΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΖΔ βάσει τῇ ΖΓ ἐδείχθη ἴση· καὶ γωνία ἄρα ἡ ὑπὸ ΖΑΔ γωνίᾳ τῇ ὑπὸ ΖΒΓ ἴση ἐστίν. καὶ ἐπεὶ πάλιν ἐδείχθη ἡ ΑΗ τῇ ΒΘ ἴση, ἀλλὰ μὴν καὶ ἡ ΖΑ τῇ ΖΒ ἴση, δύο δὴ αἱ ΖΑ, ΑΗ δυσὶ ταῖς ΖΒ, ΒΘ ἴσαι εἰσίν. καὶ γωνία ἡ ὑπὸ ΖΑΗ ἐδείχθη ἴση τῇ ὑπὸ ΖΒΘ· βάσις ἄρα ἡ ΖΗ βάσει τῇ ΖΘ ἐστιν ἴση. καὶ ἐπεὶ πάλιν ἴση ἐδείχθη ἡ ΗΕ τῇ ΕΘ, κοινὴ δὲ ἡ ΕΖ, δύο δὴ αἱ ΗΕ, ΕΖ δυσὶ ταῖς ΘΕ, ΕΖ ἴσαι εἰσίν· καὶ βάσις ἡ ΖΗ βάσει τῇ ΖΘ ἴση· γωνία ἄρα ἡ ὑπὸ ΗΕΖ γωνίᾳ τῇ ὑπὸ ΘΕΖ ἴση ἐστίν. ὀρθὴ ἄρα ἑκατέρα τῶν ὑπὸ ΗΕΖ, ΘΕΖ γωνιῶν. ἡ ΖΕ ἄρα πρὸς τὴν ΗΘ τυχόντως διὰ τοῦ Ε ἀχθεῖσαν ὀρθή ἐστιν. ὁμοίως δὴ δείξομεν, ὅτι ἡ ΖΕ καὶ πρὸς πάσας τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας. εὐθεῖα δὲ πρὸς ἐπίπεδον ὀρθή ἐστιν, ὅταν πρὸς πάσας τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ αὐτῷ ἐπιπέδῳ ὀρθὰς ποιῇ γωνίας· ἡ ΖΕ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. τὸ δὲ ὑποκείμενον ἐπίπεδόν ἐστι τὸ διὰ τῶν ΑΒ, ΓΔ εὐθειῶν. ἡ ΖΕ ἄρα πρὸς ὀρθάς ἐστι τῷ διὰ τῶν ΑΒ, ΓΔ ἐπιπέδῳ.
Ἐὰν ἄρα εὐθεῖα δύο εὐθείαις τεμνούσαις ἀλλήλας πρὸς ὀρθὰς ἐπὶ τῆς κοινῆς τομῆς ἐπισταθῇ, καὶ τῷ δι' αὐτῶν ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον XI
Ἐὰν εὐθεῖα τρισὶν εὐθείαις ἁπτομέναις ἀλλήλων πρὸς ὀρθὰς ἐπὶ τῆς κοινῆς τομῆς ἐπισταθῇ, αἱ τρεῖς εὐθεῖαι ἐν ἑνί εἰσιν ἐπιπέδῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τρισὶν εὐθείαις ταῖς ΒΓ, ΒΔ, ΒΕ πρὸς ὀρθὰς ἐπὶ τῆς κατὰ τὸ Β ἁφῆς ἐφεστάτω· λέγω, ὅτι αἱ ΒΓ, ΒΔ, ΒΕ ἐν ἑνί εἰσιν ἐπιπέδῳ.
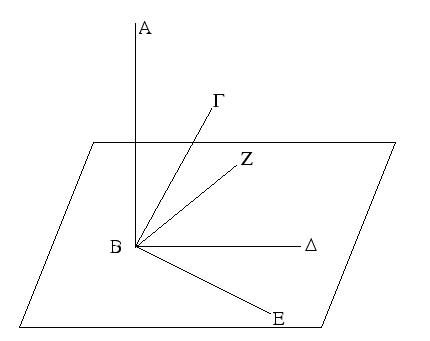
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἔστωσαν αἱ μὲν ΒΔ, ΒΕ ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ, ἡ δὲ ΒΓ ἐν μετεωροτέρῳ, καὶ ἐκβεβλήσθω τὸ διὰ τῶν ΑΒ, ΒΓ ἐπίπεδον· κοινὴν δὴ τομὴν ποιήσει ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ εὐθεῖαν. ποιείτω τὴν ΒΖ. ἐν ἑνὶ ἄρα εἰσὶν ἐπιπέδῳ τῷ διηγμένῳ διὰ τῶν ΑΒ, ΒΓ αἱ τρεῖς εὐθεῖαι αἱ ΑΒ, ΒΓ, ΒΖ. καὶ ἐπεὶ ἡ ΑΒ ὀρθή ἐστι πρὸς ἑκατέραν τῶν ΒΔ, ΒΕ, καὶ τῷ διὰ τῶν ΒΔ, ΒΕ ἄρα ἐπιπέδῳ ὀρθή ἐστιν ἡ ΑΒ. τὸ δὲ διὰ τῶν ΒΔ, ΒΕ ἐπίπεδον τὸ ὑποκείμενόν ἐστιν· ἡ ΑΒ ἄρα ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον. ὥστε καὶ πρὸς πάσας τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας ἡ ΑΒ. ἅπτεται δὲ αὐτῆς ἡ ΒΖ οὖσα ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ· ἡ ἄρα ὑπὸ ΑΒΖ γωνία ὀρθή ἐστιν. ὑπόκειται δὲ καὶ ἡ ὑπὸ ΑΒΓ ὀρθή· ἴση ἄρα ἡ ὑπὸ ΑΒΖ γωνία τῇ ὑπὸ ΑΒΓ. καί εἰσιν ἐν ἑνὶ ἐπιπέδῳ· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ΒΓ εὐθεῖα ἐν μετεωροτέρῳ ἐστὶν ἐπιπέδῳ· αἱ τρεῖς ἄρα εὐθεῖαι αἱ ΒΓ, ΒΔ, ΒΕ ἐν ἑνί εἰσιν ἐπιπέδῳ.
Ἐὰν ἄρα εὐθεῖα τρισὶν εὐθείαις ἁπτομέναις ἀλλήλων ἐπὶ τῆς ἁφῆς πρὸς ὀρθὰς ἐπισταθῇ, αἱ τρεῖς εὐθεῖαι ἐν ἑνί εἰσιν ἐπιπέδῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον XI
Ἐὰν δύο εὐθεῖαι τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ὦσιν, παράλληλοι ἔσονται αἱ εὐθεῖαι.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΓΔ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἔστωσαν· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ.
Συμβαλλέτωσαν γὰρ τῷ ὑποκειμένῳ ἐπιπέδῳ κατὰ τὰ Β, Δ σημεῖα, καὶ ἐπεζεύχθω ἡ ΒΔ εὐθεῖα, καὶ ἤχθω τῇ ΒΔ πρὸς ὀρθὰς ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ἡ ΔΕ, καὶ κείσθω τῇ ΑΒ ἴση ἡ ΔΕ, καὶ ἐπεζεύχθωσαν αἱ ΒΕ, ΑΕ, ΑΔ.
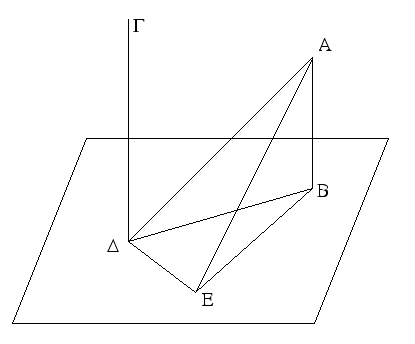
Καὶ ἐπεὶ ἡ ΑΒ ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον, καὶ πρὸς πάσας [ἄρα] τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας. ἅπτεται δὲ τῆς ΑΒ ἑκατέρα τῶν ΒΔ, ΒΕ οὖσα ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν ὑπὸ ΑΒΔ, ΑΒΕ γωνιῶν. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ὑπὸ ΓΔΒ, ΓΔΕ ὀρθή ἐστιν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΔΕ, κοινὴ δὲ ἡ ΒΔ, δύο δὴ αἱ ΑΒ, ΒΔ δυσὶ ταῖς ΕΔ, ΔΒ ἴσαι εἰσίν· καὶ γωνίας ὀρθὰς περιέχουσιν· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΒΕ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΔΕ, ἀλλὰ καὶ ἡ ΑΔ τῇ ΒΕ, δύο δὴ αἱ ΑΒ, ΒΕ δυσὶ ταῖς ΕΔ, ΔΑ ἴσαι εἰσίν· καὶ βάσις αὐτῶν κοινὴ ἡ ΑΕ· γωνία ἄρα ἡ ὑπὸ ΑΒΕ γωνίᾳ τῇ ὑπὸ ΕΔΑ ἐστιν ἴση. ὀρθὴ δὲ ἡ ὑπὸ ΑΒΕ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΕΔΑ· ἡ ΕΔ ἄρα πρὸς τὴν ΔΑ ὀρθή ἐστιν. ἔστι δὲ καὶ πρὸς ἑκατέραν τῶν ΒΔ, ΔΓ ὀρθή. ἡ ΕΔ ἄρα τρισὶν εὐθείαις ταῖς ΒΔ, ΔΑ, ΔΓ πρὸς ὀρθὰς ἐπὶ τῆς ἁφῆς ἐφέστηκεν· αἱ τρεῖς ἄρα εὐθεῖαι αἱ ΒΔ, ΔΑ, ΔΓ ἐν ἑνί εἰσιν ἐπιπέδῳ. ἐν ᾧ δὲ αἱ ΔΒ, ΔΑ, ἐν τούτῳ καὶ ἡ ΑΒ· πᾶν γὰρ τρίγωνον ἐν ἑνί ἐστιν ἐπιπέδῳ· αἱ ἄρα ΑΒ, ΒΔ, ΔΓ εὐθεῖαι ἐν ἑνί εἰσιν ἐπιπέδῳ. καί ἐστιν ὀρθὴ ἑκατέρα τῶν ὑπὸ ΑΒΔ, ΒΔΓ γωνιῶν· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ.
Ἐὰν ἄρα δύο εὐθεῖαι τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ὦσιν, παράλληλοι ἔσονται αἱ εὐθεῖαι· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον XI
Ἐὰν ὦσι δύο εὐθεῖαι παράλληλοι, ληφθῇ δὲ ἐφ' ἑκατέρας αὐτῶν τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐν τῷ αὐτῷ ἐπιπέδῳ ἐστὶ ταῖς παραλλήλοις.
Ἔστωσαν δύο εὐθεῖαι παράλληλοι αἱ ΑΒ, ΓΔ, καὶ εἰλήφθω ἐφ' ἑκατέρας αὐτῶν τυχόντα σημεῖα τὰ Ε, Ζ· λέγω, ὅτι ἡ ἐπὶ τὰ Ε, Ζ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐν τῷ αὐτῷ ἐπιπέδῳ ἐστὶ ταῖς παραλλήλοις.
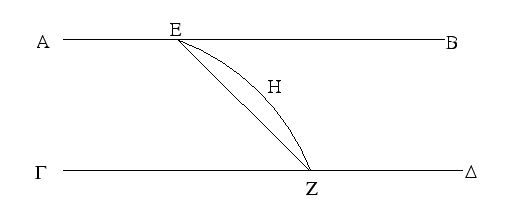
Μὴ γάρ, ἀλλ' εἰ δυνατόν, ἔστω ἐν μετεωροτέρῳ ὡς ἡ ΕΗΖ, καὶ διήχθω διὰ τῆς ΕΗΖ ἐπίπεδον· τομὴν δὴ ποιήσει ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ εὐθεῖαν. ποιείτω ὡς τὴν ΕΖ· δύο ἄρα εὐθεῖαι αἱ ΕΗΖ, ΕΖ χωρίον περιέξουσιν· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ἀπὸ τοῦ Ε ἐπὶ τὸ Ζ ἐπιζευγνυμένη εὐθεῖα ἐν μετεωροτέρῳ ἐστὶν ἐπιπέδῳ· ἐν τῷ διὰ τῶν ΑΒ, ΓΔ ἄρα παραλλήλων ἐστὶν ἐπιπέδῳ ἡ ἀπὸ τοῦ Ε ἐπὶ τὸ Ζ ἐπιζευγνυμένη εὐθεῖα.
Ἐὰν ἄρα ὦσι δύο εὐθεῖαι παράλληλοι, ληφθῇ δὲ ἐφ' ἑκατέρας αὐτῶν τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐν τῷ αὐτῷ ἐπιπέδῳ ἐστὶ ταῖς παραλλήλοις· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον XI
Ἐὰν ὦσι δύο εὐθεῖαι παράλληλοι, ἡ δὲ ἑτέρα αὐτῶν ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ λοιπὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται.
Ἔστωσαν δύο εὐθεῖαι παράλληλοι αἱ ΑΒ, ΓΔ, ἡ δὲ ἑτέρα αὐτῶν ἡ ΑΒ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἔστω· λέγω, ὅτι καὶ ἡ λοιπὴ ἡ ΓΔ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται.
Συμβαλλέτωσαν γὰρ αἱ ΑΒ, ΓΔ τῷ ὑποκειμένῳ ἐπιπέδῳ κατὰ τὰ Β, Δ σημεῖα, καὶ ἐπεζεύχθω ἡ ΒΔ· αἱ ΑΒ, ΓΔ, ΒΔ ἄρα ἐν ἑνί εἰσιν ἐπιπέδῳ. ἤχθω τῇ ΒΔ πρὸς ὀρθὰς ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ἡ ΔΕ, καὶ κείσθω τῇ ΑΒ ἴση ἡ ΔΕ, καὶ ἐπεζεύχθωσαν αἱ ΒΕ, ΑΕ, ΑΔ. καὶ ἐπεὶ ἡ ΑΒ ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν ἡ ΑΒ· ὀρθὴ ἄρα [ἐστὶν] ἑκατέρα τῶν ὑπὸ ΑΒΔ, ΑΒΕ γωνιῶν.
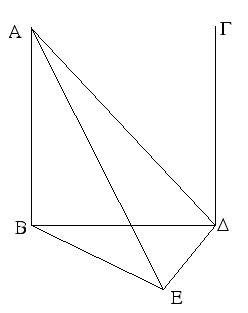
καὶ ἐπεὶ εἰς παραλλήλους τὰς ΑΒ, ΓΔ εὐθεῖα ἐμπέπτωκεν ἡ ΒΔ, αἱ ἄρα ὑπὸ ΑΒΔ, ΓΔΒ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. ὀρθὴ δὲ ἡ ὑπὸ ΑΒΔ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΓΔΒ· ἡ ΓΔ ἄρα πρὸς τὴν ΒΔ ὀρθή ἐστιν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΔΕ, κοινὴ δὲ ἡ ΒΔ, δύο δὴ αἱ ΑΒ, ΒΔ δυσὶ ταῖς ΕΔ, ΔΒ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΑΒΔ γωνίᾳ τῇ ὑπὸ ΕΔΒ ἴση· ὀρθὴ γὰρ ἑκατέρα· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΒΕ ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΑΒ τῇ ΔΕ, ἡ δὲ ΒΕ τῇ ΑΔ, δύο δὴ αἱ ΑΒ, ΒΕ δυσὶ ταῖς ΕΔ, ΔΑ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ. καὶ βάσις αὐτῶν κοινὴ ἡ ΑΕ· γωνία ἄρα ἡ ὑπὸ ΑΒΕ γωνίᾳ τῇ ὑπὸ ΕΔΑ ἐστιν ἴση. ὀρθὴ δὲ ἡ ὑπὸ ΑΒΕ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΕΔΑ· ἡ ΕΔ ἄρα πρὸς τὴν ΑΔ ὀρθή ἐστιν. ἔστι δὲ καὶ πρὸς τὴν ΔΒ ὀρθή· ἡ ΕΔ ἄρα καὶ τῷ διὰ τῶν ΒΔ, ΔΑ ἐπιπέδῳ ὀρθή ἐστιν. καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ διὰ τῶν ΒΔΑ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας ἡ ΕΔ. ἐν δὲ τῷ διὰ τῶν ΒΔΑ ἐπιπέδῳ ἐστὶν ἡ ΔΓ, ἐπειδήπερ ἐν τῷ διὰ τῶν ΒΔΑ ἐπιπέδῳ εἰσὶν αἱ ΑΒ, ΒΔ, ἐν ᾧ δὲ αἱ ΑΒ, ΒΔ, ἐν τούτῳ ἐστὶ καὶ ἡ ΔΓ. ἡ ΕΔ ἄρα τῇ ΔΓ πρὸς ὀρθάς ἐστιν· ὥστε καὶ ἡ ΓΔ τῇ ΔΕ πρὸς ὀρθάς ἐστιν. ἔστι δὲ καὶ ἡ ΓΔ τῇ ΒΔ πρὸς ὀρθάς. ἡ ΓΔ ἄρα δύο εὐθείαις τεμνούσαις ἀλλήλας ταῖς ΔΕ, ΔΒ ἀπὸ τῆς κατὰ τὸ Δ τομῆς πρὸς ὀρθὰς ἐφέστηκεν· ὥστε ἡ ΓΔ καὶ τῷ διὰ τῶν ΔΕ, ΔΒ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. τὸ δὲ διὰ τῶν ΔΕ, ΔΒ ἐπίπεδον τὸ ὑποκείμενόν ἐστιν· ἡ ΓΔ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
Ἐὰν ἄρα ὦσι δύο εὐθεῖαι παράλληλοι, ἡ δὲ μία αὐτῶν ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ λοιπὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον XI
Αἱ τῇ αὐτῇ εὐθείᾳ παράλληλοι καὶ μὴ οὖσαι αὐτῇ ἐν τῷ αὐτῷ ἐπιπέδῳ καὶ ἀλλήλαις εἰσὶ παράλληλοι.
Ἔστω γὰρ ἑκατέρα τῶν ΑΒ, ΓΔ τῇ ΕΖ παράλληλος μὴ οὖσαι αὐτῇ ἐν τῷ αὐτῷ ἐπιπέδῳ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΑΒ τῇ ΓΔ.
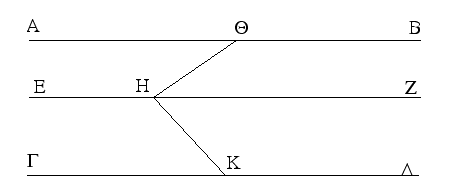
Εἰλήφθω γὰρ ἐπὶ τῆς ΕΖ τυχὸν σημεῖον τὸ Η, καὶ ἀπ' αὐτοῦ τῇ ΕΖ ἐν μὲν τῷ διὰ τῶν ΕΖ, ΑΒ ἐπιπέδῳ πρὸς ὀρθὰς ἤχθω ἡ ΗΘ, ἐν δὲ τῷ διὰ τῶν ΖΕ, ΓΔ τῇ ΕΖ πάλιν πρὸς ὀρθὰς ἤχθω ἡ ΗΚ. καὶ ἐπεὶ ἡ ΕΖ πρὸς ἑκατέραν τῶν ΗΘ, ΗΚ ὀρθή ἐστιν, ἡ ΕΖ ἄρα καὶ τῷ διὰ τῶν ΗΘ, ΗΚ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καί ἐστιν ἡ ΕΖ τῇ ΑΒ παράλληλος· καὶ ἡ ΑΒ ἄρα τῷ διὰ τῶν ΘΗΚ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΓΔ τῷ διὰ τῶν ΘΗΚ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν· ἑκατέρα ἄρα τῶν ΑΒ, ΓΔ τῷ διὰ τῶν ΘΗΚ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. ἐὰν δὲ δύο εὐθεῖαι τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ὦσιν, παράλληλοί εἰσιν αἱ εὐθεῖαι· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΓΔ· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον XI
Ἐὰν δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων ὦσι μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ, ἴσας γωνίας περιέξουσιν.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΒΓ ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας τὰς ΔΕ, ΕΖ ἁπτομένας ἀλλήλων ἔστωσαν μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ· λέγω, ὅτι ἴση ἐστὶν ἡ ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ. Ἀπειλήφθωσαν γὰρ αἱ ΒΑ, ΒΓ, ΕΔ, ΕΖ ἴσαι ἀλλήλαις, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΓΖ, ΒΕ, ΑΓ, ΔΖ. καὶ ἐπεὶ ἡ ΒΑ τῇ ΕΔ ἴση ἐστὶ καὶ παράλληλος, καὶ ἡ ΑΔ ἄρα τῇ ΒΕ ἴση ἐστὶ καὶ παράλληλος.
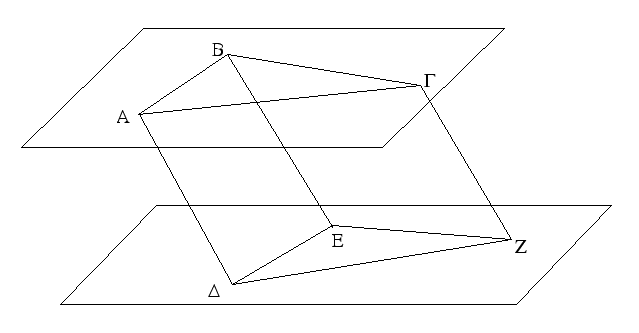
διὰ τὰ αὐτὰ δὴ καὶ ἡ ΓΖ τῇ ΒΕ ἴση ἐστὶ καὶ παράλληλος· ἑκατέρα ἄρα τῶν ΑΔ, ΓΖ τῇ ΒΕ ἴση ἐστὶ καὶ παράλληλος. αἱ δὲ τῇ αὐτῇ εὐθείᾳ παράλληλοι καὶ μὴ οὖσαι αὐτῇ ἐν τῷ αὐτῷ ἐπιπέδῳ καὶ ἀλλήλαις εἰσὶ παράλληλοι· παράλληλος ἄρα ἐστὶν ἡ ΑΔ τῇ ΓΖ καὶ ἴση. καὶ ἐπιζευγνύουσιν αὐτὰς αἱ ΑΓ, ΔΖ· καὶ ἡ ΑΓ ἄρα τῇ ΔΖ ἴση ἐστὶ καὶ παράλληλος. καὶ ἐπεὶ δύο αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΔΕ, ΕΖ ἴσαι εἰσίν, καὶ βάσις ἡ ΑΓ βάσει τῇ ΔΖ ἴση, γωνία ἄρα ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση.
Ἐὰν ἄρα δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων ὦσι μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ, ἴσας γωνίας περιέξουσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον XI
Ἀπὸ τοῦ δοθέντος σημείου μετεώρου ἐπὶ τὸ δοθὲν ἐπίπεδον κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω τὸ μὲν δοθὲν σημεῖον μετέωρον τὸ Α, τὸ δὲ δοθὲν ἐπίπεδον τὸ ὑποκείμενον· δεῖ δὴ ἀπὸ τοῦ Α σημείου ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Διήχθω γάρ τις ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ εὐθεῖα, ὡς ἔτυχεν, ἡ ΒΓ, καὶ ἤχθω ἀπὸ τοῦ Α σημείου ἐπὶ τὴν ΒΓ κάθετος ἡ ΑΔ. εἰ μὲν οὖν ἡ ΑΔ κάθετός ἐστι καὶ ἐπὶ τὸ ὑποκείμενον ἐπίπεδον, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. εἰ δὲ οὔ, ἤχθω ἀπὸ τοῦ Δ σημείου τῇ ΒΓ ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΔΕ, καὶ ἤχθω ἀπὸ τοῦ Α ἐπὶ τὴν ΔΕ κάθετος ἡ ΑΖ, καὶ διὰ τοῦ Ζ σημείου τῇ ΒΓ παράλληλος ἤχθω ἡ ΗΘ.
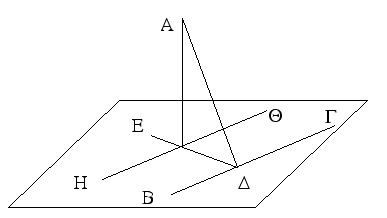
Καὶ ἐπεὶ ἡ ΒΓ ἑκατέρᾳ τῶν ΔΑ, ΔΕ πρὸς ὀρθάς ἐστιν, ἡ ΒΓ ἄρα καὶ τῷ διὰ τῶν ΕΔΑ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καί ἐστιν αὐτῇ παράλληλος ἡ ΗΘ· ἐὰν δὲ ὦσι δύο εὐθεῖαι παράλληλοι, ἡ δὲ μία αὐτῶν ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ λοιπὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· καὶ ἡ ΗΘ ἄρα τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ ὀρθή ἐστιν ἡ ΗΘ. ἅπτεται δὲ αὐτῆς ἡ ΑΖ οὖσα ἐν τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ· ἡ ΗΘ ἄρα ὀρθή ἐστι πρὸς τὴν ΖΑ· ὥστε καὶ ἡ ΖΑ ὀρθή ἐστι πρὸς τὴν ΘΗ. ἔστι δὲ ἡ ΑΖ καὶ πρὸς τὴν ΔΕ ὀρθή· ἡ ΑΖ ἄρα πρὸς ἑκατέραν τῶν ΗΘ, ΔΕ ὀρθή ἐστιν. ἐὰν δὲ εὐθεῖα δυσὶν εὐθείαις τεμνούσαις ἀλλήλας ἐπὶ τῆς τομῆς πρὸς ὀρθὰς ἐπισταθῇ, καὶ τῷ δι' αὐτῶν ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ἡ ΖΑ ἄρα τῷ διὰ τῶν ΕΔ, ΗΘ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. τὸ δὲ διὰ τῶν ΕΔ, ΗΘ ἐπίπεδόν ἐστι τὸ ὑποκείμενον· ἡ ΑΖ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
Ἀπὸ τοῦ ἄρα δοθέντος σημείου μετεώρου τοῦ Α ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετος εὐθεῖα γραμμὴ ἦκται ἡ ΑΖ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιβ΄ 12 Βιβλίον XI
Τῷ δοθέντι ἐπιπέδῳ ἀπὸ τοῦ πρὸς αὐτῷ δοθέντος σημείου πρὸς ὀρθὰς εὐθεῖαν γραμμὴν ἀναστῆσαι.
Ἔστω τὸ μὲν δοθὲν ἐπίπεδον τὸ ὑποκείμενον, τὸ δὲ πρὸς αὐτῷ σημεῖον τὸ Α· δεῖ δὴ ἀπὸ τοῦ Α σημείου τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς εὐθεῖαν γραμμὴν ἀναστῆσαι.
Νενοήσθω τι σημεῖον μετέωρον τὸ Β, καὶ ἀπὸ τοῦ Β ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετος ἤχθω ἡ ΒΓ, καὶ διὰ τοῦ Α σημείου τῇ ΒΓ παράλληλος ἤχθω ἡ ΑΔ.
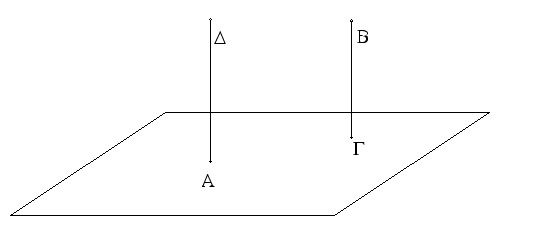
Ἐπεὶ οὖν δύο εὐθεῖαι παράλληλοί εἰσιν αἱ ΑΔ, ΓΒ, ἡ δὲ μία αὐτῶν ἡ ΒΓ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, καὶ ἡ λοιπὴ ἄρα ἡ ΑΔ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
Τῷ ἄρα δοθέντι ἐπιπέδῳ ἀπὸ τοῦ πρὸς αὐτῷ σημείου τοῦ Α πρὸς ὀρθὰς ἀνέσταται ἡ ΑΔ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιγ΄ 13 Βιβλίον XI
Ἀπὸ τοῦ αὐτοῦ σημείου τῷ αὐτῷ ἐπιπέδῳ δύο εὐθεῖαι πρὸς ὀρθὰς οὐκ ἀναστήσονται ἐπὶ τὰ αὐτὰ μέρη.
Εἰ γὰρ δυνατόν, ἀπὸ τοῦ αὐτοῦ σημείου τοῦ Α τῷ ὑποκειμένῳ ἐπιπέδῳ δύο εὐθεῖαι αἱ ΑΒ, ΑΓ πρὸς ὀρθὰς ἀνεστάτωσαν ἐπὶ τὰ αὐτὰ μέρη, καὶ διήχθω τὸ διὰ τῶν ΒΑ, ΑΓ ἐπίπεδον·
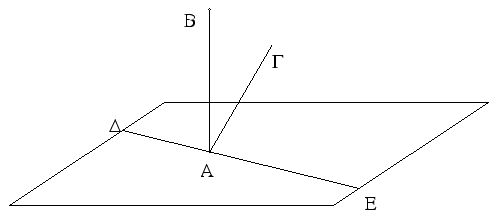
τομὴν δὴ ποιήσει διὰ τοῦ Α ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ εὐθεῖαν. ποιείτω τὴν ΔΑΕ· αἱ ἄρα ΑΒ, ΑΓ, ΔΑΕ εὐθεῖαι ἐν ἑνί εἰσιν ἐπιπέδῳ. καὶ ἐπεὶ ἡ ΓΑ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας. ἅπτεται δὲ αὐτῆς ἡ ΔΑΕ οὖσα ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ· ἡ ἄρα ὑπὸ ΓΑΕ γωνία ὀρθή ἐστιν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΒΑΕ ὀρθή ἐστιν· ἴση ἄρα ἡ ὑπὸ ΓΑΕ τῇ ὑπὸ ΒΑΕ. καί εἰσιν ἐν ἑνὶ ἐπιπέδῳ· ὅπερ ἐστὶν ἀδύνατον.
Οὐκ ἄρα ἀπὸ τοῦ αὐτοῦ σημείου τῷ αὐτῷ ἐπιπέδῳ δύο εὐθεῖαι πρὸς ὀρθὰς ἀνασταθήσονται ἐπὶ τὰ αὐτὰ μέρη· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον XI
Πρὸς ἃ ἐπίπεδα ἡ αὐτὴ εὐθεῖα ὀρθή ἐστιν, παράλληλα ἔσται τὰ ἐπίπεδα.
Εὐθεῖα γάρ τις ἡ ΑΒ πρὸς ἑκάτερον τῶν ΓΔ, ΕΖ ἐπιπέδων πρὸς ὀρθὰς ἔστω· λέγω, ὅτι παράλληλά ἐστι τὰ ἐπίπεδα.
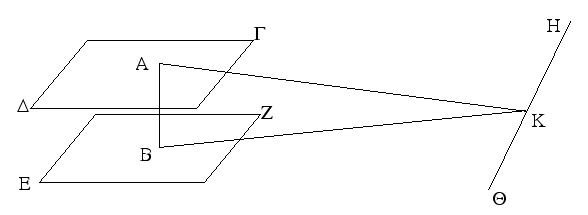
Εἰ γὰρ μή, ἐκβαλλόμενα συμπεσοῦνται. συμπιπτέτωσαν· ποιήσουσι δὴ κοινὴν τομὴν εὐθεῖαν. ποιείτωσαν τὴν ΗΘ, καὶ εἰλήφθω ἐπὶ τῆς ΗΘ τυχὸν σημεῖον τὸ Κ, καὶ ἐπεζεύχθωσαν αἱ ΑΚ, ΒΚ. καὶ ἐπεὶ ἡ ΑΒ ὀρθή ἐστι πρὸς τὸ ΕΖ ἐπίπεδον, καὶ πρὸς τὴν ΒΚ ἄρα εὐθεῖαν οὖσαν ἐν τῷ ΕΖ ἐκβληθέντι ἐπιπέδῳ ὀρθή ἐστιν ἡ ΑΒ· ἡ ἄρα ὑπὸ ΑΒΚ γωνία ὀρθή ἐστιν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΒΑΚ ὀρθή ἐστιν. τριγώνου δὴ τοῦ ΑΒΚ αἱ δύο γωνίαι αἱ ὑπὸ ΑΒΚ, ΒΑΚ δυσὶν ὀρθαῖς εἰσιν ἴσαι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΓΔ, ΕΖ ἐπίπεδα ἐκβαλλόμενα συμπεσοῦνται· παράλληλα ἄρα ἐστὶ τὰ ΓΔ, ΕΖ ἐπίπεδα.
Πρὸς ἃ ἐπίπεδα ἄρα ἡ αὐτὴ εὐθεῖα ὀρθή ἐστιν, παράλληλά ἐστι τὰ ἐπίπεδα· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον XI
Ἐὰν δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων ὦσι μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι, παράλληλά ἐστι τὰ δι' αὐτῶν ἐπίπεδα.
Δύο γὰρ εὐθεῖαι ἁπτόμεναι ἀλλήλων αἱ ΑΒ, ΒΓ παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων τὰς ΔΕ, ΕΖ ἔστωσαν μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι· λέγω, ὅτι ἐκβαλλόμενα τὰ διὰ τῶν ΑΒ, ΒΓ, ΔΕ, ΕΖ ἐπίπεδα οὐ συμπεσεῖται ἀλλήλοις.
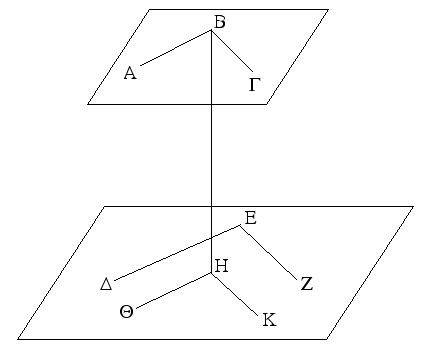
Ἤχθω γὰρ ἀπὸ τοῦ Β σημείου ἐπὶ τὸ διὰ τῶν ΔΕ, ΕΖ ἐπίπεδον κάθετος ἡ ΒΗ καὶ συμβαλλέτω τῷ ἐπιπέδῳ κατὰ τὸ Η σημεῖον, καὶ διὰ τοῦ Η τῇ μὲν ΕΔ παράλληλος ἤχθω ἡ ΗΘ, τῇ δὲ ΕΖ ἡ ΗΚ. καὶ ἐπεὶ ἡ ΒΗ ὀρθή ἐστι πρὸς τὸ διὰ τῶν ΔΕ, ΕΖ ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ διὰ τῶν ΔΕ, ΕΖ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας. ἅπτεται δὲ αὐτῆς ἑκατέρα τῶν ΗΘ, ΗΚ οὖσα ἐν τῷ διὰ τῶν ΔΕ, ΕΖ ἐπιπέδῳ· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν ὑπὸ ΒΗΘ, ΒΗΚ γωνιῶν. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΒΑ τῇ ΗΘ, αἱ ἄρα ὑπὸ ΗΒΑ, ΒΗΘ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. ὀρθὴ δὲ ἡ ὑπὸ ΒΗΘ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΗΒΑ· ἡ ΗΒ ἄρα τῇ ΒΑ πρὸς ὀρθάς ἐστιν. διὰ τὰ αὐτὰ δὴ ἡ ΗΒ καὶ τῇ ΒΓ ἐστι πρὸς ὀρθάς. ἐπεὶ οὖν εὐθεῖα ἡ ΗΒ δυσὶν εὐθείαις ταῖς ΒΑ, ΒΓ τεμνούσαις ἀλλήλας πρὸς ὀρθὰς ἐφέστηκεν, ἡ ΗΒ ἄρα καὶ τῷ διὰ τῶν ΒΑ, ΒΓ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. [διὰ τὰ αὐτὰ δὴ ἡ ΒΗ καὶ τῷ διὰ τῶν ΗΘ, ΗΚ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. τὸ δὲ διὰ τῶν ΗΘ, ΗΚ ἐπίπεδόν ἐστι τὸ διὰ τῶν ΔΕ, ΕΖ· ἡ ΒΗ ἄρα τῷ διὰ τῶν ΔΕ, ΕΖ ἐπιπέδῳ ἐστὶ πρὸς ὀρθάς. ἐδείχθη δὲ ἡ ΗΒ καὶ τῷ διὰ τῶν ΑΒ, ΒΓ ἐπιπέδῳ πρὸς ὀρθάς]. πρὸς ἃ δὲ ἐπίπεδα ἡ αὐτὴ εὐθεῖα ὀρθή ἐστιν, παράλληλά ἐστι τὰ ἐπίπεδα· παράλληλον ἄρα ἐστὶ τὸ διὰ τῶν ΑΒ, ΒΓ ἐπίπεδον τῷ διὰ τῶν ΔΕ, ΕΖ.
Ἐὰν ἄρα δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων ὦσι μὴ ἐν τῷ αὐτῷ ἐπιπέδῳ, παράλληλά ἐστι τὰ δι' αὐτῶν ἐπίπεδα· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον XI
Ἐὰν δύο ἐπίπεδα παράλληλα ὑπὸ ἐπιπέδου τινὸς τέμνηται, αἱ κοιναὶ αὐτῶν τομαὶ παράλληλοί εἰσιν.
Δύο γὰρ ἐπίπεδα παράλληλα τὰ ΑΒ, ΓΔ ὑπὸ ἐπιπέδου τοῦ ΕΖΗΘ τεμνέσθω, κοιναὶ δὲ αὐτῶν τομαὶ ἔστωσαν αἱ ΕΖ, ΗΘ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΕΖ τῇ ΗΘ.
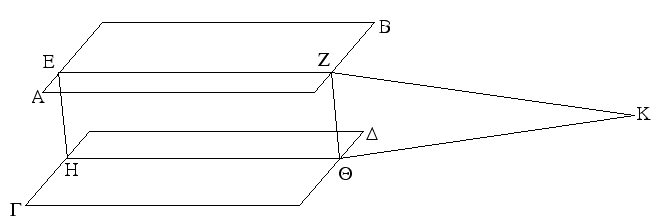
Εἰ γὰρ μή, ἐκβαλλόμεναι αἱ ΕΖ, ΗΘ ἤτοι ἐπὶ τὰ Ζ, Θ μέρη ἢ ἐπὶ τὰ Ε, Η συμπεσοῦνται. ἐκβεβλήσθωσαν ὡς ἐπὶ τὰ Ζ, Θ μέρη καὶ συμπιπτέτωσαν πρότερον κατὰ τὸ Κ. καὶ ἐπεὶ ἡ ΕΖΚ ἐν τῷ ΑΒ ἐστιν ἐπιπέδῳ, καὶ πάντα ἄρα τὰ ἐπὶ τῆς ΕΖΚ σημεῖα ἐν τῷ ΑΒ ἐστιν ἐπιπέδῳ. ἓν δὲ τῶν ἐπὶ τῆς ΕΖΚ εὐθείας σημείων ἐστὶ τὸ Κ· τὸ Κ ἄρα ἐν τῷ ΑΒ ἐστιν ἐπιπέδῳ. διὰ τὰ αὐτὰ δὴ τὸ Κ καὶ ἐν τῷ ΓΔ ἐστιν ἐπιπέδῳ· τὰ ΑΒ, ΓΔ ἄρα ἐπίπεδα ἐκβαλλόμενα συμπεσοῦνται. οὐ συμπίπτουσι δὲ διὰ τὸ παράλληλα ὑποκεῖσθαι· οὐκ ἄρα αἱ ΕΖ, ΗΘ εὐθεῖαι ἐκβαλλόμεναι ἐπὶ τὰ Ζ, Θ μέρη συμπεσοῦνται. ὁμοίως δὴ δείξομεν, ὅτι αἱ ΕΖ, ΗΘ εὐθεῖαι οὐδὲ ἐπὶ τὰ Ε, Η μέρη ἐκβαλλόμεναι συμπεσοῦνται. αἱ δὲ ἐπὶ μηδέτερα τὰ μέρη συμπίπτουσαι παράλληλοί εἰσιν. παράλληλος ἄρα ἐστὶν ἡ ΕΖ τῇ ΗΘ.
Ἐὰν ἄρα δύο ἐπίπεδα παράλληλα ὑπὸ ἐπιπέδου τινὸς τέμνηται, αἱ κοιναὶ αὐτῶν τομαὶ παράλληλοί εἰσιν· ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον XI
Ἐὰν δύο εὐθεῖαι ὑπὸ παραλλήλων ἐπιπέδων τέμνωνται εἰς τοὺς αὐτοὺς λόγους τμηθήσονται.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΓΔ ὑπὸ παραλλήλων ἐπιπέδων τῶν ΗΘ, ΚΛ, ΜΝ τεμνέσθωσαν κατὰ τὰ Α, Ε, Β, Γ, Ζ, Δ σημεῖα· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΕ εὐθεῖα πρὸς τὴν ΕΒ, οὕτως ἡ ΓΖ πρὸς τὴν ΖΔ.
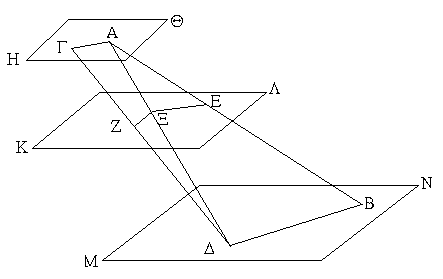
Ἐπεζεύχθωσαν γὰρ αἱ ΑΓ, ΒΔ, ΑΔ, καὶ συμβαλλέτω ἡ ΑΔ τῷ ΚΛ ἐπιπέδῳ κατὰ τὸ Ξ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΕΞ, ΞΖ. καὶ ἐπεὶ δύο ἐπίπεδα παράλληλα τὰ ΚΛ, ΜΝ ὑπὸ ἐπιπέδου τοῦ ΕΒΔΞ τέμνεται, αἱ κοιναὶ αὐτῶν τομαὶ αἱ ΕΞ, ΒΔ παράλληλοί εἰσιν. διὰ τὰ αὐτὰ δὴ ἐπεὶ δύο ἐπίπεδα παράλληλα τὰ ΗΘ, ΚΛ ὑπὸ ἐπιπέδου τοῦ ΑΞΖΓ τέμνεται, αἱ κοιναὶ αὐτῶν τομαὶ αἱ ΑΓ, ΞΖ παράλληλοί εἰσιν. καὶ ἐπεὶ τριγώνου τοῦ ΑΒΔ παρὰ μίαν τῶν πλευρῶν τὴν ΒΔ εὐθεῖα ἦκται ἡ ΕΞ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΑΕ πρὸς ΕΒ, οὕτως ἡ ΑΞ πρὸς ΞΔ. πάλιν ἐπεὶ τριγώνου τοῦ ΑΔΓ παρὰ μίαν τῶν πλευρῶν τὴν ΑΓ εὐθεῖα ἦκται ἡ ΞΖ, ἀνάλογόν ἐστιν ὡς ἡ ΑΞ πρὸς ΞΔ, οὕτως ἡ ΓΖ πρὸς ΖΔ. ἐδείχθη δὲ καὶ ὡς ἡ ΑΞ πρὸς ΞΔ, οὕτως ἡ ΑΕ πρὸς ΕΒ· καὶ ὡς ἄρα ἡ ΑΕ πρὸς ΕΒ, οὕτως ἡ ΓΖ πρὸς ΖΔ.
Ἐὰν ἄρα δύο εὐθεῖαι ὑπὸ παραλλήλων ἐπιπέδων τέμνωνται, εἰς τοὺς αὐτοὺς λόγους τμηθήσονται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον XI
Ἐὰν εὐθεῖα ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ πάντα τὰ δι' αὐτῆς ἐπίπεδα τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται.
Εὐθεῖα γάρ τις ἡ ΑΒ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἔστω· λέγω, ὅτι καὶ πάντα τὰ διὰ τῆς ΑΒ ἐπίπεδα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
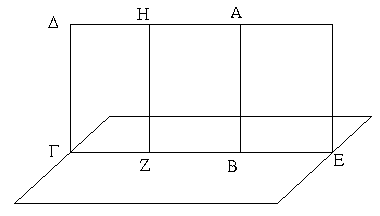
Ἐκβεβλήσθω γὰρ διὰ τῆς ΑΒ ἐπίπεδον τὸ ΔΕ, καὶ ἔστω κοινὴ τομὴ τοῦ ΔΕ ἐπιπέδου καὶ τοῦ ὑποκειμένου ἡ ΓΕ, καὶ εἰλήφθω ἐπὶ τῆς ΓΕ τυχὸν σημεῖον τὸ Ζ, καὶ ἀπὸ τοῦ Ζ τῇ ΓΕ πρὸς ὀρθὰς ἤχθω ἐν τῷ ΔΕ ἐπιπέδῳ ἡ ΖΗ. καὶ ἐπεὶ ἡ ΑΒ πρὸς τὸ ὑποκείμενον ἐπίπεδον ὀρθή ἐστιν, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθή ἐστιν ἡ ΑΒ· ὥστε καὶ πρὸς τὴν ΓΕ ὀρθή ἐστιν· ἡ ἄρα ὑπὸ ΑΒΖ γωνία ὀρθή ἐστιν. ἔστι δὲ καὶ ἡ ὑπὸ ΗΖΒ ὀρθή· παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΖΗ. ἡ δὲ ΑΒ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν· καὶ ἡ ΖΗ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καὶ ἐπίπεδον πρὸς ἐπίπεδον ὀρθόν ἐστιν, ὅταν αἱ τῇ κοινῇ τομῇ τῶν ἐπιπέδων πρὸς ὀρθὰς ἀγόμεναι εὐθεῖαι ἐν ἑνὶ τῶν ἐπιπέδων τῷ λοιπῷ ἐπιπέδῳ πρὸς ὀρθὰς ὦσιν. καὶ τῇ κοινῇ τομῇ τῶν ἐπιπέδων τῇ ΓΕ ἐν ἑνὶ τῶν ἐπιπέδων τῷ ΔΕ πρὸς ὀρθὰς ἀχθεῖσα ἡ ΖΗ ἐδείχθη τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς· τὸ ἄρα ΔΕ ἐπίπεδον ὀρθόν ἐστι πρὸς τὸ ὑποκείμενον. ὁμοίως δὴ δειχθήσεται καὶ πάντα τὰ διὰ τῆς ΑΒ ἐπίπεδα ὀρθὰ τυγχάνοντα πρὸς τὸ ὑποκείμενον ἐπίπεδον.
Ἐὰν ἄρα εὐθεῖα ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ πάντα τὰ δι' αὐτῆς ἐπίπεδα τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις ιθ΄ 19 Βιβλίον XI
Ἐὰν δύο ἐπίπεδα τέμνοντα ἄλληλα ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ κοινὴ αὐτῶν τομὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται.
Δύο γὰρ ἐπίπεδα τὰ ΑΒ, ΒΓ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἔστω, κοινὴ δὲ αὐτῶν τομὴ ἔστω ἡ ΒΔ· λέγω, ὅτι ἡ ΒΔ τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
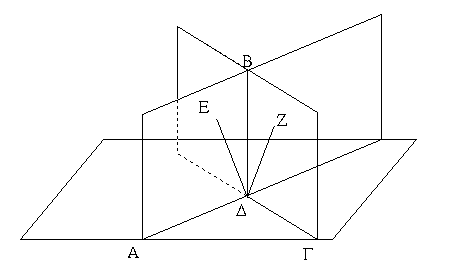
Μὴ γάρ, καὶ ἤχθωσαν ἀπὸ τοῦ Δ σημείου ἐν μὲν τῷ ΑΒ ἐπιπέδῳ τῇ ΑΔ εὐθείᾳ πρὸς ὀρθὰς ἡ ΔΕ, ἐν δὲ τῷ ΒΓ ἐπιπέδῳ τῇ ΓΔ πρὸς ὀρθὰς ἡ ΔΖ. καὶ ἐπεὶ τὸ ΑΒ ἐπίπεδον ὀρθόν ἐστι πρὸς τὸ ὑποκείμενον, καὶ τῇ κοινῇ αὐτῶν τομῇ τῇ ΑΔ πρὸς ὀρθὰς ἐν τῷ ΑΒ ἐπιπέδῳ ἦκται ἡ ΔΕ, ἡ ΔΕ ἄρα ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΔΖ ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον. ἀπὸ τοῦ αὐτοῦ ἄρα σημείου τοῦ Δ τῷ ὑποκειμένῳ ἐπιπέδῳ δύο εὐθεῖαι πρὸς ὀρθὰς ἀνεσταμέναι εἰσὶν ἐπὶ τὰ αὐτὰ μέρη· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ ἀπὸ τοῦ Δ σημείου ἀνασταθήσεται πρὸς ὀρθὰς πλὴν τῆς ΔΒ κοινῆς τομῆς τῶν ΑΒ, ΒΓ ἐπιπέδων.
Ἐὰν ἄρα δύο ἐπίπεδα τέμνοντα ἄλληλα ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ κοινὴ αὐτῶν τομὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ὅπερ ἔδει δεῖξαι.
Πρότασις κ΄ 20 Βιβλίον XI
Ἐὰν στερεὰ γωνία ὑπὸ τριῶν γωνιῶν ἐπιπέδων περιέχηται, δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι.
Στερεὰ γὰρ γωνία ἡ πρὸς τῷ Α ὑπὸ τριῶν γωνιῶν ἐπιπέδων τῶν ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ περιεχέσθω· λέγω, ὅτι τῶν ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ γωνιῶν δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι.
Εἰ μὲν οὖν αἱ ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ γωνίαι ἴσαι ἀλλήλαις εἰσίν, φανερόν, ὅτι δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσιν. εἰ δὲ οὔ, ἔστω μείζων ἡ ὑπὸ ΒΑΓ, καὶ συνεστάτω πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΔΑΒ γωνίᾳ ἐν τῷ διὰ τῶν ΒΑΓ ἐπιπέδῳ ἴση ἡ ὑπὸ ΒΑΕ, καὶ κείσθω τῇ ΑΔ ἴση ἡ ΑΕ, καὶ διὰ τοῦ Ε σημείου διαχθεῖσα ἡ ΒΕΓ τεμνέτω τὰς ΑΒ, ΑΓ εὐθείας κατὰ τὰ Β, Γ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΔΒ, ΔΓ.
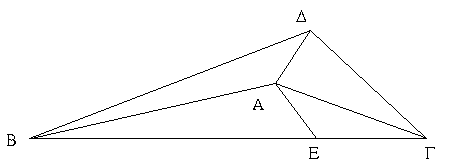
καὶ ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΑΕ, κοινὴ δὲ ἡ ΑΒ, δύο δυσὶν ἴσαι· καὶ γωνία ἡ ὑπὸ ΔΑΒ γωνίᾳ τῇ ὑπὸ ΒΑΕ ἴση· βάσις ἄρα ἡ ΔΒ βάσει τῇ ΒΕ ἐστιν ἴση. καὶ ἐπεὶ δύο αἱ ΒΔ, ΔΓ τῆς ΒΓ μείζονές εἰσιν, ὧν ἡ ΔΒ τῇ ΒΕ ἐδείχθη ἴση, λοιπὴ ἄρα ἡ ΔΓ λοιπῆς τῆς ΕΓ μείζων ἐστίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΑΕ, κοινὴ δὲ ἡ ΑΓ, καὶ βάσις ἡ ΔΓ βάσεως τῆς ΕΓ μείζων ἐστίν, γωνία ἄρα ἡ ὑπὸ ΔΑΓ γωνίας τῆς ὑπὸ ΕΑΓ μείζων ἐστίν. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΔΑΒ τῇ ὑπὸ ΒΑΕ ἴση· αἱ ἄρα ὑπὸ ΔΑΒ, ΔΑΓ τῆς ὑπὸ ΒΑΓ μείζονές εἰσιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ λοιπαὶ σύνδυο λαμβανόμεναι τῆς λοιπῆς μείζονές εἰσιν.
Ἐὰν ἄρα στερεὰ γωνία ὑπὸ τριῶν γωνιῶν ἐπιπέδων περιέχηται, δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι· ὅπερ ἔδει δεῖξαι
.Πρότασις κα΄ 21 Βιβλίον XI
Ἅπασα στερεὰ γωνία ὑπὸ ἐλασσόνων [ἢ] τεσσάρων ὀρθῶν γωνιῶν ἐπιπέδων περιέχεται.
Ἔστω στερεὰ γωνία ἡ πρὸς τῷ Α περιεχομένη ὑπὸ ἐπιπέδων γωνιῶν τῶν ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ· λέγω, ὅτι αἱ ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ τεσσάρων ὀρθῶν ἐλάσσονές εἰσιν.
Εἰλήφθω γὰρ ἐφ' ἑκάστης τῶν ΑΒ, ΑΓ, ΑΔ τυχόντα σημεῖα τὰ Β, Γ, Δ, καὶ ἐπεζεύχθωσαν αἱ ΒΓ, ΓΔ, ΔΒ. καὶ ἐπεὶ στερεὰ γωνία ἡ πρὸς τῷ Β ὑπὸ τριῶν γωνιῶν ἐπιπέδων περιέχεται τῶν ὑπὸ ΓΒΑ, ΑΒΔ, ΓΒΔ, δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσιν·
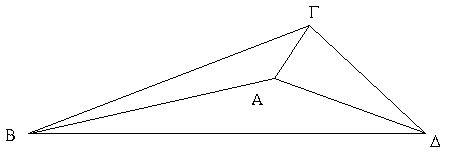
αἱ ἄρα ὑπὸ ΓΒΑ, ΑΒΔ τῆς ὑπὸ ΓΒΔ μείζονές εἰσιν. διὰ τὰ αὐτὰ δὴ καὶ αἱ μὲν ὑπὸ ΒΓΑ, ΑΓΔ τῆς ὑπὸ ΒΓΔ μείζονές εἰσιν, αἱ δὲ ὑπὸ ΓΔΑ, ΑΔΒ τῆς ὑπὸ ΓΔΒ μείζονές εἰσιν· αἱ ἓξ ἄρα γωνίαι αἱ ὑπὸ ΓΒΑ, ΑΒΔ, ΒΓΑ, ΑΓΔ, ΓΔΑ, ΑΔΒ τριῶν τῶν ὑπὸ ΓΒΔ, ΒΓΔ, ΓΔΒ μείζονές εἰσιν. ἀλλὰ αἱ τρεῖς αἱ ὑπὸ ΓΒΔ, ΒΔΓ, ΒΓΔ δυσὶν ὀρθαῖς ἴσαι εἰσίν· αἱ ἓξ ἄρα αἱ ὑπὸ ΓΒΑ, ΑΒΔ, ΒΓΑ, ΑΓΔ, ΓΔΑ, ΑΔΒ δύο ὀρθῶν μείζονές εἰσιν. καὶ ἐπεὶ ἑκάστου τῶν ΑΒΓ, ΑΓΔ, ΑΔΒ τριγώνων αἱ τρεῖς γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν, αἱ ἄρα τῶν τριῶν τριγώνων ἐννέα γωνίαι αἱ ὑπὸ ΓΒΑ, ΑΓΒ, ΒΑΓ, ΑΓΔ, ΓΔΑ, ΓΑΔ, ΑΔΒ, ΔΒΑ, ΒΑΔ ἓξ ὀρθαῖς ἴσαι εἰσίν, ὧν αἱ ὑπὸ ΑΒΓ, ΒΓΑ, ΑΓΔ, ΓΔΑ, ΑΔΒ, ΔΒΑ ἓξ γωνίαι δύο ὀρθῶν εἰσι μείζονες· λοιπαὶ ἄρα αἱ ὑπὸ ΒΑΓ, ΓΑΔ, ΔΑΒ τρεῖς [γωνίαι] περιέχουσαι τὴν στερεὰν γωνίαν τεσσάρων ὀρθῶν ἐλάσσονές εἰσιν.
Ἅπασα ἄρα στερεὰ γωνία ὑπὸ ἐλασσόνων [ἢ] τεσσάρων ὀρθῶν γωνιῶν ἐπιπέδων περιέχεται· ὅπερ ἔδει δεῖξαι.
Πρότασις κβ΄ 22 Βιβλίον XI
Ἐὰν ὦσι τρεῖς γωνίαι ἐπίπεδοι, ὧν αἱ δύο τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι, περιέχωσι δὲ αὐτὰς ἴσαι εὐθεῖαι, δυνατόν ἐστιν ἐκ τῶν ἐπιζευγνυουσῶν τὰς ἴσας εὐθείας τρίγωνον συστήσασθαι.
Ἔστωσαν τρεῖς γωνίαι ἐπίπεδοι αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ, ὧν αἱ δύο τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι, αἱ μὲν ὑπὸ ΑΒΓ, ΔΕΖ τῆς ὑπὸ ΗΘΚ, αἱ δὲ ὑπὸ ΔΕΖ, ΗΘΚ τῆς ὑπὸ ΑΒΓ, καὶ ἔτι αἱ ὑπὸ ΗΘΚ, ΑΒΓ τῆς ὑπὸ ΔΕΖ, καὶ ἔστωσαν ἴσαι αἱ ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ εὐθεῖαι, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΔΖ, ΗΚ· λέγω, ὅτι δυνατόν ἐστιν ἐκ τῶν ἴσων ταῖς ΑΓ, ΔΖ, ΗΚ τρίγωνον συστήσασθαι, τουτέστιν ὅτι τῶν ΑΓ, ΔΖ, ΗΚ δύο ὁποιαιοῦν τῆς λοιπῆς μείζονές εἰσιν.
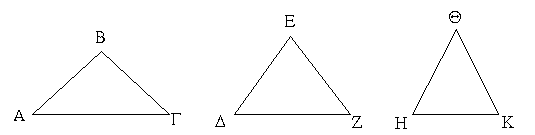
Εἰ μὲν οὖν αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ γωνίαι ἴσαι ἀλλήλαις εἰσίν, φανερόν, ὅτι καὶ τῶν ΑΓ, ΔΖ, ΗΚ ἴσων γινομένων δυνατόν ἐστιν ἐκ τῶν ἴσων ταῖς ΑΓ, ΔΖ, ΗΚ τρίγωνον συστήσασθαι. εἰ δὲ οὔ, ἔστωσαν ἄνισοι, καὶ συνεστάτω πρὸς τῇ ΘΚ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Θ τῇ ὑπὸ ΑΒΓ γωνίᾳ ἴση ἡ ὑπὸ ΚΘΛ· καὶ κείσθω μιᾷ τῶν ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ ἴση ἡ ΘΛ, καὶ ἐπεζεύχθωσαν αἱ ΚΛ, ΗΛ. καὶ ἐπεὶ δύο αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΚΘ, ΘΛ ἴσαι εἰσίν, καὶ γωνία ἡ πρὸς τῷ Β γωνίᾳ τῇ ὑπὸ ΚΘΛ ἴση, βάσις ἄρα ἡ ΑΓ βάσει τῇ ΚΛ ἴση.
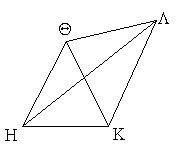
καὶ ἐπεὶ αἱ ὑπὸ ΑΒΓ, ΗΘΚ τῆς ὑπὸ ΔΕΖ μείζονές εἰσιν, ἴση δὲ ἡ ὑπὸ ΑΒΓ τῇ ὑπὸ ΚΘΛ, ἡ ἄρα ὑπὸ ΗΘΛ τῆς ὑπὸ ΔΕΖ μείζων ἐστίν. καὶ ἐπεὶ δύο αἱ ΗΘ, ΘΛ δύο ταῖς ΔΕ, ΕΖ ἴσαι εἰσίν, καὶ γωνία ἡ ὑπὸ ΗΘΛ γωνίας τῆς ὑπὸ ΔΕΖ μείζων, βάσις ἄρα ἡ ΗΛ βάσεως τῆς ΔΖ μείζων ἐστίν. ἀλλὰ αἱ ΗΚ, ΚΛ τῆς ΗΛ μείζονές εἰσιν. πολλῷ ἄρα αἱ ΗΚ, ΚΛ τῆς ΔΖ μείζονές εἰσιν. ἴση δὲ ἡ ΚΛ τῇ ΑΓ· αἱ ΑΓ, ΗΚ ἄρα τῆς λοιπῆς τῆς ΔΖ μείζονές εἰσιν. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ μὲν ΑΓ, ΔΖ τῆς ΗΚ μείζονές εἰσιν, καὶ ἔτι αἱ ΔΖ, ΗΚ τῆς ΑΓ μείζονές εἰσιν. δυνατὸν ἄρα ἐστὶν ἐκ τῶν ἴσων ταῖς ΑΓ, ΔΖ, ΗΚ τρίγωνον συστήσασθαι· ὅπερ ἔδει δεῖξαι.
Πρότασις κγ΄ 23 Βιβλίον XI
Ἐκ τριῶν γωνιῶν ἐπιπέδων, ὧν αἱ δύο τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι, στερεὰν γωνίαν συστήσασθαι· δεῖ δὴ τὰς τρεῖς τεσσάρων ὀρθῶν ἐλάσσονας εἶναι.
Ἔστωσαν αἱ δοθεῖσαι τρεῖς γωνίαι ἐπίπεδοι αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ, ὧν αἱ δύο τῆς λοιπῆς μείζονες ἔστωσαν πάντῃ μεταλαμβανόμεναι, ἔτι δὲ αἱ τρεῖς τεσσάρων ὀρθῶν ἐλάσσονες· δεῖ δὴ ἐκ τῶν ἴσων ταῖς ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ στερεὰν γωνίαν συστήσασθαι.
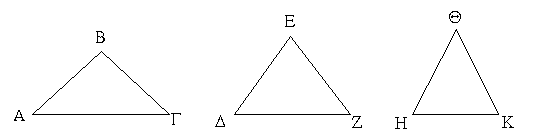
Ἀπειλήφθωσαν ἴσαι αἱ ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΔΖ, ΗΚ· δυνατὸν ἄρα ἐστὶν ἐκ τῶν ἴσων ταῖς ΑΓ, ΔΖ, ΗΚ τρίγωνον συστήσασθαι. συνεστάτω τὸ ΛΜΝ, ὥστε ἴσην εἶναι τὴν μὲν ΑΓ τῇ ΛΜ, τὴν δὲ ΔΖ τῇ ΜΝ, καὶ ἔτι τὴν ΗΚ τῇ ΝΛ, καὶ περιγεγράφθω περὶ τὸ ΛΜΝ τρίγωνον κύκλος ὁ ΛΜΝ καὶ εἰλήφθω αὐτοῦ τὸ κέντρον καὶ ἔστω τὸ Ξ, καὶ ἐπεζεύχθωσαν αἱ ΛΞ, ΜΞ, ΝΞ· λέγω, ὅτι ἡ ΑΒ μείζων ἐστὶ τῆς ΛΞ. εἰ γὰρ μή, ἤτοι ἴση ἐστὶν ἡ ΑΒ τῇ ΛΞ ἢ ἐλάττων. ἔστω πρότερον ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΛΞ, ἀλλὰ ἡ μὲν ΑΒ τῇ ΒΓ ἐστιν ἴση, ἡ δὲ ΞΛ τῇ ΞΜ, δύο δὴ αἱ ΑΒ, ΒΓ δύο ταῖς ΛΞ, ΞΜ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΑΓ βάσει τῇ ΛΜ ὑπόκειται ἴση· γωνία ἄρα ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΛΞΜ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ μὲν ὑπὸ ΔΕΖ τῇ ὑπὸ ΜΞΝ ἐστιν ἴση, καὶ ἔτι ἡ ὑπὸ ΗΘΚ τῇ ὑπὸ ΝΞΛ· αἱ ἄρα τρεῖς αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ γωνίαι τρισὶ ταῖς ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ εἰσιν ἴσαι. ἀλλὰ αἱ τρεῖς αἱ ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ τέτταρσιν ὀρθαῖς εἰσιν ἴσαι· καὶ αἱ τρεῖς ἄρα αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τέτταρσιν ὀρθαῖς ἴσαι εἰσίν. ὑπόκεινται δὲ καὶ τεσσάρων ὀρθῶν ἐλάσσονες· ὅπερ ἄτοπον. οὐκ ἄρα ἡ ΑΒ τῇ ΛΞ ἴση ἐστίν.
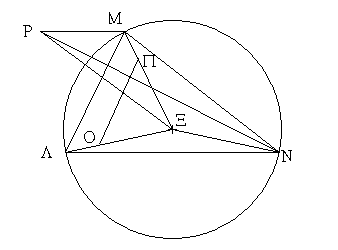
λέγω δή, ὅτι οὐδὲ ἐλάττων ἐστὶν ἡ ΑΒ τῆς ΛΞ. εἰ γὰρ δυνατόν, ἔστω· καὶ κείσθω τῇ μὲν ΑΒ ἴση ἡ ΞΟ, τῇ δὲ ΒΓ ἴση ἡ ΞΠ, καὶ ἐπεζεύχθω ἡ ΟΠ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΒΓ, ἴση ἐστὶ καὶ ἡ ΞΟ τῇ ΞΠ· ὥστε καὶ λοιπὴ ἡ ΛΟ τῇ ΠΜ ἐστιν ἴση. παράλληλος ἄρα ἐστὶν ἡ ΛΜ τῇ ΟΠ, καὶ ἰσογώνιον τὸ ΛΜΞ τῷ ΟΠΞ· ἔστιν ἄρα ὡς ἡ ΞΛ πρὸς ΛΜ, οὕτως ἡ ΞΟ πρὸς ΟΠ· ἐναλλὰξ ὡς ἡ ΛΞ πρὸς ΞΟ, οὕτως ἡ ΛΜ πρὸς ΟΠ. μείζων δὲ ἡ ΛΞ τῆς ΞΟ· μείζων ἄρα καὶ ἡ ΛΜ τῆς ΟΠ. ἀλλὰ ἡ ΛΜ κεῖται τῇ ΑΓ ἴση· καὶ ἡ ΑΓ ἄρα τῆς ΟΠ μείζων ἐστίν. ἐπεὶ οὖν δύο αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΟΞ, ΞΠ ἴσαι εἰσίν, καὶ βάσις ἡ ΑΓ βάσεως τῆς ΟΠ μείζων ἐστίν, γωνία ἄρα ἡ ὑπὸ ΑΒΓ γωνίας τῆς ὑπὸ ΟΞΠ μείζων ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ μὲν ὑπὸ ΔΕΖ τῆς ὑπὸ ΜΞΝ μείζων ἐστίν, ἡ δὲ ὑπὸ ΗΘΚ τῆς ὑπὸ ΝΞΛ. αἱ ἄρα τρεῖς γωνίαι αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τριῶν τῶν ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ μείζονές εἰσιν. ἀλλὰ αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τεσσάρων ὀρθῶν ἐλάσσονες ὑπόκεινται· πολλῷ ἄρα αἱ ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ τεσσάρων ὀρθῶν ἐλάσσονές εἰσιν. ἀλλὰ καὶ ἴσαι· ὅπερ ἐστὶν ἄτοπον. οὐκ ἄρα ἡ ΑΒ ἐλάσσων ἐστὶ τῆς ΛΞ. ἐδείχθη δέ, ὅτι οὐδὲ ἴση· μείζων ἄρα ἡ ΑΒ τῆς ΛΞ. ἀνεστάτω δὴ ἀπὸ τοῦ Ξ σημείου τῷ τοῦ ΛΜΝ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΞΡ, καὶ ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τετράγωνον τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον ἔστω τὸ ἀπὸ τῆς ΞΡ, καὶ ἐπεζεύχθωσαν αἱ ΡΛ, ΡΜ, ΡΝ. καὶ ἐπεὶ ἡ ΡΞ ὀρθή ἐστι πρὸς τὸ τοῦ ΛΜΝ κύκλου ἐπίπεδον, καὶ πρὸς ἑκάστην ἄρα τῶν ΛΞ, ΜΞ, ΝΞ ὀρθή ἐστιν ἡ ΡΞ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΛΞ τῇ ΞΜ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΞΡ, βάσις ἄρα ἡ ΡΛ βάσει τῇ ΡΜ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΡΝ ἑκατέρᾳ τῶν ΡΛ, ΡΜ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΡΛ, ΡΜ, ΡΝ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον ὑπόκειται τὸ ἀπὸ τῆς ΞΡ, τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΛΞ, ΞΡ. τοῖς δὲ ἀπὸ τῶν ΛΞ, ΞΡ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΛΡ· ὀρθὴ γὰρ ἡ ὑπὸ ΛΞΡ· τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΡΛ· ἴση ἄρα ἡ ΑΒ τῇ ΡΛ. ἀλλὰ τῇ μὲν ΑΒ ἴση ἐστὶν ἑκάστη τῶν ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ, τῇ δὲ ΡΛ ἴση ἑκατέρα τῶν ΡΜ, ΡΝ· ἑκάστη ἄρα τῶν ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ ἑκάστῃ τῶν ΡΛ, ΡΜ, ΡΝ ἴση ἐστίν. καὶ ἐπεὶ δύο αἱ ΛΡ, ΡΜ δυσὶ ταῖς ΑΒ, ΒΓ ἴσαι εἰσίν, καὶ βάσις ἡ ΛΜ βάσει τῇ ΑΓ ὑπόκειται ἴση, γωνία ἄρα ἡ ὑπὸ ΛΡΜ γωνίᾳ τῇ ὑπὸ ΑΒΓ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ μὲν ὑπὸ ΜΡΝ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση, ἡ δὲ ὑπὸ ΛΡΝ τῇ ὑπὸ ΗΘΚ.
Ἐκ τριῶν ἄρα γωνιῶν ἐπιπέδων τῶν ὑπὸ ΛΡΜ, ΜΡΝ, ΛΡΝ, αἵ εἰσιν ἴσαι τρισὶ ταῖς δοθείσαις ταῖς ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ, στερεὰ γωνία συνέσταται ἡ πρὸς τῷ Ρ περιεχομένη ὑπὸ τῶν ΛΡΜ, ΜΡΝ, ΛΡΝ γωνιῶν· ὅπερ ἔδει ποιῆσαι.
Λῆμμα
Ὃν δὲ τρόπον, ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον λαβεῖν ἔστι τὸ ἀπὸ τῆς ΞΡ, δείξομεν οὕτως. ἐκκείσθωσαν αἱ ΑΒ, ΛΞ εὐθεῖαι, καὶ ἔστω μείζων ἡ ΑΒ, καὶ γεγράφθω ἐπ᾿ αὐτῆς ἡμικύκλιον τὸ ΑΒΓ, καὶ εἰς τὸ ΑΒΓ ἡμικύκλιον ἐνηρμόσθω τῇ ΛΞ εὐθείᾳ μὴ μείζονι οὔσῃ τῆς ΑΒ διαμέτρου ἴση ἡ ΑΓ, καὶ ἐπεζεύχθω ἡ ΓΒ. ἐπεὶ οὖν ἐν ἡμικυκλίῳ τῷ ΑΓΒ γωνία ἐστὶν ἡ ὑπὸ ΑΓΒ, ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΑΓΒ.
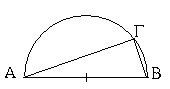
τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΓ, ΓΒ. ὥστε τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΑΓ μεῖζόν ἐστι τῷ ἀπὸ τῆς ΓΒ. ἴση δὲ ἡ ΑΓ τῇ ΛΞ. τὸ ἄρα ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ μεῖζόν ἐστι τῷ ἀπὸ τῆς ΓΒ. ἐὰν οὖν τῇ ΒΓ ἴσην τὴν ΞΡ ἀπολάβωμεν, ἔσται τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ μεῖζον τῷ ἀπὸ τῆς ΞΡ· ὅπερ προέκειτο ποιῆσαι.
Πρότασις κδ΄ 24 Βιβλίον XI
Ἐὰν στερεὸν ὑπὸ παραλλήλων ἐπιπέδων περιέχηται, τὰ ἀπεναντίον αὐτοῦ ἐπίπεδα ἴσα τε καὶ παραλληλόγραμμά ἐστιν.
Στερεὸν γὰρ τὸ ΓΔΘΗ ὑπὸ παραλλήλων ἐπιπέδων περιεχέσθω τῶν ΑΓ, ΗΖ, ΑΘ, ΔΖ, ΒΖ, ΑΕ· λέγω, ὅτι τὰ ἀπεναντίον αὐτοῦ ἐπίπεδα ἴσα τε καὶ παραλληλόγραμμά ἐστιν.
Ἐπεὶ γὰρ δύο ἐπίπεδα παράλληλα τὰ ΒΗ, ΓΕ ὑπὸ ἐπιπέδου τοῦ ΑΓ τέμνεται, αἱ κοιναὶ αὐτῶν τομαὶ παράλληλοί εἰσιν. παράλληλος ἄρα ἐστὶν ἡ ΑΒ τῇ ΔΓ. πάλιν, ἐπεὶ δύο ἐπίπεδα παράλληλα τὰ ΒΖ, ΑΕ ὑπὸ ἐπιπέδου τοῦ ΑΓ τέμνεται, αἱ κοιναὶ αὐτῶν τομαὶ παράλληλοί εἰσιν. παράλληλος ἄρα ἐστὶν ἡ ΒΓ τῇ ΑΔ. ἐδείχθη δὲ καὶ ἡ ΑΒ τῇ ΔΓ παράλληλος· παραλληλόγραμμον ἄρα ἐστὶ τὸ ΑΓ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἕκαστον τῶν ΔΖ, ΖΗ, ΗΒ, ΒΖ, ΑΕ παραλληλόγραμμόν ἐστιν.
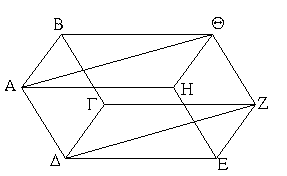
Ἐπεζεύχθωσαν αἱ ΑΘ, ΔΖ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ μὲν ΑΒ τῇ ΔΓ, ἡ δὲ ΒΘ τῇ ΓΖ, δύο δὴ αἱ ΑΒ, ΒΘ ἁπτόμεναι ἀλλήλων παρὰ δύο εὐθείας τὰς ΔΓ, ΓΖ ἁπτομένας ἀλλήλων εἰσὶν οὐκ ἐν τῷ αὐτῷ ἐπιπέδῳ· ἴσας ἄρα γωνίας περιέξουσιν· ἴση ἄρα ἡ ὑπὸ ΑΒΘ γωνία τῇ ὑπὸ ΔΓΖ. καὶ ἐπεὶ δύο αἱ ΑΒ, ΒΘ δυσὶ ταῖς ΔΓ, ΓΖ ἴσαι εἰσίν, καὶ γωνία ἡ ὑπὸ ΑΒΘ γωνίᾳ τῇ ὑπὸ ΔΓΖ ἐστιν ἴση, βάσις ἄρα ἡ ΑΘ βάσει τῇ ΔΖ ἐστιν ἴση, καὶ τὸ ΑΒΘ τρίγωνον τῷ ΔΓΖ τριγώνῳ ἴσον ἐστίν. καί ἐστι τοῦ μὲν ΑΒΘ διπλάσιον τὸ ΒΗ παραλληλόγραμμον, τοῦ δὲ ΔΓΖ διπλάσιον τὸ ΓΕ παραλληλόγραμμον· ἴσον ἄρα τὸ ΒΗ παραλληλόγραμμον τῷ ΓΕ παραλληλογράμμῳ. ὁμοίως δὴ δείξομεν, ὅτι καὶ τὸ μὲν ΑΓ τῷ ΗΖ ἐστιν ἴσον, τὸ δὲ ΑΕ τῷ ΒΖ.
Ἐὰν ἄρα στερεὸν ὑπὸ παραλλήλων ἐπιπέδων περιέχηται, τὰ ἀπεναντίον αὐτοῦ ἐπίπεδα ἴσα τε καὶ παραλληλόγραμμά ἐστιν· ὅπερ ἔδει δεῖξαι.
Πρότασις κε΄ 25 Βιβλίον XI
Ἐὰν στερεὸν παραλληλεπίπεδον ἐπιπέδῳ τμηθῇ παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔσται ὡς ἡ βάσις πρὸς τὴν βάσιν, οὕτως τὸ στερεὸν πρὸς τὸ στερεόν.
Στερεὸν γὰρ παραλληλεπίπεδον τὸ ΑΒΓΔ ἐπιπέδῳ τῷ ΖΗ τετμήσθω παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις τοῖς ΡΑ, ΔΘ· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΕΖΦ βάσις πρὸς τὴν ΕΘΓΖ βάσιν, οὕτως τὸ ΑΒΖΥ στερεὸν πρὸς τὸ ΕΗΓΔ στερεόν.
Ἐκβεβλήσθω γὰρ ἡ ΑΘ ἐφ' ἑκάτερα τὰ μέρη, καὶ κείσθωσαν τῇ μὲν ΑΕ ἴσαι ὁσαιδηποτοῦν αἱ ΑΚ, ΚΛ, τῇ δὲ ΕΘ ἴσαι ὁσαιδηποτοῦν αἱ ΘΜ, ΜΝ, καὶ συμπεπληρώσθω τὰ ΛΟ, ΚΦ, ΘΧ, ΜΣ παραλληλόγραμμα καὶ τὰ ΛΠ, ΚΡ, ΔΜ, ΜΤ στερεά. καὶ ἐπεὶ ἴσαι εἰσὶν αἱ ΛΚ, ΚΑ, ΑΕ εὐθεῖαι ἀλλήλαις, ἴσα ἐστὶ καὶ τὰ μὲν ΛΟ, ΚΦ, ΑΖ παραλληλόγραμμα ἀλλήλοις, τὰ δὲ ΚΞ, ΚΒ, ΑΗ ἀλλήλοις καὶ ἔτι τὰ ΛΨ, ΚΠ, ΑΡ ἀλλήλοις· ἀπεναντίον γάρ. διὰ τὰ αὐτὰ δὴ καὶ τὰ μὲν ΕΓ, ΘΧ, ΜΣ παραλληλόγραμμα ἴσα εἰσὶν ἀλλήλοις, τὰ δὲ ΘΗ, ΘΙ, ΙΝ ἴσα εἰσὶν ἀλλήλοις, καὶ ἔτι τὰ ΔΘ, ΜΩ, ΝΤ· τρία ἄρα ἐπίπεδα τῶν ΛΠ, ΚΡ, ΑΥ στερεῶν τρισὶν ἐπιπέδοις ἐστὶν ἴσα.
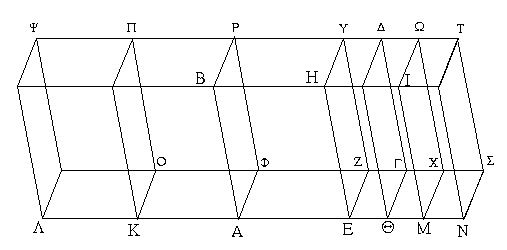
ἀλλὰ τὰ τρία τρισὶ τοῖς ἀπεναντίον ἐστὶν ἴσα· τὰ ἄρα τρία στερεὰ τὰ ΛΠ, ΚΡ, ΑΥ ἴσα ἀλλήλοις ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ τὰ τρία στερεὰ τὰ ΕΔ, ΔΜ, ΜΤ ἴσα ἀλλήλοις ἐστίν· ὁσαπλασίων ἄρα ἐστὶν ἡ ΛΖ βάσις τῆς ΑΖ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΛΥ στερεὸν τοῦ ΑΥ στερεοῦ. διὰ τὰ αὐτὰ δὴ ὁσαπλασίων ἐστὶν ἡ ΝΖ βάσις τῆς ΖΘ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΝΥ στερεὸν τοῦ ΘΥ στερεοῦ. καὶ εἰ ἴση ἐστὶν ἡ ΛΖ βάσις τῇ ΝΖ βάσει, ἴσον ἐστὶ καὶ τὸ ΛΥ στερεὸν τῷ ΝΥ στερεῷ, καὶ εἰ ὑπερέχει ἡ ΛΖ βάσις τῆς ΝΖ βάσεως, ὑπερέχει καὶ τὸ ΛΥ στερεὸν τοῦ ΝΥ στερεοῦ, καὶ εἰ ἐλλείπει, ἐλλείπει. τεσσάρων δὴ ὄντων μεγεθῶν, δύο μὲν βάσεων τῶν ΑΖ, ΖΘ, δύο δὲ στερεῶν τῶν ΑΥ, ΥΘ, εἴληπται ἰσάκις πολλαπλάσια τῆς μὲν ΑΖ βάσεως καὶ τοῦ ΑΥ στερεοῦ ἥ τε ΛΖ βάσις καὶ τὸ ΛΥ στερεόν, τῆς δὲ ΘΖ βάσεως καὶ τοῦ ΘΥ στερεοῦ ἥ τε ΝΖ βάσις καὶ τὸ ΝΥ στερεόν, καὶ δέδεικται, ὅτι εἰ ὑπερέχει ἡ ΛΖ βάσις τῆς ΖΝ βάσεως, ὑπερέχει καὶ τὸ ΛΥ στερεὸν τοῦ ΝΥ [στερεοῦ], καὶ εἰ ἴση, ἴσον, καὶ εἰ ἐλλείπει, ἐλλείπει. ἔστιν ἄρα ὡς ἡ ΑΖ βάσις πρὸς τὴν ΖΘ βάσιν, οὕτως τὸ ΑΥ στερεὸν πρὸς τὸ ΥΘ στερεόν· ὅπερ ἔδει δεῖξαι.
Πρότασις κς΄ 26 Βιβλίον XI
Πρὸς τῇ δοθείσῃ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῇ δοθείσῃ στερεᾷ γωνίᾳ ἴσην στερεὰν γωνίαν συστήσασθαι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ πρὸς αὐτῇ δοθὲν σημεῖον τὸ Α, ἡ δὲ δοθεῖσα στερεὰ γωνία ἡ πρὸς τῷ Δ περιεχομένη ὑπὸ τῶν ὑπὸ ΕΔΓ, ΕΔΖ, ΖΔΓ γωνιῶν ἐπιπέδων· δεῖ δὴ πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ πρὸς τῷ Δ στερεᾷ γωνίᾳ ἴσην στερεὰν γωνίαν συστήσασθαι.
Εἰλήφθω γὰρ ἐπὶ τῆς ΔΖ τυχὸν σημεῖον τὸ Ζ, καὶ ἤχθω ἀπὸ τοῦ Ζ ἐπὶ τὸ διὰ τῶν ΕΔ, ΔΓ ἐπίπεδον κάθετος ἡ ΖΗ, καὶ συμβαλλέτω τῷ ἐπιπέδῳ κατὰ τὸ Η, καὶ ἐπεζεύχθω ἡ ΔΗ, καὶ συνεστάτω πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ μὲν ὑπὸ ΕΔΓ γωνίᾳ ἴση ἡ ὑπὸ ΒΑΛ, τῇ δὲ ὑπὸ ΕΔΗ ἴση ἡ ὑπὸ ΒΑΚ, καὶ κείσθω τῇ ΔΗ ἴση ἡ ΑΚ, καὶ ἀνεστάτω ἀπὸ τοῦ Κ σημείου τῷ διὰ τῶν ΒΑΛ ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΚΘ, καὶ κείσθω ἴση τῇ ΗΖ ἡ ΚΘ, καὶ ἐπεζεύχθω ἡ ΘΑ· λέγω, ὅτι ἡ πρὸς τῷ Α στερεὰ γωνία περιεχομένη ὑπὸ τῶν ΒΑΛ, ΒΑΘ, ΘΑΛ γωνιῶν ἴση ἐστὶ τῇ πρὸς τῷ Δ στερεᾷ γωνίᾳ τῇ περιεχομένῃ ὑπὸ τῶν ΕΔΓ, ΕΔΖ, ΖΔΓ γωνιῶν.
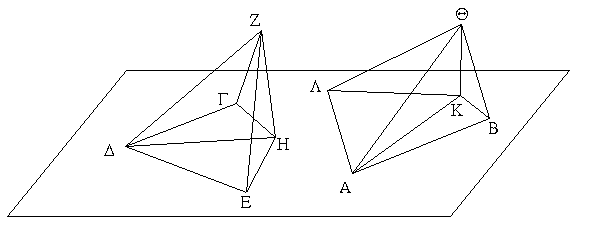
Ἀπειλήφθωσαν γὰρ ἴσαι αἱ ΑΒ, ΔΕ, καὶ ἐπεζεύχθωσαν αἱ ΘΒ, ΚΒ, ΖΕ, ΗΕ. καὶ ἐπεὶ ἡ ΖΗ ὀρθή ἐστι πρὸς τὸ ὑποκείμενον ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν ὑπὸ ΖΗΔ, ΖΗΕ γωνιῶν. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ὑπὸ ΘΚΑ, ΘΚΒ γωνιῶν ὀρθή ἐστιν. καὶ ἐπεὶ δύο αἱ ΚΑ, ΑΒ δύο ταῖς ΗΔ, ΔΕ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΚΒ βάσει τῇ ΗΕ ἴση ἐστίν. ἔστι δὲ καὶ ἡ ΚΘ τῇ ΗΖ ἴση· καὶ γωνίας ὀρθὰς περιέχουσιν· ἴση ἄρα καὶ ἡ ΘΒ τῇ ΖΕ. πάλιν ἐπεὶ δύο αἱ ΑΚ, ΚΘ δυσὶ ταῖς ΔΗ, ΗΖ ἴσαι εἰσίν, καὶ γωνίας ὀρθὰς περιέχουσιν, βάσις ἄρα ἡ ΑΘ βάσει τῇ ΖΔ ἴση ἐστίν. ἔστι δὲ καὶ ἡ ΑΒ τῇ ΔΕ ἴση· δύο δὴ αἱ ΘΑ, ΑΒ δύο ταῖς ΔΖ, ΔΕ ἴσαι εἰσίν. καὶ βάσις ἡ ΘΒ βάσει τῇ ΖΕ ἴση· γωνία ἄρα ἡ ὑπὸ ΒΑΘ γωνίᾳ τῇ ὑπὸ ΕΔΖ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΘΑΛ τῇ ὑπὸ ΖΔΓ ἐστιν ἴση [ἐπειδήπερ ἐὰν ἀπολάβωμεν ἴσας τὰς ΑΛ, ΔΓ καὶ ἐπιζεύξωμεν τὰς ΚΛ, ΘΛ, ΗΓ, ΖΓ, ἐπεὶ ὅλη ἡ ὑπὸ ΒΑΛ ὅλῃ τῇ ὑπὸ ΕΔΓ ἐστιν ἴση, ὧν ἡ ὑπὸ ΒΑΚ τῇ ὑπὸ ΕΔΗ ὑπόκειται ἴση, λοιπὴ ἄρα ἡ ὑπὸ ΚΑΛ λοιπῇ τῇ ὑπὸ ΗΔΓ ἐστιν ἴση. καὶ ἐπεὶ δύο αἱ ΚΑ, ΑΛ δυσὶ ταῖς ΗΔ, ΔΓ ἴσαι εἰσίν, καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΚΛ βάσει τῇ ΗΓ ἐστιν ἴση. ἔστι δὲ καὶ ἡ ΚΘ τῇ ΗΖ ἴση· δύο δὴ αἱ ΛΚ, ΚΘ δυσὶ ταῖς ΓΗ, ΗΖ εἰσιν ἴσαι· καὶ γωνίας ὀρθὰς περιέχουσιν· βάσις ἄρα ἡ ΘΛ βάσει τῇ ΖΓ ἐστιν ἴση. καὶ ἐπεὶ δύο αἱ ΘΑ, ΑΛ δυσὶ ταῖς ΖΔ, ΔΓ εἰσιν ἴσαι, καὶ βάσις ἡ ΘΛ βάσει τῇ ΖΓ ἐστιν ἴση, γωνία ἄρα ἡ ὑπὸ ΘΑΛ γωνίᾳ τῇ ὑπὸ ΖΔΓ ἐστιν ἴση]. ἔστι δὲ καὶ ἡ ὑπὸ ΒΑΛ τῇ ὑπὸ ΕΔΓ ἴση.
Πρὸς ἄρα τῇ δοθείσῃ εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ δοθείσῃ στερεᾷ γωνίᾳ τῇ πρὸς τῷ Δ ἴση συνέσταται· ὅπερ ἔδει ποιῆσαι.
Πρότασις κζ΄ 27 Βιβλίον XI
Ἀπὸ τῆς δοθείσης εὐθείας τῷ δοθέντι στερεῷ παραλληλεπιπέδῳ ὅμοιόν τε καὶ ὁμοίως κείμενον στερεὸν παραλληλεπίπεδον ἀναγράψαι.
Ἔστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν στερεὸν παραλληλεπίπεδον τὸ ΓΔ· δεῖ δὴ ἀπὸ τῆς δοθείσης εὐθείας τῆς ΑΒ τῷ δοθέντι στερεῷ παραλληλεπιπέδῳ τῷ ΓΔ ὅμοιόν τε καὶ ὁμοίως κείμενον στερεὸν παραλληλεπίπεδον ἀναγράψαι.
Συνεστάτω γὰρ πρὸς τῇ ΑΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ πρὸς τῷ Γ στερεᾷ γωνίᾳ ἴση ἡ περιεχομένη ὑπὸ τῶν ΒΑΘ, ΘΑΚ, ΚΑΒ, ὥστε ἴσην εἶναι τὴν μὲν ὑπὸ ΒΑΘ γωνίαν τῇ ὑπὸ ΕΓΖ, τὴν δὲ ὑπὸ ΒΑΚ τῇ ὑπὸ ΕΓΗ, τὴν δὲ ὑπὸ ΚΑΘ τῇ ὑπὸ ΗΓΖ· καὶ γεγονέτω ὡς μὲν ἡ ΕΓ πρὸς τὴν ΓΗ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΚ, ὡς δὲ ἡ ΗΓ πρὸς τὴν ΓΖ, οὕτως ἡ ΚΑ πρὸς τὴν ΑΘ. καὶ δι' ἴσου ἄρα ἐστὶν ὡς ἡ ΕΓ πρὸς τὴν ΓΖ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΘ. καὶ συμπεπληρώσθω τὸ ΘΒ παραλληλόγραμμον καὶ τὸ ΑΛ στερεόν.
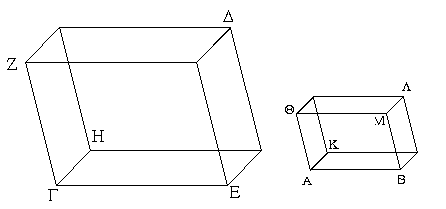
Καὶ ἐπεί ἐστιν ὡς ἡ ΕΓ πρὸς τὴν ΓΗ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΚ, καὶ περὶ ἴσας γωνίας τὰς ὑπὸ ΕΓΗ, ΒΑΚ αἱ πλευραὶ ἀνάλογόν εἰσιν, ὅμοιον ἄρα ἐστὶ τὸ ΗΕ παραλληλόγραμμον τῷ ΚΒ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΚΘ παραλληλόγραμμον τῷ ΗΖ παραλληλογράμμῳ ὅμοιόν ἐστι καὶ ἔτι τὸ ΖΕ τῷ ΘΒ· τρία ἄρα παραλληλόγραμμα τοῦ ΓΔ στερεοῦ τρισὶ παραλληλογράμμοις τοῦ ΑΛ στερεοῦ ὅμοιά ἐστιν. ἀλλὰ τὰ μὲν τρία τρισὶ τοῖς ἀπεναντίον ἴσα τέ ἐστι καὶ ὅμοια, τὰ δὲ τρία τρισὶ τοῖς ἀπεναντίον ἴσα τέ ἐστι καὶ ὅμοια· ὅλον ἄρα τὸ ΓΔ στερεὸν ὅλῳ τῷ ΑΛ στερεῷ ὅμοιόν ἐστιν.
Ἀπὸ τῆς δοθείσης ἄρα εὐθείας τῆς ΑΒ τῷ δοθέντι στερεῷ παραλληλεπιπέδῳ τῷ ΓΔ ὅμοιόν τε καὶ ὁμοίως κείμενον ἀναγέγραπται τὸ ΑΛ· ὅπερ ἔδει ποιῆσαι.
Πρότασις κη΄ 28 Βιβλίον XI
Ἐὰν στερεὸν παραλληλεπίπεδον ἐπιπέδῳ τμηθῇ κατὰ τὰς διαγωνίους τῶν ἀπεναντίον ἐπιπέδων, δίχα τμηθήσεται τὸ στερεὸν ὑπὸ τοῦ ἐπιπέδου.
Στερεὸν γὰρ παραλληλεπίπεδον τὸ ΑΒ ἐπιπέδῳ τῷ ΓΔΕΖ τετμήσθω κατὰ τὰς διαγωνίους τῶν ἀπεναντίον ἐπιπέδων τὰς ΓΖ, ΔΕ· λέγω, ὅτι δίχα τμηθήσεται τὸ ΑΒ στερεὸν ὑπὸ τοῦ ΓΔΕΖ ἐπιπέδου.
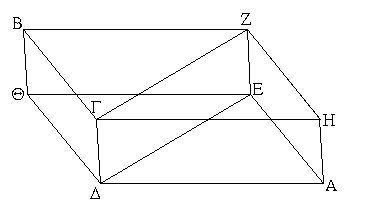
Ἐπεὶ γὰρ ἴσον ἐστὶ τὸ μὲν ΓΗΖ τρίγωνον τῷ ΓΖΒ τριγώνῳ, τὸ δὲ ΑΔΕ τῷ ΔΕΘ, ἔστι δὲ καὶ τὸ μὲν ΓΑ παραλληλόγραμμον τῷ ΕΒ ἴσον· ἀπεναντίον γάρ· τὸ δὲ ΗΕ τῷ ΓΘ, καὶ τὸ πρίσμα ἄρα τὸ περιεχόμενον ὑπὸ δύο μὲν τριγώνων τῶν ΓΗΖ, ΑΔΕ, τριῶν δὲ παραλληλογράμμων τῶν ΗΕ, ΑΓ, ΓΕ ἴσον ἐστὶ τῷ πρίσματι τῷ περιεχομένῳ ὑπὸ δύο μὲν τριγώνων τῶν ΓΖΒ, ΔΕΘ, τριῶν δὲ παραλληλογράμμων τῶν ΓΘ, ΒΕ, ΓΕ· ὑπὸ γὰρ ἴσων ἐπιπέδων περιέχονται τῷ τε πλήθει καὶ τῷ μεγέθει. ὥστε ὅλον τὸ ΑΒ στερεὸν δίχα τέτμηται ὑπὸ τοῦ ΓΔΕΖ ἐπιπέδου· ὅπερ ἔδει δεῖξαι.
Πρότασις κθ΄ 29 Βιβλίον XI
Τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν, ἴσα ἀλλήλοις ἐστίν.
Ἔστω ἐπὶ τῆς αὐτῆς βάσεως τῆς ΑΒ στερεὰ παραλληλεπίπεδα τὰ ΓΜ, ΓΝ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΑΗ, ΑΖ, ΛΜ, ΛΝ, ΓΔ, ΓΕ, ΒΘ, ΒΚ ἐπὶ τῶν αὐτῶν εὐθειῶν ἔστωσαν τῶν ΖΝ, ΔΚ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΓΜ στερεὸν τῷ ΓΝ στερεῷ.
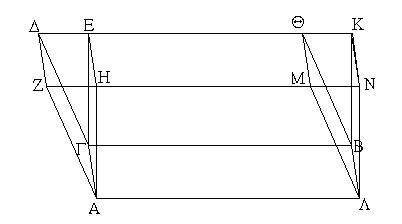
Ἐπεὶ γὰρ παραλληλόγραμμόν ἐστιν ἑκάτερον τῶν ΓΘ, ΓΚ, ἴση ἐστὶν ἡ ΓΒ ἑκατέρᾳ τῶν ΔΘ, ΕΚ· ὥστε καὶ ἡ ΔΘ τῇ ΕΚ ἐστιν ἴση. κοινὴ ἀφῃρήσθω ἡ ΕΘ· λοιπὴ ἄρα ἡ ΔΕ λοιπῇ τῇ ΘΚ ἐστιν ἴση. ὥστε καὶ τὸ μὲν ΔΓΕ τρίγωνον τῷ ΘΒΚ τριγώνῳ ἴσον ἐστίν, τὸ δὲ ΔΗ παραλληλόγραμμον τῷ ΘΝ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΑΖΗ τρίγωνον τῷ ΜΛΝ τριγώνῳ ἴσον ἐστίν. ἔστι δὲ καὶ τὸ μὲν ΓΖ παραλληλόγραμμον τῷ ΒΜ παραλληλογράμμῳ ἴσον, τὸ δὲ ΓΗ τῷ ΒΝ· ἀπεναντίον γάρ· καὶ τὸ πρίσμα ἄρα τὸ περιεχόμενον ὑπὸ δύο μὲν τριγώνων τῶν ΑΖΗ, ΔΓΕ, τριῶν δὲ παραλληλογράμμων τῶν ΑΔ, ΔΗ, ΓΗ ἴσον ἐστὶ τῷ πρίσματι τῷ περιεχομένῳ ὑπὸ δύο μὲν τριγώνων τῶν ΜΛΝ, ΘΒΚ, τριῶν δὲ παραλληλογράμμων τῶν ΒΜ, ΘΝ, ΒΝ. κοινὸν προσκείσθω τὸ στερεόν, οὗ βάσις μὲν τὸ ΑΒ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΗΕΘΜ· ὅλον ἄρα τὸ ΓΜ στερεὸν παραλληλεπίπεδον ὅλῳ τῷ ΓΝ στερεῷ παραλληλεπιπέδῳ ἴσον ἐστίν.
Τὰ ἄρα ἐπὶ τῆς αὐτῆς βάσεως ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν, ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λ΄ 30 Βιβλίον XI
Τὰ ἐπὶ τῆς αὐτῆς βάσεως ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι οὐκ εἰσὶν ἐπὶ τῶν αὐτῶν εὐθειῶν, ἴσα ἀλλήλοις ἐστίν.
Ἔστω ἐπὶ τῆς αὐτῆς βάσεως τῆς ΑΒ στερεὰ παραλληλεπίπεδα τὰ ΓΜ, ΓΝ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΑΖ, ΑΗ, ΛΜ, ΛΝ, ΓΔ, ΓΕ, ΒΘ, ΒΚ μὴ ἔστωσαν ἐπὶ τῶν αὐτῶν εὐθειῶν· λέγω, ὅτι ἴσον ἐστὶ τὸ ΓΜ στερεὸν τῷ ΓΝ στερεῷ.
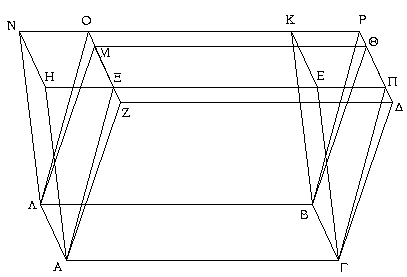
Ἐκβεβλήσθωσαν γὰρ αἱ ΝΚ, ΔΘ καὶ συμπιπτέτωσαν ἀλλήλαις κατὰ τὸ Ρ, καὶ ἔτι ἐκβεβλήσθωσαν αἱ ΖΜ, ΗΕ ἐπὶ τὰ Ο, Π, καὶ ἐπεζεύχθωσαν αἱ ΑΞ, ΛΟ, ΓΠ, ΒΡ. ἴσον δή ἐστι τὸ ΓΜ στερεόν, οὗ βάσις μὲν τὸ ΑΓΒΛ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΖΔΘΜ, τῷ ΓΟ στερεῷ, οὗ βάσις μὲν τὸ ΑΓΒΛ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΞΠΡΟ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΑΓΒΛ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΑΖ, ΑΞ, ΛΜ, ΛΟ, ΓΔ, ΓΠ, ΒΘ, ΒΡ ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν τῶν ΖΟ, ΔΡ. ἀλλὰ τὸ ΓΟ στερεόν, οὗ βάσις μέν ἐστι τὸ ΑΓΒΛ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΞΠΡΟ, ἴσον ἐστὶ τῷ ΓΝ στερεῷ, οὗ βάσις μὲν τὸ ΑΓΒΛ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΗΕΚΝ· ἐπί τε γὰρ πάλιν τῆς αὐτῆς βάσεώς εἰσι τῆς ΑΓΒΛ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΑΗ, ΑΞ, ΓΕ, ΓΠ, ΛΝ, ΛΟ, ΒΚ, ΒΡ ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν τῶν ΗΠ, ΝΡ. ὥστε καὶ τὸ ΓΜ στερεὸν ἴσον ἐστὶ τῷ ΓΝ στερεῷ.
Τὰ ἄρα ἐπὶ τῆς αὐτῆς βάσεως στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι οὐκ εἰσὶν ἐπὶ τῶν αὐτῶν εὐθειῶν, ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λα΄ 31 Βιβλίον XI
Τὰ ἐπὶ ἴσων βάσεων ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν.
Ἔστω ἐπὶ ἴσων βάσεων τῶν ΑΒ, ΓΔ στερεὰ παραλληλεπίπεδα τὰ ΑΕ, ΓΖ ὑπὸ τὸ αὐτὸ ὕψος· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΕ στερεὸν τῷ ΓΖ στερεῷ.
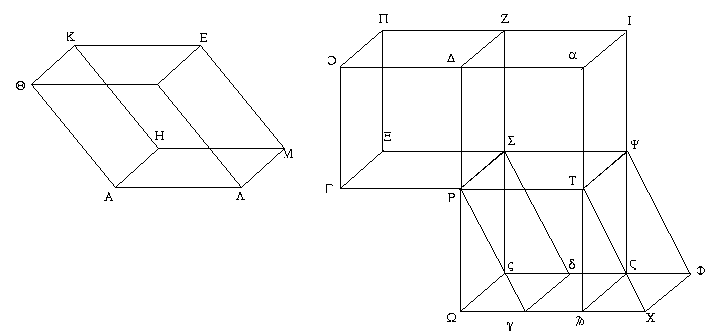
Ἔστωσαν δὴ πρότερον αἱ ἐφεστηκυῖαι αἱ ΘΚ, ΒΕ, ΑΗ, ΛΜ, ΟΠ, ΔΖ, ΓΞ, ΡΣ πρὸς ὀρθὰς ταῖς ΑΒ, ΓΔ βάσεσιν, καὶ ἐκβεβλήσθω ἐπ᾿ εὐθείας τῇ ΓΡ εὐθεῖα ἡ ΡΤ, καὶ συνεστάτω πρὸς τῇ ΡΤ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Ρ τῇ ὑπὸ ΑΛΒ γωνίᾳ ἴση ἡ ὑπὸ ΤΡΥ, καὶ κείσθω τῇ μὲν ΑΛ ἴση ἡ ΡΤ, τῇ δὲ ΛΒ ἴση ἡ ΡΥ, καὶ συμπεπληρώσθω ἥ τε ΡΧ βάσις καὶ τὸ ΨΥ στερεόν. καὶ ἐπεὶ δύο αἱ ΤΡ, ΡΥ δυσὶ ταῖς ΑΛ, ΛΒ ἴσαι εἰσίν, καὶ γωνίας ἴσας περιέχουσιν, ἴσον ἄρα καὶ ὅμοιον τὸ ΡΧ παραλληλόγραμμον τῷ ΘΛ παραλληλογράμμῳ. καὶ ἐπεὶ πάλιν ἴση μὲν ἡ ΑΛ τῇ ΡΤ, ἡ δὲ ΛΜ τῇ ΡΣ, καὶ γωνίας ὀρθὰς περιέχουσιν, ἴσον ἄρα καὶ ὅμοιόν ἐστι τὸ ΡΨ παραλληλόγραμμον τῷ ΑΜ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΛΕ τῷ ΣΥ ἴσον τέ ἐστι καὶ ὅμοιον· τρία ἄρα παραλληλόγραμμα τοῦ ΑΕ στερεοῦ τρισὶ παραλληλογράμμοις τοῦ ΨΥ στερεοῦ ἴσα τέ ἐστι καὶ ὅμοια. ἀλλὰ τὰ μὲν τρία τρισὶ τοῖς ἀπεναντίον ἴσα τέ ἐστι καὶ ὅμοια, τὰ δὲ τρία τρισὶ τοῖς ἀπεναντίον· ὅλον ἄρα τὸ ΑΕ στερεὸν παραλληλεπίπεδον ὅλῳ τῷ ΨΥ στερεῷ παραλληλεπιπέδῳ ἴσον ἐστίν. διήχθωσαν αἱ ΔΡ, ΧΥ καὶ συμπιπτέτωσαν ἀλλήλαις κατὰ τὸ Ω, καὶ διὰ τοῦ Τ τῇ ΔΩ παράλληλος ἤχθω ἡ αΤϠ, καὶ ἐκβεβλήσθω ἡ ΟΔ κατὰ τὸ α, καὶ συμπεπληρώσθω τὰ ΩΨ, ΡΙ στερεά. ἴσον δή ἐστι τὸ ΨΩ στερεόν, οὗ βάσις μέν ἐστι τὸ ΡΨ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΩϚ, τῷ ΨΥ στερεῷ, οὗ βάσις μὲν τὸ ΡΨ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΥΦ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΡΨ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΡΩ, ΡΥ, ΤϠ, ΤΧ, Σς, Σδ, ΨϚ, ΨΦ ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν τῶν ΩΧ, ςΦ. ἀλλὰ τὸ ΨΥ στερεὸν τῷ ΑΕ ἐστιν ἴσον· καὶ τὸ ΨΩ ἄρα στερεὸν τῷ ΑΕ στερεῷ ἐστιν ἴσον. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΡΥΧΤ παραλληλόγραμμον τῷ ΩΤ παραλληλογράμμῳ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΡΤ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΡΤ, ΩΧ· ἀλλὰ τὸ ΡΥΧΤ τῷ ΓΔ ἐστιν ἴσον, ἐπεὶ καὶ τῷ ΑΒ, καὶ τὸ ΩΤ ἄρα παραλληλόγραμμον τῷ ΓΔ ἐστιν ἴσον. ἄλλο δὲ τὸ ΔΤ· ἔστιν ἄρα ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ, οὕτως ἡ ΩΤ πρὸς τὴν ΔΤ. καὶ ἐπεὶ στερεὸν παραλληλεπίπεδον τὸ ΓΙ ἐπιπέδῳ τῷ ΡΖ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ βάσιν, οὕτως τὸ ΓΖ στερεὸν πρὸς τὸ ΡΙ στερεόν. διὰ τὰ αὐτὰ δή, ἐπεὶ στερεὸν παραλληλεπίπεδον τὸ ΩΙ ἐπιπέδῳ τῷ ΡΨ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ὡς ἡ ΩΤ βάσις πρὸς τὴν ΤΔ βάσιν, οὕτως τὸ ΩΨ στερεὸν πρὸς τὸ ΡΙ. ἀλλ' ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ, οὕτως ἡ ΩΤ πρὸς τὴν ΔΤ· καὶ ὡς ἄρα τὸ ΓΖ στερεὸν πρὸς τὸ ΡΙ στερεόν, οὕτως τὸ ΩΨ στερεὸν πρὸς τὸ ΡΙ. ἑκάτερον ἄρα τῶν ΓΖ, ΩΨ στερεῶν πρὸς τὸ ΡΙ τὸν αὐτὸν ἔχει λόγον· ἴσον ἄρα ἐστὶ τὸ ΓΖ στερεὸν τῷ ΩΨ στερεῷ. ἀλλὰ τὸ ΩΨ τῷ ΑΕ ἐδείχθη ἴσον· καὶ τὸ ΑΕ ἄρα τῷ ΓΖ ἐστιν ἴσον.
Μὴ ἔστωσαν δὴ αἱ ἐφεστηκυῖαι αἱ ΑΗ, ΘΚ, ΒΕ, ΛΜ, ΓΝ, ΟΠ, ΔΖ, ΡΣ πρὸς ὀρθὰς ταῖς ΑΒ, ΓΔ βάσεσιν· λέγω πάλιν, ὅτι ἴσον τὸ ΑΕ στερεὸν τῷ ΓΖ στερεῷ.
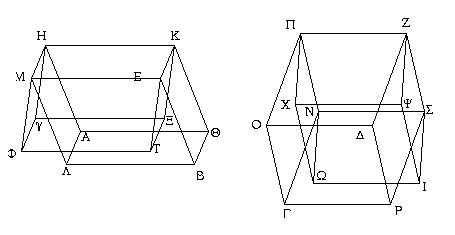
ἤχθωσαν γὰρ ἀπὸ τῶν Κ, Ε, Η, Μ, Π, Ζ, Ν, Σ σημείων ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετοι αἱ ΚΞ, ΕΤ, ΗΥ, ΜΦ, ΠΧ, ΖΨ, ΝΩ, ΣΙ, καὶ συμβαλλέτωσαν τῷ ἐπιπέδῳ κατὰ τὰ Ξ, Τ, Υ, Φ, Χ, Ψ, Ω, Ι σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΞΤ, ΞΥ, ΥΦ, ΤΦ, ΧΨ, ΧΩ, ΩΙ, ΙΨ. ἴσον δή ἐστι τὸ ΚΦ στερεὸν τῷ ΠΙ στερεῷ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΚΜ, ΠΣ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι πρὸς ὀρθάς εἰσι ταῖς βάσεσιν. ἀλλὰ τὸ μὲν ΚΦ στερεὸν τῷ ΑΕ στερεῷ ἐστιν ἴσον, τὸ δὲ ΠΙ τῷ ΓΖ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι οὔκ εἰσιν ἐπὶ τῶν αὐτῶν εὐθειῶν. καὶ τὸ ΑΕ ἄρα στερεὸν τῷ ΓΖ στερεῷ ἐστιν ἴσον.
Τὰ ἄρα ἐπὶ ἴσων βάσεων ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Πρότασις λβ΄ 32 Βιβλίον XI
Τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα στερεὰ παραλληλεπίπεδα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις.
Ἔστω ὑπὸ τὸ αὐτὸ ὕψος στερεὰ παραλληλεπίπεδα τὰ ΑΒ, ΓΔ· λέγω, ὅτι τὰ ΑΒ, ΓΔ στερεὰ παραλληλεπίπεδα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις, τουτέστιν ὅτι ἐστὶν ὡς ἡ ΑΕ βάσις πρὸς τὴν ΓΖ βάσιν, οὕτως τὸ ΑΒ στερεὸν πρὸς τὸ ΓΔ στερεόν.
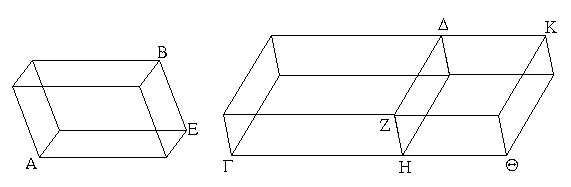
Παραβεβλήσθω γὰρ παρὰ τὴν ΖΗ τῷ ΑΕ ἴσον τὸ ΖΘ, καὶ ἀπὸ βάσεως μὲν τῆς ΖΘ, ὕψους δὲ τοῦ αὐτοῦ τῷ ΓΔ στερεὸν παραλληλεπίπεδον συμπεπληρώσθω τὸ ΗΚ. ἴσον δή ἐστι τὸ ΑΒ στερεὸν τῷ ΗΚ στερεῷ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΑΕ, ΖΘ καὶ ὑπὸ τὸ αὐτὸ ὕψος. καὶ ἐπεὶ στερεὸν παραλληλεπίπεδον τὸ ΓΚ ἐπιπέδῳ τῷ ΔΗ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ἄρα ὡς ἡ ΓΖ βάσις πρὸς τὴν ΖΘ βάσιν, οὕτως τὸ ΓΔ στερεὸν πρὸς τὸ ΔΘ στερεόν. ἴση δὲ ἡ μὲν ΖΘ βάσις τῇ ΑΕ βάσει, τὸ δὲ ΗΚ στερεὸν τῷ ΑΒ στερεῷ· ἔστιν ἄρα καὶ ὡς ἡ ΑΕ βάσις πρὸς τὴν ΓΖ βάσιν, οὕτως τὸ ΑΒ στερεὸν πρὸς τὸ ΓΔ στερεόν.
Τὰ ἄρα ὑπὸ τὸ αὐτὸ ὕψος ὄντα στερεὰ παραλληλεπίπεδα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις· ὅπερ ἔδει δεῖξαι.
Πρότασις λγ΄ 33 Βιβλίον XI
Τὰ ὅμοια στερεὰ παραλληλεπίπεδα πρὸς ἄλληλα ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν.
Ἔστω ὅμοια στερεὰ παραλληλεπίπεδα τὰ ΑΒ, ΓΔ, ὁμόλογος δὲ ἔστω ἡ ΑΕ τῇ ΓΖ· λέγω, ὅτι τὸ ΑΒ στερεὸν πρὸς τὸ ΓΔ στερεὸν τριπλασίονα λόγον ἔχει, ἤπερ ἡ ΑΕ πρὸς τὴν ΓΖ.
Ἐκβεβλήσθωσαν γὰρ ἐπ᾿ εὐθείας ταῖς ΑΕ, ΗΕ, ΘΕ αἱ ΕΚ, ΕΛ, ΕΜ, καὶ κείσθω τῇ μὲν ΓΖ ἴση ἡ ΕΚ, τῇ δὲ ΖΝ ἴση ἡ ΕΛ, καὶ ἔτι τῇ ΖΡ ἴση ἡ ΕΜ, καὶ συμπεπληρώσθω τὸ ΚΛ παραλληλόγραμμον καὶ τὸ ΚΟ στερεόν.
Καὶ ἐπεὶ δύο αἱ ΚΕ, ΕΛ δυσὶ ταῖς ΓΖ, ΖΝ ἴσαι εἰσίν, ἀλλὰ καὶ γωνία ἡ ὑπὸ ΚΕΛ γωνίᾳ τῇ ὑπὸ ΓΖΝ ἐστιν ἴση, ἐπειδήπερ καὶ ἡ ὑπὸ ΑΕΗ τῇ ὑπὸ ΓΖΝ ἐστιν ἴση διὰ τὴν ὁμοιότητα τῶν ΑΒ, ΓΔ στερεῶν, ἴσον ἄρα ἐστὶ [καὶ ὅμοιον] τὸ ΚΛ παραλληλόγραμμον τῷ ΓΝ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΚΜ παραλληλόγραμμον ἴσον ἐστὶ καὶ ὅμοιον τῷ ΓΡ [παραλληλογράμμῳ] καὶ ἔτι τὸ ΕΟ τῷ ΔΖ· τρία ἄρα παραλληλόγραμμα τοῦ ΚΟ στερεοῦ τρισὶ παραλληλογράμμοις τοῦ ΓΔ στερεοῦ ἴσα ἐστὶ καὶ ὅμοια. ἀλλὰ τὰ μὲν τρία τρισὶ τοῖς ἀπεναντίον ἴσα ἐστὶ καὶ ὅμοια, τὰ δὲ τρία τρισὶ τοῖς ἀπεναντίον ἴσα ἐστὶ καὶ ὅμοια· ὅλον ἄρα τὸ ΚΟ στερεὸν ὅλῳ τῷ ΓΔ στερεῷ ἴσον ἐστὶ καὶ ὅμοιον. συμπεπληρώσθω τὸ ΗΚ παραλληλόγραμμον, καὶ ἀπὸ βάσεων μὲν τῶν ΗΚ, ΚΛ παραλληλογράμμων, ὕψους δὲ τοῦ αὐτοῦ τῷ ΑΒ στερεὰ συμπεπληρώσθω τὰ ΕΞ, ΛΠ. καὶ ἐπεὶ διὰ τὴν ὁμοιότητα τῶν ΑΒ, ΓΔ στερεῶν ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΝ, καὶ ἡ ΕΘ πρὸς τὴν ΖΡ, ἴση δὲ ἡ μέν ΓΖ τῇ ΕΚ, ἡ δὲ ΖΝ τῇ ΕΛ, ἡ δὲ ΖΡ τῇ ΕΜ, ἔστιν ἄρα ὡς ἡ ΑΕ πρὸς τὴν ΕΚ, οὕτως ἡ ΗΕ πρὸς τὴν ΕΛ καὶ ἡ ΘΕ πρὸς τὴν ΕΜ.
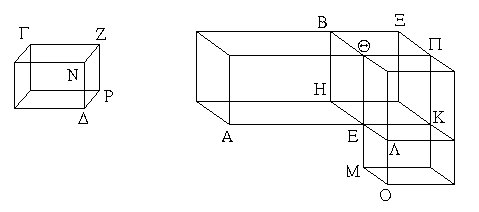
ἀλλ' ὡς μὲν ἡ ΑΕ πρὸς τὴν ΕΚ, οὕτως τὸ ΑΗ [παραλληλόγραμμον] πρὸς τὸ ΗΚ παραλληλόγραμμον, ὡς δὲ ἡ ΗΕ πρὸς τὴν ΕΛ, οὕτως τὸ ΗΚ πρὸς τὸ ΚΛ, ὡς δὲ ἡ ΘΕ πρὸς ΕΜ, οὕτως τὸ ΠΕ πρὸς τὸ ΚΜ· καὶ ὡς ἄρα τὸ ΑΗ παραλληλόγραμμον πρὸς τὸ ΗΚ, οὕτως τὸ ΗΚ πρὸς τὸ ΚΛ καὶ τὸ ΠΕ πρὸς τὸ ΚΜ. ἀλλ' ὡς μὲν τὸ ΑΗ πρὸς τὸ ΗΚ, οὕτως τὸ ΑΒ στερεὸν πρὸς τὸ ΕΞ στερεόν, ὡς δὲ τὸ ΗΚ πρὸς τὸ ΚΛ, οὕτως τὸ ΞΕ στερεὸν πρὸς τὸ ΠΛ στερεόν, ὡς δὲ τὸ ΠΕ πρὸς τὸ ΚΜ, οὕτως τὸ ΠΛ στερεὸν πρὸς τὸ ΚΟ στερεόν· καὶ ὡς ἄρα τὸ ΑΒ στερεὸν πρὸς τὸ ΕΞ, οὕτως τὸ ΕΞ πρὸς τὸ ΠΛ καὶ τὸ ΠΛ πρὸς τὸ ΚΟ. ἐὰν δὲ τέσσαρα μεγέθη κατὰ τὸ συνεχὲς ἀνάλογον ᾖ, τὸ πρῶτον πρὸς τὸ τέταρτον τριπλασίονα λόγον ἔχει ἤπερ πρὸς τὸ δεύτερον· τὸ ΑΒ ἄρα στερεὸν πρὸς τὸ ΚΟ τριπλασίονα λόγον ἔχει ἤπερ τὸ ΑΒ πρὸς τὸ ΕΞ. ἀλλ' ὡς τὸ ΑΒ πρὸς τὸ ΕΞ, οὕτως τὸ ΑΗ παραλληλόγραμμον πρὸς τὸ ΗΚ καὶ ἡ ΑΕ εὐθεῖα πρὸς τὴν ΕΚ· ὥστε καὶ τὸ ΑΒ στερεὸν πρὸς τὸ ΚΟ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΑΕ πρὸς τὴν ΕΚ. ἴσον δὲ τὸ [μὲν] ΚΟ στερεὸν τῷ ΓΔ στερεῷ, ἡ δὲ ΕΚ εὐθεῖα τῇ ΓΖ· καὶ τὸ ΑΒ ἄρα στερεὸν πρὸς τὸ ΓΔ στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος αὐτοῦ πλευρὰ ἡ ΑΕ πρὸς τὴν ὁμόλογον πλευρὰν τὴν ΓΖ.
Τὰ ἄρα ὅμοια στερεὰ παραλληλεπίπεδα ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· ὅπερ ἔδει δεῖξαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, ἔσται ὡς ἡ πρώτη πρὸς τὴν τετάρτην, οὕτω τὸ ἀπὸ τῆς πρώτης στερεὸν παραλληλεπίπεδον πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον, ἐπείπερ καὶ ἡ πρώτη πρὸς τὴν τετάρτην τριπλασίονα λόγον ἔχει ἤπερ πρὸς τὴν δευτέραν.
Πρότασις λδ΄ 34 Βιβλίον XI
Τῶν ἴσων στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· καὶ ὧν στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσα ἐστὶν ἐκεῖνα.
Ἔστω ἴσα στερεὰ παραλληλεπίπεδα τὰ ΑΒ, ΓΔ· λέγω, ὅτι τῶν ΑΒ, ΓΔ στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, καί ἐστιν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος.
Ἔστωσαν γὰρ πρότερον αἱ ἐφεστηκυῖαι αἱ ΑΗ, ΕΖ, ΛΒ, ΘΚ, ΓΜ, ΝΞ, ΟΔ, ΠΡ πρὸς ὀρθὰς ταῖς βάσεσιν αὐτῶν· λέγω, ὅτι ἐστὶν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως ἡ ΓΜ πρὸς τὴν ΑΗ.
Εἰ μὲν οὖν ἴση ἐστιν ἡ ΕΘ βάσις τῇ ΝΠ βάσει, ἔστι δὲ καὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ ἴσον, ἔσται καὶ ἡ ΓΜ τῇ ΑΗ ἴση. τὰ γὰρ ὑπὸ τὸ αὐτὸ ὕψος στερεὰ παραλληλεπίπεδα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις [εἰ γὰρ τῶν ΕΘ, ΝΠ βάσεων ἴσων οὐσῶν μὴ εἴη τὰ ΑΗ, ΓΜ ὕψη ἴσα, οὐδ' ἄρα τὸ ΑΒ στερεὸν ἴσον ἔσται τῷ ΓΔ. ὑπόκειται δὲ ἴσον· οὐκ ἄρα ἄνισόν ἐστι τὸ ΓΜ ὕψος τῷ ΑΗ ὕψει· ἴσον ἄρα]. καὶ ἔσται ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ, οὕτως ἡ ΓΜ πρὸς τὴν ΑΗ, καὶ φανερόν, ὅτι τῶν ΑΒ, ΓΔ στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν.
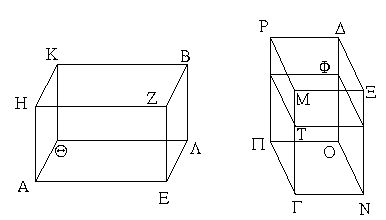
Μὴ ἔστω δὴ ἴση ἡ ΕΘ βάσις τῇ ΝΠ βάσει, ἀλλ' ἔστω μείζων ἡ ΕΘ. ἔστι δὲ καὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ ἴσον· μείζων ἄρα ἐστὶ καὶ ἡ ΓΜ τῆς ΑΗ [εἰ γὰρ μή, οὐδ' ἄρα πάλιν τὰ ΑΒ, ΓΔ στερεὰ ἴσα ἔσται· ὑπόκειται δὲ ἴσα]. κείσθω οὖν τῇ ΑΗ ἴση ἡ ΓΤ, καὶ συμπεπληρώσθω ἀπὸ βάσεως μὲν τῆς ΝΠ, ὕψους δὲ τοῦ ΓΤ, στερεὸν παραλληλεπίπεδον τὸ ΦΓ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ, ἔξωθεν δὲ τὸ ΓΦ, τὰ δὲ ἴσα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ ΑΒ στερεὸν πρὸς τὸ ΓΦ στερεόν, οὕτως τὸ ΓΔ στερεὸν πρὸς τὸ ΓΦ στερεόν. ἀλλ' ὡς μὲν τὸ ΑΒ στερεὸν πρὸς τὸ ΓΦ στερεόν, οὕτως ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν· ἰσοϋψῆ γὰρ τὰ ΑΒ, ΓΦ στερεά· ὡς δὲ τὸ ΓΔ στερεὸν πρὸς τὸ ΓΦ στερεόν, οὕτως ἡ ΜΠ βάσις πρὸς τὴν ΤΠ βάσιν καὶ ἡ ΓΜ πρὸς τὴν ΓΤ· καὶ ὡς ἄρα ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως ἡ ΜΓ πρὸς τὴν ΓΤ. ἴση δὲ ἡ ΓΤ τῇ ΑΗ· καὶ ὡς ἄρα ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως ἡ ΜΓ πρὸς τὴν ΑΗ. τῶν ΑΒ, ΓΔ ἄρα στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν.
Πάλιν δὴ τῶν ΑΒ, ΓΔ στερεῶν παραλληλεπιπέδων ἀντιπεπονθέτωσαν αἱ βάσεις τοῖς ὕψεσιν, καὶ ἔστω ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ.
Ἔστωσαν [γὰρ] πάλιν αἱ ἐφεστηκυῖαι πρὸς ὀρθὰς ταῖς βάσεσιν, καὶ εἰ μὲν ἴση ἐστὶν ἡ ΕΘ βάσις τῇ ΝΠ βάσει, καί ἐστιν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος, ἴσον ἄρα ἐστὶ καὶ τὸ τοῦ ΓΔ στερεοῦ ὕψος τῷ τοῦ ΑΒ στερεοῦ ὕψει. τὰ δὲ ἐπὶ ἴσων βάσεων στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν· ἴσον ἄρα ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ.
Μὴ ἔστω δὴ ἡ ΕΘ βάσις τῇ ΝΠ [βάσει] ἴση, ἀλλ' ἔστω μείζων ἡ ΕΘ· μεῖζον ἄρα ἐστὶ καὶ τὸ τοῦ ΓΔ στερεοῦ ὕψος τοῦ τοῦ ΑΒ στερεοῦ ὕψους, τουτέστιν ἡ ΓΜ τῆς ΑΗ. κείσθω τῇ ΑΗ ἴση πάλιν ἡ ΓΤ, καὶ συμπεπληρώσθω ὁμοίως τὸ ΓΦ στερεόν. ἐπεί ἐστιν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως ἡ ΜΓ πρὸς τὴν ΑΗ, ἴση δὲ ἡ ΑΗ τῇ ΓΤ, ἔστιν ἄρα ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως ἡ ΓΜ πρὸς τὴν ΓΤ. ἀλλ' ὡς μὲν ἡ ΕΘ [βάσις] πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ ΑΒ στερεὸν πρὸς τὸ ΓΦ στερεόν· ἰσοϋψῆ γάρ ἐστι τὰ ΑΒ, ΓΦ στερεά· ὡς δὲ ἡ ΓΜ πρὸς τὴν ΓΤ, οὕτως ἥ τε ΜΠ βάσις πρὸς τὴν ΠΤ βάσιν καὶ τὸ ΓΔ στερεὸν πρὸς τὸ ΓΦ στερεόν. καὶ ὡς ἄρα τὸ ΑΒ στερεὸν πρὸς τὸ ΓΦ στερεόν, οὕτως τὸ ΓΔ στερεὸν πρὸς τὸ ΓΦ στερεόν· ἑκάτερον ἄρα τῶν ΑΒ, ΓΔ πρὸς τὸ ΓΦ τὸν αὐτὸν ἔχει λόγον. ἴσον ἄρα ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ [ὅπερ ἔδει δεῖξαι].
Μὴ ἔστωσαν δὴ αἱ ἐφεστηκυῖαι αἱ ΖΕ, ΒΛ, ΗΑ, ΘΚ, ΞΝ, ΔΟ, ΜΓ, ΡΠ πρὸς ὀρθὰς ταῖς βάσεσιν αὐτῶν, καὶ ἤχθωσαν ἀπὸ τῶν Ζ, Η, Β, Κ, Ξ, Μ, Δ, Ρ σημείων ἐπὶ τὰ διὰ τῶν ΕΘ, ΝΠ ἐπίπεδα κάθετοι καὶ συμβαλλέτωσαν τοῖς ἐπιπέδοις κατὰ τὰ Σ, Τ, Υ, Φ, Χ, Ψ, Ω, #2, καὶ συμπεπληρώσθω τὰ ΖΦ, ΞΩ στερεά· λέγω, ὅτι καὶ οὕτως ἴσων ὄντων τῶν ΑΒ, ΓΔ στερεῶν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, καί ἐστιν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος.
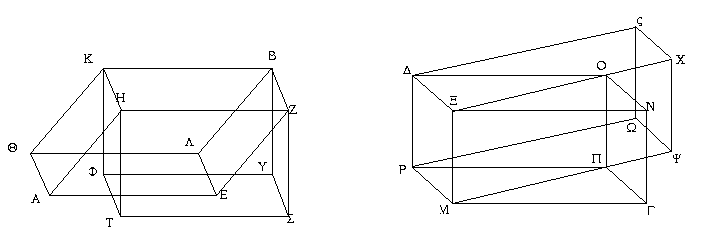
Ἐπεὶ ἴσον ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ, ἀλλὰ τὸ μὲν ΑΒ τῷ ΒΤ ἐστιν ἴσον· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΖΚ καὶ ὑπὸ τὸ αὐτὸ ὕψος [ὧν αἱ ἐφεστῶσαι οὐκ εἰσὶν ἐπὶ τῶν αὐτῶν εὐθειῶν]· τὸ δὲ ΓΔ στερεὸν τῷ ΔΨ ἐστιν ἴσον· ἐπί τε γὰρ πάλιν τῆς αὐτῆς βάσεώς εἰσι τῆς ΡΞ καὶ ὑπὸ τὸ αὐτὸ ὕψος [ὧν αἱ ἐφεστῶσαι οὐκ εἰσὶν ἐπὶ τῶν αὐτῶν εὐθειῶν]· καὶ τὸ ΒΤ ἄρα στερεὸν τῷ ΔΨ στερεῷ ἴσον ἐστίν [τῶν δὲ ἴσων στερεῶν παραλληλεπιπέδων, ὧν τὰ ὕψη πρὸς ὀρθάς ἐστι ταῖς βάσεσιν αὐτῶν, ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν]. ἔστιν ἄρα ὡς ἡ ΖΚ βάσις πρὸς τὴν ΞΡ βάσιν, οὕτως τὸ τοῦ ΔΨ στερεοῦ ὕψος πρὸς τὸ τοῦ ΒΤ στερεοῦ ὕψος. ἴση δὲ ἡ μὲν ΖΚ βάσις τῇ ΕΘ βάσει, ἡ δὲ ΞΡ βάσις τῇ ΝΠ βάσει· ἔστιν ἄρα ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΔΨ στερεοῦ ὕψος πρὸς τὸ τοῦ ΒΤ στερεοῦ ὕψος. τὰ δ' αὐτὰ ὕψη ἐστὶ τῶν ΔΨ, ΒΤ στερεῶν καὶ τῶν ΔΓ, ΒΑ· ἔστιν ἄρα ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΔΓ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος. τῶν ΑΒ, ΓΔ ἄρα στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν.
Πάλιν δὴ τῶν ΑΒ, ΓΔ στερεῶν παραλληλεπιπέδων ἀντιπεπονθέτωσαν αἱ βάσεις τοῖς ὕψεσιν, καὶ ἔστω ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒ στερεὸν τῷ ΓΔ στερεῷ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΕΘ βάσις πρὸς τὴν ΝΠ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος, ἴση δὲ ἡ μὲν ΕΘ βάσις τῇ ΖΚ βάσει, ἡ δὲ ΝΠ τῇ ΞΡ, ἔστιν ἄρα ὡς ἡ ΖΚ βάσις πρὸς τὴν ΞΡ βάσιν, οὕτως τὸ τοῦ ΓΔ στερεοῦ ὕψος πρὸς τὸ τοῦ ΑΒ στερεοῦ ὕψος. τὰ δ' αὐτὰ ὕψη ἐστὶ τῶν ΑΒ, ΓΔ στερεῶν καὶ τῶν ΒΤ, ΔΨ· ἔστιν ἄρα ὡς ἡ ΖΚ βάσις πρὸς τὴν ΞΡ βάσιν, οὕτως τὸ τοῦ ΔΨ στερεοῦ ὕψος πρὸς τὸ τοῦ ΒΤ στερεοῦ ὕψος. τῶν ΒΤ, ΔΨ ἄρα στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν [ὧν δὲ στερεῶν παραλληλεπιπέδων τὰ ὕψη πρὸς ὀρθάς ἐστι ταῖς βάσεσιν αὐτῶν, ἀντιπεπόνθασι δὲ αἱ βάσεις τοῖς ὕψεσιν, ἴσα ἐστὶν ἐκεῖνα]· ἴσον ἄρα ἐστὶ τὸ ΒΤ στερεὸν τῷ ΔΨ στερεῷ. ἀλλὰ τὸ μὲν ΒΤ τῷ ΒΑ ἴσον ἐστίν· ἐπί τε γὰρ τῆς αὐτῆς βάσεως [εἰσι] τῆς ΖΚ καὶ ὑπὸ τὸ αὐτὸ ὕψος [ὧν αἱ ἐφεστῶσαι οὐκ εἰσὶν ἐπὶ τῶν αὐτῶν εὐθειῶν]. τὸ δὲ ΔΨ στερεὸν τῷ ΔΓ στερεῷ ἴσον ἐστίν [ἐπί τε γὰρ πάλιν τῆς αὐτῆς βάσεώς εἰσι τῆς ΞΡ καὶ ὑπὸ τὸ αὐτὸ ὕψος καὶ οὐκ ἐν ταῖς αὐταῖς εὐθείαις]. καὶ τὸ ΑΒ ἄρα στερεὸν τῷ ΓΔ στερεῷ ἐστιν ἴσον· ὅπερ ἔδει δεῖξαι.
Πρότασις λε΄ 35 Βιβλίον XI
Ἐὰν ὦσι δύο γωνίαι ἐπίπεδοι ἴσαι, ἐπὶ δὲ τῶν κορυφῶν αὐτῶν μετέωροι εὐθεῖαι ἐπισταθῶσιν ἴσας γωνίας περιέχουσαι μετὰ τῶν ἐξ ἀρχῆς εὐθειῶν ἑκατέραν ἑκατέρᾳ, ἐπὶ δὲ τῶν μετεώρων ληφθῇ τυχόντα σημεῖα, καὶ ἀπ' αὐτῶν ἐπὶ τὰ ἐπίπεδα, ἐν οἷς εἰσιν αἱ ἐξ ἀρχῆς γωνίαι, κάθετοι ἀχθῶσιν, ἀπὸ δὲ τῶν γενομένων σημείων ἐν τοῖς ἐπιπέδοις ἐπὶ τὰς ἐξ ἀρχῆς γωνίας ἐπιζευχθῶσιν εὐθεῖαι, ἴσας γωνίας περιέξουσι μετὰ τῶν μετεώρων.
Ἔστωσαν δύο γωνίαι εὐθύγραμμοι ἴσαι αἱ ὑπὸ ΒΑΓ, ΕΔΖ, ἀπὸ δὲ τῶν Α, Δ σημείων μετέωροι εὐθεῖαι ἐφεστάτωσαν αἱ ΑΗ, ΔΜ ἴσας γωνίας περιέχουσαι μετὰ τῶν ἐξ ἀρχῆς εὐθειῶν ἑκατέραν ἑκατέρᾳ, τὴν μὲν ὑπὸ ΜΔΕ τῇ ὑπὸ ΗΑΒ, τὴν δὲ ὑπὸ ΜΔΖ τῇ ὑπὸ ΗΑΓ, καὶ εἰλήφθω ἐπὶ τῶν ΑΗ, ΔΜ τυχόντα σημεῖα τὰ Η, Μ, καὶ ἤχθωσαν ἀπὸ τῶν Η, Μ σημείων ἐπὶ τὰ διὰ τῶν ΒΑΓ, ΕΔΖ ἐπίπεδα κάθετοι αἱ ΗΛ, ΜΝ, καὶ συμβαλλέτωσαν τοῖς ἐπιπέδοις κατὰ τὰ Ν, Λ, καὶ ἐπεζεύχθωσαν αἱ ΛΑ, ΝΔ· λέγω, ὅτι ἴση ἐστὶν ἡ ὑπὸ ΗΑΛ γωνία τῇ ὑπὸ ΜΔΝ γωνίᾳ.
Κείσθω τῇ ΔΜ ἴση ἡ ΑΘ, καὶ ἤχθω διὰ τοῦ Θ σημείου τῇ ΗΛ παράλληλος ἡ ΘΚ. ἡ δὲ ΗΛ κάθετός ἐστιν ἐπὶ τὸ διὰ τῶν ΒΑΓ ἐπίπεδον· καὶ ἡ ΘΚ ἄρα κάθετός ἐστιν ἐπὶ τὸ διὰ τῶν ΒΑΓ ἐπίπεδον. ἤχθωσαν ἀπὸ τῶν Κ, Ν σημείων ἐπὶ τὰς ΑΒ, ΑΓ, ΔΖ, ΔΕ εὐθείας κάθετοι αἱ ΚΓ, ΝΖ, ΚΒ, ΝΕ, καὶ ἐπεζεύχθωσαν αἱ ΘΓ, ΓΒ, ΜΖ, ΖΕ. ἐπεὶ τὸ ἀπὸ τῆς ΘΑ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΘΚ, ΚΑ, τῷ δὲ ἀπὸ τῆς ΚΑ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΚΓ, ΓΑ, καὶ τὸ ἀπὸ τῆς ΘΑ ἄρα ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΘΚ, ΚΓ, ΓΑ. τοῖς δὲ ἀπὸ τῶν ΘΚ, ΚΓ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΘΓ· τὸ ἄρα ἀπὸ τῆς ΘΑ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΘΓ, ΓΑ. ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΘΓΑ γωνία. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΔΖΜ γωνία ὀρθή ἐστιν. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΓΘ γωνία τῇ ὑπὸ ΔΖΜ. ἔστι δὲ καὶ ἡ ὑπὸ ΘΑΓ τῇ ὑπὸ ΜΔΖ ἴση. δύο δὴ τρίγωνά ἐστι τὰ ΜΔΖ, ΘΑΓ δύο γωνίας δυσὶ γωνίαις ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν τὴν ΘΑ τῇ ΜΔ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει ἑκατέραν ἑκατέρᾳ.
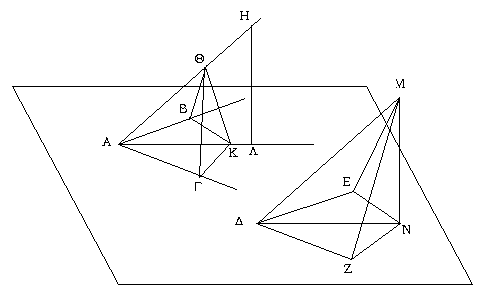
ἴση ἄρα ἐστὶν ἡ ΑΓ τῇ ΔΖ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΑΒ τῇ ΔΕ ἐστιν ἴση [οὕτως· ἐπεζεύχθωσαν αἱ ΘΒ, ΜΕ. καὶ ἐπεὶ τὸ ἀπὸ τῆς ΑΘ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΚ, ΚΘ, τῷ δὲ ἀπὸ τῆς ΑΚ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΑΒ, ΒΚ, τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΚ, ΚΘ ἴσα ἐστὶ τῷ ἀπὸ ΑΘ. ἀλλὰ τοῖς ἀπὸ τῶν ΒΚ, ΚΘ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΒΘ· ὀρθὴ γὰρ ἡ ὑπὸ ΘΚΒ γωνία διὰ τὸ καὶ τὴν ΘΚ κάθετον εἶναι ἐπὶ τὸ ὑποκείμενον ἐπίπεδον· τὸ ἄρα ἀπὸ τῆς ΑΘ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΒ, ΒΘ· ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΑΒΘ γωνία. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΔΕΜ γωνία ὀρθή ἐστιν. ἔστι δὲ καὶ ἡ ὑπὸ ΒΑΘ γωνία τῇ ὑπὸ ΕΔΜ ἴση· ὑπόκεινται γάρ· καὶ ἔστιν ἡ ΑΘ τῇ ΔΜ ἴση· ἴση ἄρα ἐστὶ καὶ ἡ ΑΒ τῇ ΔΕ]. ἐπεὶ οὖν ἴση ἐστὶν ἡ μὲν ΑΓ τῇ ΔΖ, ἡ δὲ ΑΒ τῇ ΔΕ, δύο δὴ αἱ ΓΑ, ΑΒ δυσὶ ταῖς ΖΔ, ΔΕ ἴσαι εἰσίν. ἀλλὰ καὶ γωνία ἡ ὑπὸ ΓΑΒ γωνίᾳ τῇ ὑπὸ ΖΔΕ ἐστιν ἴση· βάσις ἄρα ἡ ΒΓ βάσει τῇ ΕΖ ἴση ἐστὶ καὶ τὸ τρίγωνον τῷ τριγώνῳ καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις· ἴση ἄρα ἡ ὑπὸ ΑΓΒ γωνία τῇ ὑπὸ ΔΖΕ. ἔστι δὲ καὶ ὀρθὴ ἡ ὑπὸ ΑΓΚ ὀρθῇ τῇ ὑπὸ ΔΖΝ ἴση· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΒΓΚ λοιπῇ τῇ ὑπὸ ΕΖΝ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΓΒΚ τῇ ὑπὸ ΖΕΝ ἐστιν ἴση. δύο δὴ τρίγωνά ἐστι τὰ ΒΓΚ, ΕΖΝ [τὰς] δύο γωνίας δυσὶ γωνίαις ἴσας ἔχοντα ἑκατέραν ἑκατέρᾳ καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν πρὸς ταῖς ἴσαις γωνίαις τὴν ΒΓ τῇ ΕΖ· καὶ τὰς λοιπὰς ἄρα πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξουσιν. ἴση ἄρα ἐστὶν ἡ ΓΚ τῇ ΖΝ. ἔστι δὲ καὶ ἡ ΑΓ τῇ ΔΖ ἴση· δύο δὴ αἱ ΑΓ, ΓΚ δυσὶ ταῖς ΔΖ, ΖΝ ἴσαι εἰσίν· καὶ ὀρθὰς γωνίας περιέχουσιν. βάσις ἄρα ἡ ΑΚ βάσει τῇ ΔΝ ἴση ἐστίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΘ τῇ ΔΜ, ἴσον ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΘ τῷ ἀπὸ τῆς ΔΜ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΘ ἴσα ἐστὶ τὰ ἀπὸ τῶν ΑΚ, ΚΘ· ὀρθὴ γὰρ ἡ ὑπὸ ΑΚΘ· τῷ δὲ ἀπὸ τῆς ΔΜ ἴσα τὰ ἀπὸ τῶν ΔΝ, ΝΜ· ὀρθὴ γὰρ ἡ ὑπὸ ΔΝΜ· τὰ ἄρα ἀπὸ τῶν ΑΚ, ΚΘ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΔΝ, ΝΜ, ὧν τὸ ἀπὸ τῆς ΑΚ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΔΝ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΚΘ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΝΜ· ἴση ἄρα ἡ ΘΚ τῇ ΜΝ. καὶ ἐπεὶ δύο αἱ ΘΑ, ΑΚ δυσὶ ταῖς ΜΔ, ΔΝ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ βάσις ἡ ΘΚ βάσει τῇ ΜΝ ἐδείχθη ἴση, γωνία ἄρα ἡ ὑπὸ ΘΑΚ γωνίᾳ τῇ ὑπὸ ΜΔΝ ἐστιν ἴση.
Ἐὰν ἄρα ὦσι δύο γωνίαι ἐπίπεδοι ἴσαι καὶ τὰ ἑξῆς τῆς προτάσεως [ὅπερ ἔδει δεῖξαι].
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι, ἐὰν ὦσι δύο γωνίαι ἐπίπεδοι ἴσαι, ἐπισταθῶσι δὲ ἐπ᾿ αὐτῶν μετέωροι εὐθεῖαι ἴσαι ἴσας γωνίας περιέχουσαι μετὰ τῶν ἐξ ἀρχῆς εὐθειῶν ἑκατέραν ἑκατέρᾳ, αἱ ἀπ' αὐτῶν κάθετοι ἀγόμεναι ἐπὶ τὰ ἐπίπεδα, ἐν οἷς εἰσιν αἱ ἐξ ἀρχῆς γωνίαι, ἴσαι ἀλλήλαις εἰσίν. ὅπερ ἔδει δεῖξαι.
Πρότασις λς΄ 36 Βιβλίον XI
Ἐὰν τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, τὸ ἐκ τῶν τριῶν στερεὸν παραλληλεπίπεδον ἴσον ἐστὶ τῷ ἀπὸ τῆς μέσης στερεῷ παραλληλεπιπέδῳ ἰσοπλεύρῳ μέν, ἰσογωνίῳ δὲ τῷ προειρημένῳ.
Ἔστωσαν τρεῖς εὐθεῖαι ἀνάλογον αἱ Α, Β, Γ, ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ· λέγω, ὅτι τὸ ἐκ τῶν Α, Β, Γ στερεὸν ἴσον ἐστὶ τῷ ἀπὸ τῆς Β στερεῷ ἰσοπλεύρῳ μέν, ἰσογωνίῳ δὲ τῷ προειρημένῳ.
Ἐκκείσθω στερεὰ γωνία ἡ πρὸς τῷ Ε περιεχομένη ὑπὸ τῶν ὑπὸ ΔΕΗ, ΗΕΖ, ΖΕΔ, καὶ κείσθω τῇ μὲν Β ἴση ἑκάστη τῶν ΔΕ, ΗΕ, ΕΖ, καὶ συμπεπληρώσθω τὸ ΕΚ στερεὸν παραλληλεπίπεδον, τῇ δὲ Α ἴση ἡ ΛΜ, καὶ συνεστάτω πρὸς τῇ ΛΜ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Λ τῇ πρὸς τῷ Ε στερεᾷ γωνίᾳ ἴση στερεὰ γωνία ἡ περιεχομένη ὑπὸ τῶν ΝΛΞ, ΞΛΜ, ΜΛΝ, καὶ κείσθω τῇ μὲν Β ἴση ἡ ΛΞ, τῇ δὲ Γ ἴση ἡ ΛΝ. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Β πρὸς τὴν Γ, ἴση δὲ ἡ μὲν Α τῇ ΛΜ, ἡ δὲ Β ἑκατέρᾳ τῶν ΛΞ, ΕΔ, ἡ δὲ Γ τῇ ΛΝ, ἔστιν ἄρα ὡς ἡ ΛΜ πρὸς τὴν ΕΖ, οὕτως ἡ ΔΕ πρὸς τὴν ΛΝ.
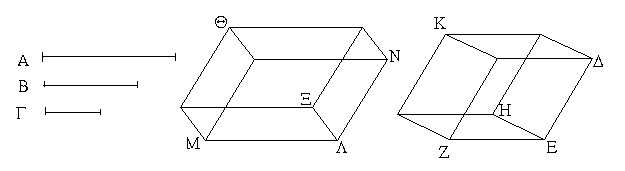
καὶ περὶ ἴσας γωνίας τὰς ὑπὸ ΝΛΜ, ΔΕΖ αἱ πλευραὶ ἀντιπεπόνθασιν· ἴσον ἄρα ἐστὶ τὸ ΜΝ παραλληλόγραμμον τῷ ΔΖ παραλληλογράμμῳ. καὶ ἐπεὶ δύο γωνίαι ἐπίπεδοι εὐθύγραμμοι ἴσαι εἰσὶν αἱ ὑπὸ ΔΕΖ, ΝΛΜ, καὶ ἐπ᾿ αὐτῶν μετέωροι εὐθεῖαι ἐφεστᾶσιν αἱ ΛΞ, ΕΗ ἴσαι τε ἀλλήλαις καὶ ἴσας γωνίας περιέχουσαι μετὰ τῶν ἐξ ἀρχῆς εὐθειῶν ἑκατέραν ἑκατέρᾳ, αἱ ἄρα ἀπὸ τῶν Η, Ξ σημείων κάθετοι ἀγόμεναι ἐπὶ τὰ διὰ τῶν ΝΛΜ, ΔΕΖ ἐπίπεδα ἴσαι ἀλλήλαις εἰσίν· ὥστε τὰ ΛΘ, ΕΚ στερεὰ ὑπὸ τὸ αὐτὸ ὕψος ἐστίν. τὰ δὲ ἐπὶ ἴσων βάσεων στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν· ἴσον ἄρα ἐστὶ τὸ ΘΛ στερεὸν τῷ ΕΚ στερεῷ. καί ἐστι τὸ μὲν ΛΘ τὸ ἐκ τῶν Α, Β, Γ στερεόν, τὸ δὲ ΕΚ τὸ ἀπὸ τῆς Β στερεόν· τὸ ἄρα ἐκ τῶν Α, Β, Γ στερεὸν παραλληλεπίπεδον ἴσον ἐστὶ τῷ ἀπὸ τῆς Β στερεῷ ἰσοπλεύρῳ μέν, ἰσογωνίῳ δὲ τῷ προειρημένῳ· ὅπερ ἔδει δεῖξαι.
Πρότασις λζ΄ 37 Βιβλίον XI
Ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, καὶ τὰ ἀπ' αὐτῶν στερεὰ παραλληλεπίπεδα ὅμοιά τε καὶ ὁμοίως ἀναγραφόμενα ἀνάλογον ἔσται· καὶ ἐὰν τὰ ἀπ' αὐτῶν στερεὰ παραλληλεπίπεδα ὅμοιά τε καὶ ὁμοίως ἀναγραφόμενα ἀνάλογον ᾖ, καὶ αὐταὶ αἱ εὐθεῖαι ἀνάλογον ἔσονται.
Ἔστωσαν τέσσαρες εὐθεῖαι ἀνάλογον αἱ ΑΒ, ΓΔ, ΕΖ, ΗΘ, ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ, καὶ ἀναγεγράφθωσαν ἀπὸ τῶν ΑΒ, ΓΔ, ΕΖ, ΗΘ ὅμοιά τε καὶ ὁμοίως κείμενα στερεὰ παραλληλεπίπεδα τὰ ΚΑ, ΛΓ, ΜΕ, ΝΗ· λέγω, ὅτι ἐστὶν ὡς τὸ ΚΑ πρὸς τὸ ΛΓ, οὕτως τὸ ΜΕ πρὸς τὸ ΝΗ.
Ἐπεὶ γὰρ ὅμοιόν ἐστι τὸ ΚΑ στερεὸν παραλληλεπίπεδον τῷ ΛΓ, τὸ ΚΑ ἄρα πρὸς τὸ ΛΓ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ πρὸς τὴν ΓΔ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΜΕ πρὸς τὸ ΝΗ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΕΖ πρὸς τὴν ΗΘ. καί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ. καὶ ὡς ἄρα τὸ ΑΚ πρὸς τὸ ΛΓ, οὕτως τὸ ΜΕ πρὸς τὸ ΝΗ.
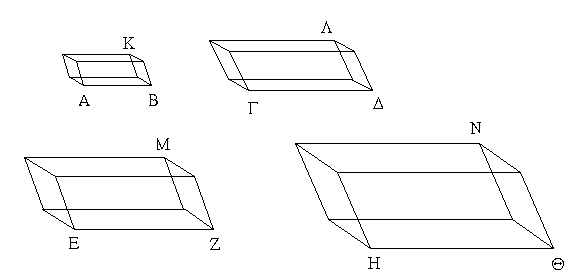
Ἀλλὰ δὴ ἔστω ὡς τὸ ΑΚ στερεὸν πρὸς τὸ ΛΓ στερεόν, οὕτως τὸ ΜΕ στερεὸν πρὸς τὸ ΝΗ· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΒ εὐθεῖα πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ.
Ἐπεὶ γὰρ πάλιν τὸ ΚΑ πρὸς τὸ ΛΓ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΑΒ πρὸς τὴν ΓΔ, ἔχει δὲ καὶ τὸ ΜΕ πρὸς τὸ ΝΗ τριπλασίονα λόγον ἤπερ ἡ ΕΖ πρὸς τὴν ΗΘ, καί ἐστιν ὡς τὸ ΚΑ πρὸς τὸ ΛΓ, οὕτως τὸ ΜΕ πρὸς τὸ ΝΗ, καὶ ὡς ἄρα ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἡ ΕΖ πρὸς τὴν ΗΘ.
Ἐὰν ἄρα τέσσαρες εὐθεῖαι ἀνάλογον ὦσι καὶ τὰ ἑξῆς τῆς προτάσεως· ὅπερ ἔδει δεῖξαι.
Πρότασις λη΄ 38 Βιβλίον XI
Ἐὰν κύβου τῶν ἀπεναντίον ἐπιπέδων αἱ πλευραὶ δίχα τμηθῶσιν, διὰ δὲ τῶν τομῶν ἐπίπεδα ἐκβληθῇ, ἡ κοινὴ τομὴ τῶν ἐπιπέδων καὶ ἡ τοῦ κύβου διάμετρος δίχα τέμνουσιν ἀλλήλας.
Κύβου γὰρ τοῦ ΑΖ τῶν ἀπεναντίον ἐπιπέδων τῶν ΓΖ, ΑΘ αἱ πλευραὶ δίχα τετμήσθωσαν κατὰ τὰ Κ, Λ, Μ, Ν, Ξ, Π, Ο, Ρ σημεῖα, διὰ δὲ τῶν τομῶν ἐπίπεδα ἐκβεβλήσθω τὰ ΚΝ, ΞΡ, κοινὴ δὲ τομὴ τῶν ἐπιπέδων ἔστω ἡ ΥΣ, τοῦ δὲ ΑΖ κύβου διαγώνιος ἡ ΔΗ. λέγω, ὅτι ἴση ἐστὶν ἡ μὲν ΥΤ τῇ ΤΣ, ἡ δὲ ΔΤ τῇ ΤΗ.
Ἐπεζεύχθωσαν γὰρ αἱ ΔΥ, ΥΕ, ΒΣ, ΣΗ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΔΞ τῇ ΟΕ, αἱ ἐναλλὰξ γωνίαι αἱ ὑπὸ ΔΞΥ, ΥΟΕ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΔΞ τῇ ΟΕ, ἡ δὲ ΞΥ τῇ ΥΟ, καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΔΥ τῇ ΥΕ ἐστιν ἴση, καὶ τὸ ΔΞΥ τρίγωνον τῷ ΟΥΕ τριγώνῳ ἐστὶν ἴσον καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι· ἴση ἄρα ἡ ὑπὸ ΞΥΔ γωνία τῇ ὑπὸ ΟΥΕ γωνίᾳ. διὰ δὴ τοῦτο εὐθεῖά ἐστιν ἡ ΔΥΕ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΒΣΗ εὐθεῖά ἐστιν, καὶ ἴση ἡ ΒΣ τῇ ΣΗ.
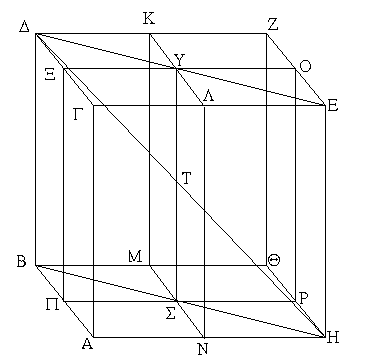
καὶ ἐπεὶ ἡ ΓΑ τῇ ΔΒ ἴση ἐστὶ καὶ παράλληλος, ἀλλὰ ἡ ΓΑ καὶ τῇ ΕΗ ἴση τέ ἐστι καὶ παράλληλος, καὶ ἡ ΔΒ ἄρα τῇ ΕΗ ἴση τέ ἐστι καὶ παράλληλος. καὶ ἐπιζευγνύουσιν αὐτὰς εὐθεῖαι αἱ ΔΕ, ΒΗ· παράλληλος ἄρα ἐστὶν ἡ ΔΕ τῇ ΒΗ. ἴση ἄρα ἡ μὲν ὑπὸ ΕΔΤ γωνία τῇ ὑπὸ ΒΗΤ· ἐναλλὰξ γάρ· ἡ δὲ ὑπὸ ΔΤΥ τῇ ὑπὸ ΗΤΣ. δύο δὴ τρίγωνά ἐστι τὰ ΔΤΥ, ΗΤΣ τὰς δύο γωνίας ταῖς δυσὶ γωνίαις ἴσας ἔχοντα καὶ μίαν πλευρὰν μιᾷ πλευρᾷ ἴσην τὴν ὑποτείνουσαν ὑπὸ μίαν τῶν ἴσων γωνιῶν τὴν ΔΥ τῇ ΗΣ· ἡμίσειαι γάρ εἰσι τῶν ΔΕ, ΒΗ· καὶ τὰς λοιπὰς πλευρὰς ταῖς λοιπαῖς πλευραῖς ἴσας ἕξει. ἴση ἄρα ἡ μὲν ΔΤ τῇ ΤΗ, ἡ δὲ ΥΤ τῇ ΤΣ.
Ἐὰν ἄρα κύβου τῶν ἀπεναντίον ἐπιπέδων αἱ πλευραὶ δίχα τμηθῶσιν, διὰ δὲ τῶν τομῶν ἐπίπεδα ἐκβληθῇ, ἡ κοινὴ τομὴ τῶν ἐπιπέδων καὶ ἡ τοῦ κύβου διάμετρος δίχα τέμνουσιν ἀλλήλας· ὅπερ ἔδει δεῖξαι.
Πρότασις λθ΄ 39 Βιβλίον XI
Ἐὰν ᾖ δύο πρίσματα ἰσοϋψῆ, καὶ τὸ μὲν ἔχῃ βάσιν παραλληλόγραμμον, τὸ δὲ τρίγωνον, διπλάσιον δὲ ᾖ τὸ παραλληλόγραμμον τοῦ τριγώνου, ἴσα ἔσται τὰ πρίσματα.
Ἔστω δύο πρίσματα ἰσοϋψῆ τὰ ΑΒΓΔΕΖ, ΗΘΚΛ ΜΝ, καὶ τὸ μὲν ἐχέτω βάσιν τὸ ΑΖ παραλληλόγραμμον, τὸ δὲ τὸ ΗΘΚ τρίγωνον, διπλάσιον δὲ ἔστω τὸ ΑΖ παραλληλόγραμμον τοῦ ΗΘΚ τριγώνου· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΒΓΔΕΖ πρίσμα τῷ ΗΘΚΛΜΝ πρίσματι.
Συμπεπληρώσθω γὰρ τὰ ΑΞ, ΗΟ στερεά. ἐπεὶ διπλάσιόν ἐστι τὸ ΑΖ παραλληλόγραμμον τοῦ ΗΘΚ τριγώνου, ἔστι δὲ καὶ τὸ ΘΚ παραλληλόγραμμον διπλάσιον τοῦ ΗΘΚ τριγώνου, ἴσον ἄρα ἐστὶ τὸ ΑΖ παραλληλόγραμμον τῷ ΘΚ παραλληλογράμμῳ.
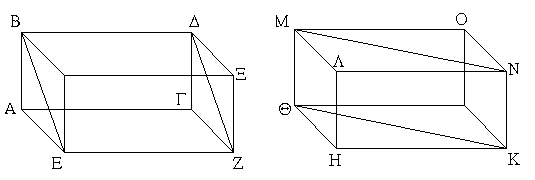
τὰ δὲ ἐπὶ ἴσων βάσεων ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν· ἴσον ἄρα ἐστὶ τὸ ΑΞ στερεὸν τῷ ΗΟ στερεῷ. καί ἐστι τοῦ μὲν ΑΞ στερεοῦ ἥμισυ τὸ ΑΒΓΔΕΖ πρίσμα, τοῦ δὲ ΗΟ στερεοῦ ἥμισυ τὸ ΗΘΚΛΜΝ πρίσμα· ἴσον ἄρα ἐστὶ τὸ ΑΒΓΔΕΖ πρίσμα τῷ ΗΘΚΛΜΝ πρίσματι.
Ἐὰν ἄρα ᾖ δύο πρίσματα ἰσοψῆ, καὶ τὸ μὲν ἔχῃ βάσιν παραλληλόγραμμον, τὸ δὲ τρίγωνον, διπλάσιον δὲ ᾖ τὸ παραλληλόγραμμον τοῦ τριγώνου, ἴσα ἐστὶ τὰ πρίσματα· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου ιβ΄
Βιβλίον XII
Προτάσεις ιη΄ 18
Πρότασις α΄ 1 Βιβλίον XII
Τὰ ἐν τοῖς κύκλοις ὅμοια πολύγωνα πρὸς ἄλληλά ἐστιν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα.
Ἔστωσαν κύκλοι οἱ ΑΒΓ, ΖΗΘ, καὶ ἐν αὐτοῖς ὅμοια πολύγωνα ἔστω τὰ ΑΒΓΔΕ, ΖΗΘΚΛ, διάμετροι δὲ τῶν κύκλων ἔστωσαν αἱ ΒΜ, ΗΝ· λέγω, ὅτι ἐστὶν ὡς τὸ ἀπὸ τῆς ΒΜ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΝ τετράγωνον, οὕτως τὸ ΑΒΓΔΕ πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΑΜ, ΗΛ, ΖΝ. καὶ ἐπεὶ ὅμοιον τὸ ΑΒΓΔΕ πολύγωνον τῷ ΖΗΘΚΛ πολυγώνῳ, ἴση ἐστὶ καὶ ἡ ὑπὸ ΒΑΕ γωνία τῇ ὑπὸ ΗΖΛ, καί ἐστιν ὡς ἡ ΒΑ πρὸς τὴν ΑΕ, οὕτως ἡ ΗΖ πρὸς τὴν ΖΛ.
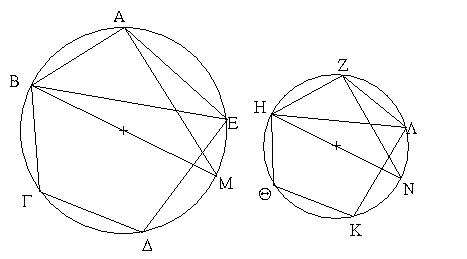
δύο δὴ τρίγωνά ἐστι τὰ ΒΑΕ, ΗΖΛ μίαν γωνίαν μιᾷ γωνίᾳ ἴσην ἔχοντα τὴν ὑπὸ ΒΑΕ τῇ ὑπὸ ΗΖΛ, περὶ δὲ τὰς ἴσας γωνίας τὰς πλευρὰς ἀνάλογον· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΕ τρίγωνον τῷ ΖΗΛ τριγώνῳ. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΕΒ γωνία τῇ ὑπὸ ΖΛΗ. ἀλλ' ἡ μὲν ὑπὸ ΑΕΒ τῇ ὑπὸ ΑΜΒ ἐστιν ἴση· ἐπὶ γὰρ τῆς αὐτῆς περιφερείας βεβήκασιν· ἡ δὲ ὑπὸ ΖΛΗ τῇ ὑπὸ ΖΝΗ· καὶ ἡ ὑπὸ ΑΜΒ ἄρα τῇ ὑπὸ ΖΝΗ ἐστιν ἴση. ἔστι δὲ καὶ ὀρθὴ ἡ ὑπὸ ΒΑΜ ὀρθῇ τῇ ὑπὸ ΗΖΝ ἴση· καὶ ἡ λοιπὴ ἄρα τῇ λοιπῇ ἐστιν ἴση. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΜ τρίγωνον τῷ ΖΗΝ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΜ πρὸς τὴν ΗΝ, οὕτως ἡ ΒΑ πρὸς τὴν ΗΖ. ἀλλὰ τοῦ μὲν τῆς ΒΜ πρὸς τὴν ΗΝ λόγου διπλασίων ἐστὶν ὁ τοῦ ἀπὸ τῆς ΒΜ τετραγώνου πρὸς τὸ ἀπὸ τῆς ΗΝ τετράγωνον, τοῦ δὲ τῆς ΒΑ πρὸς τὴν ΗΖ διπλασίων ἐστὶν ὁ τοῦ ΑΒΓΔΕ πολυγώνου πρὸς τὸ ΖΗ ΘΚΛ πολύγωνον· καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΒΜ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΗΝ τετράγωνον, οὕτως τὸ ΑΒΓΔΕ πολύγωνον πρὸς τὸ ΖΗΘΚΛ πολύγωνον.
Τὰ ἄρα ἐν τοῖς κύκλοις ὅμοια πολύγωνα πρὸς ἄλληλά ἐστιν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον XII
Οἱ κύκλοι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα.
Ἔστωσαν κύκλοι οἱ ΑΒΓΔ, ΕΖΗΘ, διάμετροι δὲ αὐτῶν [ἔστωσαν] αἱ ΒΔ, ΖΘ· λέγω, ὅτι ἐστὶν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ τετράγωνον.
Εἰ γὰρ μή ἐστιν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ, οὕτως τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ, ἔσται ὡς τὸ ἀπὸ τῆς ΒΔ πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος ἤτοι πρὸς ἔλασσόν τι τοῦ ΕΖΗΘ κύκλου χωρίον ἢ πρὸς μεῖζον. ἔστω πρότερον πρὸς ἔλασσον τὸ Σ. καὶ ἐγγεγράφθω εἰς τὸν ΕΖΗΘ κύκλον τετράγωνον τὸ ΕΖΗΘ· τὸ δὴ ἐγγεγραμμένον τετράγωνον μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ ΕΖΗΘ κύκλου, ἐπειδήπερ ἐὰν διὰ τῶν Ε, Ζ, Η, Θ σημείων ἐφαπτομένας [εὐθείας] τοῦ κύκλου ἀγάγωμεν, τοῦ περιγραφομένου περὶ τὸν κύκλον τετραγώνου ἥμισύ ἐστι τὸ ΕΖΗΘ τετράγωνον, τοῦ δὲ περιγραφέντος τετραγώνου ἐλάττων ἐστὶν ὁ κύκλος· ὥστε τὸ ΕΖΗΘ ἐγγεγραμμένον τετράγωνον μεῖζόν ἐστι τοῦ ἡμίσεως τοῦ ΕΖΗΘ κύκλου. τετμήσθωσαν δίχα αἱ ΕΖ, ΖΗ, ΗΘ, ΘΕ περιφέρειαι κατὰ τὰ Κ, Λ, Μ, Ν σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΕΚ, ΚΖ, ΖΛ, ΛΗ, ΗΜ, ΜΘ, ΘΝ, ΝΕ· καὶ ἕκαστον ἄρα τῶν ΕΚΖ, ΖΛΗ, ΗΜΘ, ΘΝΕ τριγώνων μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ κύκλου, ἐπειδήπερ ἐὰν διὰ τῶν Κ, Λ, Μ, Ν σημείων ἐφαπτομένας τοῦ κύκλου ἀγάγωμεν καὶ ἀναπληρώσωμεν τὰ ἐπὶ τῶν ΕΖ, ΖΗ, ΗΘ, ΘΕ εὐθειῶν παραλληλόγραμμα, ἕκαστον τῶν ΕΚΖ, ΖΛΗ, ΗΜΘ, ΘΝΕ τριγώνων ἥμισυ ἔσται τοῦ καθ᾿ ἑαυτὸ παραλληλογράμμου, ἀλλὰ τὸ καθ᾿ ἑαυτὸ τμῆμα ἔλαττόν ἐστι τοῦ παραλληλογράμμου· ὥστε ἕκαστον τῶν ΕΚΖ, ΖΛΗ, ΗΜΘ, ΘΝΕ τριγώνων μεῖζόν ἐστι τοῦ ἡμίσεως τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ κύκλου. τέμνοντες δὴ τὰς ὑπολειπομένας περιφερείας δίχα καὶ ἐπιζευγνύντες εὐθείας καὶ τοῦτο ἀεὶ ποιοῦντες καταλείψομέν τινα ἀποτμήματα τοῦ κύκλου, ἃ ἔσται ἐλάσσονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ ΕΖΗΘ κύκλος τοῦ Σ χωρίου.
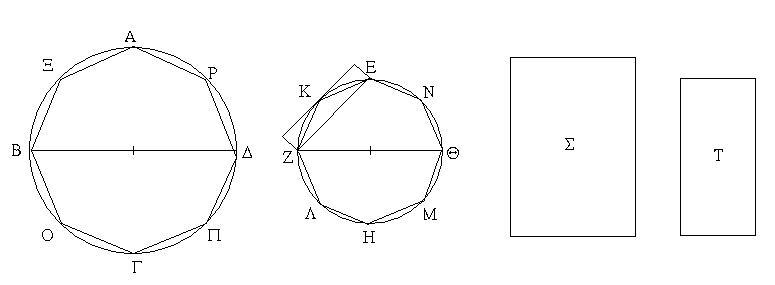
ἐδείχθη γὰρ ἐν τῷ πρώτῳ θεωρήματι τοῦ δεκάτου βιβλίου, ὅτι δύο μεγεθῶν ἀνίσων ἐκκειμένων, ἐὰν ἀπὸ τοῦ μείζονος ἀφαιρεθῇ μεῖζον ἢ τὸ ἥμισυ καὶ τοῦ καταλειπομένου μεῖζον ἢ τὸ ἥμισυ, καὶ τοῦτο ἀεὶ γίγνηται, λειφθήσεταί τι μέγεθος, ὃ ἔσται ἔλασσον τοῦ ἐκκειμένου ἐλάσσονος μεγέθους. λελείφθω οὖν, καὶ ἔστω τὰ ἐπὶ τῶν ΕΚ, ΚΖ, ΖΛ, ΛΗ, ΗΜ, ΜΘ, ΘΝ, ΝΕ τμήματα τοῦ ΕΖΗΘ κύκλου ἐλάττονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ ΕΖΗΘ κύκλος τοῦ Σ χωρίου. λοιπὸν ἄρα τὸ ΕΚΖΛΗ ΜΘΝ πολύγωνον μεῖζόν ἐστι τοῦ Σ χωρίου. ἐγγεγράφθω καὶ εἰς τὸν ΑΒΓΔ κύκλον τῷ ΕΚΖΛΗΜΘΝ πολυγώνῳ ὅμοιον πολύγωνον τὸ ΑΞΒΟΓΠΔΡ· ἔστιν ἄρα ὡς τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ τετράγωνον, οὕτως τὸ ΑΞΒΟΓΠΔΡ πολύγωνον πρὸς τὸ ΕΚΖΛ ΗΜΘΝ πολύγωνον. ἀλλὰ καὶ ὡς τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς τὸ Σ χωρίον· καὶ ὡς ἄρα ὁ ΑΒΓΔ κύκλος πρὸς τὸ Σ χωρίον, οὕτως τὸ ΑΞΒΟΓΠΔΡ πολύγωνον πρὸς τὸ ΕΚΖΛΗΜΘΝ πολύγωνον· ἐναλλὰξ ἄρα ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸ ἐν αὐτῷ πολύγωνον, οὕτως τὸ Σ χωρίον πρὸς τὸ ΕΚΖΛΗΜΘΝ πολύγωνον. μείζων δὲ ὁ ΑΒΓΔ κύκλος τοῦ ἐν αὐτῷ πολυγώνου· μεῖζον ἄρα καὶ τὸ Σ χωρίον τοῦ ΕΚΖΛΗΜΘΝ πολυγώνου. ἀλλὰ καὶ ἔλαττον· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς ἔλασσόν τι τοῦ ΕΖΗΘ κύκλου χωρίον. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ὡς τὸ ἀπὸ ΖΘ πρὸς τὸ ἀπὸ ΒΔ, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς ἔλασσόν τι τοῦ ΑΒΓΔ κύκλου χωρίον.
Λέγω δή, ὅτι οὐδὲ ὡς τὸ ἀπὸ τῆς ΒΔ πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς μεῖζόν τι τοῦ ΕΖΗΘ κύκλου χωρίον.
Εἰ γὰρ δυνατόν, ἔστω πρὸς μεῖζον τὸ Σ. ἀνάπαλιν ἄρα [ἐστὶν] ὡς τὸ ἀπὸ τῆς ΖΘ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΔΒ, οὕτως τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον. ἀλλ' ὡς τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔ κύκλου χωρίον· καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΖΘ πρὸς τὸ ἀπὸ τῆς ΒΔ, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς ἔλασσόν τι τοῦ ΑΒΓΔ κύκλου χωρίον· ὅπερ ἀδύνατον ἐδείχθη. οὐκ ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς μεῖζόν τι τοῦ ΕΖΗΘ κύκλου χωρίον. ἐδείχθη δέ, ὅτι οὐδὲ πρὸς ἔλασσον· ἔστιν ἄρα ὡς τὸ ἀπὸ τῆς ΒΔ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΖΘ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον.
Οἱ ἄρα κύκλοι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Λέγω δή, ὅτι τοῦ Σ χωρίου μείζονος ὄντος τοῦ ΕΖΗΘ κύκλου ἐστὶν ὡς τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔ κύκλου χωρίον.
Γεγονέτω γὰρ ὡς τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς τὸ Τ χωρίον. λέγω, ὅτι ἔλαττόν ἐστι τὸ Τ χωρίον τοῦ ΑΒΓΔ κύκλου. ἐπεὶ γάρ ἐστιν ὡς τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς τὸ Τ χωρίον, ἐναλλάξ ἐστιν ὡς τὸ Σ χωρίον πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς τὸ Τ χωρίον. μεῖζον δὲ τὸ Σ χωρίον τοῦ ΕΖΗΘ κύκλου· μείζων ἄρα καὶ ὁ ΑΒΓΔ κύκλος τοῦ Τ χωρίου. ὥστε ἐστὶν ὡς τὸ Σ χωρίον πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΖΗΘ κύκλος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔ κύκλου χωρίον· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον XII
Πᾶσα πυραμὶς τρίγωνον ἔχουσα βάσιν διαιρεῖται εἰς δύο πυραμίδας ἴσας τε καὶ ὁμοίας ἀλλήλαις καὶ [ὁμοίας] τῇ ὅλῃ τριγώνους ἐχούσας βάσεις καὶ εἰς δύο πρίσματα ἴσα· καὶ τὰ δύο πρίσματα μείζονά ἐστιν ἢ τὸ ἥμισυ τῆς ὅλης πυραμίδος.
Ἔστω πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον· λέγω, ὅτι ἡ ΑΒΓΔ πυραμὶς διαιρεῖται εἰς δύο πυραμίδας ἴσας ἀλλήλαις τριγώνους βάσεις ἐχούσας καὶ ὁμοίας τῇ ὅλῃ καὶ εἰς δύο πρίσματα ἴσα· καὶ τὰ δύο πρίσματα μείζονά ἐστιν ἢ τὸ ἥμισυ τῆς ὅλης πυραμίδος.
Τετμήσθωσαν γὰρ αἱ ΑΒ, ΒΓ, ΓΑ, ΑΔ, ΔΒ, ΔΓ δίχα κατὰ τὰ Ε, Ζ, Η, Θ, Κ, Λ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΘΕ, ΕΗ, ΗΘ, ΘΚ, ΚΛ, ΛΘ, ΚΖ, ΖΗ. ἐπεὶ ἴση ἐστὶν ἡ μὲν ΑΕ τῇ ΕΒ, ἡ δὲ ΑΘ τῇ ΔΘ, παράλληλος ἄρα ἐστὶν ἡ ΕΘ τῇ ΔΒ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΘΚ τῇ ΑΒ παράλληλός ἐστιν. παραλληλόγραμμον ἄρα ἐστὶ τὸ ΘΕ ΒΚ· ἴση ἄρα ἐστὶν ἡ ΘΚ τῇ ΕΒ. ἀλλὰ ἡ ΕΒ τῇ ΕΑ ἐστιν ἴση· καὶ ἡ ΑΕ ἄρα τῇ ΘΚ ἐστιν ἴση. ἔστι δὲ καὶ ἡ ΑΘ τῇ ΘΔ ἴση· δύο δὴ αἱ ΕΑ, ΑΘ δυσὶ ταῖς ΚΘ, ΘΔ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΕΑΘ γωνίᾳ τῇ ὑπὸ ΚΘΔ ἴση· βάσις ἄρα ἡ ΕΘ βάσει τῇ ΚΔ ἐστιν ἴση. ἴσον ἄρα καὶ ὅμοιόν ἐστι τὸ ΑΕΘ τρίγωνον τῷ ΘΚΔ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΑΘΗ τρίγωνον τῷ ΘΛΔ τριγώνῳ ἴσον τέ ἐστι καὶ ὅμοιον. καὶ ἐπεὶ δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων αἱ ΕΘ, ΘΗ παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων τὰς ΚΔ, ΔΛ εἰσιν οὐκ ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι, ἴσας γωνίας περιέξουσιν. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΕΘΗ γωνία τῇ ὑπὸ ΚΔΛ γωνίᾳ.
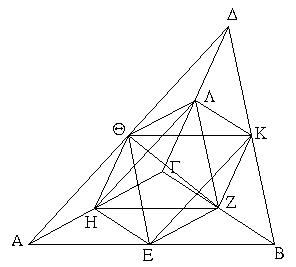
καὶ ἐπεὶ δύο εὐθεῖαι αἱ ΕΘ, ΘΗ δυσὶ ταῖς ΚΔ, ΔΛ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ γωνία ἡ ὑπὸ ΕΘΗ γωνίᾳ τῇ ὑπὸ ΚΔΛ ἐστιν ἴση, βάσις ἄρα ἡ ΕΗ βάσει τῇ ΚΛ [ἐστιν] ἴση· ἴσον ἄρα καὶ ὅμοιόν ἐστι τὸ ΕΘΗ τρίγωνον τῷ ΚΔΛ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΑΕΗ τρίγωνον τῷ ΘΚΛ τριγώνῳ ἴσον τε καὶ ὅμοιόν ἐστιν. ἡ ἄρα πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον, ἴση καὶ ὁμοία ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΘΚΛ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον. καὶ ἐπεὶ τριγώνου τοῦ ΑΔΒ παρὰ μίαν τῶν πλευρῶν τὴν ΑΒ ἦκται ἡ ΘΚ, ἰσογώνιόν ἐστι τὸ ΑΔΒ τρίγωνον τῷ ΔΘΚ τριγώνῳ, καὶ τὰς πλευρὰς ἀνάλογον ἔχουσιν· ὅμοιον ἄρα ἐστὶ τὸ ΑΔΒ τρίγωνον τῷ ΔΘΚ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΔΒΓ τρίγωνον τῷ ΔΚΛ τριγώνῳ ὅμοιόν ἐστιν, τὸ δὲ ΑΔΓ τῷ ΔΛΘ. καὶ ἐπεὶ δύο εὐθεῖαι ἁπτόμεναι ἀλλήλων αἱ ΒΑ, ΑΓ παρὰ δύο εὐθείας ἁπτομένας ἀλλήλων τὰς ΚΘ, ΘΛ εἰσιν οὐκ ἐν τῷ αὐτῷ ἐπιπέδῳ, ἴσας γωνίας περιέξουσιν. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΚΘΛ. καί ἐστιν ὡς ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΚΘ πρὸς τὴν ΘΛ· ὅμοιον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον τῷ ΘΚΛ τριγώνῳ. καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ὁμοία ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΘΚΛ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον. ἀλλὰ πυραμίς, ἧς βάσις μὲν [ἐστι] τὸ ΘΚΛ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ὁμοία ἐδείχθη πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον [ὥστε καὶ πυραμίς, ἧς βάσις μὲν τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ὁμοία ἐστὶ πυραμίδι, ἧς βάσις μὲν τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον]. ἑκατέρα ἄρα τῶν ΑΕΗΘ, ΘΚΛΔ πυραμίδων ὁμοία ἐστὶ τῇ ὅλῃ τῇ ΑΒΓΔ πυραμίδι. Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΖ τῇ ΖΓ, διπλάσιόν ἐστι τὸ ΕΒΖΗ παραλληλόγραμμον τοῦ ΗΖΓ τριγώνου. καὶ ἐπεί, ἐὰν ᾖ δύο πρίσματα ἰσοϋψῆ, καὶ τὸ μὲν ἔχῃ βάσιν παραλληλόγραμμον, τὸ δὲ τρίγωνον, διπλάσιον δὲ ᾖ τὸ παραλληλόγραμμον τοῦ τριγώνου, ἴσα ἐστὶ τὰ πρίσματα, ἴσον ἄρα ἐστὶ τὸ πρίσμα τὸ περιεχόμενον ὑπὸ δύο μὲν τριγώνων τῶν ΒΚΖ, ΕΘΗ, τριῶν δὲ παραλληλογράμμων τῶν ΕΒΖΗ, ΕΒΚΘ, ΘΚΖΗ τῷ πρίσματι τῷ περιεχομένῳ ὑπὸ δύο μὲν τριγώνων τῶν ΗΖΓ, ΘΚΛ, τριῶν δὲ παραλληλογράμμων τῶν ΚΖΓΛ, ΛΓΗΘ, ΘΚΖΗ. καὶ φανερόν, ὅτι ἑκάτερον τῶν πρισμάτων, οὗ τε βάσις τὸ ΕΒΖΗ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΘΚ εὐθεῖα, καὶ οὗ βάσις τὸ ΗΖΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΘΚΛ τρίγωνον, μεῖζόν ἐστιν ἑκατέρας τῶν πυραμίδων, ὧν βάσεις μὲν τὰ ΑΕΗ, ΘΚΛ τρίγωνα, κορυφαὶ δὲ τὰ Θ, Δ σημεῖα, ἐπειδήπερ [καὶ] ἐὰν ἐπιζεύξωμεν τὰς ΕΖ, ΕΚ εὐθείας, τὸ μὲν πρίσμα, οὗ βάσις τὸ ΕΒΖΗ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΘΚ εὐθεῖα, μεῖζόν ἐστι τῆς πυραμίδος, ἧς βάσις τὸ ΕΒΖ τρίγωνον, κορυφὴ δὲ τὸ Κ σημεῖον. ἀλλ' ἡ πυραμίς, ἧς βάσις τὸ ΕΒΖ τρίγωνον, κορυφὴ δὲ τὸ Κ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον· ὑπὸ γὰρ ἴσων καὶ ὁμοίων ἐπιπέδων περιέχονται. ὥστε καὶ τὸ πρίσμα, οὗ βάσις μὲν τὸ ΕΒΖΗ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΘΚ εὐθεῖα, μεῖζόν ἐστι πυραμίδος, ἧς βάσις μὲν τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον. ἴσον δὲ τὸ μὲν πρίσμα, οὗ βάσις τὸ ΕΒΖΗ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΘΚ εὐθεῖα, τῷ πρίσματι, οὗ βάσις μὲν τὸ ΗΖΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΘΚΛ τρίγωνον· ἡ δὲ πυραμίς, ἧς βάσις τὸ ΑΕΗ τρίγωνον, κορυφὴ δὲ τὸ Θ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις τὸ ΘΚΛ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον. τὰ ἄρα εἰρημένα δύο πρίσματα μείζονά ἐστι τῶν εἰρημένων δύο πυραμίδων, ὧν βάσεις μὲν τὰ ΑΕΗ, ΘΚΛ τρίγωνα, κορυφαὶ δὲ τὰ Θ, Δ σημεῖα.
Ἡ ἄρα ὅλη πυραμίς, ἧς βάσις τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, διῄρηται εἴς τε δύο πυραμίδας ἴσας ἀλλήλαις [καὶ ὁμοίας τῇ ὅλῃ] καὶ εἰς δύο πρίσματα ἴσα, καὶ τὰ δύο πρίσματα μείζονά ἐστιν ἢ τὸ ἥμισυ τῆς ὅλης πυραμίδος· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον XII
Ἐὰν ὦσι δύο πυραμίδες ὑπὸ τὸ αὐτὸ ὕψος τριγώνους ἔχουσαι βάσεις, διαιρεθῇ δὲ ἑκατέρα αὐτῶν εἴς τε δύο πυραμίδας ἴσας ἀλλήλαις καὶ ὁμοίας τῇ ὅλῃ καὶ εἰς δύο πρίσματα ἴσα, ἔσται ὡς ἡ τῆς μιᾶς πυραμίδος βάσις πρὸς τὴν τῆς ἑτέρας πυραμίδος βάσιν, οὕτως τὰ ἐν τῇ μιᾷ πυραμίδι πρίσματα πάντα πρὸς τὰ ἐν τῇ ἑτέρᾳ πυραμίδι πρίσματα πάντα ἰσοπληθῆ.
Ἔστωσαν δύο πυραμίδες ὑπὸ τὸ αὐτὸ ὕψος τριγώνους ἔχουσαι βάσεις τὰς ΑΒΓ, ΔΕΖ, κορυφὰς δὲ τὰ Η, Θ σημεῖα, καὶ διῃρήσθω ἑκατέρα αὐτῶν εἴς τε δύο πυραμίδας ἴσας ἀλλήλαις καὶ ὁμοίας τῇ ὅλῃ καὶ εἰς δύο πρίσματα ἴσα· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὰ ἐν τῇ ΑΒΓΗ πυραμίδι πρίσματα πάντα πρὸς τὰ ἐν τῇ ΔΕΖΘ πυραμίδι πρίσματα ἰσοπληθῆ.
Ἐπεὶ γὰρ ἴση ἐστὶν ἡ μὲν ΒΞ τῇ ΞΓ, ἡ δὲ ΑΛ τῇ ΛΓ, παράλληλος ἄρα ἐστὶν ἡ ΛΞ τῇ ΑΒ καὶ ὅμοιον τὸ ΑΒΓ τρίγωνον τῷ ΛΞΓ τριγώνῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΔΕΖ τρίγωνον τῷ ΡΦΖ τριγώνῳ ὅμοιόν ἐστιν. καὶ ἐπεὶ διπλασίων ἐστὶν ἡ μὲν ΒΓ τῆς ΓΞ, ἡ δὲ ΕΖ τῆς ΖΦ, ἔστιν ἄρα ὡς ἡ ΒΓ πρὸς τὴν ΓΞ, οὕτως ἡ ΕΖ πρὸς τὴν ΖΦ. καὶ ἀναγέγραπται ἀπὸ μὲν τῶν ΒΓ, ΓΞ ὅμοιά τε καὶ ὁμοίως κείμενα εὐθύγραμμα τὰ ΑΒΓ, ΛΞΓ, ἀπὸ δὲ τῶν ΕΖ, ΖΦ ὅμοιά τε καὶ ὁμοίως κείμενα [εὐθύγραμμα] τὰ ΔΕΖ, ΡΦΖ. ἔστιν ἄρα ὡς τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΛΞΓ τρίγωνον, οὕτως τὸ ΔΕΖ τρίγωνον πρὸς τὸ ΡΦΖ τρίγωνον· ἐναλλὰξ ἄρα ἐστὶν ὡς τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΔΕΖ [τρίγωνον], οὕτως τὸ ΛΞΓ [τρίγωνον] πρὸς τὸ ΡΦΖ τρίγωνον.
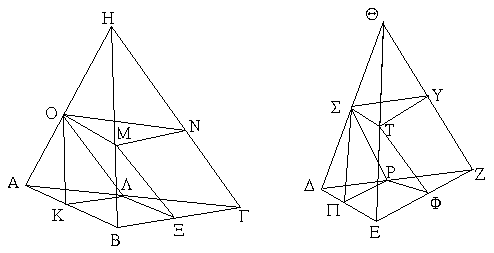
ἀλλ' ὡς τὸ ΛΞΓ τρίγωνον πρὸς τὸ ΡΦΖ τρίγωνον, οὕτως τὸ πρίσμα, οὗ βάσις μὲν [ἐστι] τὸ ΛΞΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΟΜΝ, πρὸς τὸ πρίσμα, οὗ βάσις μὲν τὸ ΡΦΖ τρίγωνον, ἀπεναντίον δὲ τὸ ΣΤΥ· καὶ ὡς ἄρα τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΔΕΖ τρίγωνον, οὕτως τὸ πρίσμα, οὗ βάσις μὲν τὸ ΛΞΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΟΜΝ, πρὸς τὸ πρίσμα, οὗ βάσις μὲν τὸ ΡΦΖ τρίγωνον, ἀπεναντίον δὲ τὸ ΣΤΥ. ὡς δὲ τὰ εἰρημένα πρίσματα πρὸς ἄλληλα, οὕτως τὸ πρίσμα, οὗ βάσις μὲν τὸ ΚΒΞΛ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΟΜ εὐθεῖα, πρὸς τὸ πρίσμα, οὗ βάσις μὲν τὸ ΠΕΦΡ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΣΤ εὐθεῖα. καὶ τὰ δύο ἄρα πρίσματα, οὗ τε βάσις μὲν τὸ ΚΒΞΛ παραλληλόγραμμον, ἀπεναντίον δὲ ἡ ΟΜ, καὶ οὗ βάσις μὲν τὸ ΛΞΓ, ἀπεναντίον δὲ τὸ ΟΜΝ, πρὸς τὰ πρίσματα, οὗ τε βάσις μὲν τὸ ΠΕΦΡ, ἀπεναντίον δὲ ἡ ΣΤ εὐθεῖα, καὶ οὗ βάσις μὲν τὸ ΡΦΖ τρίγωνον, ἀπεναντίον δὲ τὸ ΣΤΥ. καὶ ὡς ἄρα ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὰ εἰρημένα δύο πρίσματα πρὸς τὰ εἰρημένα δύο πρίσματα.
Καὶ ὁμοίως, ἐὰν διαιρεθῶσιν αἱ ΟΜΝΗ, ΣΤΥΘ πυραμίδες εἴς τε δύο πρίσματα καὶ δύο πυραμίδας, ἔσται ὡς ἡ ΟΜΝ βάσις πρὸς τὴν ΣΤΥ βάσιν, οὕτως τὰ ἐν τῇ ΟΜ ΝΗ πυραμίδι δύο πρίσματα πρὸς τὰ ἐν τῇ ΣΤΥΘ πυραμίδι δύο πρίσματα. ἀλλ' ὡς ἡ ΟΜΝ βάσις πρὸς τὴν ΣΤΥ βάσιν, οὕτως ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν· ἴσον γὰρ ἑκάτερον τῶν ΟΜΝ, ΣΤΥ τριγώνων ἑκατέρῳ τῶν ΛΞΓ, ΡΦΖ. καὶ ὡς ἄρα ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὰ τέσσαρα πρίσματα πρὸς τὰ τέσσαρα πρίσματα. ὁμοίως δὲ κἂν τὰς ὑπολειπομένας πυραμίδας διέλωμεν εἴς τε δύο πυραμίδας καὶ εἰς δύο πρίσματα, ἔσται ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὰ ἐν τῇ ΑΒ ΓΗ πυραμίδι πρίσματα πάντα πρὸς τὰ ἐν τῇ ΔΕΖΘ πυραμίδι πρίσματα πάντα ἰσοπληθῆ· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ὅτι δέ ἐστιν ὡς τὸ ΛΞΓ τρίγωνον πρὸς τὸ ΡΦΖ τρίγωνον, οὕτως τὸ πρίσμα, οὗ βάσις τὸ ΛΞΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΟΜΝ, πρὸς τὸ πρίσμα, οὗ βάσις μὲν τὸ ΡΦΖ [τρίγωνον], ἀπεναντίον δὲ τὸ ΣΤΥ, οὕτω δεικτέον.
Ἐπὶ γὰρ τῆς αὐτῆς καταγραφῆς νενοήσθωσαν ἀπὸ τῶν Η, Θ κάθετοι ἐπὶ τὰ ΑΒΓ, ΔΕΖ ἐπίπεδα, ἴσαι δηλαδὴ τυγχάνουσαι διὰ τὸ ἰσοϋψεῖς ὑποκεῖσθαι τὰς πυραμίδας. καὶ ἐπεὶ δύο εὐθεῖαι ἥ τε ΗΓ καὶ ἡ ἀπὸ τοῦ Η κάθετος ὑπὸ παραλλήλων ἐπιπέδων τῶν ΑΒΓ, ΟΜΝ τέμνονται, εἰς τοὺς αὐτοὺς λόγους τμηθήσονται. καὶ τέτμηται ἡ ΗΓ δίχα ὑπὸ τοῦ ΟΜΝ ἐπιπέδου κατὰ τὸ Ν· καὶ ἡ ἀπὸ τοῦ Η ἄρα κάθετος ἐπὶ τὸ ΑΒΓ ἐπίπεδον δίχα τμηθήσεται ὑπὸ τοῦ ΟΜΝ ἐπιπέδου. διὰ τὰ αὐτὰ δὴ καὶ ἡ ἀπὸ τοῦ Θ κάθετος ἐπὶ τὸ ΔΕΖ ἐπίπεδον δίχα τμηθήσεται ὑπὸ τοῦ ΣΤΥ ἐπιπέδου. καί εἰσιν ἴσαι αἱ ἀπὸ τῶν Η, Θ κάθετοι ἐπὶ τὰ ΑΒΓ, ΔΕΖ ἐπίπεδα· ἴσαι ἄρα καὶ αἱ ἀπὸ τῶν ΟΜΝ, ΣΤΥ τριγώνων ἐπὶ τὰ ΑΒΓ, ΔΕΖ κάθετοι. ἰσοϋψῆ ἄρα [ἐστὶ] τὰ πρίσματα, ὧν βάσεις μέν εἰσι τὰ ΛΞΓ, ΡΦΖ τρίγωνα, ἀπεναντίον δὲ τὰ ΟΜΝ, ΣΤΥ. ὥστε καὶ τὰ στερεὰ παραλληλεπίπεδα τὰ ἀπὸ τῶν εἰρημένων πρισμάτων ἀναγραφόμενα ἰσοϋψῆ καὶ πρὸς ἄλληλα [εἰσὶν] ὡς αἱ βάσεις· καὶ τὰ ἡμίση ἄρα ἐστὶν ὡς ἡ ΛΞΓ βάσις πρὸς τὴν ΡΦΖ βάσιν, οὕτως τὰ εἰρημένα πρίσματα πρὸς ἄλληλα· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον XII
Αἱ ὑπὸ τὸ αὐτὸ ὕψος οὖσαι πυραμίδες καὶ τριγώνους ἔχουσαι βάσεις πρὸς ἀλλήλας εἰσὶν ὡς αἱ βάσεις.
Ἔστωσαν ὑπὸ τὸ αὐτὸ ὕψος πυραμίδες, ὧν βάσεις μὲν τὰ ΑΒΓ, ΔΕΖ τρίγωνα, κορυφαὶ δὲ τὰ Η, Θ σημεῖα· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα.
Εἰ γὰρ μή ἐστιν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα, ἔσται ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς ἤτοι πρὸς ἔλασσόν τι τῆς ΔΕΖΘ πυραμίδος στερεὸν ἢ πρὸς μεῖζον. ἔστω πρότερον πρὸς ἔλασσον τὸ Χ, καὶ διῃρήσθω ἡ ΔΕΖΘ πυραμὶς εἴς τε δύο πυραμίδας ἴσας ἀλλήλαις καὶ ὁμοίας τῇ ὅλῃ καὶ εἰς δύο πρίσματα ἴσα· τὰ δὴ δύο πρίσματα μείζονά ἐστιν ἢ τὸ ἥμισυ τῆς ὅλης πυραμίδος. καὶ πάλιν αἱ ἐκ τῆς διαιρέσεως γινόμεναι πυραμίδες ὁμοίως διῃρήσθωσαν, καὶ τοῦτο ἀεὶ γινέσθω, ἕως οὗ λειφθῶσί τινες πυραμίδες ἀπὸ τῆς ΔΕΖΘ πυραμίδος, αἵ εἰσιν ἐλάττονες τῆς ὑπεροχῆς, ᾗ ὑπερέχει ἡ ΔΕ ΖΘ πυραμὶς τοῦ Χ στερεοῦ. λελείφθωσαν καὶ ἔστωσαν λόγου ἕνεκεν αἱ ΔΠΡΣ, ΣΤΥΘ· λοιπὰ ἄρα τὰ ἐν τῇ ΔΕ ΖΘ πυραμίδι πρίσματα μείζονά ἐστι τοῦ Χ στερεοῦ.
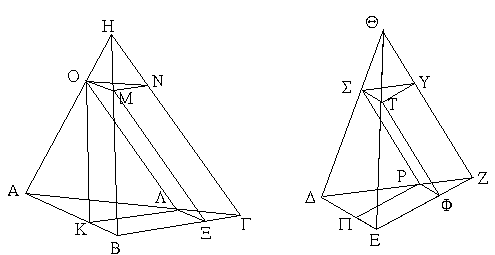
διῃρήσθω καὶ ἡ ΑΒΓΗ πυραμὶς ὁμοίως καὶ ἰσοπληθῶς τῇ ΔΕΖΘ πυραμίδι· ἔστιν ἄρα ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὰ ἐν τῇ ΑΒΓΗ πυραμίδι πρίσματα πρὸς τὰ ἐν τῇ ΔΕΖΘ πυραμίδι πρίσματα. ἀλλὰ καὶ ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὸ Χ στερεόν· καὶ ὡς ἄρα ἡ ΑΒΓΗ πυραμὶς πρὸς τὸ Χ στερεόν, οὕτως τὰ ἐν τῇ ΑΒΓΗ πυραμίδι πρίσματα πρὸς τὰ ἐν τῇ ΔΕΖΘ πυραμίδι πρίσματα· ἐναλλὰξ ἄρα ὡς ἡ ΑΒΓΗ πυραμὶς πρὸς τὰ ἐν αὐτῇ πρίσματα, οὕτως τὸ Χ στερεὸν πρὸς τὰ ἐν τῇ ΔΕΖΘ πυραμίδι πρίσματα. μείζων δὲ ἡ ΑΒΓΗ πυραμὶς τῶν ἐν αὐτῇ πρισμάτων· μεῖζον ἄρα καὶ τὸ Χ στερεὸν τῶν ἐν τῇ ΔΕΖΘ πυραμίδι πρισμάτων. ἀλλὰ καὶ ἔλαττον· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐστὶν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς ἔλασσόν τι τῆς ΔΕΖΘ πυραμίδος στερεόν. ὁμοίως δὴ δειχθήσεται, ὅτι οὐδὲ ὡς ἡ ΔΕΖ βάσις πρὸς τὴν ΑΒΓ βάσιν, οὕτως ἡ ΔΕΖΘ πυραμὶς πρὸς ἔλαττόν τι τῆς ΑΒΓΗ πυραμίδος στερεόν.
Λέγω δή, ὅτι οὐκ ἔστιν οὐδὲ ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς μεῖζόν τι τῆς ΔΕΖΘ πυραμίδος στερεόν.
Εἰ γὰρ δυνατόν, ἔστω πρὸς μεῖζον τὸ Χ· ἀνάπαλιν ἄρα ἐστὶν ὡς ἡ ΔΕΖ βάσις πρὸς τὴν ΑΒΓ βάσιν, οὕτως τὸ Χ στερεὸν πρὸς τὴν ΑΒΓΗ πυραμίδα. ὡς δὲ τὸ Χ στερεὸν πρὸς τὴν ΑΒΓΗ πυραμίδα, οὕτως ἡ ΔΕΖΘ πυραμὶς πρὸς ἔλασσόν τι τῆς ΑΒΓΗ πυραμίδος, ὡς ἔμπροσθεν ἐδείχθη· καὶ ὡς ἄρα ἡ ΔΕΖ βάσις πρὸς τὴν ΑΒΓ βάσιν, οὕτως ἡ ΔΕΖΘ πυραμὶς πρὸς ἔλασσόν τι τῆς ΑΒΓΗ πυραμίδος· ὅπερ ἄτοπον ἐδείχθη.
οὐκ ἄρα ἐστὶν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς μεῖζόν τι τῆς ΔΕΖΘ πυραμίδος στερεόν. ἐδείχθη δέ, ὅτι οὐδὲ πρὸς ἔλασσον. ἔστιν ἄρα ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον XII
Αἱ ὑπὸ τὸ αὐτὸ ὕψος οὖσαι πυραμίδες καὶ πολυγώνους ἔχουσαι βάσεις πρὸς ἀλλήλας εἰσὶν ὡς αἱ βάσεις.
Ἔστωσαν ὑπὸ τὸ αὐτὸ ὕψος πυραμίδες, ὧν [αἱ] βάσεις μὲν τὰ ΑΒΓΔΕ, ΖΗΘΚΛ πολύγωνα, κορυφαὶ δὲ τὰ Μ, Ν σημεῖα· λέγω, ὅτι ἐστὶν ὡς ἡ ΑΒΓΔΕ βάσις πρὸς τὴν ΖΗΘΚΛ βάσιν, οὕτως ἡ ΑΒΓΔΕΜ πυραμὶς πρὸς τὴν ΖΗΘΚΛΝ πυραμίδα.
Ἐπεζεύχθωσαν γὰρ αἱ ΑΓ, ΑΔ, ΖΘ, ΖΚ. ἐπεὶ οὖν δύο πυραμίδες εἰσὶν αἱ ΑΒΓΜ, ΑΓΔΜ τριγώνους ἔχουσαι βάσεις καὶ ὕψος ἴσον, πρὸς ἀλλήλας εἰσὶν ὡς αἱ βάσεις· ἔστιν ἄρα ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΑΓΔ βάσιν, οὕτως ἡ ΑΒΓΜ πυραμὶς πρὸς τὴν ΑΓΔΜ πυραμίδα. καὶ συνθέντι ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΑΓΔ βάσιν, οὕτως ἡ ΑΒΓΔΜ πυραμὶς πρὸς τὴν ΑΓΔΜ πυραμίδα. ἀλλὰ καὶ ὡς ἡ ΑΓΔ βάσις πρὸς τὴν ΑΔΕ βάσιν, οὕτως ἡ ΑΓΔΜ πυραμὶς πρὸς τὴν ΑΔΕΜ πυραμίδα.
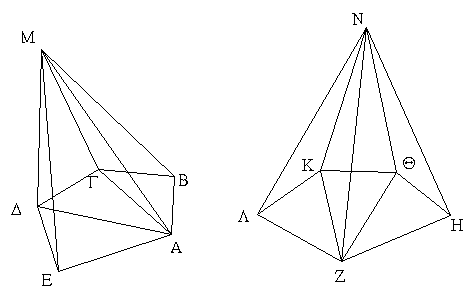
δι' ἴσου ἄρα ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΑΔΕ βάσιν, οὕτως ἡ ΑΒΓΔΜ πυραμὶς πρὸς τὴν ΑΔΕΜ πυραμίδα. καὶ συνθέντι πάλιν, ὡς ἡ ΑΒΓΔΕ βάσις πρὸς τὴν ΑΔΕ βάσιν, οὕτως ἡ ΑΒΓΔΕΜ πυραμὶς πρὸς τὴν ΑΔΕΜ πυραμίδα. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ὡς ἡ ΖΗΘΚΛ βάσις πρὸς τὴν ΖΗΘ βάσιν, οὕτως καὶ ἡ ΖΗΘΚΛΝ πυραμὶς πρὸς τὴν ΖΗΘΝ πυραμίδα. καὶ ἐπεὶ δύο πυραμίδες εἰσὶν αἱ ΑΔ ΕΜ, ΖΗΘΝ τριγώνους ἔχουσαι βάσεις καὶ ὕψος ἴσον, ἔστιν ἄρα ὡς ἡ ΑΔΕ βάσις πρὸς τὴν ΖΗΘ βάσιν, οὕτως ἡ ΑΔΕΜ πυραμὶς πρὸς τὴν ΖΗΘΝ πυραμίδα. ἀλλ' ὡς ἡ ΑΔΕ βάσις πρὸς τὴν ΑΒΓΔΕ βάσιν, οὕτως ἦν ἡ ΑΔ ΕΜ πυραμὶς πρὸς τὴν ΑΒΓΔΕΜ πυραμίδα. καὶ δι' ἴσου ἄρα ὡς ἡ ΑΒΓΔΕ βάσις πρὸς τὴν ΖΗΘ βάσιν, οὕτως ἡ ΑΒΓΔΕΜ πυραμὶς πρὸς τὴν ΖΗΘΝ πυραμίδα. ἀλλὰ μὴν καὶ ὡς ἡ ΖΗΘ βάσις πρὸς τὴν ΖΗΘΚΛ βάσιν, οὕτως ἦν καὶ ἡ ΖΗΘΝ πυραμὶς πρὸς τὴν ΖΗΘΚΛΝ πυραμίδα. καὶ δι' ἴσου ἄρα ὡς ἡ ΑΒΓΔΕ βάσις πρὸς τὴν ΖΗΘΚΛ βάσιν, οὕτως ἡ ΑΒΓΔΕΜ πυραμὶς πρὸς τὴν ΖΗΘΚΛΝ πυραμίδα· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον XII
Πᾶν πρίσμα τρίγωνον ἔχον βάσιν διαιρεῖται εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους βάσεις ἐχούσας.
Ἔστω πρίσμα, οὗ βάσις μὲν τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ· λέγω, ὅτι τὸ ΑΒΓΔΕΖ πρίσμα διαιρεῖται εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους ἐχούσας βάσεις.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΔ, ΕΓ, ΓΔ. ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΑΒΕΔ, διάμετρος δὲ αὐτοῦ ἐστιν ἡ ΒΔ, ἴσον ἄρα ἐστὶ τὸ ΑΒΔ τρίγωνον τῷ ΕΒΔ τριγώνῳ· καὶ ἡ πυραμὶς ἄρα, ἧς βάσις μὲν τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΔΕΒ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον. ἀλλὰ ἡ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΔΕΒ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἡ αὐτή ἐστι πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον· ὑπὸ γὰρ τῶν αὐτῶν ἐπιπέδων περιέχεται. καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον.
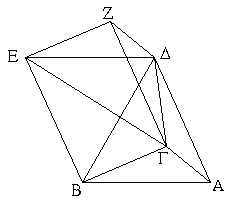
πάλιν, ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΖΓΒΕ, διάμετρος δέ ἐστιν αὐτοῦ ἡ ΓΕ, ἴσον ἐστὶ τὸ ΓΕΖ τρίγωνον τῷ ΓΒΕ τριγώνῳ. καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΒΓΕ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΓΖ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον. ἡ δὲ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΒΓΕ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐδείχθη πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον· καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΓΕΖ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μὲν [ἐστι] τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον· διῄρηται ἄρα τὸ ΑΒΓΔΕΖ πρίσμα εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους ἐχούσας βάσεις.
Καὶ ἐπεὶ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἡ αὐτή ἐστι πυραμίδι, ἧς βάσις τὸ ΓΑΒ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον· ὑπὸ γὰρ τῶν αὐτῶν ἐπιπέδων περιέχονται· ἡ δὲ πυραμίς, ἧς βάσις τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, τρίτον ἐδείχθη τοῦ πρίσματος, οὗ βάσις τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ, καὶ ἡ πυραμὶς ἄρα, ἧς βάσις τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, τρίτον ἐστὶ τοῦ πρίσματος τοῦ ἔχοντος βάσιν τὴν αὐτὴν τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι πᾶσα πυραμὶς τρίτον μέρος ἐστὶ τοῦ πρίσματος τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῇ καὶ ὕψος ἴσον [ἐπειδήπερ κἂν ἕτερόν τι σχῆμα εὐθύγραμμον ἔχῃ ἡ βάσις τοῦ πρίσματος, τοιοῦτο καὶ τὸ ἀπεναντίον, καὶ διαιρεῖται εἰς πρίσματα τρίγωνα ἔχοντα τὰς βάσεις καὶ τὰ ἀπεναντίον, καὶ ὡς ἡ ὅλη βάσις πρὸς ἕκαστον]· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον XII
Αἱ ὅμοιαι πυραμίδες καὶ τριγώνους ἔχουσαι βάσεις ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν.
Ἔστωσαν ὅμοιαι καὶ ὁμοίως κείμεναι πυραμίδες, ὧν βάσεις μέν εἰσι τὰ ΑΒΓ, ΔΕΖ τρίγωνα, κορυφαὶ δὲ τὰ Η, Θ σημεῖα· λέγω, ὅτι ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Συμπεπληρώσθω γὰρ τὰ ΒΗΜΛ, ΕΘΠΟ στερεὰ παραλληλεπίπεδα. καὶ ἐπεὶ ὁμοία ἐστὶν ἡ ΑΒΓΗ πυραμὶς τῇ ΔΕΖΘ πυραμίδι, ἴση ἄρα ἐστὶν ἡ μὲν ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ γωνίᾳ, ἡ δὲ ὑπὸ ΗΒΓ τῇ ὑπὸ ΘΕΖ, ἡ δὲ ὑπὸ ΑΒΗ τῇ ὑπὸ ΔΕΘ, καί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΔΕ, οὕτως ἡ ΒΓ πρὸς τὴν ΕΖ, καὶ ἡ ΒΗ πρὸς τὴν ΕΘ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΔΕ, οὕτως ἡ ΒΓ πρὸς τὴν ΕΖ, καὶ περὶ ἴσας γωνίας αἱ πλευραὶ ἀνάλογόν εἰσιν, ὅμοιον ἄρα ἐστὶ τὸ ΒΜ παραλληλόγραμμον τῷ ΕΠ παραλληλογράμμῳ.
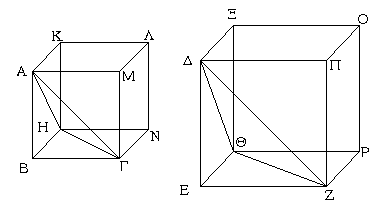
διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΒΝ τῷ ΕΡ ὅμοιόν ἐστι, τὸ δὲ ΒΚ τῷ ΕΞ· τὰ τρία ἄρα τὰ ΜΒ, ΒΚ, ΒΝ τρισὶ τοῖς ΕΠ, ΕΞ, ΕΡ ὅμοιά ἐστιν. ἀλλὰ τὰ μὲν τρία τὰ ΜΒ, ΒΚ, ΒΝ τρισὶ τοῖς ἀπεναντίον ἴσα τε καὶ ὅμοιά ἐστιν, τὰ δὲ τρία τὰ ΕΠ, ΕΞ, ΕΡ τρισὶ τοῖς ἀπεναντίον ἴσα τε καὶ ὅμοιά ἐστιν. τὰ ΒΗΜΛ, ΕΘΠΟ ἄρα στερεὰ ὑπὸ ὁμοίων ἐπιπέδων ἴσων τὸ πλῆθος περιέχεται. ὅμοιον ἄρα ἐστὶ τὸ ΒΗΜΛ στερεὸν τῷ ΕΘΠΟ στερεῷ. τὰ δὲ ὅμοια στερεὰ παραλληλεπίπεδα ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν. τὸ ΒΗΜΛ ἄρα στερεὸν πρὸς τὸ ΕΘΠΟ στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ ἡ ΒΓ πρὸς τὴν ὁμόλογον πλευρὰν τὴν ΕΖ. ὡς δὲ τὸ ΒΗΜΛ στερεὸν πρὸς τὸ ΕΘΠΟ στερεόν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα, ἐπειδήπερ ἡ πυραμὶς ἕκτον μέρος ἐστὶ τοῦ στερεοῦ διὰ τὸ καὶ τὸ πρίσμα ἥμισυ ὂν τοῦ στερεοῦ παραλληλεπιπέδου τριπλάσιον εἶναι τῆς πυραμίδος. καὶ ἡ ΑΒΓΗ ἄρα πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ· ὅπερ ἔδει δεῖξαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι καὶ αἱ πολυγώνους ἔχουσαι βάσεις ὅμοιαι πυραμίδες πρὸς ἀλλήλας ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν. διαιρεθεισῶν γὰρ αὐτῶν εἰς τὰς ἐν αὐταῖς πυραμίδας τριγώνους βάσεις ἐχούσας τῷ καὶ τὰ ὅμοια πολύγωνα τῶν βάσεων εἰς ὅμοια τρίγωνα διαιρεῖσθαι καὶ ἴσα τῷ πλήθει καὶ ὁμόλογα τοῖς ὅλοις ἔσται ὡς [ἡ] ἐν τῇ ἑτέρᾳ μία πυραμὶς τρίγωνον ἔχουσα βάσιν πρὸς τὴν ἐν τῇ ἑτέρᾳ μίαν πυραμίδα τρίγωνον ἔχουσαν βάσιν, οὕτως καὶ ἅπασαι αἱ ἐν τῇ ἑτέρᾳ πυραμίδι πυραμίδες τριγώνους ἔχουσαι βάσεις πρὸς τὰς ἐν τῇ ἑτέρᾳ πυραμίδι πυραμίδας τριγώνους βάσεις ἐχούσας, τουτέστιν αὐτὴ ἡ πολύγωνον βάσιν ἔχουσα πυραμὶς πρὸς τὴν πολύγωνον βάσιν ἔχουσαν πυραμίδα. ἡ δὲ τρίγωνον βάσιν ἔχουσα πυραμὶς πρὸς τὴν τρίγωνον βάσιν ἔχουσαν ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· καὶ ἡ πολύγωνον ἄρα βάσιν ἔχουσα πρὸς τὴν ὁμοίαν βάσιν ἔχουσαν τριπλασίονα λόγον ἔχει ἤπερ ἡ πλευρὰ πρὸς τὴν πλευράν.
Πρότασις θ΄ 9 Βιβλίον XII
Τῶν ἴσων πυραμίδων καὶ τριγώνους βάσεις ἐχουσῶν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· καὶ ὧν πυραμίδων τριγώνους βάσεις ἐχουσῶν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσαι εἰσὶν ἐκεῖναι.
Ἔστωσαν γὰρ ἴσαι πυραμίδες τριγώνους βάσεις ἔχουσαι τὰς ΑΒΓ, ΔΕΖ, κορυφὰς δὲ τὰ Η, Θ σημεῖα· λέγω, ὅτι τῶν ΑΒΓΗ, ΔΕΖΘ πυραμίδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, καί ἐστιν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὸ τῆς ΔΕΖΘ πυραμίδος ὕψος πρὸς τὸ τῆς ΑΒΓΗ πυραμίδος ὕψος.
Συμπεπληρώσθω γὰρ τὰ ΒΗΜΛ, ΕΘΠΟ στερεὰ παραλληλεπίπεδα. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒΓΗ πυραμὶς τῇ ΔΕΖΘ πυραμίδι, καί ἐστι τῆς μὲν ΑΒΓΗ πυραμίδος ἑξαπλάσιον τὸ ΒΗ ΜΛ στερεόν, τῆς δὲ ΔΕΖΘ πυραμίδος ἑξαπλάσιον τὸ ΕΘΠΟ στερεόν, ἴσον ἄρα ἐστὶ τὸ ΒΗΜΛ στερεὸν τῷ ΕΘΠΟ στερεῷ. τῶν δὲ ἴσων στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· ἔστιν ἄρα ὡς ἡ ΒΜ βάσις πρὸς τὴν ΕΠ βάσιν, οὕτως τὸ τοῦ ΕΘΠΟ στερεοῦ ὕψος πρὸς τὸ τοῦ ΒΗΜΛ στερεοῦ ὕψος. ἀλλ' ὡς ἡ ΒΜ βάσις πρὸς τὴν ΕΠ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΔΕΖ τρίγωνον. καὶ ὡς ἄρα τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΔΕΖ τρίγωνον, οὕτως τὸ τοῦ ΕΘΠΟ στερεοῦ ὕψος πρὸς τὸ τοῦ ΒΗΜΛ στερεοῦ ὕψος. ἀλλὰ τὸ μὲν τοῦ ΕΘΠΟ στερεοῦ ὕψος τὸ αὐτό ἐστι τῷ τῆς ΔΕΖΘ πυραμίδος ὕψει, τὸ δὲ τοῦ ΒΗΜΛ στερεοῦ ὕψος τὸ αὐτό ἐστι τῷ τῆς ΑΒΓΗ πυραμίδος ὕψει· ἔστιν ἄρα ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὸ τῆς ΔΕΖΘ πυραμίδος ὕψος πρὸς τὸ τῆς ΑΒΓΗ πυραμίδος ὕψος. τῶν ΑΒΓΗ, ΔΕΖΘ ἄρα πυραμίδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν.
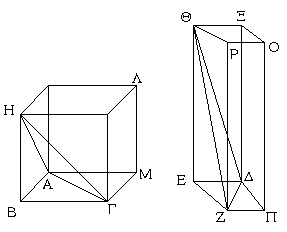
Ἀλλὰ δὴ τῶν ΑΒΓΗ, ΔΕΖΘ πυραμίδων ἀντιπεπονθέτωσαν αἱ βάσεις τοῖς ὕψεσιν, καὶ ἔστω ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὸ τῆς ΔΕΖΘ πυραμίδος ὕψος πρὸς τὸ τῆς ΑΒΓΗ πυραμίδος ὕψος· λέγω, ὅτι ἴση ἐστὶν ἡ ΑΒΓΗ πυραμὶς τῇ ΔΕΖΘ πυραμίδι.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὸ τῆς ΔΕΖΘ πυραμίδος ὕψος πρὸς τὸ τῆς ΑΒΓΗ πυραμίδος ὕψος, ἀλλ' ὡς ἡ ΑΒΓ βάσις πρὸς τὴν ΔΕΖ βάσιν, οὕτως τὸ ΒΜ παραλληλόγραμμον πρὸς τὸ ΕΠ παραλληλόγραμμον, καὶ ὡς ἄρα τὸ ΒΜ παραλληλόγραμμον πρὸς τὸ ΕΠ παραλληλόγραμμον, οὕτως τὸ τῆς ΔΕΖΘ πυραμίδος ὕψος πρὸς τὸ τῆς ΑΒΓΗ πυραμίδος ὕψος. ἀλλὰ τὸ [μὲν] τῆς ΔΕΖΘ πυραμίδος ὕψος τὸ αὐτό ἐστι τῷ τοῦ ΕΘΠΟ παραλληλεπιπέδου ὕψει, τὸ δὲ τῆς ΑΒΓΗ πυραμίδος ὕψος τὸ αὐτό ἐστι τῷ τοῦ ΒΗΜΛ παραλληλεπιπέδου ὕψει· ἔστιν ἄρα ὡς ἡ ΒΜ βάσις πρὸς τὴν ΕΠ βάσιν, οὕτως τὸ τοῦ ΕΘΠΟ παραλληλεπιπέδου ὕψος πρὸς τὸ τοῦ ΒΗΜΛ παραλληλεπιπέδου ὕψος. ὧν δὲ στερεῶν παραλληλεπιπέδων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσα ἐστὶν ἐκεῖνα· ἴσον ἄρα ἐστὶ τὸ ΒΗΜΛ στερεὸν παραλληλεπίπεδον τῷ ΕΘ ΠΟ στερεῷ παραλληλεπιπέδῳ. καί ἐστι τοῦ μὲν ΒΗΜΛ ἕκτον μέρος ἡ ΑΒΓΗ πυραμίς, τοῦ δὲ ΕΘΠΟ παραλληλεπιπέδου ἕκτον μέρος ἡ ΔΕΖΘ πυραμίς· ἴση ἄρα ἡ ΑΒΓΗ πυραμὶς τῇ ΔΕΖΘ πυραμίδι.
Τῶν ἄρα ἴσων πυραμίδων καὶ τριγώνους βάσεις ἐχουσῶν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· καὶ ὧν πυραμίδων τριγώνους βάσεις ἐχουσῶν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσαι εἰσὶν ἐκεῖναι· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον XII
Πᾶς κῶνος κυλίνδρου τρίτον μέρος ἐστὶ τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῷ καὶ ὕψος ἴσον.
Ἐχέτω γὰρ κῶνος κυλίνδρῳ βάσιν τε τὴν αὐτὴν τὸν ΑΒΓΔ κύκλον καὶ ὕψος ἴσον· λέγω, ὅτι ὁ κῶνος τοῦ κυλίνδρου τρίτον ἐστὶ μέρος, τουτέστιν ὅτι ὁ κύλινδρος τοῦ κώνου τριπλασίων ἐστίν.
Εἰ γὰρ μή ἐστιν ὁ κύλινδρος τοῦ κώνου τριπλασίων, ἔσται ὁ κύλινδρος τοῦ κώνου ἤτοι μείζων ἢ τριπλασίων ἢ ἐλάσσων ἢ τριπλασίων. ἔστω πρότερον μείζων ἢ τριπλασίων, καὶ ἐγγεγράφθω εἰς τὸν ΑΒΓΔ κύκλον τετράγωνον τὸ ΑΒΓΔ· τὸ δὴ ΑΒΓΔ τετράγωνον μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ ΑΒΓΔ κύκλου. καὶ ἀνεστάτω ἀπὸ τοῦ ΑΒΓΔ τετραγώνου πρίσμα ἰσουψὲς τῷ κυλίνδρῳ. τὸ δὴ ἀνιστάμενον πρίσμα μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ κυλίνδρου, ἐπειδήπερ κἂν περὶ τὸν ΑΒΓΔ κύκλον τετράγωνον περιγράψωμεν, τὸ ἐγγεγραμμένον εἰς τὸν ΑΒΓΔ κύκλον τετράγωνον ἥμισύ ἐστι τοῦ περιγεγραμμένου· καί ἐστι τὰ ἀπ' αὐτῶν ἀνιστάμενα στερεὰ παραλληλεπίπεδα πρίσματα ἰσοϋψῆ· τὰ δὲ ὑπὸ τὸ αὐτὸ ὕψος ὄντα στερεὰ παραλληλεπίπεδα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις· καὶ τὸ ἐπὶ τοῦ ΑΒΓΔ ἄρα τετραγώνου ἀνασταθὲν πρίσμα ἥμισύ ἐστι τοῦ ἀνασταθέντος πρίσματος ἀπὸ τοῦ περὶ τὸν ΑΒΓΔ κύκλον περιγραφέντος τετραγώνου· καί ἐστιν ὁ κύλινδρος ἐλάττων τοῦ πρίσματος τοῦ ἀνασταθέντος ἀπὸ τοῦ περὶ τὸν ΑΒΓΔ κύκλον περιγραφέντος τετραγώνου· τὸ ἄρα πρίσμα τὸ ἀνασταθὲν ἀπὸ τοῦ ΑΒΓΔ τετραγώνου ἰσοϋψὲς τῷ κυλίνδρῳ μεῖζόν ἐστι τοῦ ἡμίσεως τοῦ κυλίνδρου. τετμήσθωσαν αἱ ΑΒ, ΒΓ, ΓΔ, ΔΑ περιφέρειαι δίχα κατὰ τὰ Ε, Ζ, Η, Θ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΑΕ, ΕΒ, ΒΖ, ΖΓ, ΓΗ, ΗΔ, ΔΘ, ΘΑ· καὶ ἕκαστον ἄρα τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ ΑΒΓΔ κύκλου, ὡς ἔμπροσθεν ἐδείκνυμεν.
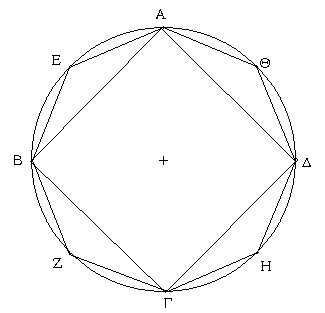
ἀνεστάτω ἐφ' ἑκάστου τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων πρίσματα ἰσοϋψῆ τῷ κυλίνδρῳ· καὶ ἕκαστον ἄρα τῶν ἀνασταθέντων πρισμάτων μεῖζόν ἐστιν ἢ τὸ ἥμισυ μέρος τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ κυλίνδρου, ἐπειδήπερ ἐὰν διὰ τῶν Ε, Ζ, Η, Θ σημείων παραλλήλους ταῖς ΑΒ, ΒΓ, ΓΔ, ΔΑ ἀγάγωμεν, καὶ συμπληρώσωμεν τὰ ἐπὶ τῶν ΑΒ, ΒΓ, ΓΔ, ΔΑ παραλληλόγραμμα, καὶ ἀπ' αὐτῶν ἀναστήσωμεν στερεὰ παραλληλεπίπεδα ἰσοϋψῆ τῷ κυλίνδρῳ, ἑκάστου τῶν ἀνασταθέντων ἡμίση ἐστὶ τὰ πρίσματα τὰ ἐπὶ τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων· καί ἐστι τὰ τοῦ κυλίνδρου τμήματα ἐλάττονα τῶν ἀνασταθέντων στερεῶν παραλληλεπιπέδων· ὥστε καὶ τὰ ἐπὶ τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων πρίσματα μείζονά ἐστιν ἢ τὸ ἥμισυ τῶν καθ᾿ ἑαυτὰ τοῦ κυλίνδρου τμημάτων. τέμνοντες δὴ τὰς ὑπολειπομένας περιφερείας δίχα καὶ ἐπιζευγνύντες εὐθείας καὶ ἀνιστάντες ἐφ' ἑκάστου τῶν τριγώνων πρίσματα ἰσοϋψῆ τῷ κυλίνδρῳ καὶ τοῦτο ἀεὶ ποιοῦντες καταλείψομέν τινα ἀποτμήματα τοῦ κυλίνδρου, ἃ ἔσται ἐλάττονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ κύλινδρος τοῦ τριπλασίου τοῦ κώνου. λελείφθω, καὶ ἔστω τὰ ΑΕ, ΕΒ, ΒΖ, ΖΓ, ΓΗ, ΗΔ, ΔΘ, ΘΑ· λοιπὸν ἄρα τὸ πρίσμα, οὗ βάσις μὲν τὸ ΑΕΒΖ ΓΗΔΘ πολύγωνον, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, μεῖζόν ἐστιν ἢ τριπλάσιον τοῦ κώνου. ἀλλὰ τὸ πρίσμα, οὗ βάσις μέν ἐστι τὸ ΑΕΒΖΓΗΔΘ πολύγωνον, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, τριπλάσιόν ἐστι τῆς πυραμίδος, ἧς βάσις μέν ἐστι τὸ ΑΕΒΖΓΗΔΘ πολύγωνον, κορυφὴ δὲ ἡ αὐτὴ τῷ κώνῳ· καὶ ἡ πυραμὶς ἄρα, ἧς βάσις μὲν [ἐστι] τὸ ΑΕΒΖΓΗΔΘ πολύγωνον, κορυφὴ δὲ ἡ αὐτὴ τῷ κώνῳ, μείζων ἐστὶ τοῦ κώνου τοῦ βάσιν ἔχοντος τὸν ΑΒ ΓΔ κύκλον. ἀλλὰ καὶ ἐλάττων· ἐμπεριέχεται γὰρ ὑπ' αὐτοῦ· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐστὶν ὁ κύλινδρος τοῦ κώνου μείζων ἢ τριπλάσιος.
Λέγω δή, ὅτι οὐδὲ ἐλάττων ἐστὶν ἢ τριπλάσιος ὁ κύλινδρος τοῦ κώνου.
Εἰ γὰρ δυνατόν, ἔστω ἐλάττων ἢ τριπλάσιος ὁ κύλινδρος τοῦ κώνου· ἀνάπαλιν ἄρα ὁ κῶνος τοῦ κυλίνδρου μείζων ἐστὶν ἢ τρίτον μέρος. ἐγγεγράφθω δὴ εἰς τὸν ΑΒΓΔ κύκλον τετράγωνον τὸ ΑΒΓΔ· τὸ ΑΒΓΔ ἄρα τετράγωνον μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ ΑΒΓΔ κύκλου. καὶ ἀνεστάτω ἀπὸ τοῦ ΑΒΓΔ τετραγώνου πυραμὶς τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ· ἡ ἄρα ἀνασταθεῖσα πυραμὶς μείζων ἐστὶν ἢ τὸ ἥμισυ μέρος τοῦ κώνου, ἐπειδήπερ, ὡς ἔμπροσθεν ἐδείκνυμεν, ὅτι ἐὰν περὶ τὸν κύκλον τετράγωνον περιγράψωμεν, ἔσται τὸ ΑΒΓΔ τετράγωνον ἥμισυ τοῦ περὶ τὸν κύκλον περιγεγραμμένου τετραγώνου· καὶ ἐὰν ἀπὸ τῶν τετραγώνων στερεὰ παραλληλεπίπεδα ἀναστήσωμεν ἰσοϋψῆ τῷ κώνῳ, ἃ καὶ καλεῖται πρίσματα, ἔσται τὸ ἀνασταθὲν ἀπὸ τοῦ ΑΒΓΔ τετραγώνου ἥμισυ τοῦ ἀνασταθέντος ἀπὸ τοῦ περὶ τὸν κύκλον περιγραφέντος τετραγώνου· πρὸς ἄλληλα γάρ εἰσιν ὡς αἱ βάσεις. ὥστε καὶ τὰ τρίτα· καὶ πυραμὶς ἄρα, ἧς βάσις τὸ ΑΒΓΔ τετράγωνον, ἥμισύ ἐστι τῆς πυραμίδος τῆς ἀνασταθείσης ἀπὸ τοῦ περὶ τὸν κύκλον περιγραφέντος τετραγώνου. καί ἐστι μείζων ἡ πυραμὶς ἡ ἀνασταθεῖσα ἀπὸ τοῦ περὶ τὸν κύκλον τετραγώνου τοῦ κώνου· ἐμπεριέχει γὰρ αὐτόν. ἡ ἄρα πυραμὶς, ἧς βάσις τὸ ΑΒΓΔ τετράγωνον, κορυφὴ δὲ ἡ αὐτὴ τῷ κώνῳ, μείζων ἐστὶν ἢ τὸ ἥμισυ τοῦ κώνου. τετμήσθωσαν αἱ ΑΒ, ΒΓ, ΓΔ, ΔΑ περιφέρειαι δίχα κατὰ τὰ Ε, Ζ, Η, Θ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΑΕ, ΕΒ, ΒΖ, ΖΓ, ΓΗ, ΗΔ, ΔΘ, ΘΑ· καὶ ἕκαστον ἄρα τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων μεῖζόν ἐστιν ἢ τὸ ἥμισυ μέρος τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ ΑΒΓΔ κύκλου. καὶ ἀνεστάτωσαν ἐφ' ἑκάστου τῶν ΑΕΒ, ΒΖΓ, ΓΗΔ, ΔΘΑ τριγώνων πυραμίδες τὴν αὐτὴν κορυφὴν ἔχουσαι τῷ κώνῳ· καὶ ἑκάστη ἄρα τῶν ἀνασταθεισῶν πυραμίδων κατὰ τὸν αὐτὸν τρόπον μείζων ἐστὶν ἢ τὸ ἥμισυ μέρος τοῦ καθ᾿ ἑαυτὴν τμήματος τοῦ κώνου. τέμνοντες δὴ τὰς ὑπολειπομένας περιφερείας δίχα καὶ ἐπιζευγνύντες εὐθείας καὶ ἀνιστάντες ἐφ' ἑκάστου τῶν τριγώνων πυραμίδα τὴν αὐτὴν κορυφὴν ἔχουσαν τῷ κώνῳ καὶ τοῦτο ἀεὶ ποιοῦντες καταλείψομέν τινα ἀποτμήματα τοῦ κώνου, ἃ ἔσται ἐλάττονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ κῶνος τοῦ τρίτου μέρους τοῦ κυλίνδρου. λελείφθω, καὶ ἔστω τὰ ἐπὶ τῶν ΑΕ, ΕΒ, ΒΖ, ΖΓ, ΓΗ, ΗΔ, ΔΘ, ΘΑ· λοιπὴ ἄρα ἡ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΕΒΖΓΗΔΘ πολύγωνον, κορυφὴ δὲ ἡ αὐτὴ τῷ κώνῳ, μείζων ἐστὶν ἢ τρίτον μέρος τοῦ κυλίνδρου. ἀλλ' ἡ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΕΒΖΓ ΗΔΘ πολύγωνον, κορυφὴ δὲ ἡ αὐτὴ τῷ κώνῳ, τρίτον ἐστὶ μέρος τοῦ πρίσματος, οὗ βάσις μέν ἐστι τὸ ΑΕΒΖΓ ΗΔΘ πολύγωνον, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ· τὸ ἄρα πρίσμα, οὗ βάσις μέν ἐστι τὸ ΑΕΒΖΓΗΔΘ πολύγωνον, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, μεῖζόν ἐστι τοῦ κυλίνδρου, οὗ βάσις ἐστὶν ὁ ΑΒΓΔ κύκλος. ἀλλὰ καὶ ἔλαττον· ἐμπεριέχεται γὰρ ὑπ' αὐτοῦ· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ὁ κύλινδρος τοῦ κώνου ἐλάττων ἐστὶν ἢ τριπλάσιος. ἐδείχθη δέ, ὅτι οὐδὲ μείζων ἢ τριπλάσιος· τριπλάσιος ἄρα ὁ κύλινδρος τοῦ κώνου· ὥστε ὁ κῶνος τρίτον ἐστὶ μέρος τοῦ κυλίνδρου.
Πᾶς ἄρα κῶνος κυλίνδρου τρίτον μέρος ἐστὶ τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῷ καὶ ὕψος ἴσον· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον XII
Οἱ ὑπὸ τὸ αὐτὸ ὕψος ὄντες κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους εἰσὶν ὡς αἱ βάσεις.
Ἔστωσαν ὑπὸ τὸ αὐτὸ ὕψος κῶνοι καὶ κύλινδροι, ὧν βάσεις μὲν [εἰσιν] οἱ ΑΒΓΔ, ΕΖΗΘ κύκλοι, ἄξονες δὲ οἱ ΚΛ, ΜΝ, διάμετροι δὲ τῶν βάσεων αἱ ΑΓ, ΕΗ· λέγω, ὅτι ἐστὶν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς τὸν ΕΝ κῶνον.
Εἰ γὰρ μή, ἔσται ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος ἤτοι πρὸς ἔλασσόν τι τοῦ ΕΝ κώνου στερεὸν ἢ πρὸς μεῖζον. ἔστω πρότερον πρὸς ἔλασσον τὸ Ξ, καὶ ᾧ ἔλασσόν ἐστι τὸ Ξ στερεὸν τοῦ ΕΝ κώνου, ἐκείνῳ ἴσον ἔστω τὸ Ψ στερεόν· ὁ ΕΝ κῶνος ἄρα ἴσος ἐστὶ τοῖς Ξ, Ψ στερεοῖς. ἐγγεγράφθω εἰς τὸν ΕΖΗΘ κύκλον τετράγωνον τὸ ΕΖΗΘ· τὸ ἄρα τετράγωνον μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ κύκλου. ἀνεστάτω ἀπὸ τοῦ ΕΖ ΗΘ τετραγώνου πυραμὶς ἰσοϋψὴς τῷ κώνῳ· ἡ ἄρα ἀνασταθεῖσα πυραμὶς μείζων ἐστὶν ἢ τὸ ἥμισυ τοῦ κώνου, ἐπειδήπερ ἐὰν περιγράψωμεν περὶ τὸν κύκλον τετράγωνον, καὶ ἀπ' αὐτοῦ ἀναστήσωμεν πυραμίδα ἰσοϋψῆ τῷ κώνῳ, ἡ ἐγγραφεῖσα πυραμὶς ἥμισύ ἐστι τῆς περιγραφείσης· πρὸς ἀλλήλας γάρ εἰσιν ὡς αἱ βάσεις· ἐλάττων δὲ ὁ κῶνος τῆς περιγραφείσης πυραμίδος. τετμήσθωσαν αἱ ΕΖ, ΖΗ, ΗΘ, ΘΕ περιφέρειαι δίχα κατὰ τὰ Ο, Π, Ρ, Σ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΘΟ, ΟΕ, ΕΠ, ΠΖ, ΖΡ, ΡΗ, ΗΣ, ΣΘ.
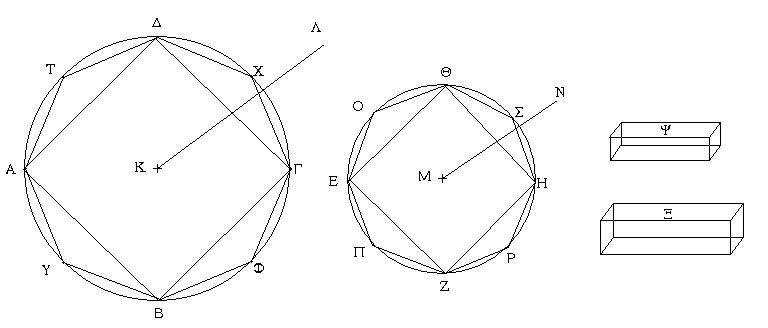
ἕκαστον ἄρα τῶν ΘΟΕ, ΕΠΖ, ΖΡΗ, ΗΣΘ τριγώνων μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ κύκλου. ἀνεστάτω ἐφ' ἑκάστου τῶν ΘΟΕ, ΕΠΖ, ΖΡΗ, ΗΣΘ τριγώνων πυραμὶς ἰσοϋψὴς τῷ κώνῳ· καὶ ἑκάστη ἄρα τῶν ἀνασταθεισῶν πυραμίδων μείζων ἐστὶν ἢ τὸ ἥμισυ τοῦ καθ᾿ ἑαυτὴν τμήματος τοῦ κώνου. τέμνοντες δὴ τὰς ὑπολειπομένας περιφερείας δίχα καὶ ἐπιζευγνύντες εὐθείας καὶ ἀνιστάντες ἐπὶ ἑκάστου τῶν τριγώνων πυραμίδας ἰσοϋψεῖς τῷ κώνῳ καὶ ἀεὶ τοῦτο ποιοῦντες καταλείψομέν τινα ἀποτμήματα τοῦ κώνου, ἃ ἔσται ἐλάσσονα τοῦ Ψ στερεοῦ. λελείφθω, καὶ ἔστω τὰ ἐπὶ τῶν ΘΟΕ, ΕΠΖ, ΖΡΗ, ΗΣΘ· λοιπὴ ἄρα ἡ πυραμίς, ἧς βάσις τὸ ΘΟΕΠΖΡΗΣ πολύγωνον, ὕψος δὲ τὸ αὐτὸ τῷ κώνῳ, μείζων ἐστὶ τοῦ Ξ στερεοῦ. ἐγγεγράφθω καὶ εἰς τὸν ΑΒΓΔ κύκλον τῷ ΘΟΕΠΖΡΗΣ πολυγώνῳ ὅμοιόν τε καὶ ὁμοίως κείμενον πολύγωνον τὸ ΔΤΑΥΒ ΦΓΧ, καὶ ἀνεστάτω ἐπ᾿ αὐτοῦ πυραμὶς ἰσοϋψὴς τῷ ΑΛ κώνῳ. ἐπεὶ οὖν ἐστιν ὡς τὸ ἀπὸ τῆς ΑΓ πρὸς τὸ ἀπὸ τῆς ΕΗ, οὕτως τὸ ΔΤΑΥΒΦΓΧ πολύγωνον πρὸς τὸ ΘΟΕ ΠΖΡΗΣ πολύγωνον, ὡς δὲ τὸ ἀπὸ τῆς ΑΓ πρὸς τὸ ἀπὸ τῆς ΕΗ, οὕτως ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, καὶ ὡς ἄρα ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως τὸ ΔΤΑΥΒΦΓΧ πολύγωνον πρὸς τὸ ΘΟΕΠΖΡΗΣ πολύγωνον. ὡς δὲ ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς τὸ Ξ στερεόν, ὡς δὲ τὸ ΔΤΑΥΒΦΓΧ πολύγωνον πρὸς τὸ ΘΟΕΠΖ ΡΗΣ πολύγωνον, οὕτως ἡ πυραμίς, ἧς βάσις μὲν τὸ ΔΤΑΥΒΦΓΧ πολύγωνον, κορυφὴ δὲ τὸ Λ σημεῖον, πρὸς τὴν πυραμίδα, ἧς βάσις μὲν τὸ ΘΟΕΠΖΡΗΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον. καὶ ὡς ἄρα ὁ ΑΛ κῶνος πρὸς τὸ Ξ στερεόν, οὕτως ἡ πυραμίς, ἧς βάσις μὲν τὸ ΔΤΑΥΒΦΓΧ πολύγωνον, κορυφὴ δὲ τὸ Λ σημεῖον, πρὸς τὴν πυραμίδα, ἧς βάσις μὲν τὸ ΘΟΕΠΖΡΗΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον· ἐναλλὰξ ἄρα ἐστὶν ὡς ὁ ΑΛ κῶνος πρὸς τὴν ἐν αὐτῷ πυραμίδα, οὕτως τὸ Ξ στερεὸν πρὸς τὴν ἐν τῷ ΕΝ κώνῳ πυραμίδα. μείζων δὲ ὁ ΑΛ κῶνος τῆς ἐν αὐτῷ πυραμίδος· μεῖζον ἄρα καὶ τὸ Ξ στερεὸν τῆς ἐν τῷ ΕΝ κώνῳ πυραμίδος. ἀλλὰ καὶ ἔλασσον· ὅπερ ἄτοπον. οὐκ ἄρα ἐστὶν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς ἔλασσόν τι τοῦ ΕΝ κώνου στερεόν. ὁμοίως δὴ δείξομεν, ὅτι οὐδέ ἐστιν ὡς ὁ ΕΖΗΘ κύκλος πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΝ κῶνος πρὸς ἔλασσόν τι τοῦ ΑΛ κώνου στερεόν.
Λέγω δή, ὅτι οὐδέ ἐστιν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς μεῖζόν τι τοῦ ΕΝ κώνου στερεόν.
Εἰ γὰρ δυνατόν, ἔστω πρὸς μεῖζον τὸ Ξ· ἀνάπαλιν ἄρα ἐστὶν ὡς ὁ ΕΖΗΘ κύκλος πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως τὸ Ξ στερεὸν πρὸς τὸν ΑΛ κῶνον. ἀλλ' ὡς τὸ Ξ στερεὸν πρὸς τὸν ΑΛ κῶνον, οὕτως ὁ ΕΝ κῶνος πρὸς ἔλασσόν τι τοῦ ΑΛ κώνου στερεόν· καὶ ὡς ἄρα ὁ ΕΖΗΘ κύκλος πρὸς τὸν ΑΒΓΔ κύκλον, οὕτως ὁ ΕΝ κῶνος πρὸς ἔλασσόν τι τοῦ ΑΛ κώνου στερεόν· ὅπερ ἀδύνατον ἐδείχθη. οὐκ ἄρα ἐστὶν ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς μεῖζόν τι τοῦ ΕΝ κώνου στερεόν. ἐδείχθη δέ, ὅτι οὐδὲ πρὸς ἔλασσον· ἔστιν ἄρα ὡς ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως ὁ ΑΛ κῶνος πρὸς τὸν ΕΝ κῶνον.
Ἀλλ' ὡς ὁ κῶνος πρὸς τὸν κῶνον, ὁ κύλινδρος πρὸς τὸν κύλινδρον· τριπλασίων γὰρ ἑκάτερος ἑκατέρου. καὶ ὡς ἄρα ὁ ΑΒΓΔ κύκλος πρὸς τὸν ΕΖΗΘ κύκλον, οὕτως οἱ ἐπ᾿ αὐτῶν ἰσοϋψεῖς [τοῖς κώνοις] κύλινδροι.
Οἱ ἄρα ὑπὸ τὸ αὐτὸ ὕψος ὄντες κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους εἰσὶν ὡς αἱ βάσεις· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον XII
Οἱ ὅμοιοι κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ἐν ταῖς βάσεσι διαμέτρων.
Ἔστωσαν ὅμοιοι κῶνοι καὶ κύλινδροι, ὧν βάσεις μὲν οἱ ΑΒΓΔ, ΕΖΗΘ κύκλοι, διάμετροι δὲ τῶν βάσεων αἱ ΒΔ, ΖΘ, ἄξονες δὲ τῶν κώνων καὶ κυλίνδρων οἱ ΚΛ, ΜΝ· λέγω, ὅτι ὁ κῶνος, οὗ βάσις μὲν [ἐστιν] ὁ ΑΒΓΔ κύκλος, κορυφὴ δὲ τὸ Λ σημεῖον, πρὸς τὸν κῶνον, οὗ βάσις μὲν [ἐστιν] ὁ ΕΖΗΘ κύκλος, κορυφὴ δὲ τὸ Ν σημεῖον, τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ.
Εἰ γὰρ μὴ ἔχει ὁ ΑΒΓΔΛ κῶνος πρὸς τὸν ΕΖΗΘΝ κῶνον τριπλασίονα λόγον ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ, ἕξει ὁ ΑΒΓΔΛ κῶνος ἢ πρὸς ἔλασσόν τι τοῦ ΕΖΗΘΝ κώνου στερεὸν τριπλασίονα λόγον ἢ πρὸς μεῖζον. ἐχέτω πρότερον πρὸς ἔλασσον τὸ Ξ, καὶ ἐγγεγράφθω εἰς τὸν ΕΖΗΘ κύκλον τετράγωνον τὸ ΕΖΗΘ· τὸ ἄρα ΕΖΗΘ τετράγωνον μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ ΕΖΗΘ κύκλου. καὶ ἀνεστάτω ἐπὶ τοῦ ΕΖΗΘ τετραγώνου πυραμὶς τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ· ἡ ἄρα ἀνασταθεῖσα πυραμὶς μείζων ἐστὶν ἢ τὸ ἥμισυ μέρος τοῦ κώνου. τετμήσθωσαν δὴ αἱ ΕΖ, ΖΗ, ΗΘ, ΘΕ περιφέρειαι δίχα κατὰ τὰ Ο, Π, Ρ, Σ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΕΟ, ΟΖ, ΖΠ, ΠΗ, ΗΡ, ΡΘ, ΘΣ, ΣΕ. καὶ ἕκαστον ἄρα τῶν ΕΟΖ, ΖΠΗ, ΗΡΘ, ΘΣΕ τριγώνων μεῖζόν ἐστιν ἢ τὸ ἥμισυ μέρος τοῦ καθ᾿ ἑαυτὸ τμήματος τοῦ ΕΖΗΘ κύκλου. καὶ ἀνεστάτω ἐφ' ἑκάστου τῶν ΕΟΖ, ΖΠΗ, ΗΡΘ, ΘΣΕ τριγώνων πυραμὶς τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ· καὶ ἑκάστη ἄρα τῶν ἀνασταθεισῶν πυραμίδων μείζων ἐστὶν ἢ τὸ ἥμισυ μέρος τοῦ καθ᾿ ἑαυτὴν τμήματος τοῦ κώνου. τέμνοντες δὴ τὰς ὑπολειπομένας περιφερείας δίχα καὶ ἐπιζευγνύντες εὐθείας καὶ ἀνιστάντες ἐφ' ἑκάστου τῶν τριγώνων πυραμίδας τὴν αὐτὴν κορυφὴν ἐχούσας τῷ κώνῳ καὶ τοῦτο ἀεὶ ποιοῦντες καταλείψομέν τινα ἀποτμήματα τοῦ κώνου, ἃ ἔσται ἐλάσσονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ ΕΖΗΘΝ κῶνος τοῦ Ξ στερεοῦ.
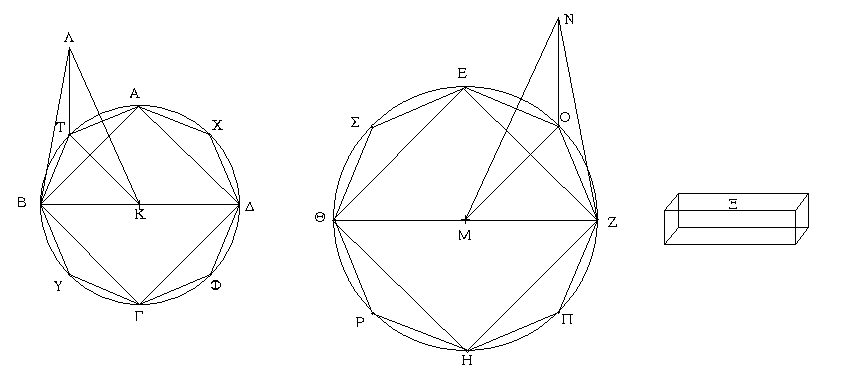
λελείφθω, καὶ ἔστω τὰ ἐπὶ τῶν ΕΟ, ΟΖ, ΖΠ, ΠΗ, ΗΡ, ΡΘ, ΘΣ, ΣΕ· λοιπὴ ἄρα ἡ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον, μείζων ἐστὶ τοῦ Ξ στερεοῦ. ἐγγεγράφθω καὶ εἰς τὸν ΑΒΓΔ κύκλον τῷ ΕΟΖΠΗΡΘΣ πολυγώνῳ ὅμοιόν τε καὶ ὁμοίως κείμενον πολύγωνον τὸ ΑΤΒΥΓΦΔΧ, καὶ ἀνεστάτω ἐπὶ τοῦ ΑΤΒΥΓΦΔΧ πολυγώνου πυραμὶς τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ, καὶ τῶν μὲν περιεχόντων τὴν πυραμίδα, ἧς βάσις μέν ἐστι τὸ ΑΤΒΥ ΓΦΔΧ πολύγωνον, κορυφὴ δὲ τὸ Λ σημεῖον, ἓν τρίγωνον ἔστω τὸ ΛΒΤ, τῶν δὲ περιεχόντων τὴν πυραμίδα, ἧς βάσις μέν ἐστι τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον, ἓν τρίγωνον ἔστω τὸ ΝΖΟ, καὶ ἐπεζεύχθωσαν αἱ ΚΤ, ΜΟ. καὶ ἐπεὶ ὅμοιός ἐστιν ὁ ΑΒΓΔΛ κῶνος τῷ ΕΖΗΘΝ κώνῳ, ἔστιν ἄρα ὡς ἡ ΒΔ πρὸς τὴν ΖΘ, οὕτως ὁ ΚΛ ἄξων πρὸς τὸν ΜΝ ἄξονα. ὡς δὲ ἡ ΒΔ πρὸς τὴν ΖΘ, οὕτως ἡ ΒΚ πρὸς τὴν ΖΜ· καὶ ὡς ἄρα ἡ ΒΚ πρὸς τὴν ΖΜ, οὕτως ἡ ΚΛ πρὸς τὴν ΜΝ. καὶ ἐναλλὰξ ὡς ἡ ΒΚ πρὸς τὴν ΚΛ, οὕτως ἡ ΖΜ πρὸς τὴν ΜΝ. καὶ περὶ ἴσας γωνίας τὰς ὑπὸ ΒΚΛ, ΖΜΝ αἱ πλευραὶ ἀνάλογόν εἰσιν· ὅμοιον ἄρα ἐστὶ τὸ ΒΚΛ τρίγωνον τῷ ΖΜΝ τριγώνῳ. πάλιν, ἐπεί ἐστιν ὡς ἡ ΒΚ πρὸς τὴν ΚΤ, οὕτως ἡ ΖΜ πρὸς τὴν ΜΟ, καὶ περὶ ἴσας γωνίας τὰς ὑπὸ ΒΚΤ, ΖΜΟ, ἐπειδήπερ, ὃ μέρος ἐστὶν ἡ ὑπὸ ΒΚΤ γωνία τῶν πρὸς τῷ Κ κέντρῳ τεσσάρων ὀρθῶν, τὸ αὐτὸ μέρος ἐστὶ καὶ ἡ ὑπὸ ΖΜΟ γωνία τῶν πρὸς τῷ Μ κέντρῳ τεσσάρων ὀρθῶν· ἐπεὶ οὖν περὶ ἴσας γωνίας αἱ πλευραὶ ἀνάλογόν εἰσιν, ὅμοιον ἄρα ἐστὶ τὸ ΒΚΤ τρίγωνον τῷ ΖΜΟ τριγώνῳ. πάλιν, ἐπεὶ ἐδείχθη ὡς ἡ ΒΚ πρὸς τὴν ΚΛ, οὕτως ἡ ΖΜ πρὸς τὴν ΜΝ, ἴση δὲ ἡ μὲν ΒΚ τῇ ΚΤ, ἡ δὲ ΖΜ τῇ ΟΜ, ἔστιν ἄρα ὡς ἡ ΤΚ πρὸς τὴν ΚΛ, οὕτως ἡ ΟΜ πρὸς τὴν ΜΝ. καὶ περὶ ἴσας γωνίας τὰς ὑπὸ ΤΚΛ, ΟΜΝ· ὀρθαὶ γάρ· αἱ πλευραὶ ἀνάλογόν εἰσιν· ὅμοιον ἄρα ἐστὶ τὸ ΛΚΤ τρίγωνον τῷ ΝΜΟ τριγώνῳ. καὶ ἐπεὶ διὰ τὴν ὁμοιότητα τῶν ΛΚΒ, ΝΜΖ τριγώνων ἐστὶν ὡς ἡ ΛΒ πρὸς τὴν ΒΚ, οὕτως ἡ ΝΖ πρὸς τὴν ΖΜ, διὰ δὲ τὴν ὁμοιότητα τῶν ΒΚΤ, ΖΜΟ τριγώνων ἐστὶν ὡς ἡ ΚΒ πρὸς τὴν ΒΤ, οὕτως ἡ ΜΖ πρὸς τὴν ΖΟ, δι' ἴσου ἄρα ὡς ἡ ΛΒ πρὸς τὴν ΒΤ, οὕτως ἡ ΝΖ πρὸς τὴν ΖΟ. πάλιν, ἐπεὶ διὰ τὴν ὁμοιότητα τῶν ΛΤΚ, ΝΟΜ τριγώνων ἐστὶν ὡς ἡ ΛΤ πρὸς τὴν ΤΚ, οὕτως ἡ ΝΟ πρὸς τὴν ΟΜ, διὰ δὲ τὴν ὁμοιότητα τῶν ΤΚΒ, ΟΜΖ τριγώνων ἐστὶν ὡς ἡ ΚΤ πρὸς τὴν ΤΒ, οὕτως ἡ ΜΟ πρὸς τὴν ΟΖ, δι' ἴσου ἄρα ὡς ἡ ΛΤ πρὸς τὴν ΤΒ, οὕτως ἡ ΝΟ πρὸς τὴν ΟΖ. ἐδείχθη δὲ καὶ ὡς ἡ ΤΒ πρὸς τὴν ΒΛ, οὕτως ἡ ΟΖ πρὸς τὴν ΖΝ. δι' ἴσου ἄρα ὡς ἡ ΤΛ πρὸς τὴν ΛΒ, οὕτως ἡ ΟΝ πρὸς τὴν ΝΖ. τῶν ΛΤΒ, ΝΟΖ ἄρα τριγώνων ἀνάλογόν εἰσιν αἱ πλευραί· ἰσογώνια ἄρα ἐστὶ τὰ ΛΤΒ, ΝΟΖ τρίγωνα· ὥστε καὶ ὅμοια. καὶ πυραμὶς ἄρα, ἧς βάσις μὲν τὸ ΒΚΤ τρίγωνον, κορυφὴ δὲ τὸ Λ σημεῖον, ὁμοία ἐστὶ πυραμίδι, ἧς βάσις μὲν τὸ ΖΜΟ τρίγωνον, κορυφὴ δὲ τὸ Ν σημεῖον· ὑπὸ γὰρ ὁμοίων ἐπιπέδων περιέχονται ἴσων τὸ πλῆθος. αἱ δὲ ὅμοιαι πυραμίδες καὶ τριγώνους ἔχουσαι βάσεις ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν. ἡ ἄρα ΒΚΤΛ πυραμὶς πρὸς τὴν ΖΜΟΝ πυραμίδα τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΚ πρὸς τὴν ΖΜ. ὁμοίως δὴ ἐπιζευγνύντες ἀπὸ τῶν Α, Χ, Δ, Φ, Γ, Υ ἐπὶ τὸ Κ εὐθείας καὶ ἀπὸ τῶν Ε, Σ, Θ, Ρ, Η, Π ἐπὶ τὸ Μ καὶ ἀνιστάντες ἐφ' ἑκάστου τῶν τριγώνων πυραμίδας τὴν αὐτὴν κορυφὴν ἐχούσας τοῖς κώνοις δείξομεν, ὅτι καὶ ἑκάστη τῶν ὁμοταγῶν πυραμίδων πρὸς ἑκάστην ὁμοταγῆ πυραμίδα τριπλασίονα λόγον ἕξει ἤπερ ἡ ΒΚ ὁμόλογος πλευρὰ πρὸς τὴν ΖΜ ὁμόλογον πλευράν, τουτέστιν ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ. καὶ ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ἔστιν ἄρα καὶ ὡς ἡ ΒΚΤΛ πυραμὶς πρὸς τὴν ΖΜΟΝ πυραμίδα, οὕτως ἡ ὅλη πυραμίς, ἧς βάσις τὸ ΑΤΒΥΓΦΔΧ πολύγωνον, κορυφὴ δὲ τὸ Λ σημεῖον, πρὸς τὴν ὅλην πυραμίδα, ἧς βάσις μὲν τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον· ὥστε καὶ πυραμίς, ἧς βάσις μὲν τὸ ΑΤΒΥΓΦΔΧ, κορυφὴ δὲ τὸ Λ, πρὸς τὴν πυραμίδα, ἧς βάσις [μὲν] τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν σημεῖον, τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ. ὑπόκειται δὲ καὶ ὁ κῶνος, οὗ βάσις [μὲν] ὁ ΑΒΓΔ κύκλος, κορυφὴ δὲ τὸ Λ σημεῖον, πρὸς τὸ Ξ στερεὸν τριπλασίονα λόγον ἔχων ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ· ἔστιν ἄρα ὡς ὁ κῶνος, οὗ βάσις μέν ἐστιν ὁ ΑΒΓΔ κύκλος, κορυφὴ δὲ τὸ Λ, πρὸς τὸ Ξ στερεόν, οὕτως ἡ πυραμίς, ἧς βάσις μὲν τὸ ΑΤΒΥΓΦΔΧ [πολύγωνον], κορυφὴ δὲ τὸ Λ, πρὸς τὴν πυραμίδα, ἧς βάσις μέν ἐστι τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν· ἐναλλὰξ ἄρα, ὡς ὁ κῶνος, οὗ βάσις μὲν ὁ ΑΒΓΔ κύκλος, κορυφὴ δὲ τὸ Λ, πρὸς τὴν ἐν αὐτῷ πυραμίδα, ἧς βάσις μὲν τὸ ΑΤΒΥΓΦΔΧ πολύγωνον, κορυφὴ δὲ τὸ Λ, οὕτως τὸ Ξ [στερεὸν] πρὸς τὴν πυραμίδα, ἧς βάσις μέν ἐστι τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν. μείζων δὲ ὁ εἰρημένος κῶνος τῆς ἐν αὐτῷ πυραμίδος· ἐμπεριέχει γὰρ αὐτήν. μεῖζον ἄρα καὶ τὸ Ξ στερεὸν τῆς πυραμίδος, ἧς βάσις μέν ἐστι τὸ ΕΟΖΠΗΡΘΣ πολύγωνον, κορυφὴ δὲ τὸ Ν. ἀλλὰ καὶ ἔλαττον· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ὁ κῶνος, οὗ βάσις ὁ ΑΒΓΔ κύκλος, κορυφὴ δὲ τὸ Λ [σημεῖον], πρὸς ἔλαττόν τι τοῦ κώνου στερεόν, οὗ βάσις μὲν ὁ ΕΖΗΘ κύκλος, κορυφὴ δὲ τὸ Ν σημεῖον, τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ὁ ΕΖΗΘΝ κῶνος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔΛ κώνου στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΖΘ πρὸς τὴν ΒΔ.
Λέγω δή, ὅτι οὐδὲ ὁ ΑΒΓΔΛ κῶνος πρὸς μεῖζόν τι τοῦ ΕΖΗΘΝ κώνου στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ.
Εἰ γὰρ δυνατόν, ἐχέτω πρὸς μεῖζον τὸ Ξ. ἀνάπαλιν ἄρα τὸ Ξ στερεὸν πρὸς τὸν ΑΒΓΔΛ κῶνον τριπλασίονα λόγον ἔχει ἤπερ ἡ ΖΘ πρὸς τὴν ΒΔ. ὡς δὲ τὸ Ξ στερεὸν πρὸς τὸν ΑΒΓΔΛ κῶνον, οὕτως ὁ ΕΖΗΘΝ κῶνος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔΛ κώνου στερεόν. καὶ ὁ ΕΖΗΘΝ ἄρα κῶνος πρὸς ἔλαττόν τι τοῦ ΑΒΓΔΛ κώνου στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΖΘ πρὸς τὴν ΒΔ· ὅπερ ἀδύνατον ἐδείχθη. οὐκ ἄρα ὁ ΑΒΓΔΛ κῶνος πρὸς μεῖζόν τι τοῦ ΕΖΗΘΝ κώνου στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ. ἐδείχθη δέ, ὅτι οὐδὲ πρὸς ἔλαττον. ὁ ΑΒΓΔΛ ἄρα κῶνος πρὸς τὸν ΕΖΗΘΝ κῶνον τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ.
Ὡς δὲ ὁ κῶνος πρὸς τὸν κῶνον, ὁ κύλινδρος πρὸς τὸν κύλινδρον· τριπλάσιος γὰρ ὁ κύλινδρος τοῦ κώνου ὁ ἐπὶ τῆς αὐτῆς βάσεως τῷ κώνῳ καὶ ἰσοϋψὴς αὐτῷ. καὶ ὁ κύλινδρος ἄρα πρὸς τὸν κύλινδρον τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΔ πρὸς τὴν ΖΘ.
Οἱ ἄρα ὅμοιοι κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ἐν ταῖς βάσεσι διαμέτρων· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον XII
Ἐὰν κύλινδρος ἐπιπέδῳ τμηθῇ παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔσται ὡς ὁ κύλινδρος πρὸς τὸν κύλινδρον, οὕτως ὁ ἄξων πρὸς τὸν ἄξονα. Κύλινδρος γὰρ ὁ ΑΔ ἐπιπέδῳ τῷ ΗΘ τετμήσθω παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις τοῖς ΑΒ, ΓΔ, καὶ συμβαλλέτω τῷ ἄξονι τὸ ΗΘ ἐπίπεδον κατὰ τὸ Κ σημεῖον· λέγω, ὅτι ἐστὶν ὡς ὁ ΒΗ κύλινδρος πρὸς τὸν ΗΔ κύλινδρον, οὕτως ὁ ΕΚ ἄξων πρὸς τὸν ΚΖ ἄξονα.
Ἐκβεβλήσθω γὰρ ὁ ΕΖ ἄξων ἐφ' ἑκάτερα τὰ μέρη ἐπὶ τὰ Λ, Μ σημεῖα, καὶ ἐκκείσθωσαν τῷ ΕΚ ἄξονι ἴσοι ὁσοιδηποτοῦν οἱ ΕΝ, ΝΛ, τῷ δὲ ΖΚ ἴσοι ὁσοιδηποτοῦν οἱ ΖΞ, ΞΜ, καὶ νοείσθω ὁ ἐπὶ τοῦ ΛΜ ἄξονος κύλινδρος ὁ ΟΧ, οὗ βάσεις οἱ ΟΠ, ΦΧ κύκλοι. καὶ ἐκβεβλήσθω διὰ τῶν Ν, Ξ σημείων ἐπίπεδα παράλληλα τοῖς ΑΒ, ΓΔ καὶ ταῖς βάσεσι τοῦ ΟΧ κυλίνδρου καὶ ποιείτωσαν τοὺς ΡΣ, ΤΥ κύκλους περὶ τὰ Ν, Ξ κέντρα. καὶ ἐπεὶ οἱ ΛΝ, ΝΕ, ΕΚ ἄξονες ἴσοι εἰσὶν ἀλλήλοις, οἱ ἄρα ΠΡ, ΡΒ, ΒΗ κύλινδροι πρὸς ἀλλήλους εἰσὶν ὡς αἱ βάσεις. ἴσαι δέ εἰσιν αἱ βάσεις· ἴσοι ἄρα καὶ οἱ ΠΡ, ΡΒ, ΒΗ κύλινδροι ἀλλήλοις.
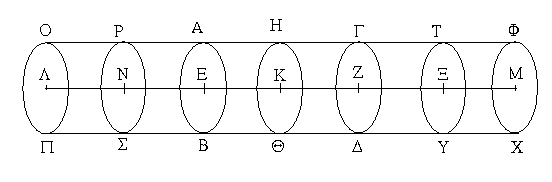
ἐπεὶ οὖν οἱ ΛΝ, ΝΕ, ΕΚ ἄξονες ἴσοι εἰσὶν ἀλλήλοις, εἰσὶ δὲ καὶ οἱ ΠΡ, ΡΒ, ΒΗ κύλινδροι ἴσοι ἀλλήλοις, καί ἐστιν ἴσον τὸ πλῆθος τῷ πλήθει, ὁσαπλασίων ἄρα ὁ ΚΛ ἄξων τοῦ ΕΚ ἄξονος, τοσαυταπλασίων ἔσται καὶ ὁ ΠΗ κύλινδρος τοῦ ΗΒ κυλίνδρου. διὰ τὰ αὐτὰ δὴ καὶ ὁσαπλασίων ἐστὶν ὁ ΜΚ ἄξων τοῦ ΚΖ ἄξονος, τοσαυταπλασίων ἐστὶ καὶ ὁ ΧΗ κύλινδρος τοῦ ΗΔ κυλίνδρου. καὶ εἰ μὲν ἴσος ἐστὶν ὁ ΚΛ ἄξων τῷ ΚΜ ἄξονι, ἴσος ἔσται καὶ ὁ ΠΗ κύλινδρος τῷ ΗΧ κυλίνδρῳ, εἰ δὲ μείζων ὁ ἄξων τοῦ ἄξονος, μείζων καὶ ὁ κύλινδρος τοῦ κυλίνδρου, καὶ εἰ ἐλάσσων, ἐλάσσων. τεσσάρων δὴ μεγεθῶν ὄντων, ἀξόνων μὲν τῶν ΕΚ, ΚΖ, κυλίνδρων δὲ τῶν ΒΗ, ΗΔ, εἴληπται ἰσάκις πολλαπλάσια, τοῦ μὲν ΕΚ ἄξονος καὶ τοῦ ΒΗ κυλίνδρου ὅ τε ΛΚ ἄξων καὶ ὁ ΠΗ κύλινδρος, τοῦ δὲ ΚΖ ἄξονος καὶ τοῦ ΗΔ κυλίνδρου ὅ τε ΚΜ ἄξων καὶ ὁ ΗΧ κύλινδρος, καὶ δέδεικται, ὅτι εἰ ὑπερέχει ὁ ΚΛ ἄξων τοῦ ΚΜ ἄξονος, ὑπερέχει καὶ ὁ ΠΗ κύλινδρος τοῦ ΗΧ κυλίνδρου, καὶ εἰ ἴσος, ἴσος, καὶ εἰ ἐλάσσων, ἐλάσσων. ἔστιν ἄρα ὡς ὁ ΕΚ ἄξων πρὸς τὸν ΚΖ ἄξονα, οὕτως ὁ ΒΗ κύλινδρος πρὸς τὸν ΗΔ κύλινδρον· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον XII
Οἱ ἐπὶ ἴσων βάσεων ὄντες κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ὕψη.
Ἔστωσαν γὰρ ἐπὶ ἴσων βάσεων τῶν ΑΒ, ΓΔ κύκλων κύλινδροι οἱ ΕΒ, ΖΔ· λέγω, ὅτι ἐστὶν ὡς ὁ ΕΒ κύλινδρος πρὸς τὸν ΖΔ κύλινδρον, οὕτως ὁ ΗΘ ἄξων πρὸς τὸν ΚΛ ἄξονα.
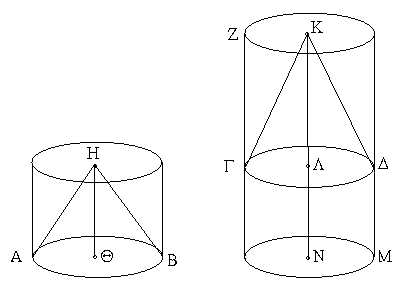
Ἐκβεβλήσθω γὰρ ὁ ΚΛ ἄξων ἐπὶ τὸ Ν σημεῖον, καὶ κείσθω τῷ ΗΘ ἄξονι ἴσος ὁ ΛΝ, καὶ περὶ ἄξονα τὸν ΛΝ κύλινδρος νενοήσθω ὁ ΓΜ. ἐπεὶ οὖν οἱ ΕΒ, ΓΜ κύλινδροι ὑπὸ τὸ αὐτὸ ὕψος εἰσίν, πρὸς ἀλλήλους εἰσὶν ὡς αἱ βάσεις. ἴσαι δέ εἰσιν αἱ βάσεις ἀλλήλαις· ἴσοι ἄρα εἰσὶ καὶ οἱ ΕΒ, ΓΜ κύλινδροι. καὶ ἐπεὶ κύλινδρος ὁ ΖΜ ἐπιπέδῳ τέτμηται τῷ ΓΔ παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ἄρα ὡς ὁ ΓΜ κύλινδρος πρὸς τὸν ΖΔ κύλινδρον, οὕτως ὁ ΛΝ ἄξων πρὸς τὸν ΚΛ ἄξονα. ἴσος δέ ἐστιν ὁ μὲν ΓΜ κύλινδρος τῷ ΕΒ κυλίνδρῳ, ὁ δὲ ΛΝ ἄξων τῷ ΗΘ ἄξονι· ἔστιν ἄρα ὡς ὁ ΕΒ κύλινδρος πρὸς τὸν ΖΔ κύλινδρον, οὕτως ὁ ΗΘ ἄξων πρὸς τὸν ΚΛ ἄξονα. ὡς δὲ ὁ ΕΒ κύλινδρος πρὸς τὸν ΖΔ κύλινδρον, οὕτως ὁ ΑΒΗ κῶνος πρὸς τὸν ΓΔΚ κῶνον. καὶ ὡς ἄρα ὁ ΗΘ ἄξων πρὸς τὸν ΚΛ ἄξονα, οὕτως ὁ ΑΒΗ κῶνος πρὸς τὸν ΓΔΚ κῶνον καὶ ὁ ΕΒ κύλινδρος πρὸς τὸν ΖΔ κύλινδρον· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον XII
Τῶν ἴσων κώνων καὶ κυλίνδρων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· καὶ ὧν κώνων καὶ κυλίνδρων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσοι εἰσὶν ἐκεῖνοι.
Ἔστωσαν ἴσοι κῶνοι καὶ κύλινδροι, ὧν βάσεις μὲν οἱ ΑΒΓΔ, ΕΖΗΘ κύκλοι, διάμετροι δὲ αὐτῶν αἱ ΑΓ, ΕΗ, ἄξονες δὲ οἱ ΚΛ, ΜΝ, οἵτινες καὶ ὕψη εἰσὶ τῶν κώνων ἢ κυλίνδρων, καὶ συμπεπληρώσθωσαν οἱ ΑΞ, ΕΟ κύλινδροι. λέγω, ὅτι τῶν ΑΞ, ΕΟ κυλίνδρων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, καί ἐστιν ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΚΛ ὕψος.
Τὸ γὰρ ΛΚ ὕψος τῷ ΜΝ ὕψει ἤτοι ἴσον ἐστὶν ἢ οὔ. ἔστω πρότερον ἴσον. ἔστι δὲ καὶ ὁ ΑΞ κύλινδρος τῷ ΕΟ κυλίνδρῳ ἴσος. οἱ δὲ ὑπὸ τὸ αὐτὸ ὕψος ὄντες κῶνοι καὶ κύλινδροι πρὸς ἀλλήλους εἰσὶν ὡς αἱ βάσεις· ἴση ἄρα καὶ ἡ ΑΒΓΔ βάσις τῇ ΕΖΗΘ βάσει. ὥστε καὶ ἀντιπέπονθεν, ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΚΛ ὕψος.
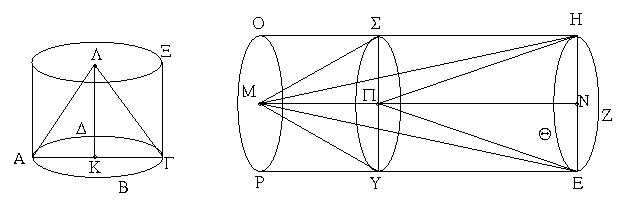
ἀλλὰ δὴ μὴ ἔστω τὸ ΛΚ ὕψος τῷ ΜΝ ἴσον, ἀλλ' ἔστω μεῖζον τὸ ΜΝ, καὶ ἀφῃρήσθω ἀπὸ τοῦ ΜΝ ὕψους τῷ ΚΛ ἴσον τὸ ΠΝ, καὶ διὰ τοῦ Π σημείου τετμήσθω ὁ ΕΟ κύλινδρος ἐπιπέδῳ τῷ ΤΥΣ παραλλήλῳ τοῖς τῶν ΕΖΗΘ, ΡΟ κύκλων ἐπιπέδοις, καὶ ἀπὸ βάσεως μὲν τοῦ ΕΖΗΘ κύκλου, ὕψους δὲ τοῦ ΝΠ κύλινδρος νενοήσθω ὁ ΕΣ. καὶ ἐπεὶ ἴσος ἐστὶν ὁ ΑΞ κύλινδρος τῷ ΕΟ κυλίνδρῳ, ἔστιν ἄρα ὡς ὁ ΑΞ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον, οὕτως ὁ ΕΟ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον. ἀλλ' ὡς μὲν ὁ ΑΞ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον, οὕτως ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ· ὑπὸ γὰρ τὸ αὐτὸ ὕψος εἰσὶν οἱ ΑΞ, ΕΣ κύλινδροι· ὡς δὲ ὁ ΕΟ κύλινδρος πρὸς τὸν ΕΣ, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΠΝ ὕψος· ὁ γὰρ ΕΟ κύλινδρος ἐπιπέδῳ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις. ἔστιν ἄρα καὶ ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΠΝ ὕψος. ἴσον δὲ τὸ ΠΝ ὕψος τῷ ΚΛ ὕψει· ἔστιν ἄρα ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΚΛ ὕψος. τῶν ἄρα ΑΞ, ΕΟ κυλίνδρων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν.
Ἀλλὰ δὴ τῶν ΑΞ, ΕΟ κυλίνδρων ἀντιπεπονθέτωσαν αἱ βάσεις τοῖς ὕψεσιν, καὶ ἔστω ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΚΛ ὕψος· λέγω, ὅτι ἴσος ἐστὶν ὁ ΑΞ κύλινδρος τῷ ΕΟ κυλίνδρῳ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων ἐπεί ἐστιν ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΚΛ ὕψος, ἴσον δὲ τὸ ΚΛ ὕψος τῷ ΠΝ ὕψει, ἔστιν ἄρα ὡς ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως τὸ ΜΝ ὕψος πρὸς τὸ ΠΝ ὕψος. ἀλλ' ὡς μὲν ἡ ΑΒΓΔ βάσις πρὸς τὴν ΕΖΗΘ βάσιν, οὕτως ὁ ΑΞ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον· ὑπὸ γὰρ τὸ αὐτὸ ὕψος εἰσίν· ὡς δὲ τὸ ΜΝ ὕψος πρὸς τὸ ΠΝ [ὕψος], οὕτως ὁ ΕΟ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον· ἔστιν ἄρα ὡς ὁ ΑΞ κύλινδρος πρὸς τὸν ΕΣ κύλινδρον, οὕτως ὁ ΕΟ κύλινδρος πρὸς τὸν ΕΣ. ἴσος ἄρα ὁ ΑΞ κύλινδρος τῷ ΕΟ κυλίνδρῳ. ὡσαύτως δὲ καὶ ἐπὶ τῶν κώνων· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον XII
Δύο κύκλων περὶ τὸ αὐτὸ κέντρον ὄντων εἰς τὸν μείζονα κύκλον πολύγωνον ἰσόπλευρόν τε καὶ ἀρτιόπλευρον ἐγγράψαι μὴ ψαῦον τοῦ ἐλάσσονος κύκλου.
Ἔστωσαν οἱ δοθέντες δύο κύκλοι οἱ ΑΒΓΔ, ΕΖΗΘ περὶ τὸ αὐτὸ κέντρον τὸ Κ· δεῖ δὴ εἰς τὸν μείζονα κύκλον τὸν ΑΒΓΔ πολύγωνον ἰσόπλευρόν τε καὶ ἀρτιόπλευρον ἐγγράψαι μὴ ψαῦον τοῦ ΕΖΗΘ κύκλου.
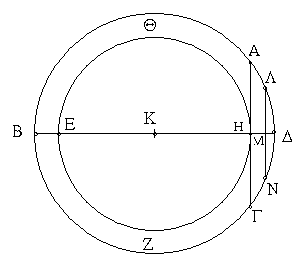
Ἤχθω γὰρ διὰ τοῦ Κ κέντρου εὐθεῖα ἡ ΒΚΔ, καὶ ἀπὸ τοῦ Η σημείου τῇ ΒΔ εὐθείᾳ πρὸς ὀρθὰς ἤχθω ἡ ΗΑ καὶ διήχθω ἐπὶ τὸ Γ· ἡ ΑΓ ἄρα ἐφάπτεται τοῦ ΕΖΗΘ κύκλου. τέμνοντες δὴ τὴν ΒΑΔ περιφέρειαν δίχα καὶ τὴν ἡμίσειαν αὐτῆς δίχα καὶ τοῦτο ἀεὶ ποιοῦντες καταλείψομεν περιφέρειαν ἐλάσσονα τῆς ΑΔ. λελείφθω, καὶ ἔστω ἡ ΛΔ, καὶ ἀπὸ τοῦ Λ ἐπὶ τὴν ΒΔ κάθετος ἤχθω ἡ ΛΜ καὶ διήχθω ἐπὶ τὸ Ν, καὶ ἐπεζεύχθωσαν αἱ ΛΔ, ΔΝ· ἴση ἄρα ἐστὶν ἡ ΛΔ τῇ ΔΝ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΛΝ τῇ ΑΓ, ἡ δὲ ΑΓ ἐφάπτεται τοῦ ΕΖΗΘ κύκλου, ἡ ΛΝ ἄρα οὐκ ἐφάπτεται τοῦ ΕΖΗΘ κύκλου· πολλῷ ἄρα αἱ ΛΔ, ΔΝ οὐκ ἐφάπτονται τοῦ ΕΖΗΘ κύκλου. ἐὰν δὴ τῇ ΛΔ εὐθείᾳ ἴσας κατὰ τὸ συνεχὲς ἐναρμόσωμεν εἰς τὸν ΑΒΓΔ κύκλον, ἐγγραφήσεται εἰς τὸν ΑΒΓΔ κύκλον πολύγωνον ἰσόπλευρόν τε καὶ ἀρτιόπλευρον μὴ ψαῦον τοῦ ἐλάσσονος κύκλου τοῦ ΕΖΗΘ· ὅπερ ἔδει ποιῆσαι.
Πρότασις ιζ΄ 17 Βιβλίον XII
Δύο σφαιρῶν περὶ τὸ αὐτὸ κέντρον οὐσῶν εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγράψαι μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Νενοήσθωσαν δύο σφαῖραι περὶ τὸ αὐτὸ κέντρον τὸ Α· δεῖ δὴ εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγράψαι μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Τετμήσθωσαν αἱ σφαῖραι ἐπιπέδῳ τινὶ διὰ τοῦ κέντρου· ἔσονται δὴ αἱ τομαὶ κύκλοι, ἐπειδήπερ μενούσης τῆς διαμέτρου καὶ περιφερομένου τοῦ ἡμικυκλίου ἐγίγνετο ἡ σφαῖρα· ὥστε καὶ καθ᾿ οἵας ἂν θέσεως ἐπινοήσωμεν τὸ ἡμικύκλιον, τὸ δι' αὐτοῦ ἐκβαλλόμενον ἐπίπεδον ποιήσει ἐπὶ τῆς ἐπιφανείας τῆς σφαίρας κύκλον. καὶ φανερόν, ὅτι καὶ μέγιστον, ἐπειδήπερ ἡ διάμετρος τῆς σφαίρας, ἥτις ἐστὶ καὶ τοῦ ἡμικυκλίου διάμετρος δηλαδὴ καὶ τοῦ κύκλου, μείζων ἐστὶ πασῶν τῶν εἰς τὸν κύκλον ἢ τὴν σφαῖραν διαγομένων [εὐθειῶν]. ἔστω οὖν ἐν μὲν τῇ μείζονι σφαίρᾳ κύκλος ὁ ΒΓΔΕ, ἐν δὲ τῇ ἐλάσσονι σφαίρᾳ κύκλος ὁ ΖΗΘ, καὶ ἤχθωσαν αὐτῶν δύο διάμετροι πρὸς ὀρθὰς ἀλλήλαις αἱ ΒΔ, ΓΕ, καὶ δύο κύκλων περὶ τὸ αὐτὸ κέντρον ὄντων τῶν ΒΓΔΕ, ΖΗΘ εἰς τὸν μείζονα κύκλον τὸν ΒΓΔΕ πολύγωνον ἰσόπλευρον καὶ ἀρτιόπλευρον ἐγγεγράφθω μὴ ψαῦον τοῦ ἐλάσσονος κύκλου τοῦ ΖΗΘ, οὗ πλευραὶ ἔστωσαν ἐν τῷ ΒΕ τεταρτημορίῳ αἱ ΒΚ, ΚΛ, ΛΜ, ΜΕ, καὶ ἐπιζευχθεῖσα ἡ ΚΑ διήχθω ἐπὶ τὸ Ν, καὶ ἀνεστάτω ἀπὸ τοῦ Α σημείου τῷ τοῦ ΒΓΔΕ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΑΞ καὶ συμβαλλέτω τῇ ἐπιφανείᾳ τῆς σφαίρας κατὰ τὸ Ξ, καὶ διὰ τῆς ΑΞ καὶ ἑκατέρας τῶν ΒΔ, ΚΝ ἐπίπεδα ἐκβεβλήσθω· ποιήσουσι δὴ διὰ τὰ εἰρημένα ἐπὶ τῆς ἐπιφανείας τῆς σφαίρας μεγίστους κύκλους. ποιείτωσαν, ὧν ἡμικύκλια ἔστω ἐπὶ τῶν ΒΔ, ΚΝ διαμέτρων τὰ ΒΞΔ, ΚΞΝ. καὶ ἐπεὶ ἡ ΞΑ ὀρθή ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον, καὶ πάντα ἄρα τὰ διὰ τῆς ΞΑ ἐπίπεδά ἐστιν ὀρθὰ πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον·
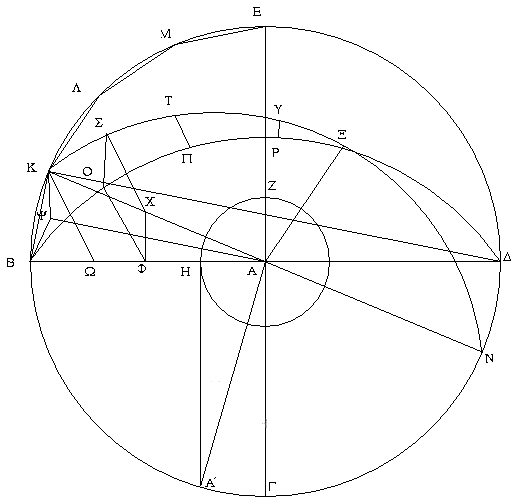
ὥστε καὶ τὰ ΒΞΔ, ΚΞΝ ἡμικύκλια ὀρθά ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον. καὶ ἐπεὶ ἴσα ἐστὶ τὰ ΒΕΔ, ΒΞΔ, ΚΞΝ ἡμικύκλια· ἐπὶ γὰρ ἴσων εἰσὶ διαμέτρων τῶν ΒΔ, ΚΝ· ἴσα ἐστὶ καὶ τὰ ΒΕ, ΒΞ, ΚΞ τεταρτημόρια ἀλλήλοις. ὅσαι ἄρα εἰσὶν ἐν τῷ ΒΕ τεταρτημορίῳ πλευραὶ τοῦ πολυγώνου, τοσαῦταί εἰσι καὶ ἐν τοῖς ΒΞ, ΚΞ τεταρτημορίοις ἴσαι ταῖς ΒΚ, ΚΛ, ΛΜ, ΜΕ εὐθείαις. ἐγγεγράφθωσαν καὶ ἔστωσαν αἱ ΒΟ, ΟΠ, ΠΡ, ΡΞ, ΚΣ, ΣΤ, ΤΥ, ΥΞ, καὶ ἐπεζεύχθωσαν αἱ ΣΟ, ΤΠ, ΥΡ, καὶ ἀπὸ τῶν Ο, Σ ἐπὶ τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον κάθετοι ἤχθωσαν· πεσοῦνται δὴ ἐπὶ τὰς κοινὰς τομὰς τῶν ἐπιπέδων τὰς ΒΔ, ΚΝ, ἐπειδήπερ καὶ τὰ τῶν ΒΞΔ, ΚΞΝ ἐπίπεδα ὀρθά ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον. πιπτέτωσαν, καὶ ἔστωσαν αἱ ΟΦ, ΣΧ, καὶ ἐπεζεύχθω ἡ ΧΦ. καὶ ἐπεὶ ἐν ἴσοις ἡμικυκλίοις τοῖς ΒΞΔ, ΚΞΝ ἴσαι ἀπειλημμέναι εἰσὶν αἱ ΒΟ, ΚΣ, καὶ κάθετοι ἠγμέναι εἰσὶν αἱ ΟΦ, ΣΧ, ἴση [ἄρα] ἐστὶν ἡ μὲν ΟΦ τῇ ΣΧ, ἡ δὲ ΒΦ τῇ ΚΧ. ἔστι δὲ καὶ ὅλη ἡ ΒΑ ὅλῃ τῇ ΚΑ ἴση· καὶ λοιπὴ ἄρα ἡ ΦΑ λοιπῇ τῇ ΧΑ ἐστιν ἴση· ἔστιν ἄρα ὡς ἡ ΒΦ πρὸς τὴν ΦΑ, οὕτως ἡ ΚΧ πρὸς τὴν ΧΑ· παράλληλος ἄρα ἐστὶν ἡ ΧΦ τῇ ΚΒ. καὶ ἐπεὶ ἑκατέρα τῶν ΟΦ, ΣΧ ὀρθή ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον, παράλληλος ἄρα ἐστὶν ἡ ΟΦ τῇ ΣΧ. ἐδείχθη δὲ αὐτῇ καὶ ἴση· καὶ αἱ ΧΦ, ΣΟ ἄρα ἴσαι εἰσὶ καὶ παράλληλοι. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΧΦ τῇ ΣΟ, ἀλλὰ ἡ ΧΦ τῇ ΚΒ ἐστι παράλληλος, καὶ ἡ ΣΟ ἄρα τῇ ΚΒ ἐστι παράλληλος. καὶ ἐπιζευγνύουσιν αὐτὰς αἱ ΒΟ, ΚΣ· τὸ ΚΒΟΣ ἄρα τετράπλευρον ἐν ἑνί ἐστιν ἐπιπέδῳ, ἐπειδήπερ, ἐὰν ὦσι δύο εὐθεῖαι παράλληλοι, καὶ ἐφ' ἑκατέρας αὐτῶν ληφθῇ τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐν τῷ αὐτῷ ἐπιπέδῳ ἐστὶ ταῖς παραλλήλοις. διὰ τὰ αὐτὰ δὴ καὶ ἑκάτερον τῶν ΣΟΠΤ, ΤΠΡΥ τετραπλεύρων ἐν ἑνί ἐστιν ἐπιπέδῳ. ἔστι δὲ καὶ τὸ ΥΡΞ τρίγωνον ἐν ἑνὶ ἐπιπέδῳ. ἐὰν δὴ νοήσωμεν ἀπὸ τῶν Ο, Σ, Π, Τ, Ρ, Υ σημείων ἐπὶ τὸ Α ἐπιζευγνυμένας εὐθείας, συσταθήσεταί τι σχῆμα στερεὸν πολύεδρον μεταξὺ τῶν ΒΞ, ΚΞ περιφερειῶν ἐκ πυραμίδων συγκείμενον, ὧν βάσεις μὲν τὰ ΚΒΟΣ, ΣΟΠΤ, ΤΠΡΥ τετράπλευρα καὶ τὸ ΥΡΞ τρίγωνον, κορυφὴ δὲ τὸ Α σημεῖον. ἐὰν δὲ καὶ ἐπὶ ἑκάστης τῶν ΚΛ, ΛΜ, ΜΕ πλευρῶν καθάπερ ἐπὶ τῆς ΒΚ τὰ αὐτὰ κατασκευάσωμεν καὶ ἔτι ἐπὶ τῶν λοιπῶν τριῶν τεταρτημορίων, συσταθήσεταί τι σχῆμα πολύεδρον ἐγγεγραμμένον εἰς τὴν σφαῖραν πυραμίσι περιεχόμενον, ὧν βάσεις [μὲν] τὰ εἰρημένα τετράπλευρα καὶ τὸ ΥΡΞ τρίγωνον καὶ τὰ ὁμοταγῆ αὐτοῖς, κορυφὴ δὲ τὸ Α σημεῖον.
Λέγω, ὅτι τὸ εἰρημένον πολύεδρον οὐκ ἐφάψεται τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν, ἐφ' ἧς ἐστιν ὁ ΖΗΘ κύκλος.
Ἤχθω ἀπὸ τοῦ Α σημείου ἐπὶ τὸ τοῦ ΚΒΟΣ τετραπλεύρου ἐπίπεδον κάθετος ἡ ΑΨ καὶ συμβαλλέτω τῷ ἐπιπέδῳ κατὰ τὸ Ψ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΨΒ, ΨΚ. καὶ ἐπεὶ ἡ ΑΨ ὀρθή ἐστι πρὸς τὸ τοῦ ΚΒΟΣ τετραπλεύρου ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ τοῦ τετραπλεύρου ἐπιπέδῳ ὀρθή ἐστιν. ἡ ΑΨ ἄρα ὀρθή ἐστι πρὸς ἑκατέραν τῶν ΒΨ, ΨΚ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΑΚ, ἴσον ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΑΚ. καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΒ ἴσα τὰ ἀπὸ τῶν ΑΨ, ΨΒ· ὀρθὴ γὰρ ἡ πρὸς τῷ Ψ· τῷ δὲ ἀπὸ τῆς ΑΚ ἴσα τὰ ἀπὸ τῶν ΑΨ, ΨΚ. τὰ ἄρα ἀπὸ τῶν ΑΨ, ΨΒ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΑΨ, ΨΚ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΑΨ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΒΨ λοιπῷ τῷ ἀπὸ τῆς ΨΚ ἴσον ἐστίν· ἴση ἄρα ἡ ΒΨ τῇ ΨΚ. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ἀπὸ τοῦ Ψ ἐπὶ τὰ Ο, Σ ἐπιζευγνύμεναι εὐθεῖαι ἴσαι εἰσὶν ἑκατέρᾳ τῶν ΒΨ, ΨΚ. ὁ ἄρα κέντρῳ τῷ Ψ καὶ διαστήματι ἑνὶ τῶν ΨΒ, ΨΚ γραφόμενος κύκλος ἥξει καὶ διὰ τῶν Ο, Σ, καὶ ἔσται ἐν κύκλῳ τὸ ΚΒΟΣ τετράπλευρον.
Καὶ ἐπεὶ μείζων ἐστὶν ἡ ΚΒ τῆς ΧΦ, ἴση δὲ ἡ ΧΦ τῇ ΣΟ, μείζων ἄρα ἡ ΚΒ τῆς ΣΟ. ἴση δὲ ἡ ΚΒ ἑκατέρᾳ τῶν ΚΣ, ΒΟ· καὶ ἑκατέρα ἄρα τῶν ΚΣ, ΒΟ τῆς ΣΟ μείζων ἐστίν. καὶ ἐπεὶ ἐν κύκλῳ τετράπλευρόν ἐστι τὸ ΚΒΟΣ, καὶ ἴσαι αἱ ΚΒ, ΒΟ, ΚΣ, καὶ ἐλάττων ἡ ΟΣ, καὶ ἐκ τοῦ κέντρου τοῦ κύκλου ἐστὶν ἡ ΒΨ, τὸ ἄρα ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΒΨ μεῖζόν ἐστιν ἢ διπλάσιον. ἤχθω ἀπὸ τοῦ Κ ἐπὶ τὴν ΒΦ κάθετος ἡ ΚΩ. καὶ ἐπεὶ ἡ ΒΔ τῆς ΔΩ ἐλάττων ἐστὶν ἢ διπλῆ, καί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΩ, οὕτως τὸ ὑπὸ τῶν ΔΒ, ΒΩ πρὸς τὸ ὑπὸ [τῶν] ΔΩ, ΩΒ, ἀναγραφομένου ἀπὸ τῆς ΒΩ τετραγώνου καὶ συμπληρουμένου τοῦ ἐπὶ τῆς ΩΔ παραλληλογράμμου καὶ τὸ ὑπὸ ΔΒ, ΒΩ ἄρα τοῦ ὑπὸ ΔΩ, ΩΒ ἔλαττόν ἐστιν ἢ διπλάσιον. καί ἐστι τῆς ΚΔ ἐπιζευγνυμένης τὸ μὲν ὑπὸ ΔΒ, ΒΩ ἴσον τῷ ἀπὸ τῆς ΒΚ, τὸ δὲ ὑπὸ τῶν ΔΩ, ΩΒ ἴσον τῷ ἀπὸ τῆς ΚΩ· τὸ ἄρα ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΚΩ ἔλασσόν ἐστιν ἢ διπλάσιον. ἀλλὰ τὸ ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΒΨ μεῖζόν ἐστιν ἢ διπλάσιον· μεῖζον ἄρα τὸ ἀπὸ τῆς ΚΩ τοῦ ἀπὸ τῆς ΒΨ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΑ τῇ ΚΑ, ἴσον ἐστὶ τὸ ἀπὸ τῆς ΒΑ τῷ ἀπὸ τῆς ΑΚ. καί ἐστι τῷ μὲν ἀπὸ τῆς ΒΑ ἴσα τὰ ἀπὸ τῶν ΒΨ, ΨΑ, τῷ δὲ ἀπὸ τῆς ΚΑ ἴσα τὰ ἀπὸ τῶν ΚΩ, ΩΑ· τὰ ἄρα ἀπὸ τῶν ΒΨ, ΨΑ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΚΩ, ΩΑ, ὧν τὸ ἀπὸ τῆς ΚΩ μεῖζον τοῦ ἀπὸ τῆς ΒΨ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΩΑ ἔλασσόν ἐστι τοῦ ἀπὸ τῆς ΨΑ. μείζων ἄρα ἡ ΑΨ τῆς ΑΩ· πολλῷ ἄρα ἡ ΑΨ μείζων ἐστὶ τῆς ΑΗ. καί ἐστιν ἡ μὲν ΑΨ ἐπὶ μίαν τοῦ πολυέδρου βάσιν, ἡ δὲ ΑΗ ἐπὶ τὴν τῆς ἐλάσσονος σφαίρας ἐπιφάνειαν· ὥστε τὸ πολύεδρον οὐ ψαύσει τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Δύο ἄρα σφαιρῶν περὶ τὸ αὐτὸ κέντρον οὐσῶν εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγέγραπται μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν· ὅπερ ἔδει ποιῆσαι.
Πόρισμα
Ἐὰν δὲ καὶ εἰς ἑτέραν σφαῖραν τῷ ἐν τῇ ΒΓΔΕ σφαίρᾳ στερεῷ πολυέδρῳ ὅμοιον στερεὸν πολύεδρον ἐγγραφῇ, τὸ ἐν τῇ ΒΓΔΕ σφαίρᾳ στερεὸν πολύεδρον πρὸς τὸ ἐν τῇ ἑτέρᾳ σφαίρᾳ στερεὸν πολύεδρον τριπλασίονα λόγον ἔχει, ἤπερ ἡ τῆς ΒΓΔΕ σφαίρας διάμετρος πρὸς τὴν τῆς ἑτέρας σφαίρας διάμετρον. διαιρεθέντων γὰρ τῶν στερεῶν εἰς τὰς ὁμοιοπληθεῖς καὶ ὁμοιοταγεῖς πυραμίδας ἔσονται αἱ πυραμίδες ὅμοιαι. αἱ δὲ ὅμοιαι πυραμίδες πρὸς ἀλλήλας ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν· ἡ ἄρα πυραμίς, ἧς βάσις μέν ἐστι τὸ ΚΒΟΣ τετράπλευρον, κορυφὴ δὲ τὸ Α σημεῖον, πρὸς τὴν ἐν τῇ ἑτέρᾳ σφαίρᾳ ὁμοιοταγῆ πυραμίδα τριπλασίονα λόγον ἔχει, ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἤπερ ἡ ΑΒ ἐκ τοῦ κέντρου τῆς σφαίρας τῆς περὶ κέντρον τὸ Α πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας. ὁμοίως καὶ ἑκάστη πυραμὶς τῶν ἐν τῇ περὶ κέντρον τὸ Α σφαίρᾳ πρὸς ἑκάστην ὁμοταγῆ πυραμίδα τῶν ἐν τῇ ἑτέρᾳ σφαίρᾳ τριπλασίονα λόγον ἕξει, ἤπερ ἡ ΑΒ πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας. καὶ ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ὥστε ὅλον τὸ ἐν τῇ περὶ κέντρον τὸ Α σφαίρᾳ στερεὸν πολύεδρον πρὸς ὅλον τὸ ἐν τῇ ἑτέρᾳ [σφαίρᾳ] στερεὸν πολύεδρον τριπλασίονα λόγον ἕξει, ἤπερ ἡ ΑΒ πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας, τουτέστιν ἤπερ ἡ ΒΔ διάμετρος πρὸς τὴν τῆς ἑτέρας σφαίρας διάμετρον· ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον XII
Αἱ σφαῖραι πρὸς ἀλλήλας ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ἰδίων διαμέτρων.
Νενοήσθωσαν σφαῖραι αἱ ΑΒΓ, ΔΕΖ, διάμετροι δὲ αὐτῶν αἱ ΒΓ, ΕΖ· λέγω, ὅτι ἡ ΑΒΓ σφαῖρα πρὸς τὴν ΔΕΖ σφαῖραν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Εἰ γὰρ μὴ ἡ ΑΒΓ σφαῖρα πρὸς τὴν ΔΕΖ σφαῖραν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ, ἕξει ἄρα ἡ ΑΒΓ σφαῖρα πρὸς ἐλάσσονά τινα τῆς ΔΕΖ σφαίρας τριπλασίονα λόγον ἢ πρὸς μείζονα ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ. ἐχέτω πρότερον πρὸς ἐλάσσονα τὴν ΗΘΚ, καὶ νενοήσθω ἡ ΔΕΖ τῇ ΗΘΚ περὶ τὸ αὐτὸ κέντρον, καὶ ἐγγεγράφθω εἰς τὴν μείζονα σφαῖραν τὴν ΔΕΖ στερεὸν πολύεδρον μὴ ψαῦον τῆς ἐλάσσονος σφαίρας τῆς ΗΘΚ κατὰ τὴν ἐπιφάνειαν, ἐγγεγράφθω δὲ καὶ εἰς τὴν ΑΒΓ σφαῖραν τῷ ἐν τῇ ΔΕΖ σφαίρᾳ στερεῷ πολυέδρῳ ὅμοιον στερεὸν πολύεδρον· τὸ ἄρα ἐν τῇ ΑΒΓ στερεὸν πολύεδρον πρὸς τὸ ἐν τῇ ΔΕΖ στερεὸν πολύεδρον τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
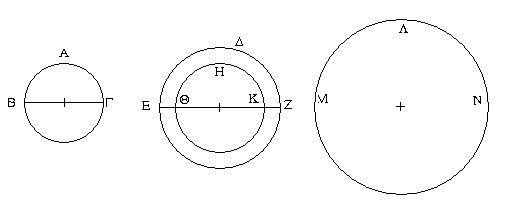
ἔχει δὲ καὶ ἡ ΑΒΓ σφαῖρα πρὸς τὴν ΗΘΚ σφαῖραν τριπλασίονα λόγον ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ· ἔστιν ἄρα ὡς ἡ ΑΒΓ σφαῖρα πρὸς τὴν ΗΘΚ σφαῖραν, οὕτως τὸ ἐν τῇ ΑΒΓ σφαίρᾳ στερεὸν πολύεδρον πρὸς τὸ ἐν τῇ ΔΕΖ σφαίρᾳ στερεὸν πολύεδρον· ἐναλλὰξ [ἄρα] ὡς ἡ ΑΒΓ σφαῖρα πρὸς τὸ ἐν αὐτῇ πολύεδρον, οὕτως ἡ ΗΘΚ σφαῖρα πρὸς τὸ ἐν τῇ ΔΕΖ σφαίρᾳ στερεὸν πολύεδρον. μείζων δὲ ἡ ΑΒΓ σφαῖρα τοῦ ἐν αὐτῇ πολυέδρου· μείζων ἄρα καὶ ἡ ΗΘΚ σφαῖρα τοῦ ἐν τῇ ΔΕΖ σφαίρᾳ πολυέδρου. ἀλλὰ καὶ ἐλάττων· ἐμπεριέχεται γὰρ ὑπ' αὐτοῦ. οὐκ ἄρα ἡ ΑΒΓ σφαῖρα πρὸς ἐλάσσονα τῆς ΔΕΖ σφαίρας τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ διάμετρος πρὸς τὴν ΕΖ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἡ ΔΕΖ σφαῖρα πρὸς ἐλάσσονα τῆς ΑΒΓ σφαίρας τριπλασίονα λόγον ἔχει ἤπερ ἡ ΕΖ πρὸς τὴν ΒΓ.
Λέγω δή, ὅτι οὐδὲ ἡ ΑΒΓ σφαῖρα πρὸς μείζονά τινα τῆς ΔΕΖ σφαίρας τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Εἰ γὰρ δυνατόν, ἐχέτω πρὸς μείζονα τὴν ΛΜΝ· ἀνάπαλιν ἄρα ἡ ΛΜΝ σφαῖρα πρὸς τὴν ΑΒΓ σφαῖραν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΕΖ διάμετρος πρὸς τὴν ΒΓ διάμετρον. ὡς δὲ ἡ ΛΜΝ σφαῖρα πρὸς τὴν ΑΒΓ σφαῖραν, οὕτως ἡ ΔΕΖ σφαῖρα πρὸς ἐλάσσονά τινα τῆς ΑΒΓ σφαίρας, ἐπειδήπερ μείζων ἐστὶν ἡ ΛΜΝ τῆς ΔΕΖ, ὡς ἔμπροσθεν ἐδείχθη. καὶ ἡ ΔΕΖ ἄρα σφαῖρα πρὸς ἐλάσσονά τινα τῆς ΑΒΓ σφαίρας τριπλασίονα λόγον ἔχει ἤπερ ἡ ΕΖ πρὸς τὴν ΒΓ· ὅπερ ἀδύνατον ἐδείχθη. οὐκ ἄρα ἡ ΑΒΓ σφαῖρα πρὸς μείζονά τινα τῆς ΔΕΖ σφαίρας τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ. ἐδείχθη δέ, ὅτι οὐδὲ πρὸς ἐλάσσονα. ἡ ἄρα ΑΒΓ σφαῖρα πρὸς τὴν ΔΕΖ σφαῖραν τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ· ὅπερ ἔδει δεῖξαι.
Στοιχεῖα Εὐκλείδου ιγ΄
Βιβλίον XIII
Προτάσεις ιη΄ 18
Πρότασις α΄ 1 Βιβλίον XIII
Ἐὰν εὐθεῖα γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, τὸ μεῖζον τμῆμα προσλαβὸν τὴν ἡμίσειαν τῆς ὅλης πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τετραγώνου.
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τετμήσθω κατὰ τὸ Γ σημεῖον, καὶ ἔστω μεῖζον τμῆμα τὸ ΑΓ, καὶ ἐκβεβλήσθω ἐπ᾿ εὐθείας τῇ ΓΑ εὐθεῖα ἡ ΑΔ, καὶ κείσθω τῆς ΑΒ ἡμίσεια ἡ ΑΔ· λέγω, ὅτι πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΓΔ τοῦ ἀπὸ τῆς ΔΑ.
Ἀναγεγράφθωσαν γὰρ ἀπὸ τῶν ΑΒ, ΔΓ τετράγωνα τὰ ΑΕ, ΔΖ, καὶ καταγεγράφθω ἐν τῷ ΔΖ τὸ σχῆμα, καὶ διήχθω ἡ ΖΓ ἐπὶ τὸ Η. καὶ ἐπεὶ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Γ, τὸ ἄρα ὑπὸ τῶν ΑΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ. καί ἐστι τὸ μὲν ὑπὸ τῶν ΑΒΓ τὸ ΓΕ, τὸ δὲ ἀπὸ τῆς ΑΓ τὸ ΖΘ· ἴσον ἄρα τὸ ΓΕ τῷ ΖΘ.
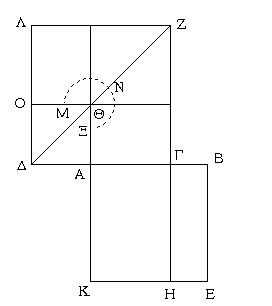
καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΒΑ τῆς ΑΔ, ἴση δὲ ἡ μὲν ΒΑ τῇ ΚΑ, ἡ δὲ ΑΔ τῇ ΑΘ, διπλῆ ἄρα καὶ ἡ ΚΑ τῆς ΑΘ. ὡς δὲ ἡ ΚΑ πρὸς τὴν ΑΘ, οὕτως τὸ ΓΚ πρὸς τὸ ΓΘ· διπλάσιον ἄρα τὸ ΓΚ τοῦ ΓΘ. εἰσὶ δὲ καὶ τὰ ΛΘ, ΘΓ διπλάσια τοῦ ΓΘ. ἴσον ἄρα τὸ ΚΓ τοῖς ΛΘ, ΘΓ. ἐδείχθη δὲ καὶ τὸ ΓΕ τῷ ΘΖ ἴσον· ὅλον ἄρα τὸ ΑΕ τετράγωνον ἴσον ἐστὶ τῷ ΜΝΞ γνώμονι. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΒΑ τῆς ΑΔ, τετραπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΑ τοῦ ἀπὸ τῆς ΑΔ, τουτέστι τὸ ΑΕ τοῦ ΔΘ. ἴσον δὲ τὸ ΑΕ τῷ ΜΝΞ γνώμονι· καὶ ὁ ΜΝΞ ἄρα γνώμων τετραπλάσιός ἐστι τοῦ ΑΟ· ὅλον ἄρα τὸ ΔΖ πενταπλάσιόν ἐστι τοῦ ΑΟ. καί ἐστι τὸ μὲν ΔΖ τὸ ἀπὸ τῆς ΔΓ, τὸ δὲ ΑΟ τὸ ἀπὸ τῆς ΔΑ· τὸ ἄρα ἀπὸ τῆς ΓΔ πενταπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΔΑ.
Ἐὰν ἄρα εὐθεῖα ἄκρον καὶ μέσον λόγον τμηθῇ, τὸ μεῖζον τμῆμα προσλαβὸν τὴν ἡμίσειαν τῆς ὅλης πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τετραγώνου· ὅπερ ἔδει δεῖξαι.
Πρότασις β΄ 2 Βιβλίον XIII
Ἐὰν εὐθεῖα γραμμὴ τμήματος ἑαυτῆς πενταπλάσιον δύνηται, τῆς διπλασίας τοῦ εἰρημένου τμήματος ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμα τὸ λοιπὸν μέρος ἐστὶ τῆς ἐξ ἀρχῆς εὐθείας.
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ τμήματος ἑαυτῆς τοῦ ΑΓ πενταπλάσιον δυνάσθω, τῆς δὲ ΑΓ διπλῆ ἔστω ἡ ΓΔ· λέγω, ὅτι τῆς ΓΔ ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΓΒ.
Ἀναγεγράφθω γὰρ ἀφ' ἑκατέρας τῶν ΑΒ, ΓΔ τετράγωνα τὰ ΑΖ, ΓΗ, καὶ καταγεγράφθω ἐν τῷ ΑΖ τὸ σχῆμα, καὶ διήχθω ἡ ΒΕ. καὶ ἐπεὶ πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΑ τοῦ ἀπὸ τῆς ΑΓ, πενταπλάσιόν ἐστι τὸ ΑΖ τοῦ ΑΘ. τετραπλάσιος ἄρα ὁ ΜΝΞ γνώμων τοῦ ΑΘ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΔΓ τῆς ΓΑ, τετραπλάσιον ἄρα ἐστὶ τὸ ἀπὸ ΔΓ τοῦ ἀπὸ ΓΑ, τουτέστι τὸ ΓΗ τοῦ ΑΘ. ἐδείχθη δὲ καὶ ὁ ΜΝΞ γνώμων τετραπλάσιος τοῦ ΑΘ· ἴσος ἄρα ὁ ΜΝΞ γνώμων τῷ ΓΗ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΔΓ τῆς ΓΑ, ἴση δὲ ἡ μὲν ΔΓ τῇ ΓΚ, ἡ δὲ ΑΓ τῇ ΓΘ [διπλῆ ἄρα καὶ ἡ ΚΓ τῆς ΓΘ], διπλάσιον ἄρα καὶ τὸ ΚΒ τοῦ ΒΘ.
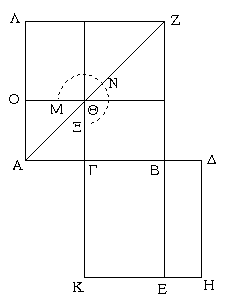
εἰσὶ δὲ καὶ τὰ ΛΘ, ΘΒ τοῦ ΘΒ διπλάσια· ἴσον ἄρα τὸ ΚΒ τοῖς ΛΘ, ΘΒ. ἐδείχθη δὲ καὶ ὅλος ὁ ΜΝΞ γνώμων ὅλῳ τῷ ΓΗ ἴσος· καὶ λοιπὸν ἄρα τὸ ΘΖ τῷ ΒΗ ἐστιν ἴσον. καί ἐστι τὸ μὲν ΒΗ τὸ ὑπὸ τῶν ΓΔΒ· ἴση γὰρ ἡ ΓΔ τῇ ΔΗ· τὸ δὲ ΘΖ τὸ ἀπὸ τῆς ΓΒ· τὸ ἄρα ὑπὸ τῶν ΓΔΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ. ἔστιν ἄρα ὡς ἡ ΔΓ πρὸς τὴν ΓΒ, οὕτως ἡ ΓΒ πρὸς τὴν ΒΔ. μείζων δὲ ἡ ΔΓ τῆς ΓΒ· μείζων ἄρα καὶ ἡ ΓΒ τῆς ΒΔ. τῆς ΓΔ ἄρα εὐθείας ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΓΒ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμήματος ἑαυτῆς πενταπλάσιον δύνηται, τῆς διπλασίας τοῦ εἰρημένου τμήματος ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμα τὸ λοιπὸν μέρος ἐστὶ τῆς ἐξ ἀρχῆς εὐθείας· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ὅτι δὲ ἡ διπλῆ τῆς ΑΓ μείζων ἐστὶ τῆς ΒΓ, οὕτως δεικτέον.
Εἰ γὰρ μή, ἔστω, εἰ δυνατόν, ἡ ΒΓ διπλῆ τῆς ΓΑ. τετραπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς ΓΑ· πενταπλάσια ἄρα τὰ ἀπὸ τῶν ΒΓ, ΓΑ τοῦ ἀπὸ τῆς ΓΑ. ὑπόκειται δὲ καὶ τὸ ἀπὸ τῆς ΒΑ πενταπλάσιον τοῦ ἀπὸ τῆς ΓΑ· τὸ ἄρα ἀπὸ τῆς ΒΑ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΓ, ΓΑ· ὅπερ ἀδύνατον. οὐκ ἄρα ἡ ΓΒ διπλασία ἐστὶ τῆς ΑΓ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἡ ἐλάττων τῆς ΓΒ διπλασίων ἐστὶ τῆς ΓΑ· πολλῷ γὰρ [μεῖζον] τὸ ἄτοπον.
Ἡ ἄρα τῆς ΑΓ διπλῆ μείζων ἐστὶ τῆς ΓΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις γ΄ 3 Βιβλίον XIII
Ἐὰν εὐθεῖα γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, τὸ ἔλασσον τμῆμα προσλαβὸν τὴν ἡμίσειαν τοῦ μείζονος τμήματος πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τοῦ μείζονος τμήματος τετραγώνου.
Εὐθεῖα γάρ τις ἡ ΑΒ ἄκρον καὶ μέσον λόγον τετμήσθω κατὰ τὸ Γ σημεῖον, καὶ ἔστω μεῖζον τμῆμα τὸ ΑΓ, καὶ τετμήσθω ἡ ΑΓ δίχα κατὰ τὸ Δ· λέγω, ὅτι πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΔ τοῦ ἀπὸ τῆς ΔΓ.
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΕ, καὶ καταγεγράφθω διπλοῦν τὸ σχῆμα. ἐπεὶ διπλῆ ἐστιν ἡ ΑΓ τῆς ΔΓ, τετραπλάσιον ἄρα τὸ ἀπὸ τῆς ΑΓ τοῦ ἀπὸ τῆς ΔΓ, τουτέστι τὸ ΡΣ τοῦ ΖΗ. καὶ ἐπεὶ τὸ ὑπὸ τῶν ΑΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ, καί ἐστι τὸ ὑπὸ τῶν ΑΒΓ τὸ ΓΕ, τὸ ἄρα ΓΕ ἴσον ἐστὶ τῷ ΡΣ.
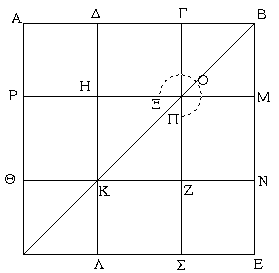
τετραπλάσιον δὲ τὸ ΡΣ τοῦ ΖΗ· τετραπλάσιον ἄρα καὶ τὸ ΓΕ τοῦ ΖΗ. πάλιν ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΔΓ, ἴση ἐστὶ καὶ ἡ ΘΚ τῇ ΚΖ. ὥστε καὶ τὸ ΗΖ τετράγωνον ἴσον ἐστὶ τῷ ΘΛ τετραγώνῳ. ἴση ἄρα ἡ ΗΚ τῇ ΚΛ, τουτέστιν ἡ ΜΝ τῇ ΝΕ· ὥστε καὶ τὸ ΜΖ τῷ ΖΕ ἐστιν ἴσον. ἀλλὰ τὸ ΜΖ τῷ ΓΗ ἐστιν ἴσον· καὶ τὸ ΓΗ ἄρα τῷ ΖΕ ἐστιν ἴσον. κοινὸν προσκείσθω τὸ ΓΝ· ὁ ἄρα ΞΟΠ γνώμων ἴσος ἐστὶ τῷ ΓΕ. ἀλλὰ τὸ ΓΕ τετραπλάσιον ἐδείχθη τοῦ ΗΖ· καὶ ὁ ΞΟΠ ἄρα γνώμων τετραπλάσιός ἐστι τοῦ ΖΗ τετραγώνου. ὁ ΞΟΠ ἄρα γνώμων καὶ τὸ ΖΗ τετράγωνον πενταπλάσιός ἐστι τοῦ ΖΗ. ἀλλὰ ὁ ΞΟΠ γνώμων καὶ τὸ ΖΗ τετράγωνόν ἐστι τὸ ΔΝ. καί ἐστι τὸ μὲν ΔΝ τὸ ἀπὸ τῆς ΔΒ, τὸ δὲ ΗΖ τὸ ἀπὸ τῆς ΔΓ. τὸ ἄρα ἀπὸ τῆς ΔΒ πενταπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΔΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις δ΄ 4 Βιβλίον XIII
Ἐὰν εὐθεῖα γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, τὸ ἀπὸ τῆς ὅλης καὶ τοῦ ἐλάσσονος τμήματος, τὰ συναμφότερα τετράγωνα, τριπλάσιά ἐστι τοῦ ἀπὸ τοῦ μείζονος τμήματος τετραγώνου.
Ἔστω εὐθεῖα ἡ ΑΒ, καὶ τετμήσθω ἄκρον καὶ μέσον λόγον κατὰ τὸ Γ, καὶ ἔστω μεῖζον τμῆμα τὸ ΑΓ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΓΑ.
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν ἡ ΑΒ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Γ, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΑΓ, τὸ ἄρα ὑπὸ τῶν ΑΒΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΓ.
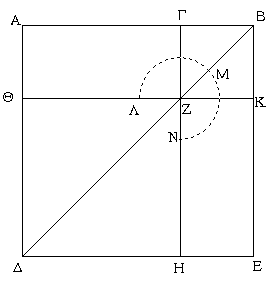
καί ἐστι τὸ μὲν ὑπὸ τῶν ΑΒΓ τὸ ΑΚ, τὸ δὲ ἀπὸ τῆς ΑΓ τὸ ΘΗ· ἴσον ἄρα ἐστὶ τὸ ΑΚ τῷ ΘΗ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΖ τῷ ΖΕ, κοινὸν προσκείσθω τὸ ΓΚ· ὅλον ἄρα τὸ ΑΚ ὅλῳ τῷ ΓΕ ἐστιν ἴσον· τὰ ἄρα ΑΚ, ΓΕ τοῦ ΑΚ ἐστι διπλάσια. ἀλλὰ τὰ ΑΚ, ΓΕ ὁ ΛΜΝ γνώμων ἐστὶ καὶ τὸ ΓΚ τετράγωνον· ὁ ἄρα ΛΜΝ γνώμων καὶ τὸ ΓΚ τετράγωνον διπλάσιά ἐστι τοῦ ΑΚ. ἀλλὰ μὴν καὶ τὸ ΑΚ τῷ ΘΗ ἐδείχθη ἴσον· ὁ ἄρα ΛΜΝ γνώμων καὶ [τὸ ΓΚ τετράγωνον διπλάσιά ἐστι τοῦ ΘΗ· ὥστε ὁ ΛΜΝ γνώμων καὶ] τὰ ΓΚ, ΘΗ τετράγωνα τριπλάσιά ἐστι τοῦ ΘΗ τετραγώνου. καί ἐστιν ὁ [μὲν] ΛΜΝ γνώμων καὶ τὰ ΓΚ, ΘΗ τετράγωνα ὅλον τὸ ΑΕ καὶ τὸ ΓΚ, ἅπερ ἐστὶ τὰ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα, τὸ δὲ ΗΘ τὸ ἀπὸ τῆς ΑΓ τετράγωνον. τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΑΓ τετραγώνου· ὅπερ ἔδει δεῖξαι.
Πρότασις ε΄ 5 Βιβλίον XIII
Ἐὰν εὐθεῖα γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, καὶ προστεθῇ αὐτῇ ἴση τῷ μείζονι τμήματι, ἡ ὅλη εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ἐξ ἀρχῆς εὐθεῖα.
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τετμήσθω κατὰ τὸ Γ σημεῖον, καὶ ἔστω μεῖζον τμῆμα ἡ ΑΓ, καὶ τῇ ΑΓ ἴση [κείσθω] ἡ ΑΔ. λέγω, ὅτι ἡ ΔΒ εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Α, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ἐξ ἀρχῆς εὐθεῖα ἡ ΑΒ.
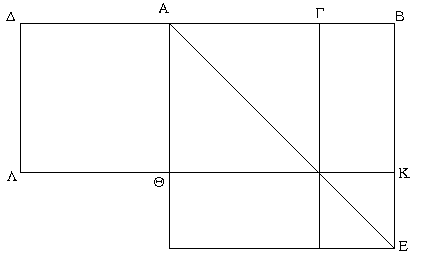
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΕ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Γ, τὸ ἄρα ὑπὸ ΑΒΓ ἴσον ἐστὶ τῷ ἀπὸ ΑΓ. καί ἐστι τὸ μὲν ὑπὸ ΑΒΓ τὸ ΓΕ, τὸ δὲ ἀπὸ τῆς ΑΓ τὸ ΓΘ· ἴσον ἄρα τὸ ΓΕ τῷ ΘΓ. ἀλλὰ τῷ μὲν ΓΕ ἴσον ἐστὶ τὸ ΘΕ, τῷ δὲ ΘΓ ἴσον τὸ ΔΘ· καὶ τὸ ΔΘ ἄρα ἴσον ἐστὶ τῷ ΘΕ [κοινὸν προσκείσθω τὸ ΘΒ]. ὅλον ἄρα τὸ ΔΚ ὅλῳ τῷ ΑΕ ἐστιν ἴσον. καί ἐστι τὸ μὲν ΔΚ τὸ ὑπὸ τῶν ΒΔ, ΔΑ· ἴση γὰρ ἡ ΑΔ τῇ ΔΛ· τὸ δὲ ΑΕ τὸ ἀπὸ τῆς ΑΒ· τὸ ἄρα ὑπὸ τῶν ΒΔΑ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ. ἔστιν ἄρα ὡς ἡ ΔΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΔ. μείζων δὲ ἡ ΔΒ τῆς ΒΑ· μείζων ἄρα καὶ ἡ ΒΑ τῆς ΑΔ.
Ἡ ἄρα ΔΒ ἄκρον καὶ μέσον λόγον τέμηται κατὰ τὸ Α, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΑΒ· ὅπερ ἔδει δεῖξαι.
Πρότασις ς΄ 6 Βιβλίον XIII
Ἐὰν εὐθεῖα ῥητὴ ἄκρον καὶ μέσον λόγον τμηθῇ, ἑκάτερον τῶν τμημάτων ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.
Ἔστω εὐθεῖα ῥητὴ ἡ ΑΒ καὶ τετμήσθω ἄκρον καὶ μέσον λόγον κατὰ τὸ Γ, καὶ ἔστω μεῖζον τμῆμα ἡ ΑΓ· λέγω, ὅτι ἑκατέρα τῶν ΑΓ, ΓΒ ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.
Ἐκβεβλήσθω γὰρ ἡ ΒΑ, καὶ κείσθω τῆς ΒΑ ἡμίσεια ἡ ΑΔ. ἐπεὶ οὖν εὐθεῖα ἡ ΑΒ τέτμηται ἄκρον καὶ μέσον λόγον κατὰ τὸ Γ, καὶ τῷ μείζονι τμήματι τῷ ΑΓ πρόσκειται ἡ ΑΔ ἡμίσεια οὖσα τῆς ΑΒ, τὸ ἄρα ἀπὸ ΓΔ τοῦ ἀπὸ ΔΑ πενταπλάσιόν ἐστιν.
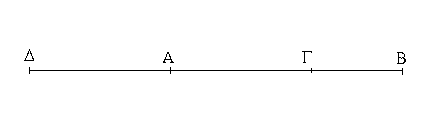
τὸ ἄρα ἀπὸ ΓΔ πρὸς τὸ ἀπὸ ΔΑ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν· σύμμετρον ἄρα τὸ ἀπὸ ΓΔ τῷ ἀπὸ ΔΑ. ῥητὸν δὲ τὸ ἀπὸ ΔΑ· ῥητὴ γὰρ [ἐστιν] ἡ ΔΑ ἡμίσεια οὖσα τῆς ΑΒ ῥητῆς οὔσης· ῥητὸν ἄρα καὶ τὸ ἀπὸ ΓΔ· ῥητὴ ἄρα ἐστὶ καὶ ἡ ΓΔ. καὶ ἐπεὶ τὸ ἀπὸ ΓΔ πρὸς τὸ ἀπὸ ΔΑ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ἀσύμμετρος ἄρα μήκει ἡ ΓΔ τῇ ΔΑ· αἱ ΓΔ, ΔΑ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΑΓ. πάλιν, ἐπεὶ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΑΓ, τὸ ἄρα ὑπὸ ΑΒ, ΒΓ τῷ ἀπὸ ΑΓ ἴσον ἐστίν. τὸ ἄρα ἀπὸ τῆς ΑΓ ἀποτομῆς παρὰ τὴν ΑΒ ῥητὴν παραβληθὲν πλάτος ποιεῖ τὴν ΒΓ. τὸ δὲ ἀπὸ ἀποτομῆς παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν πρώτην· ἀποτομὴ ἄρα πρώτη ἐστὶν ἡ ΓΒ. ἐδείχθη δὲ καὶ ἡ ΓΑ ἀποτομή.
Ἐὰν ἄρα εὐθεῖα ῥητὴ ἄκρον καὶ μέσον λόγον τμηθῇ, ἑκάτερον τῶν τμημάτων ἄλογός ἐστιν ἡ καλουμένη ἀποτομή· ὅπερ ἔδει δεῖξαι.
Πρότασις ζ΄ 7 Βιβλίον XIII
Ἐὰν πενταγώνου ἰσοπλεύρου αἱ τρεῖς γωνίαι ἤτοι αἱ κατὰ τὸ ἑξῆς ἢ αἱ μὴ κατὰ τὸ ἑξῆς ἴσαι ὦσιν, ἰσογώνιον ἔσται τὸ πεντάγωνον.
Πενταγώνου γὰρ ἰσοπλεύρου τοῦ ΑΒΓΔΕ αἱ τρεῖς γωνίαι πρότερον αἱ κατὰ τὸ ἑξῆς αἱ πρὸς τοῖς Α, Β, Γ ἴσαι ἀλλήλαις ἔστωσαν· λέγω, ὅτι ἰσογώνιόν ἐστι τὸ ΑΒΓΔΕ πεντάγωνον.
Ἐπεζεύχθωσαν γὰρ αἱ ΑΓ, ΒΕ, ΖΔ. καὶ ἐπεὶ δύο αἱ ΓΒ, ΒΑ δυσὶ ταῖς ΒΑ, ΑΕ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, καὶ γωνία ἡ ὑπὸ ΓΒΑ γωνίᾳ τῇ ὑπὸ ΒΑΕ ἐστιν ἴση, βάσις ἄρα ἡ ΑΓ βάσει τῇ ΒΕ ἐστιν ἴση, καὶ τὸ ΑΒΓ τρίγωνον τῷ ΑΒΕ τριγώνῳ ἴσον, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν, ἡ μὲν ὑπὸ ΒΓΑ τῇ ὑπὸ ΒΕΑ, ἡ δὲ ὑπὸ ΑΒΕ τῇ ὑπὸ ΓΑΒ· ὥστε καὶ πλευρὰ ἡ ΑΖ πλευρᾷ τῇ ΒΖ ἐστιν ἴση.
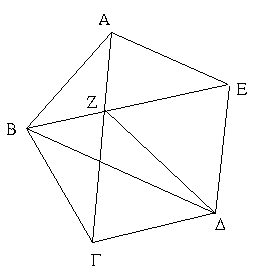
ἐδείχθη δὲ καὶ ὅλη ἡ ΑΓ ὅλῃ τῇ ΒΕ ἴση· καὶ λοιπὴ ἄρα ἡ ΖΓ λοιπῇ τῇ ΖΕ ἐστιν ἴση. ἔστι δὲ καὶ ἡ ΓΔ τῇ ΔΕ ἴση. δύο δὴ αἱ ΖΓ, ΓΔ δυσὶ ταῖς ΖΕ, ΕΔ ἴσαι εἰσίν· καὶ βάσις αὐτῶν κοινὴ ἡ ΖΔ· γωνία ἄρα ἡ ὑπὸ ΖΓΔ γωνίᾳ τῇ ὑπὸ ΖΕΔ ἐστιν ἴση. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΒΓΑ τῇ ὑπὸ ΑΕΒ ἴση· καὶ ὅλη ἄρα ἡ ὑπὸ ΒΓΔ ὅλῃ τῇ ὑπὸ ΑΕΔ ἴση. ἀλλ' ἡ ὑπὸ ΒΓΔ ἴση ὑπόκειται ταῖς πρὸς τοῖς Α, Β γωνίαις· καὶ ἡ ὑπὸ ΑΕΔ ἄρα ταῖς πρὸς τοῖς Α, Β γωνίαις ἴση ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ὑπὸ ΓΔΕ γωνία ἴση ἐστὶ ταῖς πρὸς τοῖς Α, Β, Γ γωνίαις· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓΔΕ πεντάγωνον.
Ἀλλὰ δὴ μὴ ἔστωσαν ἴσαι αἱ κατὰ τὸ ἑξῆς γωνίαι, ἀλλ' ἔστωσαν ἴσαι αἱ πρὸς τοῖς Α, Γ, Δ σημείοις· λέγω, ὅτι καὶ οὕτως ἰσογώνιόν ἐστι τὸ ΑΒΓΔΕ πεντάγωνον.
Ἐπεζεύχθω γὰρ ἡ ΒΔ. καὶ ἐπεὶ δύο αἱ ΒΑ, ΑΕ δυσὶ ταῖς ΒΓ, ΓΔ ἴσαι εἰσὶ καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΒΕ βάσει τῇ ΒΔ ἴση ἐστίν, καὶ τὸ ΑΒΕ τρίγωνον τῷ ΒΓΔ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΕΒ γωνία τῇ ὑπὸ ΓΔΒ. ἔστι δὲ καὶ ἡ ὑπὸ ΒΕΔ γωνία τῇ ὑπὸ ΒΔΕ ἴση, ἐπεὶ καὶ πλευρὰ ἡ ΒΕ πλευρᾷ τῇ ΒΔ ἐστιν ἴση. καὶ ὅλη ἄρα ἡ ὑπὸ ΑΕΔ γωνία ὅλῃ τῇ ὑπὸ ΓΔΕ ἐστιν ἴση. ἀλλὰ ἡ ὑπὸ ΓΔΕ ταῖς πρὸς τοῖς Α, Γ γωνίαις ὑπόκειται ἴση· καὶ ἡ ὑπὸ ΑΕΔ ἄρα γωνία ταῖς πρὸς τοῖς Α, Γ ἴση ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ὑπὸ ΑΒΓ ἴση ἐστὶ ταῖς πρὸς τοῖς Α, Γ, Δ γωνίαις. ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΓΔΕ πεντάγωνον· ὅπερ ἔδει δεῖξαι.
Πρότασις η΄ 8 Βιβλίον XIII
Ἐὰν πενταγώνου ἰσοπλεύρου καὶ ἰσογωνίου τὰς κατὰ τὸ ἑξῆς δύο γωνίας ὑποτείνωσιν εὐθεῖαι, ἄκρον καὶ μέσον λόγον τέμνουσιν ἀλλήλας, καὶ τὰ μείζονα αὐτῶν τμήματα ἴσα ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ.
Πενταγώνου γὰρ ἰσοπλεύρου καὶ ἰσογωνίου τοῦ ΑΒΓ ΔΕ δύο γωνίας τὰς κατὰ τὸ ἑξῆς τὰς πρὸς τοῖς Α, Β ὑποτεινέτωσαν εὐθεῖαι αἱ ΑΓ, ΒΕ τέμνουσαι ἀλλήλας κατὰ τὸ Θ σημεῖον· λέγω, ὅτι ἑκατέρα αὐτῶν ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ σημεῖον, καὶ τὰ μείζονα αὐτῶν τμήματα ἴσα ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ.
Περιγεγράφθω γὰρ περὶ τὸ ΑΒΓΔΕ πεντάγωνον κύκλος ὁ ΑΒΓΔΕ. καὶ ἐπεὶ δύο εὐθεῖαι αἱ ΕΑ, ΑΒ δυσὶ ταῖς ΑΒ, ΒΓ ἴσαι εἰσὶ καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΒΕ βάσει τῇ ΑΓ ἴση ἐστίν, καὶ τὸ ΑΒΕ τρίγωνον τῷ ΑΒΓ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΑΒΕ· διπλῆ ἄρα ἡ ὑπὸ ΑΘΕ τῆς ὑπὸ ΒΑΘ. ἔστι δὲ καὶ ἡ ὑπὸ ΕΑΓ τῆς ὑπὸ ΒΑΓ διπλῆ, ἐπειδήπερ καὶ περιφέρεια ἡ ΕΔΓ περιφερείας τῆς ΓΒ ἐστι διπλῆ· ἴση ἄρα ἡ ὑπὸ ΘΑΕ γωνία τῇ ὑπὸ ΑΘΕ· ὥστε καὶ ἡ ΘΕ εὐθεῖα τῇ ΕΑ, τουτέστι τῇ ΑΒ ἐστιν ἴση.
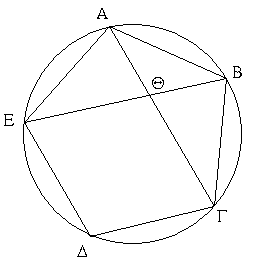
καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΑ εὐθεῖα τῇ ΑΕ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΑΒΕ τῇ ὑπὸ ΑΕΒ. ἀλλὰ ἡ ὑπὸ ΑΒΕ τῇ ὑπὸ ΒΑΘ ἐδείχθη ἴση· καὶ ἡ ὑπὸ ΒΕΑ ἄρα τῇ ὑπὸ ΒΑΘ ἐστιν ἴση. καὶ κοινὴ τῶν δύο τριγώνων τοῦ τε ΑΒΕ καὶ τοῦ ΑΒΘ ἐστιν ἡ ὑπὸ ΑΒΕ· λοιπὴ ἄρα ἡ ὑπὸ ΒΑΕ γωνία λοιπῇ τῇ ὑπὸ ΑΘΒ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΕ τρίγωνον τῷ ΑΒΘ τριγώνῳ· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΕΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΑΒ πρὸς τὴν ΒΘ. ἴση δὲ ἡ ΒΑ τῇ ΕΘ· ὡς ἄρα ἡ ΒΕ πρὸς τὴν ΕΘ, οὕτως ἡ ΕΘ πρὸς τὴν ΘΒ. μείζων δὲ ἡ ΒΕ τῆς ΕΘ· μείζων ἄρα καὶ ἡ ΕΘ τῆς ΘΒ. ἡ ΒΕ ἄρα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ, καὶ τὸ μεῖζον τμῆμα τὸ ΘΕ ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΑΓ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ, καὶ τὸ μεῖζον αὐτῆς τμῆμα ἡ ΓΘ ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ· ὅπερ ἔδει δεῖξαι.
Πρότασις θ΄ 9 Βιβλίον XIII
Ἐὰν ἡ τοῦ ἑξαγώνου πλευρὰ καὶ ἡ τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων συντεθῶσιν, ἡ ὅλη εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ τοῦ ἑξαγώνου πλευρά.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ τῶν εἰς τὸν ΑΒΓ κύκλον ἐγγραφομένων σχημάτων, δεκαγώνου μὲν ἔστω πλευρὰ ἡ ΒΓ, ἑξαγώνου δὲ ἡ ΓΔ, καὶ ἔστωσαν ἐπ᾿ εὐθείας· λέγω, ὅτι ἡ ὅλη εὐθεῖα ἡ ΒΔ ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΓΔ.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ε σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΕΒ, ΕΓ, ΕΔ, καὶ διήχθω ἡ ΒΕ ἐπὶ τὸ Α. ἐπεὶ δεκαγώνου ἰσοπλεύρου πλευρά ἐστιν ἡ ΒΓ, πενταπλασίων ἄρα ἡ ΑΓΒ περιφέρεια τῆς ΒΓ περιφερείας· τετραπλασίων ἄρα ἡ ΑΓ περιφέρεια τῆς ΓΒ. ὡς δὲ ἡ ΑΓ περιφέρεια πρὸς τὴν ΓΒ, οὕτως ἡ ὑπὸ ΑΕΓ γωνία πρὸς τὴν ὑπὸ ΓΕΒ· τετραπλασίων ἄρα ἡ ὑπὸ ΑΕΓ τῆς ὑπὸ ΓΕΒ.
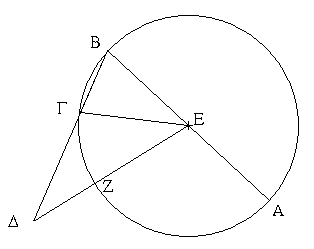
καὶ ἐπεὶ ἴση ἡ ὑπὸ ΕΒΓ γωνία τῇ ὑπὸ ΕΓΒ, ἡ ἄρα ὑπὸ ΑΕΓ γωνία διπλασία ἐστὶ τῆς ὑπὸ ΕΓΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΕΓ εὐθεῖα τῇ ΓΔ· ἑκατέρα γὰρ αὐτῶν ἴση ἐστὶ τῇ τοῦ ἑξαγώνου πλευρᾷ τοῦ εἰς τὸν ΑΒΓ κύκλον [ἐγγραφομένου]· ἴση ἐστὶ καὶ ἡ ὑπὸ ΓΕΔ γωνία τῇ ὑπὸ ΓΔΕ γωνίᾳ· διπλασία ἄρα ἡ ὑπὸ ΕΓΒ γωνία τῆς ὑπὸ ΕΔΓ. ἀλλὰ τῆς ὑπὸ ΕΓΒ διπλασία ἐδείχθη ἡ ὑπὸ ΑΕΓ· τετραπλασία ἄρα ἡ ὑπὸ ΑΕΓ τῆς ὑπὸ ΕΔΓ. ἐδείχθη δὲ καὶ τῆς ὑπὸ ΒΕΓ τετραπλασία ἡ ὑπὸ ΑΕΓ· ἴση ἄρα ἡ ὑπὸ ΕΔΓ τῇ ὑπὸ ΒΕΓ. κοινὴ δὲ τῶν δύο τριγώνων, τοῦ τε ΒΕΓ καὶ τοῦ ΒΕΔ, ἡ ὑπὸ ΕΒΔ γωνία· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΒΕΔ τῇ ὑπὸ ΕΓΒ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΕΒΔ τρίγωνον τῷ ΕΒΓ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΕΒ πρὸς τὴν ΒΓ. ἴση δὲ ἡ ΕΒ τῇ ΓΔ. ἔστιν ἄρα ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΒ. μείζων δὲ ἡ ΒΔ τῆς ΔΓ· μείζων ἄρα καὶ ἡ ΔΓ τῆς ΓΒ. ἡ ΒΔ ἄρα εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται [κατὰ τὸ Γ], καὶ τὸ μεῖζον τμῆμα αὐτῆς ἐστιν ἡ ΔΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις ι΄ 10 Βιβλίον XIII
Ἐὰν εἰς κύκλον πεντάγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ πενταγώνου πλευρὰ δύναται τήν τε τοῦ ἑξαγώνου καὶ τὴν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων.
Ἔστω κύκλος ὁ ΑΒΓΔΕ, καὶ εἰς τὸν ΑΒΓΔΕ κύκλον πεντάγωνον ἰσόπλευρον ἐγγεγράφθω τὸ ΑΒΓΔΕ. λέγω, ὅτι ἡ τοῦ ΑΒΓΔΕ πενταγώνου πλευρὰ δύναται τήν τε τοῦ ἑξαγώνου καὶ τὴν τοῦ δεκαγώνου πλευρὰν τῶν εἰς τὸν ΑΒΓΔΕ κύκλον ἐγγραφομένων.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ζ σημεῖον, καὶ ἐπιζευχθεῖσα ἡ ΑΖ διήχθω ἐπὶ τὸ Η σημεῖον, καὶ ἐπεζεύχθω ἡ ΖΒ, καὶ ἀπὸ τοῦ Ζ ἐπὶ τὴν ΑΒ κάθετος ἤχθω ἡ ΖΘ, καὶ διήχθω ἐπὶ τὸ Κ, καὶ ἐπεζεύχθωσαν αἱ ΑΚ, ΚΒ, καὶ πάλιν ἀπὸ τοῦ Ζ ἐπὶ τὴν ΑΚ κάθετος ἤχθω ἡ ΖΛ, καὶ διήχθω ἐπὶ τὸ Μ, καὶ ἐπεζεύχθω ἡ ΚΝ. ἐπεὶ ἴση ἐστὶν ἡ ΑΒΓΗ περιφέρεια τῇ ΑΕΔΗ περιφερείᾳ, ὧν ἡ ΑΒΓ τῇ ΑΕΔ ἐστιν ἴση, λοιπὴ ἄρα ἡ ΓΗ περιφέρεια λοιπῇ τῇ ΗΔ ἐστιν ἴση. πενταγώνου δὲ ἡ ΓΔ· δεκαγώνου ἄρα ἡ ΓΗ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΖΑ τῇ ΖΒ, καὶ κάθετος ἡ ΖΘ, ἴση ἄρα καὶ ἡ ὑπὸ ΑΖΚ γωνία τῇ ὑπὸ ΚΖΒ. ὥστε καὶ περιφέρεια ἡ ΑΚ τῇ ΚΒ ἐστιν ἴση· διπλῆ ἄρα ἡ ΑΒ περιφέρεια τῆς ΒΚ περιφερείας· δεκαγώνου ἄρα πλευρά ἐστιν ἡ ΑΚ εὐθεῖα. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΑΚ τῆς ΚΜ ἐστι διπλῆ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΑΒ περιφέρεια τῆς ΒΚ περιφερείας, ἴση δὲ ἡ ΓΔ περιφέρεια τῇ ΑΒ περιφερείᾳ, διπλῆ ἄρα καὶ ἡ ΓΔ περιφέρεια τῆς ΒΚ περιφερείας.
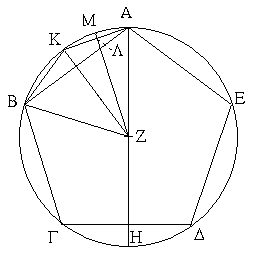
ἔστι δὲ ἡ ΓΔ περιφέρεια καὶ τῆς ΓΗ διπλῆ· ἴση ἄρα ἡ ΓΗ περιφέρεια τῇ ΒΚ περιφερείᾳ. ἀλλὰ ἡ ΒΚ τῆς ΚΜ ἐστι διπλῆ, ἐπεὶ καὶ ἡ ΚΑ· καὶ ἡ ΓΗ ἄρα τῆς ΚΜ ἐστι διπλῆ. ἀλλὰ μὴν καὶ ἡ ΓΒ περιφέρεια τῆς ΒΚ περιφερείας ἐστὶ διπλῆ· ἴση γὰρ ἡ ΓΒ περιφέρεια τῇ ΒΑ. καὶ ὅλη ἄρα ἡ ΗΒ περιφέρεια τῆς ΒΜ ἐστι διπλῆ· ὥστε καὶ γωνία ἡ ὑπὸ ΗΖΒ γωνίας τῆς ὑπὸ ΒΖΜ [ἐστι] διπλῆ. ἔστι δὲ ἡ ὑπὸ ΗΖΒ καὶ τῆς ὑπὸ ΖΑΒ διπλῆ· ἴση γὰρ ἡ ὑπὸ ΖΑΒ τῇ ὑπὸ ΑΒΖ. καὶ ἡ ὑπὸ ΒΖΝ ἄρα τῇ ὑπὸ ΖΑΒ ἐστιν ἴση. κοινὴ δὲ τῶν δύο τριγώνων, τοῦ τε ΑΒΖ καὶ τοῦ ΒΖΝ, ἡ ὑπὸ ΑΒΖ γωνία· λοιπὴ ἄρα ἡ ὑπὸ ΑΖΒ λοιπῇ τῇ ὑπὸ ΒΝΖ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΖ τρίγωνον τῷ ΒΖΝ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΑΒ εὐθεῖα πρὸς τὴν ΒΖ, οὕτως ἡ ΖΒ πρὸς τὴν ΒΝ· τὸ ἄρα ὑπὸ τῶν ΑΒΝ ἴσον ἐστὶ τῷ ἀπὸ ΒΖ. πάλιν ἐπεὶ ἴση ἐστὶν ἡ ΑΛ τῇ ΛΚ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΛΝ, βάσις ἄρα ἡ ΚΝ βάσει τῇ ΑΝ ἐστιν ἴση· καὶ γωνία ἄρα ἡ ὑπὸ ΛΚΝ γωνίᾳ τῇ ὑπὸ ΛΑΝ ἐστιν ἴση. ἀλλὰ ἡ ὑπὸ ΛΑΝ τῇ ὑπὸ ΚΒΝ ἐστιν ἴση· καὶ ἡ ὑπὸ ΛΚΝ ἄρα τῇ ὑπὸ ΚΒΝ ἐστιν ἴση. καὶ κοινὴ τῶν δύο τριγώνων τοῦ τε ΑΚΒ καὶ τοῦ ΑΚΝ ἡ πρὸς τῷ Α. λοιπὴ ἄρα ἡ ὑπὸ ΑΚΒ λοιπῇ τῇ ὑπὸ ΚΝΑ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΚΒΑ τρίγωνον τῷ ΚΝΑ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΑ εὐθεῖα πρὸς τὴν ΑΚ, οὕτως ἡ ΚΑ πρὸς τὴν ΑΝ· τὸ ἄρα ὑπὸ τῶν ΒΑΝ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΚ. ἐδείχθη δὲ καὶ τὸ ὑπὸ τῶν ΑΒΝ ἴσον τῷ ἀπὸ τῆς ΒΖ· τὸ ἄρα ὑπὸ τῶν ΑΒΝ μετὰ τοῦ ὑπὸ ΒΑΝ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΒΑ, ἴσον ἐστὶ τῷ ἀπὸ τῆς ΒΖ μετὰ τοῦ ἀπὸ τῆς ΑΚ. καί ἐστιν ἡ μὲν ΒΑ πενταγώνου πλευρά, ἡ δὲ ΒΖ ἑξαγώνου, ἡ δὲ ΑΚ δεκαγώνου.
Ἡ ἄρα τοῦ πενταγώνου πλευρὰ δύναται τήν τε τοῦ ἑξαγώνου καὶ τὴν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων· ὅπερ ἔδει δεῖξαι.
Πρότασις ια΄ 11 Βιβλίον XIII
Ἐὰν εἰς κύκλον ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Εἰς γὰρ κύκλον τὸν ΑΒΓΔΕ ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγεγράφθω τὸ ΑΒΓΔΕ· λέγω, ὅτι ἡ τοῦ [ΑΒΓΔΕ] πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ζ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΖΒ καὶ διήχθωσαν ἐπὶ τὰ Η, Θ σημεῖα, καὶ ἐπεζεύχθω ἡ ΑΓ, καὶ κείσθω τῆς ΑΖ τέταρτον μέρος ἡ ΖΚ. ῥητὴ δὲ ἡ ΑΖ· ῥητὴ ἄρα καὶ ἡ ΖΚ. ἔστι δὲ καὶ ἡ ΒΖ ῥητή· ὅλη ἄρα ἡ ΒΚ ῥητή ἐστιν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓΗ περιφέρεια τῇ ΑΔΗ περιφερείᾳ, ὧν ἡ ΑΒΓ τῇ ΑΕΔ ἐστιν ἴση, λοιπὴ ἄρα ἡ ΓΗ λοιπῇ τῇ ΗΔ ἐστιν ἴση. καὶ ἐὰν ἐπιζεύξωμεν τὴν ΑΔ, συνάγονται ὀρθαὶ αἱ πρὸς τῷ Λ γωνίαι, καὶ διπλῆ ἡ ΓΔ τῆς ΓΛ. διὰ τὰ αὐτὰ δὴ καὶ αἱ πρὸς τῷ Μ ὀρθαί εἰσιν, καὶ διπλῆ ἡ ΑΓ τῆς ΓΜ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΑΛΓ γωνία τῇ ὑπὸ ΑΜΖ, κοινὴ δὲ τῶν δύο τριγώνων τοῦ τε ΑΓΛ καὶ τοῦ ΑΜΖ ἡ ὑπὸ ΛΑΓ, λοιπὴ ἄρα ἡ ὑπὸ ΑΓΛ λοιπῇ τῇ ὑπὸ ΜΖΑ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΓΛ τρίγωνον τῷ ΑΜΖ τριγώνῳ· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΛΓ πρὸς ΓΑ, οὕτως ἡ ΜΖ πρὸς ΖΑ· καὶ τῶν ἡγουμένων τὰ διπλάσια· ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ΓΑ, οὕτως ἡ τῆς ΜΖ διπλῆ πρὸς τὴν ΖΑ. ὡς δὲ ἡ τῆς ΜΖ διπλῆ πρὸς τὴν ΖΑ, οὕτως ἡ ΜΖ πρὸς τὴν ἡμίσειαν τῆς ΖΑ· καὶ ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ΓΑ, οὕτως ἡ ΜΖ πρὸς τὴν ἡμίσειαν τῆς ΖΑ. καὶ τῶν ἑπομένων τὰ ἡμίσεα· ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ἡμίσειαν τῆς ΓΑ, οὕτως ἡ ΜΖ πρὸς τὸ τέταρτον τῆς ΖΑ.
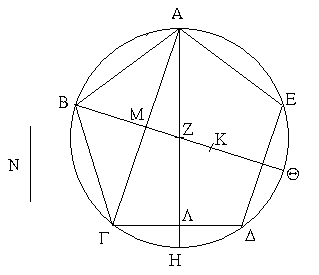
καί ἐστι τῆς μὲν ΛΓ διπλῆ ἡ ΔΓ, τῆς δὲ ΓΑ ἡμίσεια ἡ ΓΜ, τῆς δὲ ΖΑ τέταρτον μέρος ἡ ΖΚ· ἔστιν ἄρα ὡς ἡ ΔΓ πρὸς τὴν ΓΜ, οὕτως ἡ ΜΖ πρὸς τὴν ΖΚ. συνθέντι καὶ ὡς συναμφότερος ἡ ΔΓΜ πρὸς τὴν ΓΜ, οὕτως ἡ ΜΚ πρὸς ΚΖ· καὶ ὡς ἄρα τὸ ἀπὸ συναμφοτέρου τῆς ΔΓΜ πρὸς τὸ ἀπὸ ΓΜ, οὕτως τὸ ἀπὸ ΜΚ πρὸς τὸ ἀπὸ ΚΖ. καὶ ἐπεὶ τῆς ὑπὸ δύο πλευρὰς τοῦ πενταγώνου ὑποτεινούσης, οἷον τῆς ΑΓ, ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμα ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ, τουτέστι τῇ ΔΓ, τὸ δὲ μεῖζον τμῆμα προσλαβὸν τὴν ἡμίσειαν τῆς ὅλης πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τῆς ὅλης, καί ἐστιν ὅλης τῆς ΑΓ ἡμίσεια ἡ ΓΜ, τὸ ἄρα ἀπὸ τῆς ΔΓΜ ὡς μιᾶς πενταπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΓΜ. ὡς δὲ τὸ ἀπὸ τῆς ΔΓΜ ὡς μιᾶς πρὸς τὸ ἀπὸ τῆς ΓΜ, οὕτως ἐδείχθη τὸ ἀπὸ τῆς ΜΚ πρὸς τὸ ἀπὸ τῆς ΚΖ· πενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΜΚ τοῦ ἀπὸ τῆς ΚΖ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΚΖ· ῥητὴ γὰρ ἡ διάμετρος· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΜΚ· ῥητὴ ἄρα ἐστὶν ἡ ΜΚ [δυνάμει μόνον]. καὶ ἐπεὶ τετραπλασία ἐστὶν ἡ ΒΖ τῆς ΖΚ, πενταπλασία ἄρα ἐστὶν ἡ ΒΚ τῆς ΚΖ· εἰκοσιπενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΖ. πενταπλάσιον δὲ τὸ ἀπὸ τῆς ΜΚ τοῦ ἀπὸ τῆς ΚΖ· πενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ· τὸ ἄρα ἀπὸ τῆς ΒΚ πρὸς τὸ ἀπὸ ΚΜ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΚ τῇ ΚΜ μήκει. καί ἐστι ῥητὴ ἑκατέρα αὐτῶν. αἱ ΒΚ, ΚΜ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ἐὰν δὲ ἀπὸ ῥητῆς ῥητὴ ἀφαιρεθῇ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, ἡ λοιπὴ ἄλογός ἐστιν ἀποτομή· ἀποτομὴ ἄρα ἐστὶν ἡ ΜΒ, προσαρμόζουσα δὲ αὐτῇ ἡ ΜΚ. λέγω δή, ὅτι καὶ τετάρτη. ᾧ δὴ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ, ἐκείνῳ ἴσον ἔστω τὸ ἀπὸ τῆς Ν· ἡ ΒΚ ἄρα τῆς ΚΜ μεῖζον δύναται τῇ Ν. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΚΖ τῇ ΖΒ, καὶ συνθέντι σύμμετρός ἐστιν ἡ ΚΒ τῇ ΖΒ. ἀλλὰ ἡ ΒΖ τῇ ΒΘ σύμμετρός ἐστιν· καὶ ἡ ΒΚ ἄρα τῇ ΒΘ σύμμετρός ἐστιν. καὶ ἐπεὶ πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ, τὸ ἄρα ἀπὸ τῆς ΒΚ πρὸς τὸ ἀπὸ τῆς ΚΜ λόγον ἔχει, ὃν ε πρὸς ἕν. ἀναστρέψαντι ἄρα τὸ ἀπὸ τῆς ΒΚ πρὸς τὸ ἀπὸ τῆς Ν λόγον ἔχει, ὅν ε πρὸς δ. οὐχ ὃν τετράγωνος πρὸς τετράγωνον· ἀσύμετρος ἄρα ἐστὶν ἡ ΒΚ τῇ Ν· ἡ ΒΚ ἄρα τῆς ΚΜ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. ἐπεὶ οὖν ὅλη ἡ ΒΚ τῆς προσαρμοζούσης τῆς ΚΜ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ὅλη ἡ ΒΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΒΘ, ἀποτομὴ ἄρα τετάρτη ἐστὶν ἡ ΜΒ. τὸ δὲ ὑπὸ ῥητῆς καὶ ἀποτομῆς τετάρτης περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλεῖται δὲ ἐλάττων. δύναται δὲ τὸ ὑπὸ τῶν ΘΒΜ ἡ ΑΒ διὰ τὸ ἐπιζευγνυμένης τῆς ΑΘ ἰσογώνιον γίνεσθαι τὸ ΑΒΘ τρίγωνον τῷ ΑΒΜ τριγώνῳ καὶ εἶναι ὡς τὴν ΘΒ πρὸς τὴν ΒΑ, οὕτως τὴν ΑΒ πρὸς τὴν ΒΜ.
Ἡ ἄρα ΑΒ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων· ὅπερ ἔδει δεῖξαι.
Πρότασις ιβ΄ 12 Βιβλίον XIII
Ἐὰν εἰς κύκλον τρίγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ τριγώνου πλευρὰ δυνάμει τριπλασίων ἐστὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ εἰς αὐτὸν τρίγωνον ἰσόπλευρον ἐγγεγράφθω τὸ ΑΒΓ· λέγω, ὅτι τοῦ ΑΒΓ τριγώνου μία πλευρὰ δυνάμει τριπλασίων ἐστὶ τῆς ἐκ τοῦ κέντρου τοῦ ΑΒΓ κύκλου.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ ΑΒΓ κύκλου τὸ Δ, καὶ ἐπιζευχθεῖσα ἡ ΑΔ διήχθω ἐπὶ τὸ Ε, καὶ ἐπεζεύχθω ἡ ΒΕ. καὶ ἐπεὶ ἰσόπλευρόν ἐστι τὸ ΑΒΓ τρίγωνον, ἡ ΒΕΓ ἄρα περιφέρεια τρίτον μέρος ἐστὶ τῆς τοῦ ΑΒΓ κύκλου περιφερείας.
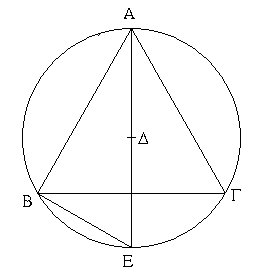
ἡ ἄρα ΒΕ περιφέρεια ἕκτον ἐστὶ μέρος τῆς τοῦ κύκλου περιφερείας· ἑξαγώνου ἄρα ἐστὶν ἡ ΒΕ εὐθεῖα· ἴση ἄρα ἐστὶ τῇ ἐκ τοῦ κέντρου τῇ ΔΕ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΑΕ τῆς ΔΕ, τετραπλάσιόν ἐστι τὸ ἀπὸ τῆς ΑΕ τοῦ ἀπὸ τῆς ΕΔ, τουτέστι τοῦ ἀπὸ τῆς ΒΕ. ἴσον δὲ τὸ ἀπὸ τῆς ΑΕ τοῖς ἀπὸ τῶν ΑΒ, ΒΕ· τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΕ τετραπλάσιά ἐστι τοῦ ἀπὸ τῆς ΒΕ. διελόντι ἄρα τὸ ἀπὸ τῆς ΑΒ τριπλάσιόν ἐστι τοῦ ἀπὸ ΒΕ. ἴση δὲ ἡ ΒΕ τῇ ΔΕ· τὸ ἄρα ἀπὸ τῆς ΑΒ τριπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΔΕ.
Ἡ ἄρα τοῦ τριγώνου πλευρὰ δυνάμει τριπλασία ἐστὶ τῆς ἐκ τοῦ κέντρου [τοῦ κύκλου]· ὅπερ ἔδει δεῖξαι.
Πρότασις ιγ΄ 13 Βιβλίον XIII
Πυραμίδα συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει ἡμιολία ἐστὶ τῆς πλευρᾶς τῆς πυραμίδος.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ, καὶ τετμήσθω κατὰ τὸ Γ σημεῖον, ὥστε διπλασίαν εἶναι τὴν ΑΓ τῆς ΓΒ· καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἤχθω ἀπὸ τοῦ Γ σημείου τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΑ· καὶ ἐκκείσθω κύκλος ὁ ΕΖΗ ἴσην ἔχων τὴν ἐκ τοῦ κέντρου τῇ ΔΓ, καὶ ἐγγεγράφθω εἰς τὸν ΕΖΗ κύκλον τρίγωνον ἰσόπλευρον τὸ ΕΖΗ· καὶ εἰλήφθω τὸ κέντρον τοῦ κύκλου τὸ Θ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΕΘ, ΘΖ, ΘΗ· καὶ ἀνεστάτω ἀπὸ τοῦ Θ σημείου τῷ τοῦ ΕΖΗ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΘΚ, καὶ ἀφῃρήσθω ἀπὸ τῆς ΘΚ τῇ ΑΓ εὐθείᾳ ἴση ἡ ΘΚ, καὶ ἐπεζεύχθωσαν αἱ ΚΕ, ΚΖ, ΚΗ. καὶ ἐπεὶ ἡ ΚΘ ὀρθή ἐστι πρὸς τὸ τοῦ ΕΖΗ κύκλου ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ τοῦ ΕΖΗ κύκλου ἐπιπέδῳ ὀρθὰς ποιήσει γωνίας. ἅπτεται δὲ αὐτῆς ἑκάστη τῶν ΘΕ, ΘΖ, ΘΗ· ἡ ΘΚ ἄρα πρὸς ἑκάστην τῶν ΘΕ, ΘΖ, ΘΗ ὀρθή ἐστιν. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΑΓ τῇ ΘΚ, ἡ δὲ ΓΔ τῇ ΘΕ, καὶ ὀρθὰς γωνίας περιέχουσιν, βάσις ἄρα ἡ ΔΑ βάσει τῇ ΚΕ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ΚΖ, ΚΗ τῇ ΔΑ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΚΕ, ΚΖ, ΚΗ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΑΓ τῆς ΓΒ, τριπλῆ ἄρα ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΔ πρὸς τὸ ἀπὸ τῆς ΔΓ, ὡς ἑξῆς δειχθήσεται. τριπλάσιον ἄρα τὸ ἀπὸ τῆς ΑΔ τοῦ ἀπὸ τῆς ΔΓ. ἔστι δὲ καὶ τὸ ἀπὸ τῆς ΖΕ τοῦ ἀπὸ τῆς ΕΘ τριπλάσιον, καί ἐστιν ἴση ἡ ΔΓ τῇ ΕΘ· ἴση ἄρα καὶ ἡ ΔΑ τῇ ΕΖ. ἀλλὰ ἡ ΔΑ ἑκάστῃ τῶν ΚΕ, ΚΖ, ΚΗ ἐδείχθη ἴση· καὶ ἑκάστη ἄρα τῶν ΕΖ, ΖΗ, ΗΕ ἑκάστῃ τῶν ΚΕ, ΚΖ, ΚΗ ἐστιν ἴση· ἰσόπλευρα ἄρα ἐστὶ τὰ τέσσαρα τρίγωνα τὰ ΕΖΗ, ΚΕΖ, ΚΖΗ, ΚΕΗ. πυραμὶς ἄρα συνέσταται ἐκ τεσσάρων τριγώνων ἰσοπλεύρων, ἧς βάσις μέν ἐστι τὸ ΕΖΗ τρίγωνον, κορυφὴ δὲ τὸ Κ σημεῖον.
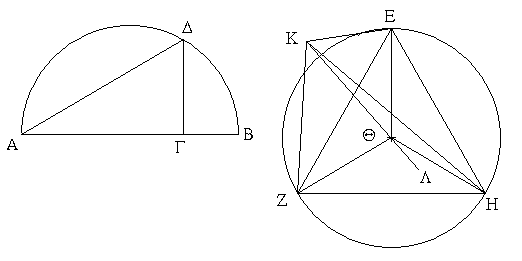
Δεῖ δὴ αὐτὴν καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος ἡμιολία ἐστὶ δυνάμει τῆς πλευρᾶς τῆς πυραμίδος.
Ἐκβεβλήσθω γὰρ ἐπ᾿ εὐθείας τῇ ΚΘ εὐθεῖα ἡ ΘΛ, καὶ κείσθω τῇ ΓΒ ἴση ἡ ΘΛ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΓ πρὸς τὴν ΓΔ, οὕτως ἡ ΓΔ πρὸς τὴν ΓΒ, ἴση δὲ ἡ μὲν ΑΓ τῇ ΚΘ, ἡ δὲ ΓΔ τῇ ΘΕ, ἡ δὲ ΓΒ τῇ ΘΛ, ἔστιν ἄρα ὡς ἡ ΚΘ πρὸς τὴν ΘΕ, οὕτως ἡ ΕΘ πρὸς τὴν ΘΛ· τὸ ἄρα ὑπὸ τῶν ΚΘ, ΘΛ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΘ. καί ἐστιν ὀρθὴ ἑκατέρα τῶν ὑπὸ ΚΘΕ, ΕΘΛ γωνιῶν· τὸ ἄρα ἐπὶ τῆς ΚΛ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Ε [ἐπειδήπερ ἐὰν ἐπιζεύξωμεν τὴν ΕΛ, ὀρθὴ γίνεται ἡ ὑπὸ ΛΕΚ γωνία διὰ τὸ ἰσογώνιον γίνεσθαι τὸ ΕΛΚ τρίγωνον ἑκατέρῳ τῶν ΕΛΘ, ΕΘΚ τριγώνων]. ἐὰν δὴ μενούσης τῆς ΚΛ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἥξει καὶ διὰ τῶν Ζ, Η σημείων ἐπιζευγνυμένων τῶν ΖΛ, ΛΗ καὶ ὀρθῶν ὁμοίως γινομένων τῶν πρὸς τοῖς Ζ, Η γωνιῶν· καὶ ἔσται ἡ πυραμὶς σφαίρᾳ περιειλημμένη τῇ δοθείσῃ. ἡ γὰρ ΚΛ τῆς σφαίρας διάμετρος ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ τῇ ΑΒ, ἐπειδήπερ τῇ μὲν ΑΓ ἴση κεῖται ἡ ΚΘ, τῇ δὲ ΓΒ ἡ ΘΛ.
Λέγω δή, ὅτι ἡ τῆς σφαίρας διάμετρος ἡμιολία ἐστὶ δυνάμει τῆς πλευρᾶς τῆς πυραμίδος.
Ἐπεὶ γὰρ διπλῆ ἐστιν ἡ ΑΓ τῆς ΓΒ, τριπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΓ· ἀναστρέψαντι ἡμιολία ἄρα ἐστὶν ἡ ΒΑ τῆς ΑΓ. ὡς δὲ ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΔ [ἐπειδήπερ ἐπιζευγνυμένης τῆς ΔΒ ἐστιν ὡς ἡ ΒΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΔΑ πρὸς τὴν ΑΓ διὰ τὴν ὁμοιότητα τῶν ΔΑΒ, ΔΑΓ τριγώνων, καὶ εἶναι ὡς τὴν πρώτην πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ἀπὸ τῆς δευτέρας]. ἡμιόλιον ἄρα καὶ τὸ ἀπὸ τῆς ΒΑ τοῦ ἀπὸ τῆς ΑΔ. καί ἐστιν ἡ μὲν ΒΑ ἡ τῆς δοθείσης σφαίρας διάμετρος, ἡ δὲ ΑΔ ἴση τῇ πλευρᾷ τῆς πυραμίδος.
Ἡ ἄρα τῆς σφαίρας διάμετρος ἡμιολία ἐστὶ τῆς πλευρᾶς τῆς πυραμίδος· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Δεικτέον, ὅτι ἐστὶν ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΔ πρὸς τὸ ἀπὸ τῆς ΔΓ.
Ἐκκείσθω γὰρ ἡ τοῦ ἡμικυκλίου καταγραφή, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἀναγεγράφθω ἀπὸ τῆς ΑΓ τετράγωνον τὸ ΕΓ, καὶ συμπεπληρώσθω τὸ ΖΒ παραλληλόγραμμον.
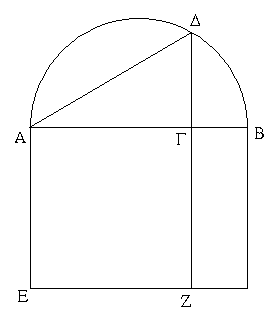
ἐπεὶ οὖν διὰ τὸ ἰσογώνιον εἶναι τὸ ΔΑΒ τρίγωνον τῷ ΔΑΓ τριγώνῳ ἐστὶν ὡς ἡ ΒΑ πρὸς τὴν ΑΔ, οὕτως ἡ ΔΑ πρὸς τὴν ΑΓ, τὸ ἄρα ὑπὸ τῶν ΒΑ, ΑΓ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΔ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ΕΒ πρὸς τὸ ΒΖ, καί ἐστι τὸ μὲν ΕΒ τὸ ὑπὸ τῶν ΒΑ, ΑΓ· ἴση γὰρ ἡ ΕΑ τῇ ΑΓ· τὸ δὲ ΒΖ τὸ ὑπὸ τῶν ΑΓ, ΓΒ, ὡς ἄρα ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ὑπὸ τῶν ΒΑ, ΑΓ πρὸς τὸ ὑπὸ τῶν ΑΓ, ΓΒ. καί ἐστι τὸ μὲν ὑπὸ τῶν ΒΑ, ΑΓ ἴσον τῷ ἀπὸ τῆς ΑΔ, τὸ δὲ ὑπὸ τῶν ΑΓΒ ἴσον τῷ ἀπὸ τῆς ΔΓ· ἡ γὰρ ΔΓ κάθετος τῶν τῆς βάσεως τμημάτων τῶν ΑΓ, ΓΒ μέση ἀνάλογόν ἐστι διὰ τὸ ὀρθὴν εἶναι τὴν ὑπὸ ΑΔΒ. ὡς ἄρα ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΔ πρὸς τὸ ἀπὸ τῆς ΔΓ· ὅπερ ἔδει δεῖξαι.
Πρότασις ιδ΄ 14 Βιβλίον XIII
Ὀκτάεδρον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὰ πρότερα, καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασία ἐστὶ τῆς πλευρᾶς τοῦ ὀκταέδρου.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ, καὶ τετμήσθω δίχα κατὰ τὸ Γ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἤχθω ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἐκκείσθω τετράγωνον τὸ ΕΖΗΘ ἴσην ἔχον ἑκάστην τῶν πλευρῶν τῇ ΔΒ, καὶ ἐπεζεύχθωσαν αἱ ΘΖ, ΕΗ, καὶ ἀνεστάτω ἀπὸ τοῦ Κ σημείου τῷ τοῦ ΕΖΗΘ τετραγώνου ἐπιπέδῳ πρὸς ὀρθὰς εὐθεῖα ἡ ΚΛ καὶ διήχθω ἐπὶ τὰ ἕτερα μέρη τοῦ ἐπιπέδου ὡς ἡ ΚΜ, καὶ ἀφῃρήσθω ἀφ' ἑκατέρας τῶν ΚΛ, ΚΜ μιᾷ τῶν ΕΚ, ΖΚ, ΗΚ, ΘΚ ἴση ἑκατέρα τῶν ΚΛ, ΚΜ, καὶ ἐπεζεύχθωσαν αἱ ΛΕ, ΛΖ, ΛΗ, ΛΘ, ΜΕ, ΜΖ, ΜΗ, ΜΘ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΚΕ τῇ ΚΘ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΕΚΘ γωνία, τὸ ἄρα ἀπὸ τῆς ΘΕ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΚ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΛΚ τῇ ΚΕ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΛΚΕ γωνία, τὸ ἄρα ἀπὸ τῆς ΕΛ διπλάσιόν ἐστι τοῦ ἀπὸ ΕΚ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΘΕ διπλάσιον τοῦ ἀπὸ τῆς ΕΚ· τὸ ἄρα ἀπὸ τῆς ΛΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΘ· ἴση ἄρα ἐστὶν ἡ ΛΕ τῇ ΕΘ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΛΘ τῇ ΘΕ ἐστιν ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΛΕΘ τρίγωνον. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ τοῦ ΕΖΗΘ τετραγώνου πλευραί, κορυφαὶ δὲ τὰ Λ, Μ σημεῖα, ἰσόπλευρόν ἐστιν· ὀκτάεδρον ἄρα συνέσταται ὑπὸ ὀκτὼ τριγώνων ἰσοπλεύρων περιεχόμενον.
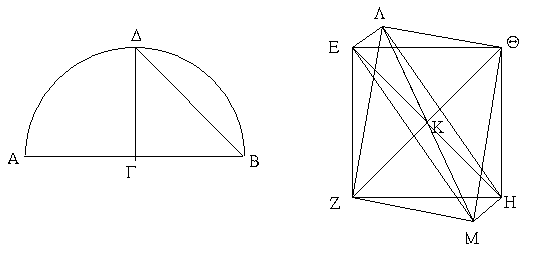
Δεῖ δὴ αὐτὸ καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασίων ἐστὶ τῆς τοῦ ὀκταέδρου πλευρᾶς.
Ἐπεὶ γὰρ αἱ τρεῖς αἱ ΛΚ, ΚΜ, ΚΕ ἴσαι ἀλλήλαις εἰσίν, τὸ ἄρα ἐπὶ τῆς ΛΜ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Ε. καὶ διὰ τὰ αὐτά, ἐὰν μενούσης τῆς ΛΜ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἥξει καὶ διὰ τῶν Ζ, Η, Θ σημείων, καὶ ἔσται σφαίρᾳ περιειλημμένον τὸ ὀκτάεδρον. λέγω δή, ὅτι καὶ τῇ δοθείσῃ. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΛΚ τῇ ΚΜ, κοινὴ δὲ ἡ ΚΕ, καὶ γωνίας ὀρθὰς περιέχουσιν, βάσις ἄρα ἡ ΛΕ βάσει τῇ ΕΜ ἐστιν ἴση. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΛΕΜ γωνία· ἐν ἡμικυκλίῳ γάρ· τὸ ἄρα ἀπὸ τῆς ΛΜ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΛΕ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, διπλασία ἐστὶν ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΔ· διπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΛΜ διπλάσιον τοῦ ἀπὸ τῆς ΛΕ. καί ἐστιν ἴσον τὸ ἀπὸ τῆς ΔΒ τῷ ἀπὸ τῆς ΛΕ· ἴση γὰρ κεῖται ἡ ΕΘ τῇ ΔΒ. ἴσον ἄρα καὶ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΛΜ· ἴση ἄρα ἡ ΑΒ τῇ ΛΜ. καί ἐστιν ἡ ΑΒ ἡ τῆς δοθείσης σφαίρας διάμετρος· ἡ ΛΜ ἄρα ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ.
Περιείληπται ἄρα τὸ ὀκτάεδρον τῇ δοθείσῃ σφαίρᾳ. καὶ συναποδέδεικται, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασίων ἐστὶ τῆς τοῦ ὀκταέδρου πλευρᾶς· ὅπερ ἔδει δεῖξαι.
Πρότασις ιε΄ 15 Βιβλίον XIII
Κύβον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὴν πυραμίδα, καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει τριπλασίων ἐστὶ τῆς τοῦ κύβου πλευρᾶς.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ καὶ τετμήσθω κατὰ τὸ Γ ὥστε διπλῆν εἶναι τὴν ΑΓ τῆς ΓΒ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς ἤχθω ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἐκκείσθω τετράγωνον τὸ ΕΖΗΘ ἴσην ἔχον τὴν πλευρὰν τῇ ΔΒ, καὶ ἀπὸ τῶν Ε, Ζ, Η, Θ τῷ τοῦ ΕΖΗΘ τετραγώνου ἐπιπέδῳ πρὸς ὀρθὰς ἤχθωσαν αἱ ΕΚ, ΖΛ, ΗΜ, ΘΝ, καὶ ἀφῃρήσθω ἀπὸ ἑκάστης τῶν ΕΚ, ΖΛ, ΗΜ, ΘΝ μιᾷ τῶν ΕΖ, ΖΗ, ΗΘ, ΘΕ ἴση ἑκάστη τῶν ΕΚ, ΖΛ, ΗΜ, ΘΝ, καὶ ἐπεζεύχθωσαν αἱ ΚΛ, ΛΜ, ΜΝ, ΝΚ· κύβος ἄρα συνέσταται ὁ ΖΝ ὑπὸ ἓξ τετραγώνων ἴσων περιεχόμενος. δεῖ δὴ αὐτὸν καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει τριπλασία ἐστὶ τῆς πλευρᾶς τοῦ κύβου.
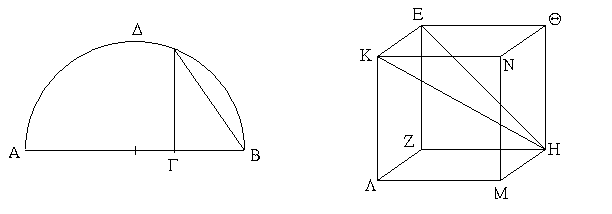
Ἐπεζεύχθωσαν γὰρ αἱ ΚΗ, ΕΗ. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΚΕΗ γωνία διὰ τὸ καὶ τὴν ΚΕ ὀρθὴν εἶναι πρὸς τὸ ΕΗ ἐπίπεδον δηλαδὴ καὶ πρὸς τὴν ΕΗ εὐθεῖαν, τὸ ἄρα ἐπὶ τῆς ΚΗ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Ε σημείου. πάλιν, ἐπεὶ ἡ ΗΖ ὀρθή ἐστι πρὸς ἑκατέραν τῶν ΖΛ, ΖΕ, καὶ πρὸς τὸ ΖΚ ἄρα ἐπίπεδον ὀρθή ἐστιν ἡ ΗΖ· ὥστε καὶ ἐὰν ἐπιζεύξωμεν τὴν ΖΚ, ἡ ΗΖ ὀρθὴ ἔσται καὶ πρὸς τὴν ΖΚ· καὶ διὰ τοῦτο πάλιν τὸ ἐπὶ τῆς ΗΚ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Ζ. ὁμοίως καὶ διὰ τῶν λοιπῶν τοῦ κύβου σημείων ἥξει. ἐὰν δὴ μενούσης τῆς ΚΗ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἔσται σφαίρᾳ περιειλημμένος ὁ κύβος. λέγω δή, ὅτι καὶ τῇ δοθείσῃ. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΗΖ τῇ ΖΕ, καί ἐστιν ὀρθὴ ἡ πρὸς τῷ Ζ γωνία, τὸ ἄρα ἀπὸ τῆς ΕΗ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΖ. ἴση δὲ ἡ ΕΖ τῇ ΕΚ· τὸ ἄρα ἀπὸ τῆς ΕΗ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΚ· ὥστε τὰ ἀπὸ τῶν ΗΕ, ΕΚ, τουτέστι τὸ ἀπὸ τῆς ΗΚ, τριπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΚ. καὶ ἐπεὶ τριπλασίων ἐστὶν ἡ ΑΒ τῆς ΒΓ, ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΔ, τριπλάσιον ἄρα τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΗΚ τοῦ ἀπὸ τῆς ΚΕ τριπλάσιον. καὶ κεῖται ἴση ἡ ΚΕ τῇ ΔΒ· ἴση ἄρα καὶ ἡ ΚΗ τῇ ΑΒ. καί ἐστιν ἡ ΑΒ τῆς δοθείσης σφαίρας διάμετρος· καὶ ἡ ΚΗ ἄρα ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ.
Τῇ δοθείσῃ ἄρα σφαίρᾳ περιείληπται ὁ κύβος· καὶ συναποδέδεικται, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει τριπλασίων ἐστὶ τῆς τοῦ κύβου πλευρᾶς· ὅπερ ἔδει δεῖξαι.
Πρότασις ις΄ 16 Βιβλίον XIII
Εἰκοσάεδρον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὰ προειρημένα σχήματα, καὶ δεῖξαι, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ καὶ τετμήσθω κατὰ τὸ Γ ὥστε τετραπλῆν εἶναι τὴν ΑΓ τῆς ΓΒ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἤχθω ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς γωνίας εὐθεῖα γραμμὴ ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἐκκείσθω κύκλος ὁ ΕΖΗΘΚ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἔστω τῇ ΔΒ, καὶ ἐγγεγράφθω εἰς τὸν ΕΖΗΘΚ κύκλον πεντάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον τὸ ΕΖΗΘΚ, καὶ τετμήσθωσαν αἱ ΕΖ, ΖΗ, ΗΘ, ΘΚ, ΚΕ περιφέρειαι δίχα κατὰ τὰ Λ, Μ, Ν, Ξ, Ο σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΛΜ, ΜΝ, ΝΞ, ΞΟ, ΟΛ, ΕΟ. ἰσόπλευρον ἄρα ἐστὶ καὶ τὸ ΛΜΝΞΟ πεντάγωνον, καὶ δεκαγώνου ἡ ΕΟ εὐθεῖα. καὶ ἀνεστάτωσαν ἀπὸ τῶν Ε, Ζ, Η, Θ, Κ σημείων τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς γωνίας εὐθεῖαι αἱ ΕΠ, ΖΡ, ΗΣ, ΘΤ, ΚΥ ἴσαι οὖσαι τῇ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου, καὶ ἐπεζεύχθωσαν αἱ ΠΡ, ΡΣ, ΣΤ, ΤΥ, ΥΠ, ΠΛ, ΛΡ, ΡΜ, ΜΣ, ΣΝ, ΝΤ, ΤΞ, ΞΥ, ΥΟ, ΟΠ. καὶ ἐπεὶ ἑκατέρα τῶν ΕΠ, ΚΥ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, παράλληλος ἄρα ἐστὶν ἡ ΕΠ τῇ ΚΥ. ἔστι δὲ αὐτῇ καὶ ἴση· αἱ δὲ τὰς ἴσας τε καὶ παραλλήλους ἐπιζευγνύουσαι ἐπὶ τὰ αὐτὰ μέρη εὐθεῖαι ἴσαι τε καὶ παράλληλοί εἰσιν. ἡ ΠΥ ἄρα τῇ ΕΚ ἴση τε καὶ παράλληλός ἐστιν. πενταγώνου δὲ ἰσοπλεύρου ἡ ΕΚ· πενταγώνου ἄρα ἰσοπλεύρου καὶ ἡ ΠΥ τοῦ εἰς τὸν ΕΖΗΘΚ κύκλον ἐγγραφομένου. διὰ τὰ αὐτὰ δὴ καὶ ἑκάστη τῶν ΠΡ, ΡΣ, ΣΤ, ΤΥ πενταγώνου ἐστὶν ἰσοπλεύρου τοῦ εἰς τὸν ΕΖΗΘΚ κύκλον ἐγγραφομένου· ἰσόπλευρον ἄρα τὸ ΠΡΣΤΥ πεντάγωνον. καὶ ἐπεὶ ἑξαγώνου μέν ἐστιν ἡ ΠΕ, δεκαγώνου δὲ ἡ ΕΟ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΠΕΟ, πενταγώνου ἄρα ἐστὶν ἡ ΠΟ· ἡ γὰρ τοῦ πενταγώνου πλευρὰ δύναται τήν τε τοῦ ἑξαγώνου καὶ τὴν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΟΥ πενταγώνου ἐστὶ πλευρά. ἔστι δὲ καὶ ἡ ΠΥ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΟΥ τρίγωνον.
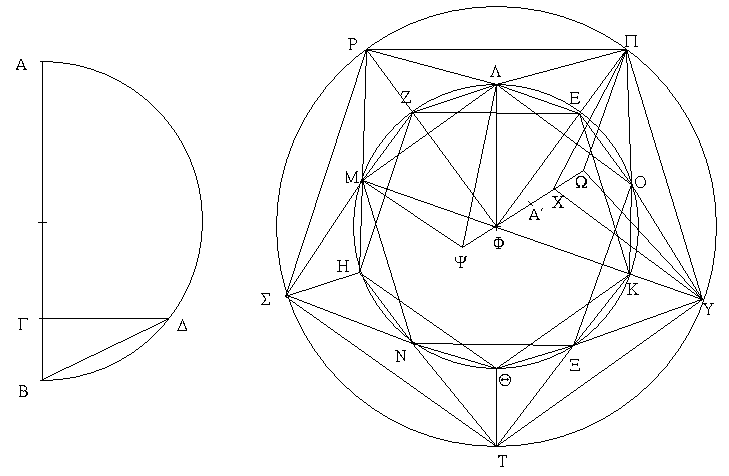
διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν ΠΛΡ, ΡΜΣ, ΣΝΤ, ΤΞΥ ἰσόπλευρόν ἐστιν. καὶ ἐπεὶ πενταγώνου ἐδείχθη ἑκατέρα τῶν ΠΛ, ΠΟ, ἔστι δὲ καὶ ἡ ΛΟ πενταγώνου, ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΛΟ τρίγωνον. διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν ΛΡΜ, ΜΣΝ, ΝΤΞ, ΞΥΟ τριγώνων ἰσόπλευρόν ἐστιν. εἰλήφθω τὸ κέντρον τοῦ ΕΖΗ ΘΚ κύκλου τὸ Φ σημεῖον· καὶ ἀπὸ τοῦ Φ τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἀνεστάτω ἡ ΦΩ, καὶ ἐκβεβλήσθω ἐπὶ τὰ ἕτερα μέρη ὡς ἡ ΦΨ, καὶ ἀφῃρήσθω ἑξαγώνου μὲν ἡ ΦΧ, δεκαγώνου δὲ ἑκατέρα τῶν ΦΨ, ΧΩ, καὶ ἐπεζεύχθωσαν αἱ ΠΩ, ΠΧ, ΥΩ, ΕΦ, ΛΦ, ΛΨ, ΨΜ. καὶ ἐπεὶ ἑκατέρα τῶν ΦΧ, ΠΕ τῷ τοῦ κύκλου ἐπιπέδῳ πρὸς ὀρθάς ἐστιν, παράλληλος ἄρα ἐστὶν ἡ ΦΧ τῇ ΠΕ. εἰσὶ δὲ καὶ ἴσαι· καὶ αἱ ΕΦ, ΠΧ ἄρα ἴσαι τε καὶ παράλληλοί εἰσιν. ἑξαγώνου δὲ ἡ ΕΦ· ἑξαγώνου ἄρα καὶ ἡ ΠΧ. καὶ ἐπεὶ ἑξαγώνου μέν ἐστιν ἡ ΠΧ, δεκαγώνου δὲ ἡ ΧΩ, καὶ ὀρθή ἐστιν ἡ ὑπὸ ΠΧΩ γωνία, πενταγώνου ἄρα ἐστὶν ἡ ΠΩ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΥΩ πενταγώνου ἐστίν, ἐπειδήπερ, ἐὰν ἐπιζεύξωμεν τὰς ΦΚ, ΧΥ, ἴσαι καὶ ἀπεναντίον ἔσονται, καί ἐστιν ἡ ΦΚ ἐκ τοῦ κέντρου οὖσα ἑξαγώνου· ἑξαγώνου ἄρα καὶ ἡ ΧΥ. δεκαγώνου δὲ ἡ ΧΩ, καὶ ὀρθὴ ἡ ὑπὸ ΥΧΩ· πενταγώνου ἄρα ἡ ΥΩ. ἔστι δὲ καὶ ἡ ΠΥ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΠΥΩ τρίγωνον. διὰ τὰ αὐτὰ δὴ καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ ΠΡ, ΡΣ, ΣΤ, ΤΥ εὐθεῖαι, κορυφὴ δὲ τὸ Ω σημεῖον, ἰσόπλευρόν ἐστιν. πάλιν, ἐπεὶ ἑξαγώνου μὲν ἡ ΦΛ, δεκαγώνου δὲ ἡ ΦΨ, καὶ ὀρθή ἐστιν ἡ ὑπὸ ΛΦΨ γωνία, πενταγώνου ἄρα ἐστὶν ἡ ΛΨ. διὰ τὰ αὐτὰ δὴ ἐὰν ἐπιζεύξωμεν τὴν ΜΦ οὖσαν ἑξαγώνου, συνάγεται καὶ ἡ ΜΨ πενταγώνου. ἔστι δὲ καὶ ἡ ΛΜ πενταγώνου· ἰσόπλευρον ἄρα ἐστὶ τὸ ΛΜΨ τρίγωνον. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ ΜΝ, ΝΞ, ΞΟ, ΟΛ, κορυφὴ δὲ τὸ Ψ σημεῖον, ἰσόπλευρόν ἐστιν. συνέσταται ἄρα εἰκοσάεδρον ὑπὸ εἴκοσι τριγώνων ἰσοπλεύρων περιεχόμενον.
Δεῖ δὴ αὐτὸ καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Ἐπεὶ γὰρ ἑξαγώνου ἐστὶν ἡ ΦΧ, δεκαγώνου δὲ ἡ ΧΩ, ἡ ΦΩ ἄρα ἄκρον καὶ μέσον λόγον τέμηται κατὰ τὸ Χ, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΦΧ· ἔστιν ἄρα ὡς ἡ ΩΦ πρὸς τὴν ΦΧ, οὕτως ἡ ΦΧ πρὸς τὴν ΧΩ. ἴση δὲ ἡ μὲν ΦΧ τῇ ΦΕ, ἡ δὲ ΧΩ τῇ ΦΨ· ἔστιν ἄρα ὡς ἡ ΩΦ πρὸς τὴν ΦΕ, οὕτως ἡ ΕΦ πρὸς τὴν ΦΨ. καί εἰσιν ὀρθαὶ αἱ ὑπὸ ΩΦΕ, ΕΦΨ γωνίαι· ἐὰν ἄρα ἐπιζεύξωμεν τὴν ΕΩ εὐθεῖαν, ὀρθὴ ἔσται ἡ ὑπὸ ΨΕΩ γωνία διὰ τὴν ὁμοιότητα τῶν ΨΕΩ, ΦΕΩ τριγώνων. διὰ τὰ αὐτὰ δὴ ἐπεί ἐστιν ὡς ἡ ΩΦ πρὸς τὴν ΦΧ, οὕτως ἡ ΦΧ πρὸς τὴν ΧΩ, ἴση δὲ ἡ μὲν ΩΦ τῇ ΨΧ, ἡ δὲ ΦΧ τῇ ΧΠ, ἔστιν ἄρα ὡς ἡ ΨΧ πρὸς τὴν ΧΠ, οὕτως ἡ ΠΧ πρὸς τὴν ΧΩ. καὶ διὰ τοῦτο πάλιν ἐὰν ἐπιζεύξωμεν τὴν ΠΨ, ὀρθὴ ἔσται ἡ πρὸς τῷ Π γωνία· τὸ ἄρα ἐπὶ τῆς ΨΩ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Π. καὶ ἐὰν μενούσης τῆς ΨΩ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἥξει καὶ διὰ τοῦ Π καὶ τῶν λοιπῶν σημείων τοῦ εἰκοσαέδρου, καὶ ἔσται σφαίρᾳ περιειλημμένον τὸ εἰκοσάεδρον. λέγω δή, ὅτι καὶ τῇ δοθείσῃ. τετμήσθω γὰρ ἡ ΦΧ δίχα κατὰ τὸ Α#. καὶ ἐπεὶ εὐθεῖα γραμμὴ ἡ ΦΩ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Χ, καὶ τὸ ἔλασσον αὐτῆς τμῆμά ἐστιν ἡ ΩΧ, ἡ ἄρα ΩΧ προσλαβοῦσα τὴν ἡμίσειαν τοῦ μείζονος τμήματος τὴν ΧΑ# πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τοῦ μείζονος τμήματος· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΩΑ# τοῦ ἀπὸ τῆς Α#Χ. καί ἐστι τῆς μὲν ΩΑ# διπλῆ ἡ ΩΨ, τῆς δὲ Α#Χ διπλῆ ἡ ΦΧ· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΩΨ τοῦ ἀπὸ τῆς ΧΦ. καὶ ἐπεὶ τετραπλῆ ἐστιν ἡ ΑΓ τῆς ΓΒ, πενταπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΔ· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΩΨ πενταπλάσιον τοῦ ἀπὸ τῆς ΦΧ. καί ἐστιν ἴση ἡ ΔΒ τῇ ΦΧ· ἑκατέρα γὰρ αὐτῶν ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου· ἴση ἄρα καὶ ἡ ΑΒ τῇ ΨΩ. καί ἐστιν ἡ ΑΒ ἡ τῆς δοθείσης σφαίρας διάμετρος· καὶ ἡ ΨΩ ἄρα ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ. τῇ ἄρα δοθείσῃ σφαίρᾳ περιείληπται τὸ εἰκοσάεδρον.
Λέγω δή, ὅτι ἡ τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων. ἐπεὶ γὰρ ῥητή ἐστιν ἡ τῆς σφαίρας διάμετρος, καί ἐστι δυνάμει πενταπλασίων τῆς ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου, ῥητὴ ἄρα ἐστὶ καὶ ἡ ἐκ τοῦ κέντρου τοῦ ΕΖΗΘΚ κύκλου· ὥστε καὶ ἡ διάμετρος αὐτοῦ ῥητή ἐστιν. ἐὰν δὲ εἰς κύκλον ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων. ἡ δὲ τοῦ ΕΖΗΘΚ πενταγώνου πλευρὰ ἡ τοῦ εἰκοσαέδρου ἐστίν. ἡ ἄρα τοῦ εἰκοσαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει πενταπλασίων ἐστὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου, ἀφ' οὗ τὸ εἰκοσάεδρον ἀναγέγραπται, καὶ ὅτι ἡ τῆς σφαίρας διάμετρος σύγκειται ἔκ τε τῆς τοῦ ἑξαγώνου καὶ δύο τῶν τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων. ὅπερ ἔδει δεῖξαι.
Πρότασις ιζ΄ 17 Βιβλίον XIII
Δωδεκάεδρον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὰ προειρημένα σχήματα, καὶ δεῖξαι, ὅτι ἡ τοῦ δωδεκαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.
Ἐκκείσθωσαν τοῦ προειρημένου κύβου δύο ἐπίπεδα πρὸς ὀρθὰς ἀλλήλοις τὰ ΑΒΓΔ, ΓΒΕΖ, καὶ τετμήσθω ἑκάστη τῶν ΑΒ, ΒΓ, ΓΔ, ΔΑ, ΕΖ, ΕΒ, ΖΓ πλευρῶν δίχα κατὰ τὰ Η, Θ, Κ, Λ, Μ, Ν, Ξ, καὶ ἐπεζεύχθωσαν αἱ ΗΚ, ΘΛ, ΜΘ, ΝΞ, καὶ τετμήσθω ἑκάστη τῶν ΝΟ, ΟΞ, ΘΠ ἄκρον καὶ μέσον λόγον κατὰ τὰ Ρ, Σ, Τ σημεῖα, καὶ ἔστω αὐτῶν μείζονα τμήματα τὰ ΡΟ, ΟΣ, ΤΠ, καὶ ἀνεστάτωσαν ἀπὸ τῶν Ρ, Σ, Τ σημείων τοῖς τοῦ κύβου ἐπιπέδοις πρὸς ὀρθὰς ἐπὶ τὰ ἐκτὸς μέρη τοῦ κύβου αἱ ΡΥ, ΣΦ, ΤΧ, καὶ κείσθωσαν ἴσαι ταῖς ΡΟ, ΟΣ, ΤΠ, καὶ ἐπεζεύχθωσαν αἱ ΥΒ, ΒΧ, ΧΓ, ΓΦ, ΦΥ. λέγω, ὅτι τὸ ΥΒΧΓΦ πεντάγωνον ἰσόπλευρόν τε καὶ ἐν ἑνὶ ἐπιπέδῳ καὶ ἔτι ἰσογώνιόν ἐστιν. ἐπεζεύχθωσαν γὰρ αἱ ΡΒ, ΣΒ, ΦΒ. καὶ ἐπεὶ εὐθεῖα ἡ ΝΟ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Ρ, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΡΟ, τὰ ἄρα ἀπὸ τῶν ΟΝ, ΝΡ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΡΟ. ἴση δὲ ἡ μὲν ΟΝ τῇ ΝΒ, ἡ δὲ ΟΡ τῇ ΡΥ· τὰ ἄρα ἀπὸ τῶν ΒΝ, ΝΡ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΡΥ. τοῖς δὲ ἀπὸ τῶν ΒΝ, ΝΡ τὸ ἀπὸ τῆς ΒΡ ἐστιν ἴσον· τὸ ἄρα ἀπὸ τῆς ΒΡ τριπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΡΥ· ὥστε τὰ ἀπὸ τῶν ΒΡ, ΡΥ τετραπλάσιά ἐστι τοῦ ἀπὸ τῆς ΡΥ. τοῖς δὲ ἀπὸ τῶν ΒΡ, ΡΥ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΒΥ· τὸ ἄρα ἀπὸ τῆς ΒΥ τετραπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΥΡ· διπλῆ ἄρα ἐστὶν ἡ ΒΥ τῆς ΡΥ. ἔστι δὲ καὶ ἡ ΦΥ τῆς ΥΡ διπλῆ, ἐπειδήπερ καὶ ἡ ΣΡ τῆς ΟΡ, τουτέστι τῆς ΡΥ, ἐστι διπλῆ· ἴση ἄρα ἡ ΒΥ τῇ ΥΦ. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἑκάστη τῶν ΒΧ, ΧΓ, ΓΦ ἑκατέρᾳ τῶν ΒΥ, ΥΦ ἐστιν ἴση. ἰσόπλευρον ἄρα ἐστὶ τὸ ΒΥΦΓΧ πεντάγωνον. λέγω δή, ὅτι καὶ ἐν ἑνί ἐστιν ἐπιπέδῳ. ἤχθω γὰρ ἀπὸ τοῦ Ο ἑκατέρᾳ τῶν ΡΥ, ΣΦ παράλληλος ἐπὶ τὰ ἐκτὸς τοῦ κύβου μέρη ἡ ΟΨ, καὶ ἐπεζεύχθωσαν αἱ ΨΘ, ΘΧ· λέγω, ὅτι ἡ ΨΘΧ εὐθεῖά ἐστιν. ἐπεὶ γὰρ ἡ ΘΠ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Τ, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΠΤ, ἔστιν ἄρα ὡς ἡ ΘΠ πρὸς τὴν ΠΤ, οὕτως ἡ ΠΤ πρὸς τὴν ΤΘ. ἴση δὲ ἡ μὲν ΘΠ τῇ ΘΟ, ἡ δὲ ΠΤ ἑκατέρᾳ τῶν ΤΧ, ΟΨ· ἔστιν ἄρα ὡς ἡ ΘΟ πρὸς τὴν ΟΨ, οὕτως ἡ ΧΤ πρὸς τὴν ΤΘ. καί ἐστι παράλληλος ἡ μὲν ΘΟ τῇ ΤΧ· ἑκατέρα γὰρ αὐτῶν τῷ ΒΔ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν· ἡ δὲ ΤΘ τῇ ΟΨ· ἑκατέρα γὰρ αὐτῶν τῷ ΒΖ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. ἐὰν δὲ δύο τρίγωνα συντεθῇ κατὰ μίαν γωνίαν, ὡς τὰ ΨΟΘ, ΘΤΧ, τὰς δύο πλευρὰς ταῖς δυσὶν ἀνάλογον ἔχοντα, ὥστε τὰς ὁμολόγους αὐτῶν πλευρὰς καὶ παραλλήλους εἶναι, αἱ λοιπαὶ εὐθεῖαι ἐπ᾿ εὐθείας ἔσονται· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΨΘ τῇ ΘΧ. πᾶσα δὲ εὐθεῖα ἐν ἑνί ἐστιν ἐπιπέδῳ· ἐν ἑνὶ ἄρα ἐπιπέδῳ ἐστὶ τὸ ΥΒΧΓΦ πεντάγωνον.
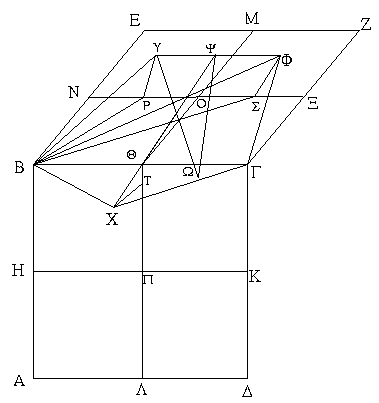
Λέγω δή, ὅτι καὶ ἰσογώνιόν ἐστιν.
Ἐπεὶ γὰρ εὐθεῖα γραμμὴ ἡ ΝΟ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Ρ, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΟΡ [ἔστιν ἄρα ὡς συναμφότερος ἡ ΝΟ, ΟΡ πρὸς τὴν ΟΝ, οὕτως ἡ ΝΟ πρὸς τὴν ΟΡ], ἴση δὲ ἡ ΟΡ τῇ ΟΣ [ἔστιν ἄρα ὡς ἡ ΣΝ πρὸς τὴν ΝΟ, οὕτως ἡ ΝΟ πρὸς τὴν ΟΣ], ἡ ΝΣ ἄρα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Ο, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΝΟ· τὰ ἄρα ἀπὸ τῶν ΝΣ, ΣΟ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΝΟ. ἴση δὲ ἡ μὲν ΝΟ τῇ ΝΒ, ἡ δὲ ΟΣ τῇ ΣΦ· τὰ ἄρα ἀπὸ τῶν ΝΣ, ΣΦ τετράγωνα τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΝΒ· ὥστε τὰ ἀπὸ τῶν ΦΣ, ΣΝ, ΝΒ τετραπλάσιά ἐστι τοῦ ἀπὸ τῆς ΝΒ. τοῖς δὲ ἀπὸ τῶν ΣΝ, ΝΒ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΣΒ· τὰ ἄρα ἀπὸ τῶν ΒΣ, ΣΦ, τουτέστι τὸ ἀπὸ τῆς ΒΦ [ὀρθὴ γὰρ ἡ ὑπὸ ΦΣΒ γωνία], τετραπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΝΒ· διπλῆ ἄρα ἐστὶν ἡ ΦΒ τῆς ΒΝ. ἔστι δὲ καὶ ἡ ΒΓ τῆς ΒΝ διπλῆ· ἴση ἄρα ἐστὶν ἡ ΒΦ τῇ ΒΓ. καὶ ἐπεὶ δύο αἱ ΒΥ, ΥΦ δυσὶ ταῖς ΒΧ, ΧΓ ἴσαι εἰσίν, καὶ βάσις ἡ ΒΦ βάσει τῇ ΒΓ ἴση, γωνία ἄρα ἡ ὑπὸ ΒΥΦ γωνίᾳ τῇ ὑπὸ ΒΧΓ ἐστιν ἴση. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ὑπὸ ΥΦΓ γωνία ἴση ἐστὶ τῇ ὑπὸ ΒΧΓ· αἱ ἄρα ὑπὸ ΒΧΓ, ΒΥΦ, ΥΦΓ τρεῖς γωνίαι ἴσαι ἀλλήλαις εἰσίν. ἐὰν δὲ πενταγώνου ἰσοπλεύρου αἱ τρεῖς γωνίαι ἴσαι ἀλλήλαις ὦσιν, ἰσογώνιον ἔσται τὸ πεντάγωνον· ἰσογώνιον ἄρα ἐστὶ τὸ ΒΥΦΓΧ πεντάγωνον. ἐδείχθη δὲ καὶ ἰσόπλευρον· τὸ ἄρα ΒΥΦΓΧ πεντάγωνον ἰσόπλευρόν ἐστι καὶ ἰσογώνιον, καί ἐστιν ἐπὶ μιᾶς τοῦ κύβου πλευρᾶς τῆς ΒΓ. ἐὰν ἄρα ἐφ' ἑκάστης τῶν τοῦ κύβου δώδεκα πλευρῶν τὰ αὐτὰ κατασκευάσωμεν, συσταθήσεταί τι σχῆμα στερεὸν ὑπὸ δώδεκα πενταγώνων ἰσοπλεύρων τε καὶ ἰσογωνίων περιεχόμενον, ὃ καλεῖται δωδεκάεδρον.
Δεῖ δὴ αὐτὸ καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τοῦ δωδεκαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.
Ἐκβεβλήσθω γὰρ ἡ ΨΟ, καὶ ἔστω ἡ ΨΩ· συμβάλλει ἄρα ἡ ΟΩ τῇ τοῦ κύβου διαμέτρῳ, καὶ δίχα τέμνουσιν ἀλλήλας· τοῦτο γὰρ δέδεικται ἐν τῷ παρατελεύτῳ θεωρήματι τοῦ ἑνδεκάτου βιβλίου. τεμνέτωσαν κατὰ τὸ Ω· τὸ Ω ἄρα κέντρον ἐστὶ τῆς σφαίρας τῆς περιλαμβανούσης τὸν κύβον, καὶ ἡ ΩΟ ἡμίσεια τῆς πλευρᾶς τοῦ κύβου. ἐπεζεύχθω δὴ ἡ ΥΩ. καὶ ἐπεὶ εὐθεῖα γραμμὴ ἡ ΝΣ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Ο, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΝΟ, τὰ ἄρα ἀπὸ τῶν ΝΣ, ΣΟ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΝΟ. ἴση δὲ ἡ μὲν ΝΣ τῇ ΨΩ, ἐπειδήπερ καὶ ἡ μὲν ΝΟ τῇ ΟΩ ἐστιν ἴση, ἡ δὲ ΨΟ τῇ ΟΣ. ἀλλὰ μὴν καὶ ἡ ΟΣ τῇ ΨΥ, ἐπεὶ καὶ τῇ ΡΟ· τὰ ἄρα ἀπὸ τῶν ΩΨ, ΨΥ τριπλάσιά ἐστι τοῦ ἀπὸ τῆς ΝΟ. τοῖς δὲ ἀπὸ τῶν ΩΨ, ΨΥ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΥΩ· τὸ ἄρα ἀπὸ τῆς ΥΩ τριπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΝΟ. ἔστι δὲ καὶ ἡ ἐκ τοῦ κέντρου τῆς σφαίρας τῆς περιλαμβανούσης τὸν κύβον δυνάμει τριπλασίων τῆς ἡμισείας τῆς τοῦ κύβου πλευρᾶς· προδέδεικται γὰρ κύβον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει τριπλασίων ἐστὶ τῆς πλευρᾶς τοῦ κύβου. εἰ δὲ ὅλη τῆς ὅλης, καὶ [ἡ] ἡμίσεια τῆς ἡμισείας· καί ἐστιν ἡ ΝΟ ἡμίσεια τῆς τοῦ κύβου πλευρᾶς· ἡ ἄρα ΥΩ ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου τῆς σφαίρας τῆς περιλαμβανούσης τὸν κύβον. καί ἐστι τὸ Ω κέντρον τῆς σφαίρας τῆς περιλαμβανούσης τὸν κύβον· τὸ Υ ἄρα σημεῖον πρὸς τῇ ἐπιφανείᾳ ἐστὶ τῆς σφαίρας. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἑκάστη τῶν λοιπῶν γωνιῶν τοῦ δωδεκαέδρου πρὸς τῇ ἐπιφανείᾳ ἐστὶ τῆς σφαίρας· περιείληπται ἄρα τὸ δωδεκάεδρον τῇ δοθείσῃ σφαίρᾳ.
Λέγω δή, ὅτι ἡ τοῦ δωδεκαέδρου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἀποτομή.
Ἐπεὶ γὰρ τῆς ΝΟ ἄκρον καὶ μέσον λόγον τετμημένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΡΟ, τῆς δὲ ΟΞ ἄκρον καὶ μέσον λόγον τετμημένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΟΣ, ὅλης ἄρα τῆς ΝΞ ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΡΣ. οἷον ἐπεί ἐστιν ὡς ἡ ΝΟ πρὸς τὴν ΟΡ, ἡ ΟΡ πρὸς τὴν ΡΝ, καὶ τὰ διπλάσια· τὰ γὰρ μέρη τοῖς ἰσάκις πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον· ὡς ἄρα ἡ ΝΞ πρὸς τὴν ΡΣ, οὕτως ἡ ΡΣ πρὸς συναμφότερον τὴν ΝΡ, ΣΞ. μείζων δὲ ἡ ΝΞ τῆς ΡΣ· μείζων ἄρα καὶ ἡ ΡΣ συναμφοτέρου τῆς ΝΡ, ΣΞ· ἡ ΝΞ ἄρα ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΡΣ. ἴση δὲ ἡ ΡΣ τῇ ΥΦ· τῆς ἄρα ΝΞ ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΥΦ. καὶ ἐπεὶ ῥητή ἐστιν ἡ τῆς σφαίρας διάμετρος καί ἐστι δυνάμει τριπλασίων τῆς τοῦ κύβου πλευρᾶς, ῥητὴ ἄρα ἐστὶν ἡ ΝΞ πλευρὰ οὖσα τοῦ κύβου. ἐὰν δὲ ῥητὴ γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, ἑκάτερον τῶν τμημάτων ἄλογός ἐστιν ἀποτομή.
Ἡ ΥΦ ἄρα πλευρὰ οὖσα τοῦ δωδεκαέδρου ἄλογός ἐστιν ἀποτομή.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι τῆς τοῦ κύβου πλευρᾶς ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ τοῦ δωδεκαέδρου πλευρά. ὅπερ ἔδει δεῖξαι.
Πρότασις ιη΄ 18 Βιβλίον XIII
Τὰς πλευρὰς τῶν πέντε σχημάτων ἐκθέσθαι καὶ συγκρῖναι πρὸς ἀλλήλας.
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ, καὶ τετμήσθω κατὰ τὸ Γ ὥστε ἴσην εἶναι τὴν ΑΓ τῇ ΓΒ, κατὰ δὲ τὸ Δ ὥστε διπλασίονα εἶναι τὴν ΑΔ τῆς ΔΒ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΕΒ, καὶ ἀπὸ τῶν Γ, Δ τῇ ΑΒ πρὸς ὀρθὰς ἤχθωσαν αἱ ΓΕ, ΔΖ, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΖΒ, ΕΒ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΑΔ τῆς ΔΒ, τριπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΔ. ἀναστρέψαντι ἡμιολία ἄρα ἐστὶν ἡ ΒΑ τῆς ΑΔ. ὡς δὲ ἡ ΒΑ πρὸς τὴν ΑΔ, οὕτως τὸ ἀπὸ τῆς ΒΑ πρὸς τὸ ἀπὸ τῆς ΑΖ· ἰσογώνιον γάρ ἐστι τὸ ΑΖΒ τρίγωνον τῷ ΑΖΔ τριγώνῳ· ἡμιόλιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΒΑ τοῦ ἀπὸ τῆς ΑΖ. ἔστι δὲ καὶ ἡ τῆς σφαίρας διάμετρος δυνάμει ἡμιολία τῆς πλευρᾶς τῆς πυραμίδος. καί ἐστιν ἡ ΑΒ ἡ τῆς σφαίρας διάμετρος· ἡ ΑΖ ἄρα ἴση ἐστὶ τῇ πλευρᾷ τῆς πυραμίδος.
Πάλιν, ἐπεὶ διπλασίων ἐστὶν ἡ ΑΔ τῆς ΔΒ, τριπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΔ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΔ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΖ· τριπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΖ. ἔστι δὲ καὶ ἡ τῆς σφαίρας διάμετρος δυνάμει τριπλασίων τῆς τοῦ κύβου πλευρᾶς. καί ἐστιν ἡ ΑΒ ἡ τῆς σφαίρας διάμετρος· ἡ ΒΖ ἄρα τοῦ κύβου ἐστὶ πλευρά.
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, διπλῆ ἄρα ἐστὶν ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΕ· διπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΕ. ἔστι δὲ καὶ ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασίων τῆς τοῦ ὀκταέδρου πλευρᾶς. καί ἐστιν ἡ ΑΒ ἡ τῆς δοθείσης σφαίρας διάμετρος· ἡ ΒΕ ἄρα τοῦ ὀκταέδρου ἐστὶ πλευρά.
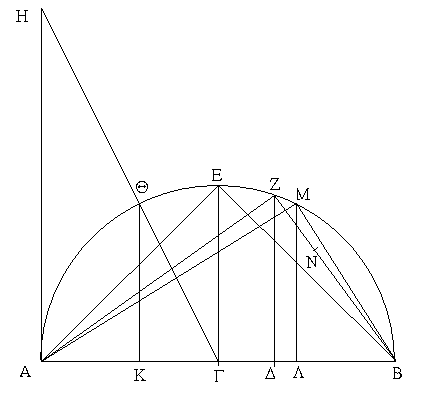
Ἤχθω δὴ ἀπὸ τοῦ Α σημείου τῇ ΑΒ εὐθείᾳ πρὸς ὀρθὰς ἡ ΑΗ, καὶ κείσθω ἡ ΑΗ ἴση τῇ ΑΒ, καὶ ἐπεζεύχθω ἡ ΗΓ, καὶ ἀπὸ τοῦ Θ ἐπὶ τὴν ΑΒ κάθετος ἤχθω ἡ ΘΚ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΗΑ τῆς ΑΓ· ἴση γὰρ ἡ ΗΑ τῇ ΑΒ· ὡς δὲ ἡ ΗΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΘΚ πρὸς τὴν ΚΓ, διπλῆ ἄρα καὶ ἡ ΘΚ τῆς ΚΓ. τετραπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΘΚ τοῦ ἀπὸ τῆς ΚΓ· τὰ ἄρα ἀπὸ τῶν ΘΚ, ΚΓ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΘΓ, πενταπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΚΓ. ἴση δὲ ἡ ΘΓ τῇ ΓΒ· πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς ΓΚ. καὶ ἐπεὶ διπλῆ ἐστιν ἡ ΑΒ τῆς ΓΒ, ὧν ἡ ΑΔ τῆς ΔΒ ἐστι διπλῆ, λοιπὴ ἄρα ἡ ΒΔ λοιπῆς τῆς ΔΓ ἐστι διπλῆ. τριπλῆ ἄρα ἡ ΒΓ τῆς ΓΔ· ἐνναπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς ΓΔ. πενταπλάσιον δὲ τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς ΓΚ· μεῖζον ἄρα τὸ ἀπὸ τῆς ΓΚ τοῦ ἀπὸ τῆς ΓΔ. μείζων ἄρα ἐστὶν ἡ ΓΚ τῆς ΓΔ. κείσθω τῇ ΓΚ ἴση ἡ ΓΛ, καὶ ἀπὸ τοῦ Λ τῇ ΑΒ πρὸς ὀρθὰς ἤχθω ἡ ΛΜ, καὶ ἐπεζεύχθω ἡ ΜΒ. καὶ ἐπεὶ πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΓ τοῦ ἀπὸ τῆς ΓΚ, καί ἐστι τῆς μὲν ΒΓ διπλῆ ἡ ΑΒ, τῆς δὲ ΓΚ διπλῆ ἡ ΚΛ, πενταπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΚΛ. ἔστι δὲ καὶ ἡ τῆς σφαίρας διάμετρος δυνάμει πενταπλασίων τῆς ἐκ τοῦ κέντρου τοῦ κύκλου, ἀφ' οὗ τὸ εἰκοσάεδρον ἀναγέγραπται. καί ἐστιν ἡ ΑΒ ἡ τῆς σφαίρας διάμετρος· ἡ ΚΛ ἄρα ἐκ τοῦ κέντρου ἐστὶ τοῦ κύκλου, ἀφ' οὗ τὸ εἰκοσάεδρον ἀναγέγραπται· ἡ ΚΛ ἄρα ἑξαγώνου ἐστὶ πλευρὰ τοῦ εἰρημένου κύκλου. καὶ ἐπεὶ ἡ τῆς σφαίρας διάμετρος σύγκειται ἔκ τε τῆς τοῦ ἑξαγώνου καὶ δύο τῶν τοῦ δεκαγώνου τῶν εἰς τὸν εἰρημένον κύκλον ἐγγραφομένων, καί ἐστιν ἡ μὲν ΑΒ ἡ τῆς σφαίρας διάμετρος, ἡ δὲ ΚΛ ἑξαγώνου πλευρά, καὶ ἴση ἡ ΑΚ τῇ ΛΒ, ἑκατέρα ἄρα τῶν ΑΚ, ΛΒ δεκαγώνου ἐστὶ πλευρὰ τοῦ ἐγγραφομένου εἰς τὸν κύκλον, ἀφ' οὗ τὸ εἰκοσάεδρον ἀναγέγραπται. καὶ ἐπεὶ δεκαγώνου μὲν ἡ ΛΒ, ἑξαγώνου δὲ ἡ ΜΛ· ἴση γάρ ἐστι τῇ ΚΛ, ἐπεὶ καὶ τῇ ΘΚ· ἴσον γὰρ ἀπέχουσιν ἀπὸ τοῦ κέντρου· καί ἐστιν ἑκατέρα τῶν ΘΚ, ΚΛ διπλασίων τῆς ΚΓ· πενταγώνου ἄρα ἐστὶν ἡ ΜΒ. ἡ δὲ τοῦ πενταγώνου ἐστὶν ἡ τοῦ εἰκοσαέδρου· εἰκοσαέδρου ἄρα ἐστὶν ἡ ΜΒ.
Καὶ ἐπεὶ ἡ ΖΒ κύβου ἐστὶ πλευρά, τετμήσθω ἄκρον καὶ μέσον λόγον κατὰ τὸ Ν, καὶ ἔστω μεῖζον τμῆμα τὸ ΝΒ· ἡ ΝΒ ἄρα δωδεκαέδρου ἐστὶ πλευρά.
Καὶ ἐπεὶ ἡ τῆς σφαίρας διάμετρος ἐδείχθη τῆς μὲν ΑΖ πλευρᾶς τῆς πυραμίδος δυνάμει ἡμιολία, τῆς δὲ τοῦ ὀκταέδρου τῆς ΒΕ δυνάμει διπλασίων, τῆς δὲ τοῦ κύβου τῆς ΖΒ δυνάμει τριπλασίων, οἵων ἄρα ἡ τῆς σφαίρας διάμετρος δυνάμει ἕξ, τοιούτων ἡ μὲν τῆς πυραμίδος τεσσάρων, ἡ δὲ τοῦ ὀκταέδρου τριῶν, ἡ δὲ τοῦ κύβου δύο. ἡ μὲν ἄρα τῆς πυραμίδος πλευρὰ τῆς μὲν τοῦ ὀκταέδρου πλευρᾶς δυνάμει ἐστὶν ἐπίτριτος, τῆς δὲ τοῦ κύβου δυνάμει διπλῆ, ἡ δὲ τοῦ ὀκταέδρου τῆς τοῦ κύβου δυνάμει ἡμιολία. αἱ μὲν οὖν εἰρημέναι τῶν τριῶν σχημάτων πλευραί, λέγω δὴ πυραμίδος καὶ ὀκταέδρου καὶ κύβου, πρὸς ἀλλήλας εἰσὶν ἐν λόγοις ῥητοῖς. αἱ δὲ λοιπαὶ δύο, λέγω δὴ ἥ τε τοῦ εἰκοσαέδρου καὶ ἡ τοῦ δωδεκαέδρου, οὔτε πρὸς ἀλλήλας οὔτε πρὸς τὰς προειρημένας εἰσὶν ἐν λόγοις ῥητοῖς· ἄλογοι γάρ εἰσιν, ἡ μὲν ἐλάττων, ἡ δὲ ἀποτομή.
Ὅτι μείζων ἐστὶν ἡ τοῦ εἰκοσαέδρου πλευρὰ ἡ ΜΒ τῆς τοῦ δωδεκαέδρου τῆς ΝΒ, δείξομεν οὕτως.
Ἐπεὶ γὰρ ἰσογώνιόν ἐστι τὸ ΖΔΒ τρίγωνον τῷ ΖΑΒ τριγώνῳ, ἀνάλογόν ἐστιν ὡς ἡ ΔΒ πρὸς τὴν ΒΖ, οὕτως ἡ ΒΖ πρὸς τὴν ΒΑ. καὶ ἐπεὶ τρεῖς εὐθεῖαι ἀνάλογόν εἰσιν, ἔστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, οὕτως τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ἀπὸ τῆς δευτέρας· ἔστιν ἄρα ὡς ἡ ΔΒ πρὸς τὴν ΒΑ, οὕτως τὸ ἀπὸ τῆς ΔΒ πρὸς τὸ ἀπὸ τῆς ΒΖ· ἀνάπαλιν ἄρα ὡς ἡ ΑΒ πρὸς τὴν ΒΔ, οὕτως τὸ ἀπὸ τῆς ΖΒ πρὸς τὸ ἀπὸ τῆς ΒΔ. τριπλῆ δὲ ἡ ΑΒ τῆς ΒΔ· τριπλάσιον ἄρα τὸ ἀπὸ τῆς ΖΒ τοῦ ἀπὸ τῆς ΒΔ. ἔστι δὲ καὶ τὸ ἀπὸ τῆς ΑΔ τοῦ ἀπὸ τῆς ΔΒ τετραπλάσιον· διπλῆ γὰρ ἡ ΑΔ τῆς ΔΒ· μεῖζον ἄρα τὸ ἀπὸ τῆς ΑΔ τοῦ ἀπὸ τῆς ΖΒ· μείζων ἄρα ἡ ΑΔ τῆς ΖΒ· πολλῷ ἄρα ἡ ΑΛ τῆς ΖΒ μείζων ἐστίν. καὶ τῆς μὲν ΑΛ ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΚΛ, ἐπειδήπερ ἡ μὲν ΛΚ ἑξαγώνου ἐστίν, ἡ δὲ ΚΑ δεκαγώνου· τῆς δὲ ΖΒ ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμά ἐστιν ἡ ΝΒ· μείζων ἄρα ἡ ΚΛ τῆς ΝΒ. ἴση δὲ ἡ ΚΛ τῇ ΛΜ· μείζων ἄρα ἡ ΛΜ τῆς ΝΒ [τῆς δὲ ΛΜ μείζων ἐστὶν ἡ ΜΒ]. πολλῷ ἄρα ἡ ΜΒ πλευρὰ οὖσα τοῦ εἰκοσαέδρου μείζων ἐστὶ τῆς ΝΒ πλευρᾶς οὔσης τοῦ δωδεκαέδρου· ὅπερ ἔδει δεῖξαι.
Λέγω δή, ὅτι παρὰ τὰ εἰρημένα πέντε σχήματα οὐ συσταθήσεται ἕτερον σχῆμα περιεχόμενον ὑπὸ ἰσοπλεύρων τε καὶ ἰσογωνίων ἴσων ἀλλήλοις.
Ὑπὸ μὲν γὰρ δύο τριγώνων ἢ ὅλως ἐπιπέδων στερεὰ γωνία οὐ συνίσταται. ὑπὸ δὲ τριῶν τριγώνων ἡ τῆς πυραμίδος, ὑπὸ δὲ τεσσάρων ἡ τοῦ ὀκταέδρου, ὑπὸ δὲ πέντε ἡ τοῦ εἰκοσαέδρου· ὑπὸ δὲ ἓξ τριγώνων ἰσοπλεύρων τε καὶ ἰσογωνίων πρὸς ἑνὶ σημείῳ συνισταμένων οὐκ ἔσται στερεὰ γωνία· οὔσης γὰρ τῆς τοῦ ἰσοπλεύρου τριγώνου γωνίας διμοίρου ὀρθῆς ἔσονται αἱ ἓξ τέσσαρσιν ὀρθαῖς ἴσαι· ὅπερ ἀδύνατον· ἅπασα γὰρ στερεὰ γωνία ὑπὸ ἐλασσόνων ἢ τεσσάρων ὀρθῶν περιέχεται. διὰ τὰ αὐτὰ δὴ οὐδὲ ὑπὸ πλειόνων ἢ ἓξ γωνιῶν ἐπιπέδων στερεὰ γωνία συνίσταται. ὑπὸ δὲ τετραγώνων τριῶν ἡ τοῦ κύβου γωνία περιέχεται· ὑπὸ δὲ τεσσάρων ἀδύνατον· ἔσονται γὰρ πάλιν τέσσαρες ὀρθαί. ὑπὸ δὲ πενταγώνων ἰσοπλεύρων καὶ ἰσογωνίων, ὑπὸ μὲν τριῶν ἡ τοῦ δωδεκαέδρου· ὑπὸ δὲ τεσσάρων ἀδύνατον· οὔσης γὰρ τῆς τοῦ πενταγώνου ἰσοπλεύρου γωνίας ὀρθῆς καὶ πέμπτου, ἔσονται αἱ τέσσαρες γωνίαι τεσσάρων ὀρθῶν μείζους· ὅπερ ἀδύνατον. οὐδὲ μὴν ὑπὸ πολυγώνων ἑτέρων σχημάτων περισχεθήσεται στερεὰ γωνία διὰ τὸ αὐτὸ ἄτοπον.
Οὐκ ἄρα παρὰ τὰ εἰρημένα πέντε σχήματα ἕτερον σχῆμα στερεὸν συσταθήσεται ὑπὸ ἰσοπλεύρων τε καὶ ἰσογωνίων περιεχόμενον· ὅπερ ἔδει δεῖξαι.
Λῆμμα
Ὅτι δὲ ἡ τοῦ ἰσοπλεύρου καὶ ἰσογωνίου πενταγώνου γωνία ὀρθή ἐστι καὶ πέμπτου, οὕτω δεικτέον.
Ἔστω γὰρ πεντάγωνον ἰσόπλευρον καὶ ἰσογώνιον τὸ ΑΒΓΔΕ, καὶ περιγεγράφθω περὶ αὐτὸ κύκλος ὁ ΑΒΓ ΔΕ, καὶ εἰλήφθω αὐτοῦ τὸ κέντρον τὸ Ζ, καὶ ἐπεζεύχθωσαν αἱ ΖΑ, ΖΒ, ΖΓ, ΖΔ, ΖΕ.
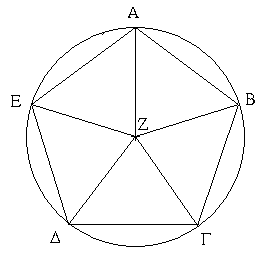
δίχα ἄρα τέμνουσι τὰς πρὸς τοῖς Α, Β, Γ, Δ, Ε τοῦ πενταγώνου γωνίας. καὶ ἐπεὶ αἱ πρὸς τῷ Ζ πέντε γωνίαι τέσσαρσιν ὀρθαῖς ἴσαι εἰσὶ καί εἰσιν ἴσαι, μία ἄρα αὐτῶν, ὡς ἡ ὑπὸ ΑΖΒ, μιᾶς ὀρθῆς ἐστι παρὰ πέμπτον· λοιπαὶ ἄρα αἱ ὑπὸ ΖΑΒ, ΑΒΖ μιᾶς εἰσιν ὀρθῆς καὶ πέμπτου. ἴση δὲ ἡ ὑπὸ ΖΑΒ τῇ ὑπὸ ΖΒΓ· καὶ ὅλη ἄρα ἡ ὑπὸ ΑΒΓ τοῦ πενταγώνου γωνία μιᾶς ἐστιν ὀρθῆς καὶ πέμπτου· ὅπερ ἔδει δεῖξαι.