Στοιχεῖα Εὐκλείδου γ΄
[Βιβλίον III]
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ις΄. [16]
Ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐκτὸς πεσεῖται τοῦ κύκλου, καὶ εἰς τὸν μεταξὺ τόπον τῆς τε εὐθείας καὶ τῆς περιφερείας ἑτέρα εὐθεῖα οὐ παρεμπεσεῖται, καὶ ἡ μὲν τοῦ ἡμικυκλίου γωνία ἁπάσης γωνίας ὀξείας εὐθυγράμμου μείζων ἐστίν, ἡ δὲ λοιπὴ ἐλάττων.
Ἔστω κύκλος ὁ ΑΒΓ περὶ κέντρον τὸ Δ καὶ διάμετρον τὴν ΑΒ· λέγω, ὅτι ἡ ἀπὸ τοῦ Α τῇ ΑΒ πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐκτὸς πεσεῖται τοῦ κύκλου.
Μὴ γάρ, ἀλλ' εἰ δυνατόν, πιπτέτω ἐντὸς ὡς ἡ ΓΑ, καὶ ἐπεζεύχθω ἡ ΔΓ.
Ἐπεὶ ἴση ἐστὶν ἡ ΔΑ τῇ ΔΓ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΔΑΓ γωνίᾳ τῇ ὑπὸ ΑΓΔ. ὀρθὴ δὲ ἡ ὑπὸ ΔΑΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΑΓΔ· τριγώνου δὴ τοῦ ΑΓΔ αἱ δύο γωνίαι αἱ ὑπὸ ΔΑΓ, ΑΓΔ δύο ὀρθαῖς ἴσαι εἰσίν· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἡ ἀπὸ τοῦ Α σημείου τῇ ΒΑ πρὸς ὀρθὰς ἀγομένη ἐντὸς πεσεῖται τοῦ κύκλου. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἐπὶ τῆς περιφερείας· ἐκτὸς ἄρα.
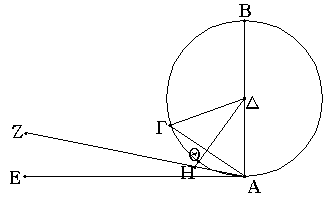
Πιπτέτω ὡς ἡ ΑΕ· λέγω δή, ὅτι εἰς τὸν μεταξὺ τόπον τῆς τε ΑΕ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἑτέρα εὐθεῖα οὐ παρεμπεσεῖται.
Εἰ γὰρ δυνατόν, παρεμπιπτέτω ὡς ἡ ΖΑ, καὶ ἤχθω ἀπὸ τοῦ Δ σημείου ἐπὶ τὴν ΖΑ κάθετος ἡ ΔΗ. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΑΗΔ, ἐλάττων δὲ ὀρθῆς ἡ ὑπὸ ΔΑΗ, μείζων ἄρα ἡ ΑΔ τῆς ΔΗ. ἴση δὲ ἡ ΔΑ τῇ ΔΘ· μείζων ἄρα ἡ ΔΘ τῆς ΔΗ, ἡ ἐλάττων τῆς μείζονος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα εἰς τὸν μεταξὺ τόπον τῆς τε εὐθείας καὶ τῆς περιφερείας ἑτέρα εὐθεῖα παρεμπεσεῖται.
Λέγω, ὅτι καὶ ἡ μὲν τοῦ ἡμικυκλίου γωνία ἡ περιεχομένη ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἁπάσης γωνίας ὀξείας εὐθυγράμμου μείζων ἐστίν, ἡ δὲ λοιπὴ ἡ περιεχομένη ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας ἁπάσης γωνίας ὀξείας εὐθυγράμμου ἐλάττων ἐστίν.
Εἰ γὰρ ἐστί τις γωνία εὐθύγραμμος μείζων μὲν τῆς περιεχομένης ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας, ἐλάττων δὲ τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας, εἰς τὸν μεταξὺ τόπον τῆς τε ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας εὐθεῖα περεμπεσεῖται, ἥτις ποιήσει μείζονα μὲν τῆς περιεχομένης ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ὑπὸ εὐθειῶν περιεχομένην, ἐλάττονα δὲ τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας. οὐ παρεμπίπτει δέ· οὐκ ἄρα τῆς περιεχομένης γωνίας ὑπό τε τῆς ΒΑ εὐθείας καὶ τῆς ΓΘΑ περιφερείας ἔσται μείζων ὀξεῖα ὑπὸ εὐθειῶν περιεχομένη, οὐδὲ μὴν ἐλάττων τῆς περιεχομένης ὑπό τε τῆς ΓΘΑ περιφερείας καὶ τῆς ΑΕ εὐθείας.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἡ τῇ διαμέτρῳ τοῦ κύκλου πρὸς ὀρθὰς ἀπ' ἄκρας ἀγομένη ἐφάπτεται τοῦ κύκλου [καὶ ὅτι εὐθεῖα κύκλου καθ᾿ ἓν μόνον ἐφάπτεται σημεῖον, ἐπειδήπερ καὶ ἡ κατὰ δύο αὐτῷ συμβάλλουσα ἐντὸς αὐτοῦ πίπτουσα ἐδείχθη]. ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου