Στοιχεῖα Εὐκλείδου α΄
[Βιβλίον I]
Αἱ Προτάσεις των Στοιχείων α΄
Προηγουμένη Πρότασις
Ἑπομὲνη Πρότασις
Πρότασις μζ΄ [47]
Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.
Ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν ὑπὸ ΒΑΓ γωνίαν· λέγω, ὅτι τὸ ἀπὸ τῆς ΒΓ τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ τετραγώνοις.
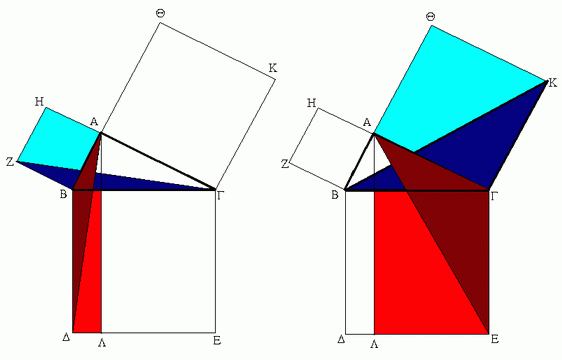
Ἀναγεγράφθω γὰρ ἀπὸ μὲν τῆς ΒΓ τετράγωνον τὸ ΒΔΕΓ, ἀπὸ δὲ τῶν ΒΑ, ΑΓ τὰ ΗΒ, ΘΓ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΒΔ, ΓΕ παράλληλος ἤχθω ἡ ΑΛ· καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΖΓ. καὶ ἐπεὶ ὀρθή ἐστιν ἑκατέρα τῶν ὑπὸ ΒΑΓ, ΒΑΗ γωνιῶν, πρὸς δή τινι εὐθείᾳ τῇ ΒΑ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α δύο εὐθεῖαι αἱ ΑΓ, ΑΗ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιοῦσιν· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΓΑ τῇ ΑΗ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΒΑ τῇ ΑΘ ἐστιν ἐπ᾿ εὐθείας. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΒΓ γωνία τῇ ὑπὸ ΖΒΑ· ὀρθὴ γὰρ ἑκατέρα· κοινὴ προσκείσθω ἡ ὑπὸ ΑΒΓ· ὅλη ἄρα ἡ ὑπὸ ΔΒΑ ὅλῃ τῇ ὑπὸ ΖΒΓ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΔΒ τῇ ΒΓ, ἡ δὲ ΖΒ τῇ ΒΑ, δύο δὴ αἱ ΔΒ, ΒΑ δύο ταῖς ΖΒ, ΒΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΔΒΑ γωνίᾳ τῇ ὑπὸ ΖΒΓ ἴση· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΖΓ [ἐστιν] ἴση, καὶ τὸ ΑΒΔ τρίγωνον τῷ ΖΒΓ τριγώνῳ ἐστὶν ἴσον· καὶ [ἐστὶ] τοῦ μὲν ΑΒΔ τριγώνου διπλάσιον τὸ ΒΛ παραλληλόγραμμον· βάσιν τε γὰρ τὴν αὐτὴν ἔχουσι τὴν ΒΔ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΒΔ, ΑΛ· τοῦ δὲ ΖΒΓ τριγώνου διπλάσιον τὸ ΗΒ τετράγωνον· βάσιν τε γὰρ πάλιν τὴν αὐτὴν ἔχουσι τὴν ΖΒ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΖΒ, ΗΓ. [τὰ δὲ τῶν ἴσων διπλάσια ἴσα ἀλλήλοις ἐστίν·] ἴσον ἄρα ἐστὶ καὶ τὸ ΒΛ παραλληλόγραμμον τῷ ΗΒ τετραγώνῳ. ὁμοίως δὴ ἐπιζευγνυμένων τῶν ΑΕ, ΒΚ δειχθήσεται καὶ τὸ ΓΛ παραλληλόγραμμον ἴσον τῷ ΘΓ τετραγώνῳ· ὅλον ἄρα τὸ ΒΔΕΓ τετράγωνον δυσὶ τοῖς ΗΒ, ΘΓ τετραγώνοις ἴσον ἐστίν. καί ἐστι τὸ μὲν ΒΔΕΓ τετράγωνον ἀπὸ τῆς ΒΓ ἀναγραφέν, τὰ δὲ ΗΒ, ΘΓ ἀπὸ τῶν ΒΑ, ΑΓ. τὸ ἄρα ἀπὸ τῆς ΒΓ πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ πλευρῶν τετραγώνοις.
Ἐν ἄρα τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν [γωνίαν] περιεχουσῶν πλευρῶν τετραγώνοις· ὅπερ ἔδει δεῖξαι.
Μετάφραση Σχόλια Διασυνδέσεις
Θεώρημα μζ΄ [47]
Στὰ ὀρθογώνια τρίγωνα τὸ τετράγωνο τῆς ὑποτείνουσας πλευρᾶς ἰσοῦται μὲ τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν ποὺ περιέχουν τὴν ὀρθή γωνία.
Ἔστω τὸ ὀρθογώνιο τρίγωνο ΑΒΓ μὲ ὀρθὴ τὴν γωνία ΒΑΓ· λέγω, ὅτι τὸ τετράγωνο τῆς πλευρᾶς ΒΓ ἰσοῦται μὲ τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν ΒΑ καὶ ΑΓ.

Ἀπὸ τὴν πλευρά ΒΓ κατασκευάζουμε τὸ τετράγωνο ΒΔΕΓ, καὶ ἀπὸ τὶς ΒΑ, ΑΓ τὰ τετράγωνα ΗΒ, ΘΓ (θεώρ_α΄46), καὶ ἀπὸ τὸ σημείο Α φέρομε παράλληλο πρὸς ὀποιαδήποτε ἀπὸ τὶς ΒΔ, ΓΕ ἔστω τὴν ΑΛ (θεώρ_α΄31)· φέρομε ἐπίσης καὶ τὶς ΑΔ, ΖΓ. Καὶ ἐπειδὴ οἱ γωνίες ΒΑΓ, ΒΑΗ εἶναι ὀρθές , τότε στὸ σημείο Α τῆς εὐθείας ΒΑ οἱ δύο εὐθεῖες ΑΓ, ΑΗ ἐφόσον δὲν κεῖνται στὰ ἴδια μέρη σχηματίζουν γωνία ἴση μὲ δύο ὀρθές · ἄρα ἡ ΓΑ καὶ ΑΗ κεῖνται σ᾿ εὐθεία (θεώρ_α΄14) . Γιά τοὺς ἴδιους λόγους καὶ οἱ ΒΑ, ΑΘ κεῖνται σ᾿ εὐθεία. Καὶ ἐπειδὴ ἡ γωνία ΔΒΓ εἶναι ἴση μὲ τὴν γωνία ΖΒΑ· ἐπειδὴ ἡ κάθε μία εἶναι ὀρθὴ · ἀν προστεθεῖ ἡ κοινή ΑΒΓ· τότε ἡ ΔΒΑ ὅλη εἶναι ἴση μὲ ὅλη τὴν ΖΒΓ (κ.ἔν.β΄). Καὶ ἐπειδή ἡ ΔΒ ἰσοῦται με τὴν ΒΓ, καὶ ἡ ΖΒ μὲ τὴν ΒΑ, καὶ ἡ γωνία ΔΒΑ ἰσοῦται μὲ τὴν ΖΒΓ, τότε τὰ τρίγωνα ΑΒΔ καὶ ΖΒΓ ἔχουν τὶς δύο πλευρές καὶ τὴν περιεχόμενη γωνία ἴσες μία πρὸς μία , ἄρα τὰ τρίγωνα εἶναι ἵσα (θεώρ_α΄4)· Καὶ εἶναι τὸ παραλληλόγραμμο ΒΛ διπλάσιο τοῦ τριγώνου ΑΒΔ · διότι ἔχουν τὴν ἴδια βάση τὴν ΒΔ καὶ κεῖνται στὶς ἴδιες παράλληλες τὶς ΒΔ, ΑΛ (θεώρ_α΄41)· ὅμοια τὸ παραλληλόγραμμο ΗΒ εἶναι διπλάσιο τοῦ τριγώνου ΖΒΓ · διότι ἔχουν τὴν ἴδια βάση τὴ ΖΒ καὶ κεῖνται στὶς ἴδιες παράλληλες τὶς ΖΒ, ΗΓ. [τὰ διπλάσια τῶν ἴσων εἶναι καὶ μεταξύ τους ἴσα·] Ἄρα τὸ παραλληλόγραμμο ΒΛ εἶναι ἴσο μὲ τὸ τετράγωνο ΗΒ. Παρόμοια λοιπὸν, φέροντας τήν ΑΕ, ΒΚ ἀποδεικνύεται ὅτι τὸ παραλληλόγραμμο ΓΛ εἶναι ἴσο μὲ τὸ τετράγωνο ΘΓ· ἄρα τὸ ὅλο τετράγωνο ΒΔΕΓ ἰσοῦται μὲ τὸ ἄθροισμα τῶν τετραγώνων ΗΒ καὶ ΘΓ. Καὶ τὸ τετράγωνο ΒΔΕΓ εἶναι αὐτὸ πού ὁρίζεται ἀπὸ τή πλευρά ΒΓ, ἐνώ τὰ ΗΒ, ΘΓ ἀπὸ τὶς πλευρές ΒΑ, ΑΓ. Ἄρα τὸ τετράγωνο τῆς πλευρᾶς ΒΓ ἰσοῦται μὲ τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν ΒΑ, ΑΓ.
Ἄρα στὰ ὀρθογώνια τρίγωνα τὸ τετράγωνο τῆς ὑποτείνουσας πλευρᾶς ἰσοῦται μὲ τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν πού περιέχουν τὴν ὀρθὴ [γωνία]· ὅπερ ἔδει δεῖξαι.
Ἑπομὲνη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις των Στοιχείων α΄
Περιεχόμενα Στοιχείων Εὐκλείδου