The normalized spherical harmonic functions Ylm (x, y, z) used in Intel IPP are real-valued polynomials of Cartesian coordinates which can be defined by the following recurrent equations:
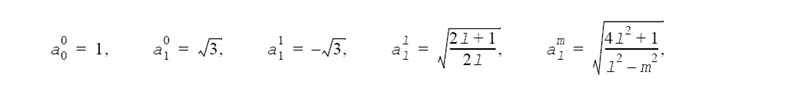
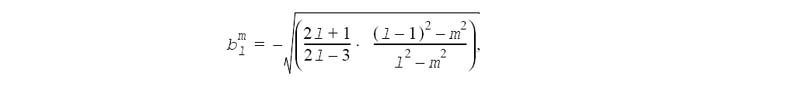
2 ≤ l ≤ L, 0 ≤ m < l .
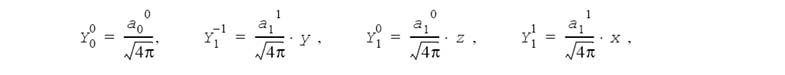
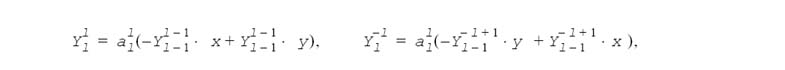
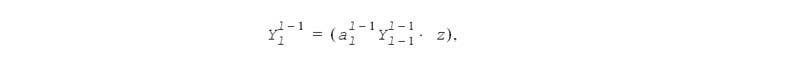
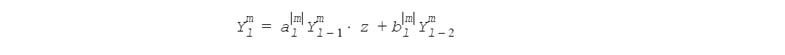
2 ≤ l ≤ L, |m| ≤ (l -1).
These equations can be derived from the three-term recurrence [see M.A.Blanco, M.Florez, M.Bermejo, "Evaluation of the rotation matrices in the basis of real spherical harmonics", Journal of Molecular Structure (Theochem), 1997, 419, 19-27, or R.Green, "Spherical harmonic lighting: The gritty details". in Game Developers' Conference, 2003] known for the associated Legendre polynomials (l-m)Pml = x(2l -1)Pml-1 - (l -1 +m)Pml-2 using the normalization factor
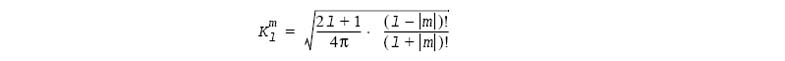
Direct formulas for normalized real-valued spherical harmonic polynomials in Cartesian coordinates can be derived from following formula (see D.A. Varshalovich A.N. Moskalev, V.K. Khersonsky, "Quantum Theory of Angular Momentum", Singapore: World Scientific Publishing, 1988):
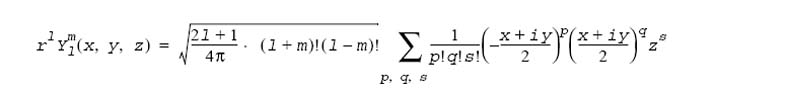
Summation is performed over p, q, s >0 such as p + q + s = l, p - q = m.
Here x2 + y2 + z2 = r2 are Cartesian coordinates.