This section describes the Intel® IPP function for spherical harmonic transformation.
Here {Ylm (x, y, z):0 ≤ l ≤ L, |m| ≤ L} denotes full set of orthogonal spherical harmonic (SH) basic functions up to order L on a unit sphere in Cartesian coordinates. So there exist (2L+1) SH functions for each order l (an SH band), and (L+1)(L+1) SH functions for all orders up to L. SH functions are indexed within the order from -m to m.
The forward spherical harmonic transform (SHT) of order L of a function f(x, y, z) on a unit sphere is a set of coefficients Clm:0 ≤ l ≤ L, |m| ≤ L, where
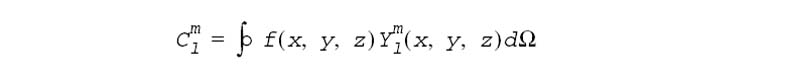
integrating over solid angle.
The inverse SHT
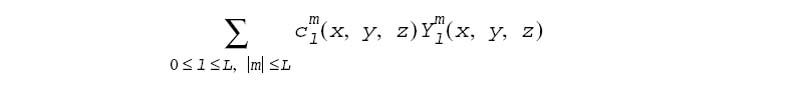
of order L is converging to the original function f(x, y, z) when L -->∞.
The SHT of a function f(x, y, z) can be approximated as
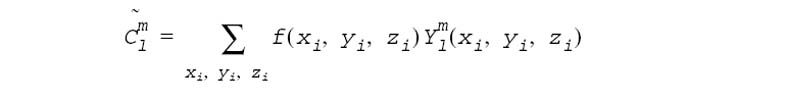
by summation over representative set of a unit sphere points.